Evolution of the Structure of EDPM Crosslinking Networks and Its Influence on the Rheological Properties of the Injection Molding Process
Abstract
1. Introduction
2. Materials and Methods
2.1. Topology of the System Subsection
2.2. Interatomic Potential Parameterization
2.3. Crosslinking Characteristics
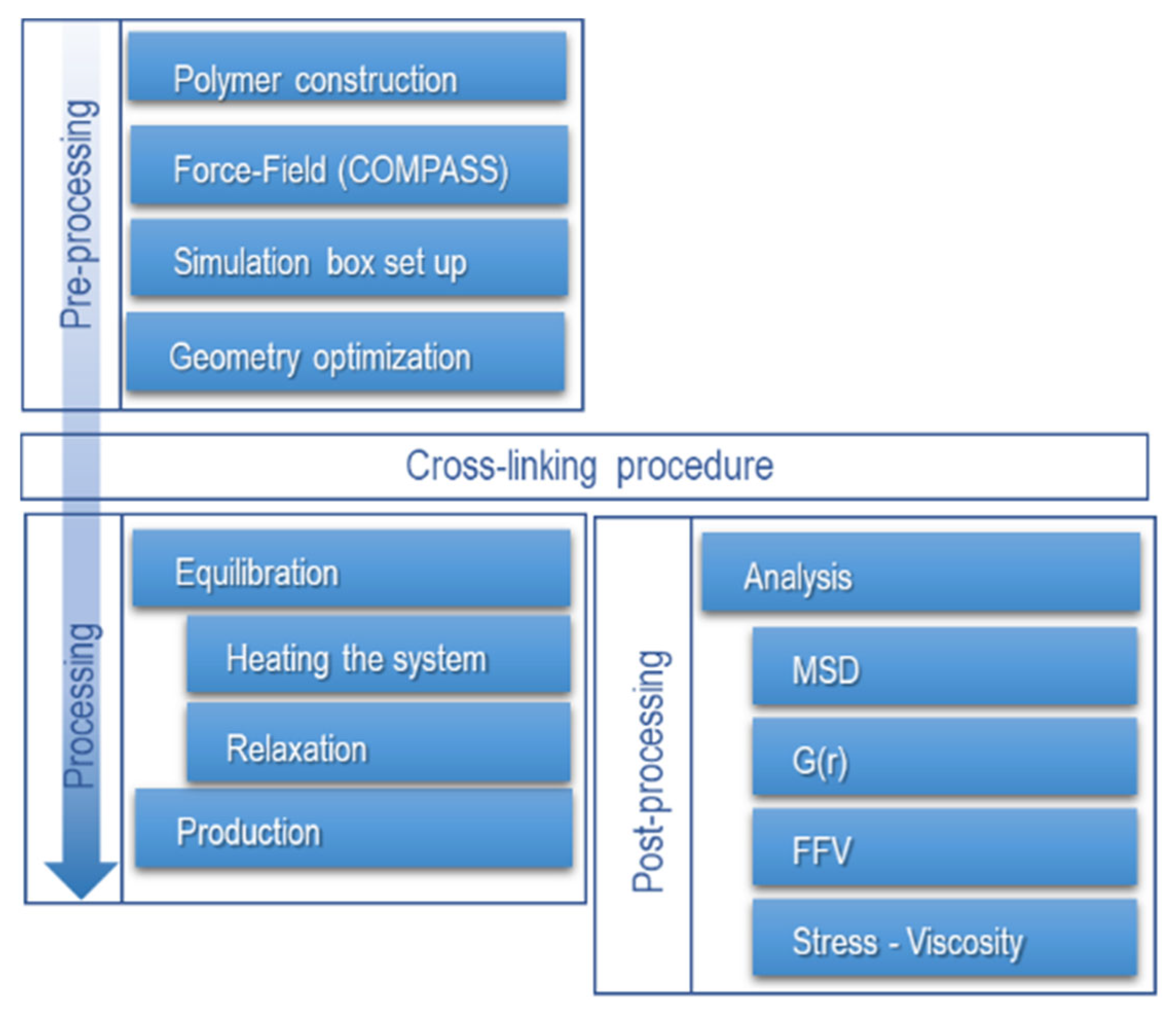
2.4. Procedure for Molecular Dynamics Simulation
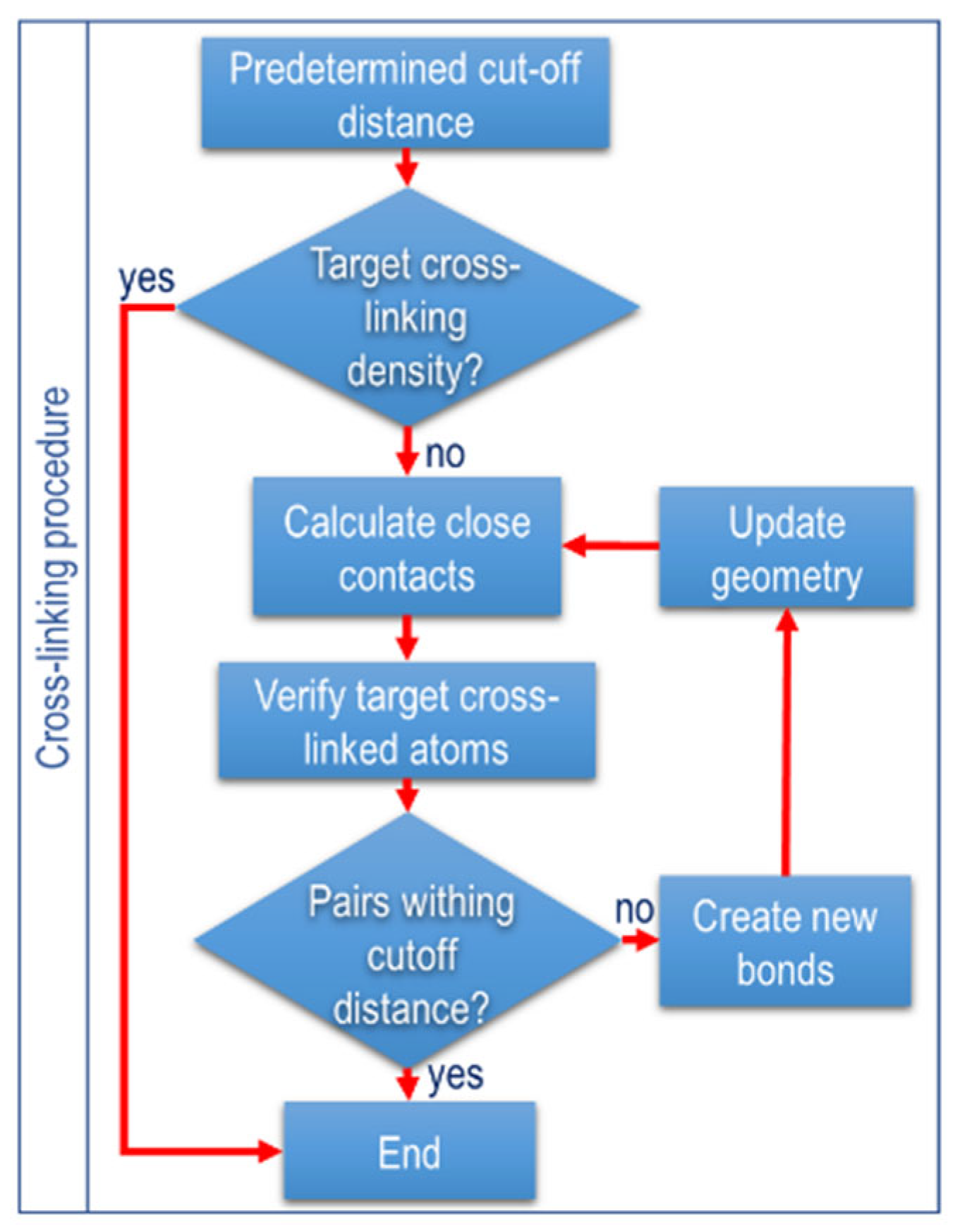
2.5. Crosslinking Procedure
2.6. Parameters for the Study of Molecular Dynamics
2.7. Equipment and Materials for Hardness Test
3. Results and Discussion
3.1. Mean Square Displacement (MSD)
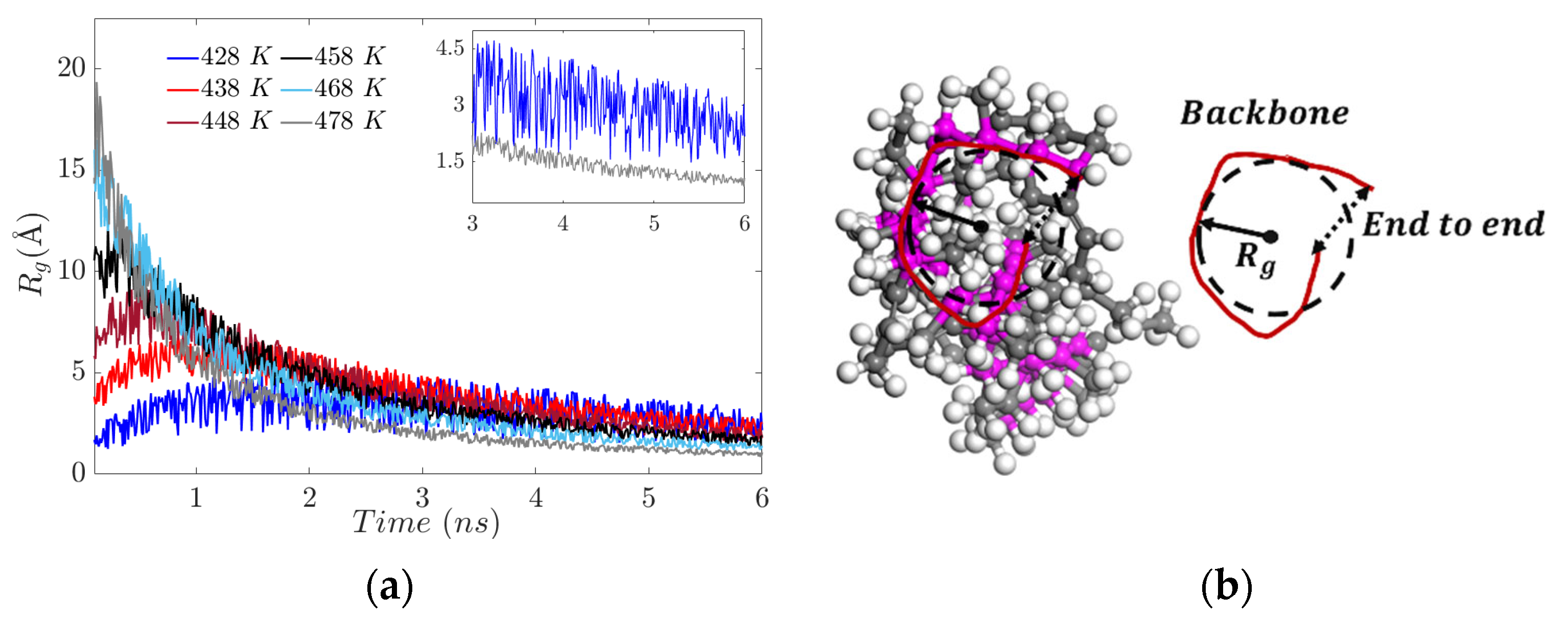
3.2. Radius of Gyration (Rg)
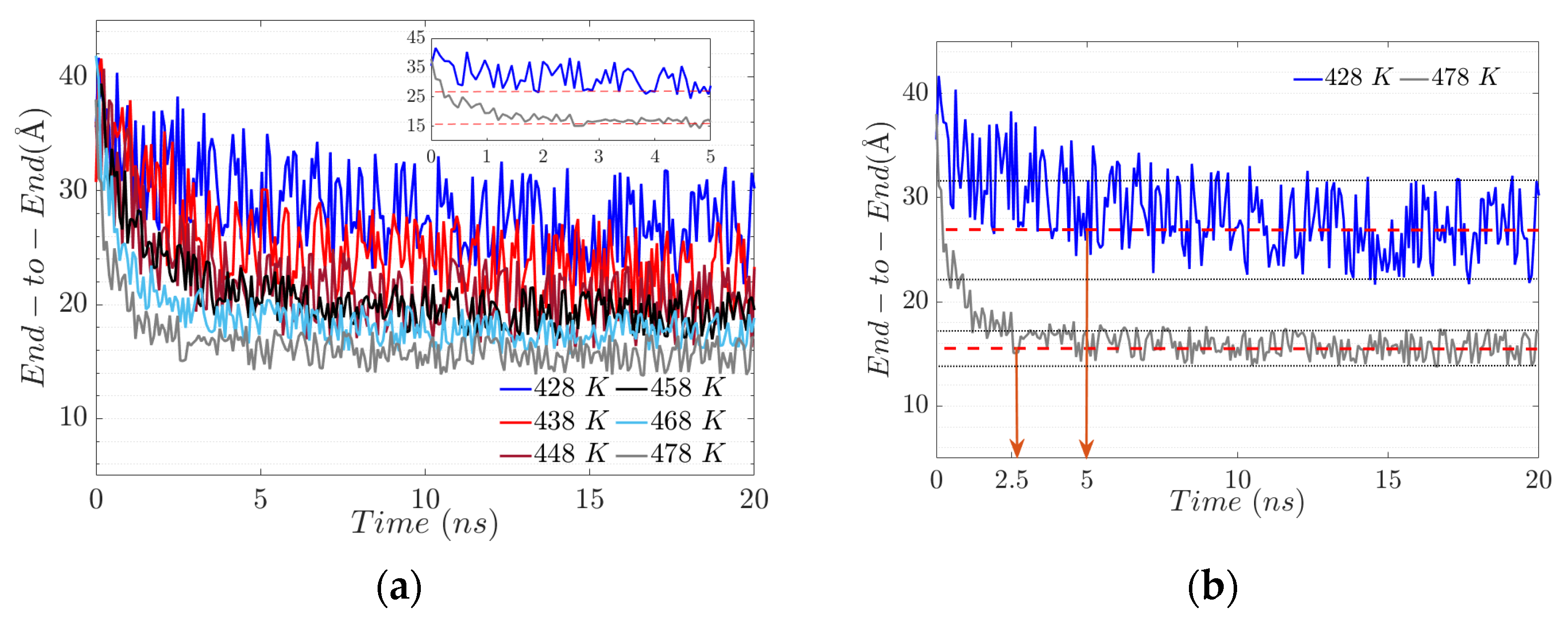
3.3. The End-to-End Vector
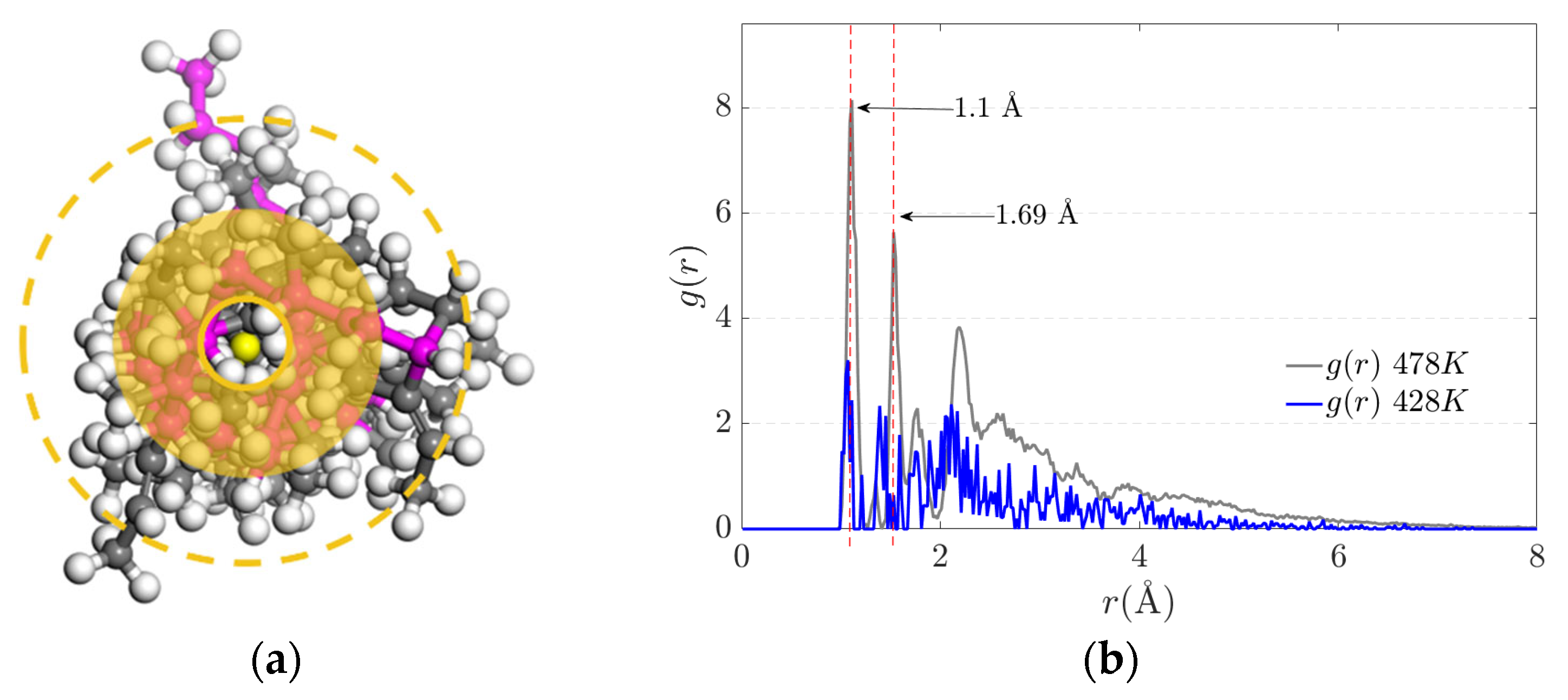
3.4. Radial Distribution Function (g(r))
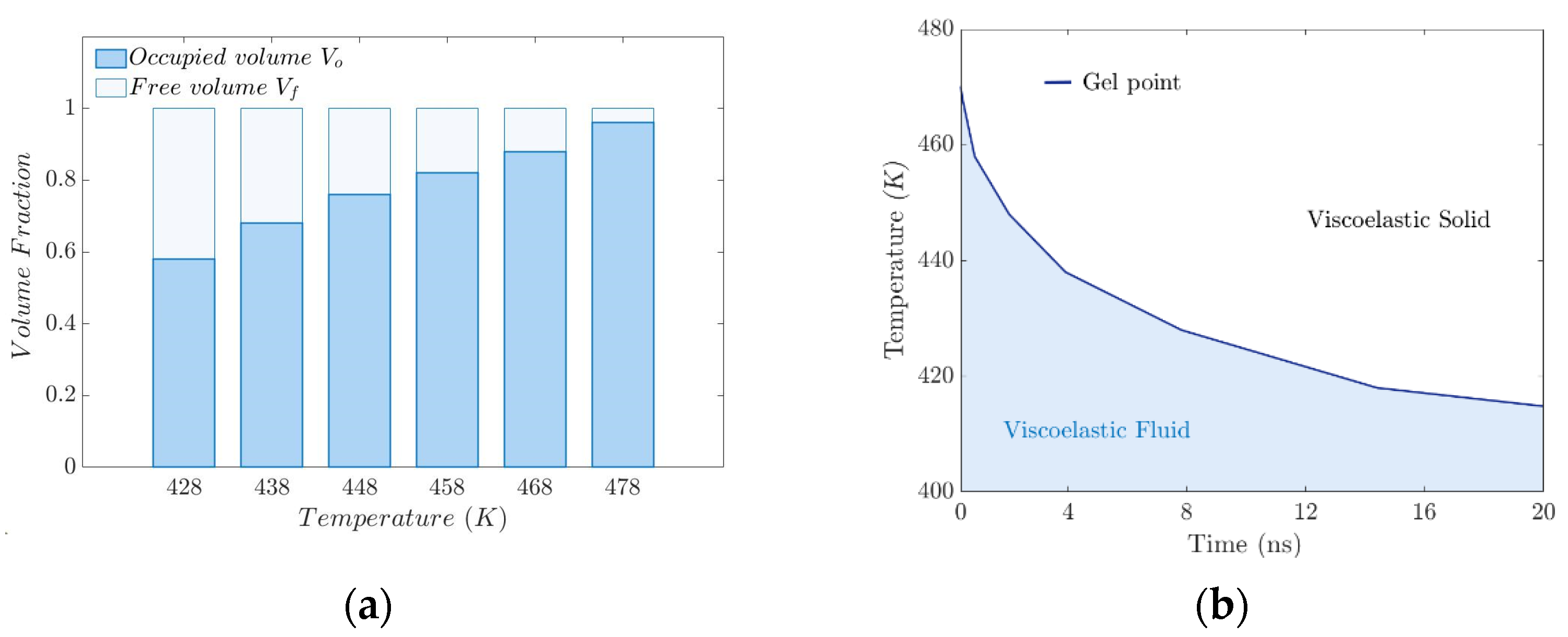
3.5. Free Volume
3.6. Hardness Test
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Li, S.; Tian, H.; Wu, H.; Ning, N.; Tian, M.; Zhang, L. Coupling effect of molecular weight and crosslinking kinetics on the formation of rubber nanoparticles and their agglomerates in EPDM/PP TPVs during dynamic vulcanization. Soft Matter 2020, 16, 2185–2198. [Google Scholar] [CrossRef]
- Bouguedad, D.; Mekhaldi, A.; Jbara, O.; Rondot, S.; Hadjadj, A.; Douglade, J.; Dony, P. Physico-chemical study of thermally aged EPDM used in power cables insulation. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3207–3215. [Google Scholar] [CrossRef]
- Ravishankar, P. Treatise on EPDM. Rubber Chem. Technol. 2012, 85, 327–349. [Google Scholar] [CrossRef]
- Shaji, R.; Kumar, N.N. Simulation of Room Temperature Vulcanized Gasket Failure at Engine T-Joints. ARAI J. Mobil. Technol. 2022, 2, 108–111. [Google Scholar] [CrossRef]
- Restrepo-Zapata, N.C.; Eagleburger, B.; Saari, T.; Osswald, T.A.; Hernández-Ortiz, J.P. Chemorheological time-temperature-transformation-viscosity diagram: Foamed EPDM rubber compound. J. Appl. Polym. Sci. 2016, 133, 43966. [Google Scholar] [CrossRef]
- Milani, G.; Milani, F. EPDM accelerated sulfur vulcanization: A kinetic model based on a genetic algorithm. J. Math. Chem. 2011, 49, 1357–1383. [Google Scholar] [CrossRef]
- Niu, W.; Li, Y.; Ma, Y.; Zhao, G. Determination and Prediction of Time-Varying Parameters of Mooney–Rivlin Model of Rubber Material Used in Natural Rubber Bearing under Alternating of Aging and Seawater Erosion. Materials 2023, 16, 4696. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Xu, J.-s.; Zhang, Z.-s.; Chen, X. Rate-dependent compressive behavior of EPDM insulation: Experimental and constitutive analysis. Mech. Mater. 2016, 96, 30–38. [Google Scholar] [CrossRef]
- Habieb, A.B.; Milani, F.; Milani, G.; Pianese, G.; Torrini, D. Vulcanization degree influence on the mechanical properties of Fiber Reinforced Elastomeric Isolators made with reactivated EPDM. Polym. Test. 2022, 108, 107496. [Google Scholar] [CrossRef]
- Shi, C.; Cao, C.; Lei, M.; Peng, L.; Shen, J. Time-dependent performance and constitutive model of EPDM rubber gasket used for tunnel segment joints. Tunn. Undergr. Space Technol. 2015, 50, 490–498. [Google Scholar] [CrossRef]
- Rashid, R.Z.A.; Yunus, N.A.; Mazlan, S.A.; Johari, N.; Aziz, S.A.A.; Nordin, N.A.; Khairi, M.H.A.; Johari, M.A.F. Temperature Dependent on Mechanical and Rheological Properties of EPDM-Based Magnetorheological Elastomers Using Silica Nanoparticles. Materials 2022, 15, 2556. [Google Scholar] [CrossRef] [PubMed]
- Hiranobe, C.T.; Ribeiro, G.D.; Torres, G.B.; Reis, E.A.P.d.; Cabrera, F.C.; Job, A.E.; Paim, L.L.; Santos, R.J.d. Cross-linked density determination of natural rubber compounds by different analytical techniques. Mater. Res. 2021, 24, e20210041. [Google Scholar] [CrossRef]
- Morovati, V.; Bahrololoumi, A.; Dargazany, R. Fatigue-induced stress-softening in cross-linked multi-network elastomers: Effect of damage accumulation. Int. J. Plast. 2021, 142, 102993. [Google Scholar] [CrossRef]
- Shen, J.; Lin, X.; Liu, J.; Li, X. Effects of Cross-Link Density and Distribution on Static and Dynamic Properties of Chemically Cross-Linked Polymers. Macromolecules 2019, 52, 121–134. [Google Scholar] [CrossRef]
- Cheng, M.; Chen, W.; Song, B. Phenomenological Modeling of the Stress-Stretch Behavior of EPDM Rubber with Loading-rate and Damage Effects. Int. J. Damage Mech. 2004, 13, 371–381. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.; Li, P.; Wang, L. The Effect of Cross-Linking Type on EPDM Elastomer Dynamics and Mechanical Properties: A Molecular Dynamics Simulation Study. Polymers 2022, 14, 1308. [Google Scholar] [CrossRef]
- Wang, A.; Vargas-Lara, F.; Younker, J.M.; Iyer, K.A.; Shull, K.R.; Keten, S. Quantifying Chemical Composition and Cross-link Effects on EPDM Elastomer Viscoelasticity with Molecular Dynamics. Macromolecules 2021, 54, 6780–6789. [Google Scholar] [CrossRef]
- Varshney, V.; Patnaik, S.S.; Roy, A.K.; Farmer, B.L. A Molecular Dynamics Study of Epoxy-Based Networks: Cross-Linking Procedure and Prediction of Molecular and Material Properties. Macromolecules 2008, 41, 6837–6842. [Google Scholar] [CrossRef]
- Papanikolaou, M.; Drikakis, D.; Asproulis, N. Molecular dynamics modelling of mechanical properties of polymers for adaptive aerospace structures. AIP Conf. Proc. 2015, 1646, 66–71. [Google Scholar] [CrossRef]
- van Duin, M.; Orza, R.; Peters, R.; Chechik, V. Mechanism of Peroxide Cross-Linking of EPDM Rubber. Macromol. Symp. 2010, 291–292, 66–74. [Google Scholar] [CrossRef]
- Tsige, M.; Taylor, P.L. Simulation study of the glass transition temperature in poly(methyl methacrylate). Phys. Rev. E 2002, 65, 021805. [Google Scholar] [CrossRef]
- Bulacu, M.; van der Giessen, E. Molecular-dynamics simulation study of the glass transition in amorphous polymers with controlled chain stiffness. Phys. Rev. E 2007, 76, 011807. [Google Scholar] [CrossRef] [PubMed]
- Duki, S.; Tsige, M.; Taylor, P. Glass transition temperature of PIB, PDMS and PMMA from small-time simulations. In Proceedings of the APS March Meeting Abstracts, Pittsburgh, PA, USA, 15–19 March 2009; p. W20. 012. [Google Scholar]
- Sun, H. COMPASS: An ab Initio Force-Field Optimized for Condensed-Phase ApplicationsOverview with Details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- McQuaid, M.J.; Sun, H.; Rigby, D. Development and validation of COMPASS force field parameters for molecules with aliphatic azide chains. J. Comput. Chem. 2004, 25, 61–71. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.; Bhowmick, A.K. An Insight into molecular structure and properties of flexible amorphous polymers: A molecular dynamics simulation approach. J. Appl. Polym. Sci. 2019, 136, 47457. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, J.; Lu, Y.; Dong, D.; Wang, W.; Zhang, L. A combined molecular dynamics simulation and experimental method to study the compatibility between elastomers and resins. Rsc Adv. 2018, 8, 14401–14413. [Google Scholar] [CrossRef]
- Yang, W.; Chen, X.; Song, X.; Hu, Y.; Pei, J.; Chen, J. Molecular dynamics study on the physical compatibility of SEBS/plasticizer blend systems. J. Mol. Model. 2024, 30, 293. [Google Scholar] [CrossRef]
- Xiang, Z.; Gao, C.; Long, T.; Ding, L.; Zhou, T.; Wu, Z. Force-Field Benchmark for Polydimethylsiloxane: Density, Heat Capacity, Isothermal Compressibility, Viscosity and Thermal Conductivity. J. Phys. Chem. B 2025, 129, 1864–1873. [Google Scholar] [CrossRef]
- Odegard, G.M.; Patil, S.U.; Deshpande, P.P.; Kanhaiya, K.; Winetrout, J.J.; Heinz, H.; Shah, S.P.; Maiaru, M. Molecular dynamics modeling of epoxy resins using the reactive interface force field. Macromolecules 2021, 54, 9815–9824. [Google Scholar] [CrossRef]
- Joseph, E.; Swaminathan, N.; Kannan, K. Material identification for improving the strength of silica/SBR interface using MD simulations. J. Mol. Model. 2020, 26, 234. [Google Scholar] [CrossRef]
- Yu, R.; Wang, Q.; Wang, W.; Xiao, Y.; Wang, Z.; Zhou, X.; Zhang, X.; Zhu, X.; Fang, C. Polyurethane/graphene oxide nanocomposite and its modified asphalt binder: Preparation, properties and molecular dynamics simulation. Mater. Des. 2021, 209, 109994. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Tao, M. Understanding Free Volume Characteristics of Ethylene-Propylene-Diene Monomer (EPDM) through Molecular Dynamics Simulations. Materials 2019, 12, 612. [Google Scholar] [CrossRef]
- Zachary, M.; Camara, S.; Whitwood, A.C.; Gilbert, B.C.; van Duin, M.; Meier, R.J.; Chechik, V. EPR study of persistent free radicals in cross-linked EPDM rubbers. Eur. Polym. J. 2008, 44, 2099–2107. [Google Scholar] [CrossRef]
- Paterlini, M.G.; Ferguson, D.M. Constant temperature simulations using the Langevin equation with velocity Verlet integration. Chem. Phys. 1998, 236, 243–252. [Google Scholar] [CrossRef]
- Yin, K.; Xiao, H.; Zhong, J.; Xu, D. A new method for Calculation of Elastic Properties of Anisotropic material by constant pressure molecular dynamics. In Proceedings of the International Conference of Computational Methods in Sciences and Engineering 2004 (ICCMSE 2004), Attica, Greece, 19–23 November 2004; pp. 586–588. [Google Scholar]
- Varadwaj, P.R. Combined Molecular Dynamics and DFT Simulation Study of the Molecular and Polymer Properties of a Catechol-Based Cyclic Oligomer of Polyether Ether Ketone. Polymers 2020, 12, 1054. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Jimenez, S.; Saucedo-Anaya, T.; Baltazar-Hernandez, V.H.; Contreras-Rodriguez, A.R. Characterization of Viscoelastic Properties of EPDM Molding Compound for Door Grommet Component Using Molecular Dynamics and Phenomenological Modeling. J. Manuf. Sci. Eng. 2023, 145, 111001. [Google Scholar] [CrossRef]
- ASTM D2084-19a; Standard Test Method for Rubber Property—Vulcanization Using Oscillating Disk. American Standard Testing for Materials ASTM: West Conshohocken, PA, USA, 2019; Volume 09.01, p. 12.
- Sun, X.; Isayev, A.I. Cure Kinetics Study of Unfilled and Carbon Black Filled Synthetic Isoprene Rubber. Rubber Chem. Technol. 2009, 82, 149–169. [Google Scholar] [CrossRef]
- Milani, G.; Leroy, E.; Milani, F.; Deterre, R. Mechanistic modeling of reversion phenomenon in sulphur cured natural rubber vulcanization kinetics. Polym. Test. 2013, 32, 1052–1063. [Google Scholar] [CrossRef]
- Gómez-Jiménez, S.; Saucedo-Anaya, T.; López-Baltazar, E.A.; Robles-Guerrero, A. Automated identification of kinetics model in elastomer vulcanization using a rheometer MDR and Rubber-K pattern recognition software. Results Mater. 2024, 21, 100516. [Google Scholar] [CrossRef]
- Antonietti, M.; Pakula, T.; Bremser, W. Rheology of Small Spherical Polystyrene Microgels: A Direct Proof for a New Transport Mechanism in Bulk Polymers besides Reptation. Macromolecules 1995, 28, 4227–4233. [Google Scholar] [CrossRef]
- Chremos, A.; Jeong, C.; Douglas, J.F. Influence of polymer architectures on diffusion in unentangled polymer melts. Soft Matter 2017, 13, 5778–5784. [Google Scholar] [CrossRef] [PubMed]
- Saleesung, T.; Reichert, D.; Saalwächter, K.; Sirisinha, C. Correlation of crosslink densities using solid state NMR and conventional techniques in peroxide-crosslinked EPDM rubber. Polymer 2015, 56, 309–317. [Google Scholar] [CrossRef]
- Xie, B.-G.; Wang, H.; Lu, R.-L.; Wang, H.; Xia, R.; Chen, P.; Qian, J.-S. A combined simulation and experiment study on polyisoprene rubber composites. Compos. Sci. Technol. 2020, 200, 108398. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Valavala, P.K.; Clancy, T.C.; Wise, K.E.; Odegard, G.M. Molecular modeling of crosslinked epoxy polymers: The effect of crosslink density on thermomechanical properties. Polymer 2011, 52, 2445–2452. [Google Scholar] [CrossRef]
- ASTM 1415-18; Standard Test Method for Rubber Property—International Hardness. American Standard Testing for Materials ASTM: West Conshohocken, PA, USA, 2018; Volume 09.01.
- P, P.; Neethirajan, J.; M.I., K.; R, R.; R, R. Thermo-oxidative aging and its influence on the performance of silica, carbon black, and silica/carbon black hybrid fillers -filled tire tread compounds. J. Polym. Res. 2025, 32, 117. [Google Scholar] [CrossRef]
- Smejda-Krzewicka, A.; Mrozowski, K. Chloroprene and Butadiene Rubber (CR/BR) Blends Cross-Linked with Metal Oxides: INFLUENCE of Vulcanization Temperature on Their Rheological, Mechanical, and Thermal Properties. Molecules 2025, 30, 2780. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Jimenez, S.; Saucedo-Anaya, T.; Guerrero-Mendez, C.; Robles-Guerrero, A.; Silva-Acosta, L.; Navarro-Solis, D.; Lopez-Betancur, D.; Contreras Rodríguez, A.R. Mooney–Rivlin Parameter Determination Model as a Function of Temperature in Vulcanized Rubber Based on Molecular Dynamics Simulations. Materials 2024, 17, 3252. [Google Scholar] [CrossRef] [PubMed]
- Shao, H.; Guo, Q.; He, A. Evolution of crosslinking networks structure and thermo-oxidative aging behavior of unfilled NR/BR blends with TBIR as extra functional compatibilizer. Polym. Test. 2022, 115, 107715. [Google Scholar] [CrossRef]
- Panyukov, S. Theory of Flexible Polymer Networks: Elasticity and Heterogeneities. Polymers 2020, 12, 767. [Google Scholar] [CrossRef]








| Substance | Function | Quantity (phr) |
|---|---|---|
| Amorphous EPDM | Base elastomer | 95–100 |
| Ethylidene norbornene (ENB) | Diene component | 2–12 |
| Sulfur | Vulcanizing agent | 1.9–2.1 |
| Carbon black (N550 semiactive, specific area ~39–55 m2/g) | Promoter | 85–95 |
| And other zinc-based processing agents (trade secret). | 17–20 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez-Jimenez, S.; Guerrero Mendez, C.; Lopez-Betancur, D.; Robles-Guerrero, A.; Navarro-Solis, D.; Silva-Acosta, L.; Lopez-Baltazar, E.A.; Ortiz-Letechipia, J.; Contreras-Rodríguez, A.R. Evolution of the Structure of EDPM Crosslinking Networks and Its Influence on the Rheological Properties of the Injection Molding Process. Polymers 2025, 17, 2438. https://doi.org/10.3390/polym17182438
Gomez-Jimenez S, Guerrero Mendez C, Lopez-Betancur D, Robles-Guerrero A, Navarro-Solis D, Silva-Acosta L, Lopez-Baltazar EA, Ortiz-Letechipia J, Contreras-Rodríguez AR. Evolution of the Structure of EDPM Crosslinking Networks and Its Influence on the Rheological Properties of the Injection Molding Process. Polymers. 2025; 17(18):2438. https://doi.org/10.3390/polym17182438
Chicago/Turabian StyleGomez-Jimenez, Salvador, Carlos Guerrero Mendez, Daniela Lopez-Betancur, Antonio Robles-Guerrero, David Navarro-Solis, Luis Silva-Acosta, Enrique A. Lopez-Baltazar, Jennifer Ortiz-Letechipia, and Ada Rebeca Contreras-Rodríguez. 2025. "Evolution of the Structure of EDPM Crosslinking Networks and Its Influence on the Rheological Properties of the Injection Molding Process" Polymers 17, no. 18: 2438. https://doi.org/10.3390/polym17182438
APA StyleGomez-Jimenez, S., Guerrero Mendez, C., Lopez-Betancur, D., Robles-Guerrero, A., Navarro-Solis, D., Silva-Acosta, L., Lopez-Baltazar, E. A., Ortiz-Letechipia, J., & Contreras-Rodríguez, A. R. (2025). Evolution of the Structure of EDPM Crosslinking Networks and Its Influence on the Rheological Properties of the Injection Molding Process. Polymers, 17(18), 2438. https://doi.org/10.3390/polym17182438










