Critical Adsorption of Polyelectrolytes onto Patchy Particles with a Low-Dielectric Interior
Abstract
1. Introduction
1.1. Adsorption, Critical Adsorption, and Complex Formation
1.2. Effects of Charge Heterogeneities and of Dielectric Boundaries
1.3. Plan of This Paper
2. Model and Simulations
2.1. Main Equations for the ES Potential
2.2. Details of Computer Simulations
3. Main Results
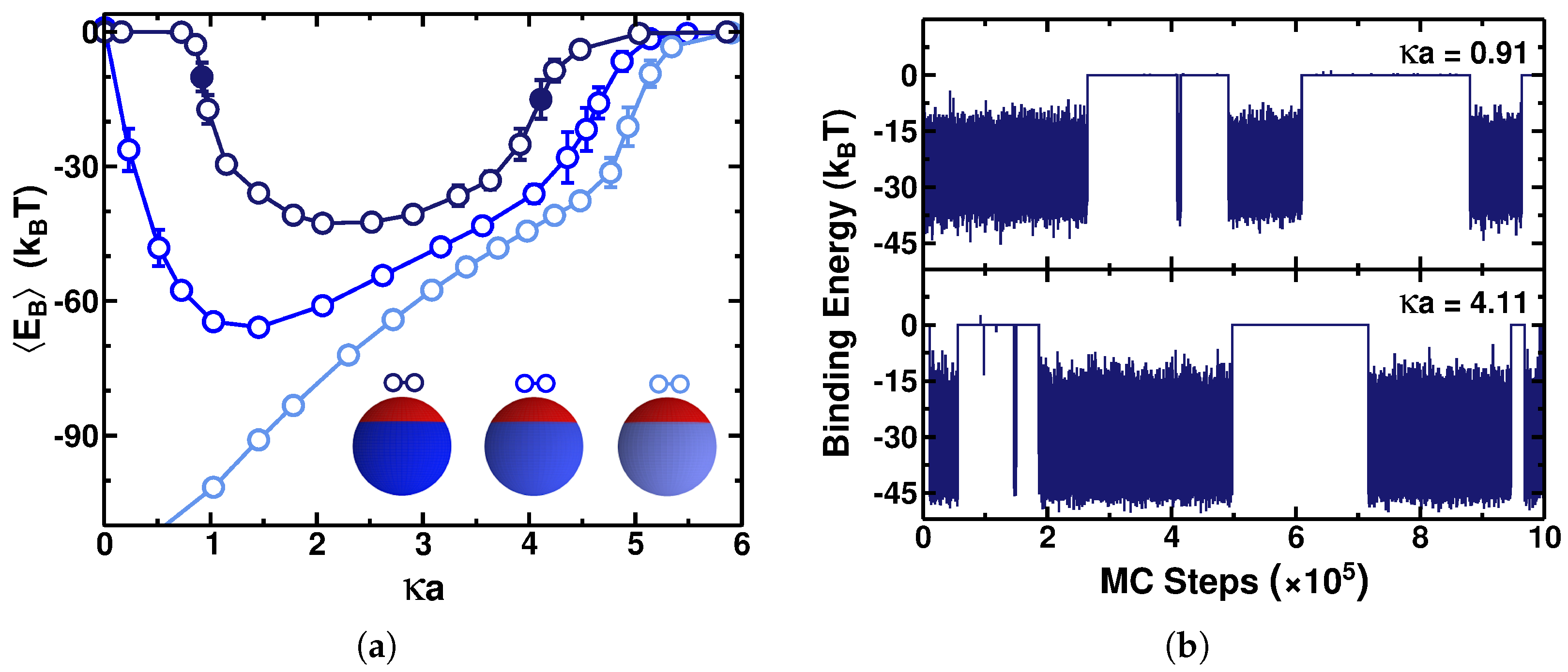
3.1. PE–Particle Binding Energy
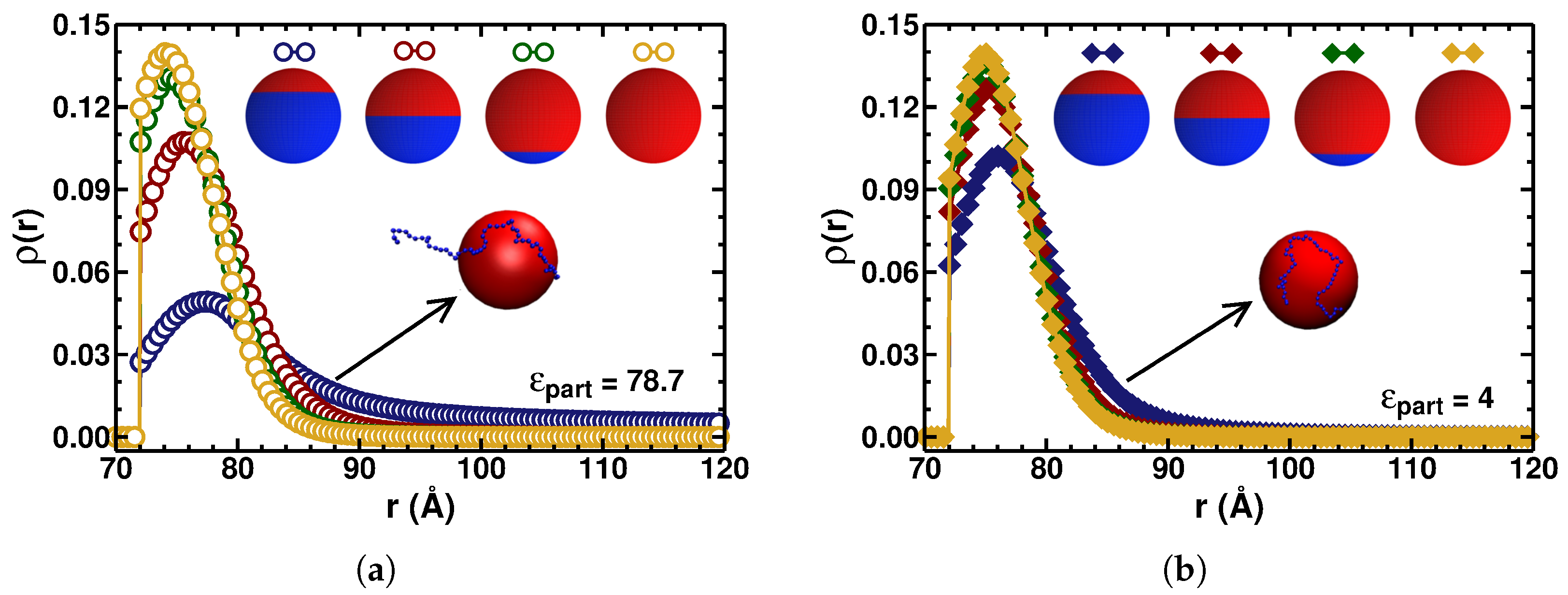
3.2. Radius of Gyration of the Polymer
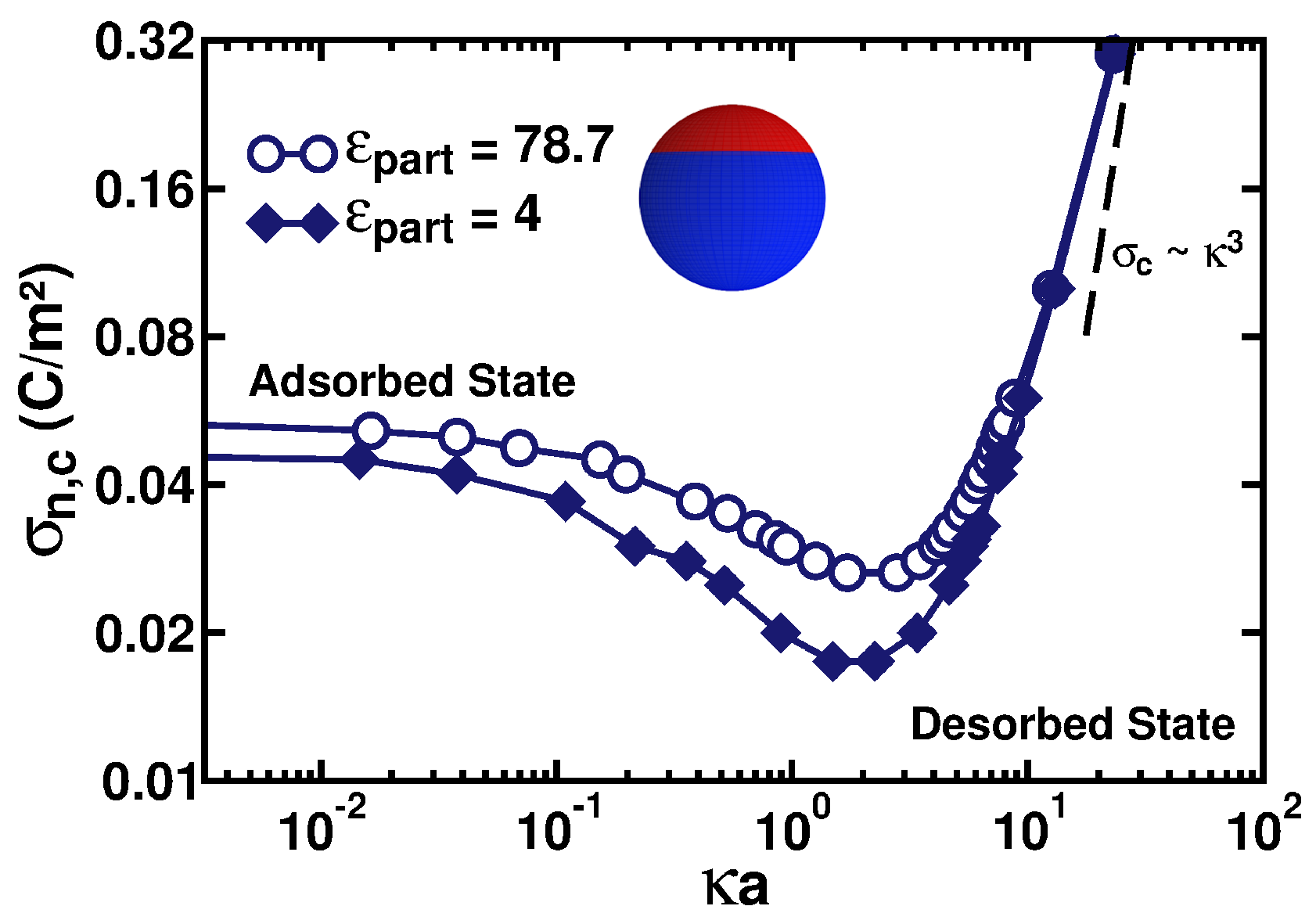
3.3. Adsorption–Desorption Curve and Critical Charge Density
3.4. Implications of Low-Dielectric Interfaces
4. Discussion, Conclusions, and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PE | polyelectrolyte |
| ES | electrostatic/electrostatics |
| WKB | Wentzel–Kramers–Brillouin |
Appendix A. ES Potential of a Patchy Particle
Appendix B. ES Potential of the Polarization Charges at the Particle Surface
References
- Oosawa, F. Polyelectrolytes; Marcel Dekker, Inc.: New York, NY, USA, 1971. [Google Scholar]
- Grosberg, A.Y.; Khokhlov, A.R. Statistical Physics of Macromolecules; AIP Press: Melville, NY, USA, 1994. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Polymer Physics; OUP Oxford: Oxford, UK, 2003. [Google Scholar]
- Muthukumar, M. 50th anniversary perspective: A perspective on polyelectrolyte solutions. Macromolecules 2017, 50, 9528–9560. [Google Scholar] [CrossRef] [PubMed]
- Wiegel, F.W. Adsorption of a macromolecule to a charged surface. J. Phys. A 1977, 10, 299–303. [Google Scholar] [CrossRef]
- Muthukumar, M. Adsorption of a polyelectrolyte chain to a charged surface. J. Chem. Phys. 1987, 86, 7230–7235. [Google Scholar] [CrossRef]
- Von Goeler, F.; Muthukumar, M. Adsorption of polyelectrolytes onto curved surfaces. J. Chem. Phys. 1994, 100, 7796–7803. [Google Scholar] [CrossRef]
- Eisenriegler, E.; Hanke, A.; Dietrich, S. Polymers interacting with spherical and rodlike particles. Phys. Rev. E 1996, 54, 1134–1152. [Google Scholar] [CrossRef]
- Kong, C.Y.; Muthukumar, M. Monte Carlo study of adsorption of a polyelectrolyte onto charged surfaces. J. Chem. Phys. 1998, 109, 1522–1527. [Google Scholar] [CrossRef]
- Netz, R.R.; Joanny, J.F. Complexation between a semiflexible polyelectrolyte and an oppositely charged sphere. Macromolecules 1999, 32, 9026–9040. [Google Scholar] [CrossRef]
- Netz, R.R.; Joanny, J.F. Adsorption of semiflexible polyelectrolytes on charged planar surfaces: Charge compensation, charge reversal, and multilayer formation. Macromolecules 1999, 32, 9013–9025. [Google Scholar] [CrossRef]
- Gurovitch, E.; Sens, P. Adsorption of polyelectrolyte onto a colloid of opposite charge. Phys. Rev. Lett. 1999, 82, 339–342. [Google Scholar] [CrossRef]
- Ellis, M.; Kong, C.Y.; Muthukumar, M. Polyelectrolyte adsorption on heterogeneously charged surfaces. J. Chem. Phys. 2000, 112, 8723–8729. [Google Scholar] [CrossRef]
- Dobrynin, A.V.; Deshkovski, A.; Rubinstein, M. Adsorption of polyelectrolytes at opppositely charged surfaces. Macromolecules 2001, 34, 3421–3436. [Google Scholar] [CrossRef]
- Stoll, S.; Chodanowski, P. Polyelectrolyte adsorption on an oppositely charged spherical particle. Chain rigidity effects. Macromolecules 2002, 35, 9556–9562. [Google Scholar] [CrossRef]
- McNamara, J.; Kong, C.Y.; Muthukumar, M. Monte Carlo studies of adsorption of a sequenced polyelectrolyte to patterned surfaces. J. Chem. Phys. 2002, 117, 5354–5360. [Google Scholar] [CrossRef]
- Huang, Y.W.; Chun, K.Y.; Gupta, V.K. Adsorption of a polyelectrolyte on surfaces with manometer sized chemical patchiness. Langmuir 2003, 19, 2175–2180. [Google Scholar] [CrossRef]
- Netz, R.R.; Andelman, D. Neutral and charged polymers at interfaces. Phys. Rep. 2003, 380, 1–95. [Google Scholar] [CrossRef]
- Dobrynin, A.V.; Rubinstein, M. Effect of short-range interactions on polyelectrolyte adsorption at charged surfaces. J. Phys. Chem. B 2003, 107, 8260–8269. [Google Scholar] [CrossRef]
- de Vries, R.; Weinbreck, F.; de Kruif, C.G. Theory of polyelectrolyte adsorption on heterogeneously charged surfaces applied to soluble protein–polyelectrolyte complexes. J. Chem. Phys. 2003, 118, 4649–4659. [Google Scholar] [CrossRef]
- de Vries, R. Monte Carlo simulations of flexible polyanions complexing with whey proteins at their isoelectric point. J. Chem. Phys. 2004, 120, 3475–3481. [Google Scholar] [CrossRef]
- Messina, R. Effect of image forces on polyelectrolyte adsorption at a charged surface. Phys. Rev. E 2004, 70, 051802. [Google Scholar] [CrossRef]
- Cherstvy, A.G.; Winkler, R.G. Complexation of semiflexible chains with oppositely charged cylinder. J. Chem. Phys. 2004, 120, 9394–9400. [Google Scholar] [CrossRef]
- Dobrynin, A.V.; Rubinstein, M. Theory of polyelectrolytes in solutions and at surfaces. Progr. Pol. Sci. 2005, 30, 1049–1118. [Google Scholar] [CrossRef]
- Cherstvy, A.G.; Winkler, R.G. Simple model for overcharging of a sphere by a wrapped oppositely charged asymmetrically neutralized polyelectrolyte: Possible effects of helical charge distribution. J. Phys. Chem. B 2005, 109, 2962–2969. [Google Scholar] [CrossRef][Green Version]
- Barroso da Silva, F.L.; Lund, M.; Jönsson, B.; Åkesson, T. On the complexation of proteins and polyelectrolytes. J. Phys. Chem. B 2006, 110, 4459–4464. [Google Scholar] [CrossRef]
- Belyi, V.A.; Muthukumar, M. Electrostatic origin of the genome packing in viruses. Proc. Natl. Acad. Sci. USA 2006, 103, 17174–17178. [Google Scholar] [CrossRef]
- Cherstvy, A.G.; Winkler, R.G. Strong and weak adsorptions of polyelectrolyte chains onto oppositely charged spheres. J. Chem. Phys. 2006, 125, 064904. [Google Scholar] [CrossRef] [PubMed]
- Winkler, R.G.; Cherstvy, A.G. Critical adsorption of polyelectrolytes onto charged spherical colloids. Phys. Rev. Lett. 2006, 96, 066103. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, S.; Seijo, M.; Stoll, S. The many facets of polyelectrolytes and oppositely charged macroions complex formation. Curr. Opin. Colloid Interface Sci. 2006, 11, 268–272. [Google Scholar] [CrossRef]
- Hoda, N.; Kumar, S. Brownian dynamics simulations of polyelectrolyte adsorption onto charged patterned surfaces. Langmuir 2007, 23, 1741–1751. [Google Scholar] [CrossRef]
- Carrillo, J.M.Y.; Dobrynin, A.V. Molecular dynamics simulations of polyelectrolyte adsorption. Langmuir 2007, 23, 2472–2482. [Google Scholar] [CrossRef]
- Winkler, R.G.; Cherstvy, A.G. Adsorption of weakly charged polyelectrolytes onto oppositely charged spherical colloids. J. Phys. Chem. B 2007, 111, 8486–8493. [Google Scholar] [CrossRef] [PubMed]
- Hoda, N.; Kumar, S. Theory of polyelectrolyte adsorption onto surfaces patterned with charge and topography. J. Chem. Phys. 2008, 128, 124907. [Google Scholar] [CrossRef]
- Hoda, N.; Kumar, S. Brownian dynamics simulations of polyelectrolyte adsorption in shear flow: Effects of solvent quality and charge patterning. J. Chem. Phys. 2008, 128, 164907. [Google Scholar] [CrossRef]
- Man, X.; Yang, S.; Yan, D.; Shi, A.C. Adsorption and depletion of polyelectrolytes in charged cylindrical system within self-consistent field theory. Macromolecules 2008, 41, 5451–5456. [Google Scholar] [CrossRef]
- Seijo, M.; Pohl, M.; Ulrich, S.; Stoll, S. Dielectric discontinuity effects on the adsorption of a linear polyelectrolyte at the surface of a neutral nanoparticle. J. Chem. Phys. 2009, 131, 174704. [Google Scholar] [CrossRef]
- da Silva, F.L.B.; Jönsson, B. Polyelectrolyte–protein complexation driven by charge regulation. Soft Matter 2009, 5, 2862–2868. [Google Scholar] [CrossRef]
- de Carvalho, S.J. First-order–like transition in salt-induced macroion-polyelectrolyte desorption. Europhys. Lett. 2010, 92, 18001. [Google Scholar] [CrossRef]
- Wang, J.; Muthukumar, M. Encapsulation of a polyelectrolyte chain by an oppositely charged spherical surface. J. Chem. Phys. 2011, 135, 194901. [Google Scholar] [CrossRef] [PubMed]
- Cherstvy, A.G.; Winkler, R.G. Polyelectrolyte adsorption onto oppositely charged interfaces: Unified approach for plane, cylinder, and sphere. Phys. Chem. Chem. Phys. 2011, 13, 11686–11693. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cherstvy, A.G. Critical polyelectrolyte adsorption under confinement: Planar slit, cylindrical pore, and spherical cavity. Biopolymers 2012, 97, 311–317. [Google Scholar] [CrossRef]
- Cherstvy, A.G.; Winkler, R.G. Polyelectrolyte adsorption onto oppositely charged interfaces: Image-charge repulsion and surface curvature. J. Phys. Chem. B 2012, 116, 9838–9845. [Google Scholar] [CrossRef]
- Nunes, S.C.C.; Pinto, P.; Pais, A.A.C.C. Nonrandom adsorption of polyelectrolyte chains on finite regularly charged surfaces. J. Comput. Chem. 2013, 34, 1198–1209. [Google Scholar] [CrossRef]
- Winkler, R.G.; Cherstvy, A.G. Strong and weak polyelectrolyte adsorption onto oppositely charged curved surfaces. In Polyelectrolyte Complexes in the Dispersed and Solid State I: Principles and Theory; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–56. [Google Scholar]
- de Carvalho, S.J.; Caetano, D.L.Z. Adsorption of polyelectrolytes onto oppositely charged cylindrical macroions. J. Chem. Phys. 2013, 138, 244909. [Google Scholar] [CrossRef]
- Kampmann, T.A.; Boltz, H.H.; Kierfeld, J. Controlling adsorption of semiflexible polymers on planar and curved substrates. J. Chem. Phys 2013, 139, 034903. [Google Scholar] [CrossRef] [PubMed]
- de Carvalho, S.J.; Metzler, R.; Cherstvy, A.G. Critical adsorption of polyelectrolytes onto charged Janus nanospheres. Phys. Chem. Chem. Phys. 2014, 16, 15539–15550. [Google Scholar] [CrossRef]
- Yigit, C.; Heyda, J.; Ballauff, M.; Dzubiella, J. Like-charged protein-polyelectrolyte complexation driven by charge patches. J. Chem. Phys. 2015, 143, 064905. [Google Scholar] [CrossRef] [PubMed]
- de Carvalho, S.J.; Metzler, R.; Cherstvy, A.G. Critical adsorption of polyelectrolytes onto planar and convex highly charged surfaces: The nonlinear Poisson-Boltzmann approach. New J. Phys. 2016, 18, 083037. [Google Scholar] [CrossRef]
- Caetano, D.L.Z.; de Carvalho, S.J.; Metzler, R.; Cherstvy, A.G. Critical adsorption of periodic and random polyampholytes onto charged surfaces. Phys. Chem. Chem. Phys. 2017, 19, 23397–23413. [Google Scholar] [CrossRef] [PubMed]
- Stornes, M.; Linse, P.; Dias, R.S. Monte Carlo simulations of complexation between weak polyelectrolytes and a charged nanoparticle. Influence of polyelectrolyte chain length and concentration. Macromolecules 2017, 50, 5978–5988. [Google Scholar] [CrossRef]
- Shojaei, H.R.; Muthukumar, M. Adsorption and encapsulation of flexible polyelectrolytes in charged spherical vesicles. J. Chem. Phys. 2017, 146, 244901. [Google Scholar] [CrossRef]
- Caetano, D.L.; de Carvalho, S.J. Conformational properties of block-polyampholytes adsorbed on charged cylindrical surfaces. Euro. Phys. J. E 2017, 40, 33. [Google Scholar] [CrossRef]
- Xu, X.; Angioletti-Uberti, S.; Lu, Y.; Dzubiella, J.; Ballauff, M. Interaction of proteins with polyelectrolytes: Comparison of theory to experiment. Langmuir 2019, 35, 5373–5391. [Google Scholar] [CrossRef]
- Bakhshandeh, A.; Segala, M. Adsorption of polyelectrolytes on charged microscopically patterned surfaces. J. Mol. Liq. 2019, 294, 111673. [Google Scholar] [CrossRef]
- Caetano, D.L.Z.; de Carvalho, S.J.; Metzler, R.; Cherstvy, A.G. Critical adsorption of multiple polyelectrolytes onto a nanosphere: Splitting the adsorption–desorption transition boundary. J. R. Soc. Interface 2020, 17, 20200199. [Google Scholar] [CrossRef]
- Kim, S.; Sureka, H.V.; Kayitmazer, A.B.; Wang, G.; Swan, J.W.; Olsen, B.D. Effect of protein surface charge distribution on protein–polyelectrolyte complexation. Biomacromolecules 2020, 21, 3026–3037. [Google Scholar] [CrossRef]
- Chang, Q.; Jiang, J. Adsorption of block-polyelectrolytes on an oppositely charged surface. Macromolecules 2021, 54, 4145–4153. [Google Scholar] [CrossRef]
- Wang, R.; Ginzburg, V.V.; Jiang, J.; Wang, Z.G. Adsorption of a polyelectrolyte chain at dielectric surfaces: Effects of surface charge distribution and relative dielectric permittivity. Macromolecules 2023, 56, 7653–7662. [Google Scholar] [CrossRef]
- Vahid, H.; Scacchi, A.; Sammalkorpi, M.; Ala-Nissila, T. Adsorption of polyelectrolytes in the presence of varying dielectric discontinuity between solution and substrate. J. Chem. Phys. 2024, 161, 134907. [Google Scholar] [CrossRef] [PubMed]
- Morrison, G.; Thirumalai, D. Scaling regimes for wormlike chains confined to cylindrical surfaces under tension. Eur. Phys. J. E 2024, 47, 6. [Google Scholar] [CrossRef]
- Africo, F.A.; Cherstvy, A.G.; Jurado de Carvalho, S. Critical adsorption of polyelectrolytes onto highly oppositely charged surfaces: Effects of charge renormalization. J. Chem. Phys. 2024, 161, 194905. [Google Scholar] [CrossRef] [PubMed]
- Martens, C.M. Critical adsorption and charge reversal in polyelectrolyte solutions: Analytical mean-field theory. J. Chem. Phys 2024, 161, 054901. [Google Scholar] [CrossRef]
- Yadav, V.; Jaiswal, P.K.; Podgornik, R.; Kumari, S. Charge regulation effect on nanoparticles interaction mediated by polyelectrolyte. arXiv 2025, arXiv:2507.00549. [Google Scholar]
- Dubin, P.L.; Rigsbee, D.R.; McQuigg, D.W. Turbidimetric and dynamic light scattering studies of mixtures of cationic polymers and anionic mixed micelles. J. Colloid Interface Sci. 1985, 105, 509–515. [Google Scholar] [CrossRef]
- Dubin, P.L.; Curran, M.E.; Hua, J. Critical linear charge density for binding of a weak polycation to an anionic/nonionic mixed micelle. Langmuir 1990, 6, 707–709. [Google Scholar] [CrossRef]
- Park, J.M.; Muhoberac, B.B.; Dubin, P.L.; Xia, J. Effects of protein charge heterogeneity in protein-polyelectrolyte complexation. Macromolecules 1992, 25, 290–295. [Google Scholar] [CrossRef]
- McQuigg, D.W.; Kaplan, J.I.; Dubin, P.L. Critical conditions for the binding of polyelectrolytes to small oppositely charged micelles. J. Phys. Chem. 1992, 96, 1973–1978. [Google Scholar] [CrossRef]
- Li, Y.; Dubin, P.L.; Spindler, R.; Tomalia, D.A. Complex formation between poly (dimethyldiallylammonium chloride) and carboxylated starburst dendrimers. Macromolecules 1995, 28, 8426–8428. [Google Scholar] [CrossRef]
- Shubin, V.; Samoshina, Y.; Menshikova, A.; Evseeva, T. Adsorption of cationic polyelectrolyte onto a model carboxylic latex and the influence of adsorbed polycation on the charge regulation at the latex surface. Colloid Polym. Sci. 1997, 275, 655–660. [Google Scholar] [CrossRef]
- Yoshida, K.; Sokhakian, S.; Dubin, P.L. Binding of polycarboxylic acids to cationic mixed micelles: Effects of polymer counterion binding and polyion charge distribution. J. Colloid Interface Sci. 1998, 205, 257–264. [Google Scholar] [CrossRef][Green Version]
- Miura, N.; Dubin, P.L.; Moorefield, C.; Newkome, G. Complex formation by electrostatic interaction between carboxyl-terminated dendrimers and oppositely charged polyelectrolytes. Langmuir 1999, 15, 4245–4250. [Google Scholar] [CrossRef]
- Zhang, H.; Ohbu, K.; Dubin, P.L. Binding of carboxy-terminated anionic/nonionic mixed micelles to a strong polycation: Critical conditions for complex formation. Langmuir 2000, 16, 9082–9086. [Google Scholar] [CrossRef]
- Feng, X.H.; Dubin, P.L.; Zhang, H.W.; Kirton, G.F.; Bahadur, P.; Parotte, J. Critical conditions for binding of dimethyldodecylamine oxide micelles to polyanions of variable charge density. Macromolecules 2001, 34, 6373–6379. [Google Scholar] [CrossRef][Green Version]
- Seyrek, E.; Dubin, P.L.; Tribet, C.; Gamble, E.A. Ionic strength dependence of protein-polyelectrolyte interactions. Biomacromolecules 2003, 4, 273–282. [Google Scholar] [CrossRef]
- Kayitmazer, A.B.; Seyrek, E.; Dubin, P.L.; Staggemeier, B.A. Influence of chain stiffness on the interaction of polyelectrolytes with oppositely charged micelles and proteins. J. Phys. Chem. B 2003, 107, 8158–8165. [Google Scholar] [CrossRef]
- Kayitmazer, A.B.; Shaw, D.; Dubin, P.L. Role of polyelectrolyte persistence length in the binding of oppositely charged micelles, dendrimers, and protein to chitosan and poly(dimethyldiallyammonium chloride). Macromolecules 2005, 38, 5198–5204. [Google Scholar] [CrossRef][Green Version]
- Cooper, C.L.; Dubin, P.L.; Kayitmazer, A.B.; Turksen, S. Polyelectrolyte–protein complexes. Curr. Opin. Colloid Interface Sci. 2005, 10, 52–78. [Google Scholar] [CrossRef]
- Kayitmazer, A.B.; Seeman, D.; Minsky, B.B.; Dubin, P.L.; Xu, Y. Protein–polyelectrolyte interactions. Soft Matter 2013, 9, 2553–2583. [Google Scholar] [CrossRef]
- Minsky, B.B.; Zheng, B.; Dubin, P.L. Inhibition of antithrombin and bovine serum albumin native state aggregation by heparin. Langmuir 2014, 30, 278–287. [Google Scholar] [CrossRef] [PubMed]
- Lunkad, R.; Barroso da Silva, F.L.; Košovan, P. Both charge-regulation and charge-patch distribution can drive adsorption on the wrong side of the isoelectric point. J. Am. Chem. Soc. 2022, 144, 1813–1825. [Google Scholar] [CrossRef]
- Boroudjerdi, H.; Kim, Y.W.; Naji, A.; Netz, R.R.; Schlagberger, X.; Serr, A. Statics and dynamics of strongly charged soft matter. Phys. Rep. 2005, 416, 129–199. [Google Scholar] [CrossRef]
- Langer, R.E. On the connection formulas and the solutions of the wave equation. Phys. Rev. 1937, 51, 669–676. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; International Series of Monographs on Physics; Clarendon Press: Oxford, UK, 1988. [Google Scholar]
- Muthukumar, M. Polymers under Confinement. In Advances in Chemical Physics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012; Chapter 4; pp. 129–196. [Google Scholar]
- Blanco, P.M.; Achetoni, M.M.; Garcés, J.L.; Madurga, S.; Mas, F.; Baieli, M.F.; Narambuena, C.F. Adsorption of flexible proteins in the ‘wrong side’ of the isoelectric point: Casein macropeptide as a model system. Colloids Surf. B Biointerfaces 2022, 217, 112617. [Google Scholar] [CrossRef]
- Simončič, M.; Hritz, J.; Lukšič, M. Biomolecular complexation on the “wrong side”: A case study of the influence of salts and sugars on the interactions between bovine serum albumin and sodium polystyrene sulfonate. Biomacromolecules 2022, 23, 4412–4426. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Russell, S.T. Calculations of electrostatic interactions in biological systems and in solutions. Q. Rev. Biophys. 1984, 17, 283–422. [Google Scholar] [CrossRef]
- Lund, M.; Åkesson, T.; Jönsson, B. Enhanced protein adsorption due to charge regulation. Langmuir 2005, 21, 8385–8388. [Google Scholar] [CrossRef]
- Lund, M.; Jönsson, B. Charge regulation in biomolecular solution. Q. Rev. Biophys. 2013, 46, 265–281. [Google Scholar] [CrossRef]
- Li, W.; Persson, B.A.; Morin, M.; Behrens, M.A.; Lund, M.; Zackrisson-Oskolkova, M. Charge-induced patchy attractions between proteins. J. Phys. Chem. B 2015, 119, 503–508. [Google Scholar] [CrossRef]
- Lund, M. Anisotropic protein–protein interactions due to ion binding. Colloids Surf. B Biointerfaces 2016, 137, 17–21. [Google Scholar] [CrossRef] [PubMed]
- Simonson, T.; Brooks, C.L. Charge screening and the dielectric constant of proteins: Insights from molecular dynamics. J. Am. Chem. Soc. 1996, 118, 8452–8458. [Google Scholar] [CrossRef]
- Cherstvy, A.G. Electrostatics of DNA complexes with cationic lipid membranes. J. Phys. Chem. B 2007, 111, 7914–7927. [Google Scholar] [CrossRef] [PubMed]
- Debye, P.; Hückel, E. Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen. Phys. Z. 1923, XXIV, 185–206. [Google Scholar]
- Cherstvy, A.G. Electrostatic interactions in biological DNA-related systems. Phys. Chem. Chem. Phys. 2011, 13, 9942–9968. [Google Scholar] [CrossRef]
- Morse, P.M.C.; Feshbach, H. Methods of Theoretical Physics; International Series in Pure and Applied Physics; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- Hasted, J.B.; Ritson, D.M.; Collie, C.H. Dielectric properties of aqueous ionic solutions. Parts I and II. J. Chem. Phys. 1948, 16, 1–21. [Google Scholar] [CrossRef]
- Levy, A.; Andelman, D.; Orland, H. Dielectric constant of ionic solutions: A field-theory approach. Phys. Rev. Lett. 2012, 108, 227801. [Google Scholar] [CrossRef] [PubMed]
- Gavish, N.; Promislow, K. Dependence of the dielectric constant of electrolyte solutions on ionic concentration: A microfield approach. Phys. Rev. E 2016, 94, 012611. [Google Scholar] [CrossRef] [PubMed]
- Yukawa, H. On the interaction of elementary particles. I. Proc. Phys.-Math. Soc. Japan. 3rd Ser. 1935, 17, 48–57. [Google Scholar]
- Cherstvy, A.G. Effect of a low-dielectric interior on DNA electrostatic response to twisting and bending. J. Phys. Chem. B 2007, 111, 12933–12937. [Google Scholar] [CrossRef]
- Netz, R.; Orland, H. Beyond Poisson-Boltzmann: Fluctuation effects and correlation functions. Eur. Phys. J. E 2000, 1, 203–214. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Grosberg, A.Y.; Shklovskii, B.I. Macroions in salty water with multivalent ions: Giant inversion of charge. Phys. Rev. Lett. 2000, 85, 1568–1571. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Nguyen, T.T.; Shklovskii, B.I. Colloquium: The physics of charge inversion in chemical and biological systems. Rev. Mod. Phys. 2002, 74, 329–345. [Google Scholar] [CrossRef]
- Levin, Y. Electrostatic correlations: From plasma to biology. Rep. Progr. Phys. 2002, 65, 1577–1632. [Google Scholar] [CrossRef]
- dos Santos, A.P.; Diehl, A.; Levin, Y. Electrostatic correlations in colloidal suspensions: Density profiles and effective charges beyond the Poisson–Boltzmann theory. J. Chem. Phys. 2009, 130, 124110. [Google Scholar] [CrossRef]
- Böttcher, C.J.F.; van Belle, O.C.; Bordewijk, P.; Rip, A.; Yue, D.D. Theory of electric polarization. J. Electrochem. Soc. 1974, 121, 211Ca. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Elsevier: London, UK, 2023. [Google Scholar]
- Teif, V.B.; Bohinc, K. Condensed DNA: Condensing the concepts. Progr. Biophys. Mol. Biol. 2011, 105, 208–222. [Google Scholar] [CrossRef]
- Cherstvy, A.G.; Teif, V.B. Electrostatic effect of H1-histone protein binding on nucleosome repeat length. Phys. Biol. 2014, 11, 044001. [Google Scholar] [CrossRef]
- Collette, D.; Dunlap, D.; Finzi, L. Macromolecular crowding and DNA: Bridging the gap between In Vitro and In Vivo. Intl. J. Mol. Sci. 2023, 24, 17502. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Caruso, I.P.; Guimaraes, G.C.; Machado, V.B.; Fossey, M.A.; Willbold, D.; Almeida, F.C.L.; Souza, F.P. Biophysical and dynamic characterization of fine-funed binding of the human Respiratory Syncytial Virus M2-1 core domain to long RNAs. J. Virol. 2020, 94, jvi.01505. [Google Scholar] [CrossRef]
- Caruso, I.P.; Panwalkar, V.; Coronado, M.A.; Dingley, A.J.; Cornélio, M.L.; Willbold, D.; Arni, R.K.; Eberle, R.J. Structure and interaction of Corynebacterium pseudotuberculosis cold shock protein A with Y-box single-stranded DNA fragment. FEBS J. 2018, 285, 372–390. [Google Scholar] [CrossRef]
- Tani, M.; Wada, H. How a soft rod wraps around a rotating cylinder. Phys. Rev. Lett. 2024, 132, 058204. [Google Scholar] [CrossRef]
- Zheng, M.; Jagota, A.; Semke, E.D.; Diner, B.A.; Mclean, R.S.; Lustig, S.R.; Richardson, R.E.; Tassi, N.G. DNA-assisted dispersion and separation of carbon nanotubes. Nat. Mat. 2003, 2, 338–342. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wen, Y.; Beltrán, L.C.; Zhu, L.; Tian, S.; Liu, J.; Zhou, X.; Chen, P.; Egelman, E.H.; Zheng, M.; et al. Understanding DNA-encoded carbon nanotube sorting and sensing via sub-nm-resolution structural determination. Scie. Adv. 2025, 11, eadt9844. [Google Scholar] [CrossRef] [PubMed]
- Eigen, M.; Wicke, E. The thermodynamics of electrolytes at higher concentration. J. Phys. Chem. 1954, 58, 702–714. [Google Scholar] [CrossRef]
- Borukhov, I.; Andelman, D.; Orland, H. Steric effects in electrolytes: A modified Poisson-Boltzmann equation. Phys. Rev. Lett. 1997, 79, 435–438. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Applied Mathematics Series; Dover Publications: Garden City, NY, USA, 1965. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anhesini, D.A.; Caetano, D.L.Z.; Caruso, I.P.; Cherstvy, A.G.; de Carvalho, S.J. Critical Adsorption of Polyelectrolytes onto Patchy Particles with a Low-Dielectric Interior. Polymers 2025, 17, 2205. https://doi.org/10.3390/polym17162205
Anhesini DA, Caetano DLZ, Caruso IP, Cherstvy AG, de Carvalho SJ. Critical Adsorption of Polyelectrolytes onto Patchy Particles with a Low-Dielectric Interior. Polymers. 2025; 17(16):2205. https://doi.org/10.3390/polym17162205
Chicago/Turabian StyleAnhesini, Dante A., Daniel L. Z. Caetano, Icaro P. Caruso, Andrey G. Cherstvy, and Sidney J. de Carvalho. 2025. "Critical Adsorption of Polyelectrolytes onto Patchy Particles with a Low-Dielectric Interior" Polymers 17, no. 16: 2205. https://doi.org/10.3390/polym17162205
APA StyleAnhesini, D. A., Caetano, D. L. Z., Caruso, I. P., Cherstvy, A. G., & de Carvalho, S. J. (2025). Critical Adsorption of Polyelectrolytes onto Patchy Particles with a Low-Dielectric Interior. Polymers, 17(16), 2205. https://doi.org/10.3390/polym17162205






