Energy Absorption Characteristics of CFRP–Aluminum Foam Composite Structure Under High-Velocity Impact: Focusing on Varying Aspect Ratios and Relative Densities
Abstract
1. Introduction
2. Experimental Methods
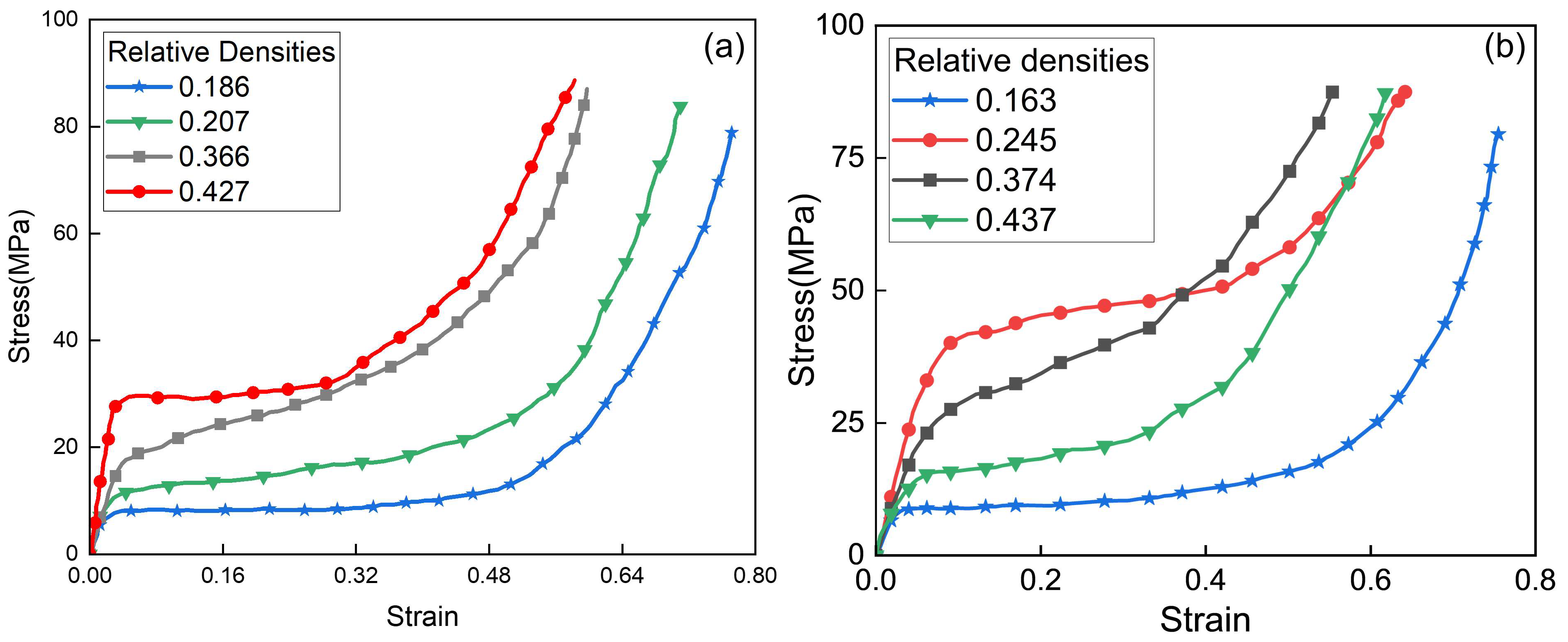
2.1. Dynamic Compression of AlF
2.2. Material Properties of CFRP
2.3. EA Characterization Indicators
3. FE Model
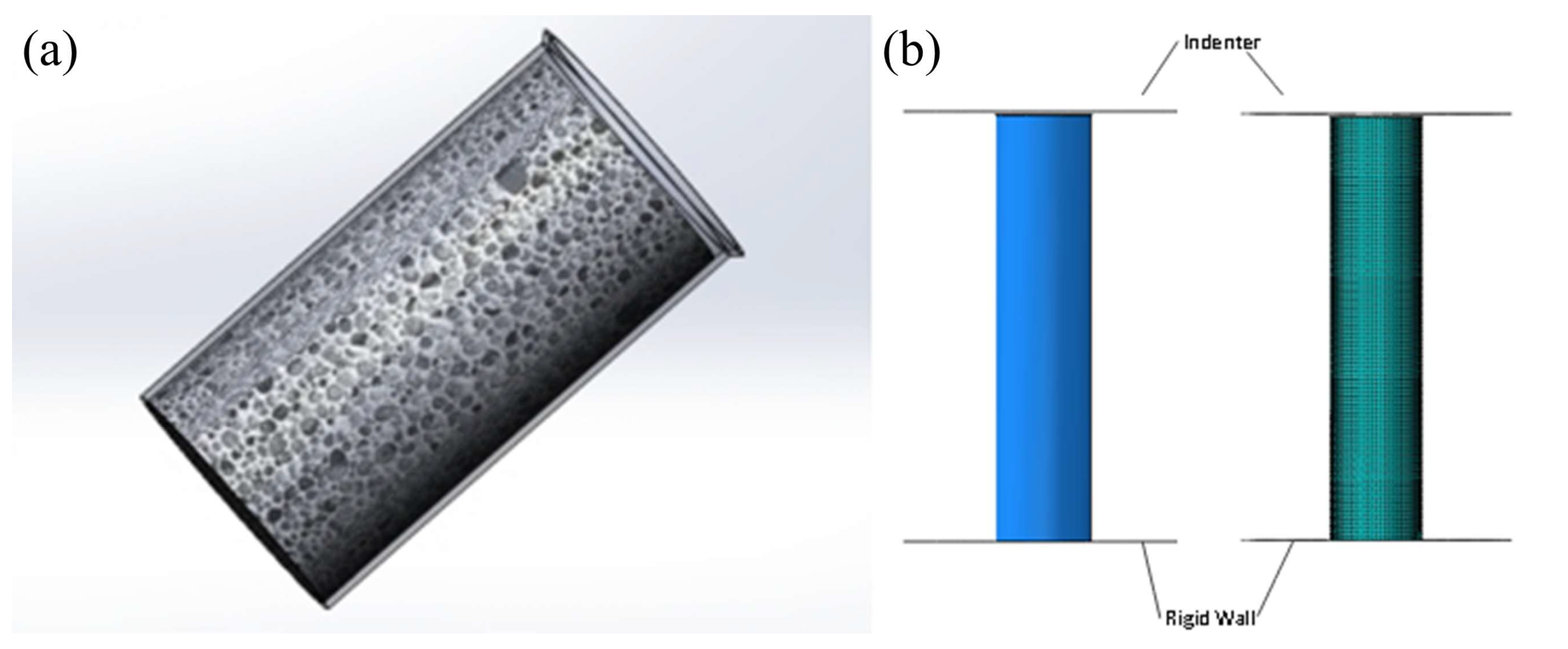
3.1. FE Modeling of CFRP-AlF Composite Structure
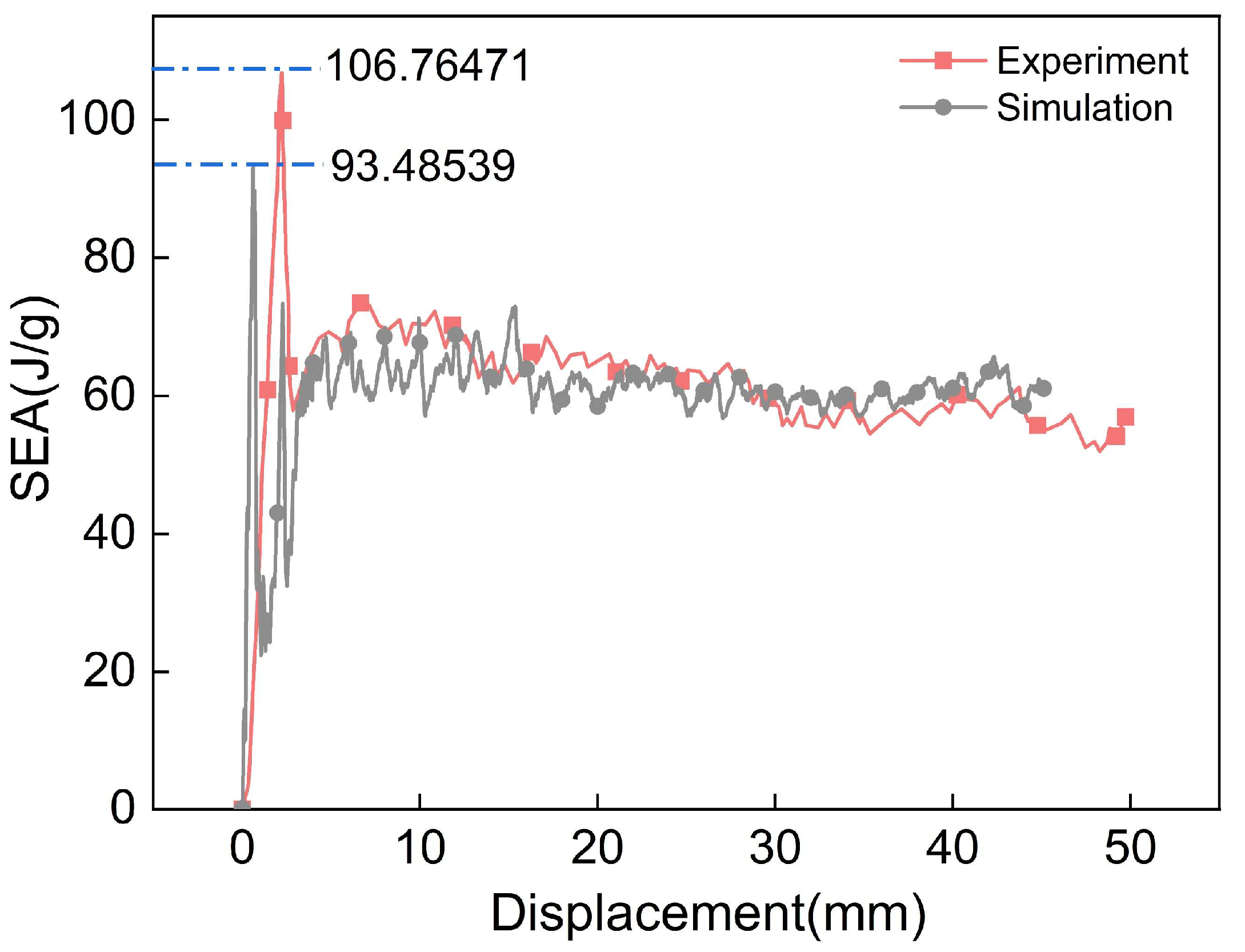
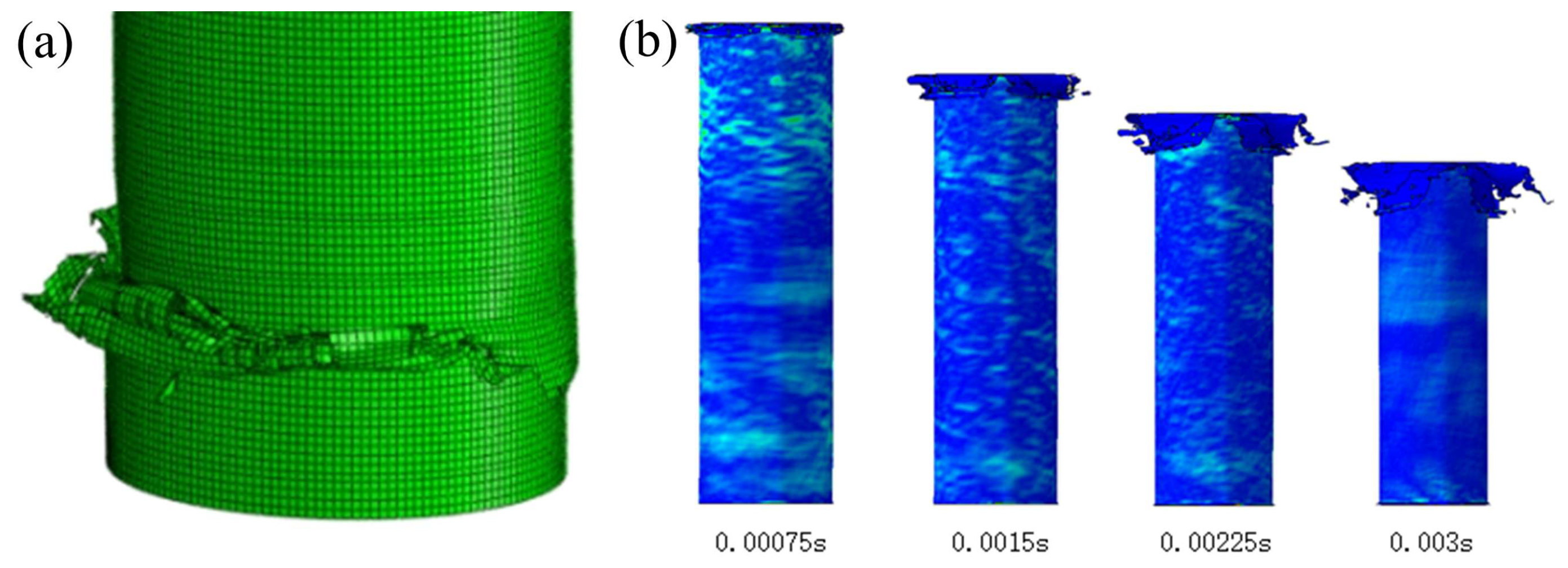
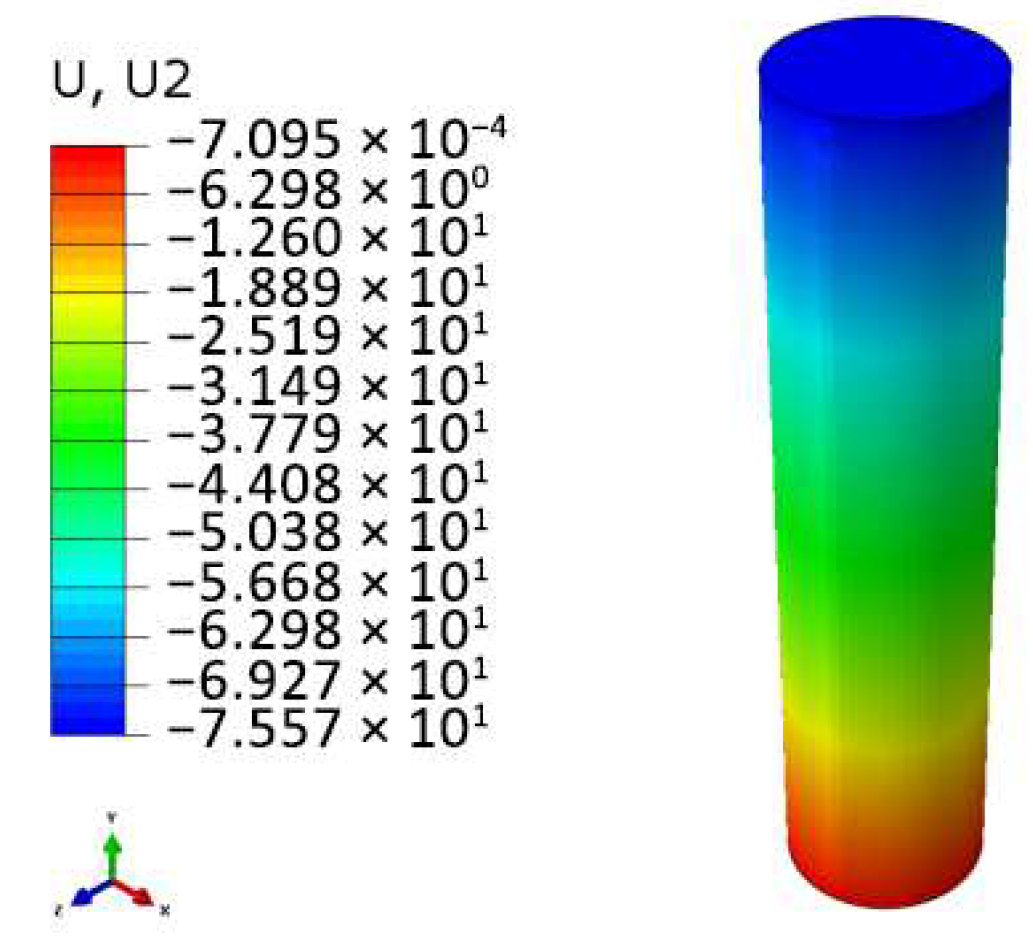
3.2. Model Validation
3.3. CFRP-AlF Composite Structures with Varying Aspect Ratios
3.4. CFRP-AlF Composite Structures with Varying AlF Relative Densities
4. Result and Discussion
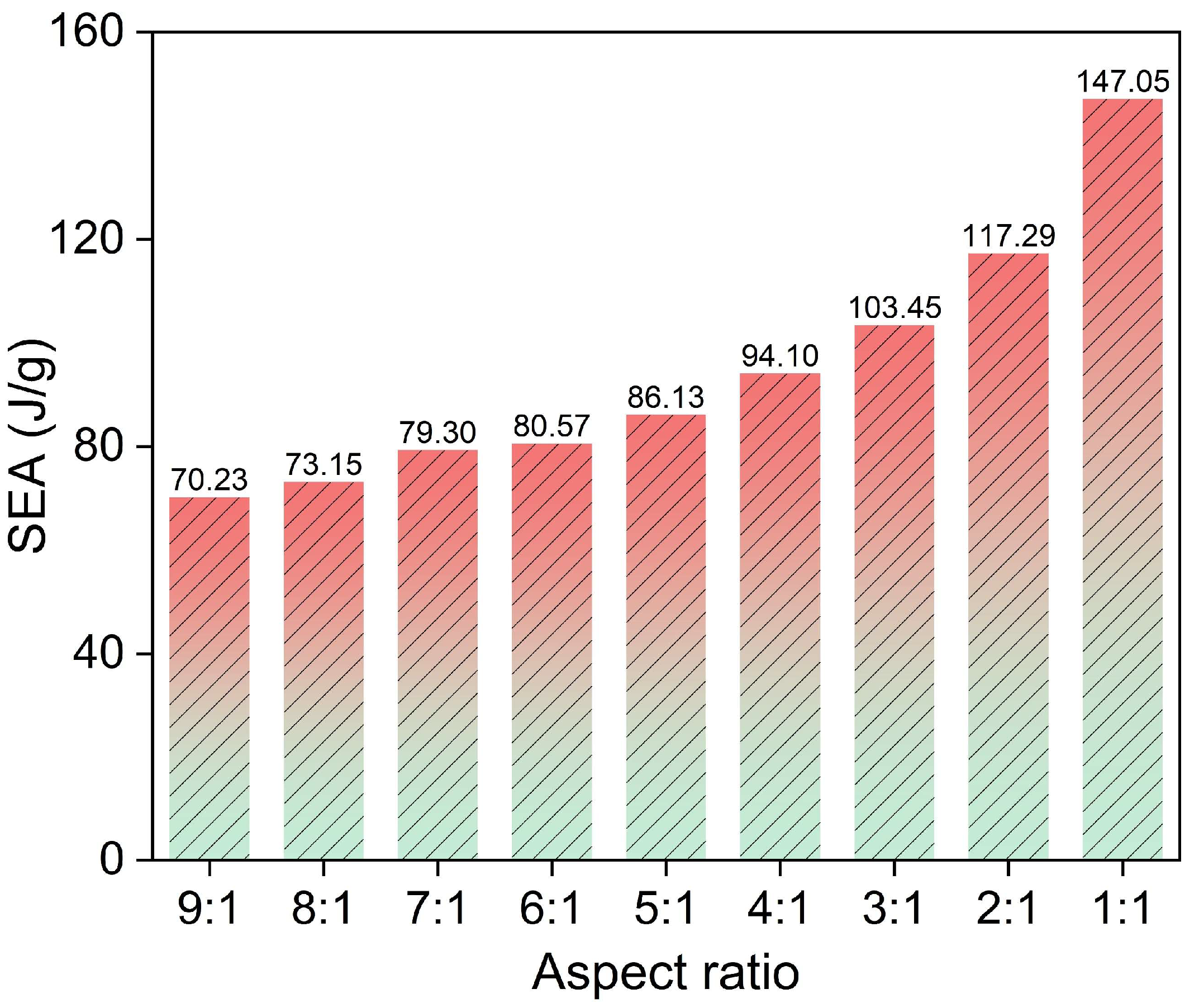
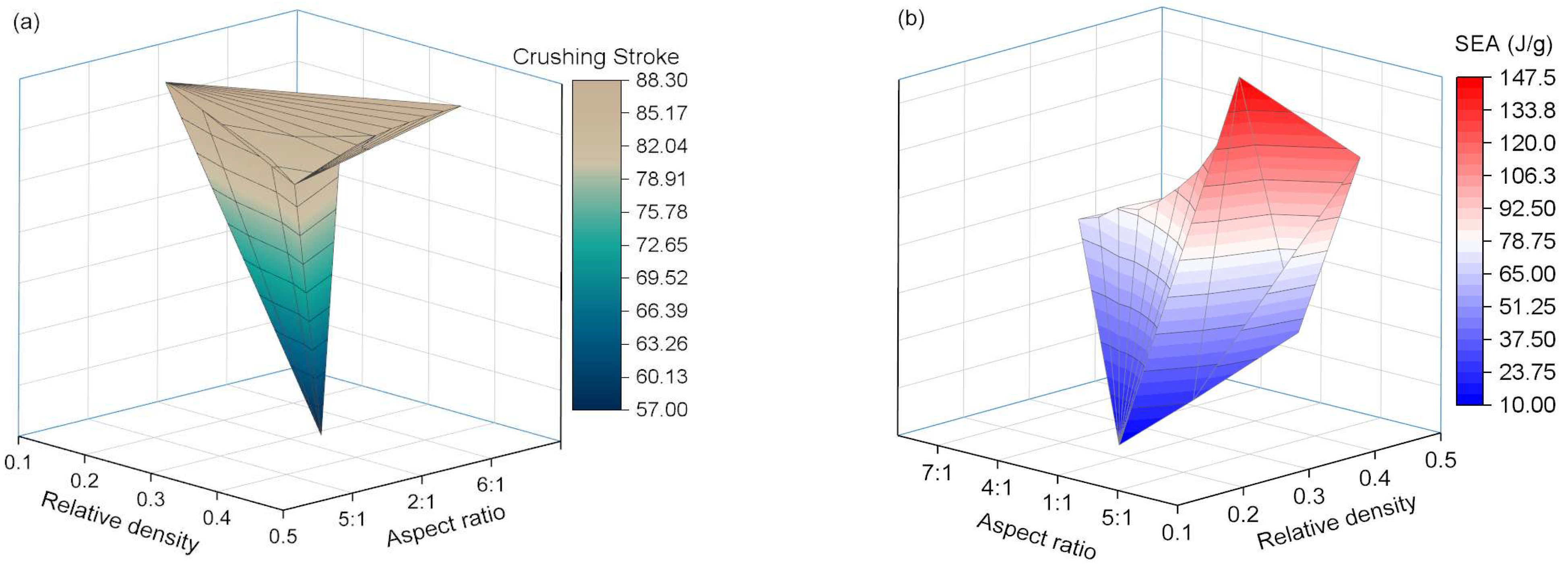
4.1. EA Characteristics of Structures with Varying Aspect Ratios
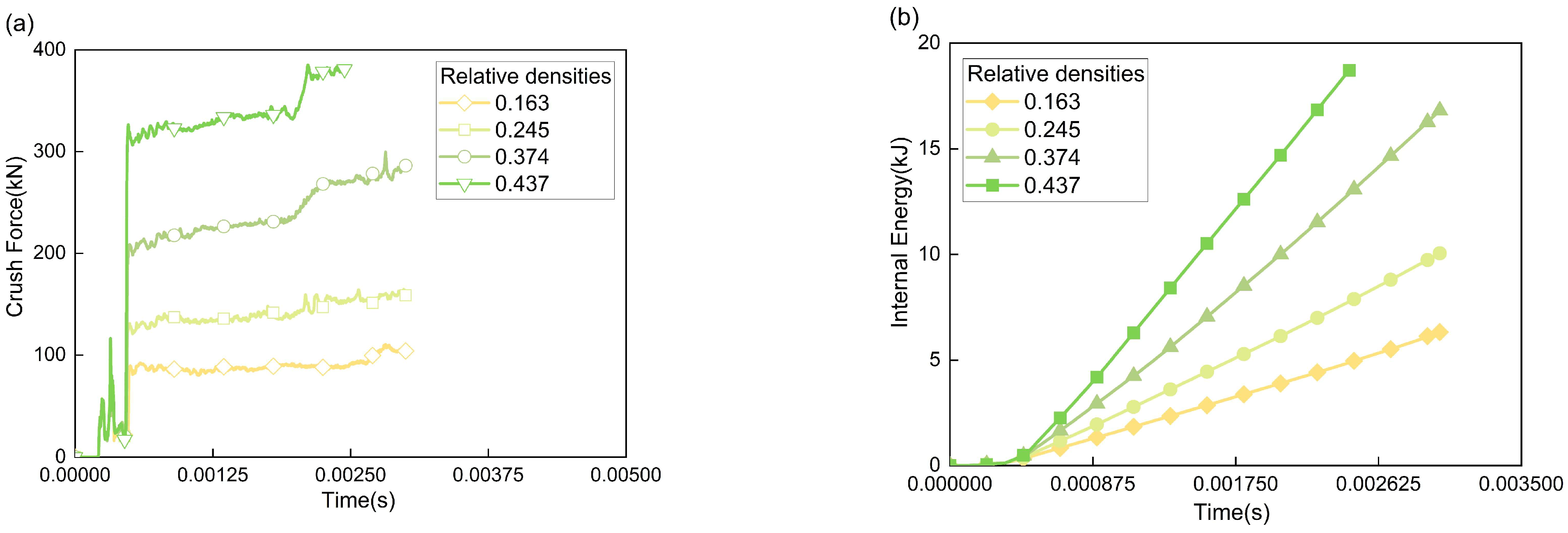
4.2. EA Characteristics of Structures with Varying AlF Relative Densities
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, S.; Wang, N.; Yang, W.; Li, H. Energy absorption performance of thin-walled metal plate due to upheaval deformation based on experiments and numerical simulation. Thin-Walled Struct. 2018, 131, 258–273. [Google Scholar] [CrossRef]
- Zhao, C.; Goh, K.L.; Lee, H.P.; Yin, C.; Zhang, K.; Zhong, J. Experimental study and finite element analysis on energy absorption of carbon fiber reinforced composite auxetic structures filled with aluminum foam. Compos. Struct. 2023, 303, 116319. [Google Scholar] [CrossRef]
- Zhao, C.; Zhong, J.; Wang, H.; Liu, C.; Li, M.; Liu, H. Impact behaviour and protection performance of a CFRP NPR skeleton filled with aluminum foam. Mater. Des. 2024, 246, 113295. [Google Scholar] [CrossRef]
- Zhao, C.; Zhou, Z.; Zhao, C.; Zhu, H.; Zhang, K.; Zhong, J.; Ren, J.; Le, G. Research on compression properties of unidirectional carbon fiber reinforced epoxy resin composite (UCFREP). J. Compos. Mater. 2021, 55, 1447–1458. [Google Scholar] [CrossRef]
- Serubibi, A.; Hazell, P.J.; Escobedo, J.P.; Wang, H.; Oromiehie, E.; Prusty, G.B.; Phillips, A.W.; St John, N.A. Fibre-metal laminate structures: High-velocity impact, penetration, and blast loading—A review. Compos. Part A Appl. Sci. Manuf. 2023, 173, 107674. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Z.; Liu, Y.; Ma, W.; Zhang, Z.; Zhao, C.; Yang, C. On the Crush Behavior and Energy Absorption of Sustainable Beverage Cans and Their Polyurethane Foam-Filled Structures: An Experimental Study. Materials 2024, 17, 2655. [Google Scholar] [CrossRef]
- Obradovic, J.; Boria, S.; Belingardi, G. Lightweight design and crash analysis of composite frontal impact energy absorbing structures. Compos. Struct. 2012, 94, 423–430. [Google Scholar] [CrossRef]
- Harris, C.E.; Starnes, J.H.; Shuart, M.J. Design and manufacturing of aerospace composite structures, state-of-the-art assessment. J. Aircr. 2002, 39, 545–560. [Google Scholar] [CrossRef]
- Liu, Q.; Guo, B.; Chen, P.; Su, J.; Arab, A.; Ding, G.; Yan, G.; Jiang, H.; Guo, F. length Investigating ballistic resistance of CFRP/polyurea composite plates subjected to ballistic impact. Thin-Walled Struct. 2021, 166, 108111. [Google Scholar] [CrossRef]
- Meric, D.; Gedikli, H. Multi-objective optimization of energy absorbing behavior of foam-filled hybrid composite tubes. Compos. Struct. 2022, 279, 114771. [Google Scholar] [CrossRef]
- Reddy, T.J.; Narayanamurthy, V.; Rao, Y.V.D. Enhancement in specific energy absorption of invertubes. Int. J. Mech. Sci. 2019, 159, 424–440. [Google Scholar] [CrossRef]
- Tang, E.; Yin, H.; Chen, C.; Han, Y.; Feng, M. Simulation of CFRP/aluminum foam sandwich structure under high velocity impact. J. Mater. Res. Technol. JMRT 2020, 9, 7273–7287. [Google Scholar] [CrossRef]
- Tang, E.; Zhang, X.; Han, Y. Experimental research on damage characteristics of CFRP/aluminum foam sandwich structure subjected to high velocity impact. J. Mater. Res. Technol. JMRT 2019, 8, 4620–4630. [Google Scholar] [CrossRef]
- Zheng, G.; Wang, Z.; Song, K. Energy absorption on metal-composite hybrid structures: Experimental and numerical simulation. Thin-Walled Struct. 2020, 150, 106571. [Google Scholar] [CrossRef]
- Zhu, G.; Wang, Z.; Huo, X.; Cheng, A.; Li, G.; Zhou, C. Experimental and numerical investigation into axial compressive behaviour of thin-walled structures filled with foams and composite skeleton. Int. J. Mech. Sci. 2017, 122, 104–119. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Z.; Chen, Y.; Wu, Y.; Song, K.; Zhu, G. Structure design of aluminum/CFRP hybrid stringers accounting for multiple impact angles. Compos. Struct. 2023, 305, 116554. [Google Scholar] [CrossRef]
- Sebaey, T.A.; Rajak, D.K.; Mehboob, H. Internally stiffened foam-filled carbon fiber reinforced composite tubes under impact loading for energy absorption applications. Compos. Struct. 2021, 255, 112910. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Q.; Fu, J.; Li, Q.; Hui, D. Dynamic crash responses of bio-inspired aluminum honeycomb sandwich structures with CFRP panels. Compos. Part B Eng. 2017, 121, 122–133. [Google Scholar] [CrossRef]
- Yang, H.; Guo, X.; Wang, H.; Qu, J.; Ma, Y.; Lei, H.; Chen, H. Low-velocity impact performance of composite-aluminum tubes prepared by mesoscopic hybridization. Compos. Struct. 2021, 274, 114348. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Wang, Z.; Li, K.; Bai, C.; Qin, Q. The influence of asymmetric faces on low-velocity impact failure of CFRP/aluminum foam composite sandwich beams. Eng. Struct. 2023, 292, 116574. [Google Scholar] [CrossRef]
- Ni, C.; Li, J.; Liu, G.; An, Q. Bending performance of carbon fiber-reinforced polymers/aluminum sandwich structure with different forming process and analysis of failure mode. J. Reinf. Plast. Compos. 2024, 43, 411–428. [Google Scholar] [CrossRef]
- Hou, W.; Xu, X.; Hu, C.; Huo, Y.; Tong, L. Failure characteristics of composite metallic foam core hat-shaped tubular T-joints under static and impact loading. Thin-Walled Struct. 2022, 174, 109064. [Google Scholar] [CrossRef]
- Gan, N.; Feng, Y.; Yin, H.; Wen, G.; Wang, D.; Huang, X. Quasi-static axial crushing experiment study of foam-filled CFRP and aluminum alloy thin-walled structures. Compos. Struct. 2016, 157, 303–319. [Google Scholar] [CrossRef]
- Zhang, Y.; Zong, Z.; Liu, Q.; Ma, J.; Wu, Y.; Li, Q. Static and dynamic crushing responses of CFRP sandwich panels filled with different reinforced materials. Mater. Des. 2017, 117, 396–408. [Google Scholar] [CrossRef]
- Sun, G.; Li, S.; Liu, Q.; Li, G.; Li, Q. Experimental study on crashworthiness of empty/aluminum foam/honeycomb-filled CFRP tubes. Compos. Struct. 2016, 152, 969–993. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Z.; Yu, H.; Gong, Z.; Li, Q. Experimental and numerical investigation into the crashworthiness of metal-foam-composite hybrid structures. Compos. Struct. 2019, 209, 535–547. [Google Scholar] [CrossRef]
- Xiao, Y.; Long, H.; Wang, Y.J.; Hu, H.L.; Liu, Y.; Wu, Q.W. Failure modes and energy absorption mechanism of CFRP thin-walled square tubes filled with gradient foam aluminum under axial compression. Mater. Today Commun. 2023, 37, 107569. [Google Scholar] [CrossRef]
- Alia, R.A.; Cantwell, W.J.; Langdon, G.S.; Yuen, S.C.K.; Nurick, G.N. The energy-absorbing characteristics of composite tube-reinforced foam structures. Compos. Part B Eng. 2014, 61, 127–135. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z.; Zhu, G. Structural design of multimaterial columns accounting for multiple loads. Int. J. Mech. Sci. 2022, 227, 107427. [Google Scholar] [CrossRef]
- Yang, C.; Chen, Z.; Yao, S.; Xu, P.; Li, S.; Alqahtani, M.S. Quasi-static and low-velocity axial crushing of polyurethane foam-filled aluminium/CFRP composite tubes: An experimental study. Compos. Struct. 2022, 299, 116083. [Google Scholar] [CrossRef]
- Yang, C.; Chen, Z.; Yao, S.; Xu, P.; Li, S.; Alqahtani, M.S. Parametric study on the crushing performance of a polyurethane foam-filled CFRP/Al composite sandwich structure. Polym. Test. 2022, 108, 107515. [Google Scholar] [CrossRef]
- Jiang, H.; Ji, Y.; Hu, Y.; Hu, X.; Ren, Y. Interfacial design and flexural property of CFRP/aluminum-honeycomb sandwich with Aramid-pulp micro/nano-fiber interlays. Compos. Struct. 2022, 289, 115486. [Google Scholar] [CrossRef]
- Chung, H.J.; Rhee, K.Y.; Lee, B.; Lee, J.H. Effect of oxygen plasma treatment on the bonding strength of CFRP/aluminum foam composite. J. Alloys Compd. 2009, 481, 214–219. [Google Scholar] [CrossRef]
- Ilinzeer, S.; Rupp, P.; Weidenmann, K.A. Influence of corrosion on the mechanical properties of hybrid sandwich structures with CFRP face sheets and aluminum foam core. Compos. Struct. 2018, 202, 142–150. [Google Scholar] [CrossRef]
- Li, Y.; Meng, X.; Xiao, S.; Xu, F. Persistent homology deep meta-transfer learning for intelligent fault diagnosis of storage stacking machinery under high-speed and heavy-load conditions. IEEE Trans. Instrum. Meas. 2024, 74, 3504814. [Google Scholar] [CrossRef]
- Ren, J.; Zhong, J.; Yao, L.; Guan, Z. Experimental Investigation and Theoretical Modelling of a High-Pressure Pneumatic Catapult Considering Dynamic Leakage and Convection. Entropy 2020, 22, 1010. [Google Scholar] [CrossRef]
- Zhong, J.; Zhao, C.; Chen, C.; Lai, W.L.; Wang, Q. Mechanical behaviors of composite auxetic structures under quasi-static compression and dynamic impact. Eur. J. Mech. A-Solids 2025, 109, 105454. [Google Scholar] [CrossRef]
- Huang, J.; Wang, X. Numerical and experimental investigations on the axial crushing response of composite tubes. Compos. Struct. 2009, 91, 222–228. [Google Scholar] [CrossRef]
- Sun, G.; Chen, D.; Zhu, G.; Li, Q. Lightweight hybrid materials and structures for energy absorption: A state-of-the-art review and outlook. Thin-Walled Struct. 2022, 172, 108760. [Google Scholar] [CrossRef]
- Zhao, C.; Meng, Z.; Yi, J.; Chen, C.Q. Auxetic metamaterials with double re-entrant configuration. Int. J. Mech. Sci. 2025, 301, 110505. [Google Scholar] [CrossRef]




| Property | Description | Value |
|---|---|---|
| Density | 1.49 g/cm3 | |
| Young’s modulus in longitudinal (fiber) direction | 142 GPa | |
| Young’s modulus in normal direction (perpendicular to fiber) | 8.12 GPa | |
| Shear modulus in 1–2 plane | 5.95 MPa | |
| v12 | Poisson’s ratio in 1–2 plane | 0.021 |
| Longitudinal tensile strength (fiber direction) | 2.15 GPa | |
| Longitudinal compressive strength (fiber direction) | 1.43 GPa | |
| Transverse tensile strength (perpendicular to fiber) | 50 MPa | |
| Transverse compressive strength (perpendicular to fiber) | 196 MPa | |
| S12 | Shear strength in 1–2 plane | 82.9 MPa |
| Sc | Shear strength of interlaminar interface | 99.7 MPa |
| Aspect Ratio | 9:1 | 8:1 | 7:1 | 6:1 | 5:1 | 4:1 | 3:1 | 2:1 | 1:1 |
|---|---|---|---|---|---|---|---|---|---|
| Crushing Stroke (mm) | 86.00 | 85.90 | 85.79 | 85.65 | 85.45 | 85.14 | 84.69 | 84.08 | 57.09 |
| EA (kJ) | 14.68 | 15.27 | 16.54 | 16.77 | 17.88 | 19.46 | 21.27 | 23.98 | 19.54 |
| SEA (J/g) | 70.23 | 73.15 | 79.30 | 80.57 | 86.13 | 94.10 | 103.45 | 117.29 | 147.05 |
| Relative Density | 0.163 | 0.245 | 0.374 | 0.437 |
|---|---|---|---|---|
| Crushing Stroke (mm) | 88.295 | 87.4755 | 85.4502 | 84.4914 |
| EA (kJ) | 6.32776 | 10.0538 | 17.8818 | 24.8181 |
| SEA (J/g) | 28.3296 | 45.5180 | 86.1259 | 116.6801 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Liu, S.; Wang, J.; Zhao, C. Energy Absorption Characteristics of CFRP–Aluminum Foam Composite Structure Under High-Velocity Impact: Focusing on Varying Aspect Ratios and Relative Densities. Polymers 2025, 17, 2162. https://doi.org/10.3390/polym17152162
Ren J, Liu S, Wang J, Zhao C. Energy Absorption Characteristics of CFRP–Aluminum Foam Composite Structure Under High-Velocity Impact: Focusing on Varying Aspect Ratios and Relative Densities. Polymers. 2025; 17(15):2162. https://doi.org/10.3390/polym17152162
Chicago/Turabian StyleRen, Jie, Shujie Liu, Jiuhe Wang, and Changfang Zhao. 2025. "Energy Absorption Characteristics of CFRP–Aluminum Foam Composite Structure Under High-Velocity Impact: Focusing on Varying Aspect Ratios and Relative Densities" Polymers 17, no. 15: 2162. https://doi.org/10.3390/polym17152162
APA StyleRen, J., Liu, S., Wang, J., & Zhao, C. (2025). Energy Absorption Characteristics of CFRP–Aluminum Foam Composite Structure Under High-Velocity Impact: Focusing on Varying Aspect Ratios and Relative Densities. Polymers, 17(15), 2162. https://doi.org/10.3390/polym17152162







