Comparison of Elastic Modulus Calculations in ASTM D7205 and CSA S806 for CFRP Rebar Under Elevated Temperature
Abstract
1. Introduction
2. Experimental Program
2.1. ASTM and CSA Tensile Test Standard for FRP Rebar
2.2. CFRP Rebar
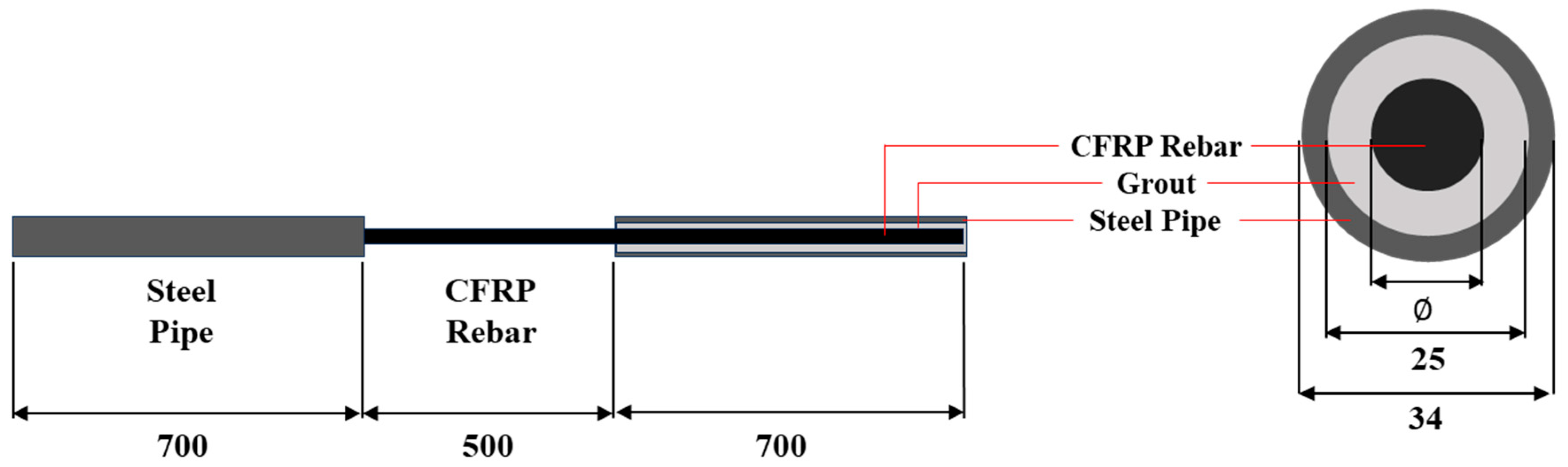
2.3. Test Specimen
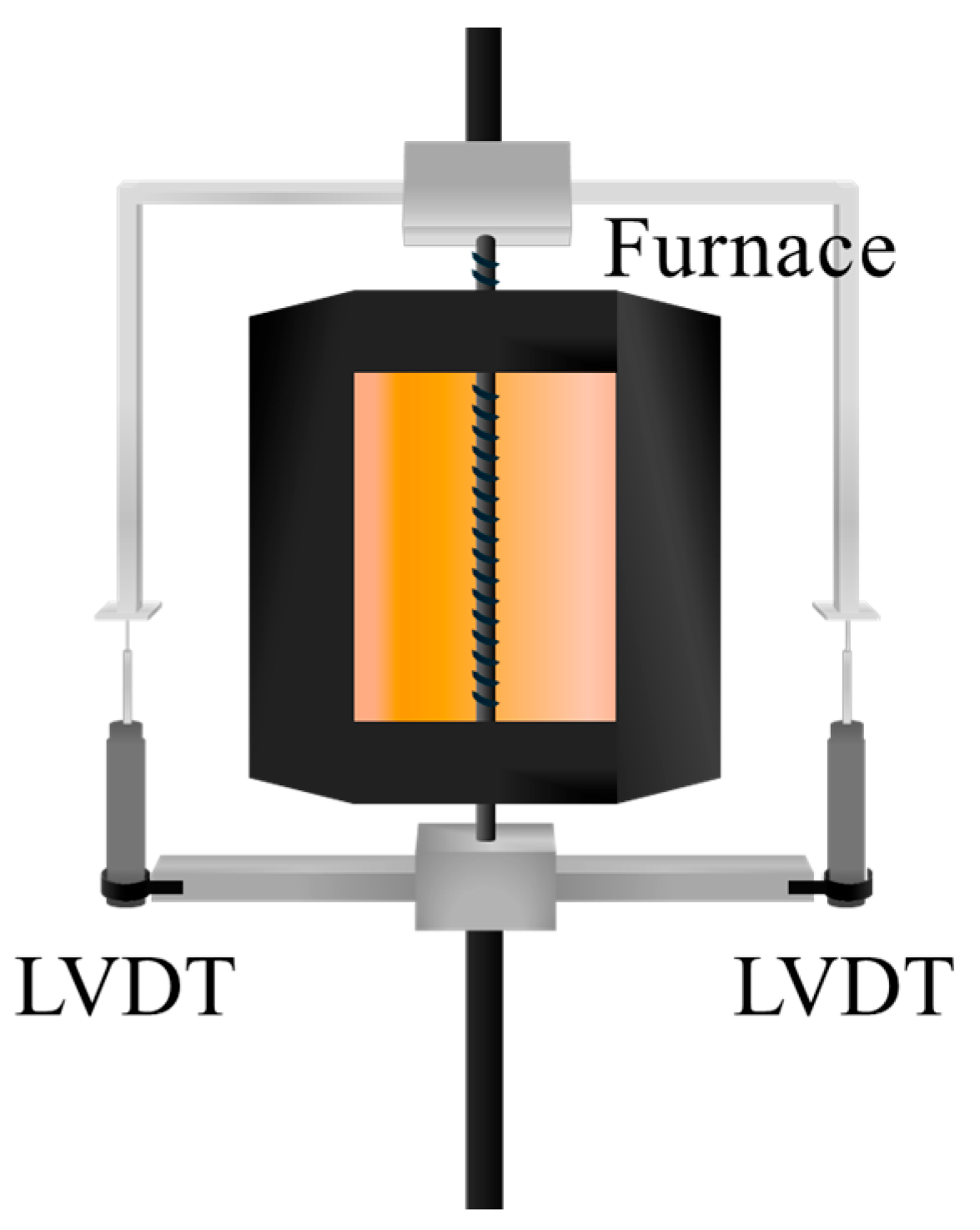
2.4. Test Set Up
3. Results and Discussion
3.1. Test Results
3.1.1. Tensile Strength
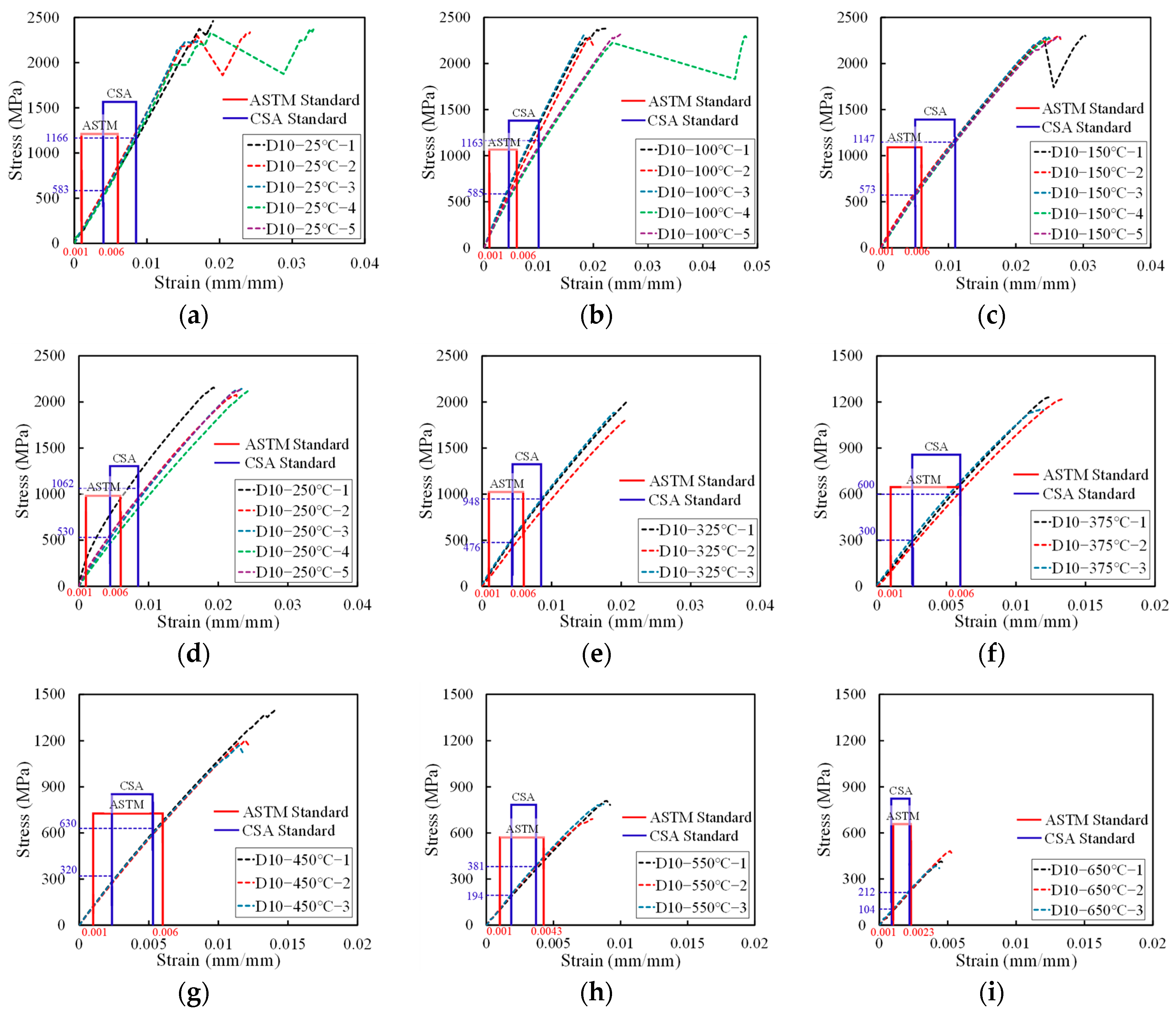
3.1.2. Elastic Modulus
3.1.3. Guaranteed Tensile Strength and Guaranteed Elastic Modulus
3.2. Experimental Equation
4. Conclusions
- The tensile strength and ultimate strain of CFRP bars increased up to 150 °C due to the post-curing effect. However, beyond 300 °C, both tensile strength and ultimate strain decreased sharply as a result of the thermal decomposition of the resin matrix. This degradation is attributed to the diminished stress transfer capability between the fibers and resin caused by resin decomposition at elevated temperatures.
- In the temperature range of 150 °C to 250 °C, which lies between the glass transition temperature (127 °C) and the resin decomposition temperature (300 °C), the elastic modulus exhibited differences of up to 21.9% between values calculated using the CSA and ASTM standards. This discrepancy arises from the presence of a transition point in the stress–strain curve, where the CSA standard incorporates post-transition data, while the ASTM standard considers only the linear pre-transition segment.
- At temperatures below 325 °C, the ASTM standard consistently defined an earlier modulus calculation interval compared to the CSA standard. Consequently, the coefficient of variation (COV) for the CSA-derived modulus values increased up to 23% due to the inclusion of post-transition data, whereas the ASTM-derived COV remained within 10%. Since the CSA standard calculates the elastic modulus based on a narrow interval (25% to 50% of the maximum load), it is less responsive to abrupt changes in the stress–strain behavior under high-temperature conditions. Therefore, further research is required to enhance the applicability of the ASTM-based CSA standard for high-temperature applications.
- Above 375 °C, after the resin fully decomposed, the elastic modulus tended to stabilize as the load-bearing capacity became dominated by the carbon fibers. Under these conditions, the modulus values calculated using both ASTM and CSA standards showed close agreement, indicating that both standards are applicable for assessing CFRP performance at temperatures exceeding 375 °C.
- Strength reduction factors used in design equations, as recommended by ACI 440.1R-15, were evaluated with reference to ASTM D7205 and CSA S806 standards. Both standards indicate that the strength reduction factor decreases as temperature increases, regardless of the reinforcement diameter. This reduction is primarily attributed to the thermal degradation of the epoxy resin at elevated temperatures, which compromises the bond between fibers and matrix, leading to diminished load-bearing capacity.
- Based on the ASTM-derived elastic modulus values, prediction models proposed by the previous studies were evaluated for their predictive accuracy under high-temperature conditions. Among the evaluated models, the model incorporating material parameters such as fiber volume fraction, glass transition temperature (127 °C), and resin decomposition temperature (300 °C) showed the closest agreement with the experimental data, exhibiting the lowest average prediction error. This suggests that incorporating these parameters is effective for predicting the high-temperature modulus degradation of CFRP reinforcements.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Kocaoz, S.; Samaranayake, V.A.; Nanni, A. Tensile characterization of glass FRP bars. Compos. Part B Eng. 2005, 36, 127–134. [Google Scholar] [CrossRef]
- Kim, S.-H.; Choi, W.; Yoon, H.-D. Determination of Mechanical Properties of Sand-Coated Carbon Fiber Reinforced Polymer (CFRP) Rebar. Polymers 2023, 15, 2186. [Google Scholar] [CrossRef]
- Wang, Y.C.; Wong, P.M.H.; Kodur, V. An experimental study of the mechanical properties of fibre reinforced polymer (FRP) and steel reinforcing bars at elevated temperatures. Compos. Struct. 2007, 80, 131–140. [Google Scholar] [CrossRef]
- Najafabadi, E.P.; Hosseini, A.; Haghani, R. The tensile performance of FRP bars embedded in concrete under elevated temperatures. Constr. Build. Mater. 2019, 211, 1138–1152. [Google Scholar] [CrossRef]
- Bazli, M.; Abolfazli, M. Mechanical Properties of Fibre Reinforced Polymers under Elevated Temperatures: An Overview. Polymers 2020, 12, 2600. [Google Scholar] [CrossRef]
- Wang, Y.C.; Kodur, V. Variation of strength and stiffness of fibre reinforced polymer reinforcing bars with temperature. Cem. Concr. Compos. 2005, 27, 864–874. [Google Scholar] [CrossRef]
- Ashrafi, H.; Bazli, M.; Najafabadi, E.P.; Oskouei, A.V. The effect of mechanical and thermal properties of FRP bars on their tensile performance under elevated temperatures. Constr. Build. Mater. 2017, 157, 1001–1010. [Google Scholar] [CrossRef]
- Hamad, R.J.; Johari, M.M.; Haddad, R.H. Mechanical properties and bond characteristics of different fiber-reinforced polymer rebars at elevated temperatures. Constr. Build. Mater. 2017, 142, 521–535. [Google Scholar] [CrossRef]
- Wu, H.; Xu, G.; Ma, M.; Yang, Y.; Xiong, H. Mechanical properties of CFRP bar with different elevated-temperature experiences. Constr. Build. Mater. 2023, 384, 131394. [Google Scholar] [CrossRef]
- Rosa, I.; Matos, A.M.; Costa, I.; Correia, J.R. Experimental study of the tensile behaviour of GFRP reinforcing bars at elevated temperatures. Compos. Struct. 2022, 280, 114844. [Google Scholar] [CrossRef]
- Yu, B.; Kodur, V. Effect of temperature on strength and stiffness properties of near-surface mounted FRP reinforcement. Compos. Part B Eng. 2014, 58, 510–517. [Google Scholar] [CrossRef]
- Zhou, F.; Zhang, J.; Song, S.; Yang, D.; Wang, C. Effect of temperature on material properties of carbon fiber reinforced polymer (CFRP) tendons: Experiments and model assessment. Materials 2019, 12, 1025. [Google Scholar] [CrossRef] [PubMed]
- Benmokrane, B.; Nazair, C.; Seynave, X.; Manalo, A. Comparison between ASTM D7205 and CSA S806 tensile-testing methods for glass fiber–reinforced polymer bars. J. Compos. Constr. 2017, 21, 04017038. [Google Scholar] [CrossRef]
- KS F ISO 10406-1; Fibre-Reinforced Polymer (FRP) Reinforcement of Concrete—Test Methods—Part 1: FRP Bars and Grids. Korean Agency for Technology and Standards (KATS): Eumseong, Republic of Korea, 2017.
- Kang, S.-B.; Kim, S.-H.; Choi, W. Evaluation of Tensile Strength of CFRP Rebar at Elevated Temperatures According to KS Standard. J. Korea Concr. Inst. 2025, 37, 347–354. [Google Scholar] [CrossRef]
- Han, S.; Lee, S.-Y.; Choi, W. Evaluation on the mechanical properties of carbon fiber rebar for substitution of steel rebar. J. Korea Concr. Inst. 2023, 35, 169–175. [Google Scholar] [CrossRef]
- ASTM D7205/D7205M-21; Standard Test Method for Tensile Properties of Fiber Reinforced Polymer Matrix Composite Bars. ASTM International: West Conshohocken, PA, USA, 2021.
- CSA S806-12; Design and Construction of Building Components with Fibre-Reinforced Polymers. Canadian Standards Association: Mississauga, ON, Canada, 2012.
- ACI 440.3R-12; Guide Test Methods for Fiber-Reinforced Polymer (FRP) Composites for Reinforcing or Strengthening Concrete and Masonry Structures. American Concrete Institute (ACI): Farmington Hills, MI, USA, 2012.
- ACI 440.1R-15; Guide for the Design and Construction of Concrete Reinforced with FRP Bars. American Concrete Institute (ACI): Farmington Hills, MI, USA, 2015.
- CSA S807-10; Specification for Fibre-Reinforced Polymers. Canadian Standards Association: Toronto, ON, Canada, 2010.
- Yun, H.-D.; Lee, S.-Y.; Kang, D.-H.; Choi, W. Retention strength of carbon fiber reinforced polymer rebar under elevated temperatures. Sci. Rep. 2025, 15, 17408. [Google Scholar] [CrossRef]
- Spagnuolo, S.; Meda, A.; Rinaldi, Z.; Nanni, A. Residual behaviour of glass FRP bars subjected to high temperatures. Compos. Struct. 2018, 203, 886–893. [Google Scholar] [CrossRef]
- Moon, D.-Y. Critical temperature for inter-laminar shear strength and effect of exposure time of FRP rebars. J. Korea Concr. Inst. 2013, 25, 45–51. [Google Scholar] [CrossRef]
- Achillides, Z.; Pilakoutas, K. Bond behavior of fiber reinforced polymer bars under direct pullout conditions. J. Compos. Constr. 2004, 8, 173–181. [Google Scholar] [CrossRef]
- You, Y.J.; Park, K.T.; Seo, D.W.; Hwang, J.H. Tensile strength of GFRP reinforcing bars with hollow section. Adv. Mater. Sci. Eng. 2015, 1, 621546. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Zhang, J.; Pan, J.; Zhang, L.; Tan, F.; Wei, H.; Zhang, W. High-temperature effect on the tensile mechanical properties of unidirectional carbon fiber-reinforced polymer plates. Materials 2021, 14, 7214. [Google Scholar] [CrossRef] [PubMed]
- Saafi, M. Effect of fire on FRP reinforced concrete members. Compos. Struct. 2002, 58, 11–20. [Google Scholar] [CrossRef]
- Ashrafi, H.; Bazli, M.; Jafari, A.; Ozbakkaloglu, T. Tensile properties of GFRP laminates after exposure to elevated temperatures: Effect of fiber configuration, sample thickness, and time of exposure. Compos. Struct. 2020, 238, 111971. [Google Scholar] [CrossRef]






| Fiber Type | Cross-Sectional Area (mm2) | Fiber Content (%) | Resin Type | Resin Content (%) | Glass Transition Temperature, Tg (°C) | Decomposition Temperature, Td (°C) |
|---|---|---|---|---|---|---|
| Carbon (D10) | 78.5 | 72.8 | Epoxy | 27.2 | 127 | 300 |
| Carbon (D13) | 132.7 | 73.5 | 26.5 |
| ID | Temperature (°C) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 25 | 100 | 150 | 250 | 325 | 375 | 450 | 550 | 650 | |
| D10 CFRP | 5 | 5 | 5 | 5 | 3 | 3 | 3 | 3 | 3 |
| D13 CFRP | 5 | 5 | 5 | 5 | 3 | 3 | 3 | 3 | 3 |
| Total | 70 | ||||||||
| ID | Tensile Strength (MPa) | Avg. Tensile Strength (MPa) | Ultimate Strain (mm/mm) | Avg. Ultimate Strain (mm/mm) |
|---|---|---|---|---|
| D10−25 °C−1 | 2461.3 | 81.6 | 0.018 | 0.0066 |
| D10−25 °C−2 | 2336.3 | 0.024 | ||
| D10−25 °C−3 | 2240.0 | 0.017 | ||
| D10−25 °C−4 | 2367.4 | 0.034 | ||
| D10−25 °C−5 | 2249.3 | 0.016 | ||
| D10−100 °C−1 | 2381.4 | 39.6 | 0.023 | 0.0108 |
| D10−100 °C−2 | 2275.0 | 0.019 | ||
| D10−100 °C−3 | 2362.7 | 0.018 | ||
| D10−100 °C−4 | 2297.4 | 0.048 | ||
| D10−100 °C−5 | 2320.4 | 0.025 | ||
| D10−150 °C−1 | 2312.6 | 14.3 | 0.030 | 0.0019 |
| D10−150 °C−2 | 2302.5 | 0.026 | ||
| D10−150 °C−3 | 2288.1 | 0.025 | ||
| D10−150 °C−4 | 2270.4 | 0.025 | ||
| D10−150 °C−5 | 2289.3 | 0.026 | ||
| D10−250 °C−1 | 2156.1 | 27.1 | 0.019 | 0.0017 |
| D10−250 °C−2 | 2076.9 | 0.023 | ||
| D10−250 °C−3 | 2141.9 | 0.023 | ||
| D10−250 °C−4 | 2116.6 | 0.024 | ||
| D10−250 °C−5 | 2130.7 | 0.023 | ||
| D10−325 °C−1 | 2003.4 | 84.6 | 0.021 | 0.0009 |
| D10−325 °C−2 | 1797.1 | 0.021 | ||
| D10−325 °C−3 | 1883.2 | 0.019 | ||
| D10−375 °C−1 | 1230.7 | 33.8 | 0.013 | 0.0007 |
| D10−375 °C−2 | 1217.6 | 0.013 | ||
| D10−375 °C−3 | 1153.4 | 0.012 | ||
| D10−450 °C−1 | 1400.9 | 101.6 | 0.014 | 0.0012 |
| D10−450 °C−2 | 1204.3 | 0.012 | ||
| D10−450 °C−3 | 1170.3 | 0.012 | ||
| D10−550 °C−1 | 808.5 | 51.4 | 0.009 | 0.0005 |
| D10−550 °C−2 | 690.7 | 0.008 | ||
| D10−550 °C−3 | 787.8 | 0.009 | ||
| D10−650 °C−1 | 414.7 | 41.3 | 0.005 | 0.0004 |
| D10−650 °C−2 | 482.4 | 0.005 | ||
| D10−650 °C−3 | 383.6 | 0.004 |
| ID | Tensile Strength (MPa) | Avg. Tensile Strength (MPa) | Ultimate Strain (mm/mm) | Avg. Ultimate Strain (mm/mm) |
|---|---|---|---|---|
| D13−25 °C−1 | 1690.7 | 1784.4 ± 134.3 | 0.015 | 0.016 ± 0.0025 |
| D13−25 °C−2 | 1579.8 | 0.015 | ||
| D13−25 °C−3 | 1806.7 | 0.014 | ||
| D13−25 °C−4 | 1943.9 | 0.021 | ||
| D13−25 °C−5 | 1900.9 | 0.015 | ||
| D13−100 °C−1 | 1812.9 | 1839.6 ± 20.2 | 0.023 | 0.025 ± 0.0008 |
| D13−100 °C−2 | 1874.7 | 0.025 | ||
| D13−100 °C−3 | 1842.4 | 0.025 | ||
| D13−100 °C−4 | 1830.7 | 0.024 | ||
| D13−100 °C−5 | 1837.4 | 0.025 | ||
| D13−150 °C−1 | 1862.5 | 1814.9 ± 53.4 | 0.037 | 0.029 ± 0.0055 |
| D13−150 °C−2 | 1784.5 | 0.035 | ||
| D13−150 °C−3 | 1791.7 | 0.024 | ||
| D13−150 °C−4 | 1745.4 | 0.026 | ||
| D13−150 °C−5 | 1890.3 | 0.025 | ||
| D13−250 °C−1 | 1801.2 | 1776.3 ± 45.8 | 0.031 | 0.028 ± 0.0027 |
| D13−250 °C−2 | 1719.3 | 0.030 | ||
| D13−250 °C−3 | 1765.0 | 0.024 | ||
| D13−250 °C−4 | 1850.7 | 0.028 | ||
| D13−250 °C−5 | 1745.4 | 0.025 | ||
| D13−325 °C−1 | 1404.5 | 1334.3 ± 54.1 | 0.027 | 0.022 ± 0.004 |
| D13−325 °C−2 | 1273.0 | 0.019 | ||
| D13−325 °C−3 | 1325.4 | 0.020 | ||
| D13−375 °C−1 | 1013.4 | 1038.9 ± 27.1 | 0.015 | 0.015 ± 0.0004 |
| D13−375 °C−2 | 1076.4 | 0.014 | ||
| D13−375 °C−3 | 1026.8 | 0.015 | ||
| D13−450 °C−1 | 1076.4 | 1095.9 ± 14.7 | 0.016 | 0.016 ± 0.001 |
| D13−450 °C−2 | 1099.2 | 0.015 | ||
| D13−450 °C−3 | 1112.0 | 0.017 | ||
| D13−550 °C−1 | 779.9 | 801.0 ± 21.0 | 0.011 | 0.011 ± 0.0004 |
| D13−550 °C−2 | 829.6 | 0.011 | ||
| D13−550 °C−3 | 793.3 | 0.010 | ||
| D13−650 °C−1 | 319.8 | 324.3 ± 18.5 | 0.005 | 0.005 ± 0.0004 |
| D13−650 °C−2 | 304.2 | 0.005 | ||
| D13−650 °C−3 | 348.8 | 0.005 |
| ID | CSA S806 | ASTM D7205 | CSA/ASTM | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Elastic Modulus (GPa) | Avg. (GPa) | SD (GPa) | COV (%) | Elastic Modulus (GPa) | Avg. (GPa) | SD (GPa) | COV (%) | Error (%) | |
| D10−25 °C−1 | 134.6 | 143.4 | 5.7 | 4.0 | 137.8 | 138.1 | 2.1 | 1.6 | 103.8 |
| D10−25 °C−2 | 147.2 | 141.6 | |||||||
| D10−25 °C−3 | 149.8 | 139.0 | |||||||
| D10−25 °C−4 | 146.4 | 135.1 | |||||||
| D10−25 °C−5 | 139.0 | 137.3 | |||||||
| D10−100 °C−1 | 127.9 | 115.7 | 13.4 | 11.5 | 137.6 | 126.3 | 11.3 | 8.9 | 91.6 |
| D10−100 °C−2 | 121.3 | 127.7 | |||||||
| D10−100 °C−3 | 129.8 | 138.9 | |||||||
| D10−100 °C−4 | 98.9 | 109.8 | |||||||
| D10−100 °C−5 | 100.5 | 117.7 | |||||||
| D10−150 °C−1 | 98.3 | 98.7 | 1.3 | 1.3 | 111.8 | 111.1 | 1.8 | 1.7 | 88.8 |
| D10−150 °C−2 | 98.8 | 111.8 | |||||||
| D10−150 °C−3 | 101.0 | 113.9 | |||||||
| D10−150 °C−4 | 98.1 | 109.4 | |||||||
| D10−150 °C−5 | 97.2 | 108.8 | |||||||
| D10−250 °C−1 | 117.2 | 101.9 | 8.2 | 8.1 | 131.8 | 113.2 | 10.5 | 9.2 | 90.0 |
| D10−250 °C−2 | 100.3 | 114.2 | |||||||
| D10−250 °C−3 | 100.9 | 109.7 | |||||||
| D10−250 °C−4 | 92.5 | 99.9 | |||||||
| D10−250 °C−5 | 98.4 | 110.2 | |||||||
| D10−325 °C−1 | 100.5 | 98.9 | 4.0 | 4.0 | 110.0 | 106.3 | 4.9 | 4.6 | 93.0 |
| D10−325 °C−2 | 93.5 | 99.4 | |||||||
| D10−325 °C−3 | 102.8 | 109.5 | |||||||
| D10−375 °C−1 | 108.5 | 106.6 | 3.0 | 2.8 | 111.1 | 108.6 | 3.1 | 2.8 | 98.2 |
| D10−375 °C−2 | 102.3 | 104.2 | |||||||
| D10−375 °C−3 | 109.0 | 110.3 | |||||||
| D10−450 °C−1 | 107.4 | 107.6 | 0.2 | 0.2 | 110.5 | 109.8 | 0.5 | 0.4 | 98.0 |
| D10−450 °C−2 | 107.6 | 109.3 | |||||||
| D10−450 °C−3 | 107.9 | 109.7 | |||||||
| D10−550 °C−1 | 95.3 | 99.8 | 3.2 | 3.2 | 96.3 | 100.5 | 3.0 | 3.0 | 99.3 |
| D10−550 °C−2 | 102.2 | 102.3 | |||||||
| D10−550 °C−3 | 101.9 | 102.9 | |||||||
| D10−650 °C−1 | 99.7 | 99.8 | 0.9 | 0.9 | 99.7 | 99.7 | 0.5 | 0.5 | 100.1 |
| D10−650 °C−2 | 98.8 | 99.1 | |||||||
| D10−650 °C−3 | 101.0 | 100.2 | |||||||
| ID | CSA S806 | ASTM D7205 | CSA/ASTM | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Elastic Modulus (GPa) | Avg. (GPa) | SD (GPa) | COV (%) | Elastic Modulus (GPa) | Avg. (GPa) | SD (GPa) | COV (%) | Error (%) | |
| D13−25 °C−1 | 111.6 | 105.2 | 19.0 | 18.0 | 108.3 | 107.3 | 10.6 | 9.9 | 98.0 |
| D13−25 °C−2 | 97.6 | 96.6 | |||||||
| D13−25 °C−3 | 127.3 | 121.2 | |||||||
| D13−25 °C−4 | 72.5 | 94.1 | |||||||
| D13−25 °C−5 | 117.1 | 116.3 | |||||||
| D13−100 °C−1 | 79.2 | 77.2 | 2.1 | 2.7 | 89.1 | 86.8 | 3.1 | 3.5 | 88.9 |
| D13−100 °C−2 | 79.2 | 90.3 | |||||||
| D13−100 °C−3 | 75.2 | 83.8 | |||||||
| D13−100 °C−4 | 78.1 | 88.3 | |||||||
| D13−100 °C−5 | 74.3 | 82.5 | |||||||
| D13−150 °C−1 | 46.11 | 62.0 | 10.6 | 17.1 | 83.0 | 80.8 | 6.1 | 7.6 | 76.7 |
| D13−150 °C−2 | 53.05 | 69.1 | |||||||
| D13−150 °C−3 | 74.13 | 86.9 | |||||||
| D13−150 °C−4 | 69.25 | 82.0 | |||||||
| D13−150 °C−5 | 67.62 | 83.2 | |||||||
| D13−250 °C−1 | 58.8 | 65.5 | 11.1 | 16.9 | 79.3 | 82.5 | 2.7 | 3.3 | 79.4 |
| D13−250 °C−2 | 49.7 | 82.7 | |||||||
| D13−250 °C−3 | 75.7 | 82.8 | |||||||
| D13−250 °C−4 | 63.3 | 80.6 | |||||||
| D13−250 °C−5 | 79.9 | 87.2 | |||||||
| D13−325 °C−1 | 46.02 | 68.1 | 15.7 | 23.0 | 69.1 | 77.8 | 6.4 | 8.3 | 87.5 |
| D13−325 °C−2 | 77.52 | 79.8 | |||||||
| D13−325 °C−3 | 80.69 | 84.4 | |||||||
| D13−375 °C−1 | 79.3 | 81.3 | 1.4 | 1.7 | 81.3 | 82.7 | 1.4 | 1.7 | 98.3 |
| D13−375 °C−2 | 82.9 | 84.7 | |||||||
| D13−375 °C−3 | 80.7 | 82.2 | |||||||
| D13−450 °C−1 | 83.93 | 82.0 | 1.5 | 1.9 | 85.4 | 83.9 | 1.0 | 1.2 | 97.74 |
| D13−450 °C−2 | 80.15 | 83.5 | |||||||
| D13−450 °C−3 | 81.80 | 82.9 | |||||||
| D13−550 °C−1 | 80.89 | 81.1 | 2.3 | 2.8 | 81.7 | 82.1 | 1.8 | 2.1 | 98.8 |
| D13−550 °C−2 | 78.38 | 80.2 | |||||||
| D13−550 °C−3 | 83.90 | 84.4 | |||||||
| D13−650 °C−1 | 83.40 | 84.9 | 1.2 | 1.4 | 83.2 | 84.9 | 1.3 | 1.5 | 100 |
| D13−650 °C−2 | 86.33 | 86.0 | |||||||
| D13−650 °C−3 | 84.96 | 85.7 | |||||||
| ID | CSA S806 | |||
|---|---|---|---|---|
| Guaranteed Tensile Strength (MPa) | GTS */ATS ** | Guaranteed Elastic Modulus (MPa) | GEM ***/AEM **** | |
| D10−25 °C | 2141.42 | 0.92 | 143.4 | 1.00 |
| D10−100 °C | 2234.29 | 0.96 | 86.3 | 0.75 |
| D10−150 °C | 2258.71 | 0.99 | 98.7 | 1.00 |
| D10−250 °C | 2060.48 | 0.97 | 83.5 | 0.82 |
| D10−325 °C | 1684.02 | 0.89 | 98.9 | 1.00 |
| D10−375 °C | 1115.18 | 0.93 | 106.6 | 1.00 |
| D10−450 °C | 1013.65 | 0.81 | 107.6 | 1.00 |
| D10−550 °C | 636.96 | 0.84 | 99.8 | 1.00 |
| D10−650 °C | 328.75 | 0.77 | 99.8 | 1.00 |
| D13−25 °C | 1481.45 | 0.83 | 65.2 | 0.62 |
| D13−100 °C | 1791.90 | 0.97 | 77.2 | 1.00 |
| D13−150 °C | 1690.47 | 0.93 | 39.5 | 0.64 |
| D13−250 °C | 1669.30 | 0.94 | 42.0 | 0.64 |
| D13−325 °C | 1198.41 | 0.90 | 34.6 | 0.51 |
| D13−375 °C | 970.28 | 0.93 | 81.3 | 1.00 |
| D13−450 °C | 1058.24 | 0.97 | 82.0 | 1.00 |
| D13−550 °C | 747.83 | 0.93 | 81.1 | 1.00 |
| D13−650 °C | 278.76 | 0.86 | 84.9 | 1.00 |
| ID | ASTM D7205 | |||
|---|---|---|---|---|
| Guaranteed Tensile Strength (MPa) | GTS */ATS ** | Guaranteed Elastic Modulus (MPa) | GEM ***/AEM **** | |
| D10−25 °C | 2086 | 0.89 | 138.1 | 1.00 |
| D10−100 °C | 2208.6 | 0.95 | 126.3 | 1.00 |
| D10−150 °C | 2249.7 | 0.98 | 111.1 | 1.00 |
| D10−250 °C | 2043.1 | 0.96 | 113.2 | 1.00 |
| D10−325 °C | 1640.8 | 0.87 | 106.3 | 1.00 |
| D10−375 °C | 1099.2 | 0.92 | 108.6 | 1.00 |
| D10−450 °C | 953.7 | 0.76 | 109.8 | 1.00 |
| D10−550 °C | 608.1 | 0.80 | 100.5 | 1.00 |
| D10−650 °C | 303 | 0.71 | 99.7 | 1.00 |
| D13−25 °C | 1381.5 | 0.77 | 107.3 | 1.00 |
| D13−100 °C | 1779 | 0.97 | 86.8 | 1.00 |
| D13−150 °C | 1654.7 | 0.91 | 80.8 | 1.00 |
| D13−250 °C | 1638.9 | 0.92 | 82.5 | 1.00 |
| D13−325 °C | 1171.1 | 0.88 | 77.8 | 1.00 |
| D13−375 °C | 957.6 | 0.92 | 82.7 | 1.00 |
| D13−450 °C | 1051.8 | 0.96 | 83.9 | 1.00 |
| D13−550 °C | 738 | 0.92 | 82.1 | 1.00 |
| D13−650 °C | 268.8 | 0.83 | 84.9 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, S.-B.; Kang, D.-H.; Choi, W. Comparison of Elastic Modulus Calculations in ASTM D7205 and CSA S806 for CFRP Rebar Under Elevated Temperature. Polymers 2025, 17, 2143. https://doi.org/10.3390/polym17152143
Kang S-B, Kang D-H, Choi W. Comparison of Elastic Modulus Calculations in ASTM D7205 and CSA S806 for CFRP Rebar Under Elevated Temperature. Polymers. 2025; 17(15):2143. https://doi.org/10.3390/polym17152143
Chicago/Turabian StyleKang, Seung-Beom, Dae-Hee Kang, and Wonchang Choi. 2025. "Comparison of Elastic Modulus Calculations in ASTM D7205 and CSA S806 for CFRP Rebar Under Elevated Temperature" Polymers 17, no. 15: 2143. https://doi.org/10.3390/polym17152143
APA StyleKang, S.-B., Kang, D.-H., & Choi, W. (2025). Comparison of Elastic Modulus Calculations in ASTM D7205 and CSA S806 for CFRP Rebar Under Elevated Temperature. Polymers, 17(15), 2143. https://doi.org/10.3390/polym17152143








