Complexation and Thermal Stabilization of Protein–Polyelectrolyte Systems via Experiments and Molecular Simulations: The Poly(acrylic acid)/Lysozyme Case
Abstract
1. Introduction
2. Systems and Methods
2.1. Experimental Details
2.1.1. Materials and Sample Preparation
2.1.2. Static and Dynamic Light Scattering
2.1.3. Fourier Transform Infrared Spectroscopy
2.1.4. Circular Dichroism
2.1.5. Electrophoretic Light Scattering
2.1.6. UV–Visible Spectroscopy
2.2. Simulation Details
3. Results and Discussion
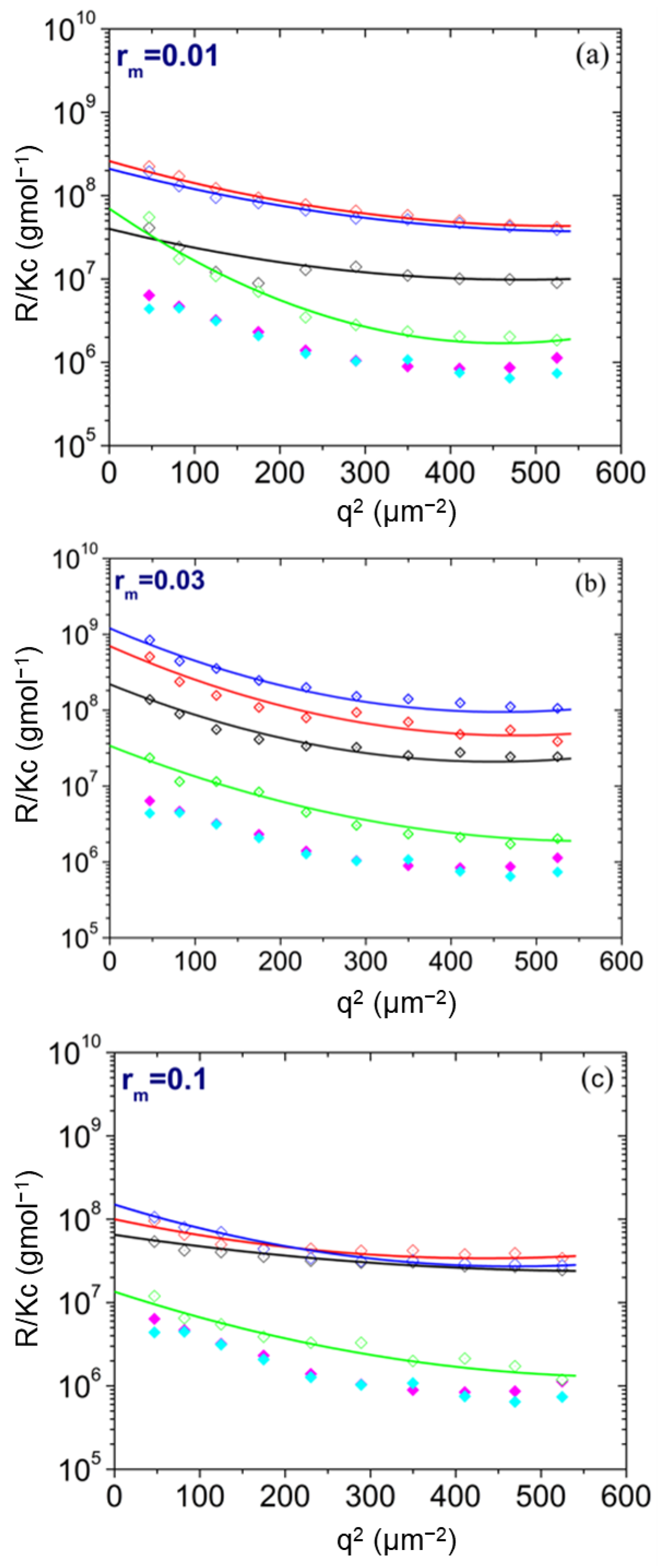
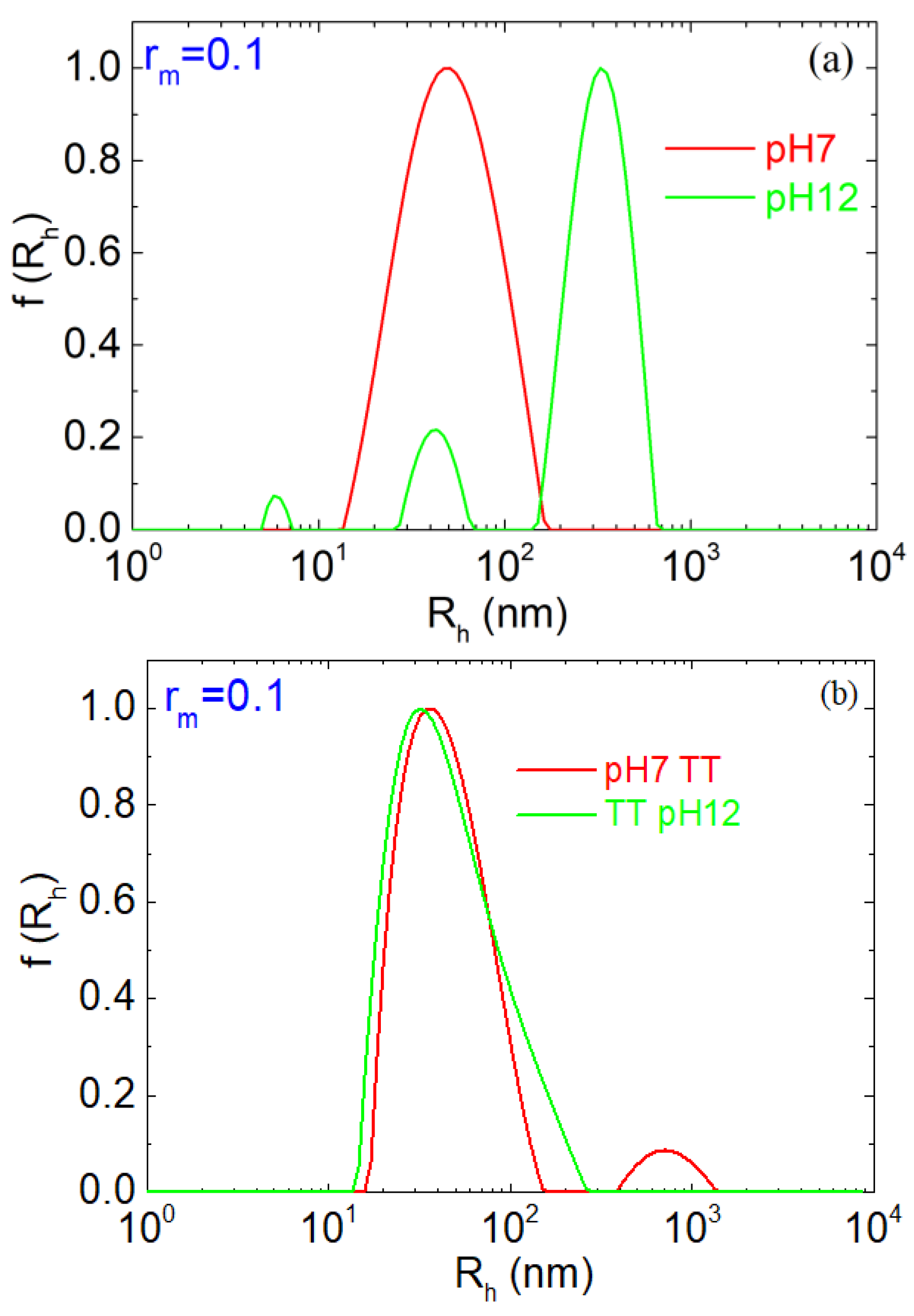
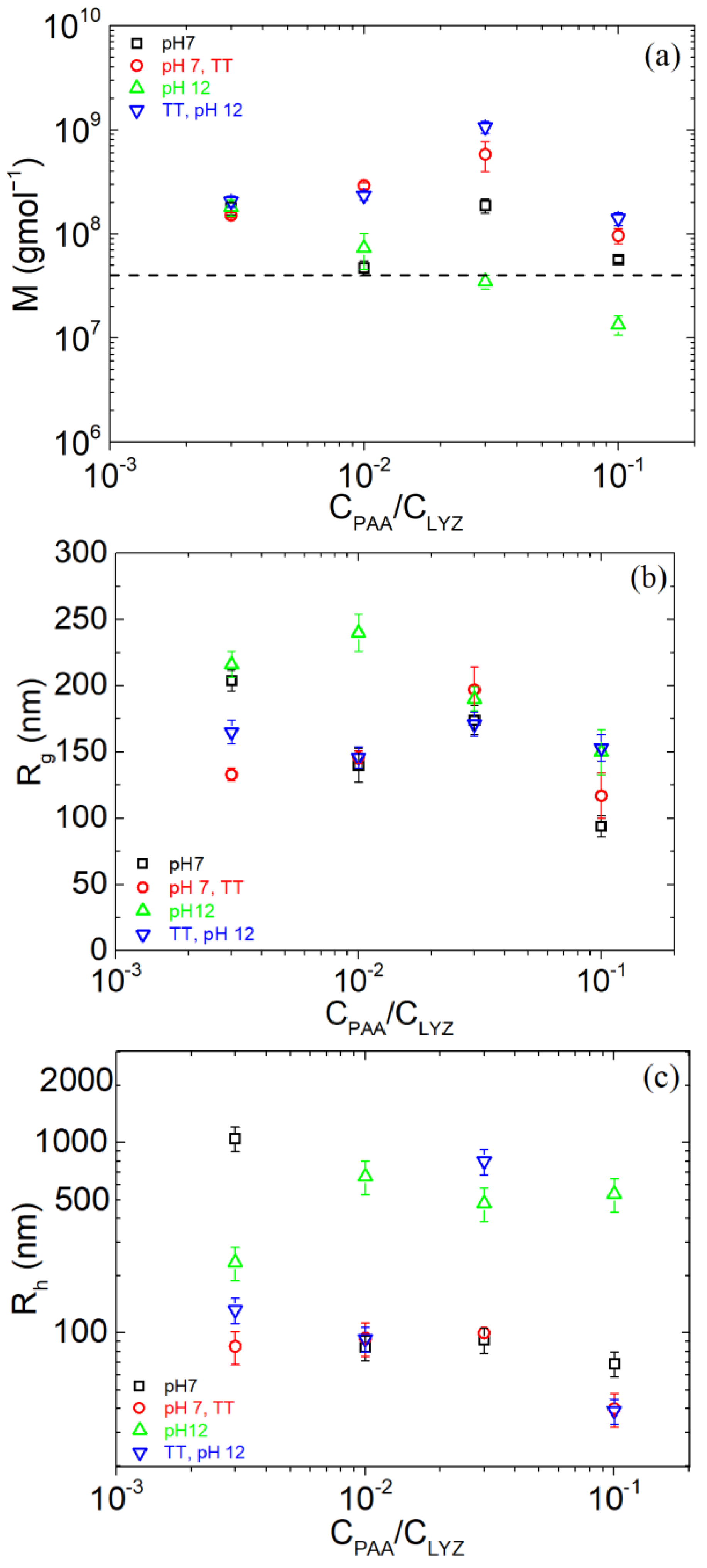
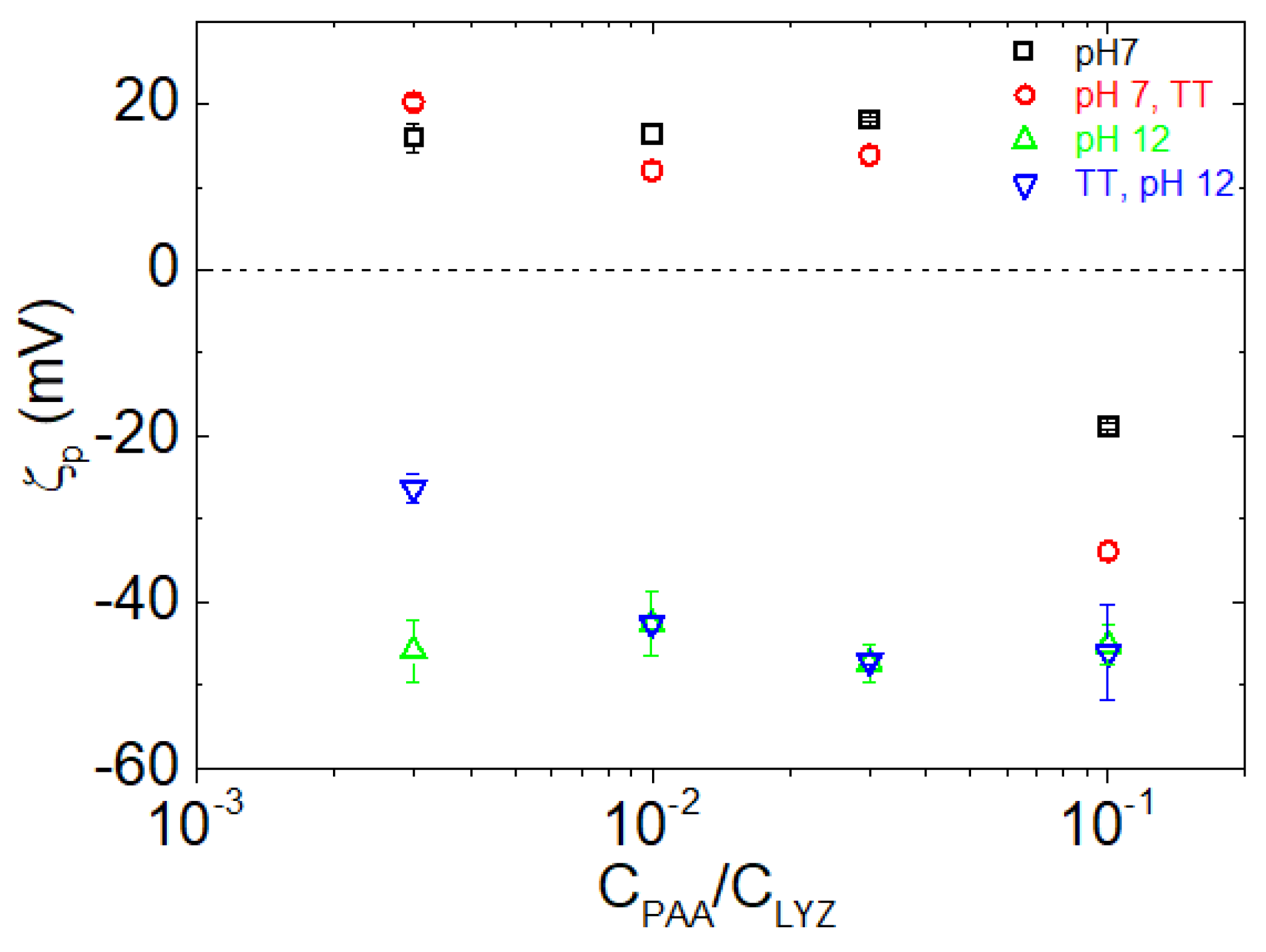
3.1. Experimental Results
3.2. Simulation Results
3.2.1. Post-Simulation Snapshots
3.2.2. Energetic Calculations
3.2.3. Association Rates
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Cooper, C.L.; Dubin, P.L.; Kayitmazer, A.B.; Turksen, S. Polyelectrolyte–Protein Complexes. Curr. Opin. Colloid Interface Sci. 2005, 10, 52–78. [Google Scholar] [CrossRef]
- Gao, S.; Holkar, A.; Srivastava, S. Protein–Polyelectrolyte Complexes and Micellar Assemblies. Polymers 2019, 11, 1097. [Google Scholar] [CrossRef]
- Schmitt, C.; Turgeon, S.L. Protein/Polysaccharide Complexes and Coacervates in Food Systems. Adv. Colloid Interface Sci. 2011, 167, 63–70. [Google Scholar] [CrossRef] [PubMed]
- Black, K.A.; Priftis, D.; Perry, S.L.; Yip, J.; Byun, W.Y.; Tirrell, M. Protein Encapsulation via Polypeptide Complex Coacervation. ACS Macro Lett. 2014, 3, 1088–1091. [Google Scholar] [CrossRef] [PubMed]
- Kučuk, N.; Primožič, M.; Knez, Ž.; Leitgeb, M. Sustainable Biodegradable Biopolymer-Based Nanoparticles for Healthcare Applications. Int. J. Mol. Sci. 2023, 24, 3188. [Google Scholar] [CrossRef]
- Wang, C.; Surat’man, N.E.B.; Chang, J.J.; Ong, Z.L.; Li, B.; Fan, X.; Loh, X.J.; Li, Z. Polyelectrolyte Hydrogels for Tissue Engineering and Regenerative Medicine. Chem. Asian J. 2022, 17, e202200604. [Google Scholar] [CrossRef]
- Dakhara, S.; Anajwala, C. Polyelectrolyte Complex: A Pharmaceutical Review. Syst. Rev. Pharm. 2010, 1, 121. [Google Scholar] [CrossRef]
- Buriuli, M.; Verma, D. Polyelectrolyte Complexes (PECs) for Biomedical Applications. In Advances in Biomaterials for Biomedical Applications; Tripathi, A., Melo, J.S., Eds.; Springer: Singapore, 2017; pp. 45–93. ISBN 978-981-10-3328-5. [Google Scholar]
- Joye, I.J.; McClements, D.J. Biopolymer-Based Nanoparticles and Microparticles: Fabrication, Characterization, and Application. Curr. Opin. Colloid Interface Sci. 2014, 19, 417–427. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Q.; Zhang, Y. Biopolymer-Based Nanotechnology Approaches To Deliver Bioactive Compounds for Food Applications: A Perspective on the Past, Present, and Future. J. Agric. Food Chem. 2020, 68, 12993–13000. [Google Scholar] [CrossRef]
- Vodyashkin, A.; Kezimana, P.; Vetcher, A.; Stanishevskiy, Y. Biopolymeric Nanoparticles–Multifunctional Materials of the Future. Polymers 2022, 14, 2287. [Google Scholar] [CrossRef]
- Kumar, S.S.D.; Rajendran, N.K.; Houreld, N.N.; Abrahamse, H. Recent Advances on Silver Nanoparticle and Biopolymer-Based Biomaterials for Wound Healing Applications. Int. J. Biol. Macromol. 2018, 115, 165–175. [Google Scholar] [CrossRef]
- Vlassi, E.; Papagiannopoulos, A. Nanoformulation of Fibrinogen by Thermal Stabilization of Its Electrostatic Complexes with Hyaluronic Acid. Int. J. Biol. Macromol. 2020, 158, 251–257. [Google Scholar] [CrossRef] [PubMed]
- Kumari, A.; Yadav, S.K.; Yadav, S.C. Biodegradable Polymeric Nanoparticles Based Drug Delivery Systems. Colloids Surf. B Biointerfaces 2010, 75, 1–18. [Google Scholar] [CrossRef]
- Hong, S.; Choi, D.W.; Kim, H.N.; Park, C.G.; Lee, W.; Park, H.H. Protein-Based Nanoparticles as Drug Delivery Systems. Pharmaceutics 2020, 12, 604. [Google Scholar] [CrossRef] [PubMed]
- Lohcharoenkal, W.; Wang, L.; Chen, Y.C.; Rojanasakul, Y. Protein Nanoparticles as Drug Delivery Carriers for Cancer Therapy. BioMed Res. Int. 2014, 2014, 180549. [Google Scholar] [CrossRef] [PubMed]
- Jones, O.G.; McClements, D.J. Functional Biopolymer Particles: Design, Fabrication, and Applications. Compr. Rev. Food Sci. Food Saf. 2010, 9, 374–397. [Google Scholar] [CrossRef]
- Papagiannopoulos, A.; Vlassi, E. Stimuli-Responsive Nanoparticles by Thermal Treatment of Bovine Serum Albumin inside Its Complexes with Chondroitin Sulfate. Food Hydrocoll. 2019, 87, 602–610. [Google Scholar] [CrossRef]
- Blanco, F.G.; Hernández, N.; Rivero-Buceta, V.; Maestro, B.; Sanz, J.M.; Mato, A.; Hernández-Arriaga, A.M.; Prieto, M.A. From Residues to Added-Value Bacterial Biopolymers as Nanomaterials for Biomedical Applications. Nanomaterials 2021, 11, 1492. [Google Scholar] [CrossRef]
- Jacob, J.; Haponiuk, J.T.; Thomas, S.; Gopi, S. Biopolymer Based Nanomaterials in Drug Delivery Systems: A Review. Mater. Today Chem. 2018, 9, 43–55. [Google Scholar] [CrossRef]
- Papagiannopoulos, A.; Sklapani, A.; Tsouko, E.; Spiliopoulos, N. Green Preparation of Nanoparticles with Potential as Nanocarriers for Bioactive Compounds Using the Valorisable Biopolymers Hyaluronic Acid and Hemoglobin. Food Biosci. 2024, 61, 104912. [Google Scholar] [CrossRef]
- Papagiannopoulos, A. Current Research on Polyelectrolyte Nanostructures: From Molecular Interactions to Biomedical Applications. Macromol 2021, 1, 155–172. [Google Scholar] [CrossRef]
- Papagiannopoulos, A.; Selianitis, D.; Chroni, A.; Allwang, J.; Li, Y.; Papadakis, C.M. Preparation of Trypsin-Based Nanoparticles, Colloidal Properties and Ability to Bind Bioactive Compounds. Int. J. Biol. Macromol. 2022, 208, 678–687. [Google Scholar] [CrossRef] [PubMed]
- Lu, R.; Li, W.-W.; Katzir, A.; Raichlin, Y.; Yu, H.-Q.; Mizaikoff, B. Probing the Secondary Structure of Bovine Serum Albumin during Heat-Induced Denaturation Using Mid-Infrared Fiberoptic Sensors. Analyst 2015, 140, 765–770. [Google Scholar] [CrossRef]
- Xu, C.; Yan, Y.; Tan, J.; Yang, D.; Jia, X.; Wang, L.; Xu, Y.; Cao, S.; Sun, S. Biodegradable Nanoparticles of Polyacrylic Acid–Stabilized Amorphous CaCO3 for Tunable pH-Responsive Drug Delivery and Enhanced Tumor Inhibition. Adv. Funct. Mater. 2019, 29, 1808146. [Google Scholar] [CrossRef]
- Rizwan, M.; Yahya, R.; Hassan, A.; Yar, M.; Azzahari, A.; Selvanathan, V.; Sonsudin, F.; Abouloula, C. pH Sensitive Hydrogels in Drug Delivery: Brief History, Properties, Swelling, and Release Mechanism, Material Selection and Applications. Polymers 2017, 9, 137. [Google Scholar] [CrossRef] [PubMed]
- Lesnierowski, G.; Kijowski, J. Lysozyme. In Bioactive Egg Compounds; Huopalahti, R., López-Fandiño, R., Anton, M., Schade, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 33–42. ISBN 978-3-540-37883-9. [Google Scholar]
- Ferraboschi, P.; Ciceri, S.; Grisenti, P. Applications of Lysozyme, an Innate Immune Defense Factor, as an Alternative Antibiotic. Antibiotics 2021, 10, 1534. [Google Scholar] [CrossRef]
- Nawaz, N.; Wen, S.; Wang, F.; Nawaz, S.; Raza, J.; Iftikhar, M.; Usman, M. Lysozyme and Its Application as Antibacterial Agent in Food Industry. Molecules 2022, 27, 6305. [Google Scholar] [CrossRef]
- Wu, T.; Jiang, Q.; Wu, D.; Hu, Y.; Chen, S.; Ding, T.; Ye, X.; Liu, D.; Chen, J. What Is New in Lysozyme Research and Its Application in Food Industry? A Review. Food Chem. 2019, 274, 698–709. [Google Scholar] [CrossRef]
- Bergamo, A.; Sava, G. Lysozyme: A Natural Product with Multiple and Useful Antiviral Properties. Molecules 2024, 29, 652. [Google Scholar] [CrossRef]
- Cousin, F.; Gummel, J.; Combet, S.; Boué, F. The Model Lysozyme–PSSNa System for Electrostatic Complexation: Similarities and Differences with Complex Coacervation. Adv. Colloid Interface Sci. 2011, 167, 71–84. [Google Scholar] [CrossRef]
- Chang, J.-Y.; Li, L. The Unfolding Mechanism and the Disulfide Structures of Denatured Lysozyme. FEBS Lett. 2002, 511, 73–78. [Google Scholar] [CrossRef]
- Xu, W.; Jin, W.; Wang, Y.; Li, J.; Huang, K.; Shah, B.R.; Li, B. Effect of Physical Interactions on Structure of Lysozyme in Presence of Three Kinds of Polysaccharides. J. Food Sci. Technol. 2018, 55, 3056–3064. [Google Scholar] [CrossRef]
- Yang, M.; Dutta, C.; Tiwari, A. Disulfide-Bond Scrambling Promotes Amorphous Aggregates in Lysozyme and Bovine Serum Albumin. J. Phys. Chem. B 2015, 119, 3969–3981. [Google Scholar] [CrossRef] [PubMed]
- Zein, H.F.; Alam, I.; Asanithi, P.; Sutthibutpong, T. Molecular Dynamics Study on the Effects of Charged Amino Acid Distribution Under Low pH Condition to the Unfolding of Hen Egg White Lysozyme and Formation of Beta Strands. PLoS ONE 2021, 17, e0249742. [Google Scholar] [CrossRef]
- Ermakova, E.A.; Makshakova, O.N.; Zuev, Y.F.; Sedov, I.A. Fibril Fragments from the Amyloid Core of Lysozyme: An Accelerated Molecular Dynamics Study. J. Mol. Graph. Model. 2021, 106, 107917. [Google Scholar] [CrossRef] [PubMed]
- Raccosta, S.; Manno, M.; Bulone, D.; Giacomazza, D.; Militello, V.; Martorana, V.; Biagio, P.L.S. Irreversible Gelation of Thermally Unfolded Proteins: Structural and Mechanical Properties of Lysozyme Aggregates. Eur. Biophys. J. 2010, 39, 1007–1017. [Google Scholar] [CrossRef] [PubMed]
- Islam, S.; Shahzadi, Z.; Mukhopadhyay, C. Temperature Dependent Aggregation Mechanism and Pathway of Lysozyme: By All Atom and Coarse Grained Molecular Dynamics Simulation. J. Mol. Graph. Model. 2021, 103, 107816. [Google Scholar] [CrossRef]
- Thermal Inactivation and Aggregation of Lysozyme in the Presence of Nano-TiO2 and Nano-SiO2 in Neutral pH. Available online: https://jns.kashanu.ac.ir/article_5468_871.html (accessed on 19 May 2025).
- Sharma, P.; Verma, N.; Singh, P.K.; Korpole, S.; Ashish. Characterization of Heat Induced Spherulites of Lysozyme Reveals New Insight on Amyloid Initiation. Sci. Rep. 2016, 6, 22475. Available online: https://www.nature.com/articles/srep22475 (accessed on 19 May 2025). [CrossRef]
- Wang, X.; Bowman, J.; Tu, S.; Nykypanchuk, D.; Kuksenok, O.; Minko, S. Polyethylene Glycol Crowder’s Effect on Enzyme Aggregation, Thermal Stability, and Residual Catalytic Activity. Langmuir 2021, 37, 8474–8485. [Google Scholar] [CrossRef]
- Nikfarjam, S.; Ghorbani, M.; Adhikari, S.; Karlsson, A.J.; Jouravleva, E.V.; Woehl, T.J.; Anisimov, M.A. Irreversible Nature of Mesoscopic Aggregates in Lysozyme Solutions. Colloid J. 2019, 81, 546–554. [Google Scholar] [CrossRef]
- Kudou, M.; Shiraki, K.; Fujiwara, S.; Imanaka, T.; Takagi, M. Prevention of Thermal Inactivation and Aggregation of Lysozyme by Polyamines. Eur. J. Biochem. 2003, 270, 4547–4554. [Google Scholar] [CrossRef] [PubMed]
- Kaumbekova, S.; Shah, D. Thermal Stability and Refolding of Hen Egg-White Lysozyme in Aqueous Deep Eutectic Solvent Solutions. J. Mol. Liq. 2023, 389, 122939. [Google Scholar] [CrossRef]
- Huda, M.M.; Adawiyah, R.; Pradana, A.R. Thermodynamic and Conformational Analysis of GTRNase and Lysozyme Proteins Under Thermal Variations Using Molecular Dynamics Simulations. J. Pijar MIPA 2024, 19, 946–953. [Google Scholar] [CrossRef]
- Hao, G.-F.; Xu, W.-F.; Yang, S.-G.; Yang, G.-F. Multiple Simulated Annealing-Molecular Dynamics (MSA-MD) for Conformational Space Search of Peptide and Miniprotein. Sci. Rep. 2015, 5, 15568. [Google Scholar] [CrossRef]
- Wu, H.; Xu, D.; Yang, M.; Zhang, X. Surface Structure of Hydroxyapatite from Simulated Annealing Molecular Dynamics Simulations. Langmuir 2016, 32, 4643–4652. Available online: https://pubs.acs.org/doi/full/10.1021/acs.langmuir.5b04667?casa_token=iuzCoA2kgWAAAAAA%3Ag9EdSf0fLNFs4vr3JdPcytr0vRPuJOdZSczx6lABJH3roZtlm5KpROOCYR7K67uO1mTMO_mboUyQ5w (accessed on 6 May 2025). [CrossRef]
- Sakae, Y.; Hiroyasu, T.; Miki, M.; Okamoto, Y. Protein Structure Predictions by Parallel Simulated Annealing Molecular Dynamics Using Genetic Crossover. J. Comput. Chem. 2011, 32, 1353–1360. [Google Scholar] [CrossRef]
- Masterson, L.R.; Shi, L.; Metcalfe, E.; Gao, J.; Taylor, S.S.; Veglia, G. Dynamically Committed, Uncommitted, and Quenched States Encoded in Protein Kinase A Revealed by NMR Spectroscopy. Proc. Natl. Acad. Sci. USA 2011, 108, 6969–6974. [Google Scholar] [CrossRef]
- Goldberg, J.M.; Batjargal, S.; Petersson, E.J. Thioamides as Fluorescence Quenching Probes: Minimalist Chromophores To Monitor Protein Dynamics. J. Am. Chem. Soc. 2010, 132, 14718–14720. [Google Scholar] [CrossRef]
- Arnittali, M.; Tegopoulos, S.N.; Kyritsis, A.; Harmandaris, V.; Papagiannopoulos, A.; Rissanou, A.N. Exploring the Origins of Association of Poly(Acrylic Acid) Polyelectrolyte with Lysozyme in Aqueous Environment through Molecular Simulations and Experiments. Polymers 2024, 16, 2565. [Google Scholar] [CrossRef]
- Rissanou, A.N.; Ektirici, S.; Harmandaris, V. Investigating the Effects of Ph and Temperature on the Properties of Lysozyme-Polyacrylic Acid Complexes. ACS Omega 2025. [Google Scholar] [CrossRef]
- Borsali, R.; Pecora, R. (Eds.) Soft Matter Characterization; SpringerLink Bücher; Springer: Dordrecht, The Netherlands, 2008; ISBN 978-1-4020-4464-9. [Google Scholar]
- Bruce, J.; Berne; Pecora, R. Dynamic Light Scattering with Applications to Chemistry, Biology, and Physics; John Wiley & Sons, Inc.: Mineola, NY, USA, 2000. [Google Scholar]
- Micsonai, A.; Wien, F.; Kernya, L.; Lee, Y.-H.; Goto, Y.; Réfrégiers, M.; Kardos, J. Accurate Secondary Structure Prediction and Fold Recognition for Circular Dichroism Spectroscopy. Proc. Natl. Acad. Sci. USA 2015, 112, E3095–E3103. [Google Scholar] [CrossRef]
- Corbett, J.C.; McNeil-Watson, F. Electrophoretic Light Scattering. In Encyclopedia of Biophysics; European Biophysical Societies, Roberts, G., Watts, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–10. ISBN 978-3-642-35943-9. [Google Scholar]
- Hunter, R.J.; Ottewill, R.H.; Rowell, R.L. Zeta Potential in Colloid Science: Principles and Applications; Elsevier Science: Burlington, MA, USA, 2013; ISBN 978-1-4832-1408-5. [Google Scholar]
- Ohshima, H. Electrophoretic Mobility of a Spherical Colloidal Particle in a Salt-Free Medium. J. Colloid Interface Sci. 2002, 248, 499–503. [Google Scholar] [CrossRef]
- Sarimov, R.M.; Matveyeva, T.A.; Mozhaeva, V.A.; Kuleshova, A.I.; Ignatova, A.A.; Simakin, A.V. Optical Study of Lysozyme Molecules in Aqueous Solutions after Exposure to Laser-Induced Breakdown. Biomolecules 2022, 12, 1613. [Google Scholar] [CrossRef]
- Swift, T.; Swanson, L.; Geoghegan, M.; Rimmer, S. The pH-Responsive Behaviour of Poly(Acrylic Acid) in Aqueous Solution Is Dependent on Molar Mass. Soft Matter 2016, 12, 2542–2549. [Google Scholar] [CrossRef]
- Lamch, Ł.; Ronka, S.; Moszyńska, I.; Warszyński, P.; Wilk, K.A. Hydrophobically Functionalized Poly(Acrylic Acid) Comprising the Ester-Type Labile Spacer: Synthesis and Self-Organization in Water. Polymers 2020, 12, 1185. [Google Scholar] [CrossRef]
- Harris, J.A.; Liu, R.; Martins De Oliveira, V.; Vázquez-Montelongo, E.A.; Henderson, J.A.; Shen, J. GPU-Accelerated All-Atom Particle-Mesh Ewald Continuous Constant pH Molecular Dynamics in Amber. J. Chem. Theory Comput. 2022, 18, 7510–7527. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a Molecular Dynamics Force Field for Both Folded and Disordered Protein States. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef]
- Carballo-Pacheco, M.; Strodel, B. Comparison of Force Fields for Alzheimer’s A: A Case Study for Intrinsically Disordered Proteins. Protein Sci. 2017, 26, 174–185. [Google Scholar] [CrossRef] [PubMed]
- Petrović, D.; Wang, X.; Strodel, B. How Accurately Do Force Fields Represent Protein Side Chain Ensembles? Proteins 2018, 86, 935–944. [Google Scholar] [CrossRef] [PubMed]
- Jana, K.; Kepp, K.P. Force-Field Benchmarking by Alternatives: A Systematic Study of Ten Small α- and β-Proteins. bioRxiv 2020. [Google Scholar] [CrossRef]
- Somavarapu, A.K.; Kepp, K.P. The Dependence of Amyloid-β Dynamics on Protein Force Fields and Water Models. ChemPhysChem 2015, 16, 3278–3289. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Chatterjee, S.; Debenedetti, P.G.; Stillinger, F.H.; Lynden-Bell, R.M. A Computational Investigation of Thermodynamics, Structure, Dynamics and Solvation Behavior in Modified Water Models. J. Chem. Phys. 2008, 128, 124511. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; Van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Baron, F.; Nau, F.; Guérin-Dubiard, C.; Bonnassie, S.; Gautier, M.; Andrews, S.C.; Jan, S. Egg White versus Salmonella Enteritidis! A Harsh Medium Meets a Resilient Pathogen. Food Microbiol. 2016, 53, 82–93. [Google Scholar] [CrossRef]
- Steudle, A.; Pleiss, J. Modelling of Lysozyme Binding to a Cation Exchange Surface at Atomic Detail: The Role of Flexibility. Biophys. J. 2011, 100, 3016–3024. [Google Scholar] [CrossRef]
- Parmar, A.S.; Muschol, M. Hydration and Hydrodynamic Interactions of Lysozyme: Effects of Chaotropic versus Kosmotropic Ions. Biophys. J. 2009, 97, 590–598. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, S.; Oda, Y.; Ataka, M.; Onuma, K.; Fujiwara, S.; Yonezawa, Y. Denaturation and Aggregation of Hen Egg Lysozyme in Aqueous Ethanol Solution Studied by Dynamic Light Scattering. Biopolymers 2001, 59, 370–379. [Google Scholar] [CrossRef]
- Papagiannopoulos, A.; Sklapani, A. Xanthan-Based Polysaccharide/Protein Nanoparticles: Preparation, Characterization, Encapsulation and Stabilization of Curcumin. Carbohydr. Polym. Technol. Appl. 2021, 2, 100075. [Google Scholar] [CrossRef]
- Fu, K.; Griebenow, K.; Hsieh, L.; Klibanov, A.M.; Langer, R. FTIR characterization of the secondary structure of proteins encapsulated within PLGA microspheres. J. Control. Release Off. J. Control. Release Soc. 1999, 58, 357–366. [Google Scholar] [CrossRef]
- Sadat, A.; Joye, I.J. Peak Fitting Applied to Fourier Transform Infrared and Raman Spectroscopic Analysis of Proteins. Appl. Sci. 2020, 10, 5918. [Google Scholar] [CrossRef]
- Krimm, S.; Bandekar, J. Vibrational Spectroscopy and Conformation of Peptides, Polypeptides, and Proteins. In Advances in Protein Chemistry; Elsevier: Amsterdam, The Netherlands, 1986; Volume 38, pp. 181–364. ISBN 978-0-12-034238-9. [Google Scholar]
- Katti, D.; Vasita, R. Structural and Functional Characterization of Proteins Adsorbed on Hydrophilized Polylactide-Co-Glycolide Microfibers. IJN 2011, 7, 61–71. [Google Scholar] [CrossRef]
- Kong, J.; Yu, S. Fourier Transform Infrared Spectroscopic Analysis of Protein Secondary Structures. ABBS 2007, 39, 549–559. [Google Scholar] [CrossRef]
- DeFlores, L.P.; Ganim, Z.; Nicodemus, R.A.; Tokmakoff, A. Amide I′−II′ 2D IR Spectroscopy Provides Enhanced Protein Secondary Structural Sensitivity. J. Am. Chem. Soc. 2009, 131, 3385–3391. [Google Scholar] [CrossRef] [PubMed]
- Zandomeneghi, G.; Krebs, M.R.H.; McCammon, M.G.; Fändrich, M. FTIR Reveals Structural Differences between Native Β-sheet Proteins and Amyloid Fibrils. Protein Sci. 2004, 13, 3314–3321. [Google Scholar] [CrossRef]

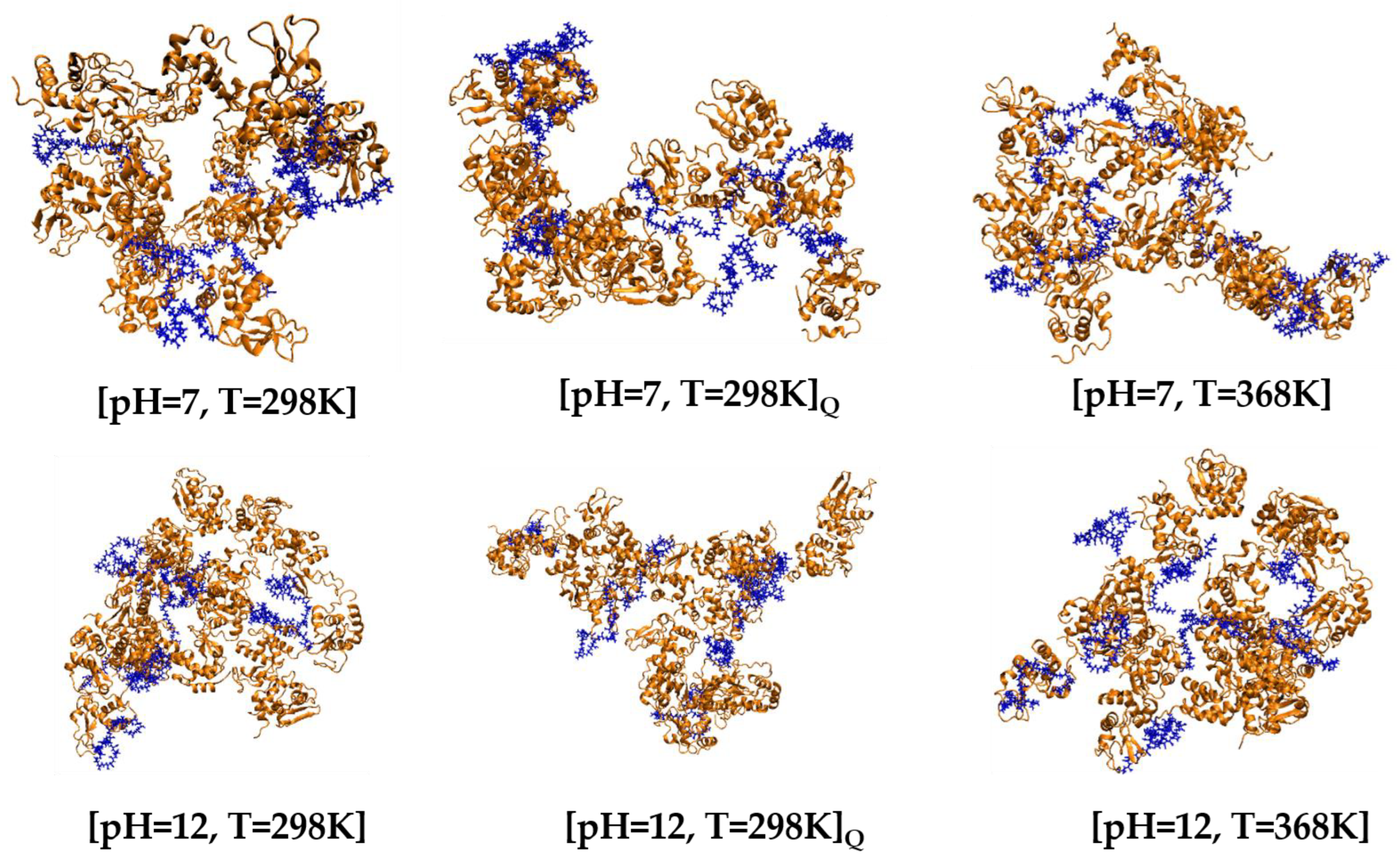
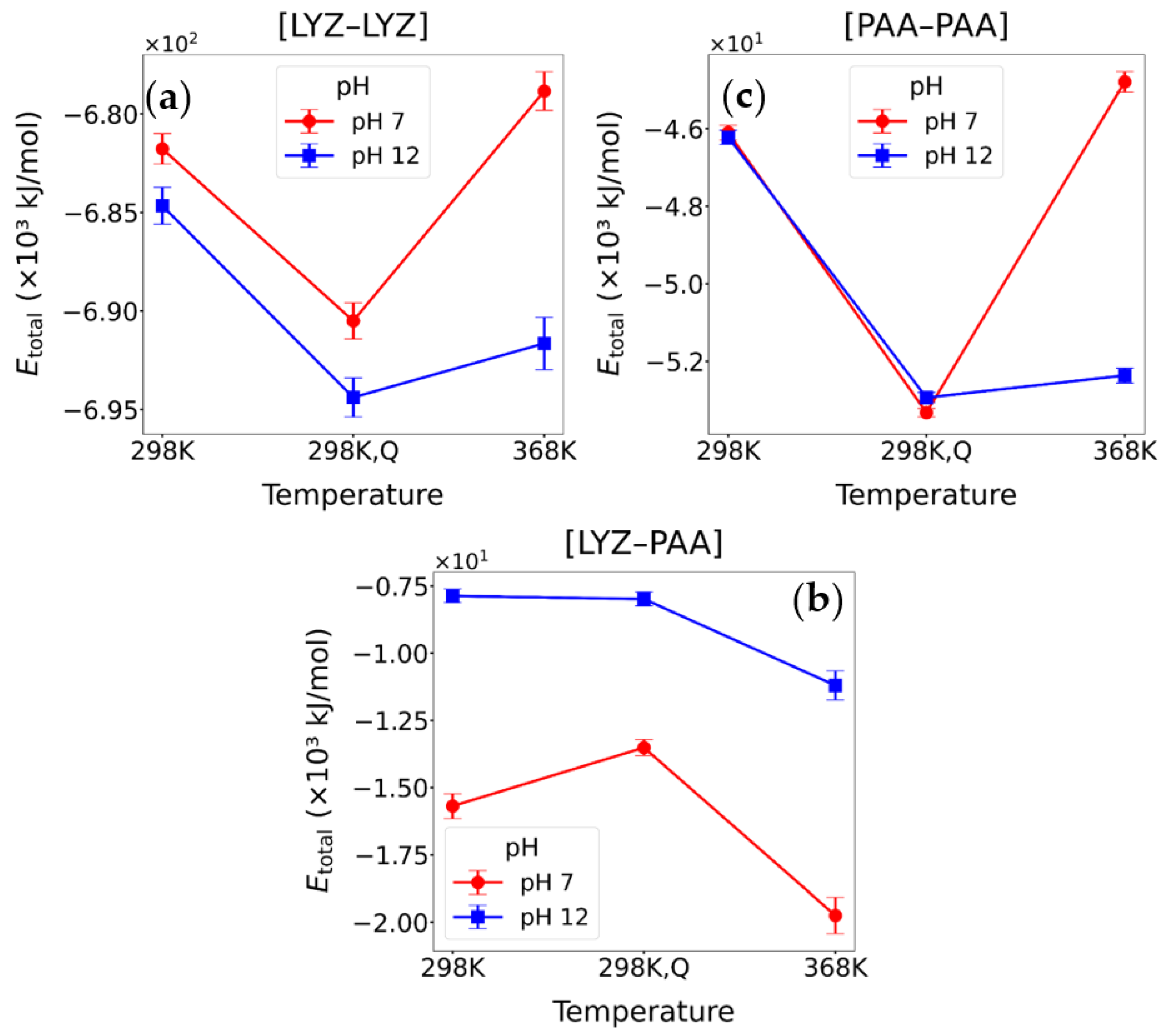
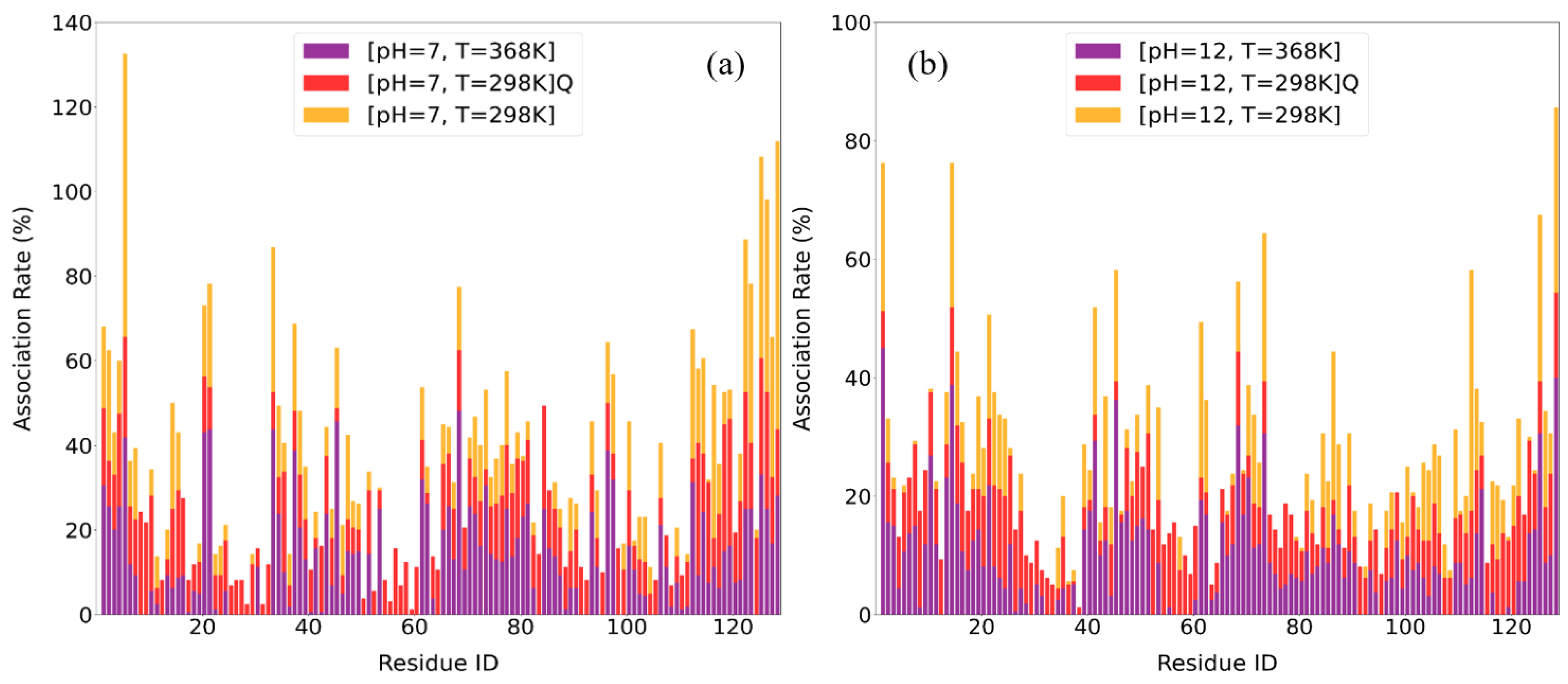

| pH | Total Number of Atoms | Number of Water Atoms | Number of LYZ Atoms | Number of NA Atoms | Number of CL Atoms |
|---|---|---|---|---|---|
| 7 | 403,211 | 368,343 | 31,360 | 402 | 370 |
| 12 | 403,282 | 368,286 | 31,296 | 594 | 370 |
| System | Condition | ΔEsolv | ΔGbinding |
|---|---|---|---|
| [LYZ-PAA] | pH = 7, T = 298 K | 564,909.0 ± 269.2 | −10,291.8 ± 7.9 |
| [LYZ-PAA]Q | pH = 7, T = 298 K | 500,421.5 ± 828.5 | −9364.3 ± 19.3 |
| [LYZ-PAA] | pH = 7, T = 368 K | 576,917.5 ± 748.9 | −11,161.2 ± 15.5 |
| [LYZ-PAA] | pH = 12, T = 298 K | −189,394.4 ± 307.0 | 673.2 ± 5.4 |
| [LYZ-PAA]Q | pH = 12, T = 298 K | −188,468.5 ± 381.4 | 854.7 ± 5.3 |
| [LYZ-PAA] | pH = 12, T = 368 K | −178,359.4 ± 524.9 | 581.2 ± 9.2 |
| System | Conditions | ELJ | ECoul | ETotal |
|---|---|---|---|---|
| [LYZ-LYZ] | pH = 7, T = 298 K | −63,504.9 ± 233.9 | −618,261.5 ± 774.8 | −681,766.4 ± 775.2 |
| [LYZ-LYZ]Q | pH = 7, T = 298 K | −61,795.4 ± 303.0 | −628,704.3 ± 804.1 | −690,499.7 ± 918.6 |
| [LYZ-LYZ] | pH = 7, T = 368 K | −62,750.5 ± 259.5 | −616,088.9 ± 970.3 | −678,839.3 ± 979.1 |
| [LYZ-LYZ] | pH = 12, T = 298 K | −60,626.1 ± 239.1 | −624,033.2 ± 902.2 | −684,659.1 ± 934.7 |
| [LYZ-LYZ]Q | pH = 12, T = 298 K | −58,959.4 ± 271.7 | −635,424.6 ± 914.4 | −694,383.9 ± 986.8 |
| [LYZ-LYZ] | pH = 12, T = 368 K | −56,963.7 ± 399.4 | −634,682.5 ± 1206.5 | −691,646.2 ± 1329.1 |
| [LYZ-PAA] | pH = 7, T = 298 K | −2506.5 ± 95.5 | −13,183.4 ± 442.7 | −15,689.9 ± 463.3 |
| [LYZ-PAA]Q | pH = 7, T = 298 K | −2989.4 ± 88.2 | −10,526.1 ± 302.4 | −13,515.5 ± 299.5 |
| [LYZ-PAA] | pH = 7, T = 368 K | −3295.8 ± 118.8 | −16,453.1 ± 653.8 | −19,748.9 ± 674.4 |
| [LYZ-PAA] | pH = 12, T = 298 K | −1517.8 ± 116.1 | −6351.9 ± 241.1 | −7869.7 ± 251.9 |
| [LYZ-PAA]Q | pH = 12, T = 298 K | −2253.9 ± 83.8 | −5731.5 ± 255.2 | −7985.5 ± 260.5 |
| [LYZ-PAA] | pH = 12, T = 368 K | −2535.5 ± 116.4 | −8665.1 ± 514.8 | −11,200.6 ± 541.3 |
| [PAA-PAA] | pH = 7, T = 298 K | −2325.1 ± 48.1 | −43,775.7 ± 190.7 | −46,100.7 ± 190.2 |
| [PAA-PAA]Q | pH = 7, T = 298 K | −2184.6 ± 55.8 | −51,141.2 ± 99.3 | −53,325.8 ± 107.1 |
| [PAA-PAA] | pH = 7, T = 368 K | −2154.1 ± 61.8 | −42,635.4 ± 257.5 | −44,789.5 ± 260.1 |
| [PAA-PAA] | pH = 12, T = 298 K | −2494.9 ± 64.9 | −43,724.1 ± 198.1 | −46,218.9 ± 183.8 |
| [PAA-PAA]Q | pH = 12, T = 298 K | −2422.3 ± 55.5 | −50,515.9 ± 125.9 | −52,938.3 ± 129.7 |
| [PAA-PAA] | pH = 12, T = 368 K | −2638.5 ± 73.4 | −49,728.6 ± 180.3 | −52,367.2 ± 189.2 |
| Condition | [LYZ-LYZ] | [LYZ-W] | [LYZ-PAA] | [PAA-PAA] | [PAA-W] |
|---|---|---|---|---|---|
| [pH = 7, T = 298 K] | 102.5 ± 1.2 | 259.7 ± 2.2 | 11.6 ± 0.5 | 1.4 ± 0.3 | 108.1 ± 2.4 |
| [pH = 7, T = 298 K]Q | 101.2 ± 1.2 | 259.2 ± 2.2 | 12.2 ± 0.5 | 1.3 ± 0.3 | 105.5 ± 2.2 |
| [pH = 7, T = 368 K] | 98.1 ± 1.3 | 231.1 ± 2.4 | 14.1 ± 0.7 | 1.3 ± 0.3 | 86.8 ± 2.5 |
| [pH = 12, T = 298 K] | 99.2 ± 1.2 | 268.6 ± 2.4 | 7.6 ± 0.4 | 1.4 ± 0.3 | 109.5 ± 2.6 |
| [pH = 12, T = 298 K]Q | 98.6 ± 1.3 | 268.2 ± 2.7 | 7.4 ± 0.4 | 1.5 ± 0.3 | 104.5 ± 2.7 |
| [pH = 12, T = 368 K] | 95.8 ± 1.6 | 232.3 ± 3.2 | 10.1 ± 0.6 | 1.8 ± 0.4 | 81.5 ± 2.7 |
| Condition | Top 10 Residues with Highest Association Rates |
|---|---|
| [pH = 7, T = 298 K] | ARG5, ARG128, ARG125, TRP123, GLY126, LYS33, ALA122, CYS127, ARG112, LYS116 |
| [pH = 7, T = 298 K]Q | ASN113, THR118, ASP119, ALA122, ARG125, GLY126, LEU129, LEU8, LEU84, ARG5 |
| [pH = 7, T = 368 K] | ARG21, ARG45, ARG68, ARG5, TYR20, LYS33, LYS96, ASN37, ARG125, LYS1 |
| [pH = 12, T = 298 K] | ARG112, ARG128, LYS1, ARG14, ARG61, SER86, ARG125, ASN19, ARG21, GLN41 |
| [pH = 12, T = 298 K]Q | LEU 129, LEU8, THR51, SER24, LEU56, TRP123, GLY16, TYR23, LEU25, VAL120 |
| [pH = 12, T = 368 K] | LYS1, ARG14, ARG45, ARG128, ARG68, ARG125, ALA10, LYS13, GLN41, ARG73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tegopoulos, S.N.; Ektirici, S.; Harmandaris, V.; Kyritsis, A.; Rissanou, A.N.; Papagiannopoulos, A. Complexation and Thermal Stabilization of Protein–Polyelectrolyte Systems via Experiments and Molecular Simulations: The Poly(acrylic acid)/Lysozyme Case. Polymers 2025, 17, 2125. https://doi.org/10.3390/polym17152125
Tegopoulos SN, Ektirici S, Harmandaris V, Kyritsis A, Rissanou AN, Papagiannopoulos A. Complexation and Thermal Stabilization of Protein–Polyelectrolyte Systems via Experiments and Molecular Simulations: The Poly(acrylic acid)/Lysozyme Case. Polymers. 2025; 17(15):2125. https://doi.org/10.3390/polym17152125
Chicago/Turabian StyleTegopoulos, Sokratis N., Sisem Ektirici, Vagelis Harmandaris, Apostolos Kyritsis, Anastassia N. Rissanou, and Aristeidis Papagiannopoulos. 2025. "Complexation and Thermal Stabilization of Protein–Polyelectrolyte Systems via Experiments and Molecular Simulations: The Poly(acrylic acid)/Lysozyme Case" Polymers 17, no. 15: 2125. https://doi.org/10.3390/polym17152125
APA StyleTegopoulos, S. N., Ektirici, S., Harmandaris, V., Kyritsis, A., Rissanou, A. N., & Papagiannopoulos, A. (2025). Complexation and Thermal Stabilization of Protein–Polyelectrolyte Systems via Experiments and Molecular Simulations: The Poly(acrylic acid)/Lysozyme Case. Polymers, 17(15), 2125. https://doi.org/10.3390/polym17152125











