Recrystallization During Annealing of Low-Density Polyethylene Non-Woven Fabric by Melt Electrospinning
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
2.3. Characterization
2.3.1. DSC
2.3.2. SAXS
2.3.3. Scanning Electron Microscopy (SEM)
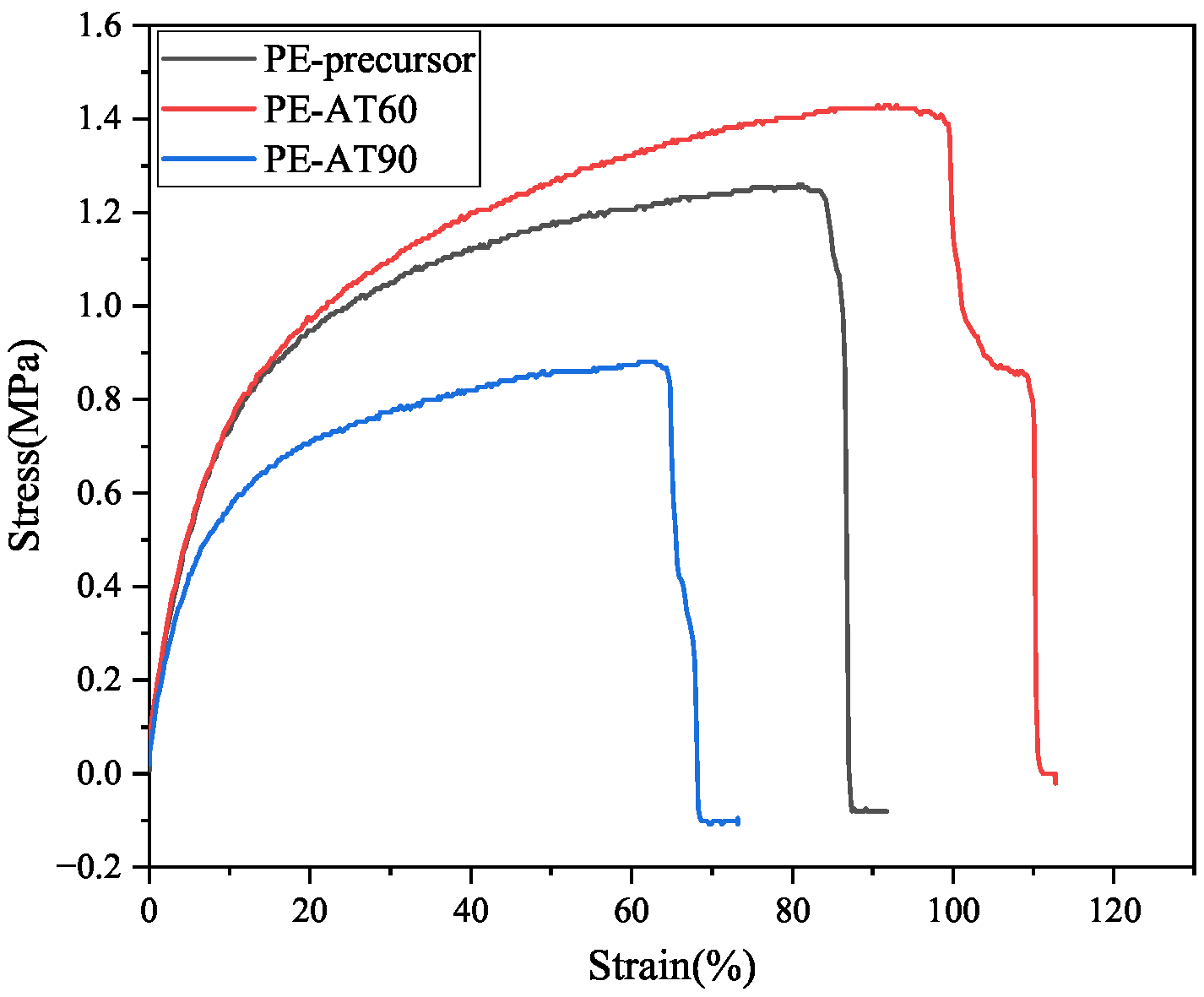
2.3.4. Tensile Properties
3. Results and Discussion
3.1. Morphology of LDPE Fibers in Non-Woven Fabric
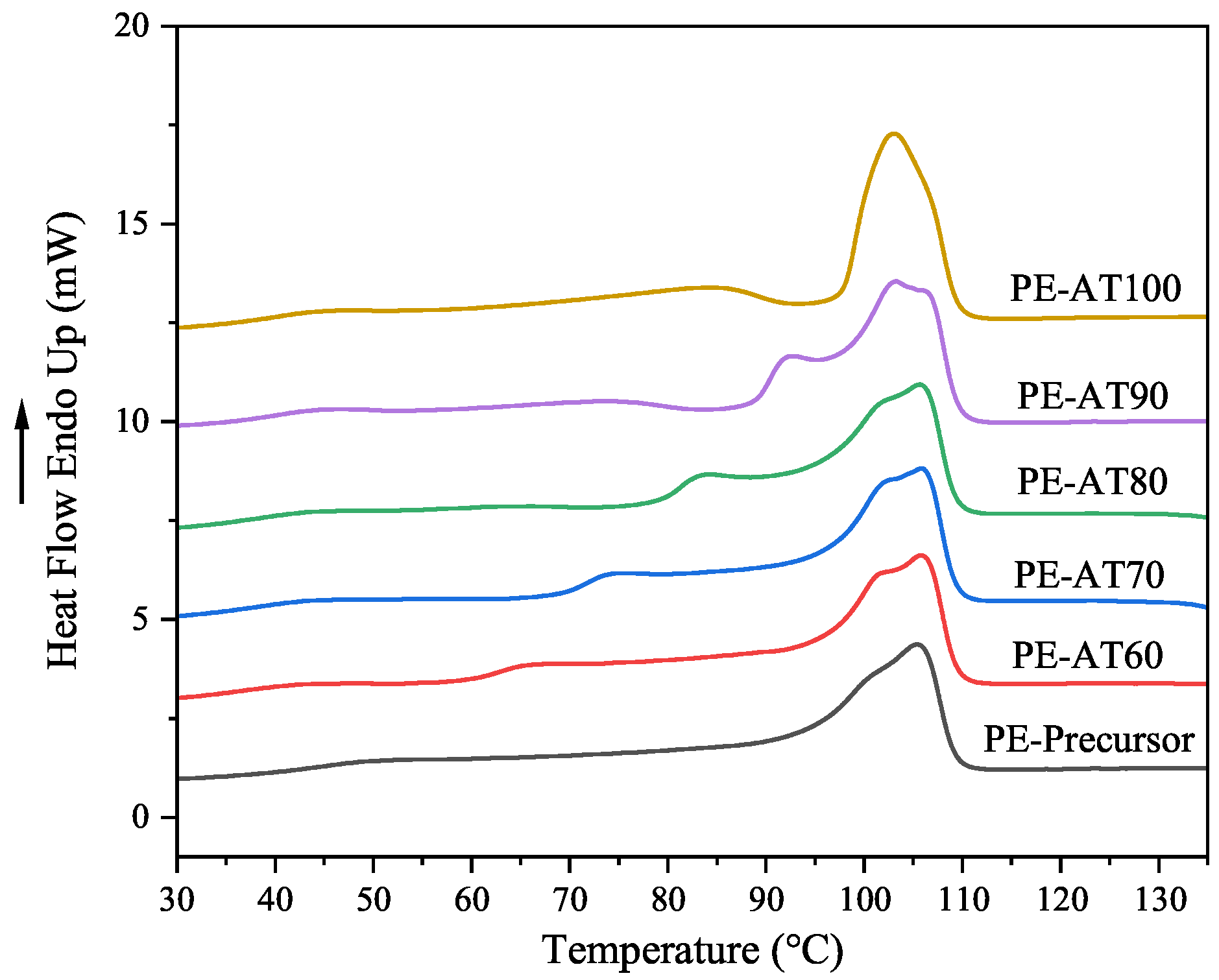
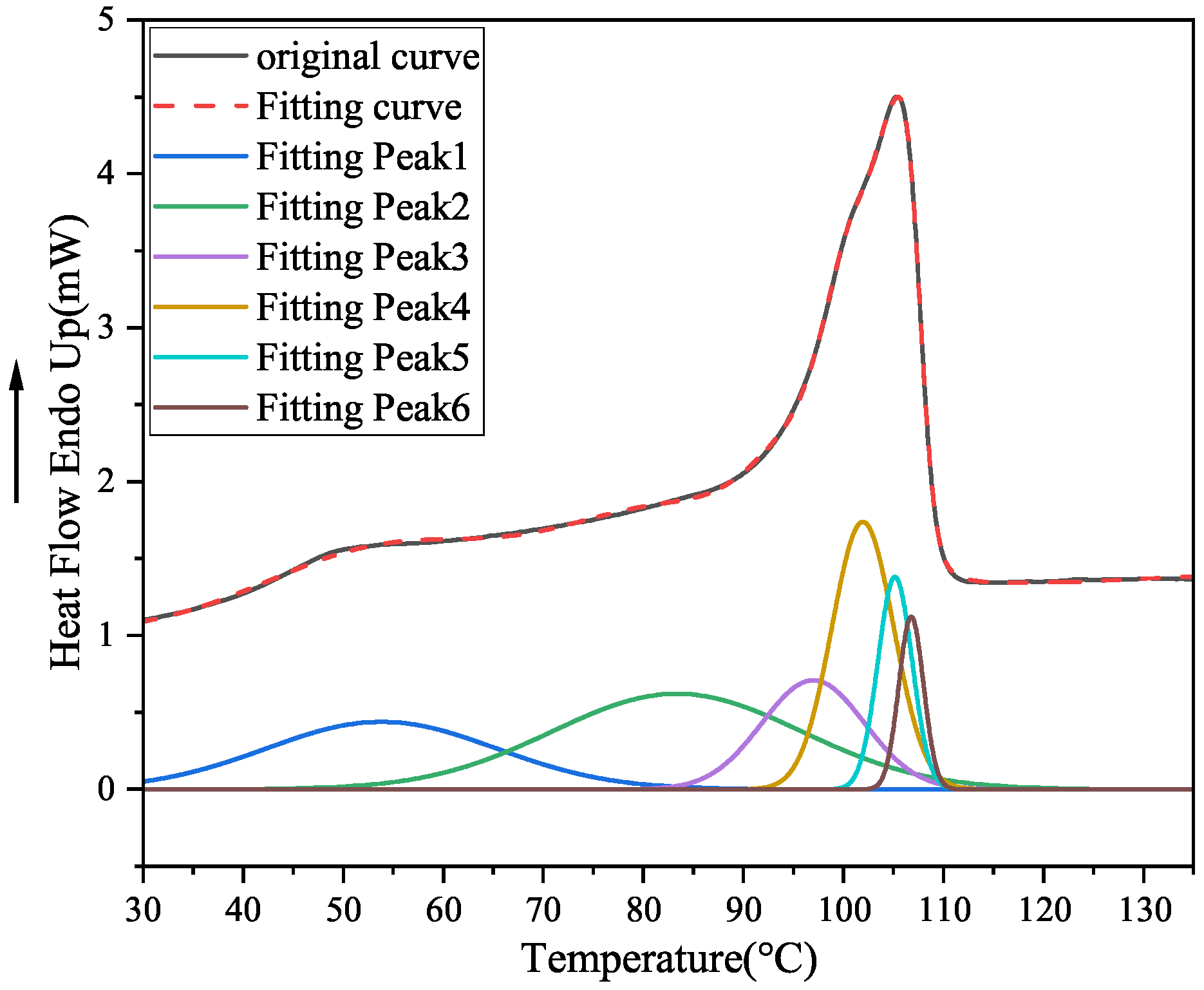
3.2. Changes in Thermodynamic Behavior of LDPE Non-Woven Fabric During Annealing
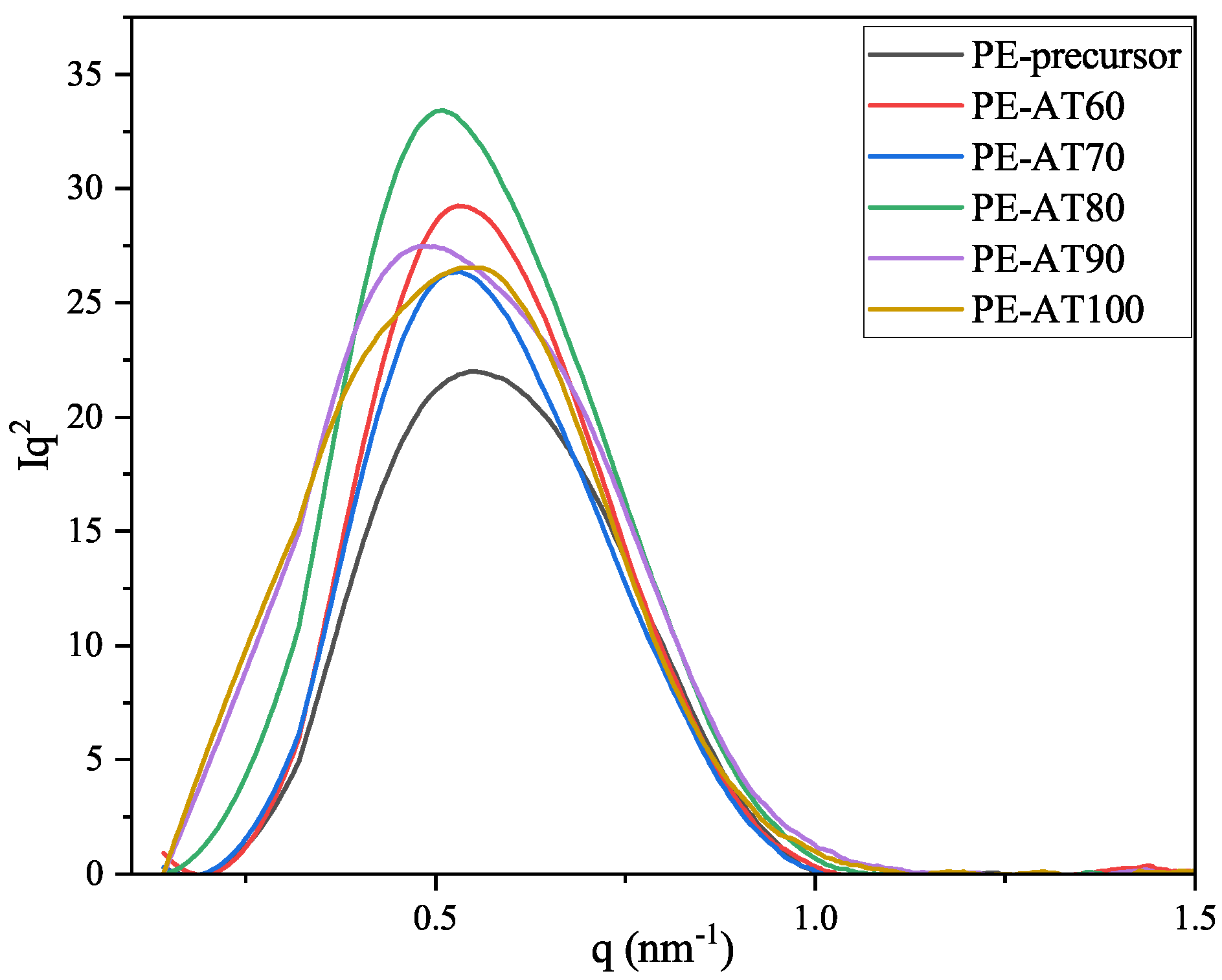
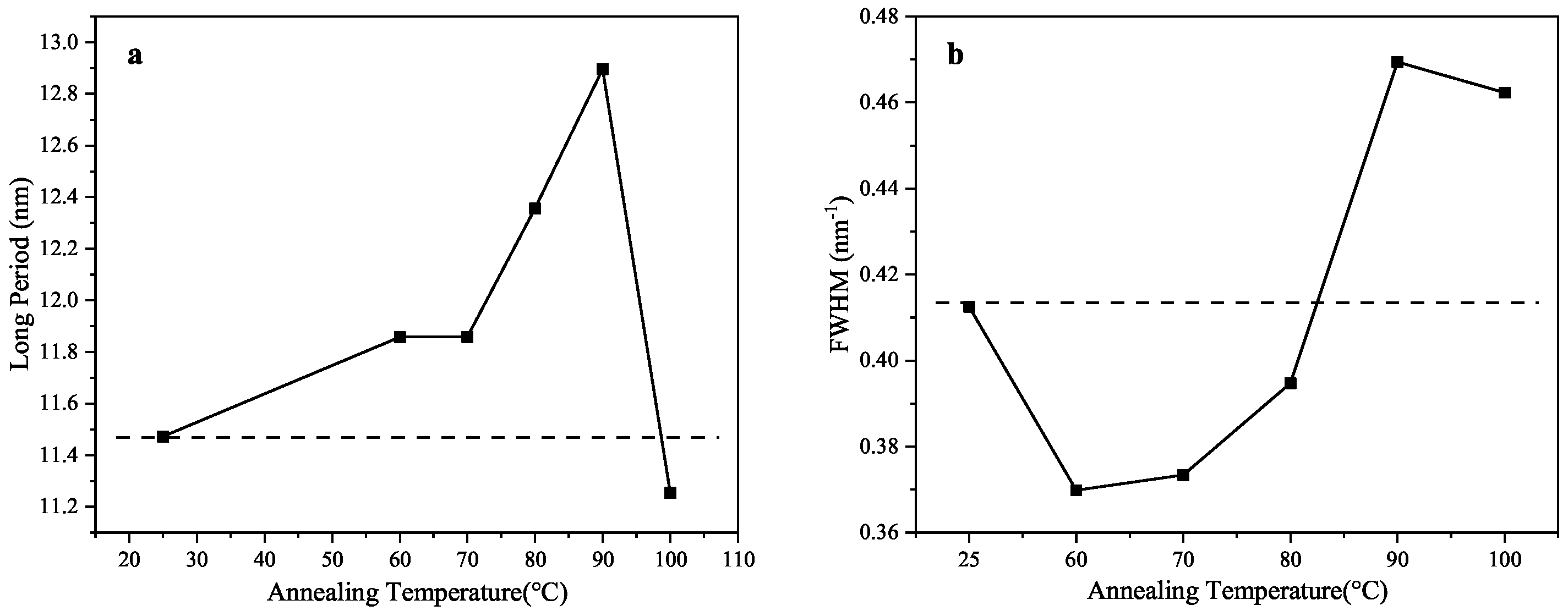
3.3. Variations in Microstructure, Including Crystalline Phase and Amorphous Phase, of LDPE During Annealing
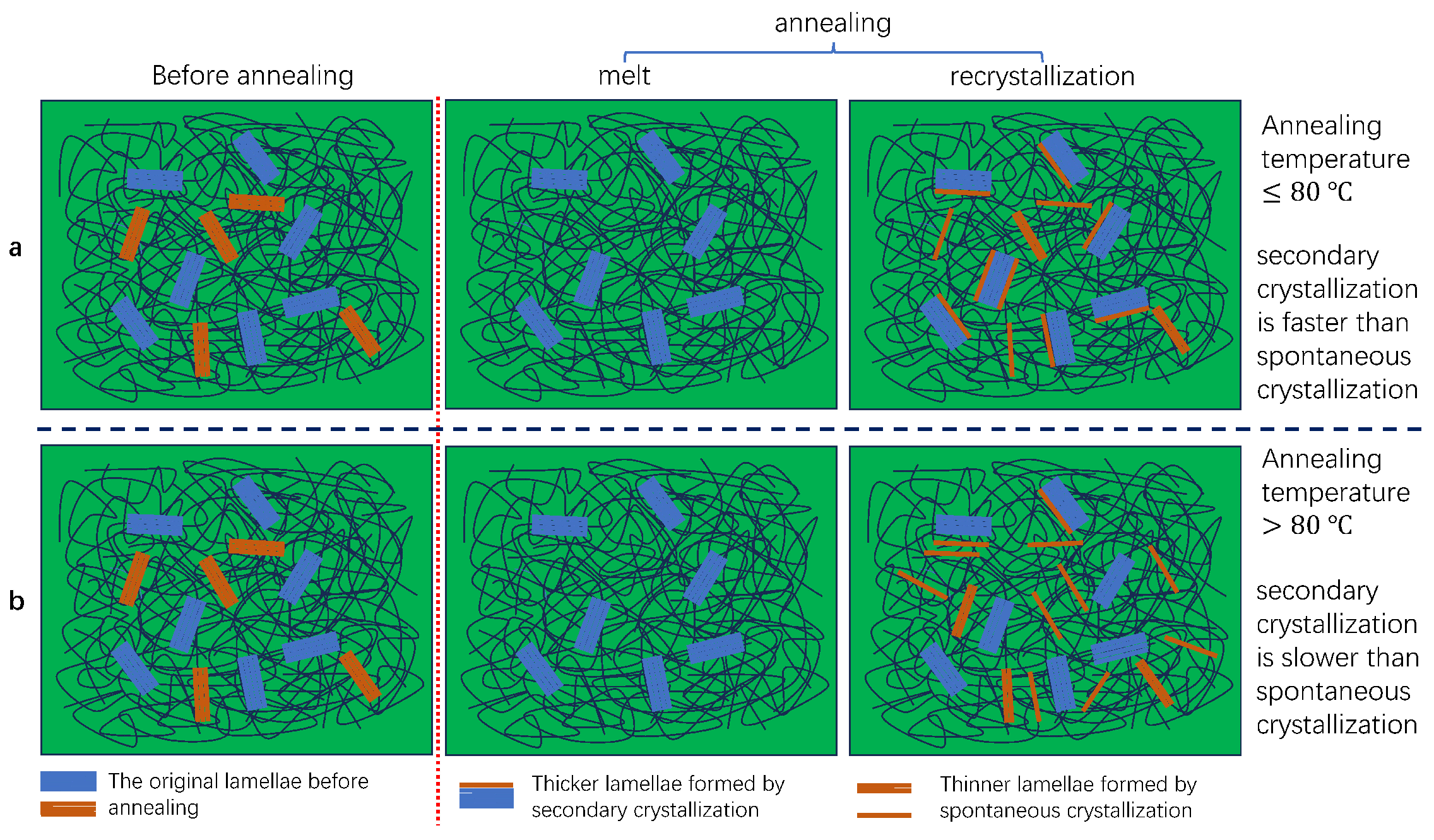
3.4. Discussion of Theoretical Mechanism for Microstructural Changes in LDPE During Annealing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, M.; Dong, R.H.; Yan, X.; Yu, G.F.; You, M.H.; Ning, X.; Long, Y.Z. Recent Advances in Needleless Electrospinning of Ultrathin Fibers: From Academia to Industrial Production. Macromol. Mater. Eng. 2017, 302, 1700002. [Google Scholar] [CrossRef]
- Frenot, A.; Chronakis, I.S. Polymer nanofibers assembled by electrospinning. Curr. Opin. Colloid Interface Sci. 2003, 8, 64–75. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, Y.; Deng, H.; Lyu, T.; Tan, J.; Yang, W.; Li, H.; Ramakrishna, S. Melt differential electrospinning of polyphenylene sulfide nanofibers for flue gas filtration. Polym. Eng. Sci. 2020, 60, 2887–2894. [Google Scholar] [CrossRef]
- Deng, R.J.; Liu, Y.; Ding, Y.M.; Yang, W.M. Investigation on producing micro-nano fibers by melt electrospinning. Mater. Sci. Technol. 2010, 18, 425 428+433. [Google Scholar]
- Huang, W.; Zhang, Y.; Chen, B.; Yang, H.; Shen, K.; Gao, X.; Fu, Q. The effect of annealing time on morphology, mechanical properties, and thermal conductivity of HDPE pipes produced by rotational shear. Mater. Today Commun. 2022, 31, 103321. [Google Scholar] [CrossRef]
- Sánchez González, C.; Pérez Jiménez, A.; Malvé, M.; Díaz Jiménez, C. Effect of Annealing on the Mechanical Properties of Composites of PLA Mixed with Mg and with HA. Polymers 2025, 17, 1207. [Google Scholar] [CrossRef]
- Lam, R.; Geil, P.H. Single Crystals of Linear Polyethylene Crystallized from the Glass. Science 1979, 205, 1388–1389. [Google Scholar] [CrossRef]
- Maxwell, A.S.; Unwin, A.P.; Ward, I.M. The effect of high pressure annealing on the molecular network in polyethylene. Polymer 1996, 37, 3293–3301. [Google Scholar] [CrossRef]
- Bai, S.J.; Huang, Y.F.; Wu, C.C.; Young, T.F. Molecular configuration of thermally annealed polyethylene studied by small-angle neutron scattering. Phys. Chem. Solids 1999, 60, 1337–1341. [Google Scholar] [CrossRef]
- Tiemprateeb, S.; Hemachandra, K.; Suwanprateeb, J. A comparison of degree of properties enhancement produced by thermal annealing between polyethylene and calcium carbonate–polyethylene composites. Polym. Test. 2000, 19, 329–339. [Google Scholar] [CrossRef]
- Lu, P.; He, T. Annealing behavior of ultrahigh molecular weight polyethylene investigated by confocal micro-Raman spectroscopy combined with two-dimensional correlation spectroscopy. Int. J. Polym. Anal. Charact. 2017, 22, 17–26. [Google Scholar] [CrossRef]
- Minoda, Y.; Hata, K.; Goto, K.; Itohara, T.; Nakamura, H. Sequentially annealed highly cross-linked polyethylene reduced in vivo wear particle generation in total knee arthroplasty. J. Orthop. Surg. 2017, 25, 230949901771890. [Google Scholar] [CrossRef]
- Song, S.; Feng, J.; Wu, P. Annealing of melt-crystallized polyethylene and its influence on microstructure and mechanical properties: A comparative study on branched and linear polyethylenes. J. Polym. Sci. Part B—Polym. Phys. 2011, 49, 1347–1359. [Google Scholar] [CrossRef]
- Fernández, C.; Puig, C.C. CHANGES IN MELTING BEHAVIOR AND MORPHOLOGY ON ANNEALING OF LINEAR AND BRANCHED POLYETHYLENE. J. Macromol. Sci. Part B 2002, 41, 991–1005. [Google Scholar] [CrossRef]
- Cser, F.; Hopewell, J.L.; Shanks, R.A. X-ray diffraction studies on reverse-annealed polyethylenes. Appl. Polym. Sci. 2001, 81, 340–349. [Google Scholar] [CrossRef]
- Cerrada, M.L.; Benavente, R.; Sierra, C.A. A Significant Enhance of Impact Strength with Thermal Annealing in High Density Polyethylene. Polym. J. 2001, 33, 270–276. [Google Scholar] [CrossRef]
- Jia, Y.; Mao, Z.; Huang, W.; Zhang, J. Effect of temperature and crystallinity on the thermal conductivity of semi-crystalline polymers: A case study of polyethylene. Mater. Chem. Phys. 2022, 287, 126325. [Google Scholar] [CrossRef]
- Liu, Z.; Jin, J.; Chen, S.; Zhang, J. Effect of crystal form and particle size of titanium dioxide on the photodegradation behaviour of ethylene-vinyl acetate copolymer/low density polyethylene composite. Polym. Degrad. Stab. 2011, 96, 43–50. [Google Scholar] [CrossRef]
- Strobl, G.R.; Schneider, M. Direct evaluation of the electron density correlation function of partially crystalline polymers. J. Polym. Sci. 1980, 18, 1343–1359. [Google Scholar] [CrossRef]
- Strobl, G.R.; Schneider, M.J.; Voigt-Martin, I.G. Model of partial crystallization and melting derived from small-angle X-ray scattering and electron microscopic studies on low-density polyethylene. J. Polym. Sci. 1980, 18, 1361–1381. [Google Scholar] [CrossRef]
- Moyses, S.C.; Zukermann-Schpector, J. Annealing in Low Density Polyethylene at Several Temperatures. Polym. J. 2004, 36, 679–683. [Google Scholar] [CrossRef]
- Hu, W. Principles of Polymer Crystallization; Chemical Industry Press: Shanghai, China, 2013. [Google Scholar]
- Tang, Y.; Men, Y. Influence of Shear on Polypropylene Crystallization and Morphology. Chem. J. Chin. U 2016, 37, 367–372. [Google Scholar][Green Version]
- Bair, H.E.; Salovey, R.; Huseby, T.W. Melting and annealing of polyethylene single crystals. Polymer 1967, 8, 9–20. [Google Scholar] [CrossRef]
- DeFoor, F.; Groeninckx, G.; Reynaers, H.; Schouterden, P.; Van der Heijden, B. Molecular, thermal, and morphological characterization of narrowly branched fractions of 1-octene linear low-density polyethylene. 3. Lamellar and spherulitic morphology. Macromolecules 1993, 26, 2575–2582. [Google Scholar] [CrossRef]
- Bassett, D.C.; Carder, D.R. Oriented chain-extended polyethylene. Philos. Mag. 1973, 28, 513–533. [Google Scholar] [CrossRef]






| Trade Name | Supplier | MFR (g/10min) (190 °C, 2.16kg) | Density (g/cm3) | (°C) | (°C) | PDI | |
|---|---|---|---|---|---|---|---|
| MG6000 | Sinopec | 60 | 0.9186 | 108.01 | 90.19 | 52042 | 4.99 |
| Sample | PE Precursor | PE-AT60 | PE-AT70 | PE-AT80 | PE-AT90 | PE-AT100 |
|---|---|---|---|---|---|---|
| () | 105.38 | 105.78 | 105.82 | 105.64 | 103.28 | 103.05 |
| (j/g) | 108.8 | 117.65 | 111.45 | 111.47 | 106.58 | 108.64 |
| Crystallinity (%) | 39.26 | 42.46 | 40.22 | 40.23 | 38.46 | 39.21 |
| Peak Value | PE Precursor | PE-AT60 | PE-AT70 | PE-AT80 | PE-AT90 | PE-AT100 |
|---|---|---|---|---|---|---|
| Fitting peak 1 () | 53.81 | 45.83 | 45.47 | 43.24 | 45.62 | 46.24 |
| Fitting peak 2 () | 83.35 | 66.76 | 58.16 | 63.77 | 71.68 | 71.78 |
| Fitting peak 3 () | 96.98 | 86.69 | 77.63 | 84.39 | 92.00 | 85.52 |
| Fitting peak 4 () | 101.94 | 98.37 | 96.01 | 96.38 | 96.89 | 94.88 |
| Fitting peak 5 () | 105.16 | 102.78 | 102.93 | 102.95 | 103.70 | 102.38 |
| Fitting peak 6 () | 106.78 | 106.50 | 106.48 | 106.41 | 107.04 | 106.47 |
| Sample | PE Precursor | PE-AT60 | PE-AT70 | PE-AT80 | PE-AT90 | PE-AT100 |
|---|---|---|---|---|---|---|
| Long Period (nm) | 11.47 | 11.86 | 11.86 | 12.36 | 12.90 | 11.25 |
| FWHM () | 0.4125 | 0.3698 | 0.3734 | 0.3947 | 0.4694 | 0.4623 |
| Sample | (nm) | (nm) | (nm) |
|---|---|---|---|
| PE precursor | 12.96 | 4.24 | 8.72 |
| PE-AT60 | 12.53 | 4.44 | 8.09 |
| PE-AT70 | 12.74 | 4.48 | 8.26 |
| PE-AT80 | 13.17 | 4.56 | 8.61 |
| PE-AT90 | 14.04 | 4.54 | 9.5 |
| PE-AT100 | 13.60 and 19.87 | 4.70 | 8.98 and 15.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Li, C.; Ren, M.; Gao, D.; Tang, Y.; Wu, C.; Chu, L.; Zhang, Q.; Zhang, S. Recrystallization During Annealing of Low-Density Polyethylene Non-Woven Fabric by Melt Electrospinning. Polymers 2025, 17, 2121. https://doi.org/10.3390/polym17152121
Ren Y, Li C, Ren M, Gao D, Tang Y, Wu C, Chu L, Zhang Q, Zhang S. Recrystallization During Annealing of Low-Density Polyethylene Non-Woven Fabric by Melt Electrospinning. Polymers. 2025; 17(15):2121. https://doi.org/10.3390/polym17152121
Chicago/Turabian StyleRen, Yueming, Changjin Li, Minqiao Ren, Dali Gao, Yujing Tang, Changjiang Wu, Liqiu Chu, Qi Zhang, and Shijun Zhang. 2025. "Recrystallization During Annealing of Low-Density Polyethylene Non-Woven Fabric by Melt Electrospinning" Polymers 17, no. 15: 2121. https://doi.org/10.3390/polym17152121
APA StyleRen, Y., Li, C., Ren, M., Gao, D., Tang, Y., Wu, C., Chu, L., Zhang, Q., & Zhang, S. (2025). Recrystallization During Annealing of Low-Density Polyethylene Non-Woven Fabric by Melt Electrospinning. Polymers, 17(15), 2121. https://doi.org/10.3390/polym17152121






