Evaluation of Polypropylene Reusability Using a Simple Mechanical Model Derived from Injection-Molded Products
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Extrusion Molding
2.3. Injection Molding
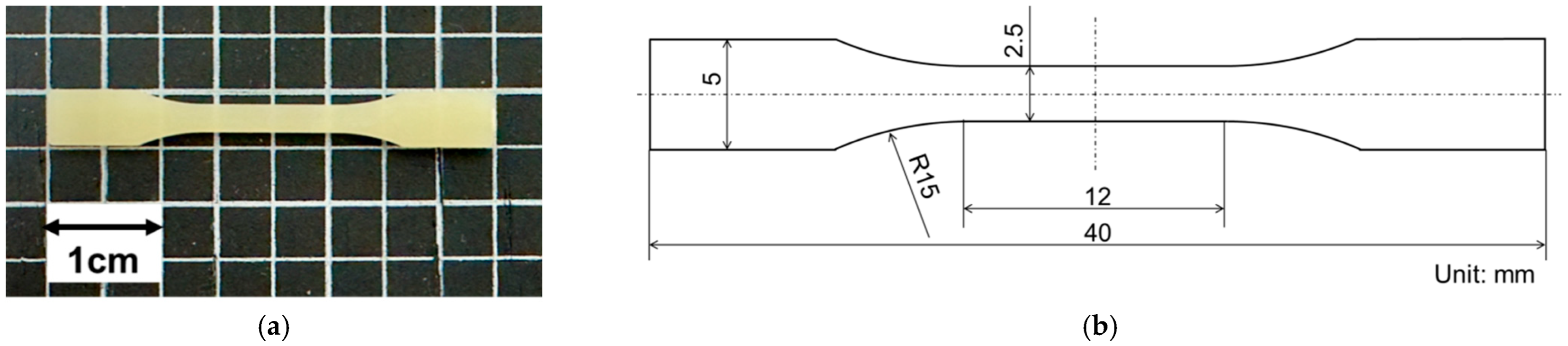
2.4. Evaluation of Poisson’s Ratio by Tensile Testing
2.5. Evaluation of Critical Expansion Stress
2.6. Differential Scanning Calorimetry (DSC)
2.7. Chemiluminescence Measurement
3. Results
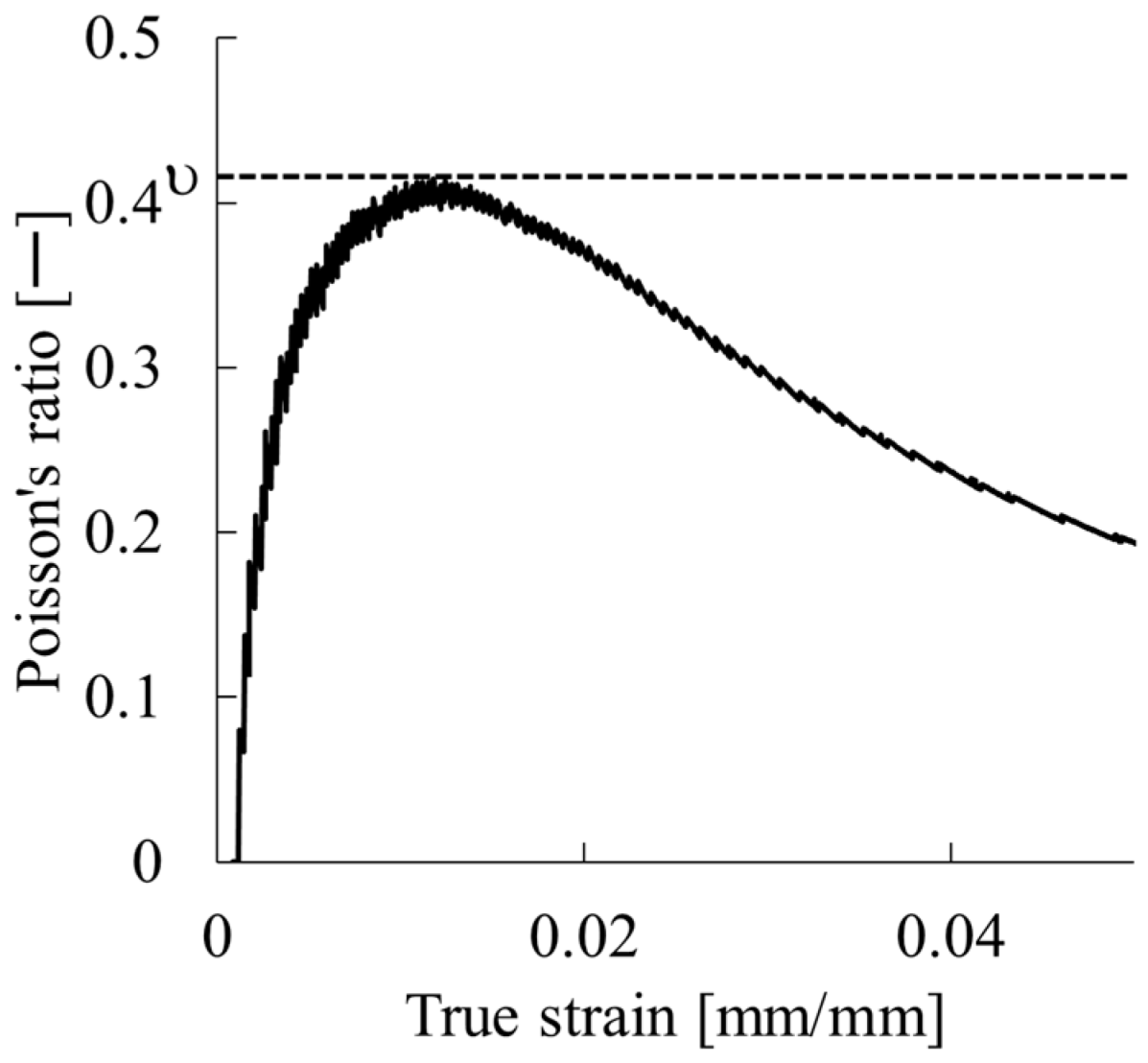
3.1. Validity of Poisson’s Ratio Determined from Tensile Testing
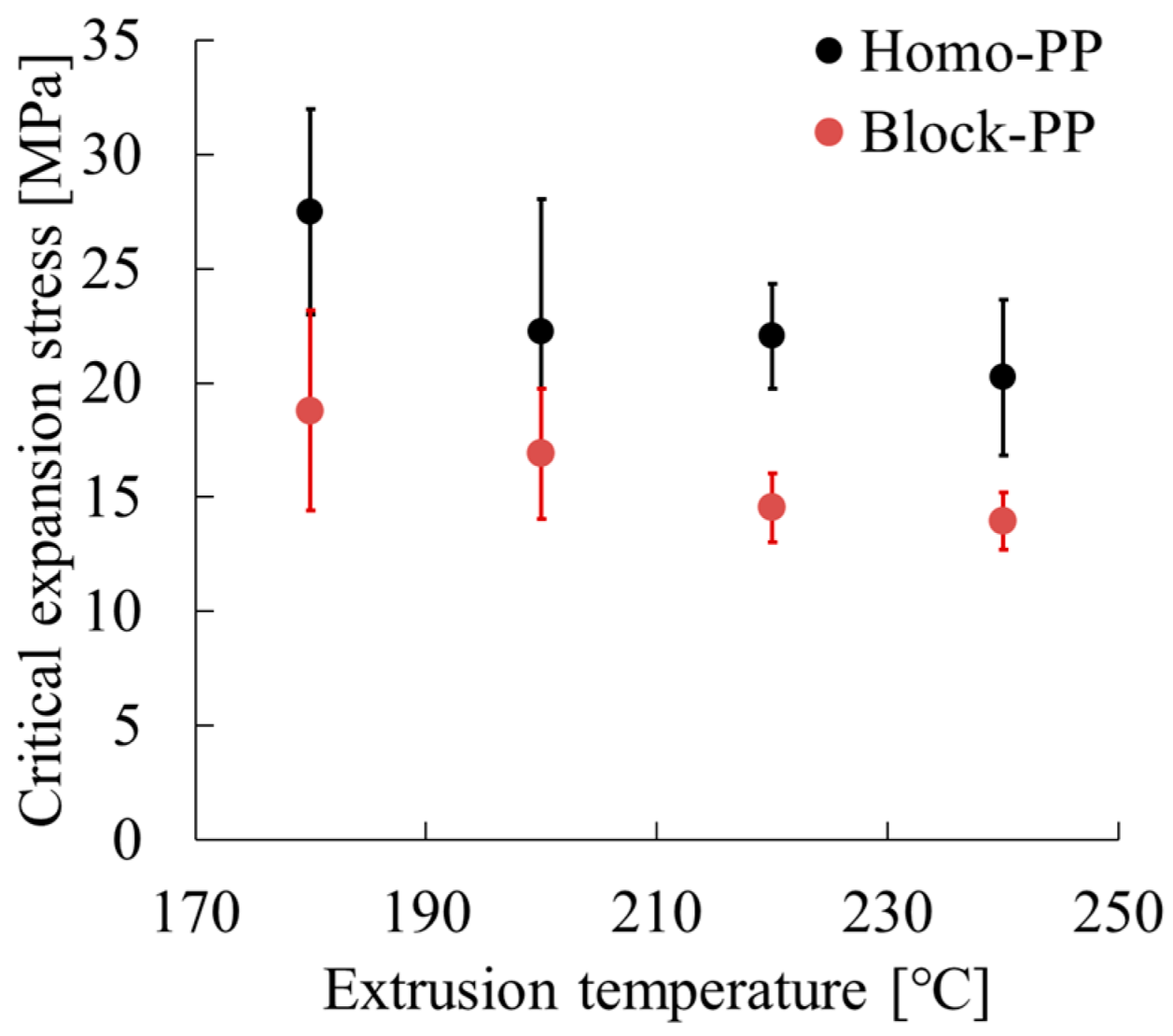
3.2. Extrusion Temperature Effects on the Critical Expansion Stress of Polypropylene
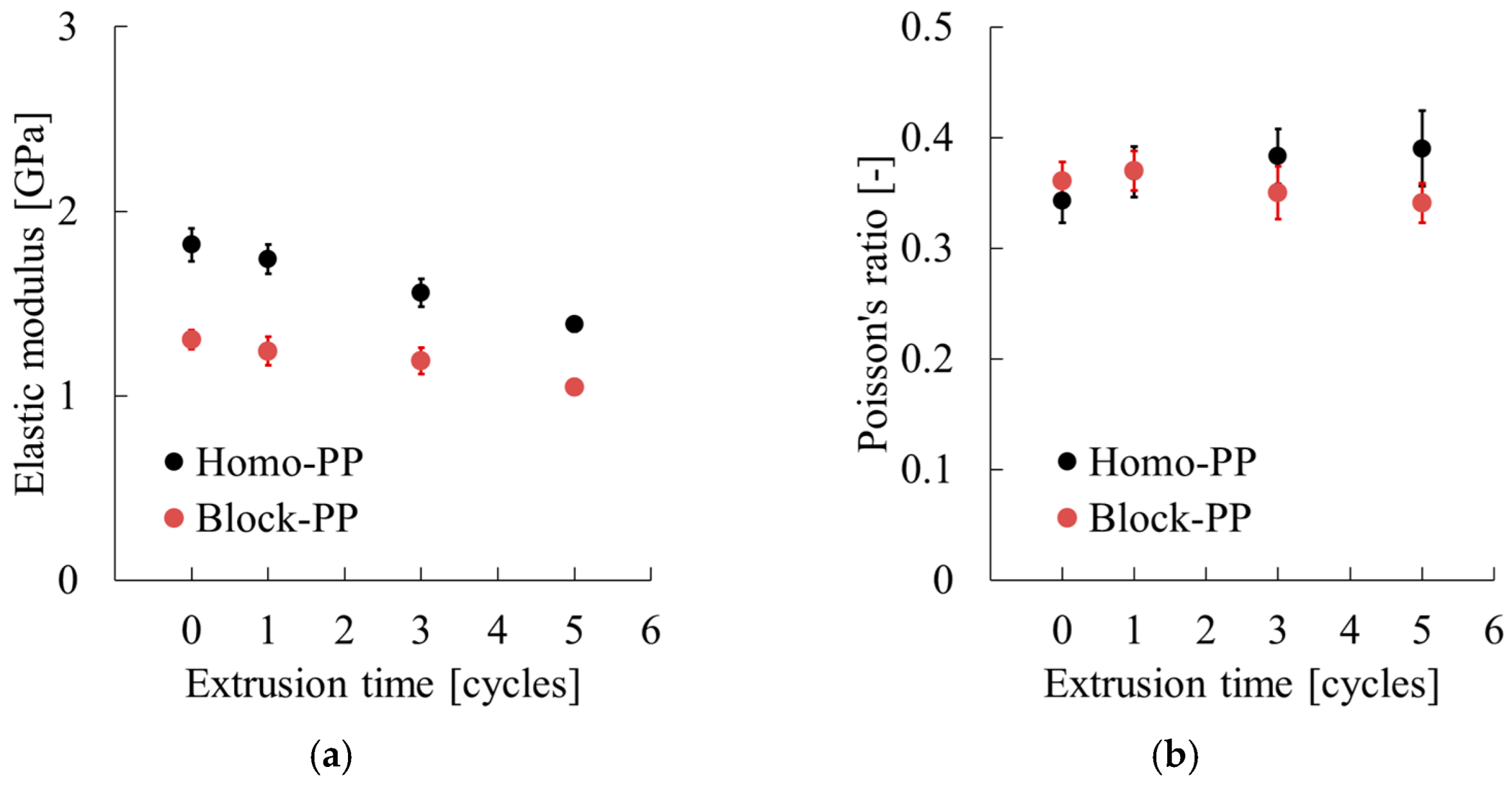
3.3. Repeated Extrusion Effects on the Critical Expansion Stress of Polypropylene
4. Discussion
4.1. Influence of Extrusion Temperature on the Critical Expansion Stress of Polypropylene
4.2. Influence of Repeated Extrusion on the Critical Expansion Stress
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Boffito, E.; Riva, M.; Vinciguerra, B.; Altomare, C.; Ranzato, S. Synthesis and Use of Thermoplastic Polymers for Tissue Engineering Purposes. Int. J. Pharm. X 2025, 9, 100313. [Google Scholar]
- Suzuki, G.; Uchida, N.; Tanaka, K.; Higashi, O.; Takahashi, Y.; Kuramochi, H.; Yamaguchi, N.; Osako, M. Global dis charge of microplastics from mechanical recycling of plastic waste. Environ. Pollut. 2024, 348, 123855. [Google Scholar] [CrossRef]
- Lamtai, A.; Elkoun, S.; Robert, M.; Mighri, F.; Diez, C. Mechanical Recycling of Thermoplastics: A Review of Key Issues. Waste 2023, 1, 860–883. [Google Scholar] [CrossRef]
- Takayama, T.; Motoyama, Y. Injection Molding Temperature Dependence of Elastic Coefficients Obtained Using Three-Point Bending Tests to Ascertain Thermoplastic Polymer Coefficients. Mech. Eng. J. 2021, 8, 20–00414. [Google Scholar] [CrossRef]
- Takayama, T.; Shibazaki, R. Mechanical Anisotropy of Injection-Molded PP/PS Polymer Blends and Correlation with Morphology. Polymers 2023, 15, 4167. [Google Scholar] [CrossRef]
- Takayama, T. Inorganic Particles Contribute to the Compatibility of Polycarbonate/Polystyrene Polymer Blends. Materials 2023, 16, 1536. [Google Scholar] [CrossRef]
- Cozar, I.R.; Arbelaez-Toro, J.J.; Maimi, P.; Otero, F.; Gonzalez, E.V.; Turon, A.; Camanho, P.P. A Novel Methodology to Measure the Transverse Poisson’s Ratio in the Elastic and Plastic Regions for Composite Materials. Compos. Part B Eng. 2024, 272, 111098. [Google Scholar] [CrossRef]
- Xu, Y.-X.; Juang, J.-Y. Measurement of Nonlinear Poisson’s Ratio of Thermoplastic Polyurethanes under Cyclic Softening Using 2D Digital Image Correlation. Polymers 2021, 13, 1498. [Google Scholar] [CrossRef] [PubMed]
- Takayama, T.; Nagasawa, Y. Poisson’s Ratio Prediction of Injection Molded Thermoplastics Using Differential Scanning Calorimetry. Polymers 2024, 16, 1956. [Google Scholar] [CrossRef] [PubMed]
- Podara, C.; Termine, S.; Modestou, M.; Semitekolos, D.; Tsirogiannis, C.; Karamitrou, M.; Trompeta, A.; Milickovic, T.; Charitidis, C. Recent Trends of Recycling and Upcycling of Polymers and Composites: A Comprehensive Review. Recycling 2024, 9, 37. [Google Scholar] [CrossRef]
- Uzosike, C.C.; Yee, L.H.; Padilla, R.V. Small-Scale Mechanical Recycling of Solid Thermoplastic Wastes: A Review of PET, PEs, and PP. Energies 2023, 16, 1406. [Google Scholar] [CrossRef]
- Von Vacano, B.; Reich, O.; Huber, G.; Türkoglu, G. Elucidating pathways of polypropylene chain cleavage and stabilization for multiple loop mechanical recycling. J. Polym. Sci. 2023, 61, 1849–1858. [Google Scholar] [CrossRef]
- Rust, N.; Ferg, E.E.; Masalova, I. A degradation study of isotactic virgin and recycled polypropylene used in lead acid battery casings. Polym. Test. 2006, 25, 130–139. [Google Scholar] [CrossRef]
- Bernagozzi, G.; Arrigo, R.; Ponzielli, G.; Frache, A. Towards effective recycling routes for polypropylene: Influence of a repair additive on flow characteristics and processability. Polym. Degrad. Stab. 2024, 223, 110714. [Google Scholar] [CrossRef]
- Mrozik, J.; Bras, S.; Burnet, J.-M.; Cazaux, L.; Ferry, L.; Michaud, V. Mechanical Recycling: Compatibilization of Mixed Thermoplastic Wastes. Polym. Degrad. Stab. 2018, 147, 245–266. [Google Scholar] [CrossRef]
- Grigorescu, R.M.; Gherghe, P.; Ilie, L.; Draghici, M.E.; Radu, E.A.; Filip, M.I.; Lupescu, R.-M.; Vasile, Z.; Anghel, I.; Socol, I.-E.; et al. Development of Thermoplastic Composites Based on Recycled Polypropylene and Waste Printed Circuit Boards. Waste Manag. 2020, 118, 391–401. [Google Scholar] [CrossRef] [PubMed]
- ISO 527-1:2019; Plastics—Determination of Tensile Properties—Part 1: General Principles. The British Standards Institution: London, UK, 2019.
- Barker, R.E. An Approximate Relation Between Elastic Moduli and Thermal Expansivities. J. Appl. Phys. 1963, 34, 107–116. [Google Scholar] [CrossRef]
- TA Instruments. TN048: Polymer Heats of Fusion; TA Instruments: New Castle, DE, USA, 2022. [Google Scholar]
- Parathodika, A.R.; Naskar, K. Ultra-High Molecular Weight EPDM Composites via Crossover Curing Agents: Stabilized Crosslink Network Structure and Performance Properties. Polym. Degrad. Stab. 2024, 219, 110603. [Google Scholar] [CrossRef]
- Nomura, T.; Nishio, T.; Imaizumi, K.; Ueda, Y.; Oyamada, H. Physical Properties and the Crystal Structure of Polypropylene Polymers. Kobunshi Ronbunshu 1996, 53, 389–397. [Google Scholar] [CrossRef]
- Iedema, P.D.; Remerie, K.; Seegers, D.; McAuley, K.B. Tacticity Changes during Controlled Degradation of Polypropylene. Macromolecules 2021, 54, 8921–8935. [Google Scholar] [CrossRef]
- Sonohata, H.; Manago, G.; Seike, S.; Kitawaki, H.; Tanabe, T. Evaluation of Plastic Waste Degradation Using Terahertz Spectroscopy for Material Recycling. Recycling 2025, 10, 134. [Google Scholar] [CrossRef]












| Material | Code | Manufacturer | Grade |
|---|---|---|---|
| Polypropylene | PP | Japan Polypropylene Co., Ltd., Tokyo, Japan | Novatec-PP MA1B |
| Polyoxymethylene | POM | Asahi Kasei Corp., Tokyo, Japan | TENAC 3010 |
| ABS copolymer | ABS | Nippon A&L Inc., Osaka, Japan | Kralastic GA-101 |
| Polycarbonate | PC | Mitsubishi Engineering-Plastics Corp., Tokyo, Japan | Iupilon H-3000 |
| Material | Code | Manufacturer | Grade |
|---|---|---|---|
| Homo-type Polypropylene | Homo-PP | Japan Polypropylene Co., Ltd., Tokyo, Japan | Novatec-PP MA3 |
| Block-type Polypropylene | Block-PP | Japan Polypropylene Co., Ltd., Tokyo, Japan | Novatec-PP BC03AD |
| Code | Tinj [°C] | Tmold [°C] | Vinj [m/s] | Phold [MPa] | Tinj [s] | Tcool [s] |
|---|---|---|---|---|---|---|
| PP | 210/230/250 | 50 | 10 | 42 | 45 | 15 |
| POM | 200/210/220 | 100 | 30 | 70 | 15 | 10 |
| ABS | 250/270/290 | 50 | 30 | 49 | 15 | 10 |
| PC | 280/290/300 | 100 | 30 | 11 | 30 | 10 |
| Code | Tinj [°C] | Tmold [°C] | Vinj [m/s] | Phold [MPa] | Tinj [s] | Tcool [s] |
|---|---|---|---|---|---|---|
| Homo-PP | 200 | 50 | 10 | 56 | 45 | 15 |
| Block-PP | 200 | 50 | 10 | 49 | 45 | 15 |
| Code | Tinj [°C] | E [MPa] | Poisson’s Ratio [—] | Poisson’s Ratio [9] [—] |
|---|---|---|---|---|
| PP | 210 | 1491 (37) | 0.413 (0.003) | 0.390 |
| 230 | 1433 (68) | 0.411 (0.014) | 0.405 | |
| 250 | 1375 (56) | 0.420 (0.020) | 0.417 | |
| POM | 200 | 2498 (16) | 0.362 (0.002) | 0.361 |
| 210 | 2537 (26) | 0.369 (0.006) | 0.372 | |
| 220 | 2417 (49) | 0.368 (0.008) | 0.380 | |
| ABS | 250 | 2400 (22) | 0.378 (0.008) | 0.367 |
| 270 | 2376 (14) | 0.390 (0.001) | 0.384 | |
| 290 | 2352 (5) | 0.402 (0.013) | 0.397 | |
| PC | 280 | 2078 (12) | 0.359 (0.008) | 0.373 |
| 290 | 2011 (23) | 0.370 (0.024) | 0.380 | |
| 300 | 1994 (29) | 0.374 (0.007) | 0.386 |
| Code | Extrusion Temp. [°C] | E [MPa] | Eυ [MPa] | υ [—] | εB [—] | σy [MPa] | f0 [—] | σv [MPa] |
|---|---|---|---|---|---|---|---|---|
| Homo-PP | 180 | 1642 (63) | 1142 (59) | 0.374 (0.013) | 1.63 (0.01) | 23.9 (1.1) | 0.103 (0.005) | 27.5 (4.5) |
| 200 | 1658 (89) | 1191 (111) | 0.368 (0.025) | 1.42 (0.16) | 25.4 (0.9) | 0.105 (0.008) | 22.3 (5.8) | |
| 220 | 1573 (96) | 1188 (99) | 0.374 (0.016) | 1.39 (0.14) | 24.2 (0.7) | 0.101 (0.008) | 22.1 (2.3) | |
| 240 | 1361 (92) | 954 (99) | 0.377 (0.029) | 1.68 (0.10) | 22.6 (1.0) | 0.115 (0.007) | 20.3 (3.4) | |
| Block-PP | 180 | 1455 (64) | 1004 (91) | 0.368 (0.010) | 1.44 (0.18) | 22.6 (0.7) | 0.112 (0.006) | 18.8 (4.4) |
| 200 | 1256 (71) | 878 (97) | 0.362 (0.015) | 1.63 (0.05) | 21.8 (1.4) | 0.120 (0.009) | 16.9 (2.9) | |
| 220 | 1182 (52) | 813 (45) | 0.360 (0.015) | 1.59 (0.05) | 21.2 (1.3) | 0.124 (0.005) | 14.6 (1.5) | |
| 240 | 1116 (23) | 763 (42) | 0.351 (0.010) | 1.68 (0.04) | 21.1 (0.6) | 0.130 (0.005) | 14.0 (1.3) |
| Code | Extrusion Time [Cycles] | E [MPa] | Eυ [MPa] | υ [—] | εB [—] | σy [MPa] | f0 [—] | σv [MPa] |
|---|---|---|---|---|---|---|---|---|
| Homo-PP | 0 | 1819 (89) | 1261 (120) | 0.345 (0.020) | 1.33 (0.07) | 27.6 (1.2) | 0.105 (0.007) | 21.7 (2.5) |
| 1 | 1740 (81) | 1279 (106) | 0.369 (0.023) | 1.25 (0.07) | 25.6 (2.2) | 0.099 (0.008) | 21.4 (3.1) | |
| 3 | 1550 (60) | 1027 (102) | 0.385 (0.027 | 1.42 (0.26) | 23.0 (1.3) | 0.108 (0.007) | 15.4 (6.8) | |
| 5 | 1388 (40) | 909 (50) | 0.390 (0.034) | 1.21 (0.09) | 22.6 (1.0) | 0.119 (0.006) | 13.5 (3.2) | |
| Block-PP | 0 | 1305 (50) | 910 (71) | 0.361 (0.017) | 1.63 (0.07) | 22.2 (1.2) | 0.118 (0.007) | 17.7 (2.5) |
| 1 | 1241 (77) | 888 (49) | 0.370 (0.018) | 1.67 (0.05) | 21.4 (1.9) | 0.116 (0.006) | 18.0 (2.0) | |
| 3 | 1190 (72) | 780 (68) | 0.350 (0.024) | 1.66 (0.02) | 21.4 (2.0) | 0.129 (0.007) | 14.3 (1.9) | |
| 5 | 1046 (35) | 662 (44) | 0.341 (0.018) | 1.70 (0.02) | 20.3 (0.9) | 0.141 (0.008) | 11.3 (1.4) |
| Code | Extrusion Temp. [°C] | Tm [°C] | Xc [—] | f [—] |
|---|---|---|---|---|
| Homo-PP | 180 | 163.8 | 0.465 | 0.0717 |
| 200 | 163.2 | 0.475 | 0.0709 | |
| 220 | 163.2 | 0.473 | 0.0711 | |
| 240 | 164.3 | 0.465 | 0.0716 | |
| Block-PP | 180 | 164.9 | 0.521 | 0.0666 |
| 200 | 165.2 | 0.501 | 0.0684 | |
| 220 | 165.2 | 0.505 | 0.0680 | |
| 240 | 164.7 | 0.516 | 0.0671 |
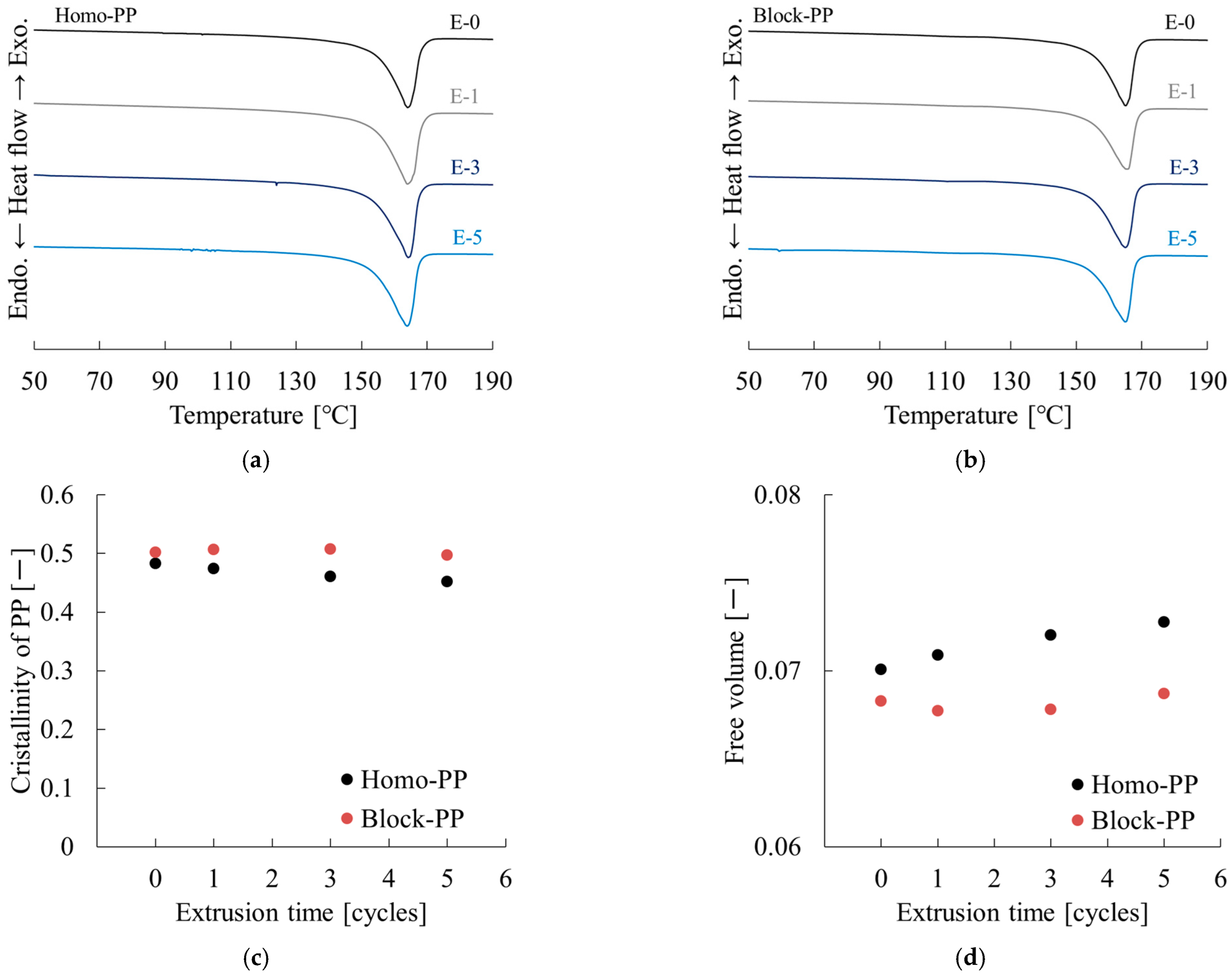
| Code | Extrusion Time [Cycles] | Tm [°C] | Xc [—] | f [—] |
|---|---|---|---|---|
| Homo-PP | 0 | 164.1 | 0.483 | 0.0701 |
| 1 | 164.0 | 0.474 | 0.0709 | |
| 3 | 164.2 | 0.461 | 0.0720 | |
| 5 | 164.0 | 0.452 | 0.0728 | |
| Block-PP | 0 | 165.2 | 0.502 | 0.0683 |
| 1 | 165.8 | 0.507 | 0.0677 | |
| 3 | 165.0 | 0.508 | 0.0678 | |
| 5 | 165.0 | 0.497 | 0.0687 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takayama, T.; Takahashi, R.; Konno, N.; Sato, N. Evaluation of Polypropylene Reusability Using a Simple Mechanical Model Derived from Injection-Molded Products. Polymers 2025, 17, 2107. https://doi.org/10.3390/polym17152107
Takayama T, Takahashi R, Konno N, Sato N. Evaluation of Polypropylene Reusability Using a Simple Mechanical Model Derived from Injection-Molded Products. Polymers. 2025; 17(15):2107. https://doi.org/10.3390/polym17152107
Chicago/Turabian StyleTakayama, Tetsuo, Rikuto Takahashi, Nao Konno, and Noriyuki Sato. 2025. "Evaluation of Polypropylene Reusability Using a Simple Mechanical Model Derived from Injection-Molded Products" Polymers 17, no. 15: 2107. https://doi.org/10.3390/polym17152107
APA StyleTakayama, T., Takahashi, R., Konno, N., & Sato, N. (2025). Evaluation of Polypropylene Reusability Using a Simple Mechanical Model Derived from Injection-Molded Products. Polymers, 17(15), 2107. https://doi.org/10.3390/polym17152107






