Mesoscale Damage Evolution, Localization, and Failure in Solid Propellants Under Strain Rate and Temperature Effects
Abstract
1. Introduction
2. Model and Methodology
2.1. Viscoelastic Model for Polymer Binder
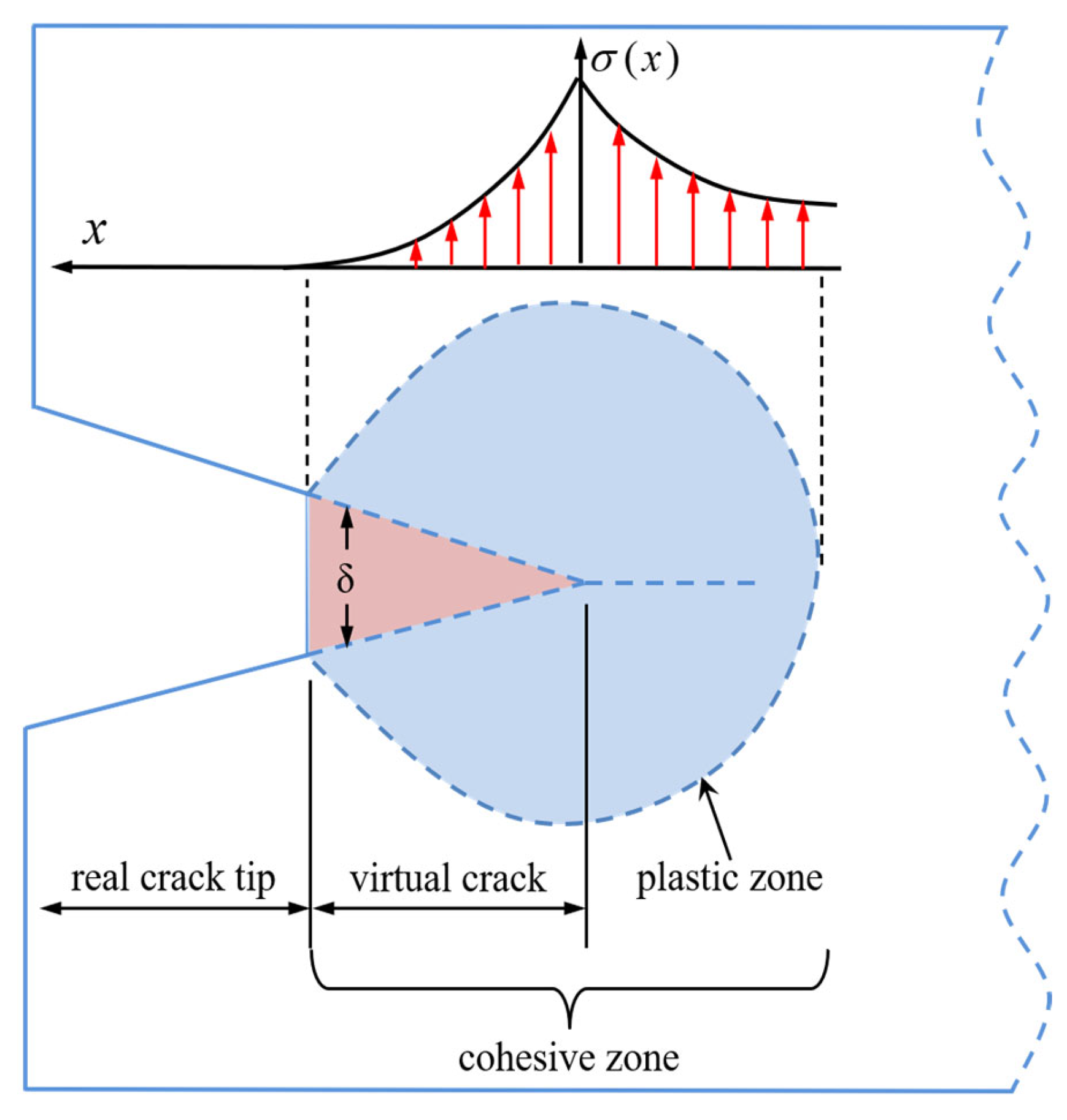
2.2. Thermomechanical Cohesive Zone Element
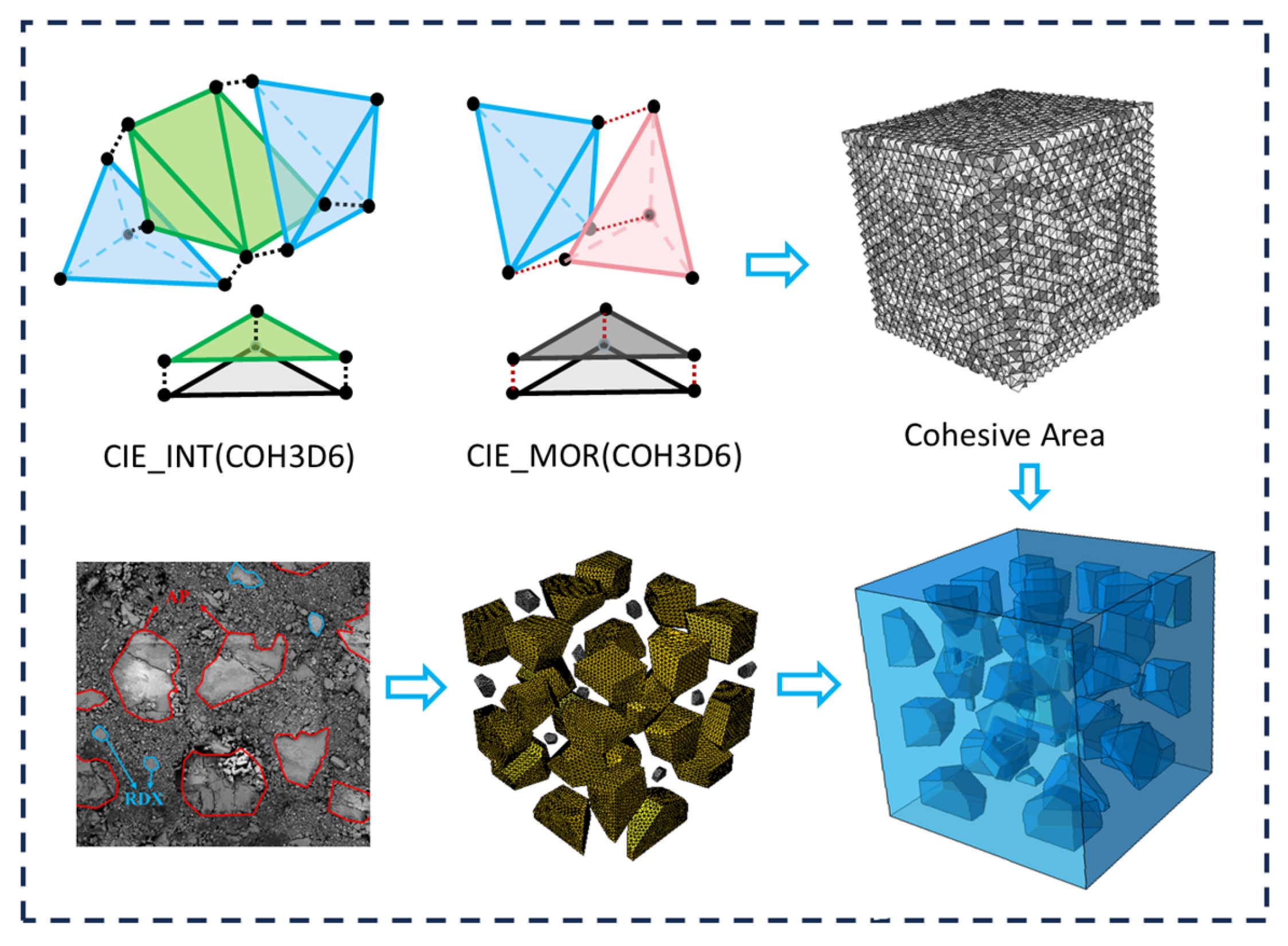
2.3. Fine-Grained Modeling
3. Model Validation
3.1. Modeling Parameters
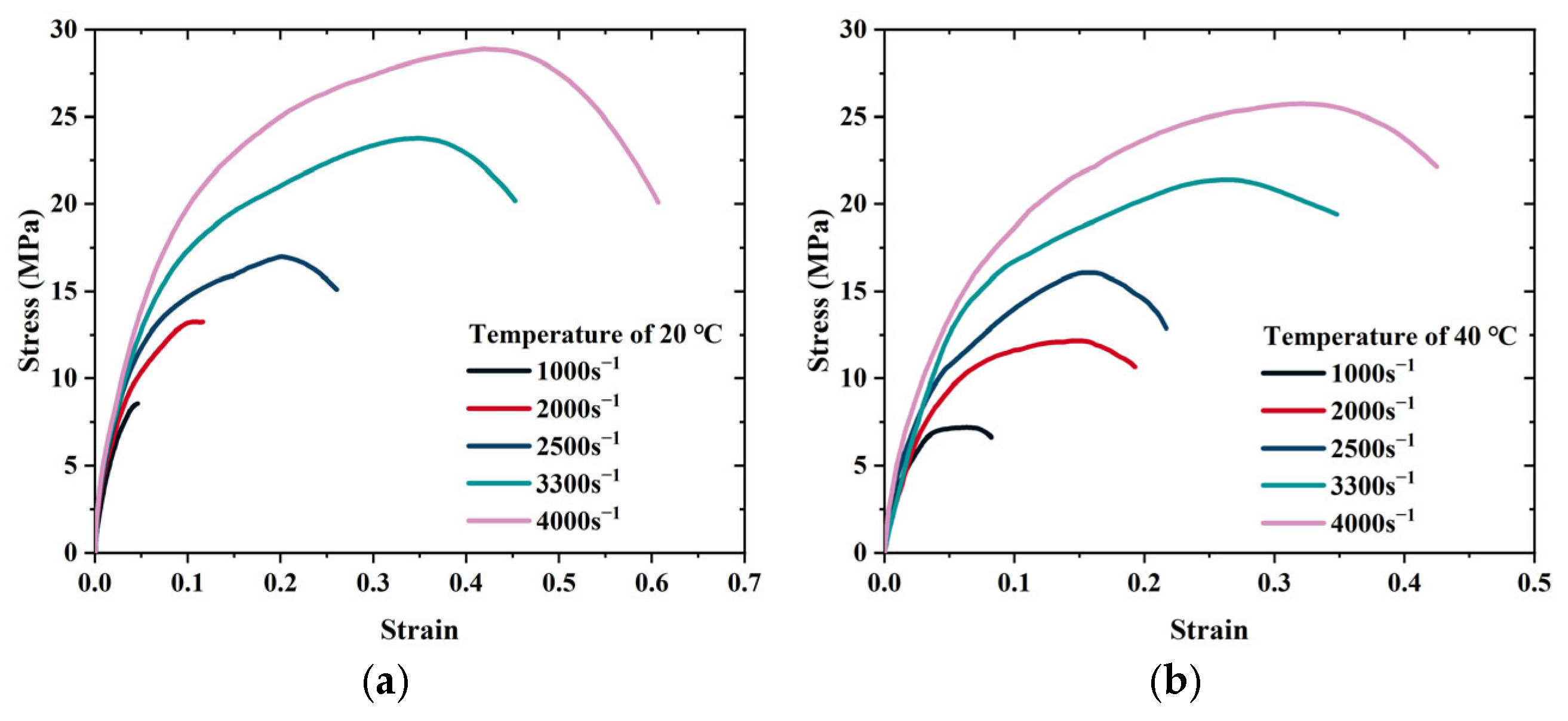
3.2. Mechanical Characterization of Solid Propellants
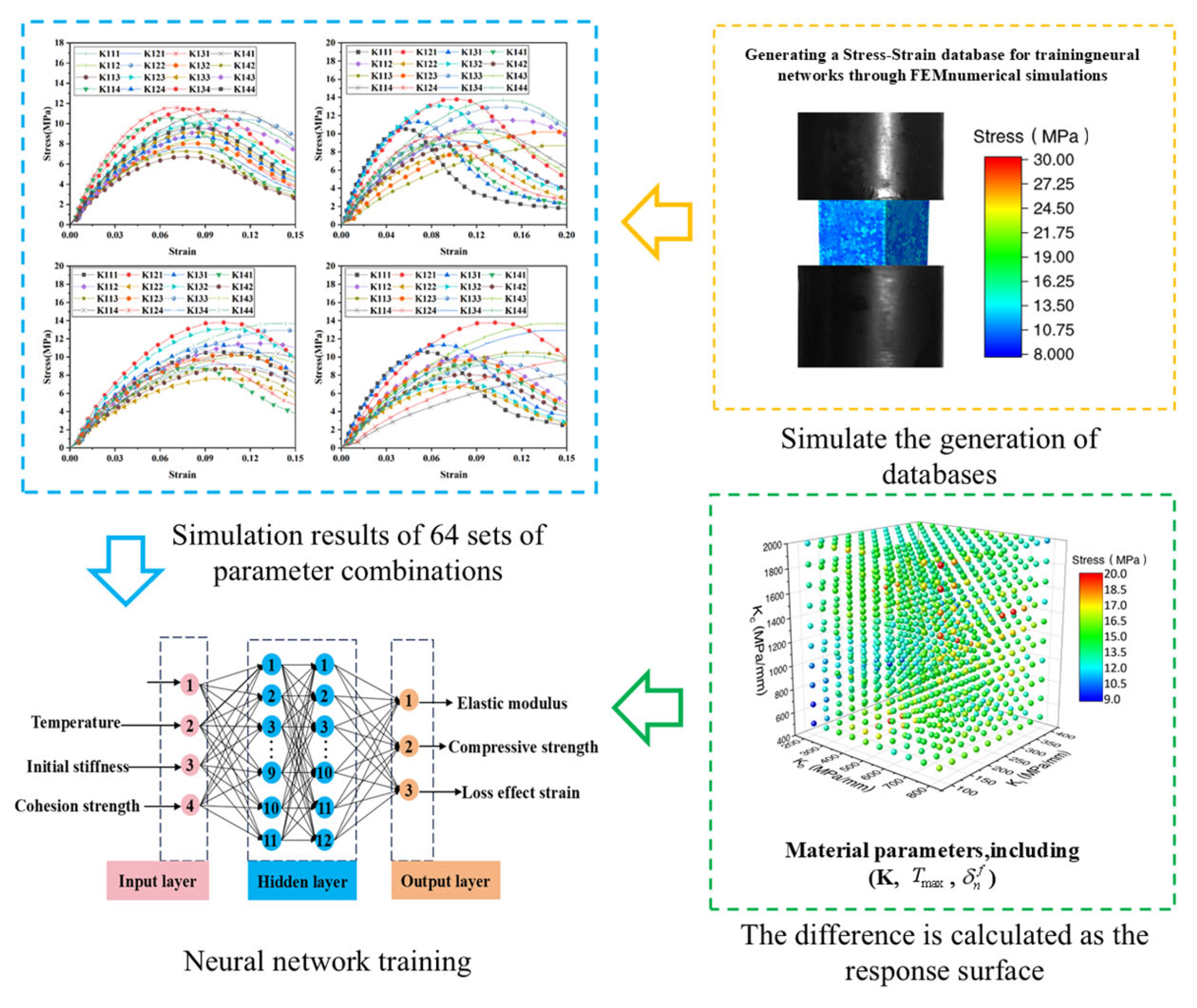
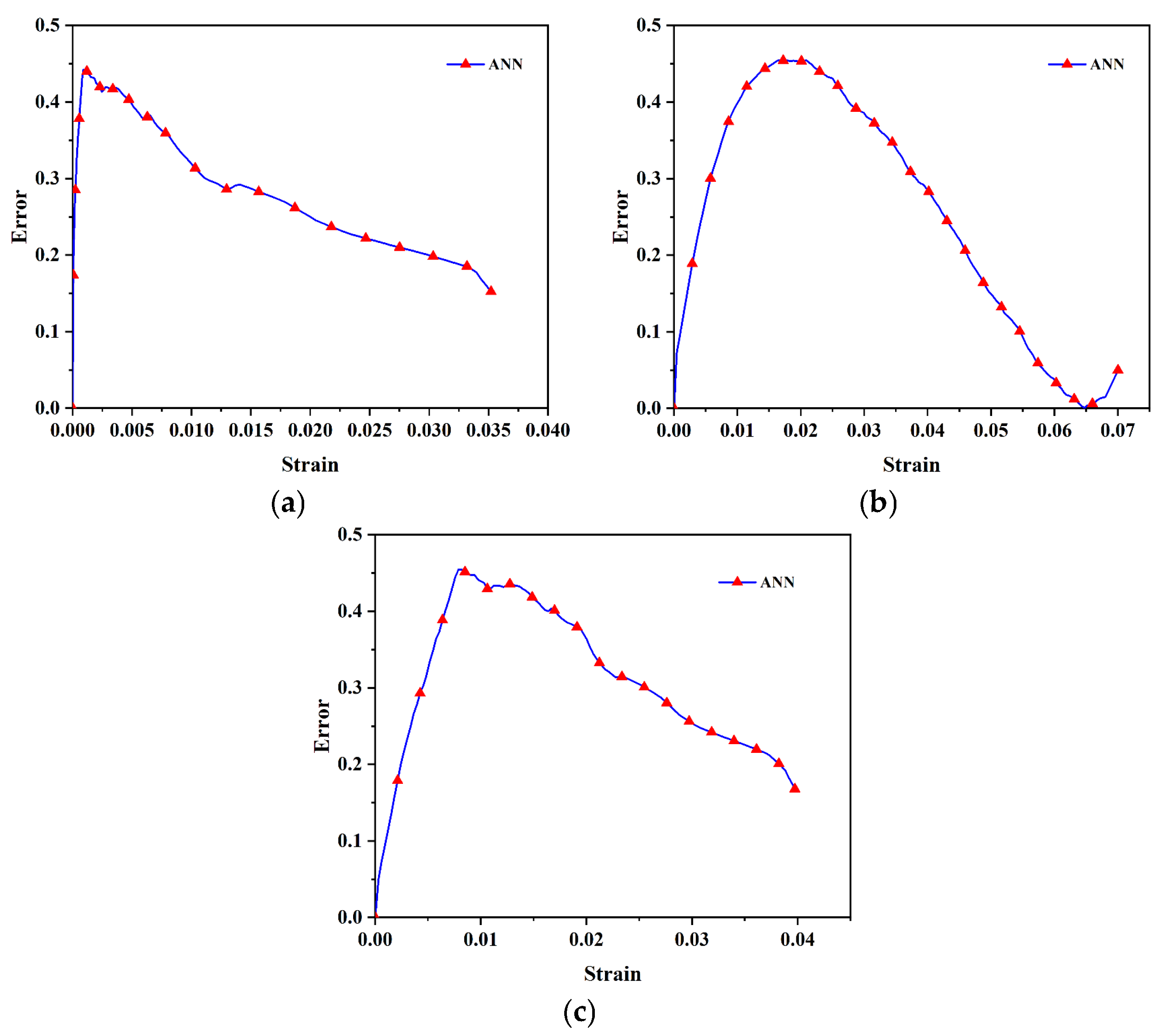
3.3. Inverse Optimization for Cohesive Model Parameters
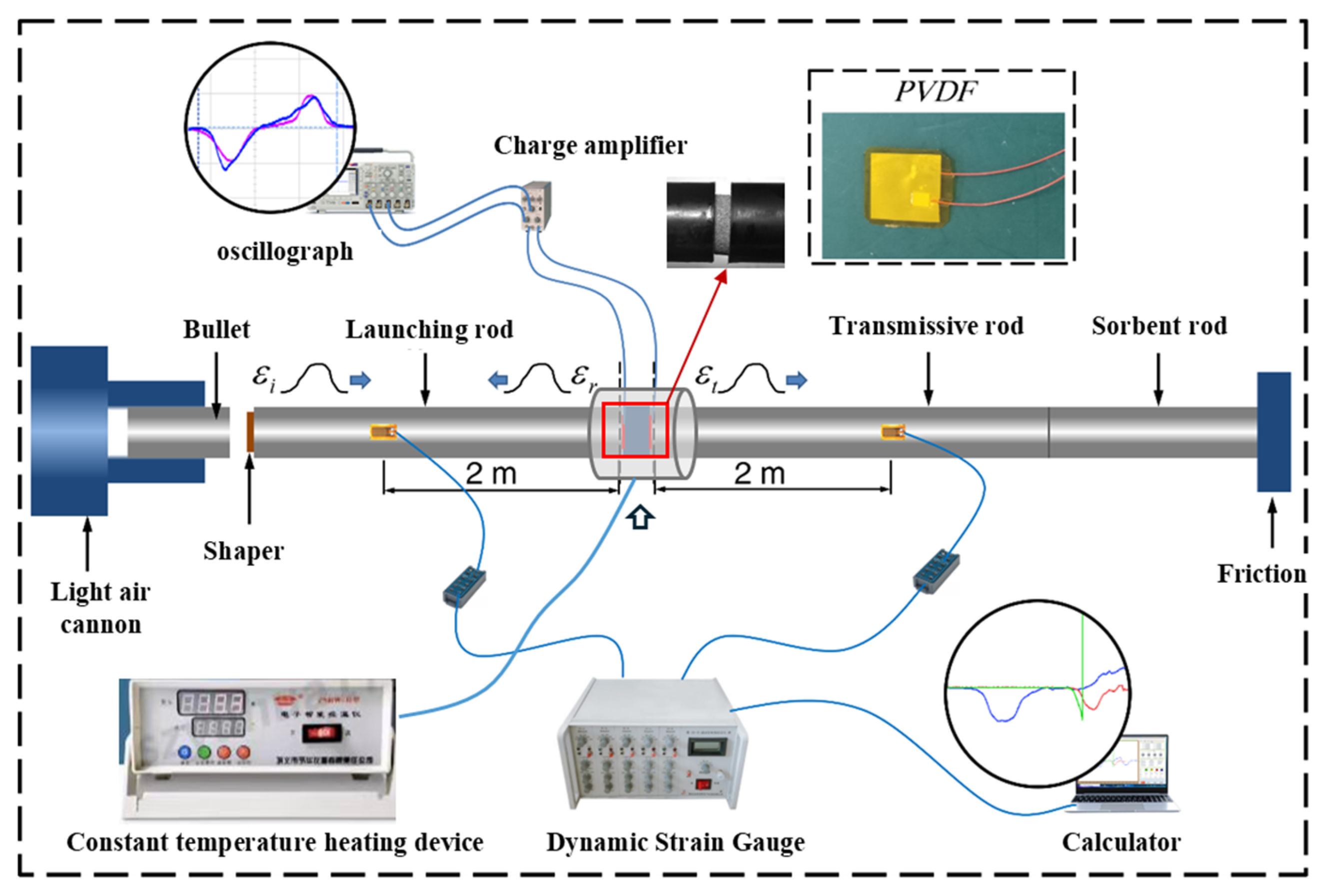
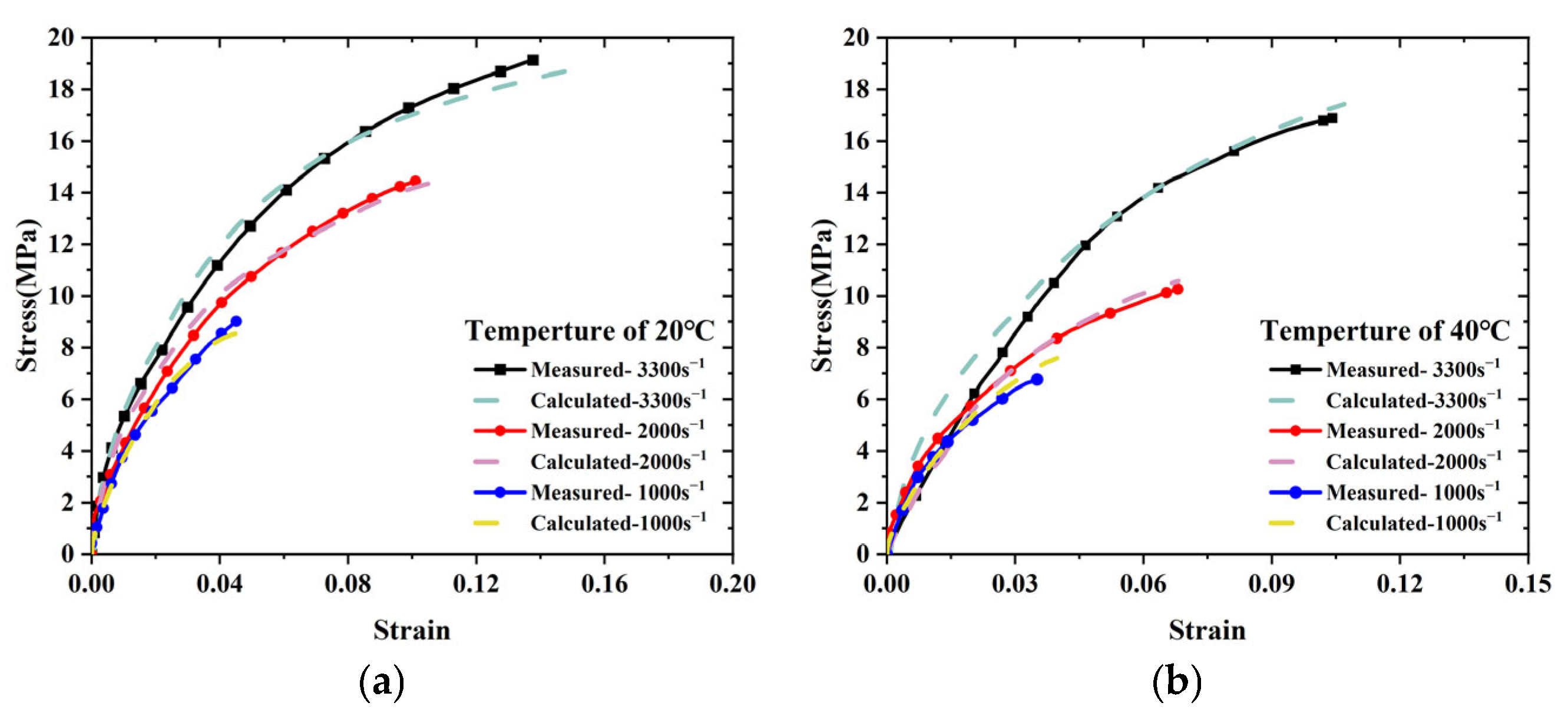
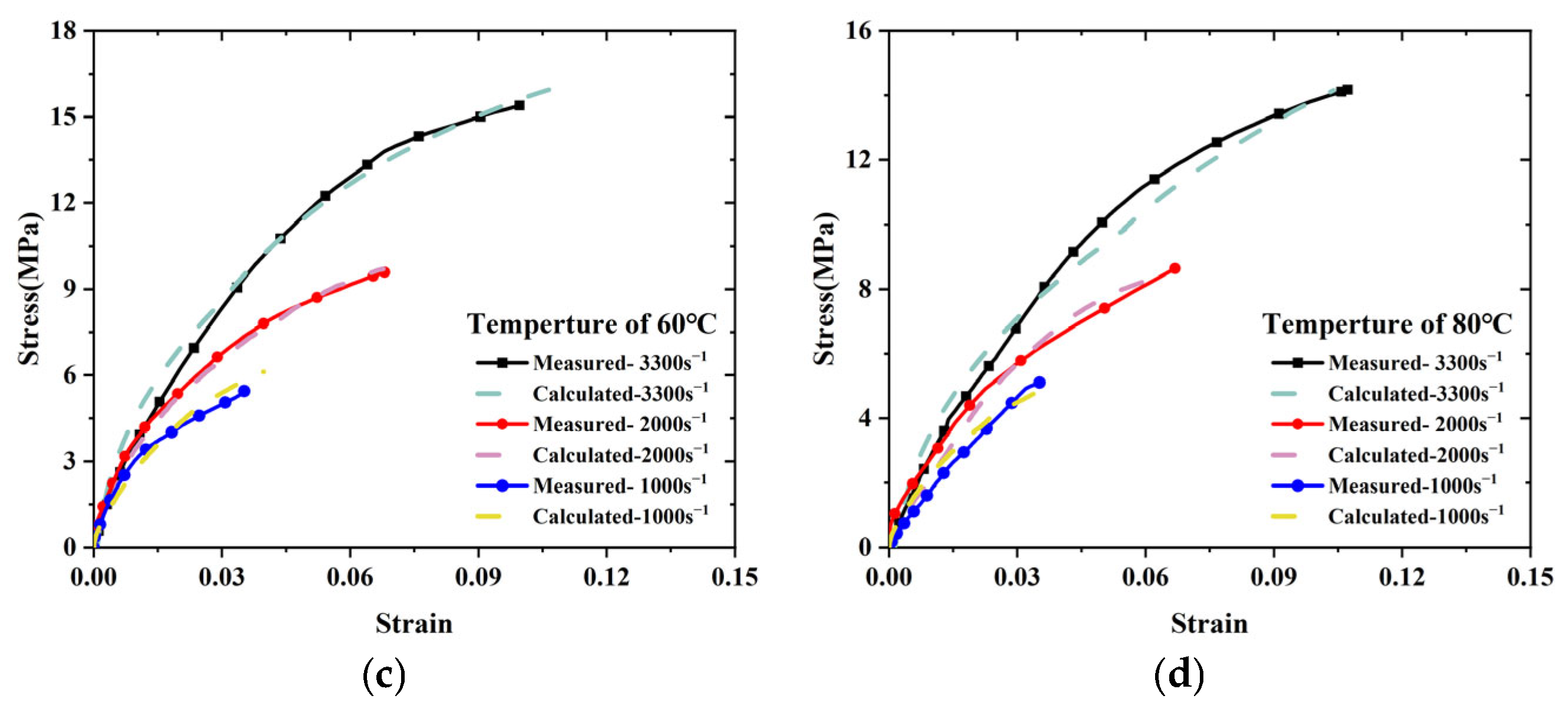
3.4. Experiment-Based Validation
4. Analysis and Discussion
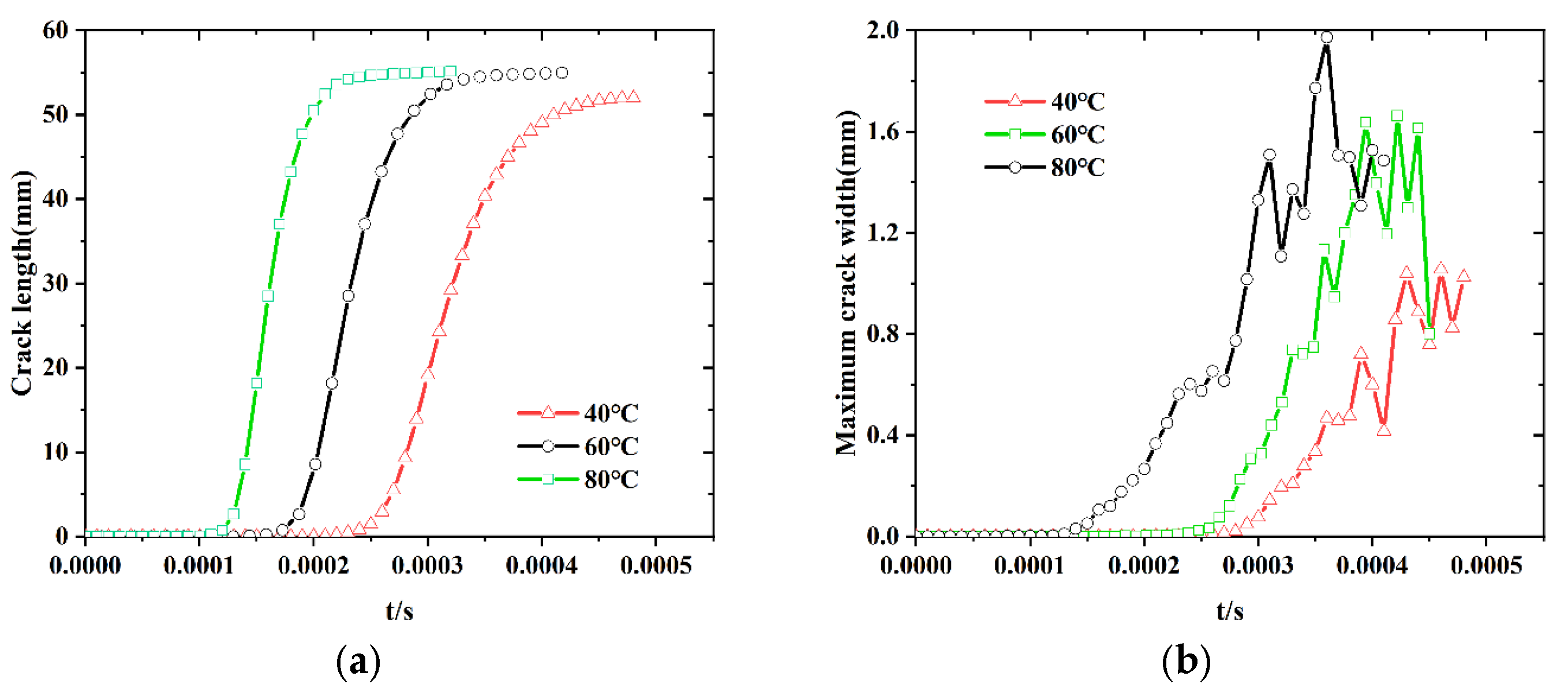
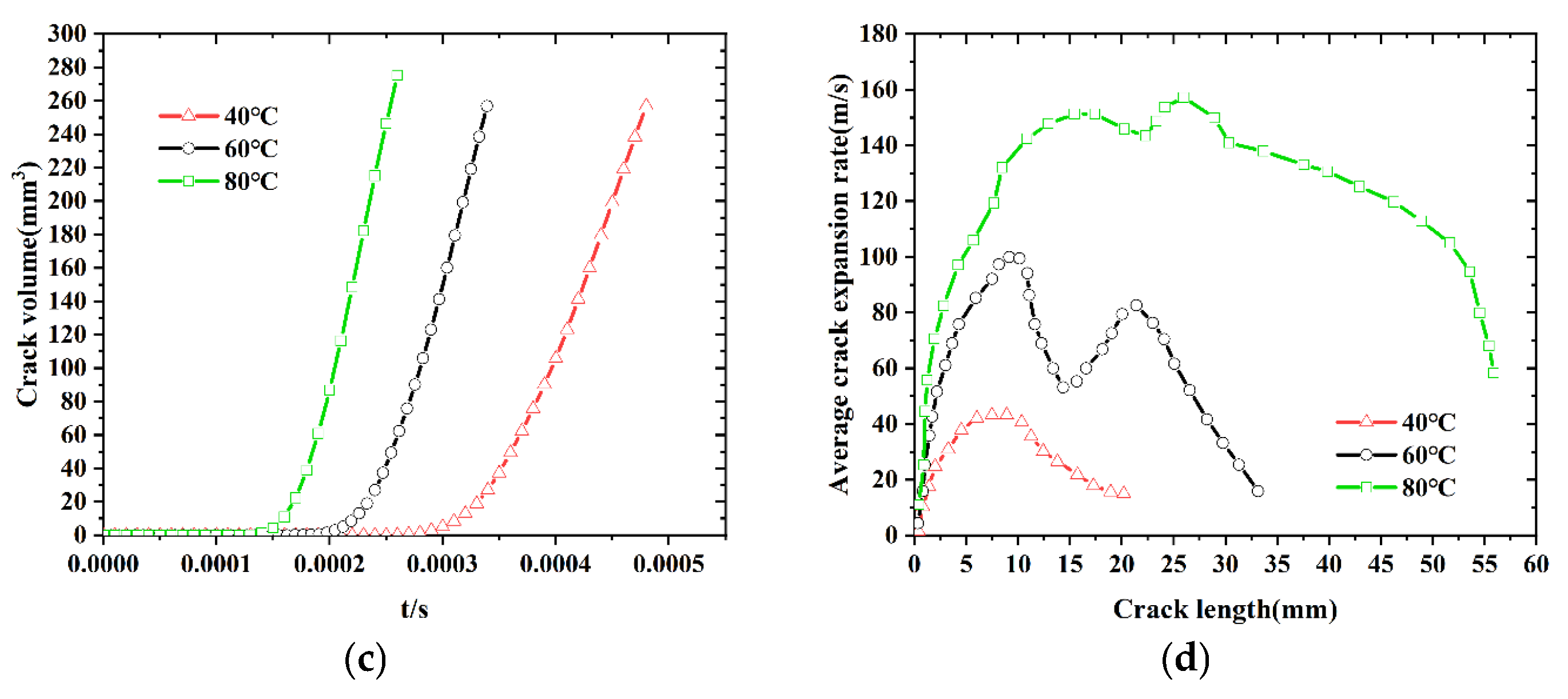
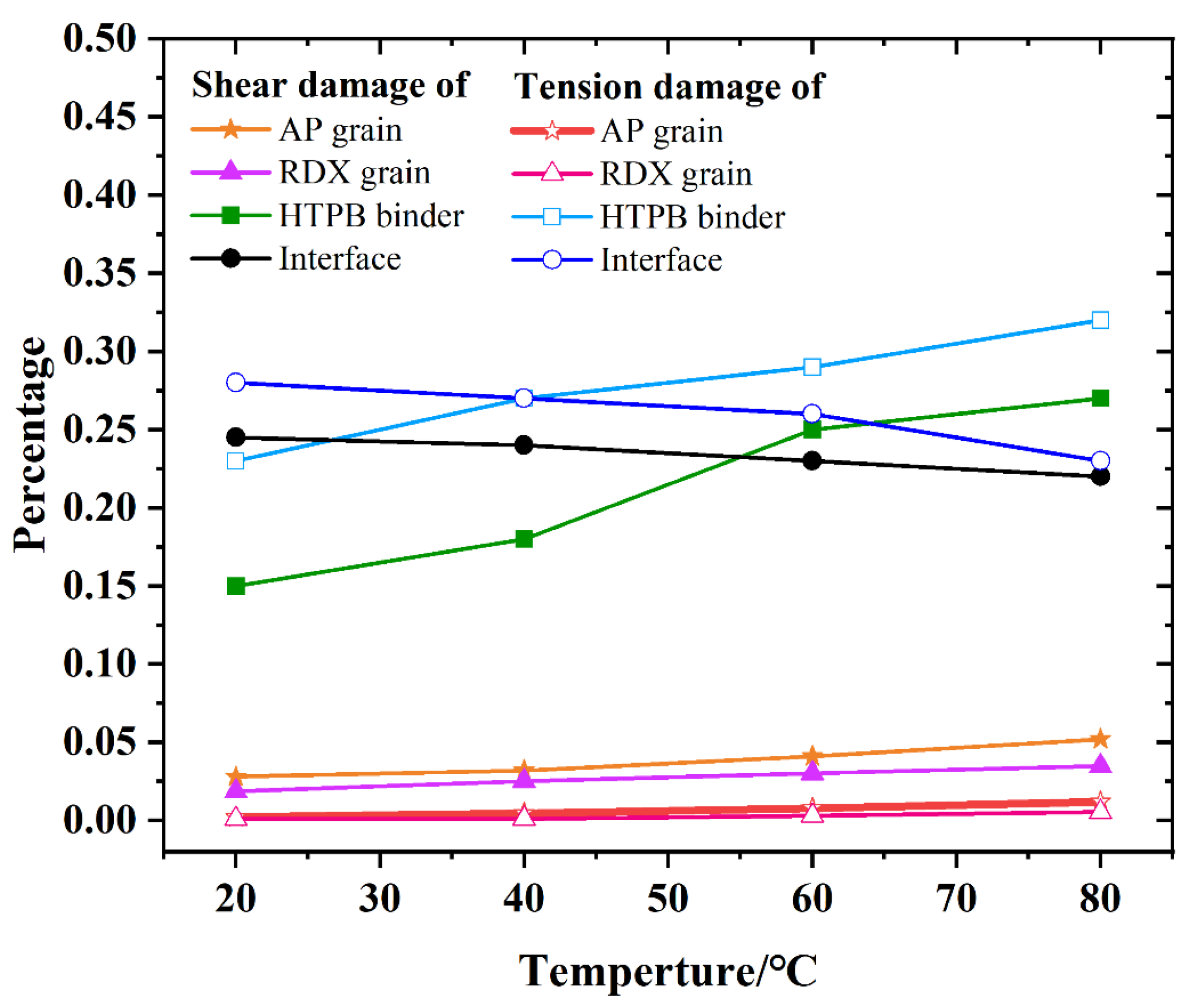
4.1. Thermal Damage Behavior of Propellants at Different Temperatures
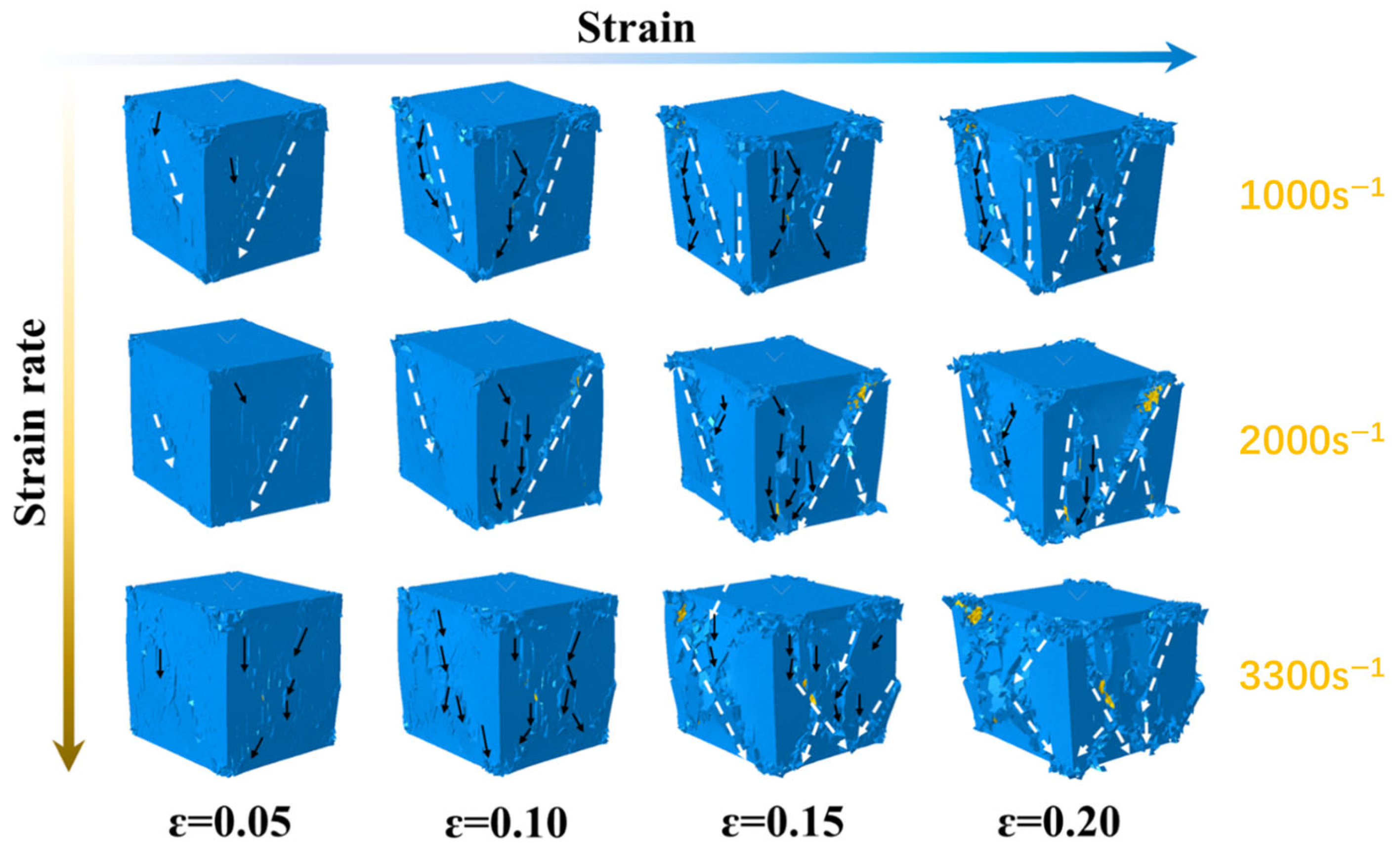
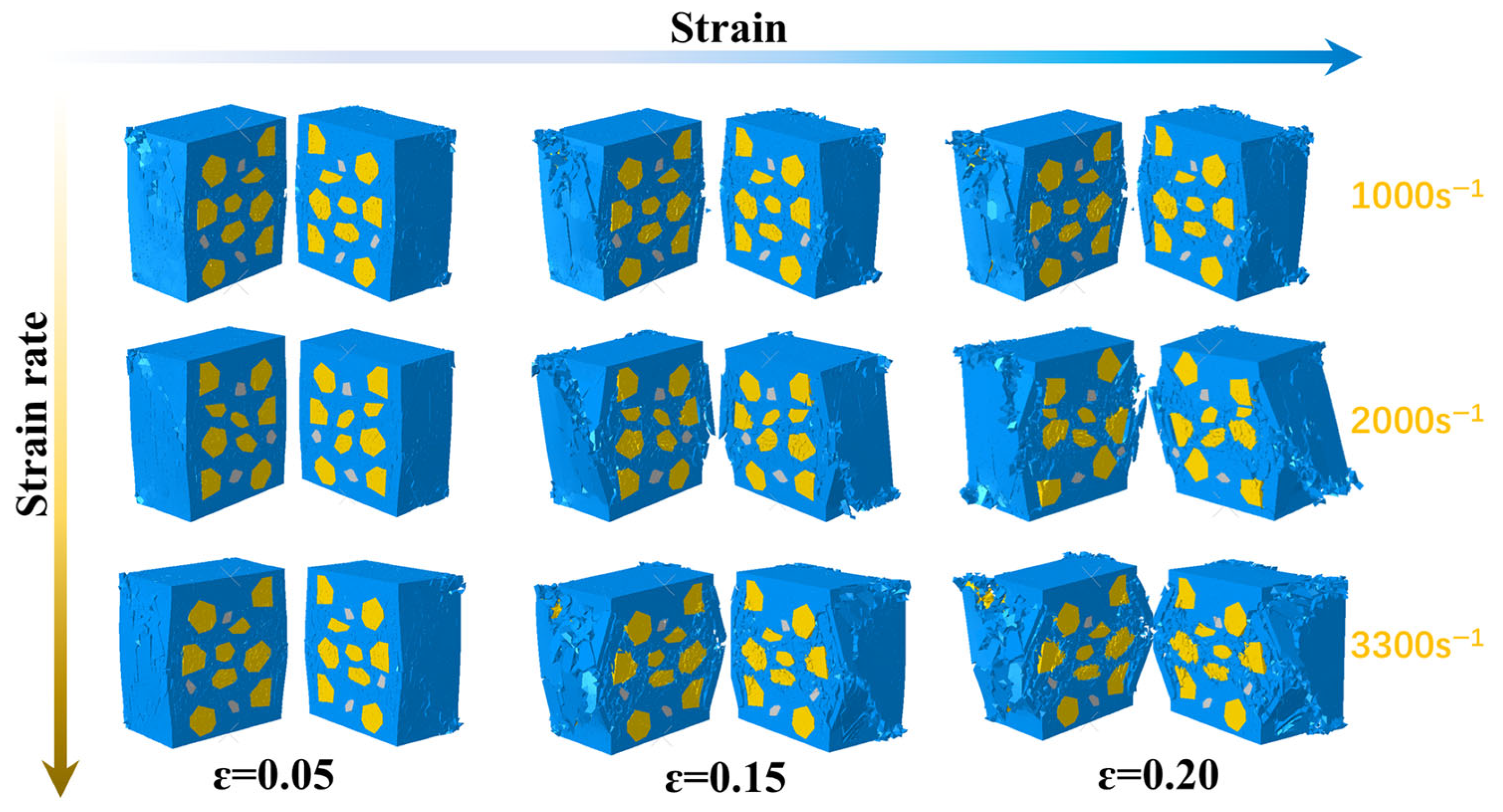
4.2. Damage Behavior of Propellant at Different Strain Rates
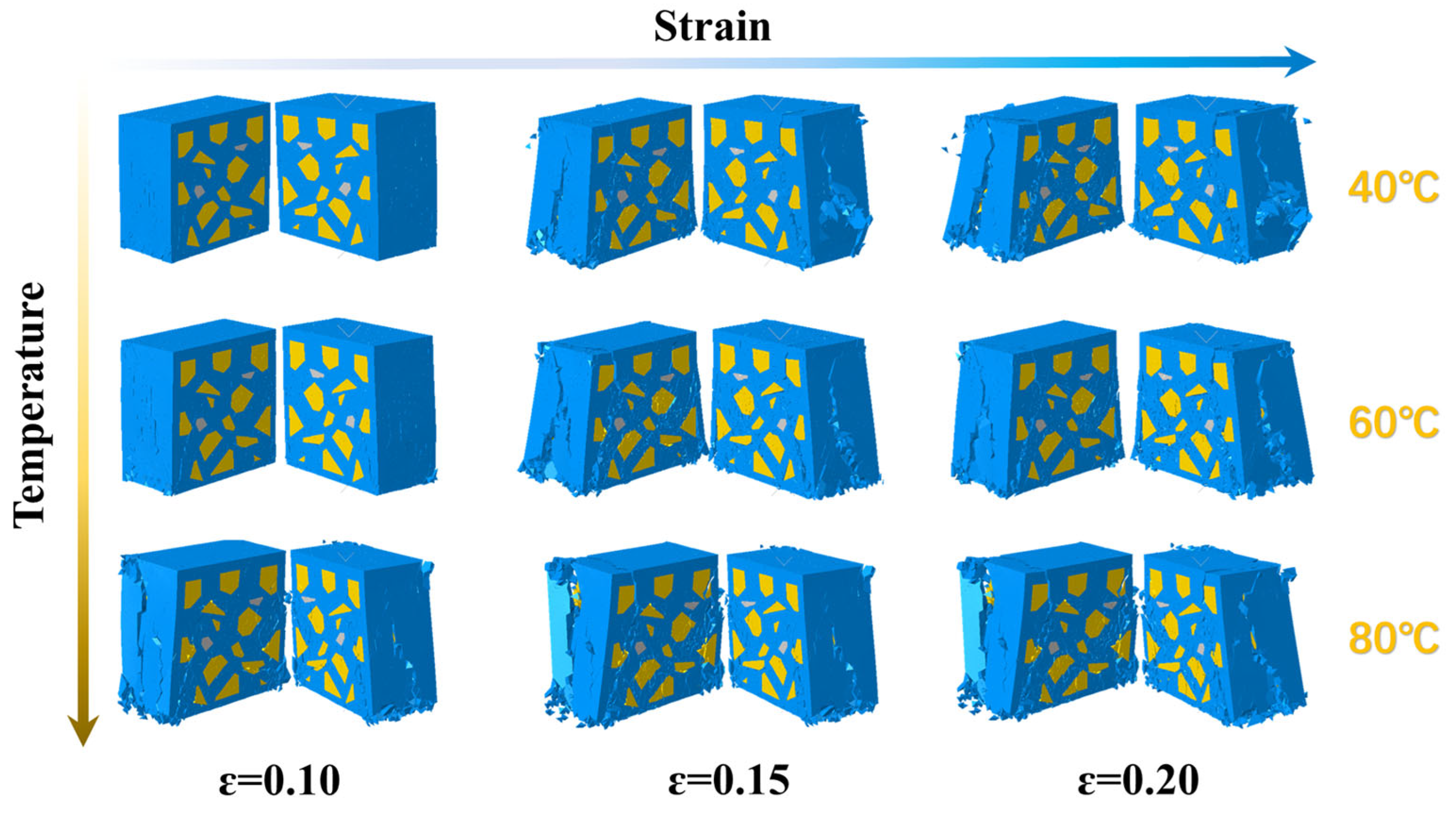
4.3. Damage Behavior of Propellant at Different Temperatures
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zou, Z.; Qiang, H.; Zhang, F.; Wang, X.; Li, Y. Research on mechanical behavior of particle/matrix interface in composite solid propellant. Eur. J. Mech.-A/Solids 2025, 109, 105498. [Google Scholar] [CrossRef]
- Xing, R.; Wang, L.; Zhang, F.; Hou, C. Mechanical behavior and constitutive model of NEPE solid propellant in finite deformation. Mech. Mater. 2022, 172, 104383. [Google Scholar] [CrossRef]
- Gouhier, F.; Diani, J.; Vandenbroucke, A. A finite strain viscoelastic model with damage and tension–compression asymmetry considerations for solid propellants. Mech. Mater. 2024, 199, 105152. [Google Scholar] [CrossRef]
- Kokash, Y.; Regueiro, R.; Miller, N.; Zhang, Y. A non-isothermal breakage-damage model for plastic-bonded granular materials incorporating temperature, pressure, and rate dependencies. Int. J. Solids Struct. 2024, 305, 113085. [Google Scholar] [CrossRef]
- Wang, G.; Wu, Y.; Yang, K.; Xia, Q.; Huang, F. Optimization of mechanical and safety properties by designing interface characteristics within energetic composites. Def. Technol. 2024, 42, 59–72. [Google Scholar] [CrossRef]
- Lu, D.; Zhang, B.; Liu, L.; Zhang, H.; Cao, L.; Zhou, Y. Three-dimensional cohesive finite element simulations coupled with machine learning to predict mechanical properties of polymer-bonded explosives. Compos. Sci. Technol. 2025, 259, 110947. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Dave, P.N. Nano-metal oxide: Potential catalyst on thermal decomposition of ammonium perchlorate. J. Exp. Nanosci. 2012, 7, 205–231. [Google Scholar] [CrossRef]
- Arora, H.; Tarleton, E.; Li-Mayer, J.; Charalambides, M.; Lewis, D. Modelling the damage and deformation process in a plastic bonded explosive microstructure under tension using the finite element method. Comput. Mater. Sci. 2015, 110, 91–101. [Google Scholar] [CrossRef]
- Zhang, X.; Luo, G.; Zhou, H.; Wei, Q.; Yang, X.; Zhu, Y.; Cao, P.; Shen, Q. Damage behavior of high particle volume fraction composites with initial damage by finite element meso-modeling. Compos. Struct. 2024, 329, 117785. [Google Scholar] [CrossRef]
- Yang, D.O.; Qin, C.; Qin, X.; Xie, Q.; Nian, X. The thermal response of the ignition and combustion of high-energy material projectiles under the influence of heat. Case Stud. Therm. Eng. 2024, 55, 104168. [Google Scholar] [CrossRef]
- Guo, Z.; Xu, J.; Chen, X.; Wang, T.; Liu, J.; Zhang, H.; Chen, Y.; Song, Q. Effects of dynamic loading and temperature on NEPE propellant: Damage and ignition analysis. Mech. Time-Depend. Mater. 2024, 28, 1927–1945. [Google Scholar] [CrossRef]
- Geng, T.; Qiang, H.; Wang, Z.; Wang, X.; Zhu, Z.; Qiao, D. Macroscopic and mesoscopic properties of HTPB propellant under low temperature dynamic biaxial compression loading. Polym. Test. 2023, 119, 107922. [Google Scholar] [CrossRef]
- Keyhani, A.; Kim, S.; Horie, Y.; Zhou, M. Energy dissipation in polymer-bonded explosives with various levels of constituent plasticity and internal friction. Comput. Mater. Sci. 2019, 159, 136–149. [Google Scholar] [CrossRef]
- Deng, X.; Huang, Y.; Zhao, J. Numerical investigation of damage and ignition behaviors of PBX under punch loading. Eng. Fract. Mech. 2024, 298, 109903. [Google Scholar] [CrossRef]
- Xia, Q.-Z.; Wu, Y.-Q.; Huang, F.-L. Effect of interface behaviour on damage and instability of PBX under combined tension–shear loading. Def. Technol. 2023, 23, 137–151. [Google Scholar] [CrossRef]
- Rae, P.; Goldrein, H.; Palmer, S.; Field, J.; Lewis, A. Quasi–static studies of the deformation and failure of β–HMX based polymer bonded explosives. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2002, 458, 743–762. [Google Scholar] [CrossRef]
- Lei, M.; Wang, J.; Cheng, J.; Xiao, J.; Wen, L.; Lu, H.; Hou, X. A constitutive model of the solid propellants considering the interface strength and dewetting. Compos. Sci. Technol. 2020, 185, 107893. [Google Scholar] [CrossRef]
- Oberth, A.; Bruenner, R. Tear phenomena around solid inclusions in castable elastomers. Trans. Soc. Rheol. 1965, 9, 165–185. [Google Scholar] [CrossRef]
- Hou, Y.; Xu, J.; Zhou, C.; Chen, X. Microstructural simulations of debonding, nucleation, and crack propagation in an HMX-MDB propellant. Mater. Des. 2021, 207, 109854. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, R.; Chen, P.; Zhou, B.; Hu, G.; Han, C.; Lv, K.; Zhu, S. Mechanical behavior of PBX with different HMX crystal size during die pressing: Experimental study and DEM simulation. Compos. Sci. Technol. 2022, 222, 109378. [Google Scholar] [CrossRef]
- Liu, C.; Shi, Y.; Liang, X. DEM study on hot spots formation of heterogeneous explosives under shock loading. Chin. J. Comput. Phys. 2014, 31, 523. [Google Scholar]
- Ahmadi, M.; Sadighi, M.; Hosseini-Toudeshky, H. Microstructure-based deformation and fracture modeling of particulate reinforced composites with ordinary state-based peridynamic theory. Compos. Struct. 2022, 279, 114734. [Google Scholar] [CrossRef]
- McDonald, B.A.; Rice, J.R.; Kirkham, M.W. Humidity induced burning rate degradation of an iron oxide catalyzed ammonium perchlorate/HTPB composite propellant. Combust. Flame 2014, 161, 363–369. [Google Scholar] [CrossRef]
- Di Benedetto, G.L.; van Ramshorst, M.C.; Duvalois, W.; Hooijmeijer, P.A.; van der Heijden, A. In-situ tensile testing of propellants in SEM. Propellants Explos. Pyrotech. 2017, 42, 1396–1400. [Google Scholar] [CrossRef]
- Hu, R.; Prakash, C.; Tomar, V.; Harr, M.; Gunduz, I.E.; Oskay, C. Experimentally-validated mesoscale modeling of the coupled mechanical–thermal response of AP–HTPB energetic material under dynamic loading. Int. J. Fract. 2017, 203, 277–298. [Google Scholar] [CrossRef]
- de Francqueville, F.; Gilormini, P.; Diani, J.; Vandenbroucke, A. Comparison of the finite strain macroscopic behavior and local damage of a soft matrix highly reinforced by spherical or polyhedral particles. Eur. J. Mech.-A/Solids 2020, 84, 104070. [Google Scholar] [CrossRef]
- Liu, Y.; Qian, W.; Wang, L.; Xue, Y.; Hou, C.; Wu, S. In situ X-ray tomography study on internal damage evolution of solid propellant for carrier rockets. Mater. Sci. Eng. A 2023, 882, 145451. [Google Scholar] [CrossRef]
- Dai, K.; Lu, B.; Chen, P.; Chen, J. Modelling microstructural deformation and the failure process of plastic bonded explosives using the cohesive zone model. Materials 2019, 12, 3661. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, K.; Liu, Q.; Wang, C. NEPE Propellant Mesoscopic Modeling and Damage Mechanism Study Based on Inversion Algorithm. Materials 2024, 17, 1289. [Google Scholar] [CrossRef]
- Zhang, X.; Chang, X.; Lai, J.; Hu, K. Comparative research of tensile and compressive mechanical properties of HTPB propellant at low temperature. J. Solid Rocket Technol. 2013, 36, 771–774. [Google Scholar]
- Xu, Y.; Zhao, S.; Jin, G.; Wang, X.; Liang, L. Ductile fracture of solder-Cu interface and inverse identification of its interfacial model parameters. Mech. Mater. 2017, 114, 279–292. [Google Scholar] [CrossRef]
- Xiao, Y.; Sun, Y.; Yang, Z.; Guo, L. Study of the dynamic mechanical behavior of PBX by Eshelby theory. Acta Mech. 2017, 228, 1993–2003. [Google Scholar] [CrossRef]
- Xu, X.-P.; Needleman, A. Numerical simulations of fast crack growth in brittle solids. J. Mech. Phys. Solids 1994, 42, 1397–1434. [Google Scholar] [CrossRef]
- Gu, X.; Liu, X.; Dong, C.; Zhang, G.; Zhang, L.; Zhang, F. The Mesoscopic Numerical Simulation of GAP/CL20/AP Composite Solid Propellant Based on MPM and FEM. Appl. Sci. 2023, 13, 4552. [Google Scholar] [CrossRef]
- Li, M.-M.; Li, F.-S.; Shen, R.-Q. Molecular dynamics study of RDX/AMMO propellant. Chin. J. Chem. Phys. 2011, 24, 199. [Google Scholar] [CrossRef]
- Xiao, Y.C.; Sun, Y.; Li, X.; Zhang, Q.; Liu, S.; Yang, H. Dynamic mechanical behavior of PBX. Propellants Explos. Pyrotech. 2016, 41, 629–636. [Google Scholar] [CrossRef]
- Gergesova, M.; Zupančič, B.; Saprunov, I.; Emri, I. The closed form tTP shifting (CFS) algorithm. J. Rheol. 2011, 55, 1–16. [Google Scholar] [CrossRef]
- Ho, S.-Y. High strain-rate constitutive models for solid rocket propellants. J. Propuls. Power 2002, 18, 1106–1111. [Google Scholar] [CrossRef]
- Xu, J.; Chen, X.; Wang, H.; Zheng, J.; Zhou, C. Thermo-damage-viscoelastic constitutive model of HTPB composite propellant. Int. J. Solids Struct. 2014, 51, 3209–3217. [Google Scholar] [CrossRef]
- Duncan, E.; Margetson, J. A nonlinear viscoelastic theory for solid rocket propellants based on a cumulative damage approach. Propellants Explos. Pyrotech. 1998, 23, 94–104. [Google Scholar] [CrossRef]
- Prakash, C.; Gunduz, I.E.; Oskay, C.; Tomar, V. Effect of interface chemistry and strain rate on particle-matrix delamination in an energetic material. Eng. Fract. Mech. 2018, 191, 46–64. [Google Scholar] [CrossRef]
- Olokun, A.M.; Prakash, C.; Emre Gunduz, I.; Tomar, V. The role of microstructure in the impact induced temperature rise in hydroxyl terminated polybutadiene (HTPB)–cyclotetramethylene-tetranitramine (HMX) energetic materials using the cohesive finite element method. J. Appl. Phys. 2020, 128, 065901. [Google Scholar] [CrossRef]
- Ambos, A.; Willot, F.; Jeulin, D.; Trumel, H. Numerical modeling of the thermal expansion of an energetic material. Int. J. Solids Struct. 2015, 60, 125–139. [Google Scholar] [CrossRef]
- Wiegand, D.A.; Pinto, J.J. The composition of polymer composite fracture surfaces as studied by XPS. MRS Online Proc. Libr. (OPL) 1995, 409, 281. [Google Scholar] [CrossRef]
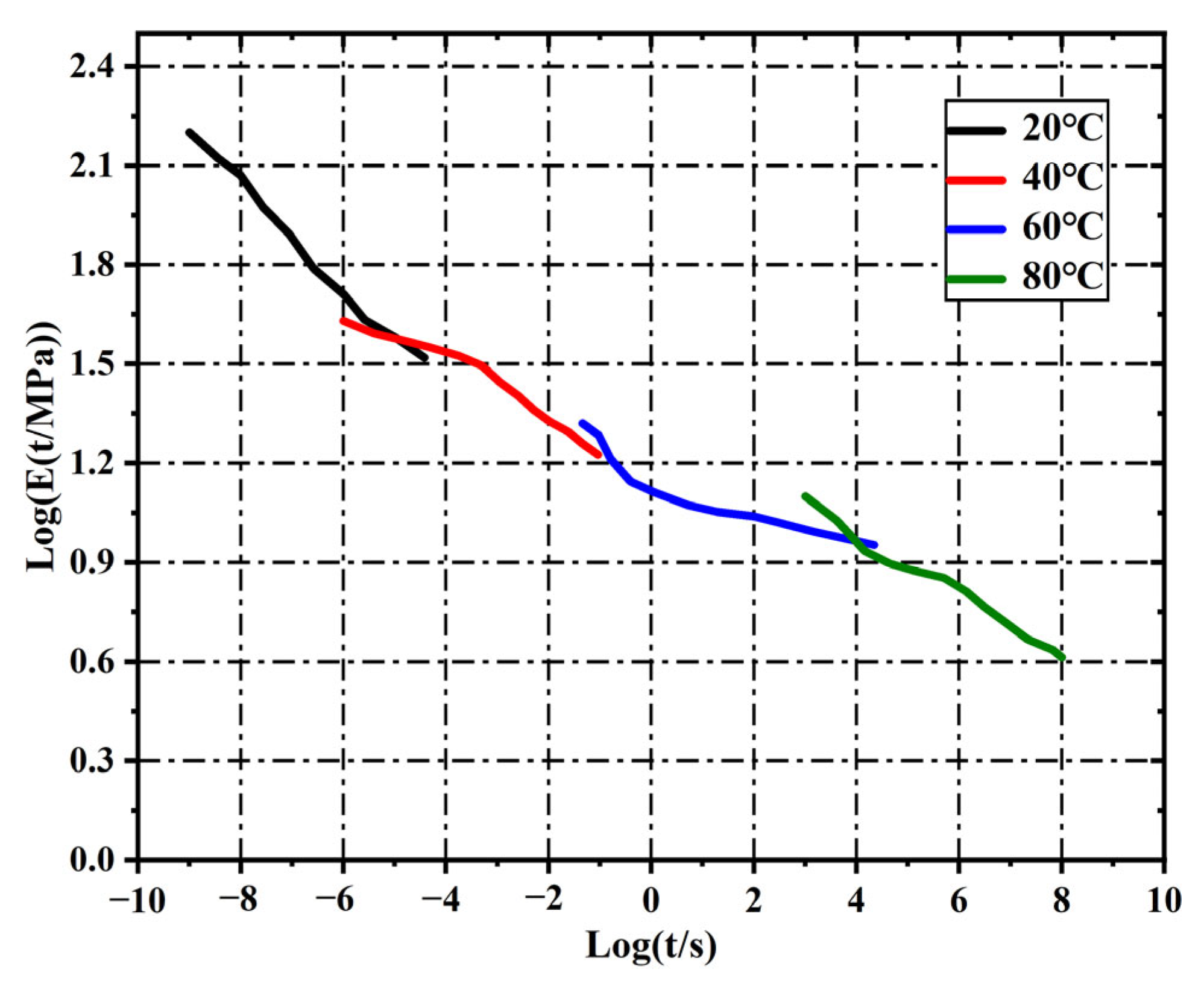





| i | Log (E(t)) | Log () | i | Log (E(t)) | Log () |
|---|---|---|---|---|---|
| 1 | 2.213 | −9 | 10 | 1.112 | 0 |
| 2 | 2.072 | −8 | 11 | 1.063 | 1 |
| 3 | 1.896 | −7 | 12 | 1.038 | 2 |
| 4 | 1.731 | −6 | 13 | 0.982 | 3 |
| 5 | 1.588 | −5 | 14 | 0.931 | 4 |
| 6 | 1.541 | −4 | 15 | 0.858 | 5 |
| 7 | 1.452 | −3 | 16 | 0.816 | 6 |
| 8 | 1.336 | −2 | 17 | 0.724 | 7 |
| 9 | 1.235 | −1 | 18 | 0.619 | 8 |
| Type | Property | 20 °C | 40 °C | 60 °C | 80 °C |
|---|---|---|---|---|---|
| AP Particle | Initial stiffness Kn (MPa/mm) | 647 | 580 | 520 | 460 |
| Maximum traction Sn (MPa) | 32.4 | 30.2 | 28.6 | 26.5 | |
| Critical separations δn, δt (mm) | 0.008 | 0.007 | 0.006 | 0.005 | |
| RDX Particle | Initial stiffness Kn (MPa/mm) | 820 | 780 | 740 | 650 |
| Maximum traction Tn (MPa) | 52.4 | 48.2 | 46.4 | 44.3 | |
| Critical separations δn, δt (mm) | 0.01 | 0.009 | 0.008 | 0.007 | |
| HTPB Binder | Initial stiffness Kn (MPa/mm) | 368 | 282 | 221 | 165 |
| Maximum traction Sn (MPa) | 12.7 | 10.6 | 8.6 | 6.4 | |
| Critical separations δn, δt (mm) | 0.005 | 0.004 | 0.003 | 0.002 | |
| Interface | Initial stiffness Kn (MPa/mm) | 134 | 88 | 42 | 21 |
| Maximum traction Sn (MPa) | 9.8 | 8.1 | 7.2 | 5.7 | |
| Critical separations δn, δt (mm) | 0.003 | 0.002 | 0.0015 | 0.001 |
| Evaluation Index | MSE | RMSE | R2 |
|---|---|---|---|
| Initial stiffness Kn (MPa/mm) | 0.0465 | 0.232 | 0.976 |
| Maximum traction Sn (MPa) | 0.142 | 0.383 | 0.955 |
| Critical separations δn, δt (mm) | 1.32 × 10−8 | 1.1 × 10−4 | 0.963 |
| Evaluation Index | MSE | RMSE | R2 |
|---|---|---|---|
| Initial stiffness Kn (MPa/mm) | 0.0476 | 0.245 | 0.948 |
| Maximum traction Sn (MPa) | 0.145 | 0.396 | 0.941 |
| Critical separations δn, δt (mm) | 1.57 × 10−8 | 1.3 × 10−4 | 0.951 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, B.; Xiao, Y.; Yu, W.; Qu, K.; Sun, Y. Mesoscale Damage Evolution, Localization, and Failure in Solid Propellants Under Strain Rate and Temperature Effects. Polymers 2025, 17, 2093. https://doi.org/10.3390/polym17152093
Gao B, Xiao Y, Yu W, Qu K, Sun Y. Mesoscale Damage Evolution, Localization, and Failure in Solid Propellants Under Strain Rate and Temperature Effects. Polymers. 2025; 17(15):2093. https://doi.org/10.3390/polym17152093
Chicago/Turabian StyleGao, Bo, Youcai Xiao, Wanqian Yu, Kepeng Qu, and Yi Sun. 2025. "Mesoscale Damage Evolution, Localization, and Failure in Solid Propellants Under Strain Rate and Temperature Effects" Polymers 17, no. 15: 2093. https://doi.org/10.3390/polym17152093
APA StyleGao, B., Xiao, Y., Yu, W., Qu, K., & Sun, Y. (2025). Mesoscale Damage Evolution, Localization, and Failure in Solid Propellants Under Strain Rate and Temperature Effects. Polymers, 17(15), 2093. https://doi.org/10.3390/polym17152093





