Process Parameters Optimization and Mechanical Properties of Additively Manufactured Ankle–Foot Orthoses Based on Polypropylene
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Equipment
2.2. Characterization Methods
2.2.1. Differential Scanning Calorimetry
- -
- Heating the sample from −60 °C to 210 °C, followed by a 1 min isotherm at 210 °C to erase thermal history.
- -
- Cooling to −60 °C.
- -
- Second heating cycle up to 210 °C.
- -
- Final cooling to 25 °C before ending the analysis.
2.2.2. Measurement of Specific Heat Capacity as a Function of Temperature
- -
- Stabilizing the sample temperature at 20 °C.
- -
- Heating the sample from 20 °C to 210 °C at 20 °C/min, followed by a 1 min isotherm at 210 °C.
- -
- Cooling back to 20 °C at 20 °C/min.
2.2.3. Thermogravimetric Analysis
2.2.4. Thermomechanical Analysis
2.2.5. Thermal Conductivity
2.2.6. Dynamic Mechanical Analysis
2.2.7. Rheometry
2.2.8. PvT Behavior
2.2.9. Emissivity
2.2.10. Tensile Testing
2.3. Optimization: Experimental Approach
2.3.1. Design of Experiments
2.3.2. Mechanical Property Evaluation Methods
Three-Point Bending Test
Short-Beam Bending Test
2.3.3. Analysis Method
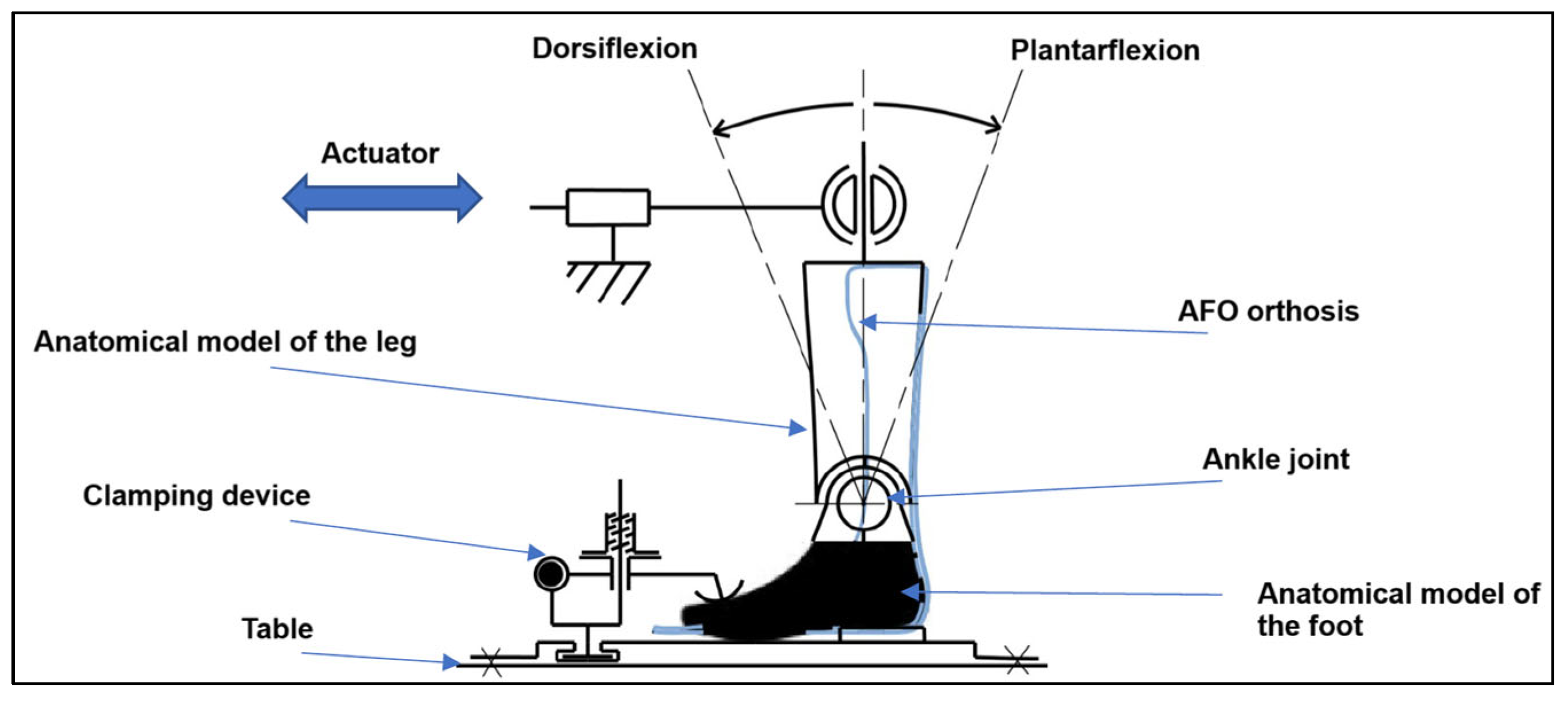
2.3.4. Mechanical Testing of the Orthosis
2.3.5. Optimization: Numerical Approach
Material Characterization
Modeling and Simulation Conditions
3. Results and Discussion
3.1. Material Characterization
3.1.1. Thermal Properties of PP Pellets and PP Filaments
3.1.2. Specific Heat Capacity as a Function of Temperature
3.1.3. Crystallization Kinetics Data
3.1.4. TGA Results
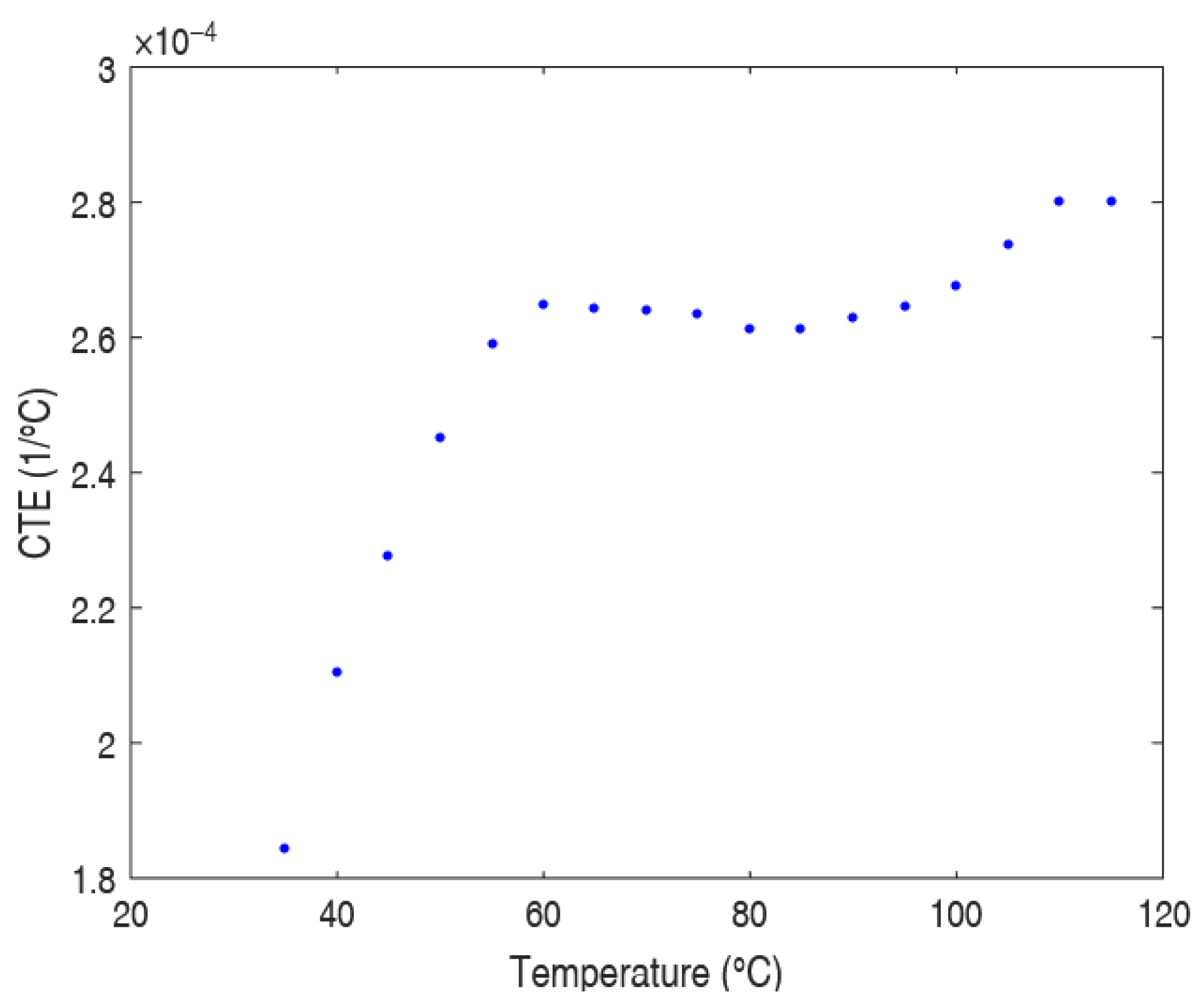
3.1.5. TMA Results
3.1.6. Thermal Conductivity Data
3.1.7. DMA Data
3.1.8. PvT Data
3.1.9. Emissivity
3.1.10. Tensile Testing
3.2. Results of the Design of Experiments
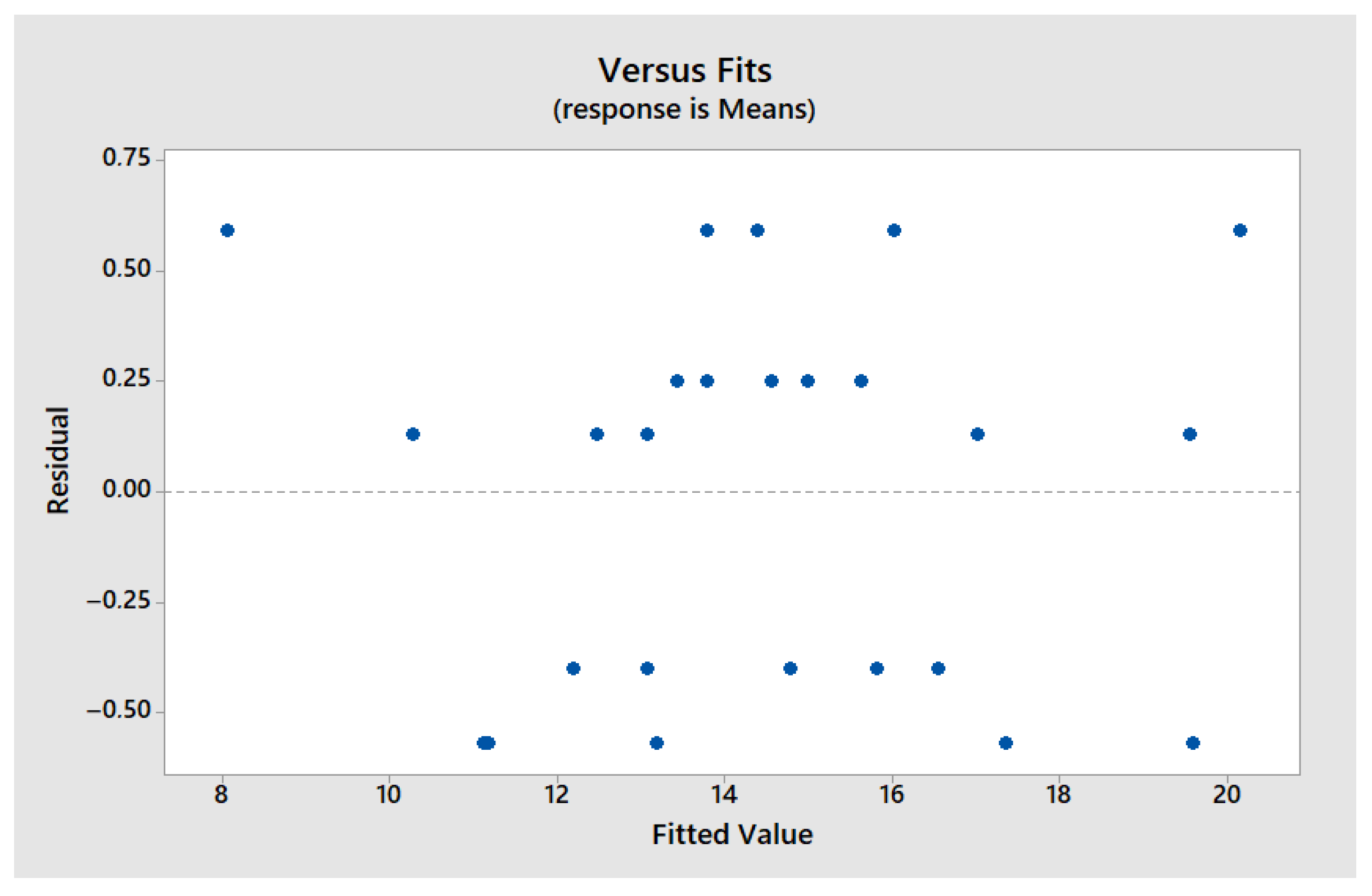
3.2.1. Normal Probability of Residuals
3.2.2. Three-Point Bending Test
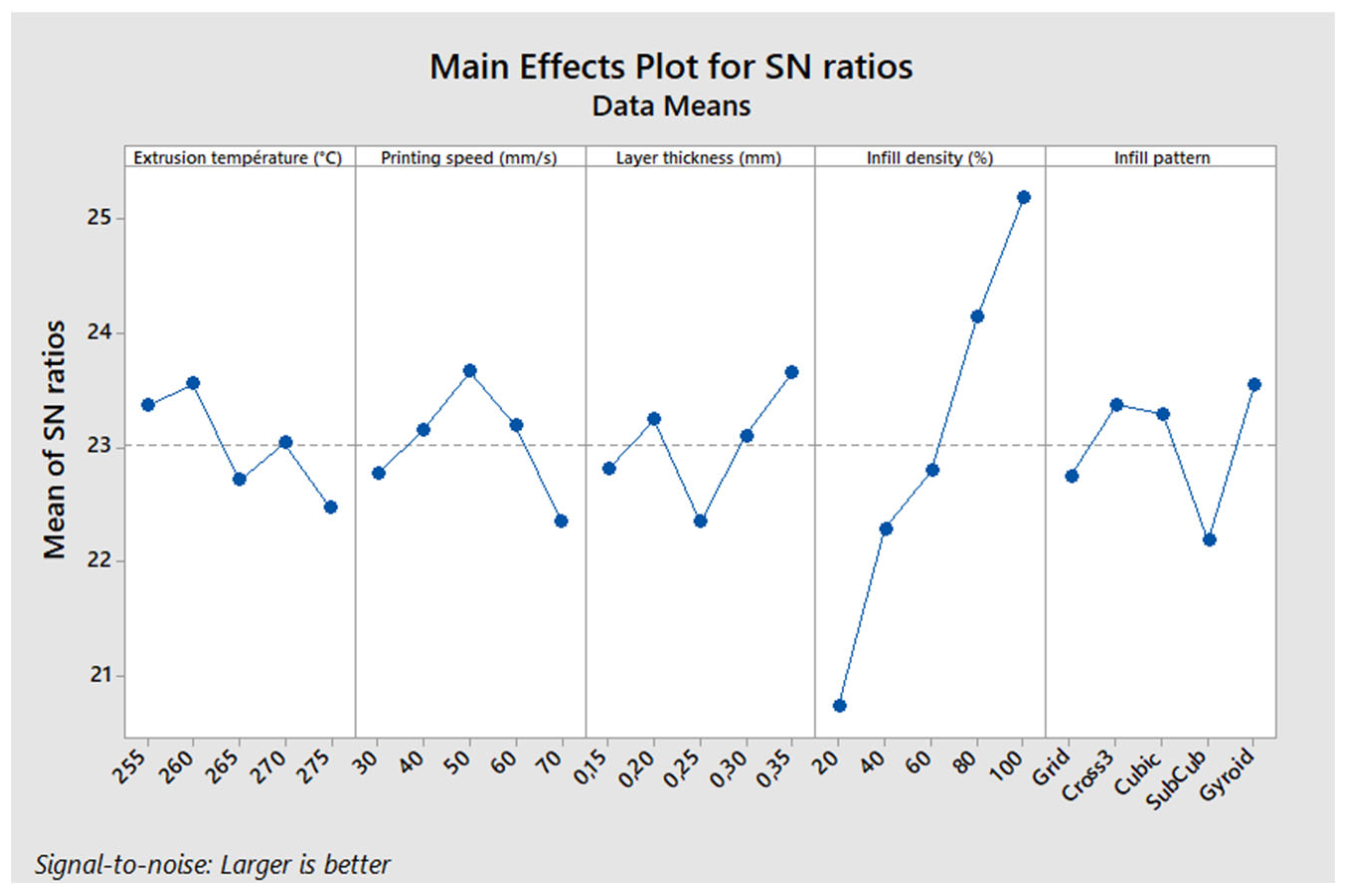
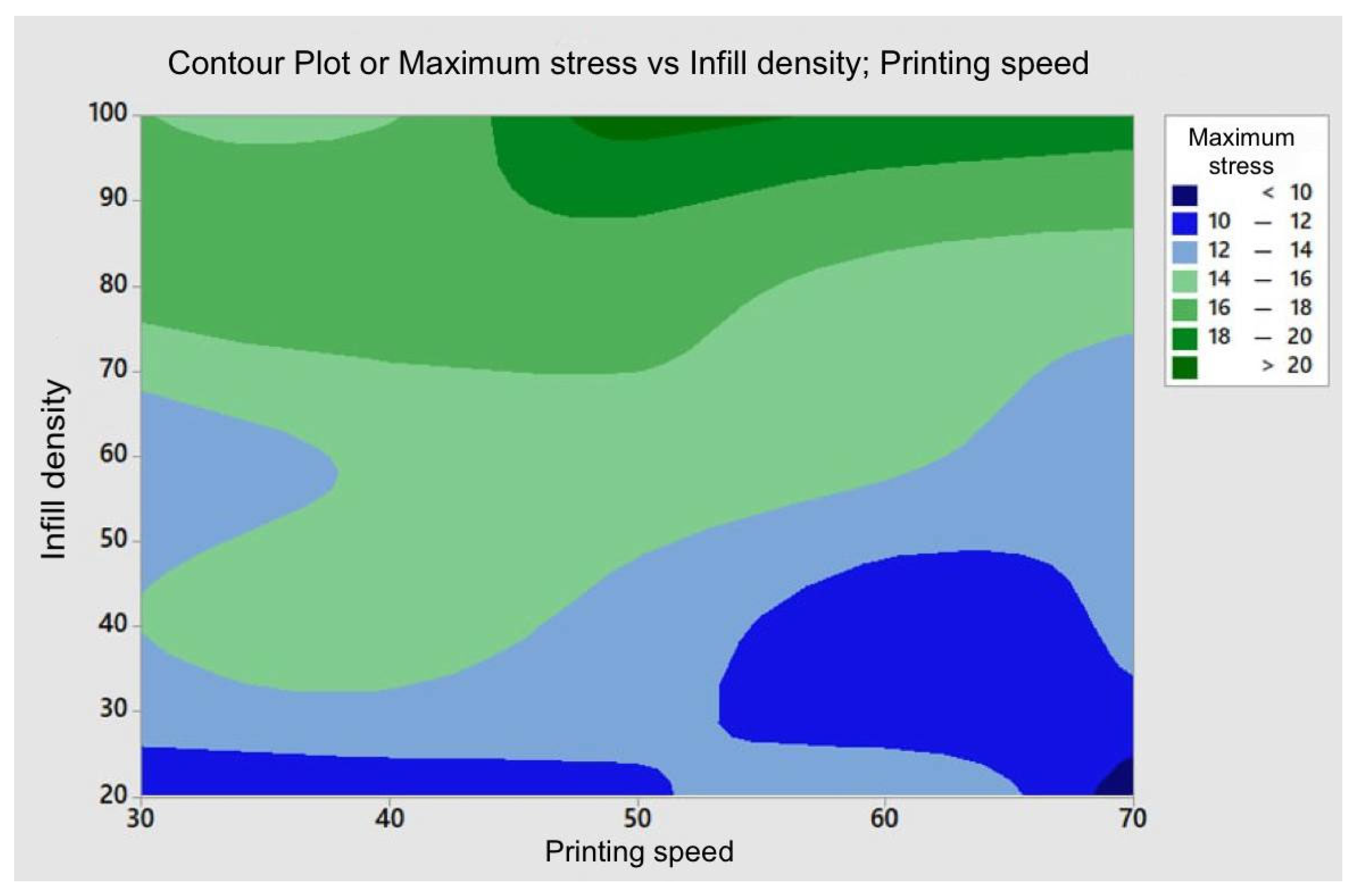
Effect of Parameters on Maximum Stress
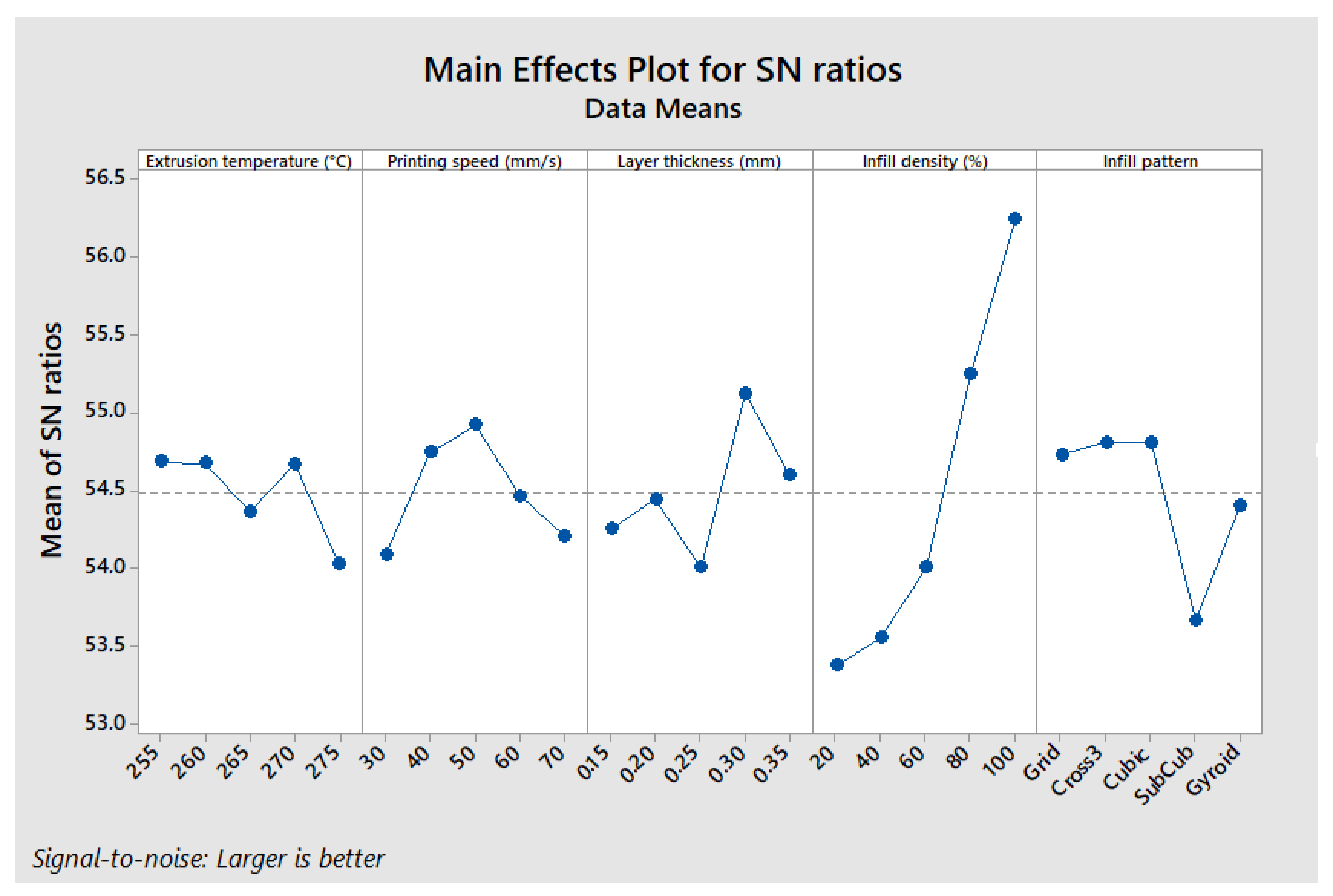
Effect of Parameters on Flexural Modulus
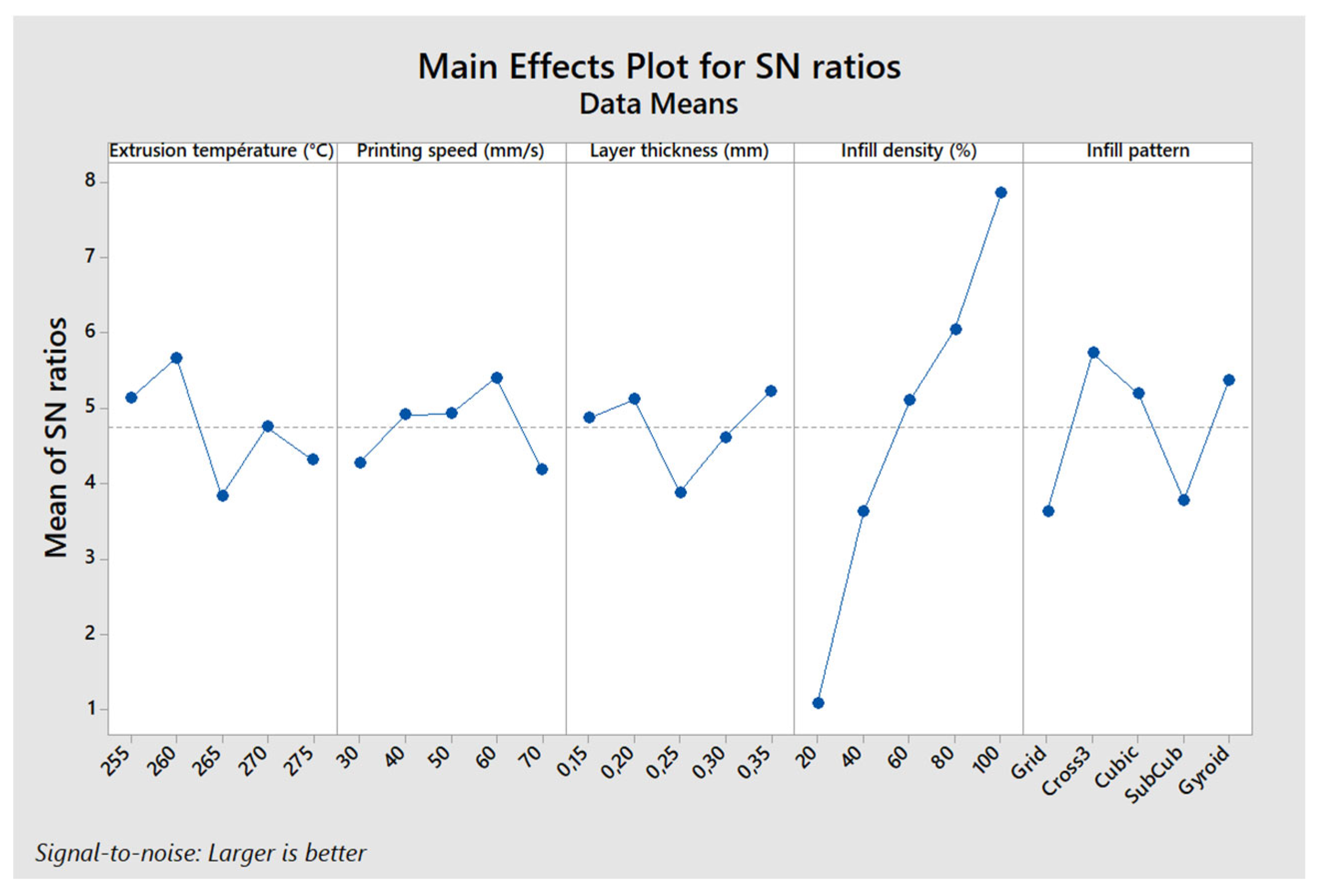
Effect of Parameters on Printing Time
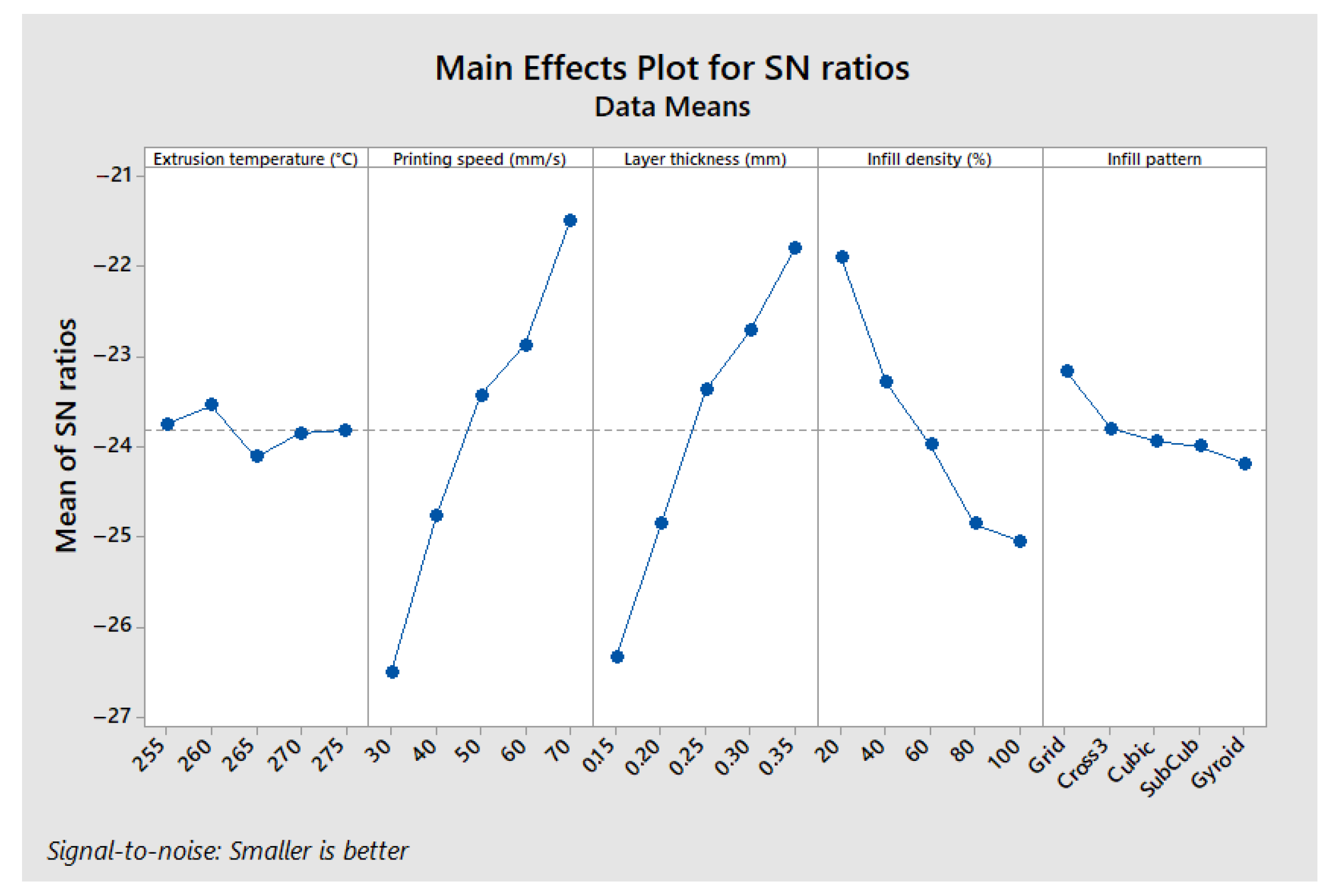
3.2.3. Short-Beam Bending Test
3.2.4. Optimal Parameters
- -
- Configuration 1: ILSS optimization (A2, B4, C5, D5, and E3)
- -
- Configuration 2: Flexural modulus optimization (A4, B3, C4, D5, and E2)
- -
- Configuration 3: Maximum stress optimization (A2, B3, C5, D5, and E5)
3.2.5. Tests on Orthoses
3.3. Numerical Simulation Results
3.3.1. Optimal Orthosis Configurations
3.3.2. Influence of Print Orientation
3.3.3. Warpage Compensation
3.3.4. Optimal Configuration
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hammond, B.; Abu, K.A.; Anyittey-Kokor, D.; Baidoo, P.K.; Leat, M.; Awoonor-Williams, R.; Konadu-Yeboah, D.; Wilson, A.A.; Vormawor, K.K.; Bukari, M.I.S. Determinants of utilization of prostheses and orthoses following lower limb amputation in Sub-Saharan Africa: A systematic review. J. Orthop. Rep. 2025, 4, 100528. [Google Scholar] [CrossRef]
- Delbruel, V. Use of additive manufacturing technologies for functional rehabilitation. Ph.D. Thesis, INSA Lyon, Villeurbanne, France, 2024. [Google Scholar]
- Karimi, A.; Rahmatabadi, D.; Baghani, M. Various FDM mechanisms used in the fabrication of continuous-fiber reinforced composites: A review. Polymers 2024, 16, 831. [Google Scholar] [CrossRef]
- Kaplan, K.; Ulkir, O.; Kuncan, F. Optimization and prediction of mechanical properties of TPU-Based wrist hand orthosis using Bayesian and machine learning models. Measurement 2025, 252, 117405. [Google Scholar] [CrossRef]
- Requena, C.; Bascou, J.; Loiret, I.; Bonnet, X.; Thomas-Pohl, M.; Duraffourg, C.; Calistri, L.; Pillet, H. Effectiveness of a New Microprocessor-Controlled Knee–Ankle–Foot System for Transfemoral Amputees: A Randomized Controlled Trial. Prosthesis 2024, 6, 1591–1606. [Google Scholar] [CrossRef]
- Wojciechowski, E.; Chang, A.Y.; Balassone, D.; Ford, J.; Cheng, T.L.; Little, D.; Menezes, M.P.; Hogan, S.; Burns, J. Feasibility of designing, manufacturing and delivering 3D printed ankle-foot orthoses: A systematic review. J. Foot Ankle Res. 2019, 12, 11. [Google Scholar] [CrossRef]
- Convery, P.; Greig, R.; Ross, R.; Sockalingam, S. A three centre study of the variability of ankle foot orthoses due to fabrication and grade of polypropylene. Prosthet. Orthot. Int. 2004, 28, 175–182. [Google Scholar] [CrossRef]
- Christakopoulos, F.; van Heugten, P.M.; Tervoort, T.A. Additive manufacturing of polyolefins. Polymers 2022, 14, 5147. [Google Scholar] [CrossRef]
- Bregman, D.J.; De Groot, V.; Van Diggele, P.; Meulman, H.; Houdijk, H.; Harlaar, J. Polypropylene ankle foot orthoses to overcome drop-foot gait in central neurological patients: A mechanical and functional evaluation. Prosthet. Orthot. Int. 2010, 34, 293–304. [Google Scholar] [CrossRef] [PubMed]
- Beckerman, H.; Becher, J.; Lankhorst, G.J.; Verbeek, A.M. Walking ability of stroke patients: Efficacy of tibial nerve blocking and a polypropylene ankle-foot orthosis. Arch. Phys. Med. Rehabil. 1996, 77, 1144–1151. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.D.; Abu-Hasaballah, K.S.; Cooper, P.S. Design enhancement of a solid ankle-foot orthosis: Real-time contact pressures evaluation. J. Rehabil. Res. Dev. 2000, 37, 273–282. [Google Scholar]
- Spoerk, M.; Holzer, C.; Gonzalez-Gutierrez, J. Material extrusion-based additive manufacturing of polypropylene: A review on how to improve dimensional inaccuracy and warpage. J. Appl. Polym. Sci. 2020, 137, 48545. [Google Scholar] [CrossRef]
- Wojtyła, S.; Klama, P.; Baran, T. Is 3D printing safe? Analysis of the thermal treatment of thermoplastics: ABS, PLA, PET, and nylon. J. Occup. Environ. Hyg. 2017, 14, D80–D85. [Google Scholar] [CrossRef]
- Walbran, M.; Turner, K.; McDaid, A. Customized 3D printed ankle-foot orthosis with adaptable carbon fibre composite spring joint. Cogent Eng. 2016, 3, 1227022. [Google Scholar] [CrossRef]
- Ali, M.H.; Smagulov, Z.; Otepbergenov, T. Finite element analysis of the CFRP-based 3D printed ankle-foot orthosis. Procedia Comput. Sci. 2021, 179, 55–62. [Google Scholar] [CrossRef]
- Seo, K.-J.; Kim, B.; Mun, D. Development of customized ankle-foot-orthosis using 3D scanning and printing technologies. J. Mech. Sci. Technol. 2023, 37, 6131–6142. [Google Scholar] [CrossRef]
- Totah, D.; Kovalenko, I.; Saez, M.; Barton, K. Manufacturing choices for ankle-foot orthoses: A multi-objective optimization. Procedia Cirp 2017, 65, 145–150. [Google Scholar] [CrossRef]
- Totah, D.; Menon, M.; Jones-Hershinow, C.; Barton, K.; Gates, D.H. The impact of ankle-foot orthosis stiffness on gait: A systematic literature review. Gait Posture 2019, 69, 101–111. [Google Scholar] [CrossRef] [PubMed]
- Sharma, K.; Kumar, K.; Singh, K.R.; Rawat, M. Optimization of FDM 3D printing process parameters using Taguchi technique. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; Volume 1168, p. 012022. [Google Scholar]
- Delbruel, V.; Banoune, A.; Tardif, N.; Duchet-Rumeau, J.; Elguedj, T.; Chevalier, J. Quantifying the effect of material stiffness and wall thickness on the mechanical properties of ankle–foot orthoses manufactured by material extrusion. Prog. Addit. Manuf. 2025, 10, 1447–1459. [Google Scholar] [CrossRef]
- ISO 22007-2:2008; Plastics—Determination of Thermal Conductivity and Thermal Diffusivity—Part 2: Transient Plane Heat Source (Hot Disc) Method. International Organization for Standardization (ISO): Geneva, Switzerland, 2008.
- He, Y. Rapid thermal conductivity measurement with a hot disk sensor: Part 1. Theoretical considerations. Thermochim. Acta 2005, 436, 122–129. [Google Scholar] [CrossRef]
- Yousfi, M.; Belhadj, A.; Lamnawar, K.; Maazouz, A. 3D printing of PLA and PMMA multilayered model polymers: An innovative approach for a better-controlled pellet multi-extrusion process. ESAFORM 2021. [Google Scholar] [CrossRef]
- ISO 527-2:1997; Plastics—Determination of Tensile Properties. International Organization for Standardization (ISO): Geneva, Switzerland, 1997.
- Palo, R.D.; Cavalieri, C. Use of Propylene Based Filament in 3D Printing. Patent WO2017182209A1; Basell Poliolefine: Ferrara, Italy, 26 October 2017. [Google Scholar]
- ISO 178:2019; Plastics–Determination of Flexural Properties. International Organization for Standardization (ISO): Geneva, Switzerland, 2019.
- ASTM D2344:2016; Standard Test Method for Short-Beam Strength of Polymer Matrix Composite Materials and Their Laminates. ASTM International: West Conshohocken, PA, USA, 2016.
- ISO 22675:2006; Prosthetics—Testing of Ankle-Foot Devices and Foot Units—Requirements and Test Methods. International Organization for Standardization (ISO): Geneva, Switzerland, 2006.
- ASTM E1269–11:2012; Standard Test Method for Determining Specific Heat Capacity by Differential Scanning Calorimetry. ASTM International: West Conshohocken, PA, USA, 2012.
- Al Rashid, A.; Koç, M. Numerical predictions and experimental validation on the effect of material properties in filament material extrusion. J. Manuf. Process. 2023, 94, 403–412. [Google Scholar] [CrossRef]
- Yu, Y.; Jiang, B.; Chen, Y.; Ye, L. Modelling and characterising FFF process of semi-crystalline polymers: Warpage formation and mechanism analysis. Polym. Polym. Compos. 2024, 32, 09673911241273654. [Google Scholar] [CrossRef]
- Santoro, L.A.; Fischer, M.; Spoerer, Y.; Stommel, M.; Kuehnert, I. Experimental Determination of the Nakamura Crystallization Model Parameters of Isotactic Polypropylene (Ipp). SSRN. Available online: https://ssrn.com/abstract=4791987 (accessed on 15 June 2025).
- Coppola, F.; Greco, R.; Martuscelli, E.; Kammer, H.; Kummerlowe, C. Mechanical properties and morphology of isotactic polypropylene/ethylene-propylene copolymer blends. Polymer 1987, 28, 47–56. [Google Scholar] [CrossRef]
- Zoller, P. Pressure–volume–temperature relationships of solid and molten polypropylene and poly (butene-1). J. Appl. Polym. Sci. 1979, 23, 1057–1061. [Google Scholar] [CrossRef]
- Hakoume, D.; Dombrovsky, L.; Delaunay, D.; Rousseau, B. Effect of Processing Temperature on Radiative Properties of Polypropylene and Heat Transfer in the Pure and Glassfibre Reinforced Polymer. In International Heat Transfer Conference Digital Library; Begel House Inc.: Danbury, CT, USA, 2014. [Google Scholar]
- Peng, C.; Tran, P.; Lalor, S.; Tirosh, O.; Rutz, E. Tuning the mechanical responses of 3D-printed ankle-foot orthoses: A numerical study. Int. J. Bioprinting 2024, 10, 3390. [Google Scholar] [CrossRef]
- Jin, Y.; Joe Qin, S.; Huang, Q. Offline predictive control of out-of-plane shape deformation for additive manufacturing. J. Manuf. Sci. Eng. 2016, 138, 121005. [Google Scholar] [CrossRef]




| Variables | Values |
|---|---|
| Infill Density/Pattern | 100%/concentric |
| Layer Width/Thickness | 0.6 mm/0.2 mm |
| Number of Outlines | 2 |
| Build Plate/Nozzle Temperature | 23/260 °C |
| Infill/External/Initial Speed Build Plate Adhesion | 50/30/20 mm/min PP plate + raft |
| Variables | Units | 1 | 2 | 3 | 4 | 5 | Symbol |
|---|---|---|---|---|---|---|---|
| Extrusion temperature | °C | 255 | 260 | 265 | 270 | 275 | A |
| Printing speed | mm/s | 30 | 40 | 50 | 60 | 70 | B |
| Layer thickness | mm | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | C |
| Infill density | % | 20 | 40 | 60 | 80 | 100 | D |
| Infill pattern | Grid | Cross 3D | Cubic | Cubic subdivision | Gyroid | E |
| Test | Variables | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| 1 | 255 | 30 | 0.15 | 20 | Grid |
| 2 | 255 | 40 | 0.2 | 40 | Cross 3D |
| 3 | 255 | 50 | 0.25 | 60 | Cubic |
| 4 | 255 | 60 | 0.3 | 80 | Cubic subdivision |
| 5 | 255 | 70 | 0.35 | 100 | Gyroid |
| 6 | 260 | 30 | 0.2 | 60 | Cubic subdivision |
| 7 | 260 | 40 | 0.25 | 80 | Gyroid |
| 8 | 260 | 50 | 0.3 | 100 | Grid |
| 9 | 260 | 60 | 0.35 | 20 | Cross 3D |
| 10 | 260 | 70 | 0.15 | 40 | Cubic |
| 11 | 265 | 30 | 0.25 | 100 | Cross 3D |
| 12 | 265 | 40 | 0.3 | 20 | Cubic |
| 13 | 265 | 50 | 0.35 | 40 | Cubic subdivision |
| 14 | 265 | 60 | 0.15 | 60 | Gyroid |
| 15 | 265 | 70 | 0.2 | 80 | Grid |
| 16 | 270 | 30 | 0.3 | 40 | Gyroid |
| 17 | 270 | 40 | 0.35 | 60 | Grid |
| 18 | 270 | 50 | 0.15 | 80 | Cross 3D |
| 19 | 270 | 60 | 0.2 | 100 | Cubic |
| 20 | 270 | 70 | 0.25 | 20 | Cubic subdivision |
| 21 | 275 | 30 | 0.35 | 80 | Cubic |
| 22 | 275 | 40 | 0.15 | 100 | Cubic subdivision |
| 23 | 275 | 50 | 0.2 | 20 | Gyroid |
| 24 | 275 | 60 | 0.25 | 40 | Grid |
| 25 | 275 | 70 | 0.3 | 60 | Cross 3D |
| Property | Test Method | Standard |
|---|---|---|
| Thermal transition | DSC | – |
| Heat capacity (Cp) vs. temperature | DSC (heat flow) | ASTM E-1269-11 [29] |
| Thermal stability index (TSI) | TGA | – |
| Coefficient of thermal expansion (CTE) vs. temperature | TMA | ASTM E831-14/ISO 11359-2 |
| Thermal conductivity vs. temperature | TPS (Transient Plane Source) | ASTM E1530-19 |
| Specific volume vs. temperature | PvT | ISO 17744:2004 |
| Young’s modulus vs. temperature | DMA | ASTM D5279/ISO 6721/ASTM D4065 |
| Crystallization kinetics | Isothermal DSC (Nakamura–Weibull model) | ASTM 1269-11 |
| Parameter | Value |
|---|---|
| Shape parameter | 2.5 |
| Scale parameter | 148 |
| Magnitude parameter | 2.8 |
| Avrami index | 2.93 |
| Symbol | Unit | Value |
|---|---|---|
| Property | Elastic Stress (MPa) | Ultimate Stress (MPa) | Strain at Elastic Limit (%) | Strain at Break (%) |
|---|---|---|---|---|
| Datasheet | 17 | 15 | 6 | 500 |
| Experimental results | 17.6 | 17.4 | - | 452 |
| Test | Variables | Three-Point Bending Responses | Short-Beam Bending Responses | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | Flexural Modulus (MPa) | Maximum Stress (MPa) | Time (min) | ILSS (MPa) | Time (min) | |
| 1 | 255 | 30 | 0.15 | 20 | Grid | 477 ± 22 | 10 ± 0 | 19.7 | 0.98 ± 0.03 | 7.3 |
| 2 | 255 | 40 | 0.2 | 40 | Cross 3D | 549 ± 21 | 15 ± 0.3 | 18.3 | 1.93 ± 0.01 | 5.7 |
| 3 | 255 | 50 | 0.25 | 60 | Cubic | 535 ± 26 | 15 ± 0.2 | 14.7 | 1.96 ± 0.05 | 4.3 |
| 4 | 255 | 60 | 0.3 | 80 | Sub. cubic | 567 ± 45 | 15 ± 0.1 | 14.0 | 1.92 ± 0.06 | 3.7 |
| 5 | 255 | 70 | 0.35 | 100 | Gyroid | 590 ± 44 | 19 ± 0.6 | 11.7 | 2.71 ± 0.04 | 3.3 |
| 6 | 260 | 30 | 0.2 | 60 | Sub. cubic | 405 ± 5 | 13 ± 0.2 | 25.0 | 1.74 ± 0.03 | 7.0 |
| 7 | 260 | 40 | 0.25 | 80 | Gyroid | 597 ± 1 | 17 ± 0.5 | 17.7 | 2.16 ± 0.02 | 5.0 |
| 8 | 260 | 50 | 0.3 | 100 | Grid | 818 ± 26 | 21 ± 0.6 | 13.7 | 2.48 ± 0.01 | 4.0 |
| 9 | 260 | 60 | 0.35 | 20 | Cross 3D | 504 ± 16 | 14 ± 0.3 | 8.7 | 1.72 ± 0.02 | 3.3 |
| 10 | 260 | 70 | 0.15 | 40 | Cubic | 467 ± 6 | 13 ± 0.3 | 14.7 | 1.63 ± 0.01 | 6.0 |
| 11 | 265 | 30 | 0.25 | 100 | Cross 3D | 589 ± 5 | 16 ± 0.2 | 24.0 | 2.06 ± 0.04 | 6.7 |
| 12 | 265 | 40 | 0.3 | 20 | Cubic | 484 ± 17 | 11 ± 0.4 | 13.3 | 1.06 ± 0.02 | 4.3 |
| 13 | 265 | 50 | 0.35 | 40 | Sub. cubic | 476 ± 7.1 | 13 ± 0.2 | 11.0 | 1.29 ± 0.04 | 3.7 |
| 14 | 265 | 60 | 0.15 | 60 | Gyroid | 505 ± 27 | 14 ± 0.5 | 20.7 | 1.95 ± 0.07 | 6.3 |
| 15 | 265 | 70 | 0.2 | 80 | Grid | 571 ± 39 | 15 ± 0.2 | 14.7 | 1.66 ± 0.13 | 4.7 |
| 16 | 270 | 30 | 0.3 | 40 | Gyroid | 500 ± 8 | 14 ± 0.3 | 18.7 | 1.63 ± 0.04 | 5.3 |
| 17 | 270 | 40 | 0.35 | 60 | Grid | 539 ± 17 | 14 ± 0.2 | 13.0 | 1.65 ± 0.02 | 4.0 |
| 18 | 270 | 50 | 0.15 | 80 | Cross 3D | 573 ± 10 | 17 ± 0.3 | 23.3 | 2.29 ± 0.08 | 6.3 |
| 19 | 270 | 60 | 0.2 | 100 | Cubic | 714 ± 15 | 20 ± 0.5 | 17.3 | 2.85 ± 0.26 | 5.0 |
| 20 | 270 | 70 | 0.25 | 20 | Sub. cubic | 421 ± 16 | 9 ± 0.1 | 9.3 | 0.88 ± 0.02 | 3.7 |
| 21 | 275 | 30 | 0.35 | 80 | Cubic | 584 ± 19 | 17 ± 0.2 | 19.3 | 2.06 ± 0.02 | 5.3 |
| 22 | 275 | 40 | 0.15 | 100 | Sub. cubic | 566 ± 20 | 16 ± 0.3 | 27.7 | 2.32 ± 0.03 | 7.3 |
| 23 | 275 | 50 | 0.2 | 20 | Gyroid | 450 ± 8 | 12 ± 0.1 | 14.0 | 1.19 ± 0.03 | 5.0 |
| 24 | 275 | 60 | 0.25 | 40 | Grid | 400 ± 8 | 11 ± 0.4 | 12.0 | 1.22 ± 0.04 | 4.3 |
| 25 | 275 | 70 | 0.3 | 60 | Cross 3D | 538 ± 20 | 13 ± 1.5 | 10.0 | 1.73 ± 0.15 | 3.7 |
| Source | DF | Seq SS | Adj SS | Adj MS | F | p | % of Contribution |
|---|---|---|---|---|---|---|---|
| Temperature | 4 | 4.03 | 4.03 | 1.01 | 2.42 | 0.21 | 4.99 |
| Printing speed | 4 | 4.84 | 4.84 | 1.21 | 2.91 | 0.16 | 6 |
| Layer thickness | 4 | 4.77 | 4.77 | 1.19 | 2.86 | 0.17 | 5.91 |
| Infill density | 4 | 59.09 | 59.09 | 14.77 | 35.5 | 0 | 73.23 |
| Infill pattern | 4 | 6.29 | 6.29 | 1.57 | 3.77 | 0.11 | 7.79 |
| Residual error | 4 | 1.67 | 1.67 | 0.42 | |||
| Total | 24 | 80.68 |
| Source | DF | Seq SS | Adj SS | Adj MS | F | p | % of Contribution |
|---|---|---|---|---|---|---|---|
| Temperature | 4 | 1.69 | 1.69 | 0.42 | 0.32 | 0.853 | 3.54 |
| Printing speed | 4 | 2.47 | 2.47 | 0.62 | 0.47 | 0.76 | 5.18 |
| Layer thickness | 4 | 3.54 | 3.54 | 0.89 | 0.67 | 0.646 | 7.43 |
| Infill density | 4 | 29.97 | 29.97 | 7.49 | 5.67 | 0.061 | 62.86 |
| Infill pattern | 4 | 4.72 | 4.72 | 1.18 | 0.89 | 0.542 | 9.91 |
| Residual error | 4 | 5.28 | 5.28 | 1.32 | |||
| Total | 24 | 47.68 |
| Source | DF | Seq SS | Adj SS | Adj MS | F | p | % of Contribution |
|---|---|---|---|---|---|---|---|
| Temperature | 4 | 0.85 | 0.85 | 0.21 | 0.41 | 0.793 | 0.48 |
| Printing speed | 4 | 73.52 | 73.52 | 18.38 | 35.8 | 0.002 | 41.4 |
| Layer thickness | 4 | 64.93 | 64.93 | 16.23 | 31.61 | 0.003 | 36.56 |
| Infill pattern | 4 | 33.14 | 33.14 | 8.29 | 16.14 | 0.01 | 18.66 |
| Infill Pattern | 4 | 3.09 | 3.09 | 0.77 | 1.5 | 0.351 | 1.74 |
| Residual error | 4 | 2.05 | 2.05 | 0.51 | |||
| Total | 24 | 177.6 |
| Source | DF | Seq SS | Adj SS | Adj MS | F | p | % of Contribution |
|---|---|---|---|---|---|---|---|
| Temperature | 4 | 10.02 | 10.02 | 2.51 | 3.75 | 0.115 | 5.76 |
| Printing speed | 4 | 5.09 | 5.09 | 1.27 | 1.9 | 0.275 | 2.92 |
| Layer thickness | 4 | 5.76 | 5.76 | 1.44 | 2.15 | 0.238 | 3.31 |
| Infill density | 4 | 130.82 | 130.82 | 32.7 | 48.9 | 0.001 | 75.16 |
| Infill pattern | 4 | 18.69 | 18.69 | 4.67 | 6.98 | 0.043 | 10.74 |
| Residual error | 4 | 2.68 | 2.68 | 0.67 | |||
| Total | 24 | 173.05 |
| Config | ILSS (MPa) (Predicted/Experimental) | % Error | Max Stress (MPa) (Predicted/Experimental) | % Error | Flexural Modulus (MPa) (Predicted/Experimental) |
|---|---|---|---|---|---|
| 1 | 2.98/2.01 | 32.5 | 20.7/17.5 | 15.6 | 694/611 |
| 2 | 2.69/1.5 | 44.2 | 20.1/19.6 | 2.5 | 760/685 |
| 3 | 2.87/1.89 | 34.1 | 21.9/19.6 | 10.5 | 704/668 |
| Orthosis | Extrusion Temp (°C) | Printing Speed (mm/s) | Layer Height (mm) | Infill Density (%) | Infill Pattern | Print Time (h) |
|---|---|---|---|---|---|---|
| 1 | 260 | 50 | 0.2 | 99 | Grid | 34 h |
| 2 | 260 | 50 | 0.35 | 99 | Gyroid | 21 h 55 |
| 3 | 270 | 60 | 0.2 | 100 | Cubic | 28 h 40 |
| 4 | 260 | 50 | 0.25 | 85 | Cubic | 22 h 21 |
| 5 | 270 | 50 | 0.3 | 100 | Cross 3D | 21 h 28 |
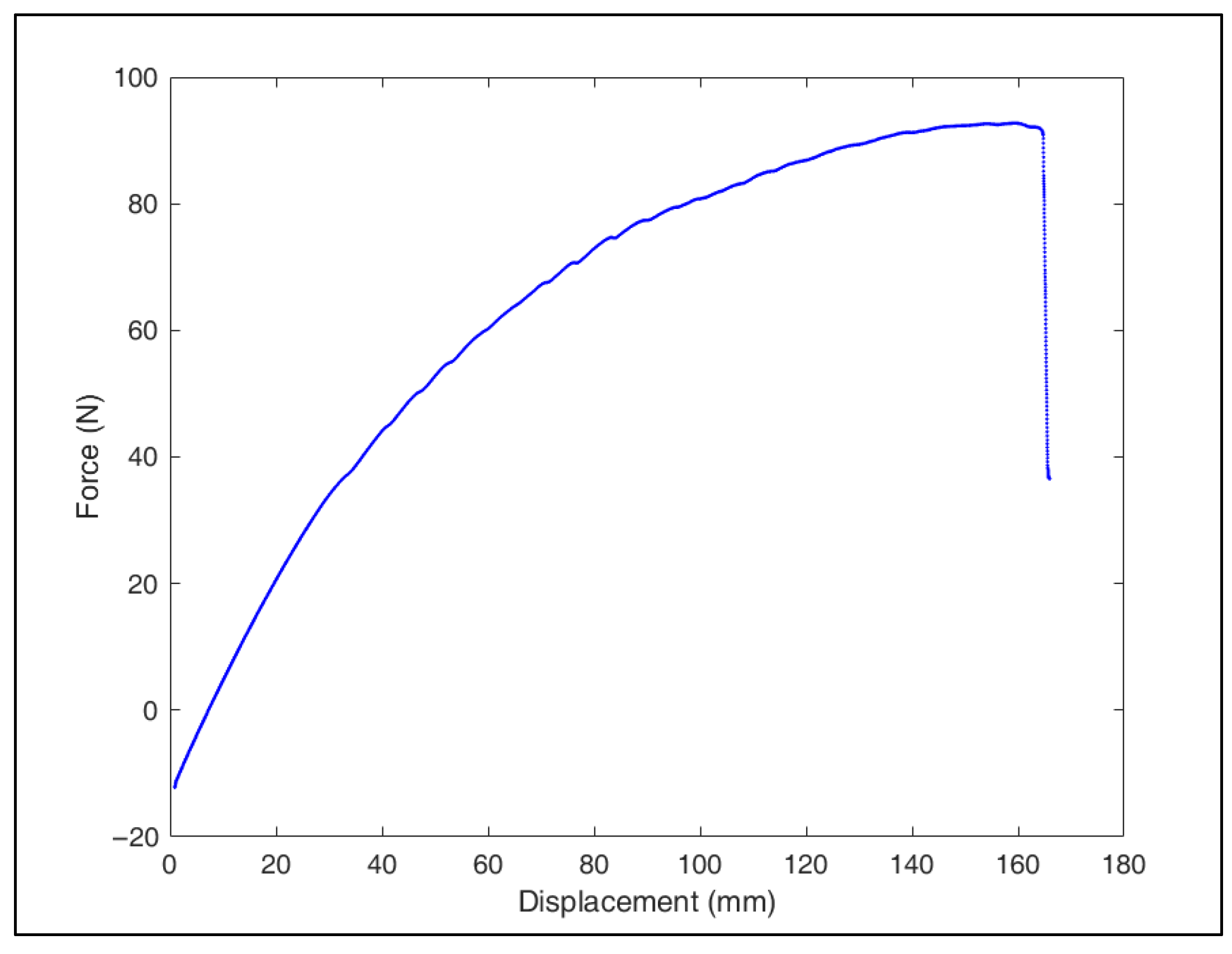
| Orthosis | Breaking Force (N) | Breaking Displacement (mm) |
|---|---|---|
| 1 | 98.5 | 147.2 |
| 2 | 91.0 | 136.9 |
| 3 | 105.2 | 169.2 |
| 4 | 92.7 | 159.5 |
| 5 | 82.8 | 100.82 |
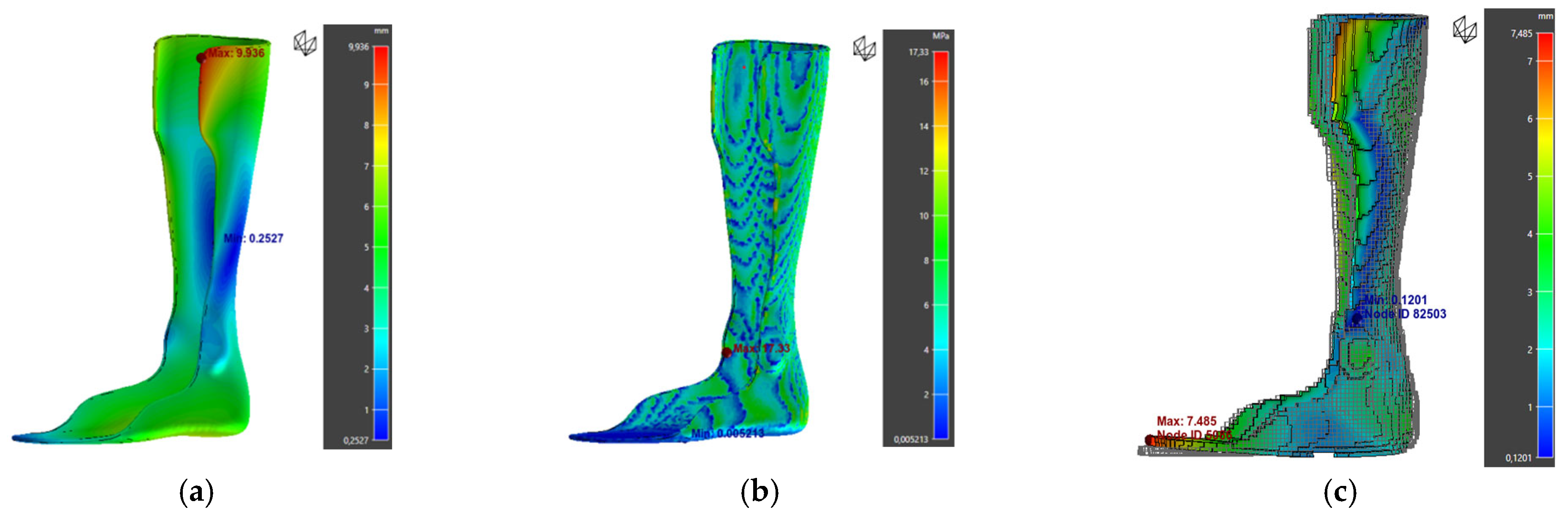
| Orthosis | Maximum Warpage (mm) | von Mises Stress (MPa) |
|---|---|---|
| 1 | 9.93 | 17.33 |
| 2 | 6.04 | 10.72 |
| 3 | 5.41 | 18 |
| 4 | 6.98 | 3.94 |
| 5 | 6.41 | 7.56 |
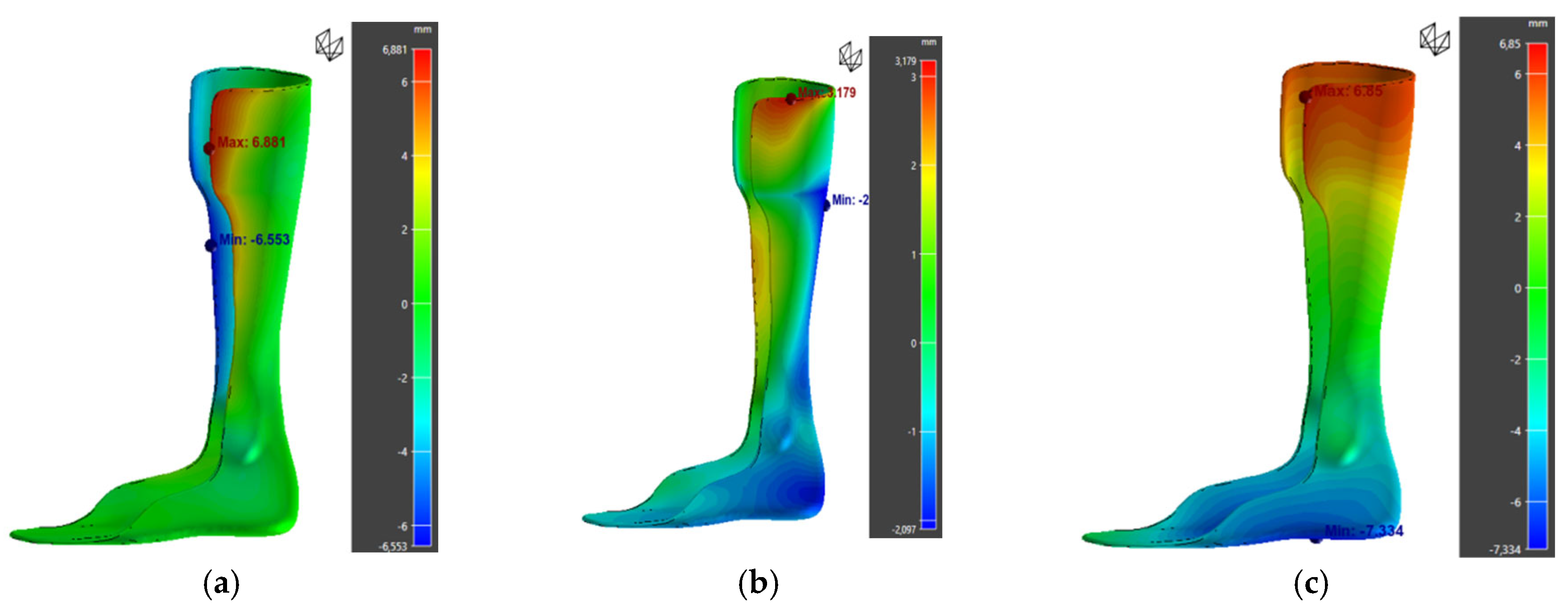
| Orientation | Maximum Warpage (mm) | von Mises Stress (MPa) |
|---|---|---|
| 90° | 5.41 | 18 |
| 45° | 33.61 | 21.24 |
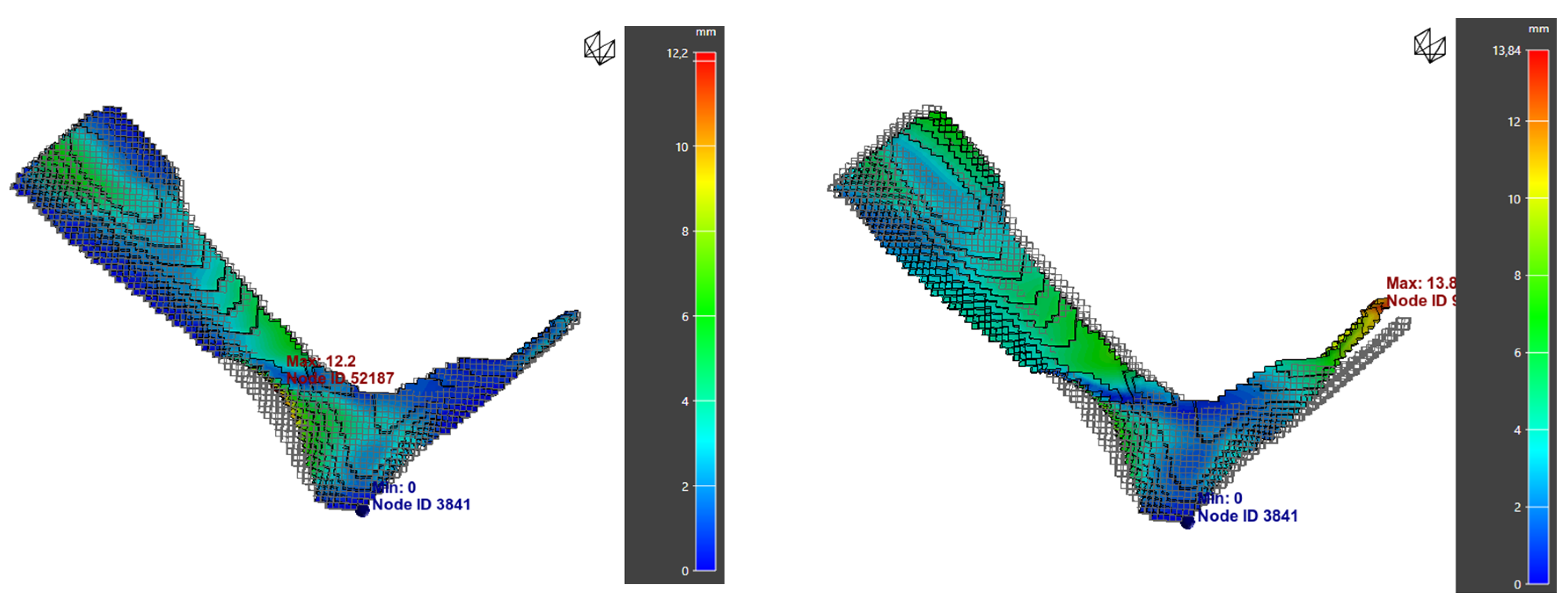
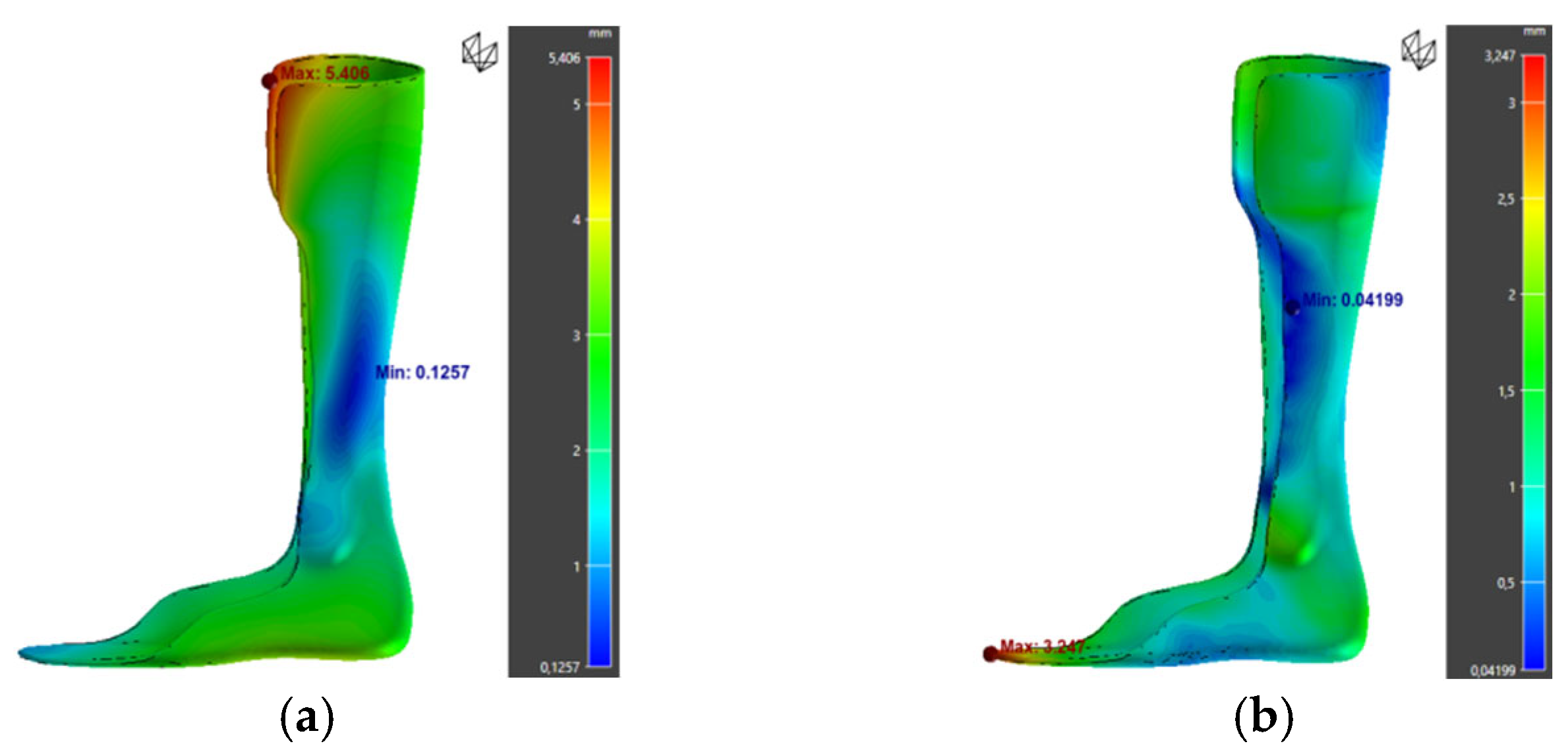
| Orthosis | Maximum Warpage (mm) | von Mises Stress (MPa) |
|---|---|---|
| Normal model | 5.41 | 18 |
| Compensated model | 3.25 | 12.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swesi, S.; Yousfi, M.; Tardif, N.; Banoune, A. Process Parameters Optimization and Mechanical Properties of Additively Manufactured Ankle–Foot Orthoses Based on Polypropylene. Polymers 2025, 17, 1921. https://doi.org/10.3390/polym17141921
Swesi S, Yousfi M, Tardif N, Banoune A. Process Parameters Optimization and Mechanical Properties of Additively Manufactured Ankle–Foot Orthoses Based on Polypropylene. Polymers. 2025; 17(14):1921. https://doi.org/10.3390/polym17141921
Chicago/Turabian StyleSwesi, Sahar, Mohamed Yousfi, Nicolas Tardif, and Abder Banoune. 2025. "Process Parameters Optimization and Mechanical Properties of Additively Manufactured Ankle–Foot Orthoses Based on Polypropylene" Polymers 17, no. 14: 1921. https://doi.org/10.3390/polym17141921
APA StyleSwesi, S., Yousfi, M., Tardif, N., & Banoune, A. (2025). Process Parameters Optimization and Mechanical Properties of Additively Manufactured Ankle–Foot Orthoses Based on Polypropylene. Polymers, 17(14), 1921. https://doi.org/10.3390/polym17141921







