Error Modeling and Error Control Study of PA/Pine Wood Biomass Composites
Abstract
1. Introduction
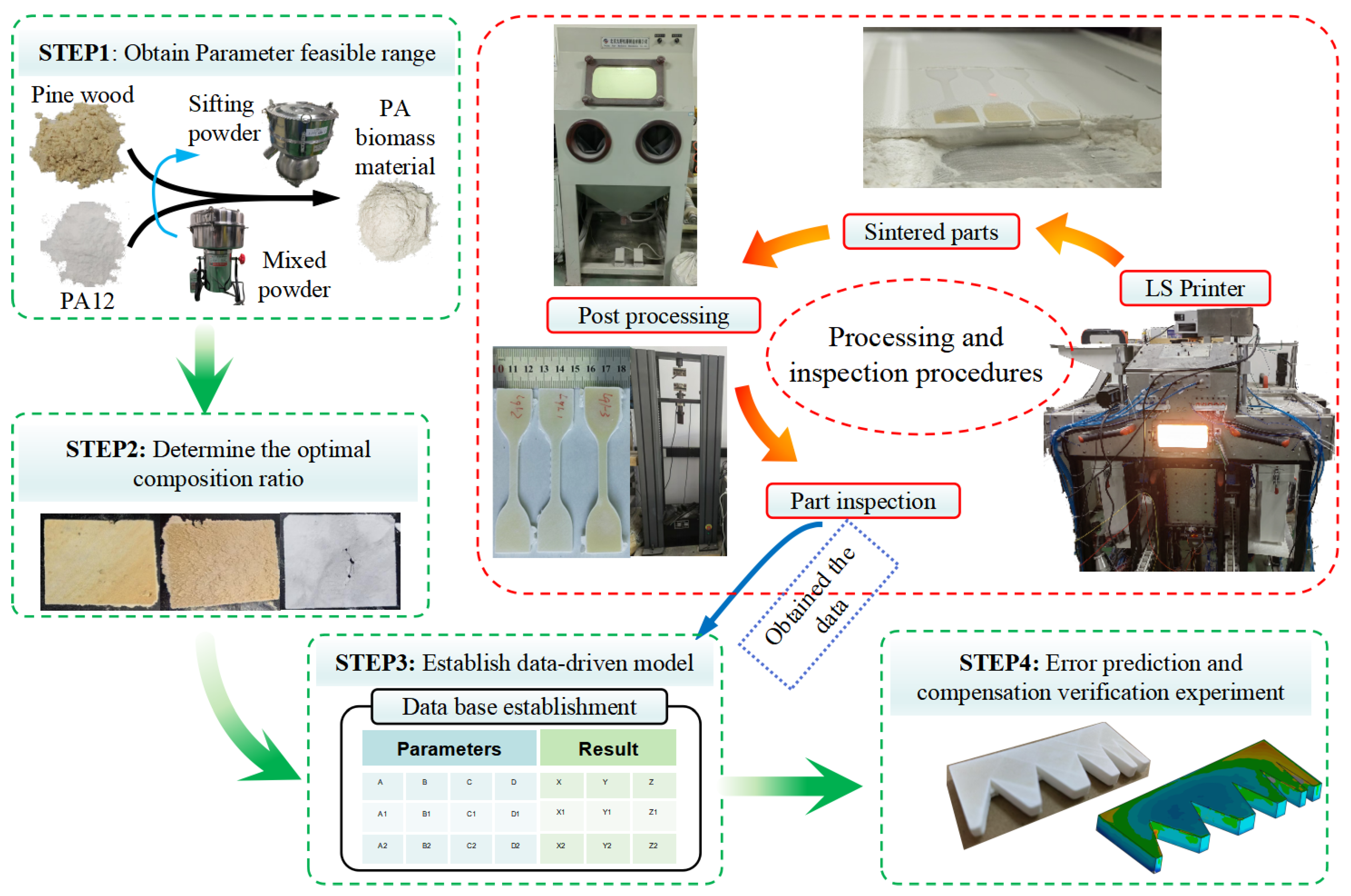
2. Experimental Methods and Procedures
2.1. Experimental Process and Equipment
2.2. Experimental Characterization and Testing
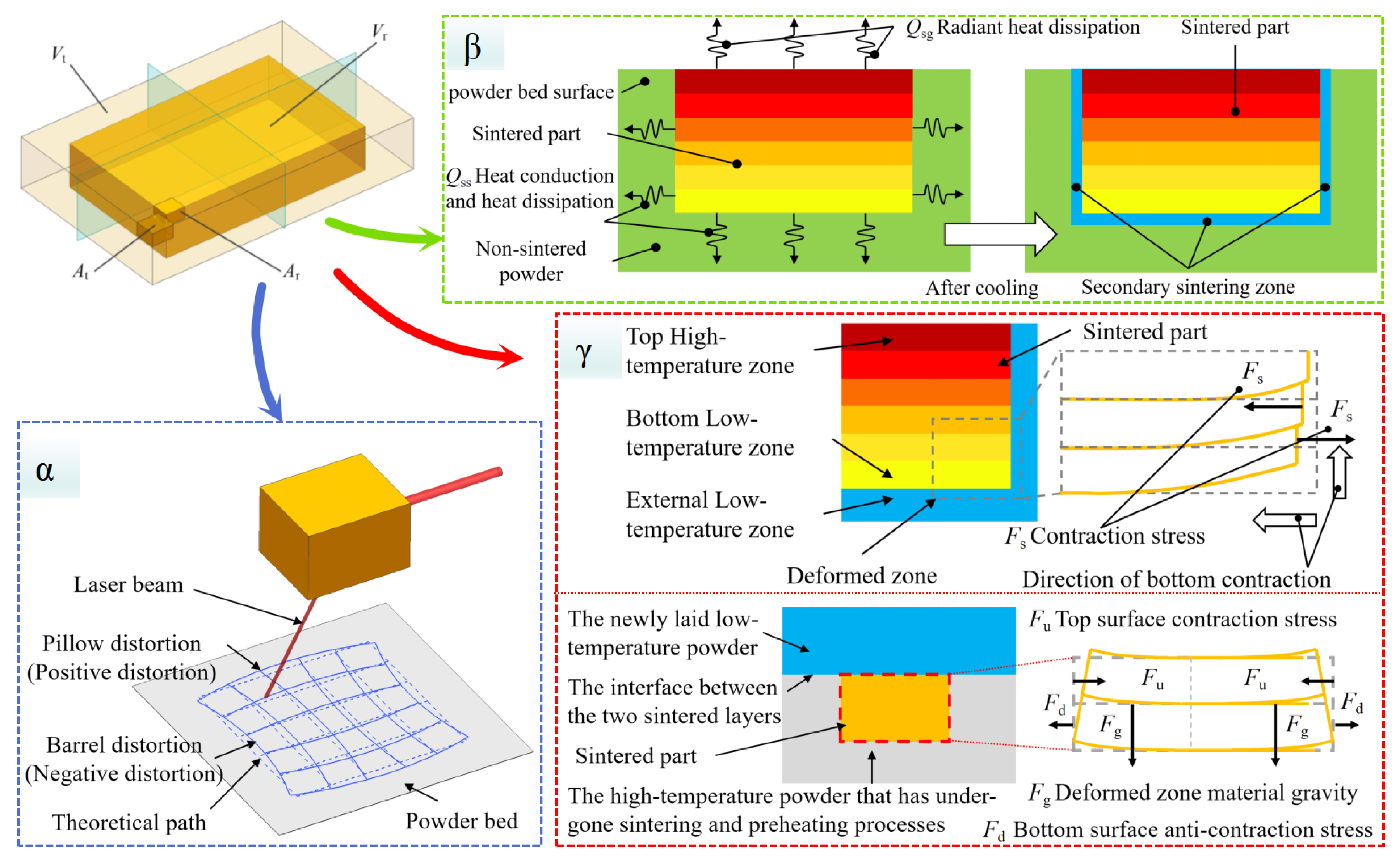
2.3. Error Modeling
2.3.1. Theoretical Mathematical Model
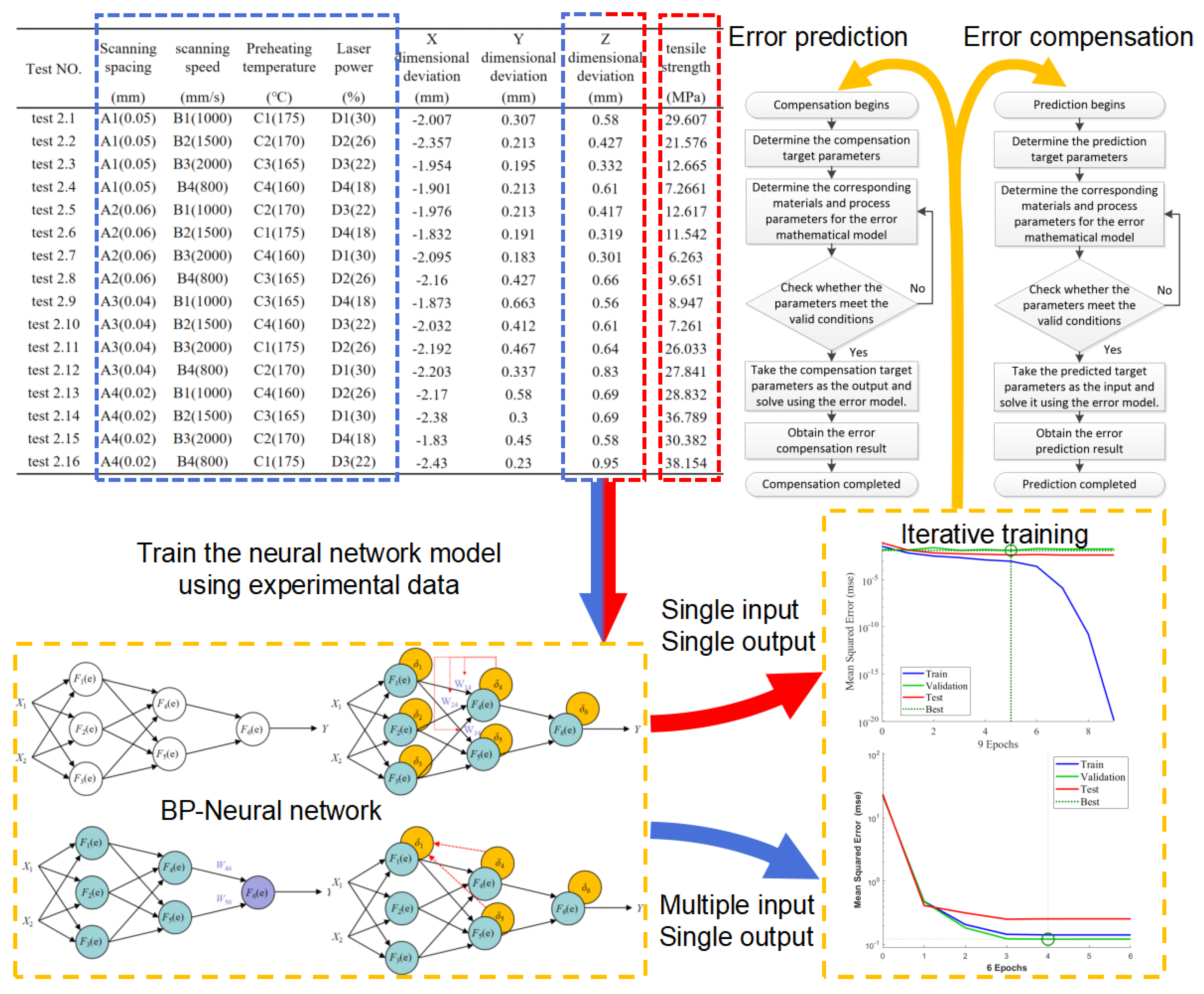
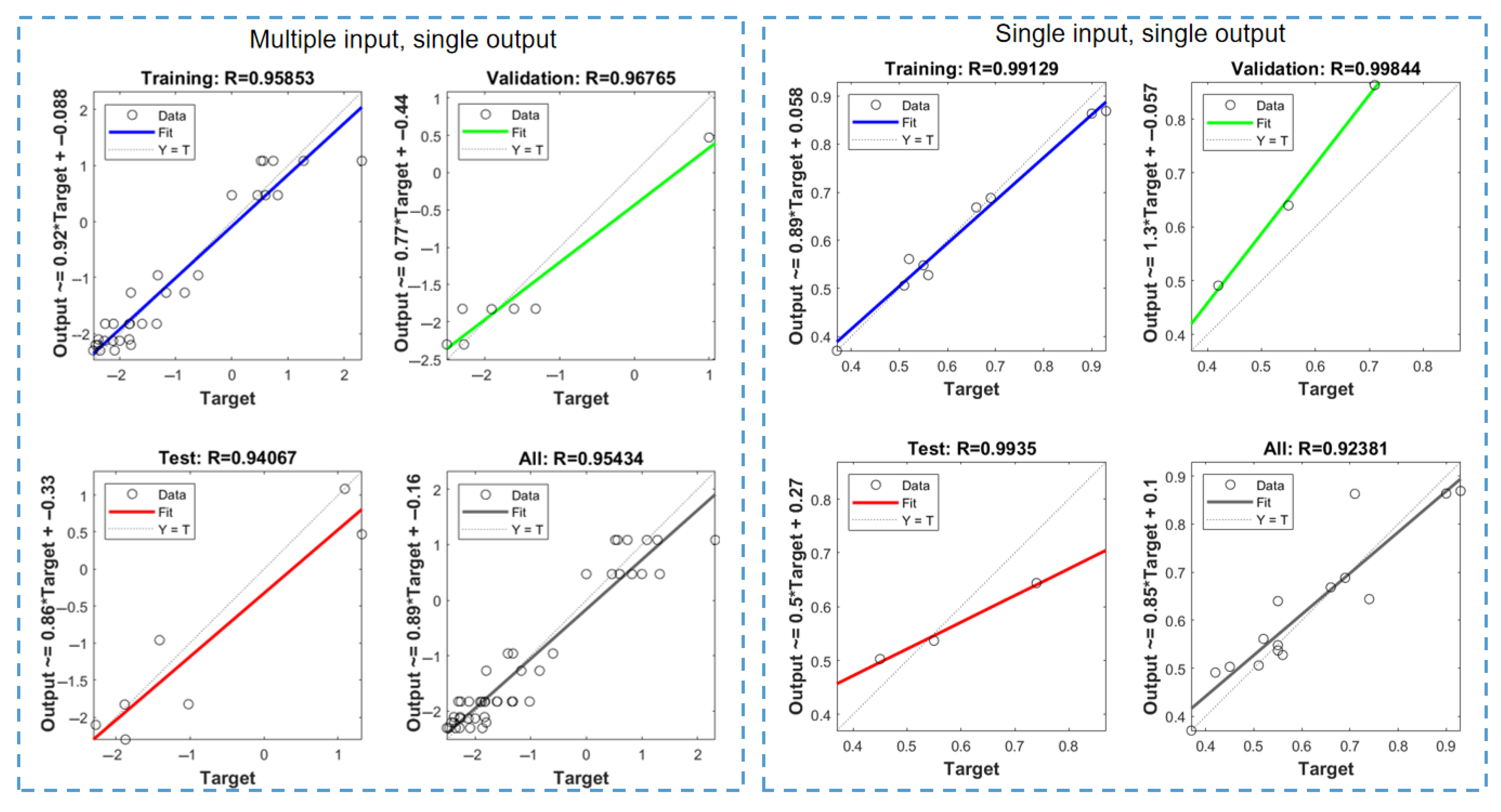
2.3.2. Data-Driven Model
- Single-Input–Single-Output Data-Driven Model (referred to as Model 1):
- 2.
- Multiple-Input–Single-Output Data-Driven Model (referred to as Model 2):
3. Results and Discussion
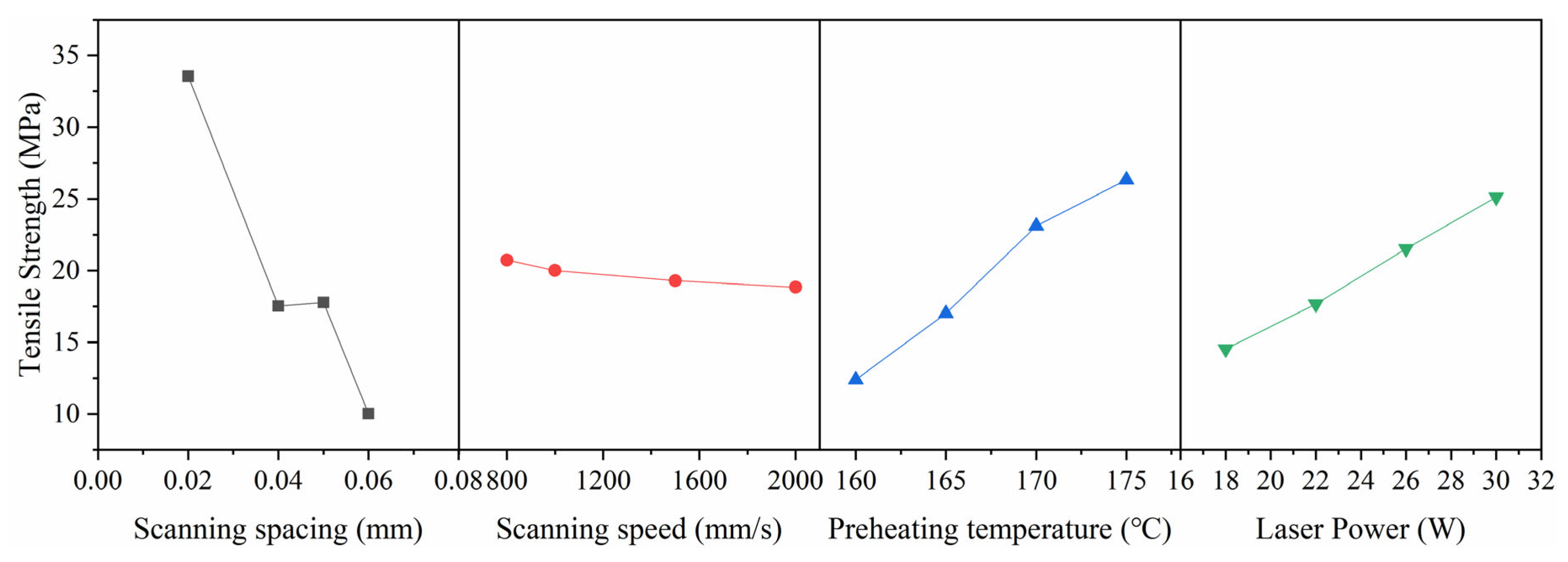
3.1. Material Performance Experiments
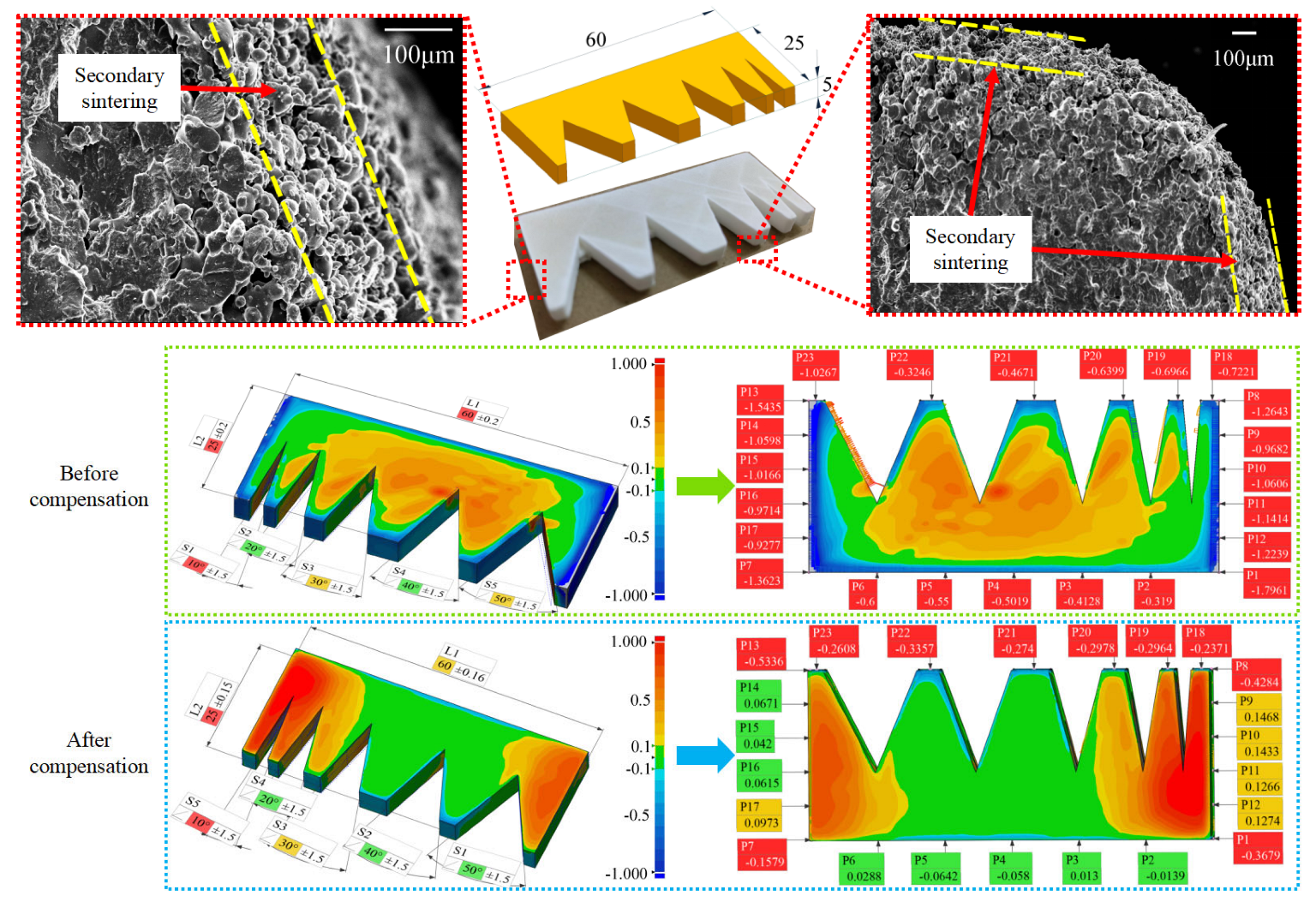
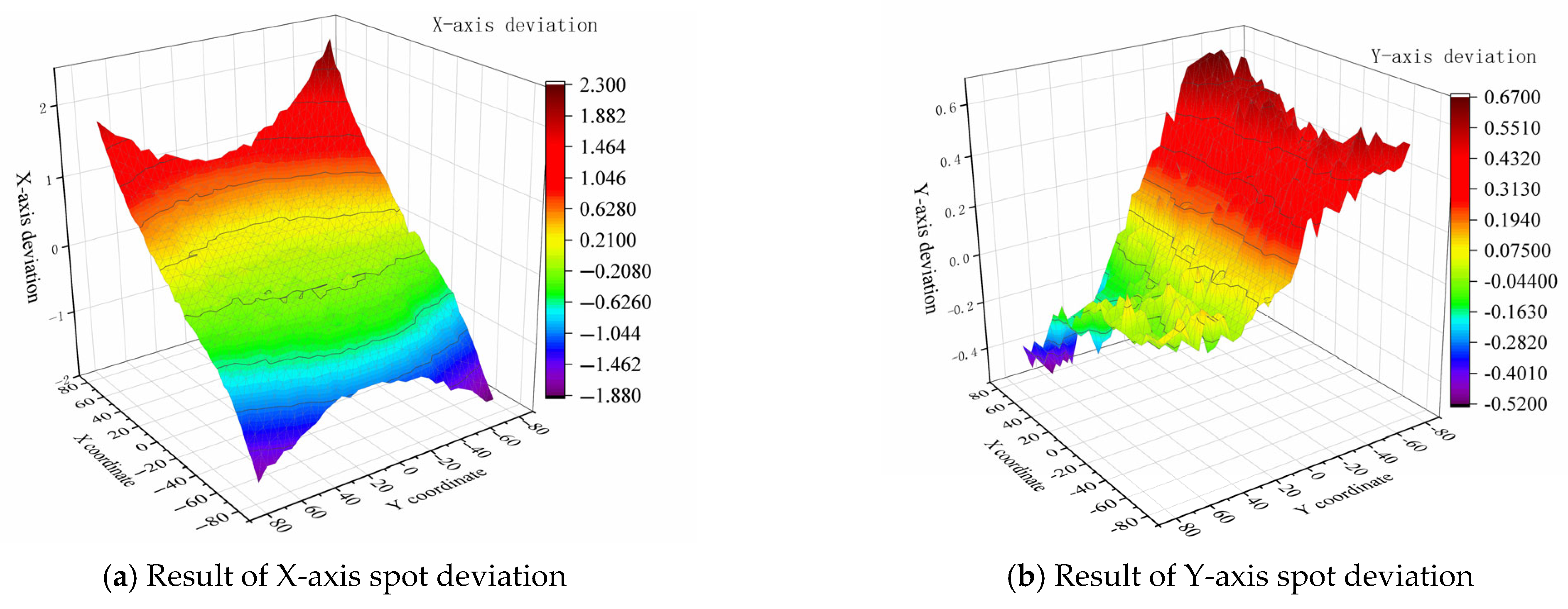
3.2. Error Model Experiment
4. Conclusions
5. Challenges and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, G.; Zhang, X.; Chen, X.; He, Y.; Cheng, L.; Huo, M.; Yin, J.; Hao, F.; Chen, S.; Wang, P.; et al. Additive manufacturing of structural materials. Mater. Sci. Eng. R Rep. 2021, 145, 100596. [Google Scholar] [CrossRef]
- Kafle, A.; Luis, E.; Silwal, R.; Pan, H.M.; Shrestha, P.L.; Bastola, A.K. 3D/4D printing of polymers: Fused deposition modelling (FDM), selective laser sintering (SLS), and stereolithography (SLA). Polymers 2021, 13, 3101. [Google Scholar] [CrossRef] [PubMed]
- Soundararajan, B.; Sofia, D.; Barletta, D.; Poletto, M. Review on modeling techniques for powder bed fusion processes based on physical principles. Addit. Manuf. 2021, 47, 102336. [Google Scholar] [CrossRef]
- Li, Y.; Ren, X.; Zhu, L.; Li, C. Biomass 3D printing: Principles, materials, post-processing and applications. Polymers 2023, 15, 2692. [Google Scholar] [CrossRef]
- Arioli, M.; Puiggalí, J.; Franco, L. Nylons with applications in energy generators, 3D printing and biomedicine. Molecules 2024, 29, 2443. [Google Scholar] [CrossRef]
- Han, W.; Kong, L.; Xu, M. Advances in selective laser sintering of polymers. Int. J. Extrem. Manuf. 2022, 4, 042002. [Google Scholar] [CrossRef]
- Mei, S.; Wang, J.; Li, Z.; Ding, B.; Li, S.; Chen, X.; Zhao, W.; Zhang, Y.; Zhang, X.; Cui, Z.; et al. 4D printing of polyamide 1212 based shape memory thermoplastic polyamide elastomers by selective laser sintering. J. Manuf. Process. 2023, 92, 157–164. [Google Scholar] [CrossRef]
- Cai, C.; Tey, W.S.; Chen, J.; Zhu, W.; Liu, X.; Liu, T.; Zhao, L.; Zhou, K. Comparative study on 3D printing of polyamide 12 by selective laser sintering and multi jet fusion. J. Mater. Process. Technol. 2021, 288, 116882. [Google Scholar] [CrossRef]
- Guo, S.; Li, J.; Zhang, L.; Li, Y. Preparation of high-porosity biomass-based carbon electrodes by selective laser sintering. Mater. Lett. 2023, 330, 133300. [Google Scholar] [CrossRef]
- Zhang, H.; Bourell, D.; Guo, Y.; Zhang, X.; Zhuang, Y.; Yu, Y.; Jiang, K.; Helal, W.M.K. Study on laser sintering of pine/co-PES composites and the investment casting process. Rapid Prototyp. J. 2019, 25, 1349–1358. [Google Scholar] [CrossRef]
- Senthilkumaran, K.; Pandey, P.M.; Rao, P.V.M. Influence of building strategies on the accuracy of parts in selective laser sintering. Mater. Des. 2009, 30, 2946–2954. [Google Scholar] [CrossRef]
- Pilipović, A.; Ilinčić, P.; Tujmer, M.; Rujnić Havstad, M. Impact of part positioning along chamber Z-Axis and processing parameters in selective laser sintering on polyamide properties. Appl. Sci. 2024, 14, 976. [Google Scholar] [CrossRef]
- Malashin, I.; Tynchenko, V.; Martysyuk, D.; Shchipakov, N.; Krysko, N.; Degtyarev, M.; Nelyub, V.; Gantimurov, A.; Borodulin, A.; Galinovsky, A. Assessment of anisotropic acoustic properties in additively manufactured materials: Experimental, computational, and deep learning approaches. Sensors 2024, 24, 4488. [Google Scholar] [CrossRef]
- Tu, R.; Majewski, C.; Gitman, I. Data-driven approaches for predicting mechanical properties and determining processing parameters of selective laser sintered nylon-12 components. Discov. Mech. Eng. 2025, 4, 10. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, Q.; Zhang, H.; Lei, J. Deep-learning-based localized porosity analysis for laser-sintered Al2O3 ceramic paste. Ceram. Int. 2023, 49, 23426–23436. [Google Scholar] [CrossRef]
- Ng, W.L.; Goh, G.L.; Goh, G.D.; Ten, J.S.J.; Yeong, W.Y. Progress and opportunities for machine learning in materials and processes of additive manufacturing. Adv. Mater. 2024, 36, 2310006. [Google Scholar] [CrossRef]
- Salazar, A.; Rico, A.; Rodríguez, J.; Escudero, J.S.; Seltzer, R.; de la Escalera Cutillas, F.M. Fatigue crack growth of SLS polyamide 12: Effect of reinforcement and temperature. Compos. Part B Eng. 2014, 59, 285–292. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, X.; Zhang, Z.; Li, S.; Fang, Q. Analysis of preheating temperature field characteristics in selective laser sintering. Adv. Mech. Eng. 2022, 14, 16878140211072397. [Google Scholar] [CrossRef]
- Qiang, T.; Kaihua, X.; Shan, Y. Accuracy and Performance Controlling of Part Made by Selective Laser Sintering Based on Secondary Sintering Region Regulation. Chin. J. Lasers 2018, 45, 62–69. [Google Scholar]
- Dai, J.; Guo, Y.; Li, J.; Guo, S.; Meng, D.; Zhang, H.; Guo, Y. Construction and Compensation of a Dimensional Accuracy Model of a Powder Bed via Laser Sintering. Polymers 2023, 15, 3417. [Google Scholar] [CrossRef]
- Westphal, E.; Seitz, H. A machine learning method for defect detection and visualization in selective laser sintering based on convolutional neural networks. Addit. Manuf. 2021, 41, 101965. [Google Scholar] [CrossRef]
- Paturi, U.M.R.; Vanga, D.G.; Duggem, R.B.; Kotkunde, N.; Reddy, N.S.; Dutta, S. Estimation of surface roughness of direct metal laser sintered AlSi10Mg using artificial neural networks and response surface methodology. Mater. Manuf. Process. 2023, 38, 1798–1808. [Google Scholar] [CrossRef]
- Guo, X.; Li, S.; Guan, Y.; Zhou, H.; Cui, L.; Xi, J.; Gu, M. Multi-objective optimization on the parameters of variable laser spot for the SL printing with a new path planning algorithm. J. Mech. Sci. Technol. 2024, 38, 6859–6872. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Q.; Ren, Y.; Chen, W.; Li, W.; Chen, J.; Zhou, L. Influence of energy density on the microstructure and property regulation of additive manufactured pure nickel. Adv. Mech. Eng. 2024, 16, 16878132241230228. [Google Scholar] [CrossRef]
- Idriss, A.I.B.; Li, J.; Wang, Y.; Guo, Y.; Elfaki, E.A. Effects of various processing parameters on the mechanical properties of sisal fiber/PES composites produced via selective laser sintering. BioResources 2020, 15, 5710–5724. [Google Scholar] [CrossRef]
- ISO 2768-1:1989; Tolerances for Linear and Angular Dimensions Without Individual Tolerance Indications. ISO: Geneva, Switzerland, 1989.


| (1) | |||||
| Test No. | Scanning Spacing | Scanning Speed | Preheating Temperature | Laser Power | |
| (mm) | (mm/s) | (°C) | (%) | ||
| test 1.1 | A1(0.05) | B1(1000) | C1(175) | D1(30) | |
| test 1.2 | A1(0.05) | B2(1500) | C2(170) | D5(24) | |
| test 1.3 | A1(0.05) | B3(2000) | C5(167) | D4(18) | |
| test 1.4 | A5(0.08) | B1(1000) | C2(170) | D4(18) | |
| test 1.5 | A5(0.08) | B2(1500) | C5(167) | D1(30) | |
| test 1.6 | A5(0.08) | B3(2000) | C1(175) | D5(24) | |
| test 1.7 | A4(0.02) | B1(1000) | C5(167) | D5(24) | |
| test 1.8 | A4(0.02) | B2(1500) | C1(175) | D4(18) | |
| test 1.9 | A4(0.02) | B3(2000) | C2(170) | D1(30) | |
| (2) | |||||
| Base Plate Temperature | Scanning Spacing | Scanning Speed | Preheating Temperature | Laser Power | |
| unit | °C | mm | mm/s | °C | % |
| value | 165 | 0.04 | 1000 | 173 | 10 |
| (3) | |||||
| Test No. | Scanning Spacing | Scanning Speed | Preheating Temperature | Laser Power | |
| (mm) | (mm/s) | (°C) | (%) | ||
| test 2.1 | A1(0.05) | B1(1000) | C1(175) | D1(30) | |
| test 2.2 | A1(0.05) | B2(1500) | C2(170) | D2(26) | |
| test 2.3 | A1(0.05) | B3(2000) | C3(165) | D3(22) | |
| test 2.4 | A1(0.05) | B4(800) | C4(160) | D4(18) | |
| test 2.5 | A2(0.06) | B1(1000) | C2(170) | D3(22) | |
| test 2.6 | A2(0.06) | B2(1500) | C1(175) | D4(18) | |
| test 2.7 | A2(0.06) | B3(2000) | C4(160) | D1(30) | |
| test 2.8 | A2(0.06) | B4(800) | C3(165) | D2(26) | |
| test 2.9 | A3(0.04) | B1(1000) | C3(165) | D4(18) | |
| test 2.10 | A3(0.04) | B2(1500) | C4(160) | D3(22) | |
| test 2.11 | A3(0.04) | B3(2000) | C1(175) | D2(26) | |
| test 2.12 | A3(0.04) | B4(800) | C2(170) | D1(30) | |
| test 2.13 | A4(0.02) | B1(1000) | C4(160) | D2(26) | |
| test 2.14 | A4(0.02) | B2(1500) | C3(165) | D1(30) | |
| test 2.15 | A4(0.02) | B3(2000) | C2(170) | D4(18) | |
| test 2.16 | A4(0.02) | B4(800) | C1(175) | D3(22) | |
| (4) | |||||
| Symbol | Description | ||||
| The i-th theoretical unit. | |||||
| The i-th practical unit. | |||||
| The displacement set from theoretical units to practical units. | |||||
| The displacement vector from the theoretical unit to the practical unit of the i-th element. | |||||
| A(xi,yi,zi) | The coordinate representation of the i-th element. | ||||
| The practical X-coordinate of the i-th element. | |||||
| The theoretical X-coordinate of the i-th element. | |||||
| Theoretical geometry. | |||||
| Practical geometry. | |||||
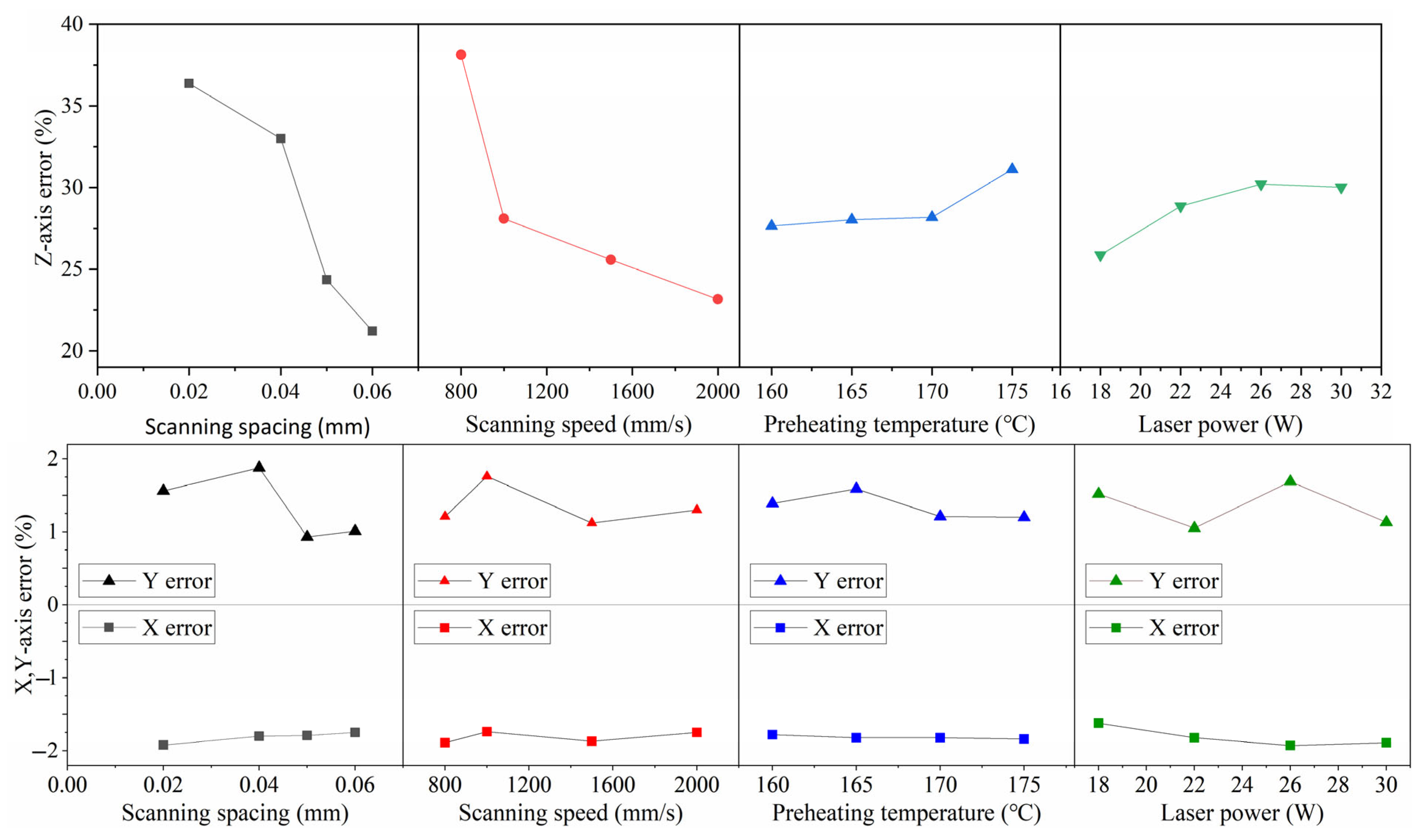
| Test NO. | Scanning Spacing | Scanning Speed | Preheating Temperature | Laser Power | X Dimensional Deviation | Y Dimensional Deviation | Z Dimensional Deviation | Tensile Strength |
|---|---|---|---|---|---|---|---|---|
| (mm) | (mm/s) | (°C) | (%) | (mm) | (mm) | (mm) | (MPa) | |
| Test 2.1 | A1(0.05) | B1(1000) | C1(175) | D1(30) | −2.007 | 0.307 | 0.58 | 29.607 |
| Test 2.2 | A1(0.05) | B2(1500) | C2(170) | D2(26) | −2.357 | 0.213 | 0.427 | 21.576 |
| Test 2.3 | A1(0.05) | B3(2000) | C3(165) | D3(22) | −1.954 | 0.195 | 0.332 | 12.665 |
| Test 2.4 | A1(0.05) | B4(800) | C4(160) | D4(18) | −1.901 | 0.213 | 0.61 | 7.2661 |
| Test 2.5 | A2(0.06) | B1(1000) | C2(170) | D3(22) | −1.976 | 0.213 | 0.417 | 12.617 |
| Test 2.6 | A2(0.06) | B2(1500) | C1(175) | D4(18) | −1.832 | 0.191 | 0.319 | 11.542 |
| Test 2.7 | A2(0.06) | B3(2000) | C4(160) | D1(30) | −2.095 | 0.183 | 0.301 | 6.263 |
| Test 2.8 | A2(0.06) | B4(800) | C3(165) | D2(26) | −2.16 | 0.427 | 0.66 | 9.651 |
| Test 2.9 | A3(0.04) | B1(1000) | C3(165) | D4(18) | −1.873 | 0.663 | 0.56 | 8.947 |
| Test 2.10 | A3(0.04) | B2(1500) | C4(160) | D3(22) | −2.032 | 0.412 | 0.61 | 7.261 |
| Test 2.11 | A3(0.04) | B3(2000) | C1(175) | D2(26) | −2.192 | 0.467 | 0.64 | 26.033 |
| Test 2.12 | A3(0.04) | B4(800) | C2(170) | D1(30) | −2.203 | 0.337 | 0.83 | 27.841 |
| Test 2.13 | A4(0.02) | B1(1000) | C4(160) | D2(26) | −2.17 | 0.58 | 0.69 | 28.832 |
| Test 2.14 | A4(0.02) | B2(1500) | C3(165) | D1(30) | −2.38 | 0.3 | 0.69 | 36.789 |
| Test 2.15 | A4(0.02) | B3(2000) | C2(170) | D4(18) | −1.83 | 0.45 | 0.58 | 30.382 |
| Test 2.16 | A4(0.02) | B4(800) | C1(175) | D3(22) | −2.43 | 0.23 | 0.95 | 38.154 |
| NO. | A Scanning Spacing | A Norm. | B Scanning Speed | B Norm. | C Preheating Temperature | C Norm. | D Laser Power | D Norm. |
|---|---|---|---|---|---|---|---|---|
| (mm) | (mm/s) | (°C)> | (%) | |||||
| TS_K1 | (A1)17.8 | 0.33 | (B1)20.0 | 0.62 | (C1)26.3 | 1.00 | (D1)25.2 | 1.00 |
| TS_K2 | (A2)10.0 | 0.00 | (B2)19.3 | 0.25 | (C2)23.1 | 0.77 | (D2)21.5 | 0.66 |
| TS_K3 | (A3)17.5 | 0.32 | (B3)18.8 | 0.00 | (C3)17.0 | 0.33 | (D3)17.7 | 0.30 |
| TS_K4 | (A4)33.5 | 1.00 | (B4)20.7 | 1.00 | (C4)12.4 | 0.00 | (D4)14.5 | 0.00 |
| Range KR_L | 23.5 | — | 1.91 | — | 13.9 | — | 10.6 | — |
| RE_X K5 | (A1)2.06 | 0.21 | (B1)2.00 | 0.00 | (C1)2.12 | 1.00 | (D1)2.17 | 0.86 |
| RE_X K6 | (A2)2.02 | 0.00 | (B2)2.15 | 0.86 | (C2)2.09 | 0.63 | (D2)2.22 | 1.00 |
| RE_X K7 | (A3)2.08 | 0.32 | (B3)2.02 | 0.07 | (C3)2.09 | 0.65 | (D3)2.10 | 0.66 |
| RE_X K8 | (A4)2.20 | 1.00 | (B4)2.17 | 1.00 | (C4)2.05 | 0.00 | (D4)1.86 | 0.00 |
| Range_KR_X | 0.187 | — | 0.167 | — | 0.065 | — | 0.361 | — |
| RE_Z K9 | (A1)0.487 | 0.21 | (B1)0.562 | 0.33 | (C1)0.622 | 1.00 | (D1)0.600 | 0.95 |
| RE_Z K10 | (A2)0.424 | 0.00 | (B2)0.511 | 0.16 | (C2)0.564 | 0.16 | (D2)0.604 | 1.00 |
| RE_Z K11 | (A3)0.660 | 0.78 | (B3)0.463 | 0.00 | (C3)0.560 | 0.10 | (D3)0.577 | 0.69 |
| RE_Z K12 | (A4)0.728 | 1.00 | (B4)0.762 | 1.00 | (C4)0.553 | 0.00 | (D4)0.517 | 0.00 |
| Range_KR_Z | 0.304 | — | 0.299 | — | 0.069 | — | 0.087 | — |
| Param. A | Normalized Weight Value | Param. B | Normalized Weight Value | Param. C | Normalized Weight Value | Param. D | Normalized Weight Value |
|---|---|---|---|---|---|---|---|
| A1 | 0.06 | B1 | 0.2275 | C1 | 0 | D1 | 0.0475 |
| A2 | 0 | B2 | −0.13 | C2 | 0.1875 | D2 | −0.17 |
| A3 | −0.115 | B3 | −0.0175 | C3 | −0.0225 | D3 | −0.1875 |
| A4 | 0 | B4 | 0 | C4 | 0 | D4 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, J.; Guo, Y.; Zhang, H. Error Modeling and Error Control Study of PA/Pine Wood Biomass Composites. Polymers 2025, 17, 1920. https://doi.org/10.3390/polym17141920
Dai J, Guo Y, Zhang H. Error Modeling and Error Control Study of PA/Pine Wood Biomass Composites. Polymers. 2025; 17(14):1920. https://doi.org/10.3390/polym17141920
Chicago/Turabian StyleDai, Jiaming, Yanling Guo, and Haoyu Zhang. 2025. "Error Modeling and Error Control Study of PA/Pine Wood Biomass Composites" Polymers 17, no. 14: 1920. https://doi.org/10.3390/polym17141920
APA StyleDai, J., Guo, Y., & Zhang, H. (2025). Error Modeling and Error Control Study of PA/Pine Wood Biomass Composites. Polymers, 17(14), 1920. https://doi.org/10.3390/polym17141920






