Abstract
Combining Brownian dynamics simulations and self-consistent field theory, we demonstrate that stable assembled structures, such as vesicles, toroidal micelles, bowl-like micelles, sheet-like micelles, non-spherical vesicles, and cylindrical micelles, are dependent on the molecular parameters of amphiphilic comb-like copolymers. Importantly, we find that vesicle formation involves two intermediate states, sheet-like and bowl-like micelles, and the difference in their free energies is minimal, which illustrates the coexisting phase between them. Moreover, the assembled vesicles can be modulated in the membrane thickness with overall size, unchanged only by adjusting the backbone length. We also demonstrate the coexistence of toroidal and cylindrical micelles because neither structure has a significant advantage over the other in free energy. Our work points out how to obtain different morphologies by adjusting the molecular parameters of amphiphilic comb-like copolymers, instilling confidence in their potential for stable drug encapsulation and enhanced targeted drug delivery.
1. Introduction
Copolymer self-assembly has been a topic of great interest because of its ability to form functional micelles or vesicles, which, in turn, determine the potential applications of copolymers [1,2,3,4,5]. For example, spherical micelles and vesicles exhibit stable drug encapsulation and enhanced targeted drug delivery [6,7,8,9,10]. Toroidal micelles have applications in delivery systems that mimic bacteriophages and vertebrate DNA rings [11,12]. In biomedical sensing, self-assembled length-controlled cylindrical micelle brushes are used to enhance the signal recognition capability of detectors [13].
The self-assembled morphologies of copolymers in solution are influenced by numerous factors, with molecular structure being the most intrinsic. To date, the self-assembling mechanisms of linear block copolymers [7,14,15], comb-like copolymers [16,17,18,19], hyperbranched copolymers [20,21], and other topologically structured copolymers continue to be subjects of ongoing exploration in both simulation and experimental studies [22]. Among them, the self-assembly of non-linear polymers, such as graft copolymers, emerges as a more promising component in self-assembled materials [23,24,25,26,27,28,29,30]. This is attributed to their lower critical micelle concentration [31] and higher interfacial stability [32], making them withstand rigorous environments such as high pressure and heat, and strong alkalis and acids [33,34].
Given this, many researchers have used different graft molecular models to explore their self-assembly morphologies. For instance, Wang et al. employed dissipative particle dynamics (DPD) simulations to investigate the self-assembly of amphiphilic comb-like copolymers, specifically using the and models (the subscript numbers 6, 2, and 3, respectively, represent the backbone length, side-chain length, and grafting number), which results in monolayer vesicles [35]. Lin et al. combined self-consistent field theory (SCFT) with DPD simulations to study the -graft- model, revealing the formation of segmented, multi-layered composite vesicles [10]. Liu et al. focused on the spontaneous formation and fusion of onion-like vesicles using DPD simulations with the model [19]. Additionally, Khokhlov et al. used Monte Carlo (MC) simulations to examine the conformational transitions of a single amphiphilic comb-like copolymer, observing structural changes from spherical to elongated ellipsoids and pearl-necklace configurations as the grafting density increased [36]. Sheng and Tsao et al. separately employed comb-like graft copolymers composed of a backbone of poly((N-vinylcarbazole)-co-(4-vinylbenzyl chloride)) (P(NVK-co-VBC)) and side chains of poly(((2-dimethylamino)ethyl methacrylate)-co-(tert-butyl acrylate)) (P(DMAEMA-co-tBA)) to regulate the formation of vesicles from unilamellar to multilamellar structures using the DPD method. They found that variations in grafting density can modulate the thickness and the number of layers in the hydrophobic region [37,38]. These studies highlight the critical role of molecular model selection in determining the self-assembly morphologies of amphiphilic comb-like copolymers. However, a significant challenge remains: the diversity of molecular models makes direct comparisons between different studies difficult. This limitation hinders the ability to establish a precise relationship between molecular parameters and the resulting self-assembled morphologies.
In the current study, we systematically investigate the relationship between the molecular parameters and self-assembled morphologies of amphiphilic comb-like chains in solution by employing Brownian dynamics (BD) simulations. The objective is to control the self-assembly structures by tuning these molecular parameters for diverse applications. The study revealed that various self-assembled morphologies could be observed, including toroid micelles, bowl-like micelles, vesicles, sheet-like micelles, cylindrical micelles, and non-spherical vesicles, by adjusting the length of the backbone and side chains, and the grafting density. In addition, we reveal the transition mechanisms between different morphologies by calculating the free energy of different self-assembled morphologies using SCFT. The remainder of this article is organized as follows. Section 2 provides the model and simulation details. Section 3 constructs the morphological phase diagram, elucidates the self-assembly mechanism, and provides the relationship between the molecular parameters and self-assembled morphologies. Section 4 presents the conclusion and future outlook.
2. Model and Methods
BD simulations: We conduct BD simulations to investigate the self-assembly dynamics of amphiphilic comb-like chains. As demonstrated in our previous work and related simulations, the coarse-grained model is employed, which can reasonably capture the essential interactions and structural features with the reduced unit system [31,32,39,40,41,42,43,44,45]. As illustrated in Figure 1, the amphiphilic comb-like chains are modeled as bead-spring chains: The hydrophilic side chains B (red) are randomly grafted onto the hydrophobic backbone A (yellow). We denote amphiphilic comb-like chains as -comb-, where x and y represent the lengths of the backbone and side chains, respectively, and n denotes the grafting number. All bonded interactions, including the adjacent beads of the backbone and the side chains, and the grafting points between the beads of the backbone and the side chains, are calculated by the finite extensible nonlinear elastic (FENE) potential [46], i.e.,
where denotes the spring constant and is the maximum separation distance for the bead–bead distance r.
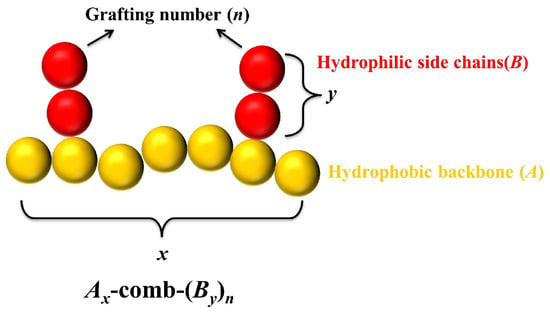
Figure 1.
Coarse-grained model of amphiphilic comb-like copolymers: -comb-, composed of a hydrophobic backbone with a length of x (represented by A, yellow) and n hydrophilic side chains with a length of y (represented by B, red), where .
The non-bonded interactions between two beads accounted for the excluded-volume interactions described through the Lennard-Jones (LJ) potential, i.e.,
Here, and represent the energy and length parameters, respectively. Implicit solvents are used in the simulation system. For the interactions between hydrophobic beads, we specify a cutoff distance for the LJ potential, corresponding to a poor solvent condition [14,47]. For the other pairwise beads, we set the cutoff to , corresponding to a good solvent condition [48]. Additionally, both LJ potentials are shifted separately to ensure at .
We employ BD simulations, where the motion for bead i is given by [49]
represents the potentials from all FENE and LJ interactions as discussed, and denotes the friction coefficient experienced by a bead in the solvent. The random force is generated based on the thermal bath model using a Gaussian-distributed random number generator, satisfying the fluctuation–dissipation theorem: , where is Boltzmann’s constant, T is the temperature, and denotes the unit tensor. Equation (3) neglects inertial effects and can be efficiently integrated using the Euler method. In this work, we disregard hydrodynamic interactions between different beads, which enables us to compute the steps for a longer time with reduced computational effort.
We adopt length, mass, and energy units as , m, and , respectively. Consequently, the unit of time can be described as . We set the temperature as , the time step as , and the friction coefficient as . Furthermore, we fix the parameters of the FENE potential as and to prevent chain crossing [50]. We conduct simulations within a cubic box with periodic boundary conditions. All samples are fixed with the same volume fraction and are simulated with – time steps. In addition, independent simulations are carried out 5–10 times with different random seeds.
SCFT: In the SCFT calculations, we consider an incompressible blending system composed of AB comb-like copolymers and solvent molecules of short A homopolymer. Under the approximations of the mean-field treatment and Gaussian-chain model, the free energy in the canonical ensemble can be expressed as
where is the mean-field conjugating to the volume fraction ( or ). The spatial function is a Lagrange multiplier used to enforce the incompressibility condition, . The two quantities and are the partition functions of single copolymer chain and single homopolymer chain interacting with the mean fields of and , respectively.
The A1-comb-(B1)1, which can be seen as the repeating units of Ax-comb-(By)n at in the BD simulation, is modelled as an AB2 star copolymer with and N segments in the SCFT. In other words, segments of the comb-like copolymer in the SCFT correspond to 1 bead of the copolymer model in the BD. By setting the number of total segments for the solvent to be and the interaction parameter between A and B components to be 15 ( denotes the Flory–Huggins parameter), we observed the order–disorder transitions and self-assembled structures in the SCFT similar to that in the BD. More details of the SCFT can be found in references [51,52] or the Supporting Information.
3. Results and Discussion
As shown in Figure 2, we initially fix , that is -comb-, to explore the possible self-assembling structures. The results reveal that when , the system cannot form a stable structure and is in the dispersed phase. At this time, each bead on the backbone is grafted with a side chain. As we reported earlier, at this time, the hydrophobic backbone chain is surrounded by the hydrophilic side chains to form a better encapsulation layer, that is to say, the formation of a single molecule micelle [40], which leads to the difficulty of further self-assembly with other chains. As n decreases, we begin to be able to observe various structures. For example, first, one can self-assemble to form cylindrical micelles; however, when x is small, the coexistence of cylindrical micelles and toroidal micelles can also be observed. The next larger percentage is sheet-like micelles. In addition, when , the structures obtained are more abundant; for example, the coexistence of sheet-like micelles and vesicles, and non-spherical vesicles and cylindrical micelles can be obtained when x is small.
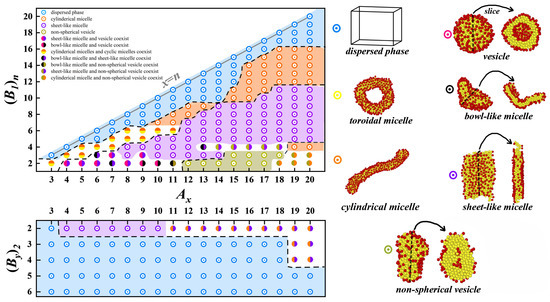
Figure 2.
Phase diagrams of -comb- and -comb-, respectively, where the blue region represents the dispersed phase, the yellow region denotes toroidal micelle, the orange region indicates cylindrical micelle, the pink region represents vesicle, the black region signifies bowl-like micelle, the purple region denotes sheet-like micelle, and the gray region indicates non-spherical vesicle. The corresponding simulation snapshots for each region are indicated on the right, where the arrows point to the cross-sectional slice of the structures. The two colored circles represent the coexistence state of two structures simulated under the same starting conditions.
We then fix , that is, -comb-, to investigate the self-assembling structures with two side chains. Our results indicate that most stable self-assembled structures cannot be formed. This implies that the desired self-assembled structure will be formed only if the molecular parameters are tuned to a suitable range. We find that only sheet-like micelles and cylindrical micelles can be formed with small y. When x is larger, it is in the coexistence phase of sheet-like micelles and cylindrical micelles. As reported in the literature, stabilized micelles and vesicles with different shapes have very many promising applications [6,7,8,9,10]. Therefore, we proceed to further analyze the self-assembly process of toroidal micelles, cylindrical micelles, and vesicles, as well as the free energy of their structures.
We trace the dynamic process of vesicle formation, as shown in Figure 3a. The chains rapidly aggregate into numerous small clusters at the initial stage and assemble into sheet-like micelles. At this stage, two distinct scenarios emerge, one where the system always maintains the sheet-like structure, accompanying occasional minor bending. The other is the gradual bending of the sheet-like micelles, transitioning into bowl-like structures. Similarly, the system either remains in the bowl-like micelles or the bowl’s opening gradually narrows until completely closed, forming a spherical vesicle. This suggests that vesicle formation involves two intermediate states, sheet-like and bowl-like micelles, rather than direct formation. This closely resembles the findings of Gianneschi et al., who utilized in situ liquid-cell transmission electron microscopy to observe the formation of bicontinuous micelle structures during the transition of amphiphilic block copolymer micelles into higher-order vesicle structures [53].
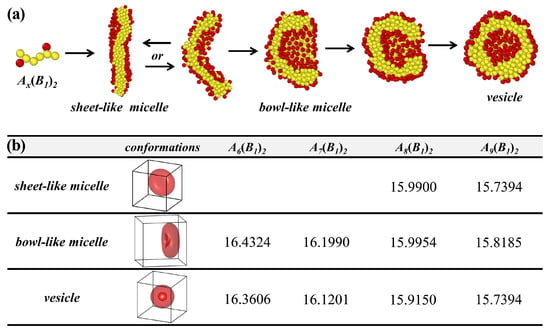
Figure 3.
(a) Self-assembly roadmap of amphiphilic comb-like copolymers with the molecular parameters , which indicates that they first form sheet-like micelles, then the structure bends and forms bowl-like micelles, or may revert to sheet-like micelles, and finally the structure closes to form vesicles. (b) Free energies calculated by SCFT for the sheet-like micelles, the bowl-like micelles, and the vesicles correspond representatively to (a).
As shown in Figure 2, the simulation results indicate the coexistence of vesicles, bowl-like micelles, and sheet-like micelles. To justify this coexistence of states, we calculate their formation and the corresponding free energies using SCFT, as shown in Figure 3b. Consistently, we observe the coexistence of vesicles and bowl-like micelles as well as sheet-like micelles, except that and failure to form the sheet-like micelles. Although the results of the coexisting phases do not fully agree with the simulation results of BD, the results show that the difference in the free energy of the different phases is minimal for the same molecular parameters, which confirms that this coexisting phase is reasonable. It also shows that this system’s potential barrier for vesicle formation is low, which opens up new possibilities for self-assembly to form vesicles.
The control of vesicle size and membrane thickness has been a widely studied topic [8,10,35,54,55]. In Figure 4a, we statistically analyze the density distribution of self-assembled vesicles with molecular parameters of -comb-, where , 8, 10, and 14, respectively. Here, r represents the distance from the vesicle center, and denotes the average density of the vesicle at on the spherical shell. Specifically, the vesicle’s center of mass is first determined. Then, the number of hydrophilic beads at different radial distances within concentric spherical shells of equal thickness is counted to obtain the distribution profile. We observe two peaks with increasing r, except , which further demonstrates the formation of vesicles. When , corresponding to non-spherical vesicles, the density distribution no longer follows the pattern of two peaks. As x increases, the first peak continuously shifts towards the vesicle’s center. However, the second peak is almost unchanged, suggesting that the membrane thickness is increasing while the overall dimensions remain constant, which matches the calculated values. This is a promising method for controlling vesicle size to modulate membrane thickness, which infers that the assembled vesicles formed by comb-like copolymers with larger gap lengths (i.e., fewer grafting points) possess thicker hydrophobic membranes and smaller cavities.
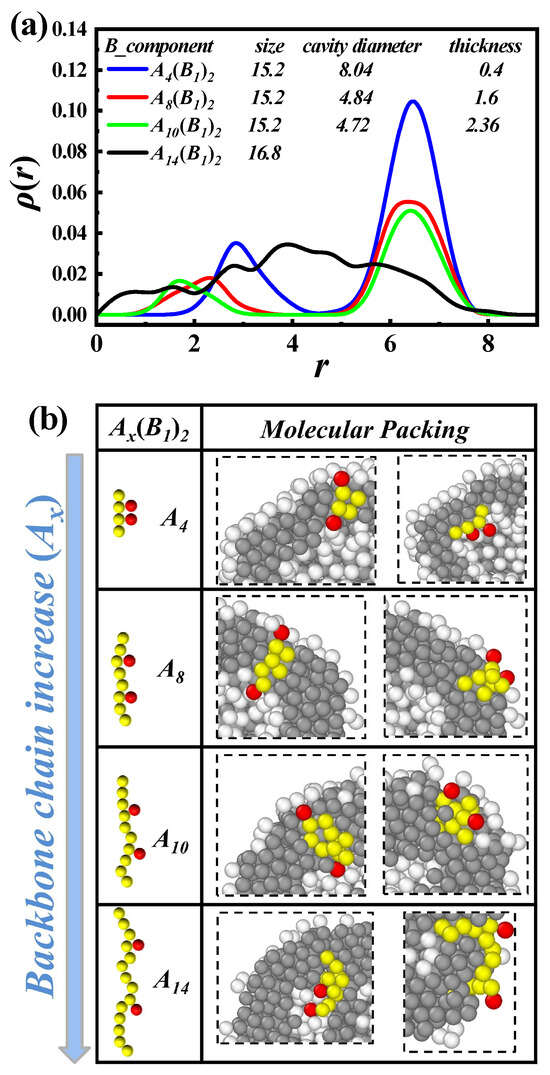
Figure 4.
(a) Average density [] of the hydrophilic beads (B) as a function of the distance r from the center of the assembled vesicles, which are composed of and , 8, 10, and 14, respectively. The overall size of the vesicles, the cavity diameters, and the membrane thicknesses are also listed. (b) Amplified molecular packing of the vesicles corresponds to the cases of (a).
To clarify the molecular mechanism of such size-invariant but membrane-thickness-variable vesicles, we give amplified molecular packing, as illustrated in Figure 4b. When , due to the high graft density of hydrophilic side chains, most hydrophobic backbones exhibit a straighter shape, and the average distance from backbone end to end is approximately 4. However, when , with side chains spaced farther apart, the backbone tends to bend, and the average distance from the backbone end to end is approximately . As hydrophobic backbones tend to aggregate, thicker hydrophobic membranes are formed. Furthermore, when increased to “overloaded” lengths, such as , the hydrophobic portion of the packing is not constrained, resulting in a non-spherical vesicle.
Figure 2 shows a large coexistence zone for toroidal and cylindrical micelles. To explore their formation mechanism and to verify the rationality of their coexistence, we calculate the radius of gyration during their formation respectively and calculate the free energy of their steady states using SCFT, as shown in Figure 5. The comb-like chains rapidly aggregate at the initial simulation. Partial aggregates gradually become straight, which may be attributed to the rearrangement of comb-like chains, causing the formation of cylindrical micelles. Differing from that of cylindrical micelles, the middle of the aggregate gradually broke open, eventually forming toroidal micelles. As depicted in Figure 5a,b, when the structure of the toroidal and cylindrical micelles is gradually stabilized, their radii of gyration are also only stable, accompanied by small fluctuations. We then calculate their free energies using SCFT in Figure 5c and find their values almost identical. This suggests that under the same molecular parameter conditions, neither structure has a significant advantage over the other, and thus, coexisting phases can easily occur.
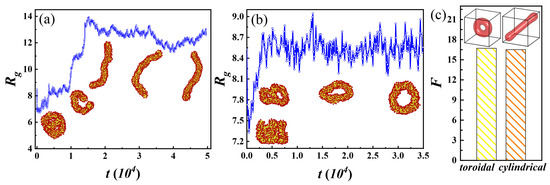
Figure 5.
Gyration radius () during the formation of cylindrical micelles (a) and toroidal micelles (b) as a function of simulation time (t). The insets show representative simulation snapshots captured during the self-assembly process. (c) Free energy (F) for toroidal and cylindrical micelles, where the insets exhibit stable states.
4. Conclusions
In this work, we systematically investigate the relationship between the molecular parameters and self-assembled morphologies of amphiphilic comb-like chains -comb- in solution by employing BD and SCFT. The results indicate that the adjustments in x and n lead to different arrangements of chains, resulting in stable states such as vesicles, toroidal micelles, bowl-like micelles, sheet-like micelles, non-spherical vesicles, and cylindrical micelles. Importantly, we find that vesicle formation involves two intermediate states, sheet-like and bowl-like micelles, and the difference in their free energies is minimal, which illustrates the coexisting phase between them. Moreover, the assembled vesicles can be modulated in the membrane thickness with overall size unchanged by only adjusting the backbone length. We also demonstrate the coexistence of toroidal and cylindrical micelles because neither structure has a significant advantage over the other in free energy. Our work shows how to obtain different morphologies by adjusting -comb-, especially the size-invariant but membrane-thickness-variable vesicles and toroidal and cylindrical micelles, which provides insight into their applications such as stable drug encapsulation and enhanced targeted drug delivery. Of course, the interaction strength of hydrophobic beads is another critical factor influencing the outcomes, alongside molecular parameters. The synergistic effects of these factors warrant further investigation. Additionally, the availability of efficient sampling methods to obtain the distribution of coexisting phases is a question worth exploring. Furthermore, future studies could extend to environmentally responsive dynamic assembly, investigating phenomena such as temperature-gradient-induced dynamic phase transitions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/polym17131870/s1, SCFT Method.
Author Contributions
Methodology, Q.C., K.T., R.Z. and Z.X.; Software, K.T.; Formal analysis, K.T. and R.Z.; Investigation, Q.C. and K.T.; Data curation, Q.C.; Writing—original draft, Q.C. and R.Z.; Writing—review & editing, M.D. and Z.X.; Supervision, M.D. and Z.X.; Project administration, M.D.; Funding acquisition, Q.C. and M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work is financially supported by the Research Program for Universities in Xinjiang Uygur Autonomous Region (No. XJEDU2024P69) and the National Natural Science Foundation of China (No. 22373025).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mei, G.; Zheng, Y.; Fu, Y.; Huo, M. Polymerization-induced self-assembly of random bottlebrush copolymers. Polym. Chem. 2022, 13, 5389–5396. [Google Scholar] [CrossRef]
- MacFarlane, L.; Zhao, C.; Cai, J.; Qiu, H.; Manners, I. Emerging applications for living crystallization-driven self-assembly. Chem. Sci. 2021, 12, 4661–4682. [Google Scholar] [CrossRef]
- Wen, W.; Huang, T.; Guan, S.; Zhao, Y.; Chen, A. Self-assembly of single chain janus nanoparticles with tunable liquid crystalline properties from stilbene-containing block copolymers. Macromolecules 2019, 52, 2956–2964. [Google Scholar] [CrossRef]
- Shi, H.; Zhao, Y.; Dong, X.; Zhou, Y.; Wang, D. Frustrated crystallisation and hierarchical self-assembly behaviour of comb-like polymers. Chem. Soc. Rev. 2013, 42, 2075–2099. [Google Scholar] [CrossRef]
- Sugihara, S.; Blanazs, A.; Armes, S.P.; Ryan, A.J.; Lewis, A.L. Aqueous dispersion polymerization: A new paradigm for in situ block copolymer self-assembly in concentrated solution. J. Am. Chem. Soc. 2011, 133, 15707–15713. [Google Scholar] [CrossRef] [PubMed]
- Rösler, A.; Vandermeulen, G.W.; Klok, H.A. Advanced drug delivery devices via self-assembly of amphiphilic block copolymers. Adv. Drug Deliv. Rev. 2001, 53, 95–108. [Google Scholar] [CrossRef]
- Ding, M.; Hou, L.; Duan, X.; Shi, T.; Li, W.; Shi, A.C. Translocation of micelles through a nanochannelNanochannel. Macromolecules 2022, 55, 6487–6492. [Google Scholar] [CrossRef]
- Nishimura, T.; Sasaki, Y.; Akiyoshi, K. Biotransporting self-assembled nanofactories using polymer vesicles with molecular permeability for enzyme prodrug cancer therapy. Adv. Mater. 2017, 29, 1702406. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Ezzat, M.; Huang, C.J. Lysolipid-inspired amphiphilic polymer nanostructures: Implications for drug delivery. ACS Appl. Nano Mater. 2022, 5, 107–112. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, T.; Lin, J. Self-assembly of graft copolymers in backbone-selective solvents: A route toward stable hierarchical vesicles. RSC Adv. 2013, 3, 19481–19491. [Google Scholar] [CrossRef]
- van den Broek, B.; Noom, M.C.; van Mameren, J.; Battle, C.; MacKintosh, F.C.; Wuite, G.J.L. Visualizing the formation and collapse of DNA toroids. Biophys. J. 2010, 98, 1902–1910. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Gao, L.; Cai, C.; Lin, J.; Wang, L.; Tian, X. Polymeric toroidal self-assemblies: Diverse formation mechanisms and functions. Adv. Funct 2021, 32, 2106036. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, L.; Sun, Y.; Lin, G.; Manners, I.; Qiu, H. Surface-Initiated Living Self-Assembly of Polythiophene-Based Conjugated Block Copolymer into Erect Micellar Brushes. Angew. Chem. Int. Ed. 2024, 63, e202315740. [Google Scholar] [CrossRef]
- Ding, M.; Chen, Q.; Duan, X.; Shi, T. Flow-driven translocation of a diblock copolymer through a nanopore. J. Phys. Chem. B 2019, 123, 8848–8852. [Google Scholar] [CrossRef] [PubMed]
- Shi, Q.; Wu, J.; Chen, H.; Xu, X.; Yang, Y.B.; Ding, M. Inertial migration of polymer micelles in a square microchannel. Soft Matter 2024, 20, 1760–1766. [Google Scholar] [CrossRef] [PubMed]
- Qi, H.; Liu, D.; Ding, M. Flow-driven translocation of strung micelles formed by core–shell bottle-brush copolymers and the accompanying morphological transformation through a nanochannel. Macromolecules 2024, 57, 2786–2791. [Google Scholar] [CrossRef]
- Phan, Q.T.; Zhang, H.; Pham, D.A.; Rabanel, J.M.; Filippini, A.; Boffito, D.; Banquy, X. Multicompartment micro- and nanoparticles using supramolecular assembly of core–shell bottlebrush polymers. ACS Macro Lett. 2023, 12, 1589–1594. [Google Scholar] [CrossRef]
- Qi, H.; Zhou, H.W.; Duan, C.; Li, W.H.; Ding, M.M. Self-assembled conformations of a core-shell comb-like chain with adjustable architectural parameters. Chin. J. Polym. Sci. 2023, 41, 1439–1446. [Google Scholar] [CrossRef]
- Liu, Y.T.; Li, Y.R.; Wang, X. Spontaneous onion shape vesicle formation and fusion of comb-like block copolymers studied by dissipative particle dynamics. RSC Adv. 2017, 7, 5130–5135. [Google Scholar] [CrossRef]
- Selianitis, D.; Pispas, S. Multi-responsive poly(oligo(ethylene glycol)methyl methacrylate)-co-poly(2-(diisopropylamino)ethyl methacrylate) hyperbranched copolymers via reversible addition fragmentation chain transfer polymerization. Polym. Chem. 2021, 12, 6582–6593. [Google Scholar] [CrossRef]
- Qi, M.; Li, K.; Zheng, Y.; Rasheed, T.; Zhou, Y. Hyperbranched multiarm copolymers with a ucst phase transition: Topological effect and the mechanism. Langmuir 2018, 34, 3058–3067. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, N.; Lee, J.H.; Akiba, I.; Nishimura, T. Exploring the effects of glyco-copolymer architectures on the solution self-assembly of amphiphilic thermoresponsive linear, star, and cyclic polymers. Polym. Chem. 2023, 14, 3834–3842. [Google Scholar] [CrossRef]
- Mukkamala, R.S.; Hore, M.J.A. Simulation and analysis of molecular bottlebrush dynamics in dilute solutions. Macromolecules 2024, 57, 445–455. [Google Scholar] [CrossRef]
- Mohammadi, E.; Joshi, S.Y.; Deshmukh, S.A. A review of computational studies of bottlebrush polymers. Comp. Mater. Sci. 2021, 199, 110720. [Google Scholar] [CrossRef]
- Li, Z.; Tang, M.; Liang, S.; Zhang, M.; Biesold, G.M.; He, Y.; Hao, S.M.; Choi, W.; Liu, Y.; Peng, J.; et al. Bottlebrush polymers: From controlled synthesis, self-assembly, properties to applications. Prog. Polym. Sci. 2021, 116, 101387. [Google Scholar] [CrossRef]
- Zhao, B. Shape-changing bottlebrush polymers. J. Phys. Chem. B 2021, 125, 6373–6389. [Google Scholar] [CrossRef] [PubMed]
- Xie, G.; Martinez, M.R.; Olszewski, M.; Sheiko, S.S.; Matyjaszewski, K. Molecular bottlebrushes as novel materials. Biomacromolecules 2019, 20, 27–54. [Google Scholar] [CrossRef] [PubMed]
- Rzayev, J. Molecular bottlebrushes: New opportunities in nanomaterials fabrication. ACS Macro Lett. 2012, 1, 1146–1149. [Google Scholar] [CrossRef]
- Kent, E.W.; Lewoczko, E.M.; Zhao, B. Effect of buffer anions on pearl-necklace morphology of tertiary amine-containing binary heterografted linear molecular bottlebrushes in acidic aqueous buffers. Langmuir 2020, 36, 13320–13330. [Google Scholar] [CrossRef]
- Nese, A.; Li, Y.; Averick, S.; Kwak, Y.; Konkolewicz, D.; Sheiko, S.S.; Matyjaszewski, K. Synthesis of amphiphilic poly(n-vinylpyrrolidone)-b-poly(vinyl acetate) molecular bottlebrushes. ACS Macro Lett. 2012, 1, 227–231. [Google Scholar] [CrossRef]
- Lyubimov, I.; Wessels, M.G.; Jayaraman, A. Molecular dynamics simulation and PRISM theory study of assembly in solutions of amphiphilic bottlebrush block copolymers. Macromolecules 2018, 51, 7586–7599. [Google Scholar] [CrossRef]
- He, Y.; Li, L.; Ding, M.; Li, W. Flow-driven translocation of comb-like copolymer micelles through a nanochannel. Soft Matter 2023, 19, 9166–9172. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, T.; Gou, J.; Zhang, L.; Tao, X.; Tian, B.; Tian, P.; Yu, D.; Song, J.; Liu, X.; et al. Strategies for improving the payload of small molecular drugs in polymeric micelles. J. Control. Release 2017, 261, 352–366. [Google Scholar] [CrossRef] [PubMed]
- De Nicola, A.; Hezaveh, S.; Zhao, Y.; Kawakatsu, T.; Roccatano, D.; Milano, G. Micellar drug nanocarriers and biomembranes: How do they interact? Phys. Chem. Chem. Phys. 2014, 16, 5093–5105. [Google Scholar] [CrossRef]
- Liu, Y.T.; Li, Y.R.; Wang, X. Dynamic evolution of a vesicle formed by comb-like block copolymer-tethered nanoparticles: A dissipative particle dynamics simulation study. Phys. Chem. Chem. Phys. 2017, 19, 27313–27319. [Google Scholar] [CrossRef]
- Kramarenko, E.Y.; Pevnaya, O.S.; Khokhlov, A.R. Stoichiometric polyelectrolyte complexes as comb copolymers. J. Chem. Phys. 2005, 122, 084902. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.Y.; Lin, Y.L.; Sheng, Y.J.; Tsao, H.K. Structural characteristics and fusion pathways of onion-like multilayered polymersome formed by amphiphilic comb-like graft copolymers. Macromolecules 2013, 46, 5644–5656. [Google Scholar] [CrossRef]
- Li, M.; Li, G.L.; Zhang, Z.; Li, J.; Neoh, K.G.; Kang, E.T. Self-assembly of pH-responsive and fluorescent comb-like amphiphilic copolymers in aqueous media. Polymer 2010, 51, 3377–3386. [Google Scholar] [CrossRef]
- Tang, Z.; Pan, X.; Zhou, H.; Li, L.; Ding, M. Conformation of a comb-like chain free in solution and confined in a nanochannel: From linear to bottlebrush structure. Macromolecules 2022, 55, 8668–8675. [Google Scholar] [CrossRef]
- Hao, P.; Mai, X.; Chen, Q.; Ding, M. Conformation of an amphiphilic comb-like copolymer in a selective solvent. Chin. J. Polym. Sci. 2023, 41, 1386–1391. [Google Scholar] [CrossRef]
- Yethiraj, A. A Monte Carlo simulation study of branched polymers. J. Chem. Phys. 2006, 125, 204901. [Google Scholar] [CrossRef] [PubMed]
- Hsu, H.P.; Paul, W.; Rathgeber, S.; Binder, K. Characteristic length scales and radial monomer density profiles of molecular bottle-brushes: Simulation and experiment. Macromolecules 2010, 43, 1592–1601. [Google Scholar] [CrossRef]
- Wessels, M.G.; Jayaraman, A. Molecular dynamics simulation study of linear, bottlebrush, and star-like amphiphilic block polymer assembly in solution. Soft Matter 2019, 15, 3987–3998. [Google Scholar] [CrossRef]
- Bejagam, K.K.; Singh, S.K.; Ahn, R.; Deshmukh, S.A. Unraveling the conformations of backbone and side chains in thermosensitive bottlebrush polymers. Macromolecules 2019, 52, 9398–9408. [Google Scholar] [CrossRef]
- Dutta, S.; Wade, M.A.; Walsh, D.J.; Guironnet, D.; Rogers, S.A.; Sing, C.E. Dilute solution structure of bottlebrush polymers. Soft Matter 2019, 15, 2928–2941. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Reddy, G.; Yethiraj, A. Implicit and explicit solvent models for the simulation of dilute polymer solutions. Macromolecules 2006, 39, 8536–8542. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Ermak, D.L.; McCammon, J.A. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978, 69, 1352–1360. [Google Scholar] [CrossRef]
- Kumar, S.; Larson, R.G. Brownian dynamics simulations of flexible polymers with spring–spring repulsions. J. Chem. Phys. 2001, 114, 6937–6941. [Google Scholar] [CrossRef]
- Zhang, L.; Lin, J.; Lin, S. Effect of molecular architecture on phase behavior of graft copolymers. J. Phys. Chem. B 2008, 112, 9720–9728. [Google Scholar] [CrossRef] [PubMed]
- Duan, C.; Li, W.; Qiu, F.; Shi, A.C. lanet-satellite micellar superstructures formed by abcb terpolymers in solution. ACS Macro Lett. 2017, 6, 257–261. [Google Scholar] [CrossRef] [PubMed]
- Parent, L.R.; Bakalis, E.; Ramirez-Hernandez, A.; Kammeyer, J.K.; Park, C.; de Pablo, J.J.; Zerbetto, F.; Patterson, J.P.; Gianneschi, N.C. Directly Observing Micelle Fusion and Growth in Solution by Liquid-Cell Transmission Electron Microscopy. J. Am. Chem. Soc. 2017, 139, 17140–17151. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.W.; Li, Y.; Park, J.H.; Lee, D.S. pH-triggered unimer/vesicle-transformable and biodegradable polymersomes based on PEG-b-PCL–grafted poly (β-amino ester) for anti-cancer drug delivery. Polymer 2013, 54, 102–110. [Google Scholar] [CrossRef]
- Tseng, Y.C.; Chang, H.Y.; Sheng, Y.J.; Tsao, H.K. Atypical vesicles and membranes with monolayer and multilayer structures formed by graft copolymers with diblock side-chains: Nonlamellar structures and curvature-enhanced permeability. Soft Matter 2022, 18, 7559–7568. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).