Modeling and Compensation Methods for Trajectory Errors in Continuous Fiber-Reinforced Thermoplastic Composites Using 3D Printing
Abstract
1. Introduction
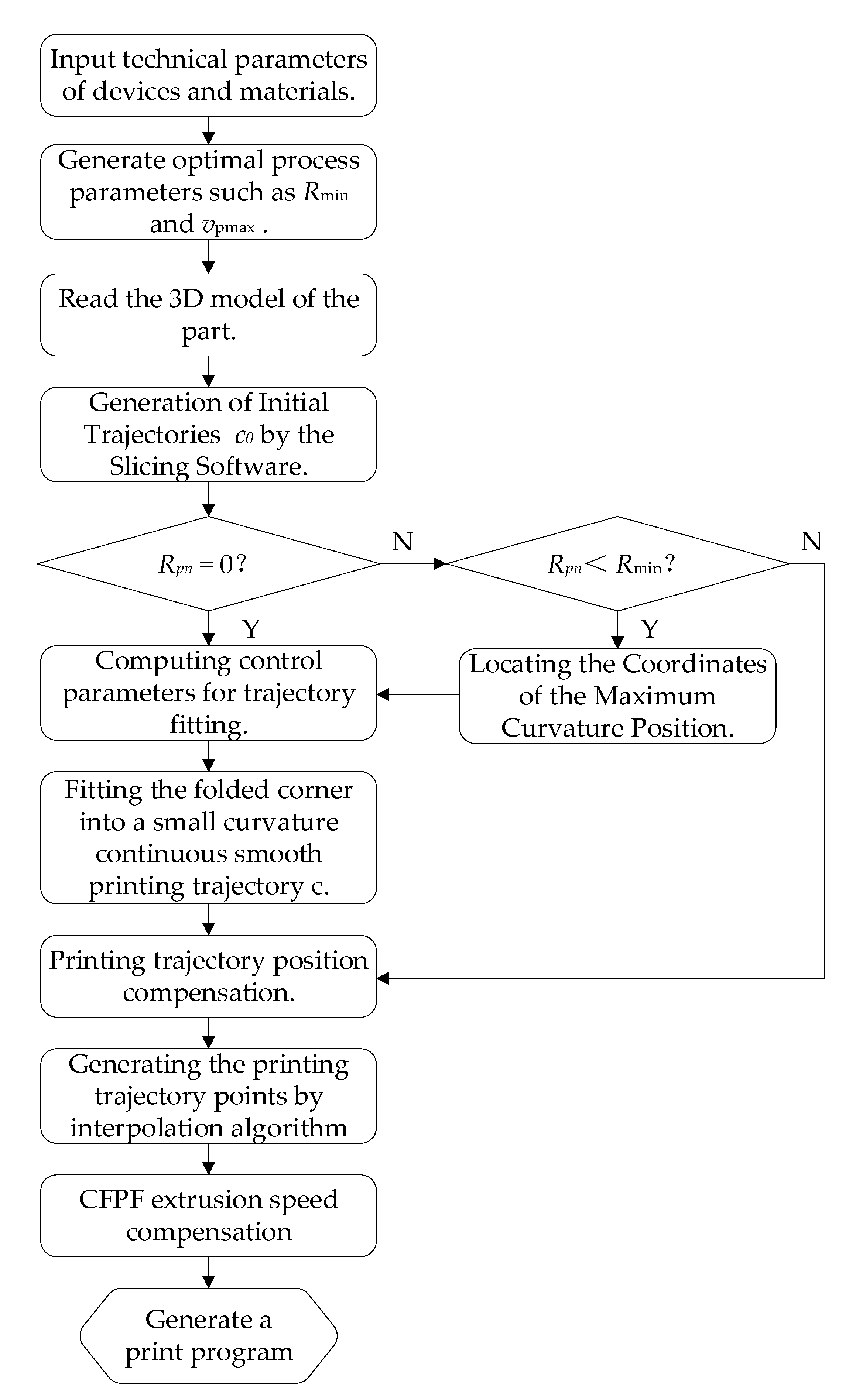
2. Theory and Method
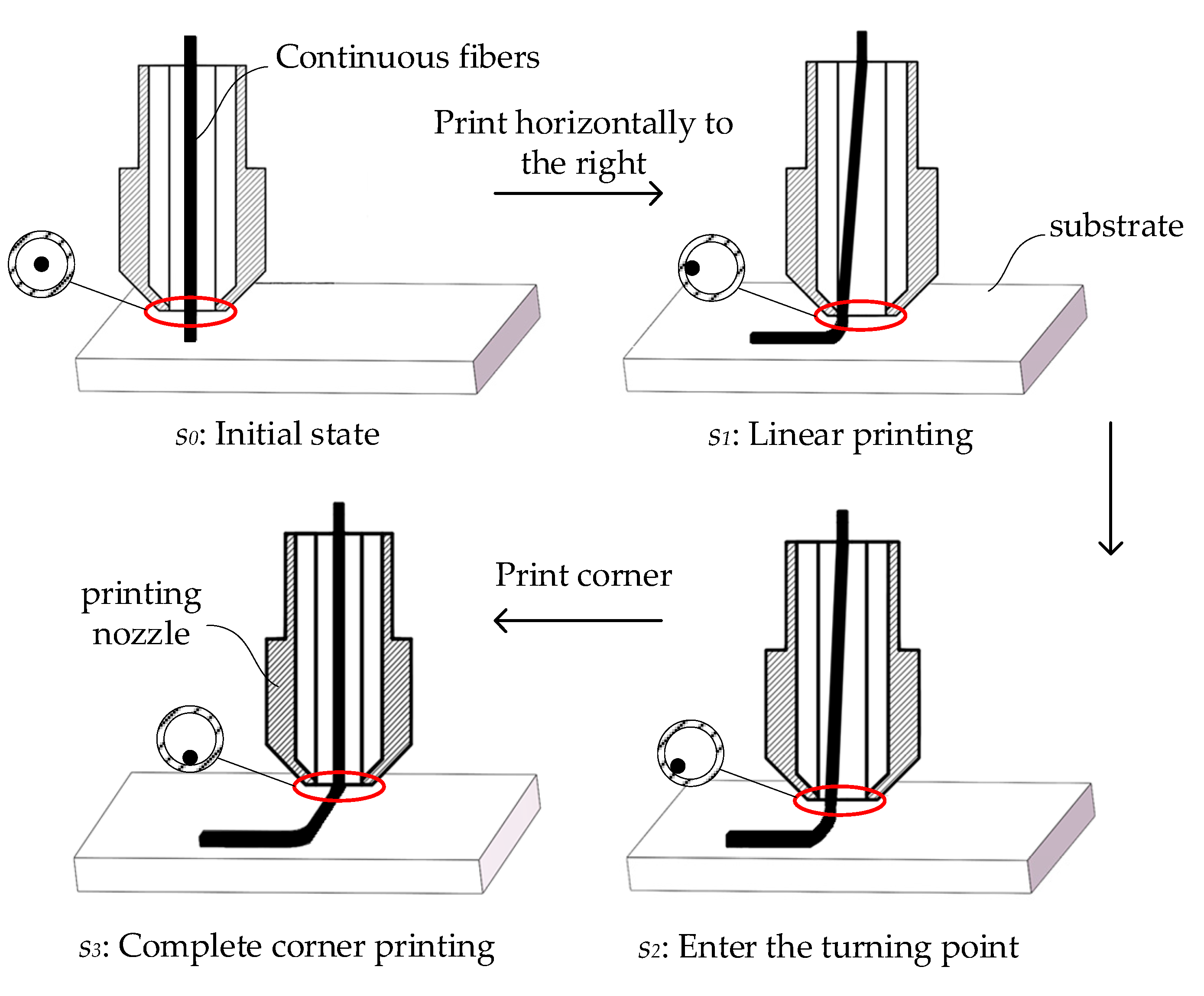
2.1. Assumption of Follow-Up Theory
- Disregarding the impacts of adhesion, elasticity, and inertia forces of the CFPF;
- The impact of the motion precision of 3D printing equipment is disregarded.
- Within the nozzle, the CFPF is passively extruded and subjected to tension.
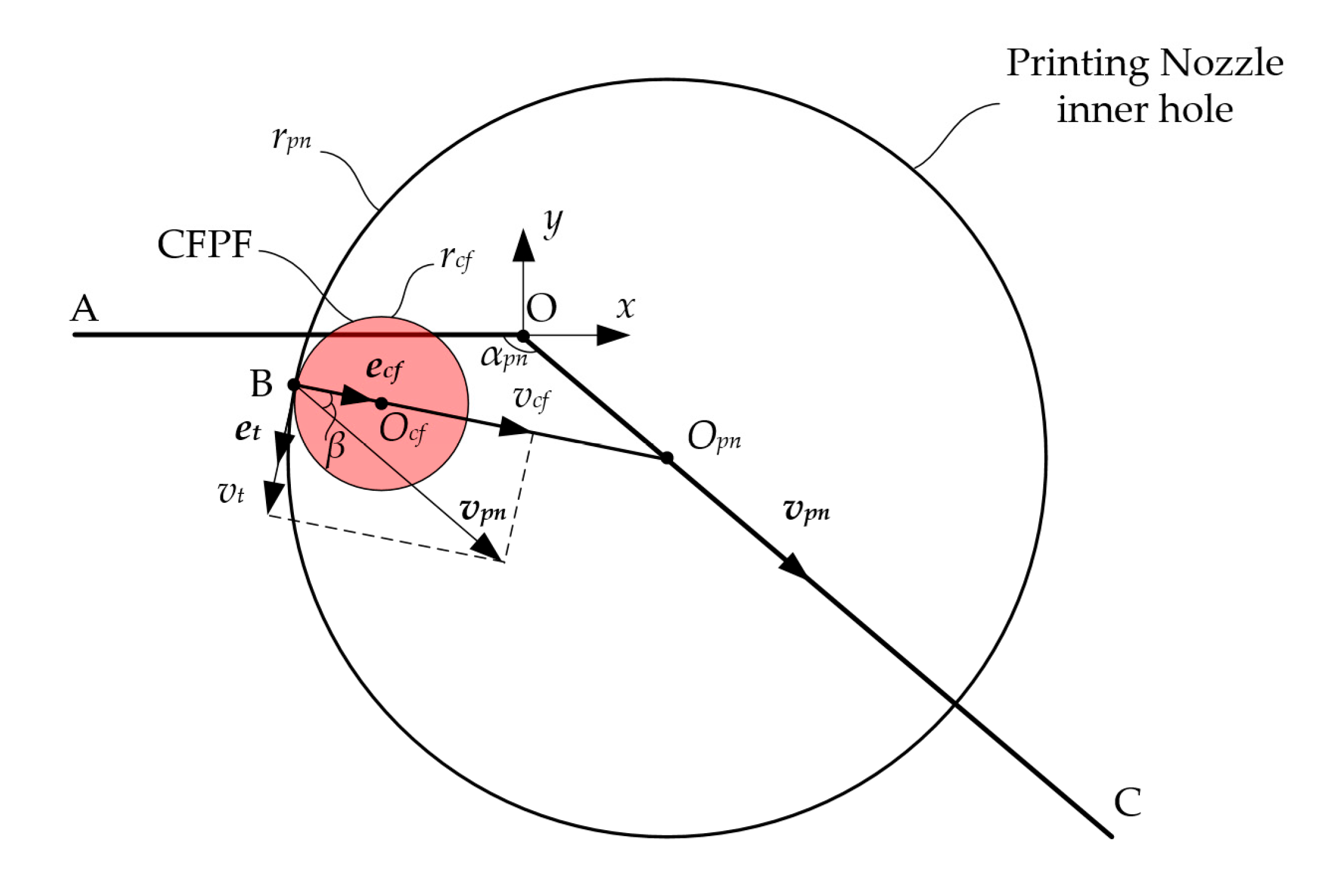
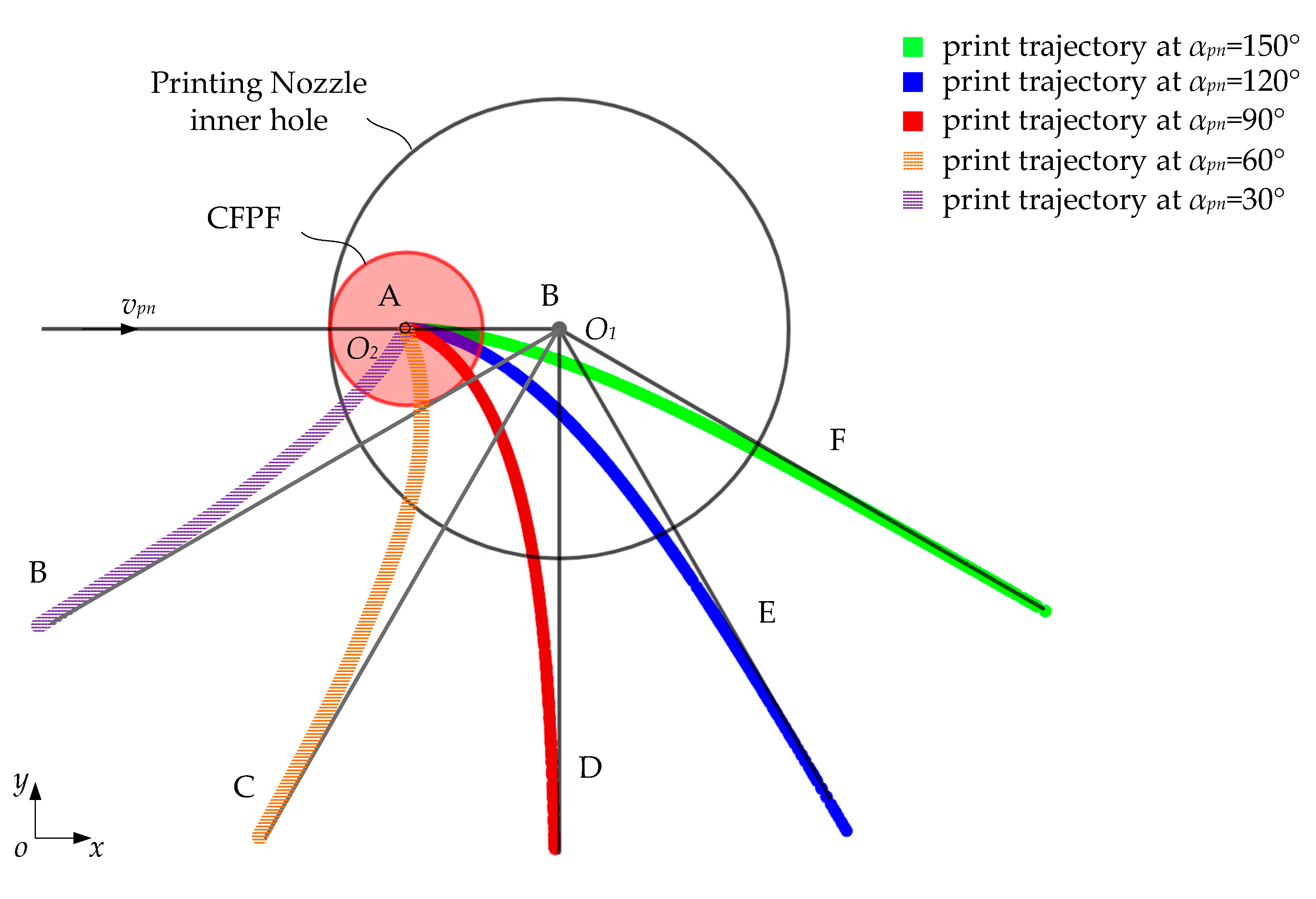
2.2. Mechanism of Printed Trajectory Error Formation
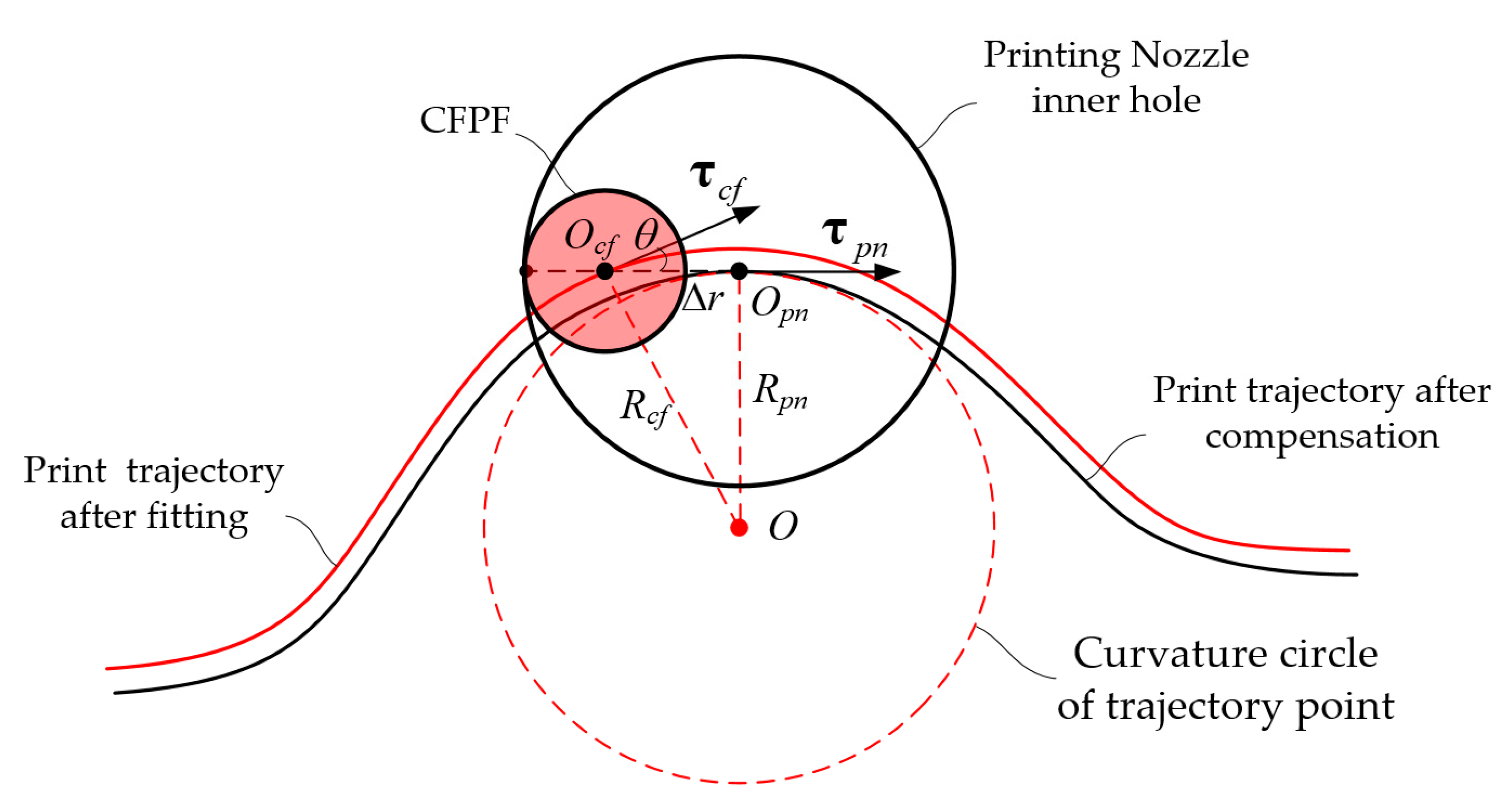
- The dragging effect of the nozzle’s inner wall on the CFPF results in a lag at the actual printing point. This subsequently leads to deviations in both the shape and position of the S-shaped printing trajectory.
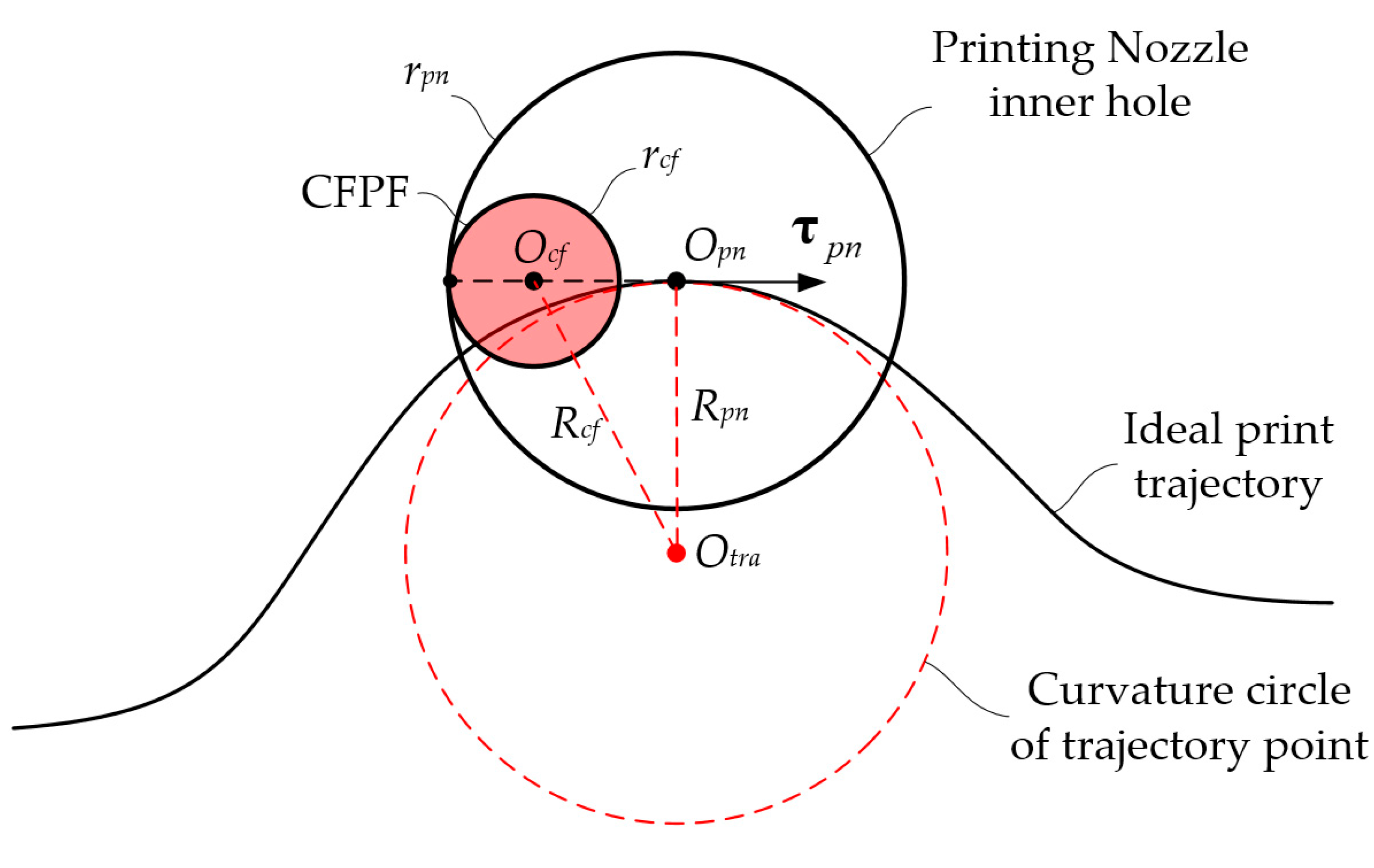
- The greater the curvature of the ideal printing trajectory, the greater the printing trajectory error; at the inflection point A where the curvature is zero, the ideal printing trajectory coincides with the actual printing trajectory.
- As the curvature of the actual printing trajectory decreases, the printed trajectory elongates, and consequently, the envelope area of the printed trajectory expands.
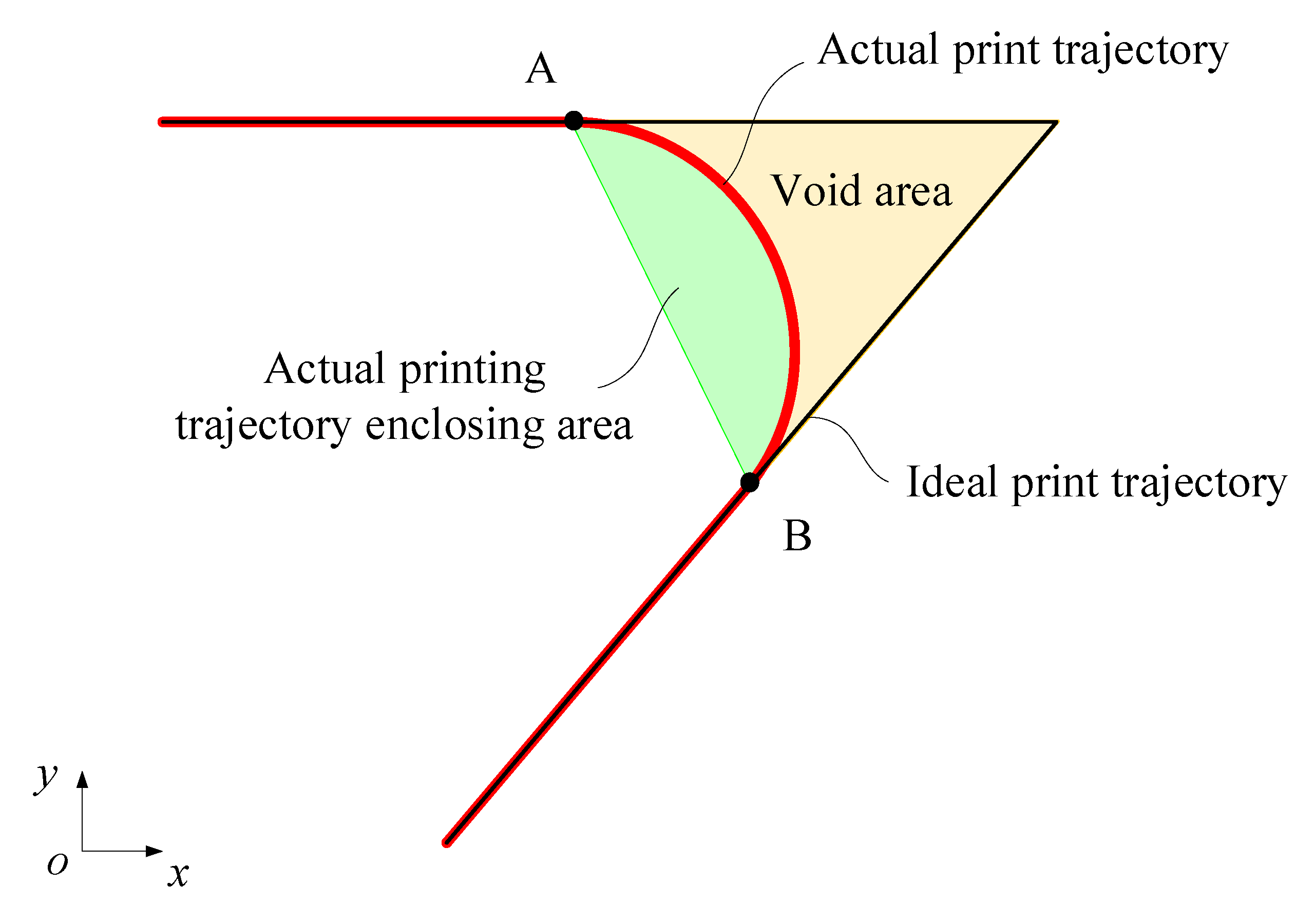
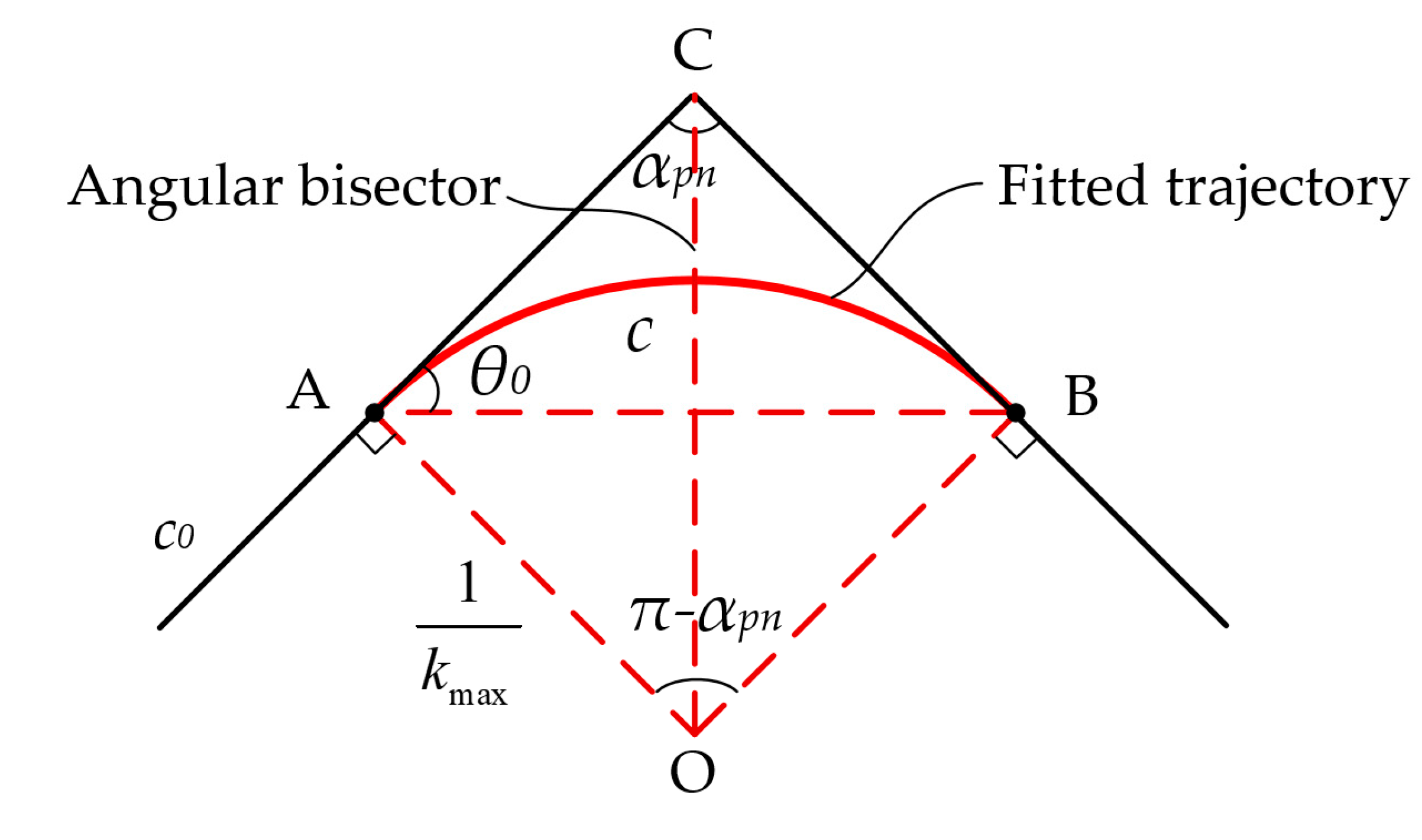
2.3. Modeling the Error in Printing Trajectory
- Line profile
- Deviation kurtosis
- Deviation area ratio
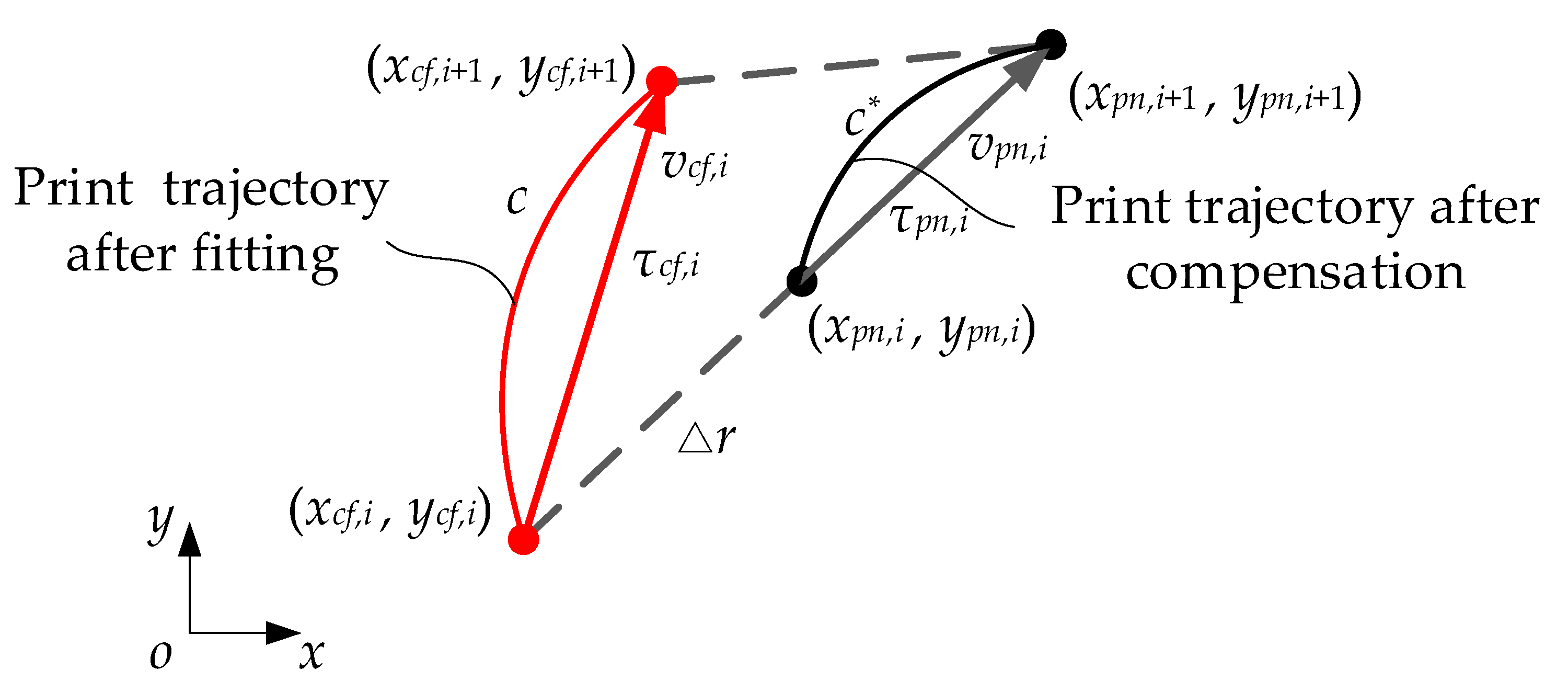
2.4. Compensation for Printing Trajectory Errors
3. Results and Analysis
3.1. Printing Devices Materials and Parameters
3.2. Maximum Printable Curvature Measurement
3.3. Simulation and Printing Experiments
4. Conclusions
- The error model provides accurate predictions of the printed trajectory error, particularly when the printed trajectory forms an obtuse angle. The average prediction deviations for line profile, deviation kurtosis, and deviation area ratio are 36.029%, 47.238%, and 2.045%, respectively.
- The layer height demonstrates a low sensitivity to printing trajectory errors. However, the emergence of wave-shaped defects may be observed when the layer height exceeds 0.25 mm. Consequently, it is suggested that the optimal layer height be maintained within the range of 0.1 to 0.2 mm.
- The correlation between the printed trajectory errors observed before and after compensation and the corner angle is markedly negative. A sharper corner in the printed trajectory corresponds to a larger trajectory error.
- After compensation, both fiber bundle twisting and folding defects were effectively mitigated. The deviation area ratio decreased by an average of 15.502%, while there was an observed increase in the line profile by an average of 0.824 mm. Additionally, the deviation kurtosis experienced an average increase of 0.66%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parveez, B.; Kittur, M.I.; Badruddin, I.A.; Kamangar, S.; Hussien, M.; Umarfarooq, M.A. Scientific advancements in composite materials for aircraft applications: A review. Polymers 2022, 14, 5007. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Lin, G.; Vaidya, U.; Wang, H. Past, present and future prospective of global carbon fiber composite developments and applications. Compos. Part B Eng. 2023, 250, 110463. [Google Scholar]
- Trzepieciński, T.; Batu, T.; Kibrete, F.; Lemu, H.G. Application of composite materials for energy generation devices. J. Compos. Sci. 2023, 7, 55. [Google Scholar]
- Van de Werken, N.; Tekinalp, H.; Khanbolouki, P.; Ozcan, S.; Williams, A.; Tehrani, M. Additively Manufactured Carbon Fiber-Reinforced Composites: State of the Art and Perspective. Addit. Manuf. 2019, 31, 100962. [Google Scholar] [CrossRef]
- Goh, G.D.; Yap, Y.L.; Agarwala, S.; Yeong, W.Y. Recent progress in additive manufacturing of fiber reinforced polymer composite. Adv. Mater. Technol. 2019, 4, 1800271. [Google Scholar]
- Dong, K.; Ke, H.; Panahi-Sarmad, M.; Yang, T.; Huang, X.; Xiao, X. Mechanical properties and shape memory effect of 4D printed cellular structure composite with a novel continuous fiber-reinforced printing path. Mater. Des. 2021, 198, 109303. [Google Scholar]
- Lincoln, R.L.; Scarpa, F.; Ting, V.P.; Trask, R.S. Multifunctional composites: A metamaterial perspective. Multifunct. Mater. 2019, 2, 043001. [Google Scholar]
- Frketic, J.; Dickens, T.; Ramakrishnan, S. Automated manufacturing and processing of fiber-reinforced polymer (FRP) composites: An additive review of contemporary and modern techniques for advanced materials manufacturing. Addit. Manuf. 2017, 14, 69–86. [Google Scholar]
- Cheng, Y.; Li, J.; Qian, X.; Rudykh, S. 3D printed recoverable honeycomb composites reinforced by continuous carbon fibers. Compos. Struct. 2021, 268, 113974. [Google Scholar]
- Fidan, I.; Imeri, A.; Gupta, A.; Hasanov, S.; Nasirov, A.; Elliott, A.; Alifui-Segbaya, F.; Nanami, N. The trends and challenges of fiber reinforced additive manufacturing. Int. J. Adv. Manuf. Technol. 2019, 102, 1801–1818. [Google Scholar]
- Matsuzaki, R.; Ueda, M.; Namiki, M.; Jeong, T.K.; Asahara, H.; Horiguchi, K.; Nakamura, T.; Todoroki, A.; Hirano, Y. Three-dimensional printing of continuous-fiber composites by in-nozzle impregnation. Sci. Rep. 2016, 6, 23058. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Liu, T.; Yang, C.; Wang, Q.; Li, D. Interface and performance of 3D printed continuous carbon fiber reinforced PLA composites. Compos. Part A Appl. Sci. Manuf. 2016, 88, 198–205. [Google Scholar] [CrossRef]
- Dickson, A.N.; Barry, J.N.; McDonnell, K.A.; Dowling, D.P. Fabrication of continuous carbon, glass and Kevlar fibre reinforced polymer composites using additive manufacturing. Addit. Manuf. 2017, 16, 146–152. [Google Scholar] [CrossRef]
- Araya-Calvo, M.; López-Gómez, I.; Chamberlain-Simon, N.; León-Salazar, J.L.; Guillén-Girón, T.; Corrales-Cordero, J.S.; Sánchez-Brenes, O. Evaluation of compressive and flexural properties of continuous fiber fabrication additive manufacturing technology. Addit. Manuf. 2018, 22, 157–164. [Google Scholar] [CrossRef]
- Chacón, J.M.; Caminero, M.A.; Núñez, P.J.; García-Plaza, E.; García-Moreno, I.; Reverte, J.M. Additive manufacturing of continuous fiber reinforced thermoplastic composites using fused deposition modeling: Effect of process parameters on mechanical properties. Compos. Sci. Technol. 2019, 181, 107688. [Google Scholar] [CrossRef]
- Naranjo-Lozada, J.; Ahuett-Garza, H.; Orta-Castañón, P.; Verbeeten, W.M.H.; Sáiz-González, D. Tensile properties and failure behavior of chopped and continuous carbon fiber composites produced by additive manufacturing. Addit. Manuf. 2019, 26, 227–241. [Google Scholar] [CrossRef]
- Uşun, A.; Gümrük, R. The mechanical performance of the 3D printed composites produced with continuous carbon fiber reinforced filaments obtained via melt impregnation. Addit. Manuf. 2021, 46, 102112. [Google Scholar] [CrossRef]
- Dreifus, G.; Goodrick, K.; Giles, S.; Patel, M.; Foster, R.M.; Williams, C.; Lindahl, J.; Post, B.; Roschli, A.; Love, L.; et al. Path optimization along lattices in additive manufacturing using the Chinese postman problem. 3D Print. Addit. Manuf. 2017, 4, 98–104. [Google Scholar] [CrossRef]
- Liu, J.; Kang, Y.; Ma, C.; Wang, Y. Research on a Fiber Corner Compensation Algorithm in a 3D Printing Layer of Continuous Fiber-Reinforced Composite Materials. Appl. Sci. 2022, 12, 6687. [Google Scholar] [CrossRef]
- Shiratori, H.; Todoroki, A.; Ueda, M.; Matsuzaki, R.; Hirano, Y. Mechanism of folding a fiber bundle in the curved section of 3D printed carbon fiber reinforced plastics. Adv. Compos. Mater. 2020, 29, 247–257. [Google Scholar] [CrossRef]
- Matsuzaki, R.; Nakamura, T.; Sugiyama, K.; Ueda, M.; Todoroki, A.; Hirano, Y.; Yamagata, Y. Effects of set curvature and fiber bundle size on the printed radius of curvature by a continuous carbon fiber composite 3D printer. Addit. Manuf. 2018, 24, 93–102. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Yu, Y.; Zhang, Q.; Li, H.; Shi, G. Research on the Simulation Model of Continuous Fiber-Reinforced Composites Printing Track. Polymers 2022, 14, 2730. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J.; Yang, D. Fibre misalignment and breakage in 3D printing of continuous carbon fibre reinforced thermoplastic composites. Addit. Manuf. 2021, 38, 101775. [Google Scholar] [CrossRef]
- Grant, C. Automated processes for composite aircraft structure. Ind. Robot 2006, 33, 117–121. [Google Scholar] [CrossRef]
- Yamawaki, M.; Kouno, Y. Fabrication and mechanical characterization of continuous carbon fiber-reinforced thermoplastic using a preform by three-dimensional printing and via hot-press molding. Adv. Compos. Mater. 2017, 27, 209–219. [Google Scholar] [CrossRef]
- Shang, J.; Tian, X.; Luo, M.; Zhu, W.; Li, D.; Qin, Y.; Shan, Z. Controllable inter-line bonding performance and fracture patterns of continuous fiber reinforced composites by sinusoidal-path 3D printing. Compos. Sci. Technol. 2020, 192, 108096. [Google Scholar] [CrossRef]
- Kim, B.C.; Weaver, P.M.; Potter, K. Computer aided modelling of variable angle tow composites manufactured by continuous tow shearing. Compos. Struct. 2015, 129, 256–267. [Google Scholar] [CrossRef]
- Wang, Y. Research on Key Technology of “Independent Extrusion” Continuous Fiber Reinforced Composites 3D Printing. PhD Thesis, University of Science and Technology Beijing, Beijing, China, 2022. [Google Scholar]
- Hao, P.; Liu, D.; Wang, Y.; Liu, X.; Wang, B.; Li, G.; Feng, S. Design of manufacturable fiber path for variable-stiffness panels based on lamination parameters. Compos. Struct. 2019, 219, 158–169. [Google Scholar] [CrossRef]
- Niu, X.; Liu, Y.; Wu, J.; Yang, T. Curvature-controlled trajectory planning for variable stiffness composite laminates. Compos. Struct. 2022, 238, 111986. [Google Scholar] [CrossRef]
- Karimi, A.; Rahmatabadi, D.; Baghani, M. Various FDM Mechanisms Used in the Fabrication of Continuous-Fiber Reinforced Composites: A Review. Polymers 2024, 16, 831. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, X.; Yang, T.; Song, L.; Yang, L. Research progress on process defects and failure behaviors of continuous fiber-reinforced composite materials via 3D printing. Acta Mater. Compos. Sin. 2024, 41, 4478–4501. [Google Scholar]









| PAHT | CFPF | ||
|---|---|---|---|
| Parameters | Value | Parameters | Value |
| Filament diameter, mm | 1.75 | Filament diameter, mm | 0.4 |
| Density, g/cm3 | 1.21 | Tensile strength, MPa | 1200 |
| Tensile strength, MPa | 69.29 ± 1.17 | Printing speed, mm/min | 300~1000 |
| Bending strength, MPa | 112.64 ± 1.6 | Printing temperature, °C | 260~300 |
| Printing temperature, °C | 280~320 | Fiber Type | 1.5 k |
| Base plate temperature, °C | 80~100 | prepreg resin | PAHT |
| Corner Angle | Error Prediction | ||
|---|---|---|---|
| /(mm) | |||
| 30° | 0.4 | 2.1% | 62% |
| 60° | 0.38 | 2.69% | 55% |
| 90° | 0.267 | 2.23% | 39% |
| 120° | 0.166 | 1.7% | 35% |
| 150° | 0.077 | 1.1% | 38% |
| No. | Influencing Factors | Uncompensated | Compensated | |||||
|---|---|---|---|---|---|---|---|---|
| /(°) | /(mm) | /(mm) | /(mm) | |||||
| 1 | 30 | 0.15 | 1.56 | 14% | 69% | 3.8 | 13.8% | 66% |
| 2 | 60 | 0.25 | 1.31 | 11% | 53% | 2.9 | 12.1% | 52% |
| 3 | 90 | 0.1 | 0.39 | 4.1% | 43% | 0.57 | 4.7% | 43% |
| 4 | 120 | 0.2 | 0.28 | 3.3% | 37% | 0.35 | 4% | 37% |
| 5 | 150 | 0.3 | 0.12 | 2.1% | 35% | 0.16 | 3.2% | 34% |
| Evaluation Index | ||||||
|---|---|---|---|---|---|---|
| Mean value | 50.687% | 60.452% | 2.502% | 36.029% | 47.238% | 2.045% |
| Standard deviation | 18.218% | 16.484% | 7.417% | 3.749% | 1.204% | 7.674% |
| Max value | 74.359% | 85% | 10.145% | 40.714% | 48.485% | 9.302% |
| Min value | 31.538% | 45.61% | −8.571% | 31.538% | 45.61% | −8.571% |
| Extreme deviations | 42.821% | 39.39% | 18.716% | 9.176% | 2.875% | 17.874% |
| Evaluation Index | Uncompensated | Compensated | ||||
|---|---|---|---|---|---|---|
| /(mm) | /(mm) | |||||
| Mean value | 0.732 | 6.9% | 47.4% | 1.556 | 7.56% | 31.898% |
| Standard deviation | 0.586 | 4.713% | 12.484% | 1.498 | 4.459% | 11.569% |
| Max value | 1.56 | 14% | 69% | 3.8 | 13.8% | 66% |
| Min value | 0.12 | 2.1% | 35% | 0.16 | 3.2% | 34% |
| Extreme deviations | 1.44 | 11.9% | 34% | 3.64 | 10.6% | 32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Qu, S.; Li, S.; Yan, X.; Li, W.; Wang, Y. Modeling and Compensation Methods for Trajectory Errors in Continuous Fiber-Reinforced Thermoplastic Composites Using 3D Printing. Polymers 2025, 17, 1865. https://doi.org/10.3390/polym17131865
Liu M, Qu S, Li S, Yan X, Li W, Wang Y. Modeling and Compensation Methods for Trajectory Errors in Continuous Fiber-Reinforced Thermoplastic Composites Using 3D Printing. Polymers. 2025; 17(13):1865. https://doi.org/10.3390/polym17131865
Chicago/Turabian StyleLiu, Manxian, Sheng Qu, Shuo Li, Xiaoqiang Yan, Wei Li, and Yesong Wang. 2025. "Modeling and Compensation Methods for Trajectory Errors in Continuous Fiber-Reinforced Thermoplastic Composites Using 3D Printing" Polymers 17, no. 13: 1865. https://doi.org/10.3390/polym17131865
APA StyleLiu, M., Qu, S., Li, S., Yan, X., Li, W., & Wang, Y. (2025). Modeling and Compensation Methods for Trajectory Errors in Continuous Fiber-Reinforced Thermoplastic Composites Using 3D Printing. Polymers, 17(13), 1865. https://doi.org/10.3390/polym17131865








