Transfer Learning-Enhanced Prediction of Glass Transition Temperature in Bismaleimide-Based Polyimides
Abstract
1. Introduction
2. Materials and Methods
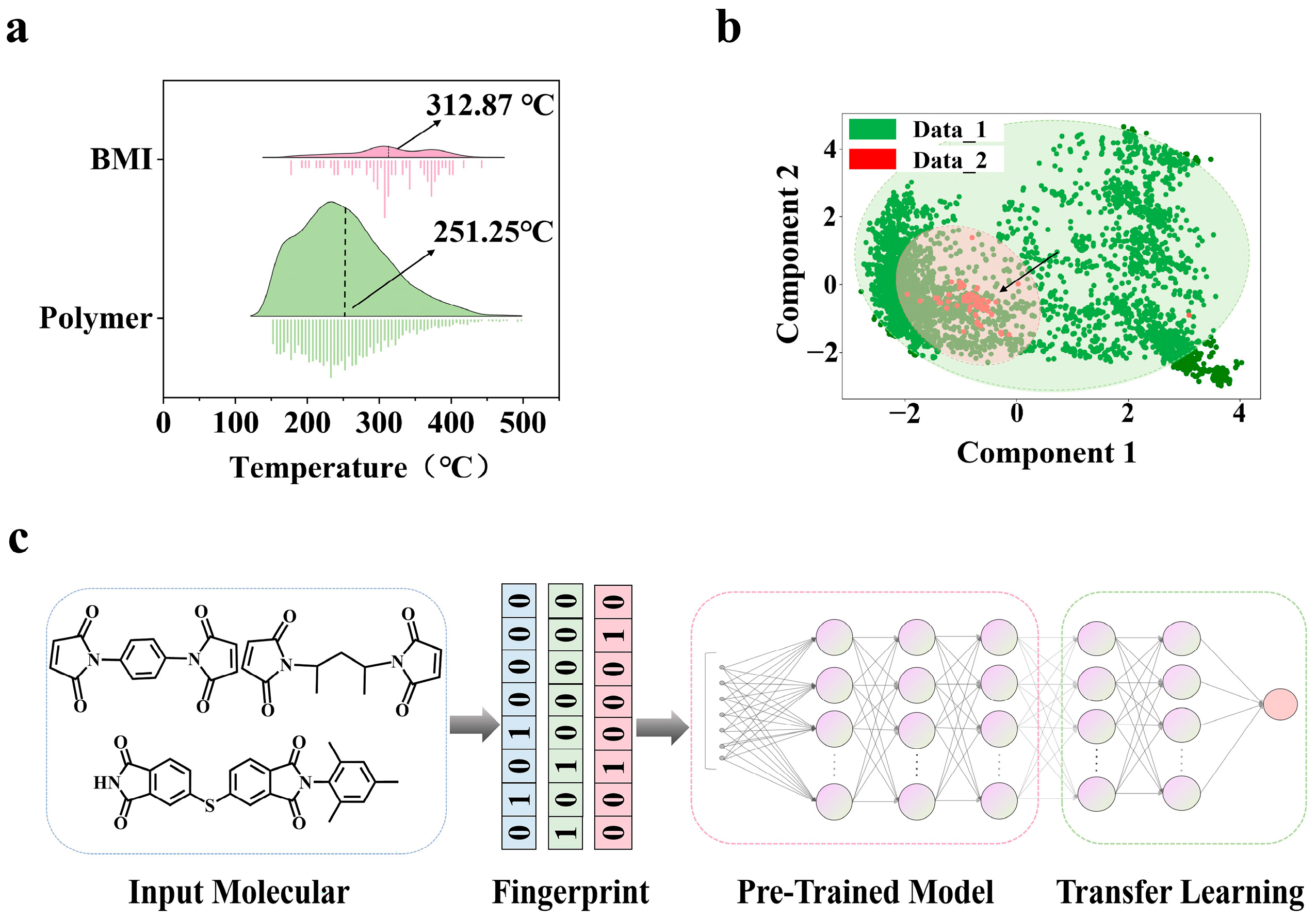
2.1. Data Collection
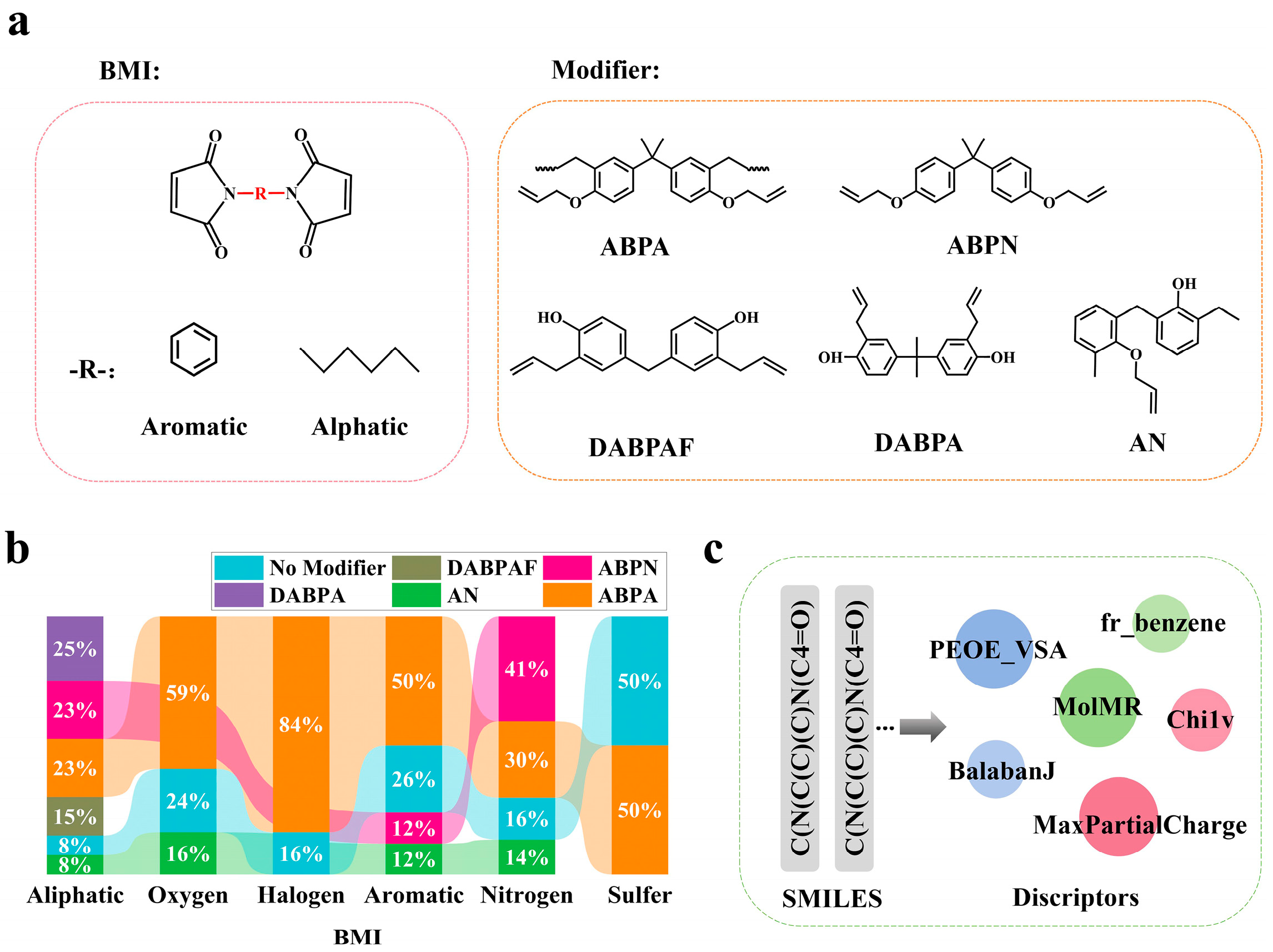
2.2. Feature Engineering
2.3. Training Strategy of Transfer Learning Model
2.4. Virtual Structure Proposed
2.5. Descriptor Calculated
2.6. Interpretable Model
2.7. SHAP Analysis
3. Results and Discussion
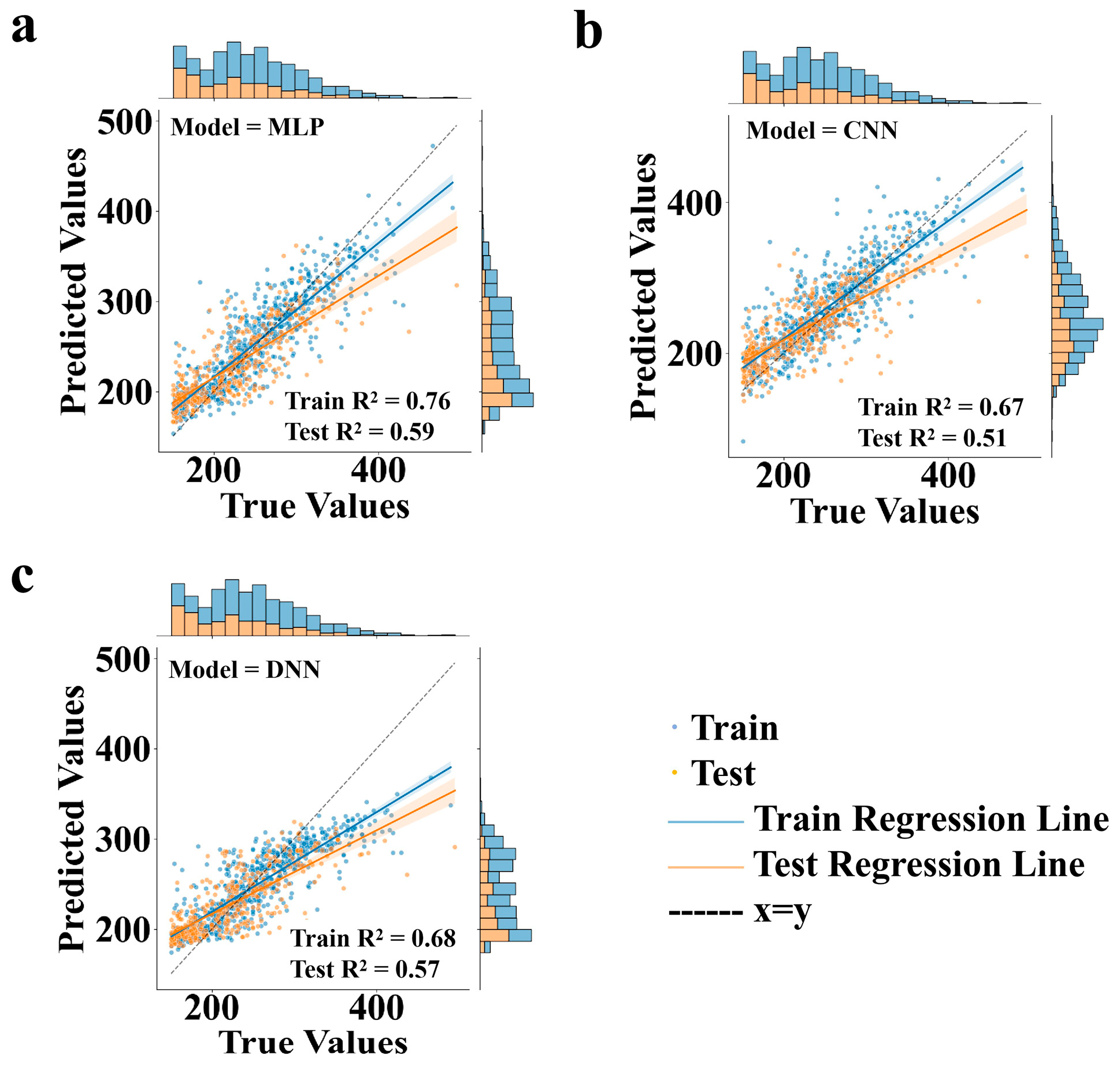
3.1. Performance Comparison of Different Neural Network Frameworks as Pre-Trained Models in Transfer Learning
3.2. Necessity and Technical Advantages of Transfer Learning
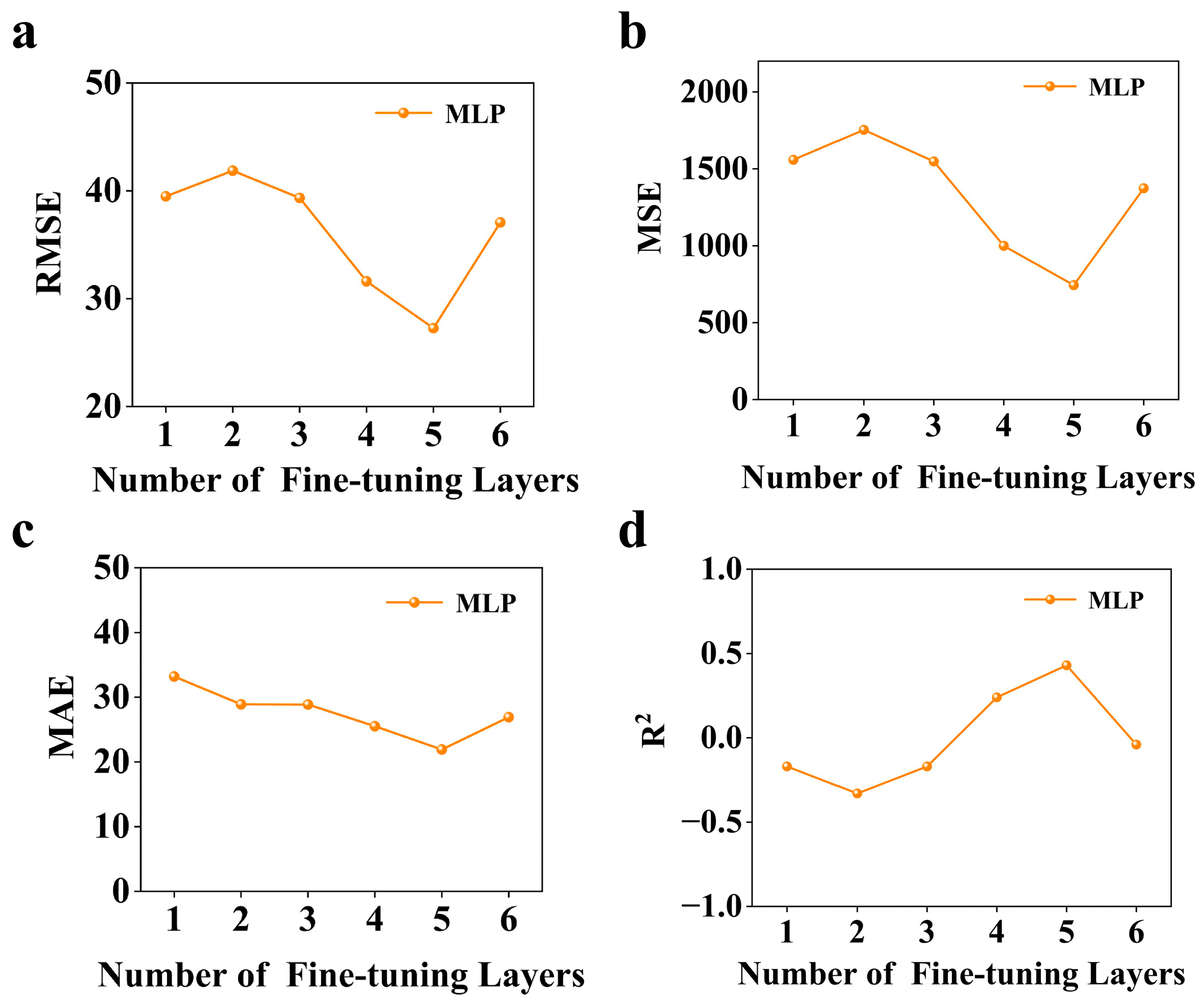
3.3. Optimizing Transfer Learning Performance Through Layer-Wise Fine-Tuning in MLP Architectures
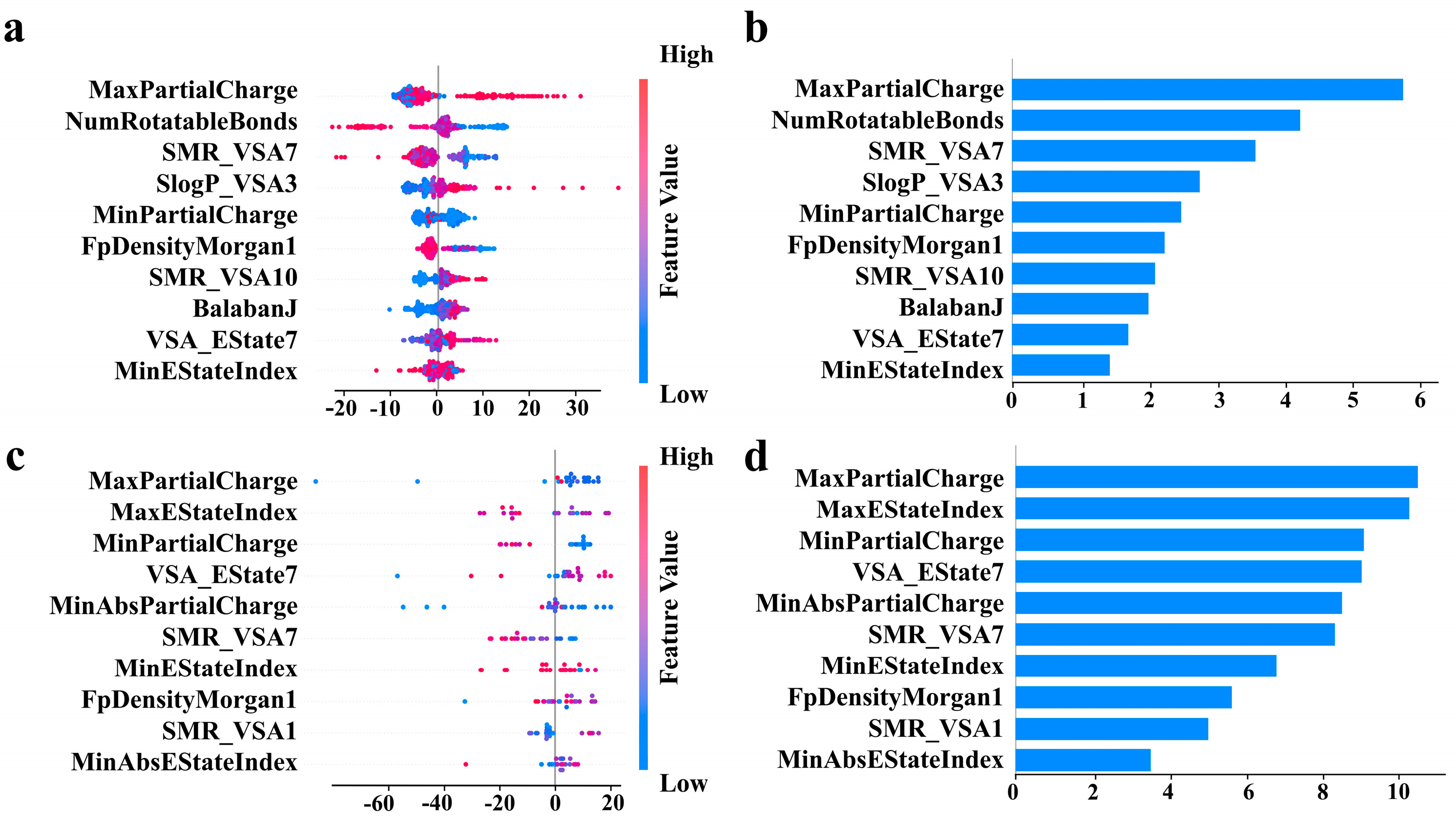
3.4. Feature Interpretability Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, Z.; Liu, F.; Yang, X.; Xie, Z.; Liu, L.; Chen, W. High-velocity impact and post-impact fatigue response of Bismaleimide resin composite laminates. Eur. J. Mech. A/Solids 2025, 112, 105655. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Chen, Y.; Zhu, F.; Wang, Y.; Wei, W.; Feng, Y. Polymer-Based Electronic Packaging Molding Compounds, Specifically Thermal Performance Improvement: An Overview. ACS Appl. Polym. Mater. 2024, 6, 14948–14969. [Google Scholar] [CrossRef]
- Xu, J.; Chen, P.; Ma, S.; Zhu, G.; Wu, L. Synthesis and thermal properties of novel bismaleimides containing cardo and oxazine structures and the thermal transition behaviors of their polymer structures. Thermochim. Acta 2023, 719, 179401. [Google Scholar] [CrossRef]
- Feng, Y.; Sun, Q.; Guo, J.; Wang, C. High-Performance Bismaleimide Resin with an Ultralow Coefficient of Thermal Expansion and High Thermostability. Macromolecules 2024, 57, 1808–1818. [Google Scholar] [CrossRef]
- Melissaris, A.P.; Mikroyannidis, J.A. Bismaleimides chain-extended by imidized benzophenone tetracarboxylic dianhydride and their polymerization to high temperature matrix resins. J. Polym. Sci. Part A Polym. Chem. 1988, 26, 1165–1178. [Google Scholar] [CrossRef]
- Grenier-Loustalot, M.-F.; Da Cunha, L. Sterically hindered bismaleimide monomer: Molten state reactivity and kinetics of polymerization. Eur. Polym. J. 1998, 34, 95–102. [Google Scholar] [CrossRef]
- Graser, J.; Kauwe, S.K.; Sparks, T.D. Machine Learning and Energy Minimization Approaches for Crystal Structure Predictions: A Review and New Horizons. Chem. Mater. 2018, 30, 3601–3612. [Google Scholar] [CrossRef]
- Radue, M.S.; Varshney, V.; Baur, J.W.; Roy, A.K.; Odegard, G.M. Molecular Modeling of Cross-Linked Polymers with Complex Cure Pathways: A Case Study of Bismaleimide Resins. Macromolecules 2018, 51, 1830–1840. [Google Scholar] [CrossRef]
- Han, J.; Gee, R.H.; Boyd, R.H. Glass Transition Temperatures of Polymers from Molecular Dynamics Simulations. Macromolecules 1994, 27, 7781–7784. [Google Scholar] [CrossRef]
- Buchholz, J.; Paul, W.; Varnik, F.; Binder, K. Cooling rate dependence of the glass transition temperature of polymer melts: Molecular dynamics study. J. Chem. Phys. 2002, 117, 7364–7372. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, S.; Chai, Y.; Yu, J.; Zhu, W.; Li, L.; Li, B.A.-O. Prediction and Interpretability Study of the Glass Transition Temperature of Polyimide Based on Machine Learning with Quantitative Structure-Property Relationship (Tg-QSPR). J. Phys. Chem. B 2024, 128, 8807–8817. [Google Scholar] [CrossRef]
- Babbar, A.; Ragunathan, S.; Mitra, D.; Dutta, A.; Patra, T.K. Explainability and extrapolation of machine learning models for predicting the glass transition temperature of polymers. J. Polym. Sci. 2024, 62, 1175–1186. [Google Scholar] [CrossRef]
- Kang, S.; Cho, K. Conditional Molecular Design with Deep Generative Models. J. Chem. Inf. Model. 2019, 59, 43–52. [Google Scholar] [CrossRef]
- Preuer, K.; Renz, P.; Unterthiner, T.; Hochreiter, S.; Klambauer, G.A.-O. Fréchet ChemNet Distance: A Metric for Generative Models for Molecules in Drug Discovery. J. Chem. Inf. Model. 2018, 58, 1736–1741. [Google Scholar] [CrossRef]
- Arús-Pous, J.A.-O.; Blaschke, T.; Ulander, S.; Reymond, J.L.; Chen, H.; Engkvist, O. Exploring the GDB-13 chemical space using deep generative models. J. Chemin. 2019, 11, 20. [Google Scholar] [CrossRef]
- Tao, L.; Varshney, V.; Li, Y. Benchmarking Machine Learning Models for Polymer Informatics: An Example of Glass Transition Temperature. J. Chem. Inf. Model. 2021, 61, 5395–5413. [Google Scholar] [CrossRef]
- He, X.; Yu, M.; Han, J.-P.; Jiang, J.; Jia, Q.; Wang, Q.; Luo, Z.-H.; Yan, F.; Zhou, Y.-N. Leveraging data-driven strategy for accelerating the discovery of polyesters with targeted glass transition temperatures. AIChE J. 2024, 70, e18409. [Google Scholar] [CrossRef]
- Zhang, B.; Li, X.; Xu, X.; Cao, J.; Zeng, M.; Zhang, W. Multi-property prediction and high-throughput screening of polyimides: An application case for interpretable machine learning. Polymer 2024, 312, 127603. [Google Scholar] [CrossRef]
- Oviedo, F.; Ferres, J.L.; Buonassisi, T.; Butler, K.T. Interpretable and Explainable Machine Learning for Materials Science and Chemistry. Acc. Mater. Res. 2022, 3, 597–607. [Google Scholar] [CrossRef]
- Nguyen, T.; Bavarian, M. A Machine Learning Framework for Predicting the Glass Transition Temperature of Homopolymers. Ind. Eng. Chem. Res. 2022, 61, 12690–12698. [Google Scholar] [CrossRef]
- Pilania, G.; Iverson, C.N.; Lookman, T.; Marrone, B.L. Machine-Learning-Based Predictive Modeling of Glass Transition Temperatures: A Case of Polyhydroxyalkanoate Homopolymers and Copolymers. J. Chem. Inf. Model. 2019, 59, 5013–5025. [Google Scholar] [CrossRef]
- Alcobaça, E.; Mastelini, S.M.; Botari, T.; Pimentel, B.A.; Cassar, D.R.; de Carvalho, A.C.P.d.L.F.; Zanotto, E.D. Explainable Machine Learning Algorithms For Predicting Glass Transition Temperatures. Acta Mater. 2020, 188, 92–100. [Google Scholar] [CrossRef]
- Xu, P.; Ji, X.; Li, M.; Lu, W. Small data machine learning in materials science. npj Comput. Mater. 2023, 9, 42. [Google Scholar] [CrossRef]
- Zhu, L.; Zhou, J.; Sun, Z. Materials Data toward Machine Learning: Advances and Challenges. J. Phys. Chem. Lett. 2022, 13, 3965–3977. [Google Scholar] [CrossRef]
- Rodrigues, J.F., Jr.; Florea, L.; de Oliveira, M.C.F.; Diamond, D.; Oliveira, O.N., Jr. Big data and machine learning for materials science. Discov. Mater. 2021, 1, 12. [Google Scholar] [CrossRef]
- King-Smith, E. Transfer learning for a foundational chemistry model. Chem. Sci. 2024, 15, 5143–5151. [Google Scholar] [CrossRef]
- Yamada, H.; Liu, C.; Wu, S.; Koyama, Y.; Ju, S.; Shiomi, J.; Morikawa, J.; Yoshida, R. Predicting Materials Properties with Little Data Using Shotgun Transfer Learning. ACS Cent. Sci. 2019, 5, 1717–1730. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Liu, Q.; Wu, D. Predicting stress–strain curves using transfer learning: Knowledge transfer across polymer composites. Mater. Des. 2022, 218, 110700. [Google Scholar] [CrossRef]
- Kazemi-Khasragh, E.; González, C.; Haranczyk, M. Toward diverse polymer property prediction using transfer learning. Comput. Mater. Sci. 2024, 244, 113206. [Google Scholar] [CrossRef]
- Otsuka, S.; Kuwajima, I.; Hosoya, J.; Xu, Y.; Yamazaki, M. PoLyInfo: Polymer Database for Polymeric Materials Design. In Proceedings of the 2011 International Conference on Emerging Intelligent Data and Web Technologies, Tirana, Albania, 7–9 September 2011; pp. 22–29. [Google Scholar]
- Zhang, H.; Li, H.; Xin, H.; Zhang, J. Property Prediction and Structural Feature Extraction of Polyimide Materials Based on Machine Learning. J. Chem. Inf. Model. 2023, 63, 5473–5483. [Google Scholar] [CrossRef]
- Zhu, J.; Xia, Y.; Liu, L.; Yan, S.; Zeng, Y.; Zhang, R.; Zhang, X.; Sheng, Y. Comparative study of the kinetic behaviors and properties of aromatic and aliphatic bismaleimides. Thermochim. Acta 2024, 737, 179768. [Google Scholar] [CrossRef]
- Lyu, J.; Tang, J.; Ji, B.; Wu, N.; Liao, W.; Yin, C.; Bai, S.; Xing, S. Fluorinated polyetherimide as the modifier for synergistically enhancing the mechanical, thermal and dielectric properties of bismaleimide resin and its composites. Compos. Commun. 2024, 51, 102035. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, H.; Li, S.; Chen, Y.; Liang, M.; Heng, Z.; Zou, H. Design of high-performance resin by tuning cross-linked network topology to improve CF/bismaleimide composite compressive properties. Compos. Sci. Technol. 2023, 242, 110170. [Google Scholar] [CrossRef]
- Hsiao, C.-C.; Lee, J.-J.; Liu, Y.-L. Meldrum’s acid-functionalized bismaleimide, polyaspartimide and their thermally crosslinked resins: Synthesis and properties. React. Funct. Polym. 2024, 202, 105988. [Google Scholar] [CrossRef]
- Peng, H.; Wang, Y.; Zhan, Y.; Lei, F.; Wang, P.; Li, K.; Li, Y.; Yang, X. Hierarchical curing mechanism in epoxy/bismaleimide composites: Enhancing mechanical properties without compromising thermal stabilities. Eur. Polym. J. 2025, 222, 113604. [Google Scholar] [CrossRef]
- Liu, B.; Yuan, Z.; Liu, C.; Sun, M.; Zhang, X.; Derradji, M.; Zhang, B.; Li, J.; Zhao, M.; Song, C.; et al. Synthesis, curing kinetics and processability of a low melting point aliphatic silicon-containing bismaleimide. Mater. Today Commun. 2024, 41, 110845. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Yuan, Q.; Zheng, Q.; Wan, L.; Huang, F. Bismaleimide resin modified by a propargyl substituted aromatic amine with ultrahigh glass transition temperature, thermomechanical stability and intrinsic flame retardancy. React. Funct. Polym. 2023, 193, 105740. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, W.; Ye, W.; Chu, F.; Hu, W.; Song, L.; Hu, Y. Design of reactive linear polyphosphazene to improve the dielectric properties and fire safety of bismaleimide composites. Chem. Eng. J. 2024, 482, 148867. [Google Scholar] [CrossRef]
- Chen, S.; Yu, L.; Zhang, S.; Sun, X.; Qu, B.; Wang, R.; Zheng, Y.; Liu, X.; Li, W.; Gao, J.; et al. Synergistic strengthening and toughening of 3D printing photosensitive resin by bismaleimide and acrylic liquid-crystal resin. J. Sci. Adv. Mater. Devices 2023, 8, 100565. [Google Scholar] [CrossRef]
- Ning, Y.; Li, D.-s.; Jiang, L. Thermally stable and deformation-reversible eugenol-derived bismaleimide resin: Synthesis and structure-property relationships. React. Funct. Polym. 2022, 173, 105236. [Google Scholar] [CrossRef]
- Sheng, X.; Yun, S.; Wang, S.; Gao, Y.; Zuo, X.; Miao, X.; Shi, X.; Qin, J.; Ma, Z.; Zhang, G. Highly heat-resistant and mechanically strong co-crosslinked polyimide/bismaleimide rigid foams with superior thermal insulation and flame resistance. Mater. Today Phys. 2023, 36, 101154. [Google Scholar] [CrossRef]
- Ge, M.; Liang, G.; Gu, A. A facile strategy and mechanism to achieve biobased bismaleimide resins with high thermal-resistance and strength through copolymerizing with unique propargyl ether-functionalized allyl compound. React. Funct. Polym. 2023, 186, 105570. [Google Scholar] [CrossRef]
- Wu, T.; Jiang, P.; Zhang, X.; Guo, Y.; Ji, Z.; Jia, X.; Wang, X.; Zhou, F.; Liu, W. Additively manufacturing high-performance bismaleimide architectures with ultraviolet-assisted direct ink writing. Mater. Des. 2019, 180, 107947. [Google Scholar] [CrossRef]
- Xiong, X.; Ma, X.; Chen, P.; Zhou, L.; Ren, R.; Liu, S. New chain-extended bismaleimides with aryl-ether-imide and phthalide cardo skeleton (I): Synthesis, characterization and properties. React. Funct. Polym. 2018, 129, 29–37. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Bao, Y.; Wei, W.; Fei, X.; Li, X.; Liu, X. Bismaleimide/Phenolic/Epoxy Ternary Resin System for Molding Compounds in High-Temperature Electronic Packaging Applications. Ind. Eng. Chem. Res. 2022, 61, 4191–4201. [Google Scholar] [CrossRef]
- Ning, L.; Yuan, L.; Liang, G.; Gu, A. Thermally resistant and strong remoldable triple-shape memory thermosets based on bismaleimide with transesterification. J. Mater. Sci. 2021, 56, 3623–3637. [Google Scholar] [CrossRef]
- Pu, Z.; Wu, F.; Wang, X.; Zhong, J.; Liu, X.; Pan, Y.; Wang, Y.; Jiang, D.; Ning, Z. Strategy to achieve low-dielectric-constant for benzoxazine-phthalonitriles: Introduction of 2,2′-bis [4-(4-Maleimidephen-oxy)phenyl)]propane by in-situ polymerization. J. Polym. Res. 2024, 31, 140. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, Y.; He, X. Design of acetylene-modified bio-based tri-functional benzoxazine and its copolymerization with bismaleimide for performance enhancement. Polym. Bull. 2023, 80, 12065–12077. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, K. Strategies for improving the performance of diallyl bisphenol A-based benzoxazine resin: Chemical modification via acetylene and physical blending with bismaleimide. React. Funct. Polym. 2021, 165, 104958. [Google Scholar] [CrossRef]
- Yu, P.; Zhang, Y.-l.; Yang, X.; Pan, L.-j.; Dai, Z.-y.; Xue, M.-z.; Liu, Y.-g.; Wang, W. Synthesis and characterization of asymmetric bismaleimide oligomers with improved processability and thermal/mechanical properties. Polym. Eng. Sci. 2019, 59, 2265–2272. [Google Scholar] [CrossRef]
- Liu, C.; Qiao, Y.; Li, N.; Hu, F.; Chen, Y.; Du, G.; Wang, J.; Jian, X. Toughened of bismaleimide resin with improved thermal properties using amino-terminated Poly(phthalazinone ether nitrile sulfone)s. Polymer 2020, 206, 122887. [Google Scholar] [CrossRef]
- Xue, K.; Zhang, P.; Song, Z.; Guo, F.; Hua, Z.; You, T.; Li, S.; Cui, C.; Liu, L. Preparation of eugenol-based flame retardant epoxy resin with an ultrahigh glass transition temperature via a dual-curing mechanism. Polym. Degrad. Stab. 2025, 231, 111092. [Google Scholar] [CrossRef]
- Ma, R.; Liu, Z.; Zhang, Q.; Liu, Z.; Luo, T. Evaluating Polymer Representations via Quantifying Structure–Property Relationships. J. Chem. Inf. Model. 2019, 59, 3110–3119. [Google Scholar] [CrossRef]
- Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Lyu, J.; Ji, B.; Wu, N.; Liao, W.; Yin, C.; Bai, S.; Xing, S. The effect of substituent group in allyl benzoxazine on the thermal, mechanical and dielectric properties of modified bismaleimide. React. Funct. Polym. 2023, 191, 105673. [Google Scholar] [CrossRef]
- Srinivasan, S.; Saravanamuthu, S.K.S.; Syed Mohammed, S.R.; Jeyaraj Pandian, D.; Chinnaswamy Thangavel, V. Low-temperature processable glass fiber reinforced aromatic diamine chain extended bismaleimide composites with improved mechanical properties. Polym. Compos. 2022, 43, 6987–6997. [Google Scholar] [CrossRef]
- Gao, H.; Ding, L.; Li, W.; Ma, G.; Bai, H.; Li, L. Hyper-Cross-Linked Organic Microporous Polymers Based on Alternating Copolymerization of Bismaleimide. ACS Macro Lett. 2016, 5, 377–381. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Taunk, K.; De, S.; Verma, S.; Swetapadma, A. A Brief Review of Nearest Neighbor Algorithm for Learning and Classification. In Proceedings of the 2019 International Conference on Intelligent Computing and Control Systems (ICCS), Madurai, India, 15–17 May 2019; pp. 1255–1260. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Cherkassky, V. The Nature Of Statistical Learning Theory. IEEE Trans. Neural Netw. 1997, 8, 1564. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Iredale, R.J.; Ward, C.; Hamerton, I. Modern advances in bismaleimide resin technology: A 21st century perspective on the chemistry of addition polyimides. Prog. Polym. Sci. 2017, 69, 1–21. [Google Scholar] [CrossRef]
- Ohtsuka, K.; Nakao, S.; Hatanaka, Y. Toughening of bismaleimide and benzoxazine alloy with allyl group by incorporation of polyrotaxane. Polymer 2025, 320, 127979. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, L.; Liang, G.; Gu, A. Achieving ultrahigh glass transition temperature, halogen-free and phosphorus-free intrinsic flame retardancy for bismaleimide resin through building network with diallyloxydiphenyldisulfide. Polymer 2020, 203, 122769. [Google Scholar] [CrossRef]
| Metrics | Data_1 Standalone | Data_2 Standalone | Transfer Learning (from Data_1 to Data_2) |
|---|---|---|---|
| RMSE (°C) | 97.53 | 82.15 | 27.27 |
| MSE | 9512.74 | 6747.92 | 743.61 |
| MAE (°C) | 89.49 | 79.47 | 21.92 |
| R2 | −6.19 | −4.10 | 0.44 |
| Model | Dataset | RMSE (°C) | MSE | MAE (°C) | R2 |
|---|---|---|---|---|---|
| RF | Data_2 | 43.18 | 1864.35 | 36.42 | −0.81 |
| Data_3 | 17.32 | 299.97 | 12.27 | 0.62 | |
| Ridge | Data_2 | 37.39 | 1398.15 | 30.72 | −0.36 |
| Data_3 | 21.75 | 472.98 | 15.33 | 0.40 | |
| KNN | Data_2 | 64.09 | 4107.56 | 48.96 | −2.98 |
| Data_3 | 20.45 | 418.29 | 13.65 | 0.47 | |
| Bayesian | Data_2 | 37.39 | 1397.86 | 30.33 | −0.36 |
| Data_3 | 21.60 | 466.51 | 15.18 | 0.41 | |
| SVR | Data_2 | 37.02 | 1370.61 | 30.39 | −0.33 |
| Data_3 | 19.07 | 363.58 | 13.38 | 0.54 | |
| XGBoost | Data_2 | 48.35 | 2337.33 | 39.91 | −1.97 |
| Data_3 | 17.06 | 290.98 | 12.09 | 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liu, Y.; Xu, X.; Zhang, J.; Li, Z.; Zheng, L.; Kang, P. Transfer Learning-Enhanced Prediction of Glass Transition Temperature in Bismaleimide-Based Polyimides. Polymers 2025, 17, 1833. https://doi.org/10.3390/polym17131833
Wang Z, Liu Y, Xu X, Zhang J, Li Z, Zheng L, Kang P. Transfer Learning-Enhanced Prediction of Glass Transition Temperature in Bismaleimide-Based Polyimides. Polymers. 2025; 17(13):1833. https://doi.org/10.3390/polym17131833
Chicago/Turabian StyleWang, Ziqi, Yu Liu, Xintong Xu, Jiale Zhang, Zhen Li, Lei Zheng, and Peng Kang. 2025. "Transfer Learning-Enhanced Prediction of Glass Transition Temperature in Bismaleimide-Based Polyimides" Polymers 17, no. 13: 1833. https://doi.org/10.3390/polym17131833
APA StyleWang, Z., Liu, Y., Xu, X., Zhang, J., Li, Z., Zheng, L., & Kang, P. (2025). Transfer Learning-Enhanced Prediction of Glass Transition Temperature in Bismaleimide-Based Polyimides. Polymers, 17(13), 1833. https://doi.org/10.3390/polym17131833







