Conductivity of Filled Diblock Copolymer Systems: Identifying the Main Influencing Factors
Abstract
1. Introduction
2. Multiscale Model of the Conductivity of Filled DBC System
2.1. Structure of the Model
2.2. Unfilled DBC System in an External Field: Phase Field Model
2.3. Filled DBC System: Immersion Energy of Fillers
2.4. Localization of Fillers in DBC System Predicted by Monte-Carlo Simulations
2.5. Calculation of the Conductivity of a Filled DBC System
3. Main Simulation Results and Discussion
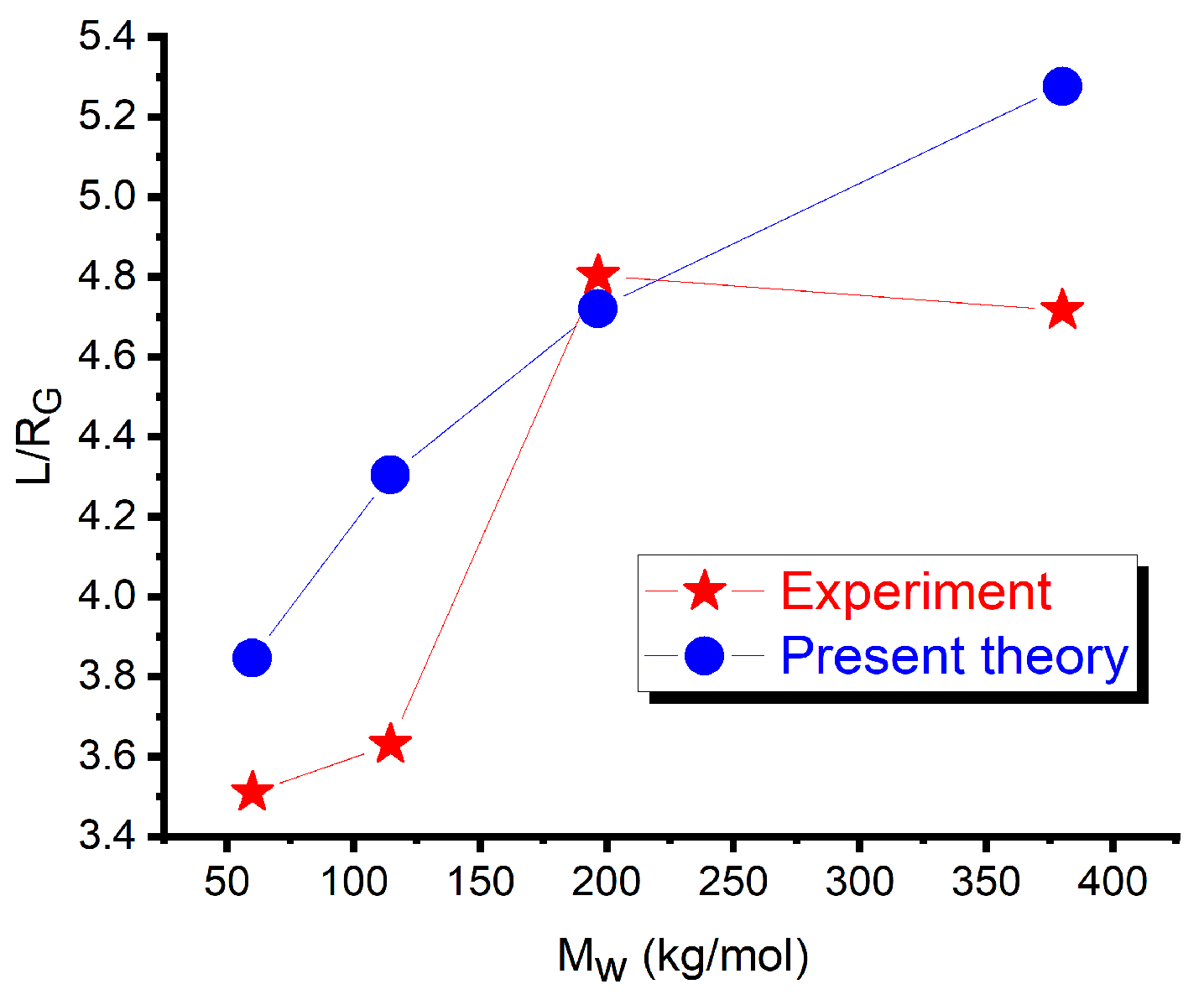
3.1. Elementary Test of the Phase-Field Model for an Unfilled DBC System
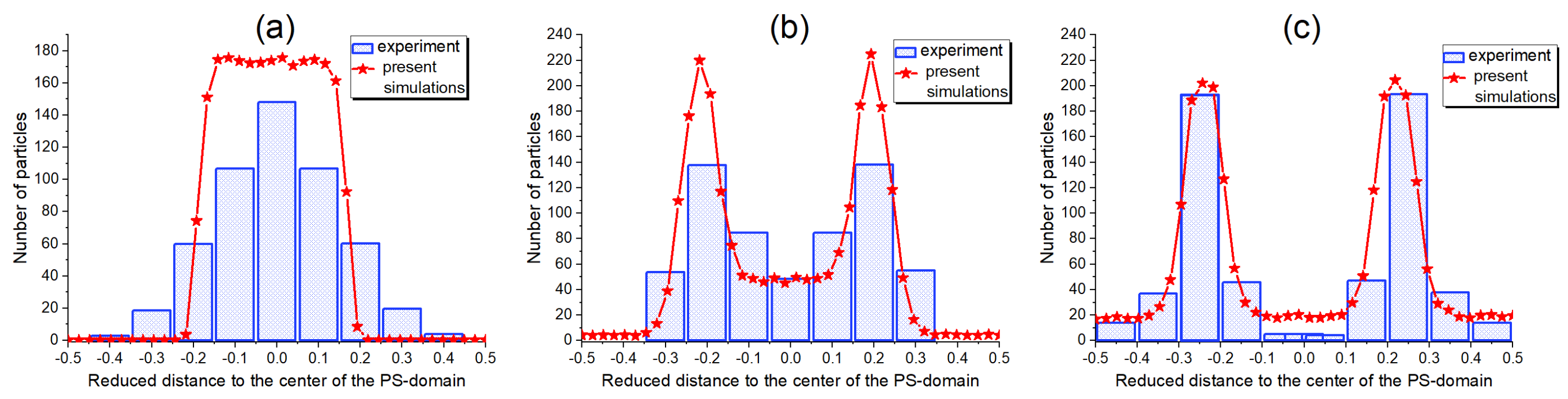
3.2. Localization of Fillers in DBC System
3.2.1. Effect of the Filler Affinity Contrast
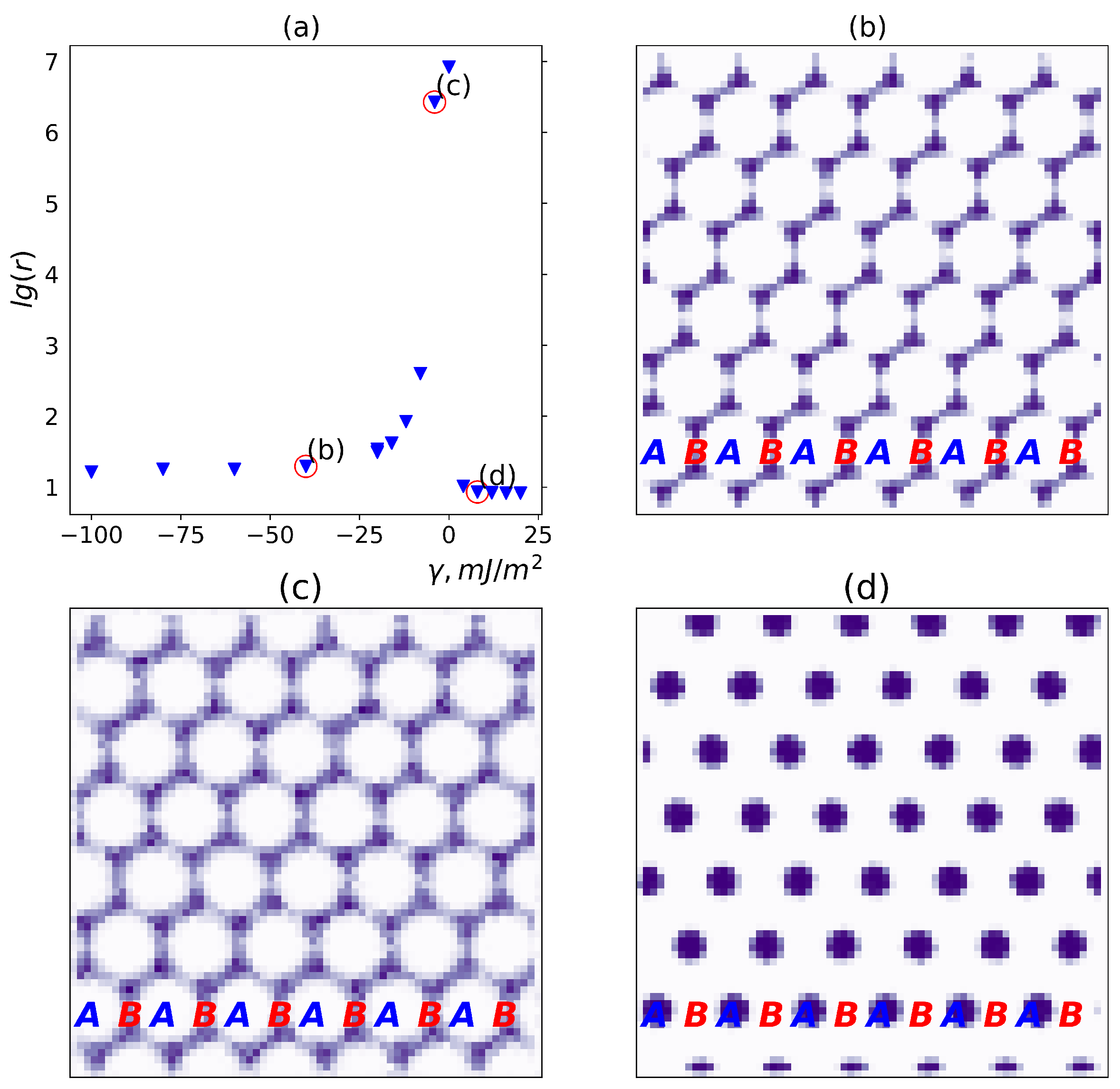
3.2.2. Effect of the Interaction Between Fillers
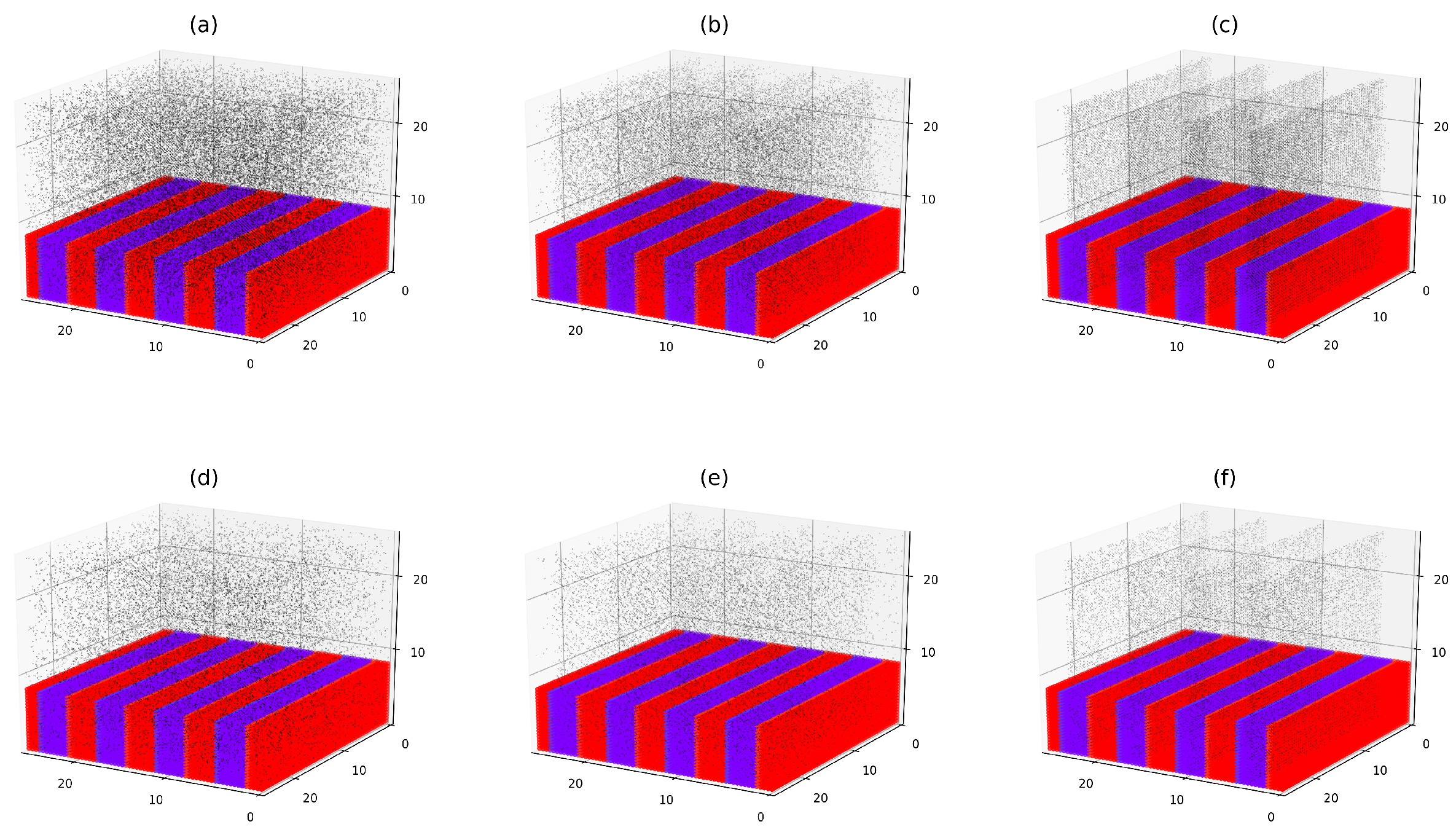
3.2.3. Effect of the DBC Morphology
3.2.4. Effect Caused by Changing the Composite Temperature
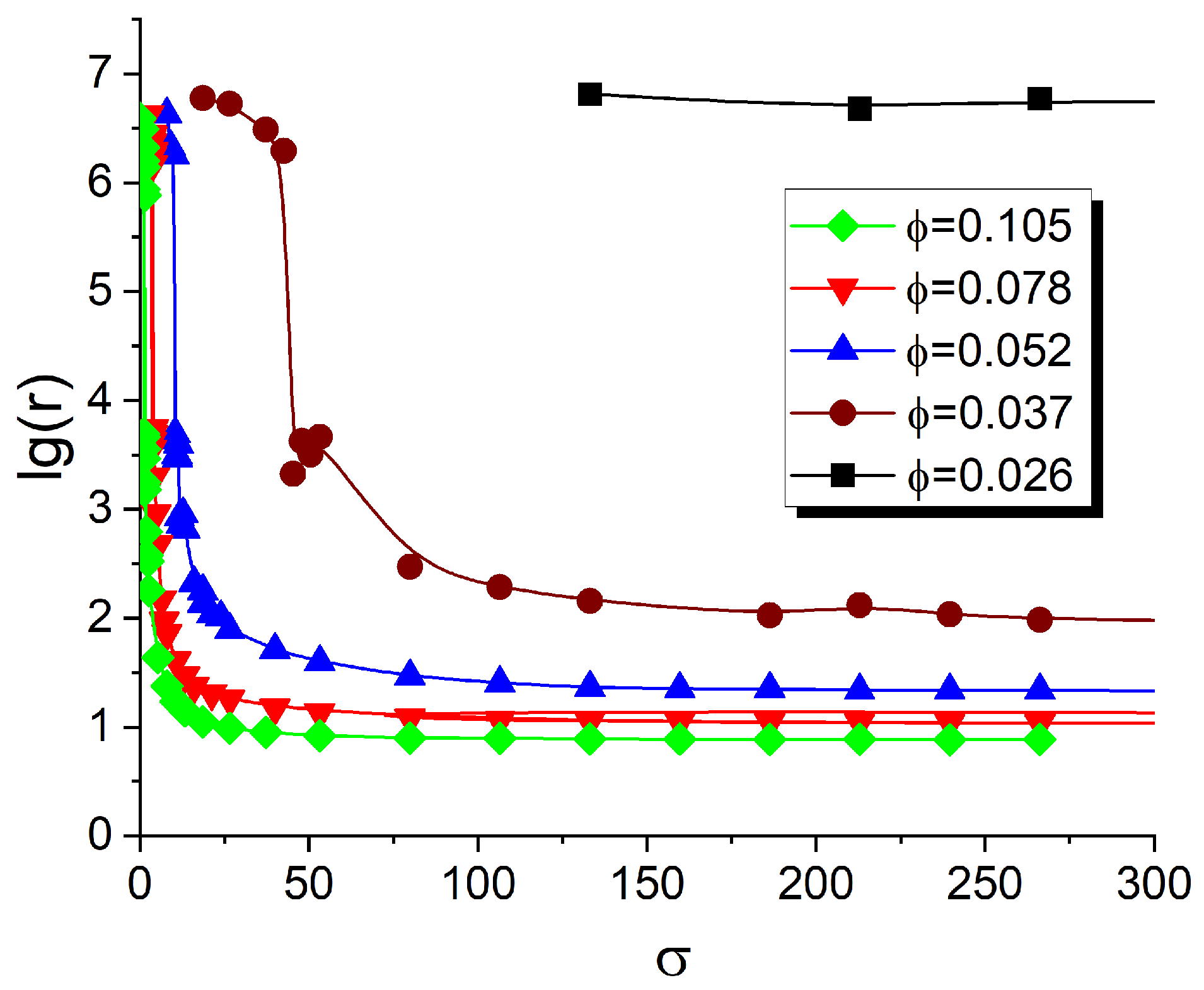
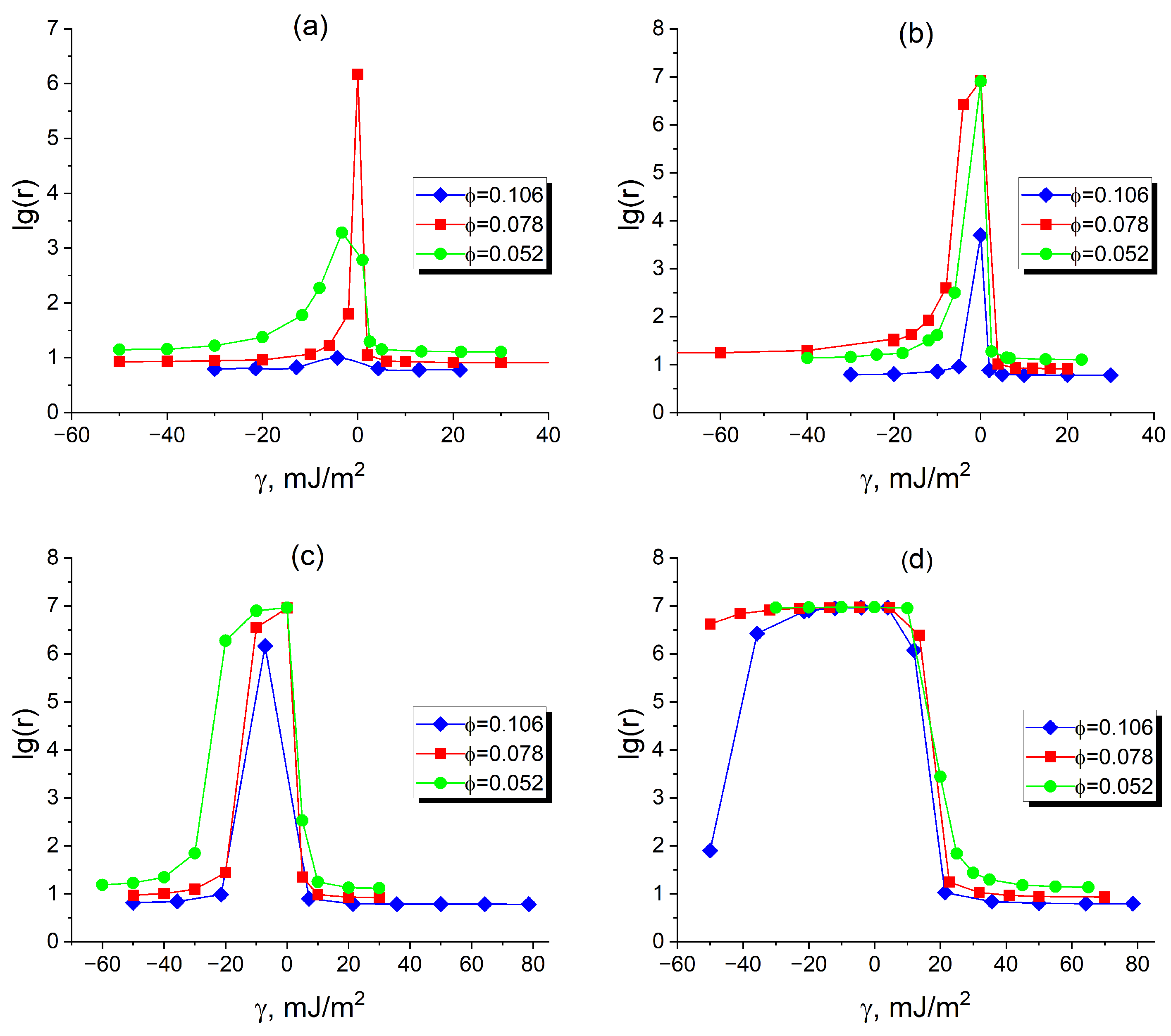
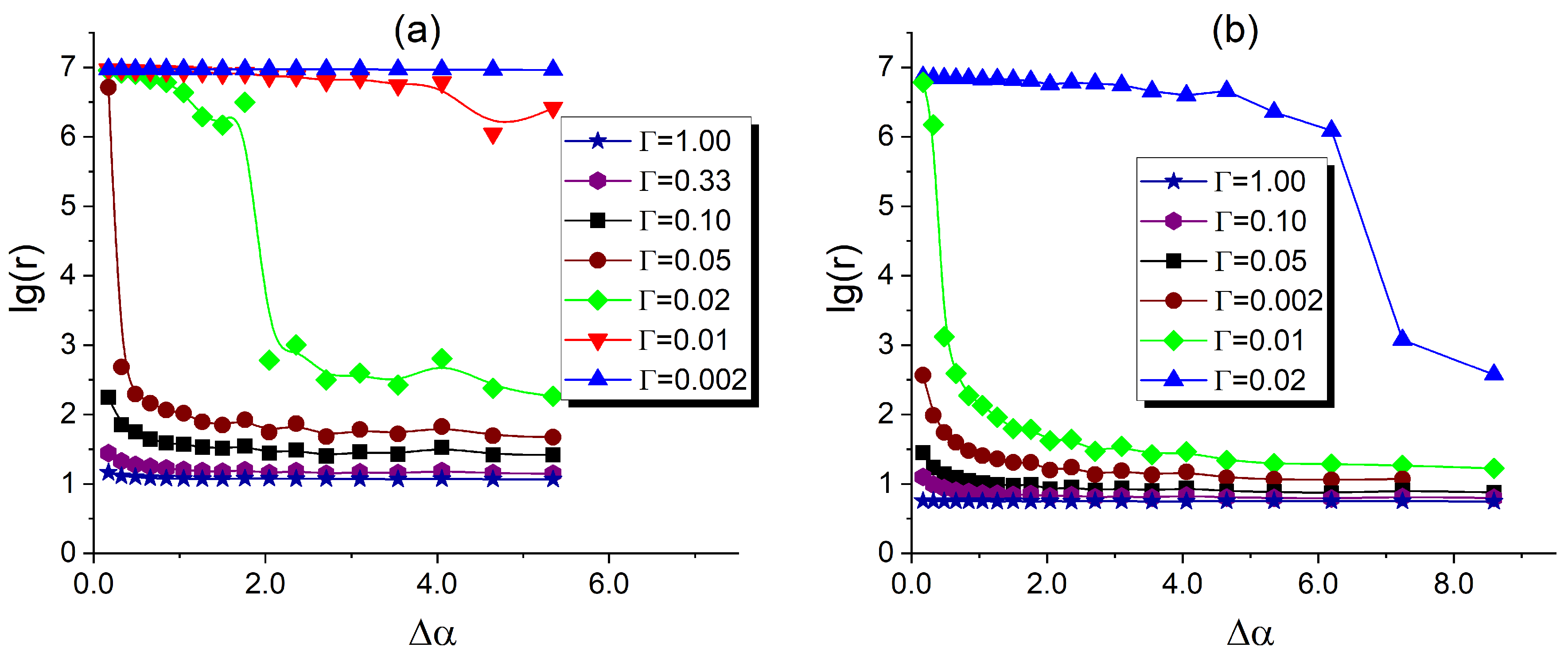
3.3. Conductivity of Filled DBC System
3.3.1. Effect of the Filler Affinity Contrast
3.3.2. Effect of the Interaction Between Fillers
3.3.3. Effect Caused by Changing the Composite Temperature
3.3.4. Effect of the DBC Morphology
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DBCs | diblock copolymers |
| MC | Monte Carlo |
| OOT | odrer–order transition |
| r.(l.)h.s. | right (left)-hand side |
References
- Huh, J.; Ginzburg, V.; Balazs, A. Thermodynamic behavior of particle/diblock copolymer mixtures: Simulation and theory. Macromolecules 2000, 33, 8085–8096. [Google Scholar] [CrossRef]
- Chervanyov, A.I.; Balazs, A. Effect of particle size and shape on the order-disorder phase transition in diblock copolymers. J. Chem. Phys. 2003, 119, 3529–3534. [Google Scholar] [CrossRef]
- Chervanyov, A.I. Spinodal Decomposition of Filled Polymer Blends: The Role of the Osmotic Effect of Fillers. Polymers 2024, 16, 38. [Google Scholar] [CrossRef]
- Heinrich, G.; Kluppel, M.; Vilgis, T. Reinforcement of elastomers. Curr. Opin. Solid State Mater. Sci. 2002, 6, 195–203. [Google Scholar] [CrossRef]
- Alig, I.; Skipa, T.; Engel, M.; Lellinger, D.; Pegel, S.; Poetschke, P. Electrical conductivity recovery in carbon nanotube polymer composites after transient shear. Phys. Status Solidi B-Basic Solid State Phys. 2007, 244, 4223–4226. [Google Scholar] [CrossRef]
- Sniegowski, J.; de Boer, M. IC-compatible polysilicon surface micromachining. Annu. Rev. Mater. Sci. 2000, 30, 299–333. [Google Scholar] [CrossRef]
- Polla, D.; Erdman, A.; Robbins, W.; Markus, D.; Diaz-Diaz, J.; Rizq, R.; Nam, Y.; Brickner, H.; Wang, A.; Krulevitch, P. Microdevices in medicine. Annu. Rev. Biomed. Eng. 2000, 2, 551–576. [Google Scholar] [CrossRef]
- Chen, D.; Pei, Q. Electronic Muscles and Skins: A Review of Soft Sensors and Actuators. Chem. Rev. 2017, 117, 11239–11268. [Google Scholar] [CrossRef]
- Knite, M.; Teteris, V.; Kiploka, A.; Kaupuzs, J. Polyisoprene-carbon black nanocomposites as tensile strain and pressure sensor materials. Sens. Actuators A-Phys. 2004, 110, 142–149. [Google Scholar] [CrossRef]
- Gao, L.; Chou, T.W.; Thostenson, E.T.; Zhang, Z.; Coulaud, M. In situ sensing of impact damage in epoxy/glass fiber composites using percolating carbon nanotube networks. Carbon 2011, 49, 3382–3385. [Google Scholar] [CrossRef]
- Chen, L.; Chen, G.; Lu, L. Piezoresistive behavior study on finger-sensing silicone rubber/graphite nanosheet nanocomposites. Adv. Funct. Mater. 2007, 17, 898–904. [Google Scholar] [CrossRef]
- Wang, P.; Geng, S.; Ding, T. Effects of carboxyl radical on electrical resistance of multi-walled carbon nanotube filled silicone rubber composite under pressure. Compos. Sci. Technol. 2010, 70, 1571–1573. [Google Scholar] [CrossRef]
- Taya, M.; Kim, W.; Ono, K. Piezoresistivity of a short fiber/elastomer matrix composite. Mech. Mater. 1998, 28, 53–59. [Google Scholar] [CrossRef]
- Ryvkina, N.; Tchmutin, I.; Vilcakova, J.; Peliskova, M.; Saha, P. The deformation behavior of conductivity in composites where charge carrier transport is by tunneling: Theoretical modeling and experimental results. Synth. Met. 2005, 148, 141–146. [Google Scholar] [CrossRef]
- Soo, P.; Huang, B.; Jang, Y.; Chiang, Y.; Sadoway, D.; Mayes, A. Rubbery block copolymer electrolytes for solid-state rechargeable lithium batteries. J. Electrochem. Soc. 1999, 146, 32–37. [Google Scholar] [CrossRef]
- Liu, T.; Liu, G. Block copolymers for supercapacitors, dielectric capacitors and batteries. J. Phys.-Condens. Matter 2019, 31, 233001. [Google Scholar] [CrossRef]
- Heinrich, G.; Kluppel, M. Recent advances in the theory of filler networking in elastomers. In Filled Elastomers Drug Divery Systems; Lee, K., Ed.; Advances in Polymer Science; Springer: Berlin/Heidelberg, Germany, 2002; Volume 160, pp. 1–44. [Google Scholar]
- Semeriyanov, F.F.; Chervanyov, A.I.; Jurk, R.; Subramaniam, K.; Koenig, S.; Roscher, M.; Das, A.; Stoeckelhuber, K.W.; Heinrich, G. Non-monotonic dependence of the conductivity of carbon nanotube-filled elastomers subjected to uniaxial compression/decompression. J. Appl. Phys. 2013, 113, 103706. [Google Scholar] [CrossRef]
- Selvan, N.T.; Eshwaran, S.B.; Das, A.; Stoeckelhuber, K.W.; Wiessner, S.; Poetschke, P.; Nando, G.B.; Chervanyov, A.I.; Heinrich, G. Piezoresistive natural rubber-multiwall carbon nanotube nanocomposite for sensor applications. Sens. Actuators A-Phys. 2016, 239, 102–113. [Google Scholar] [CrossRef]
- Alig, I.; Poetschke, P.; Lellinger, D.; Skipa, T.; Pegel, S.; Kasaliwal, G.R.; Villmow, T. Establishment, morphology and properties of carbon nanotube networks in polymer melts. Polymer 2012, 53, 4–28. [Google Scholar] [CrossRef]
- Stoeckelhuber, K.W.; Svistkov, A.S.; Pelevin, A.G.; Heinrich, G. Impact of Filler Surface Modification on Large Scale Mechanics of Styrene Butadiene/Silica Rubber Composites. Macromolecules 2011, 44, 4366–4381. [Google Scholar] [CrossRef]
- Chervanyov, A.I.; Heinrich, G. Pragmatic Approach to the Evaluation of the Polymer-Mediated Force and Stability Ratio of Nano-Fillers Immersed in Rubber Materials. Soft Mater. 2014, 12, S90–S97. [Google Scholar] [CrossRef]
- Chervanyov, A.I. Polymer-mediated interactions and their effect on the coagulation-fragmentation of nano-colloids: A self-consistent field theory approach. Soft Matter 2015, 11, 1038–1053. [Google Scholar] [CrossRef] [PubMed]
- Chervanyov, A.I. Effect of the Interplay between Polymer-Filler and Filler-Filler Interactions on the Conductivity of a Filled Diblock Copolymer System. Polymers 2024, 16, 104. [Google Scholar] [CrossRef] [PubMed]
- Chervanyov, A.I. Conductivity of Insulating Diblock Copolymer System Filled with Conductive Particles Having Different Affinities for Dissimilar Copolymer Blocks. Polymers 2020, 12, 1659. [Google Scholar] [CrossRef]
- Chervanyov, A.I. Conductivity of diblock copolymer system filled with conducting nano-particles: Effect of copolymer morphology. J. Polym. Sci. 2022, 60, 221–232. [Google Scholar] [CrossRef]
- Chervanyov, A.I. Temperature dependence of the conductivity of filled diblock copolymers. Phys. Rev. E 2020, 102, 052504. [Google Scholar] [CrossRef]
- Bates, F.; Fredrickson, G. Block Copolymer Thermodynamics—Theory and Experiment. Annu. Rev. Phys. Chem. 1990, 41, 525–557. [Google Scholar] [CrossRef]
- Bates, F.; Fredrickson, G. Block copolymers—Designer soft materials. Phys. Today 1999, 52, 32–38. [Google Scholar] [CrossRef]
- Matsen, M.; Schick, M. Stable and unstable phases of a diblock copolymer melt. Phys. Rev. Lett. 1994, 72, 2660–2663. [Google Scholar] [CrossRef]
- Leibler, L. Theory of microphase separation in block co-polymers. Macromolecules 1980, 13, 1602–1617. [Google Scholar] [CrossRef]
- Mueller, M.; Rey, J.C.O. Continuum models for directed self-assembly. Mol. Syst. Des. Eng. 2018, 3, 295–313. [Google Scholar] [CrossRef]
- Ganss, M.; Staudinger, U.; Satapathy, B.K.; Leuteritz, A.; Weidisch, R. Mechanism of strengthening and toughening of a nanostructured styrene-butadiene based block copolymer by oligostyrene-modified montmorillonites. Polymer 2021, 213, 123328. [Google Scholar] [CrossRef]
- Staudinger, U.; Satapathy, B.K.; Jehnichen, D. Nanofiller Dispersion, Morphology, Mechanical Behavior, and Electrical Properties of Nanostructured Styrene-Butadiene-Based Triblock Copolymer/CNT Composites. Polymers 2019, 11, 1831. [Google Scholar] [CrossRef]
- Staudinger, U.; Janke, A.; Steinbach, C.; Reuter, U.; Ganss, M.; Voigt, O. Influence of CNT Length on Dispersion, Localization, and Electrical Percolation in a Styrene-Butadiene-Based Star Block Copolymer. Polymers 2022, 14, 2715. [Google Scholar] [CrossRef]
- Chiu, J.J.; Kim, B.J.; Yi, G.R.; Bang, J.; Kramer, E.J.; Pine, D.J. Distribution of nanoparticles in lamellar domains of block copolymers. Macromolecules 2007, 40, 3361–3365. [Google Scholar] [CrossRef]
- Schultz, A.; Hall, C.; Genzer, J. Computer simulation of block copolymer/nanoparticle composites. Macromolecules 2005, 38, 3007–3016. [Google Scholar] [CrossRef]
- Thompson, R.; Ginzburg, V.; Matsen, M.; Balazs, A. Predicting the mesophases of copolymer-nanoparticle composites. Science 2001, 292, 2469–2472. [Google Scholar] [CrossRef]
- Thompson, R.; Ginzburg, V.; Matsen, M.; Balazs, A. Block copolymer-directed assembly of nanoparticles: Forming mesoscopically ordered hybrid materials. Macromolecules 2002, 35, 1060–1071. [Google Scholar] [CrossRef]
- Kim, B.J.; Bang, J.; Hawker, C.J.; Chiu, J.J.; Pine, D.J.; Jang, S.G.; Yang, S.M.; Kramer, E.J. Creating surfactant nanoparticles for block copolymer composites through surface chemistry. Langmuir 2007, 23, 12693–12703. [Google Scholar] [CrossRef]
- Matsen, M.W.; Thompson, R.B. Particle distributions in a block copolymer nanocomposite. Macromolecules 2008, 41, 1853–1860. [Google Scholar] [CrossRef]
- Diaz, J.; Pinna, M.; Zvelindovsky, V.A.; Pagonabarraga, I. Phase Behavior of Block Copolymer Nanocomposite Systems. Adv. Theory Simul. 2018, 1, 1800066. [Google Scholar] [CrossRef]
- Sides, S.W.; Kim, B.J.; Kramer, E.J.; Fredrickson, G.H. Hybrid particle-field simulations of polymer nanocomposites. Phys. Rev. Lett. 2006, 96, 250601. [Google Scholar] [CrossRef] [PubMed]
- Diaz, J.; Pinna, M.; Zvelindovsky, A.V.; Pagonabarraga, I.; Shenhar, R. Block CopolymerRod Interaction and Confinement. Macromolecules 2020, 53, 3234–3249. [Google Scholar] [CrossRef]
- Ohta, T.; Kawasaki, K. Equilibrium morphology of block copolymer melts. Macromolecules 1986, 19, 2621–2632. [Google Scholar] [CrossRef]
- Helgand, E.; Tagami, Y. Theory of interface between immiscible polymers. J. Chem. Phys. 1972, 57, 1812–1813. [Google Scholar] [CrossRef]
- Fredrickson, G.H.; Helfand, E. Fluctuation effects in the theory of microphase separation in block copolymers. J. Chem. Phys. 1987, 87, 697–705. [Google Scholar] [CrossRef]
- Matsen, M.W. Field theoretic approach for block polymer melts: SCFT and FTS. J. Chem. Phys. 2020, 152, 110901. [Google Scholar] [CrossRef]
- Dalcin, L.; Collier, N.; Vignal, P.; Cortes, A.M.A.; Calo, V.M. PetIGA: A framework for high-performance isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2016, 308, 151–181. [Google Scholar] [CrossRef]
- Kim, B.; Chiu, J.; Yi, G.R.; Pine, D.; Kramer, E. Nanoparticle-Induced Phase Transitions in Diblock-Copolymer Films. Adv. Mater. 2005, 17, 2618–2622. [Google Scholar] [CrossRef]
- Bockstaller, M.R.; Lapetnikov, Y.; Margel, S.; Thomas, E.L. Size-Selective Organization of Enthalpic Compatibilized Nanocrystals in Ternary Block Copolymer/Particle Mixtures. J. Am. Chem. Soc. 2003, 125, 5276–5277. [Google Scholar] [CrossRef]
- Chiu, J.J.; Kim, B.J.; Kramer, E.J.; Pine, D.J. Control of Nanoparticle Location in Block Copolymers. J. Am. Chem. Soc. 2005, 127, 5036–5037. [Google Scholar] [CrossRef] [PubMed]
- Lo, C.T.; Chang, Y.C.; Wu, S.C.; Lee, C.L. Effect of particle size on the phase behavior of block copolymer/nanoparticle composites. Colloids Surf. A Physicochem. Eng. Asp. 2010, 368, 6–12. [Google Scholar] [CrossRef]
- Wang, Q.; Nealey, P.; de Pablo, J. Behavior of single nanoparticle/homopolymer chain in ordered structures of diblock copolymers. J. Chem. Phys. 2003, 118, 11278–11285. [Google Scholar] [CrossRef]
- Chervanyov, A.I.; Heinrich, G. Immersion energy and polymer-mediated depletion interactions between nanocolloids as studied by analytic self-consistent field theory. Phys. Rev. E 2012, 86, 021801. [Google Scholar] [CrossRef]
- Chervanyov, A.I.; Heinrich, G. Rates of the colloid coagulation in the presence of irreversibly adsorbing and non-adsorbing polymers. Polym. Compos. 2013, 34, 187–193. [Google Scholar] [CrossRef]
- Widom, B. Some topics in theory of fluids. J. Chem. Phys. 1963, 39, 2808–2812. [Google Scholar] [CrossRef]
- Chervanyov, A.I. Analytic liquid state theory of the polymer-mediated depletion interaction between colloids beyond preaveraging approximation. J. Chem. Phys. 2019, 150, 144906. [Google Scholar] [CrossRef]
- Chervanyov, A.I. Effective interaction between colloids immersed in a polymer blend and their effect on the equation of state of this blend. J. Colloid Interface Sci. 2020, 563, 156–167. [Google Scholar] [CrossRef]
- Chervanyov, A.I. Depletion interaction between colloids mediated by an athermal polymer blend. Phys. Rev. E 2018, 97, 032508. [Google Scholar] [CrossRef]
- Binder, K. Applications of Monte Carlo methods to statistical physics. Rep. Prog. Phys. 1997, 60, 487–559. [Google Scholar] [CrossRef]
- Li, L.; Han, L.; Hu, H.; Zhang, R. A review on polymers and their composites for flexible electronics. Mater. Adv. 2023, 4, 726–746. [Google Scholar] [CrossRef]
- Ditte, K.; Perez, J.; Chae, S.; Hambsch, M.; Al-Hussein, M.; Komber, H.; Formanek, P.; Mannsfeld, S.C.B.; Fery, A.; Kiriy, A.; et al. Ultrasoft and High-Mobility Block Copolymers for Skin-Compatible Electronics. Adv. Mater. 2021, 33, 2005416. [Google Scholar] [CrossRef] [PubMed]
- Villmow, T.; John, A.; Poetschke, P.; Heinrich, G. Polymer/carbon nanotube composites for liquid sensing: Selectivity against different solvents. Polymer 2012, 53, 2908–2918. [Google Scholar] [CrossRef]
- Tang, X.; Poetschke, P.; Pionteck, J.; Li, Y.; Formanek, P.; Voit, B. Tuning the Piezoresistive Behavior of Poly(Vinylidene Fluoride)/Carbon Nanotube Composites Using Poly(Methyl Methacrylate). ACS Appl. Mater. Interfaces 2020, 12, 43125–43137. [Google Scholar] [CrossRef]
- Tang, X.; Pionteck, J.; Krause, B.; Poetschke, P.; Voit, B. Highly Tunable Piezoresistive Behavior of Carbon Nanotube-Containing Conductive Polymer Blend Composites Prepared from Two Polymers Exhibiting Crystallization-Induced Phase Separation. ACS Appl. Mater. Interfaces 2021, 13, 43333–43347. [Google Scholar] [CrossRef]
- Narongthong, J.; Das, A.; Le, H.H.; Wiessner, S.; Sirisinha, C. An efficient highly flexible strain sensor: Enhanced electrical conductivity, piezoresistivity and flexibility of a strongly piezoresistive composite based on conductive carbon black and an ionic liquid. Compos. Part A-Appl. Sci. Manuf. 2018, 113, 330–338. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chervanyov, A.I. Conductivity of Filled Diblock Copolymer Systems: Identifying the Main Influencing Factors. Polymers 2025, 17, 1502. https://doi.org/10.3390/polym17111502
Chervanyov AI. Conductivity of Filled Diblock Copolymer Systems: Identifying the Main Influencing Factors. Polymers. 2025; 17(11):1502. https://doi.org/10.3390/polym17111502
Chicago/Turabian StyleChervanyov, A. I. 2025. "Conductivity of Filled Diblock Copolymer Systems: Identifying the Main Influencing Factors" Polymers 17, no. 11: 1502. https://doi.org/10.3390/polym17111502
APA StyleChervanyov, A. I. (2025). Conductivity of Filled Diblock Copolymer Systems: Identifying the Main Influencing Factors. Polymers, 17(11), 1502. https://doi.org/10.3390/polym17111502





