Investigation of PBT-AP Interactions in PBT-Based Solid Propellants: A Combined Density Functional Theory and Molecular Dynamics Study
Abstract
1. Introduction
2. Theoretical Models and Computational Methods
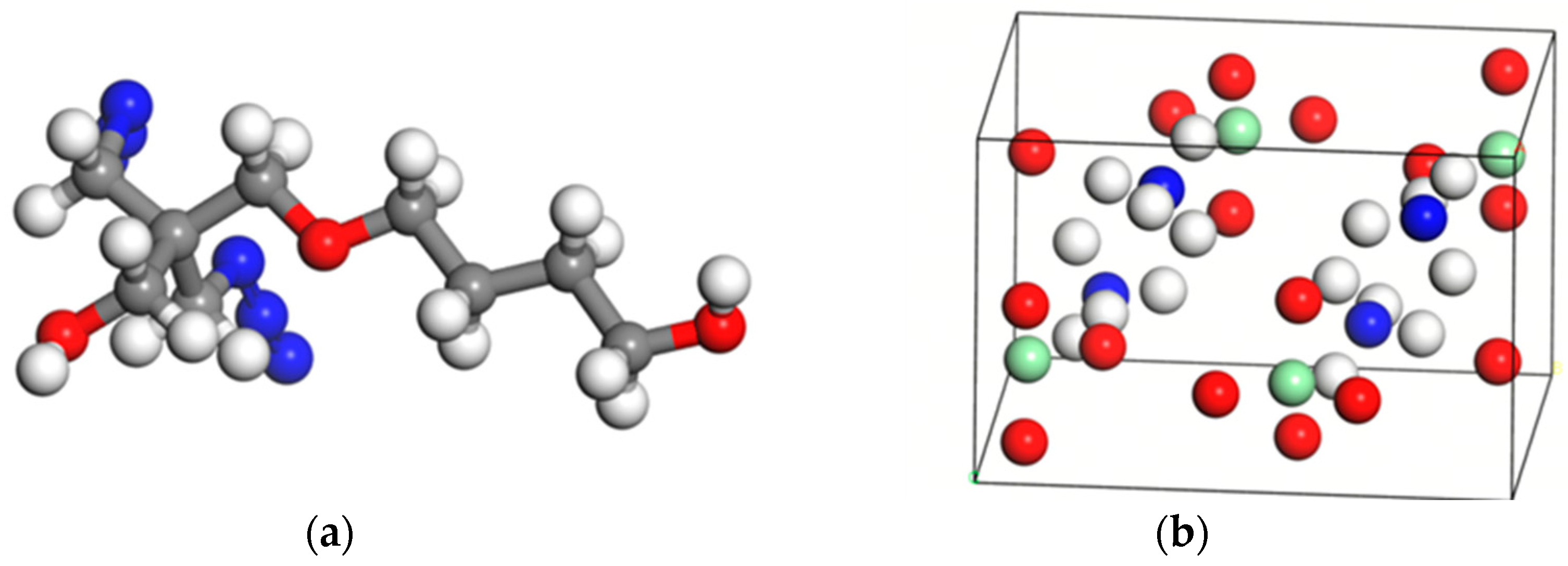
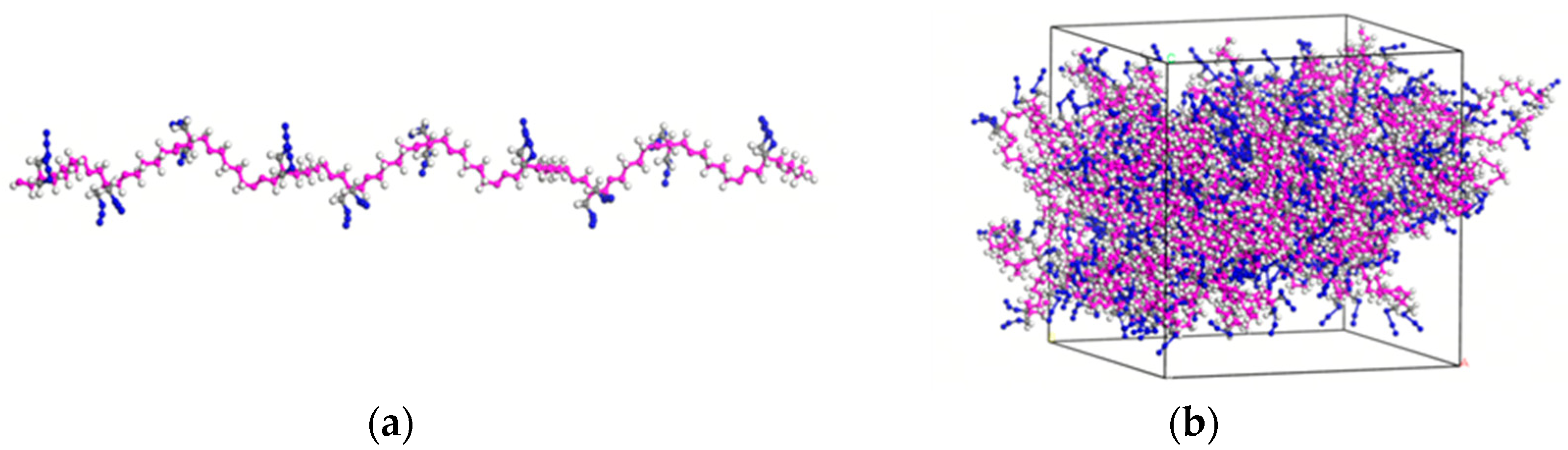
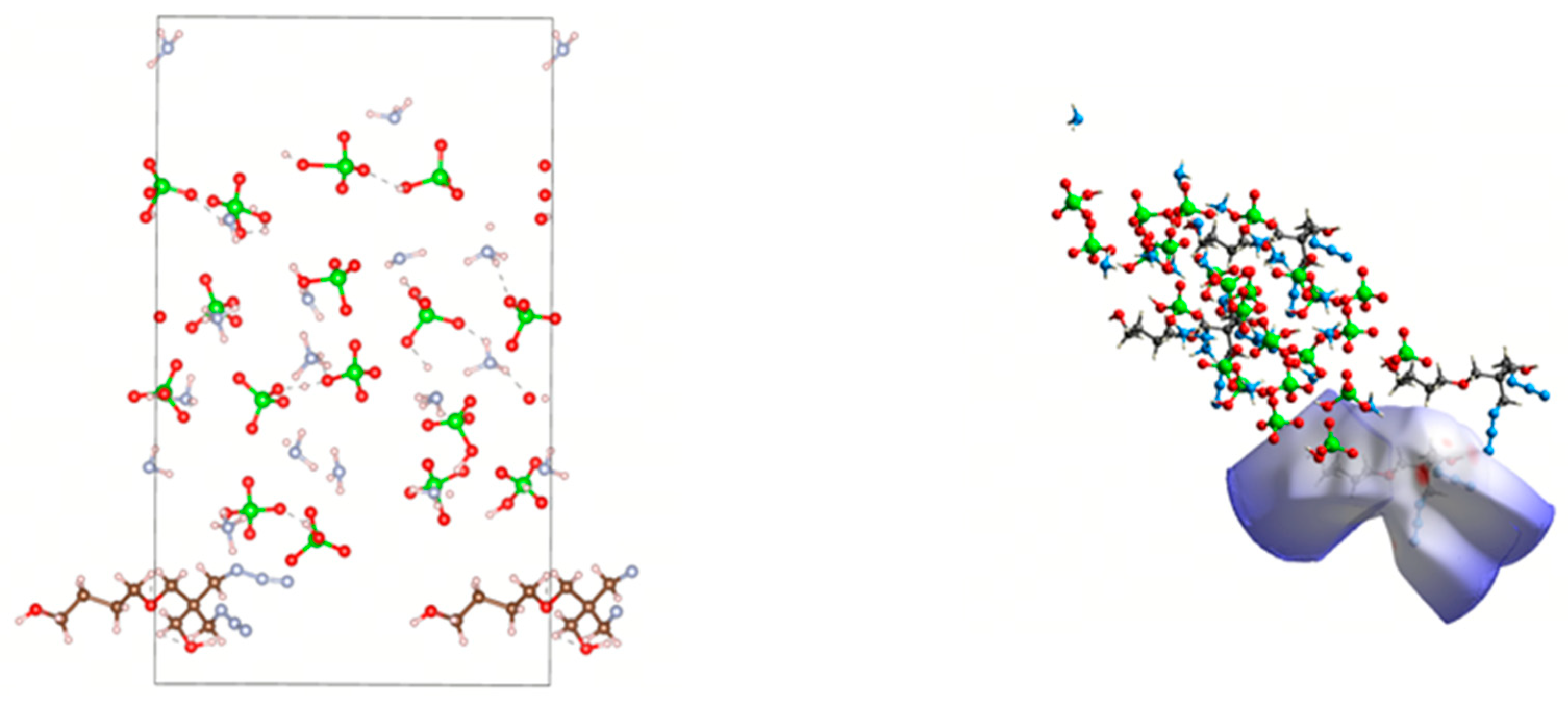
2.1. Model Construction
2.2. Selection of Computational Methods
3. Results and Data Analysis
3.1. DFT Calculations
3.1.1. DFT Calculations and Adsorption Energy Analysis
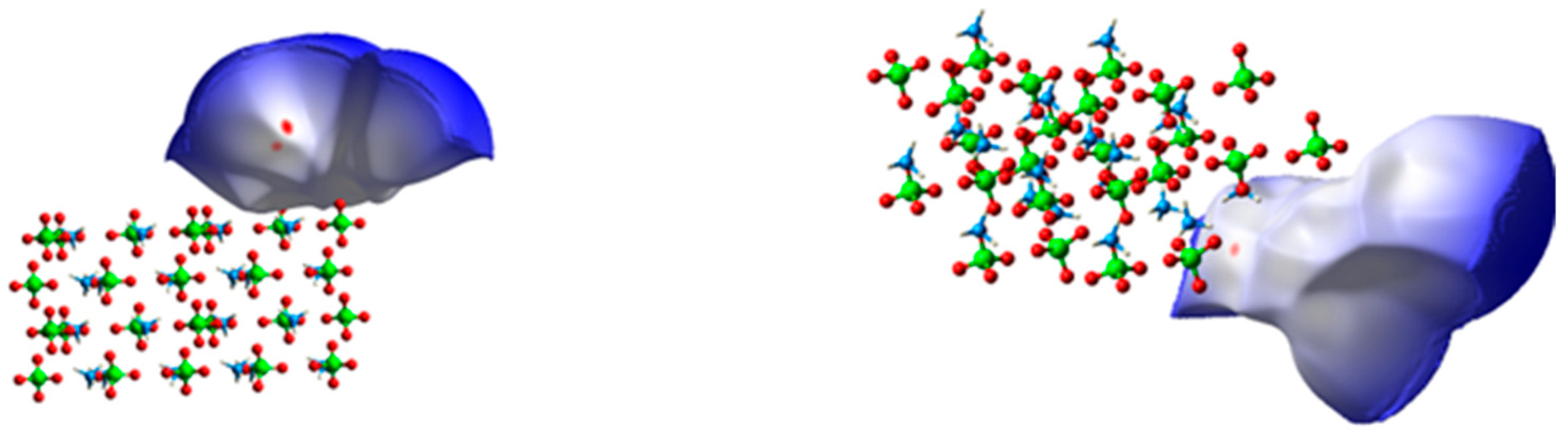
3.1.2. Charge Density Analysis
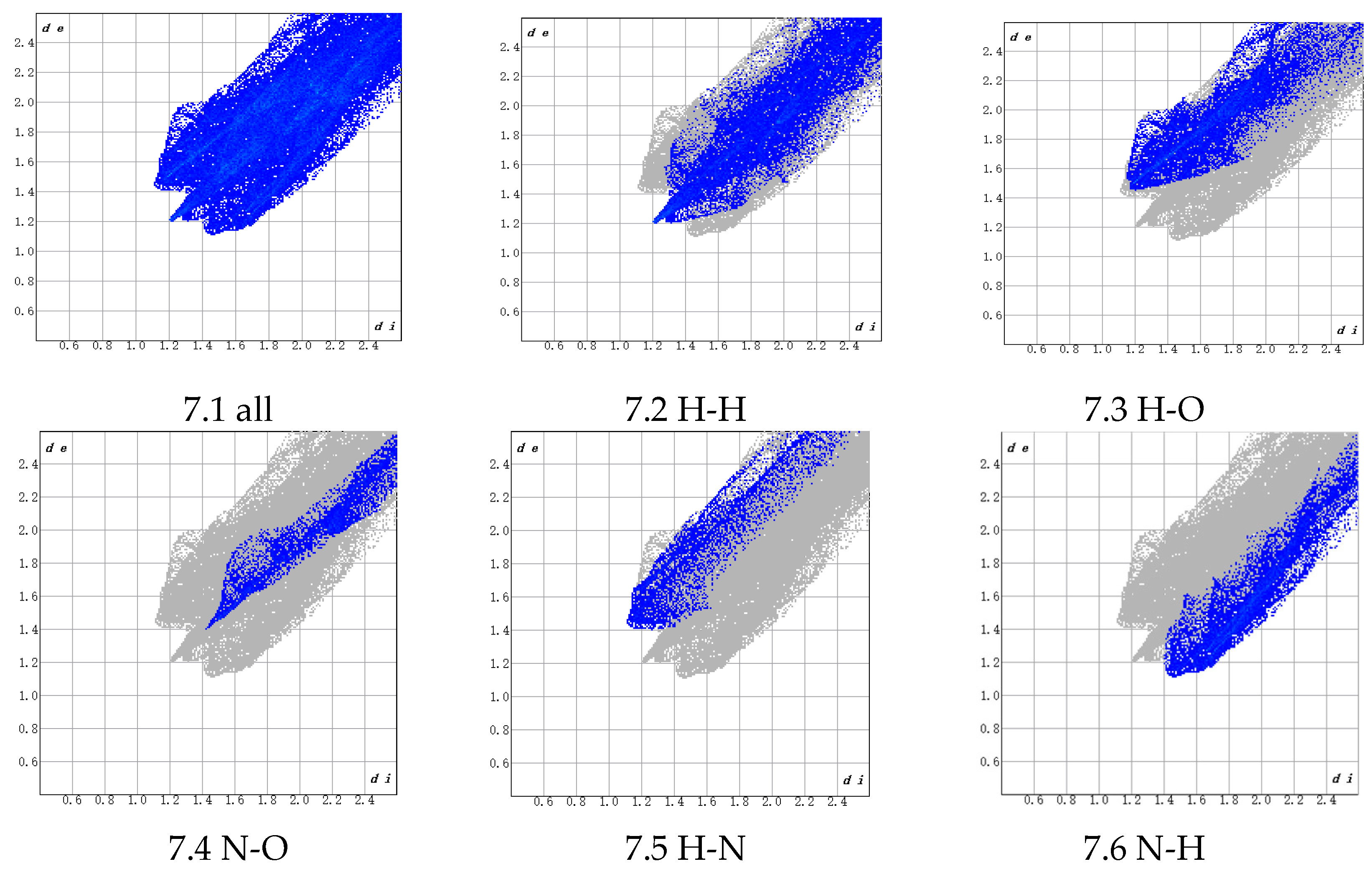
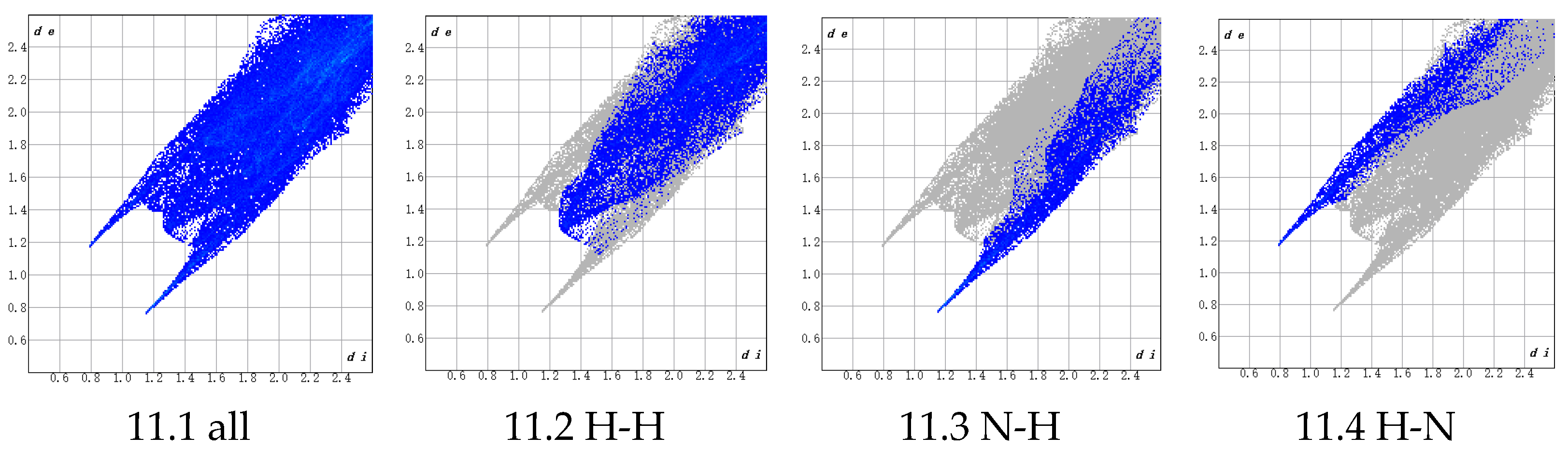
3.1.3. Atomic Distance and Bonding Analysis
- (1)
- H (PBT)–H (AP) interactions (45.3% contribution), which are predominantly driven by van der Waals forces and belong to non-bonded weak interactions. Although individual H-H interactions are weak, their high proportion suggests extensive van der Waals contacts between H atoms in the NH4+ groups on the AP crystal surface and H atoms in the THF chain segments (-CH2-CH2-O-) of PBT within the interfacial region. These interactions are enhanced by the cumulative effect of their abundance. The THF chain’s flexible structure further enables conformational adjustments to maximize the contact area, thereby improving adhesion.
- (2)
- N (PBT)–H (AP) interactions (20.8% contribution), whose physical nature involves dipole–dipole interactions or weak hydrogen bonding. These originate from the partial negative charge (δ−) on the electronegative N atoms in PBT’s azide groups (-N3) interacting with the partially positive H atoms (δ⁺) in the NH4+ groups on the AP surface. These interactions, stronger than pure van der Waals forces, provide additional binding energy to the interface, enhancing adhesion stability.
3.2. Molecular Dynamics Simulations
3.2.1. Analysis of Simulated Annealing Results
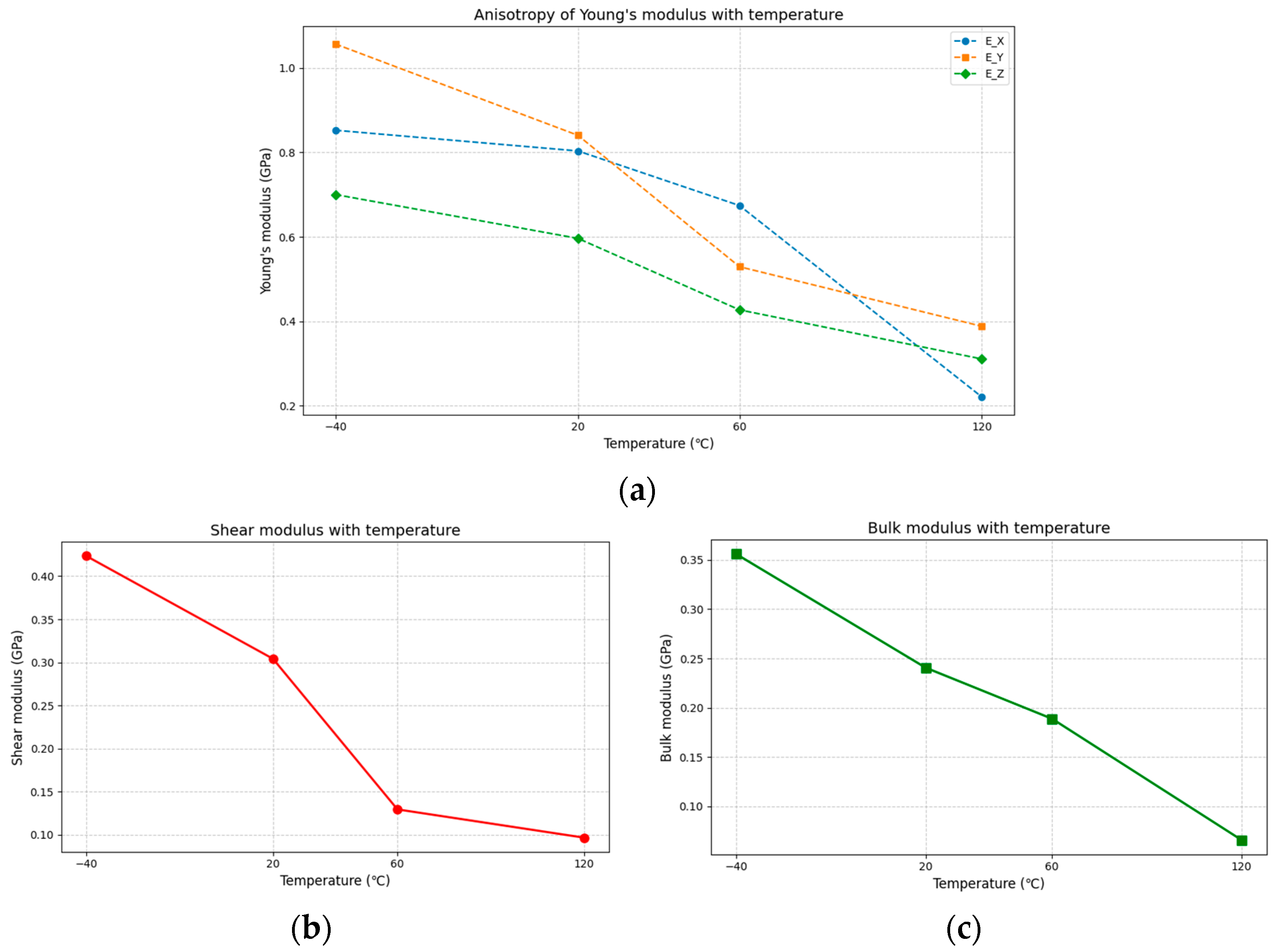
3.2.2. Analysis of Mechanical Properties
3.2.3. Tensile Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MD | molecular dynamics |
| DFT | Density functional theory |
| AP | ammonium perchlorate |
| PBT | poly(3,3-bis-azidomethyl oxetane)-tetrahydrofuran |
| vdW | van der Waals |
| CTPB | carboxyl-terminated polybutadiene |
| HTPB | hydroxyl-terminated polybutadiene |
| PAW | Projected Augmented Wave |
| PBE | Perdew–Burke–Ernzerhof |
| GGA | generalized gradient approximation |
References
- Sivabalan, R.; Talawar, M.B.; Senthilkumar, N.; Kavitha, B.; Asthana, S.N. Studies on azotetrazolate based high nitrogen content high energy materials potential additives for rocket propellants. J. Therm. Anal. Calorim. 2004, 78, 781–792. [Google Scholar] [CrossRef]
- Li, H.P.; He, J.L.; Liang, D.L.; Liu, J.Z.; Wei, M.H. Research Progress of Solid Propellant Micro-Thruster. J. Ordnance Equip. Eng. 2018, 39, 188–194. [Google Scholar]
- Sikder, A.K.; Nirmala, S. A review of advanced high performance, insensitive and thermally stable energetic materials emerging for military and space applications. J. Hazard. Mater. 2004, 112, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Badgujar, D.M.; Talawar, M.B.; Asthana, S.N.; Mahulikar, P.P. Advances in science and technology of modern energetic materials: An overview. J. Hazard. Mater. 2008, 151, 289–305. [Google Scholar] [CrossRef]
- Toshio, M.; Naminosuke, K. Energetics of BAMO. Propellants Explos. Pyrotechics 1992, 17, 5–9. [Google Scholar]
- Chen, C.; Pan, H.Q.; Tu, J.Y.; Chen, J.F.; Zhang, X.Y.; Mao, C.L.; Zhou, X. Thermal aging mechanism of PBT energetic elastomer based on the evolution of microstructure. Mater. Today Chem. 2023, 32, 101655. [Google Scholar] [CrossRef]
- Xie, W.X.; Zhao, Y.; Liu, Y.F.; Huang, H.; Zhang, W. Influence factors on mechanical properties of 3, 3-diazide methyloxybutyl-tetrahydrofuran copolyether propellant. New Chem. Mater. 2022, 48, 163–165. [Google Scholar]
- Jia, X.Z.; Tang, L.J.; Liu, R.P.; Liao, H.J.; Cao, L.; Tang, X.Q.; Cao, P. Analysis of interfacial adhesion properties between PBT azide propellant matrix and defective AP fillers using molecular dynamics simulations. Polymers 2024, 16, 3497. [Google Scholar] [CrossRef]
- Chen, H.R.; Zhou, J.W.; Chen, J.F.; Wan, D.H.; Zhang, H.K.; Mao, C.L.; Wang, R. Study on the reaction mechanism of PBT with curing agent. Chin. J. At. Mol. Phys. 2022, 39, 7. [Google Scholar]
- Zhang, P.; Pang, A.; Tang, G.; Deng, J. Molecular dynamics simulation study on the mechanism of NPBA enhancing interface strength of NEPE propellant. Appl. Surf. Sci. 2019, 493, 131–138. [Google Scholar] [CrossRef]
- Long, Y.; Liu, Y.; Nie, F.; Chen, J. Theoretical study of breaking and slipping processes for HMX/graphite interface. Appl. Surf. Sci. 2012, 258, 2384–2392. [Google Scholar] [CrossRef]
- Pan, A.; Wang, W.; Xie, J.; Zhang, H.; Hao, S. Molecular dynamics simulations of interface structure and deformation mechanisms in metal/ceramic composites under tension. Mech. Mater. 2023, 184, 104688. [Google Scholar] [CrossRef]
- Attarian, S.; Xiao, S. Investigating the strength of Ti/TiB interfaces at multiple scales using density functional theory, molecular dynamics, and cohesive zone modeling. Ceram. Int. 2022, 48, 33185–33199. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Khan, M.A.S.; Vijayalakshmi, R.; Singh, A.; Nandi, A.K.; Talawar, M.B. Morphology of ammonium perchlorate in the presence of ethylene glycol as an additive: A first principle study. CrystEngComm 2019, 21, 7519–7527. [Google Scholar] [CrossRef]
- Yeh, I.C.; Andzelm, J.W. Computational Study of Structural and Energetic Properties of Ammonium Perchlorate at Interfaces. J. Phys. Chem. C 2021, 125, 12297–12304. [Google Scholar] [CrossRef]
- Kang, L.; Li, S.; Wang, B.; Zeng, Q. Exploration of the Energetic Material Ammonium Perchlorate at High Pressures: Combined Raman Spectroscopy and X-ray Diffraction Study. J. Phys. Chem. C 2018, 122, 15937–15944. [Google Scholar] [CrossRef]
- Mao, Y.; Hu, P. Identification of the active sites and mechanism for partial methane oxidation to methanol over copper-exchanged CHA zeolites. Sci. China Chem. 2020, 63, 850–859. [Google Scholar] [CrossRef]
- Dion, M.; Rydberg, H.; Schröder, E.; Langreth, D.C.; Lundqvist, B.I. Van der Waals Density Functional for General Geometries. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef]
- Bhatta, R.S.; Pellicane, G.; Tsige, M. Tuning range-separated DFT functionals for accurate orbital energy modeling of conjugated molecules. Comput. Theor. Chem. 2015, 1070, 14–20. [Google Scholar] [CrossRef]
- Bhattacharjee, D.; Mishra, B.K.; Chakrabartty, A.K.; Deka, R.C. DFT and QTAIM studies on structure and stability of beryllium doped gold Clusters. Comput. Theor. Chem. 2014, 1034, 61–72. [Google Scholar] [CrossRef]
- Yang, J.; Gong, X.; Wang, G. Theoretical studies on the plasticizing effect of DIANP on NC with various esterification degrees. Comput. Mater. Sci. 2014, 95, 129–135. [Google Scholar] [CrossRef]
- Sun, T.; Xiao, J.; Liu, Q.; Zhao, F.; Xiao, H. Comparative study on structure, energetic and mechanical properties of a ε-CL-20/HMX cocrystal and its composite with molecular dynamics simulation. J. Mater. Chem. A 2014, 2, 13898–13904. [Google Scholar] [CrossRef]
- Taylor, D.E.; Strawhecker, K.; Shanholtz, E.R.; Sorescu, D.C.; Sausa, R.C. Investigations of the intermolecular forces between RDX and polyethylene by forcedistance spectroscopy and molecular dynamics simulations. J. Phys. Chem. A 2014, 118, 5083–5097. [Google Scholar] [CrossRef]
- Cordatos, H.; Ford, D.; Gorte, R.J. Simulated Annealing Study of the Structure and Reducibility in Ceria Clusters. J. Phys. Chem. 1996, 100, 18128–18132. [Google Scholar] [CrossRef]
- Park, Y.H.; Hijazi, I. Monte Carlo Simulation for Structure of Metallic Clusters. In Proceedings of the ASME 2010 Pressure Vessels and Piping Conference, Bellevue, WA, USA, 18–22 July 2010; Volume 2, pp. 355–358. [Google Scholar]
- Tang, Q.; Fan, X.; Li, J.; Bi, F.; Fu, X.; Zhai, L. Experimental and theoretical studies on stability of new stabilizers for N-methyl-Pnitroaniline derivative in CMDB propellants. J. Hazard. Mater. 2017, 327, 187–196. [Google Scholar] [CrossRef]
- Huang, X.; Wang, X.; Wang, Q.; Xu, X.; Zhao, S. Promoting Cross-Link Reaction of Polymers by the Matrix–Filler Interface Effect: Role of Coupling Agents and Intermediate Linkers. J. Phys. Chem. B 2024, 128, 5534–5541. [Google Scholar] [CrossRef]
- Sun, H.; Jin, Z.; Yang, C.; Akkermans, R.L.C.; Robertson, S.H.; Spenley, N.A.; Miller, S.; Todd, S.M. COMPASS II: Extended coverage for polymer and drug-like molecule databases. J. Mol. Model. 2016, 22, 47. [Google Scholar] [CrossRef]
- Li, M.; Li, F.; Shen, R.; Guo, X. Molecular dynamics study of the structures and properties of RDX/GAP propellant. J. Hazard. Mater. 2011, 186, 2031–2036. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, X.; Zhang, W.; Xu, H.; Xie, W.; Du, J.; Liu, Y. Simulation and experimental on the solvation interaction between the GAP matrix and insensitive energetic plasticizers in solid propellants. J. Phys. Chem. A 2016, 120, 765–770. [Google Scholar] [CrossRef] [PubMed]
- Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef] [PubMed]
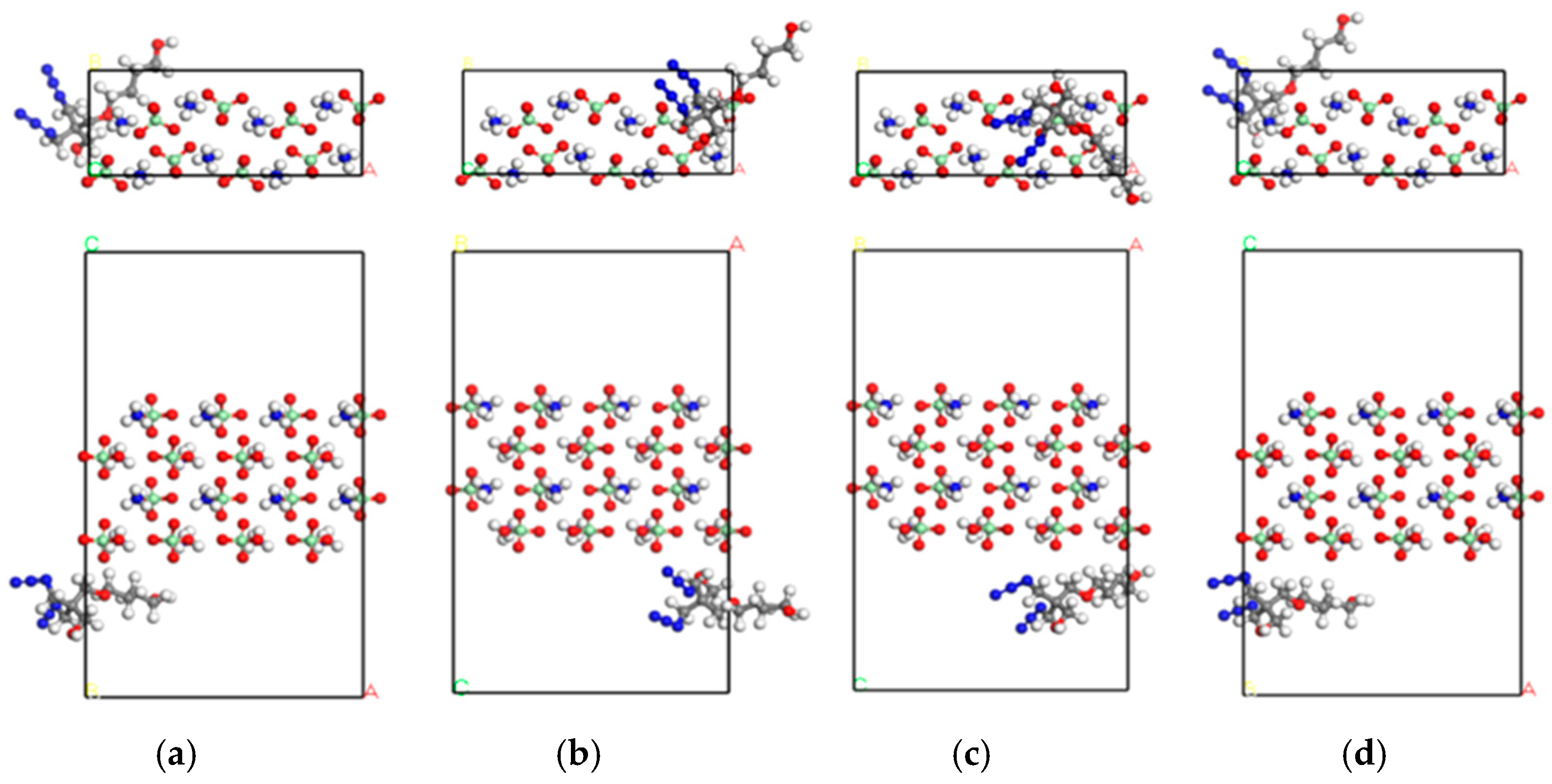





| Esuf (eV) | Eclean (eV) | Etotal (eV) | Eab (eV) | |
|---|---|---|---|---|
| a | −212.917 | −748.900 | −971.857 | −10.039 |
| b | −212.917 | −748.900 | −971.758 | −9.940 |
| c | −212.917 | −748.900 | −971.628 | −9.810 |
| d | −212.917 | −748.900 | −971.743 | −9.925 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Cheng, X. Investigation of PBT-AP Interactions in PBT-Based Solid Propellants: A Combined Density Functional Theory and Molecular Dynamics Study. Polymers 2025, 17, 1492. https://doi.org/10.3390/polym17111492
Liu K, Cheng X. Investigation of PBT-AP Interactions in PBT-Based Solid Propellants: A Combined Density Functional Theory and Molecular Dynamics Study. Polymers. 2025; 17(11):1492. https://doi.org/10.3390/polym17111492
Chicago/Turabian StyleLiu, Kun, and Xinlu Cheng. 2025. "Investigation of PBT-AP Interactions in PBT-Based Solid Propellants: A Combined Density Functional Theory and Molecular Dynamics Study" Polymers 17, no. 11: 1492. https://doi.org/10.3390/polym17111492
APA StyleLiu, K., & Cheng, X. (2025). Investigation of PBT-AP Interactions in PBT-Based Solid Propellants: A Combined Density Functional Theory and Molecular Dynamics Study. Polymers, 17(11), 1492. https://doi.org/10.3390/polym17111492





