A Unified Equation for Predicting Crack Growth in Rubber Composites Across All Crack Growth Rates
Abstract
1. Introduction
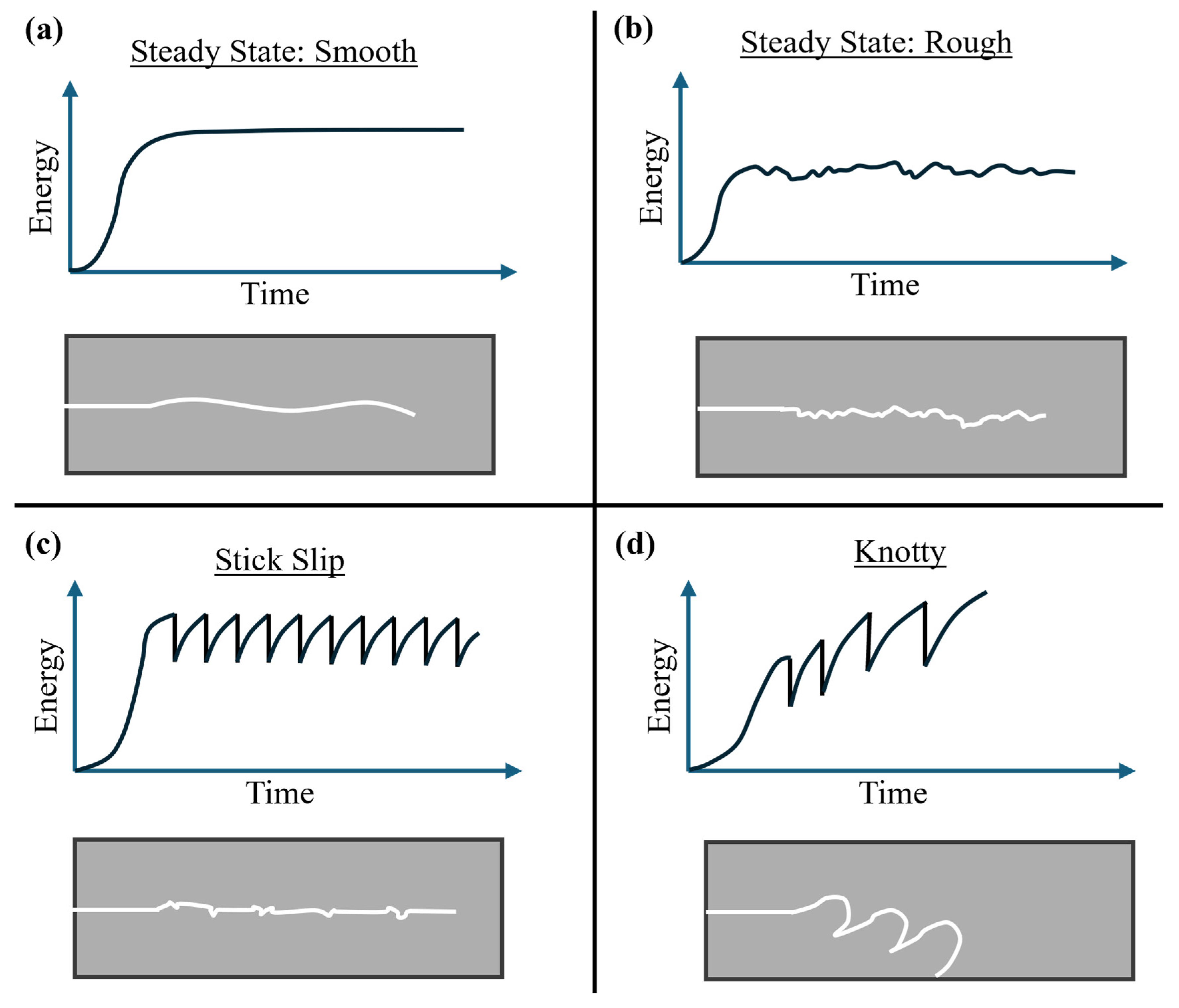
1.1. Tearing Energy Versus Crack Growth Rate
1.2. Viscoelastic Energy Dissipation During Crack Growth
1.3. Tearing Energy Experiment Geometries
2. Materials and Methods
2.1. New Method for Modeling Tearing Energy Versus Crack Growth Rate
2.2. Materials
2.3. Trouser Tear Tests
3. Results
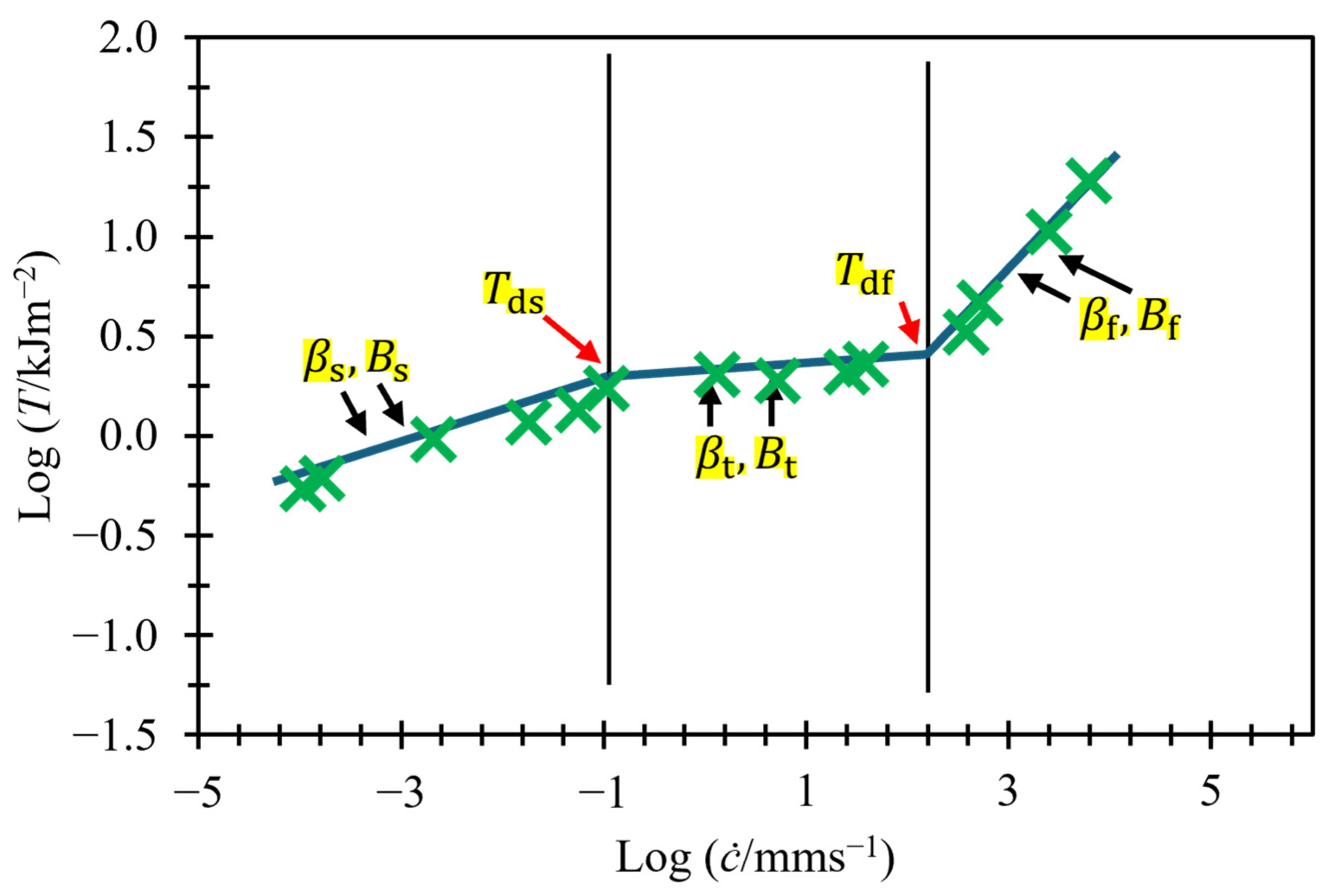
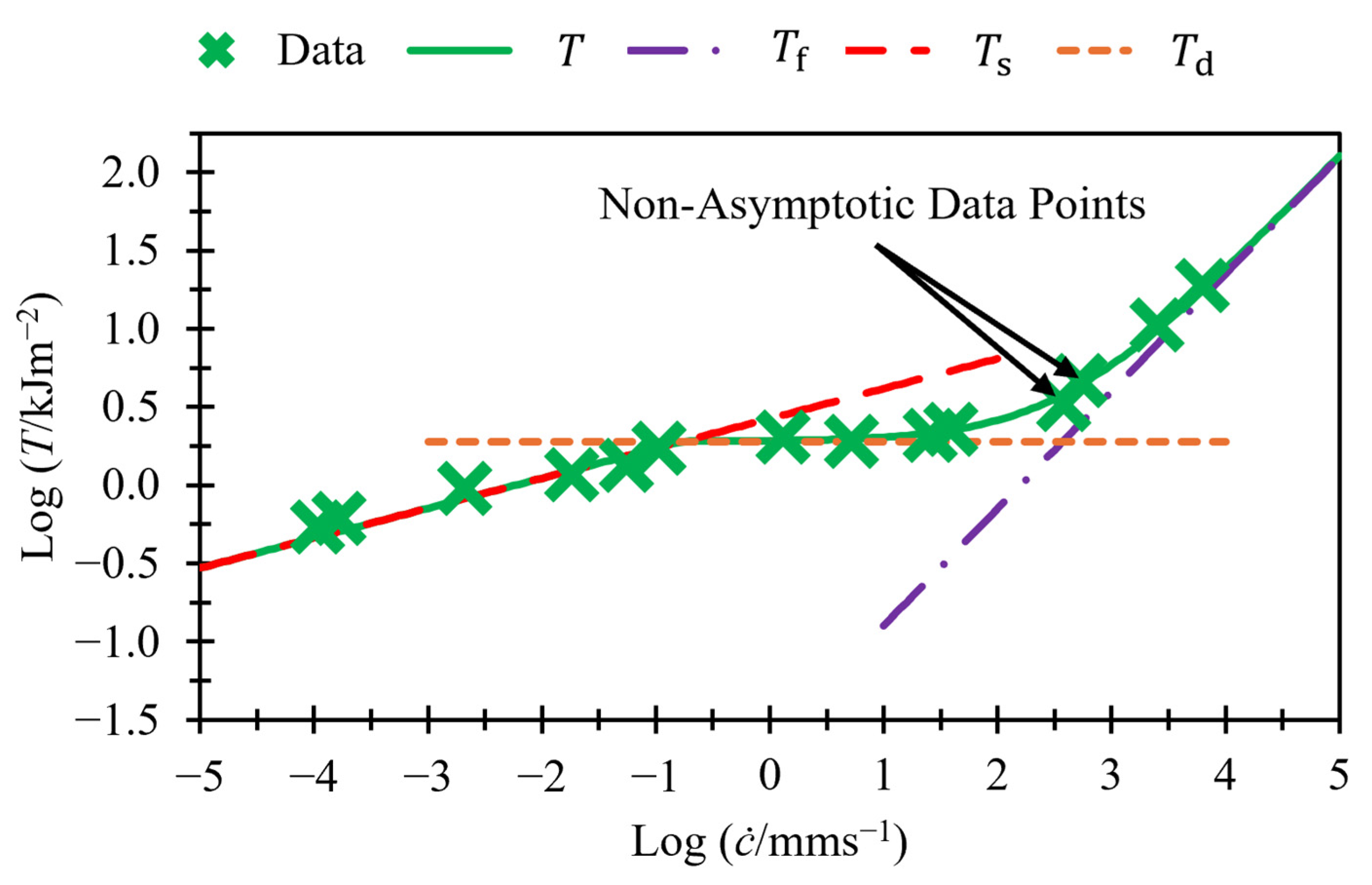
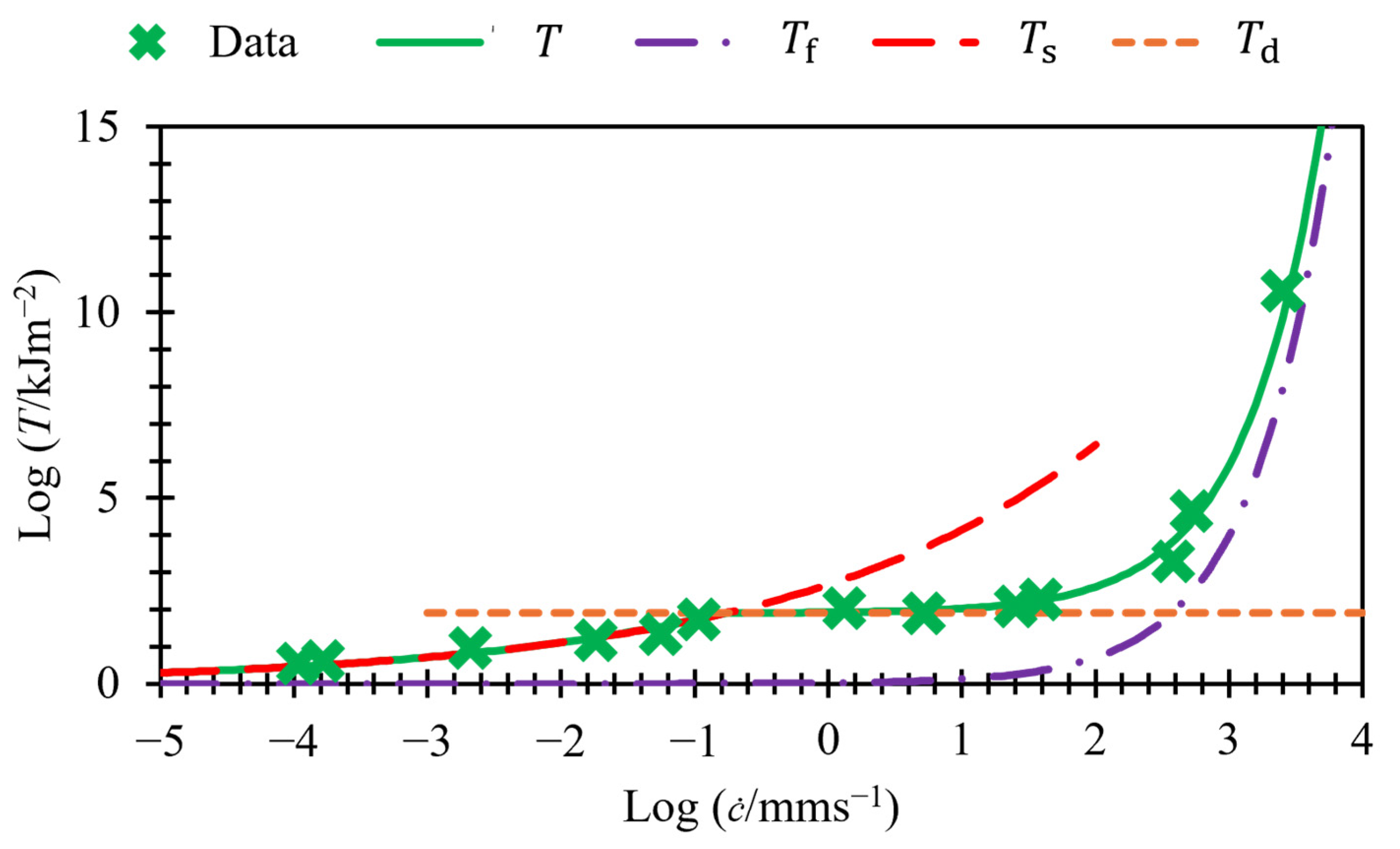
3.1. Fitting of Tearing Energy Data
3.2. Relating Variables
3.3. Predicting Transition and Fast Crack Growth Tearing Energies from Slow Tearing Energy
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NBR | Nitrile butadiene rubber |
| SBR | Styrene-butadiene rubber |
| BR | Butadiene rubber |
| DMA | Dynamical mechanical analysis |
References
- Greensmith, H.W. Rupture of Rubber. IV. Tear Properties of Vulcanizates Containing Carbon Black. Rubber Chem. Technol. 1957, 30, 584–595. [Google Scholar] [CrossRef]
- Greensmith, H.W. Rupture of Rubber. VIII. Comparisons of Tear and Tensile Rupture Measurements. J. Appl. Polym. Sci. 1960, 3, 183–193. [Google Scholar] [CrossRef]
- Greensmith, H.W.; Thomas, A.G. Rupture of Rubber. III. Determination of Tear Properties. Rubber Chem. Technol. 1956, 29, 372–381. [Google Scholar] [CrossRef]
- Lake, G.J.; Lindley, P.B.; Thomas, A.G. Fracture Mechanics of Rubber. In Proceedings of the 2nd International Conference on Fracture, Brighton, UK, 13–18 April 1969; pp. 25–45. [Google Scholar]
- Lindley, P.B. Energy for Crack Growth in Model Rubber Components. J. Strain Anal. Eng. Des. 1972, 7, 132–140. [Google Scholar] [CrossRef]
- Thomas, A.G. Rupture of Rubber. VI. Further Experiments on the Tear Criterion. J. Appl. Polym. Sci. 1960, 3, 168–174. [Google Scholar] [CrossRef]
- Rivlin, R.S.; Thomas, A.G. Rupture of Rubber. I. Characteristic Energy for Tearing. J. Polym. Sci. 1953, 10, 291–318. [Google Scholar] [CrossRef]
- Greensmith, H.W.; Mullins, L.; Thomas, A.G. Rupture of Rubber. Trans. Soc. Rheol. 1960, 4, 179–189. [Google Scholar] [CrossRef]
- Ahagon, A.; Gent, A.N. Threshold Fracture Energies for Elastomers. J. Polym. Sci. Polym. Phys. Ed. 1975, 13, 1903–1911. [Google Scholar] [CrossRef]
- Sakulkaew, K.; Thomas, A.G.; Busfield, J.J.C. The Effect of Temperature on the Tearing of Rubber. Polym. Test. 2013, 32, 86–93. [Google Scholar] [CrossRef]
- Sakulkaew, K. Tearing of Rubber; Queen Mary University of London: London, UK, 2012. [Google Scholar]
- Mullins, L. Rupture of Rubber, Part IX: Role of Hysteresis in the Tearing of Rubber. Trans. IRI 1985, 35, 213–222. [Google Scholar]
- Kadir, A.; Thomas, A.G. Tear Behavior of Rubbers over a Wide Range of Rates. Rubber Chem. Technol. 1981, 54, 15–23. [Google Scholar] [CrossRef]
- Tsunoda, K. The Role of Visco-Elasticity on the Crack Growth Behaviour of Rubber; Queen Mary University of London: London, UK, 2001. [Google Scholar]
- Tsunoda, K.; Busfield, J.J.C.; Davies, C.K.L.; Thomas, A.G. Effect of Materials Variables on the Tear Behaviour of a Non-Crystallising Elastomer. J. Mater. Sci. 2000, 35, 5187–5198. [Google Scholar] [CrossRef]
- Sakulkaew, K.; Thomas, A.G.; Busfield, J.J.C. The Effect of the Rate of Strain on Tearing in Rubber. Polym. Test. 2011, 30, 163–172. [Google Scholar] [CrossRef]
- Thomas, A.G. Rupture of Rubber. V. Cut Growth in Natural Rubber Vulcanizates. J. Polym. Sci. 1958, 31, 467–480. [Google Scholar] [CrossRef]
- Glucklich, J.; Landel, R.F. The Tearing Test as a Means for Estimating the Ultimate Properties of Rubber. J. Appl. Polym. Sci. 1976, 20, 121–137. [Google Scholar] [CrossRef]
- Busfield, J.J.C.; Tsunoda, K.; Davies, C.K.L.; Thomas, A.G. Contributions of Time Dependent and Cyclic Crack Growth to the Crack Growth Behavior of Non Strain-Crystallizing Elastomers. Rubber Chem. Technol. 2002, 75, 643–656. [Google Scholar] [CrossRef]
- Thomas, A.G. The Development of Fracture Mechanics for Elastomers. Rubber Chem. Technol. 1994, 67, 50–67. [Google Scholar] [CrossRef]
- Höfer, P.; Lion, A. Modelling of Frequency-and Amplitude-Dependent Material Properties of Filler-Reinforced Rubber. J. Mech. Phys. Solids 2009, 57, 500–520. [Google Scholar] [CrossRef]
- ASTM D1938-19; Standard Test Method for Tear-Propagation Resistance (Trouser Tear) of Plastic Film and Thin Sheeting by a Single-Tear Method. ASTM: West Conshohocken, PA, USA, 2019.
- Windslow, R.J.; Duncan, A.M.; Hohenberger, T.W.; Busfield, J.J.C. Evaluating the Crack Tip Formation and Propagation Energy of a Trouser Tear Specimen. Rubber Chem. Technol. 2023, 96, 551–563. [Google Scholar] [CrossRef]
- Andrews, E.H. A Generalized Theory of Fracture Mechanics. J. Mater. Sci. 1974, 9, 887–894. [Google Scholar] [CrossRef]
- Fukahori, Y.; Sakulkaew, K.; Busfield, J.J.C. Elastic–Viscous Transition in Tear Fracture of Rubbers. Polymer 2013, 54, 1905–1915. [Google Scholar] [CrossRef]
- Fukahori, Y.; Sakulkaew, K.; Busfield, J.J.C. A New Physical Aspect for Elastic-Viscous Transition and Velocity Jump in Fracture of Rubbers. Polymer 2017, 125, 30–39. [Google Scholar] [CrossRef]



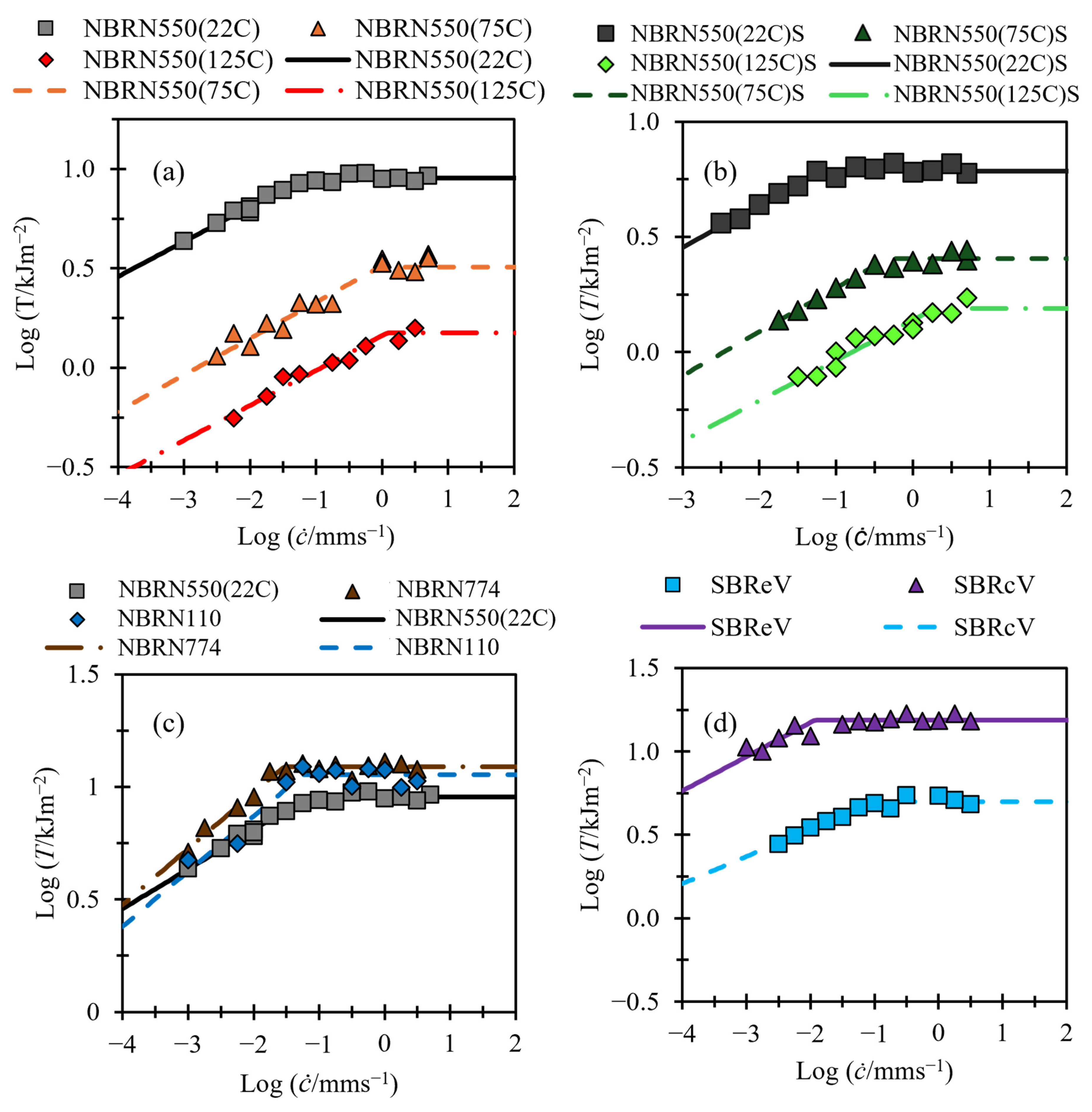
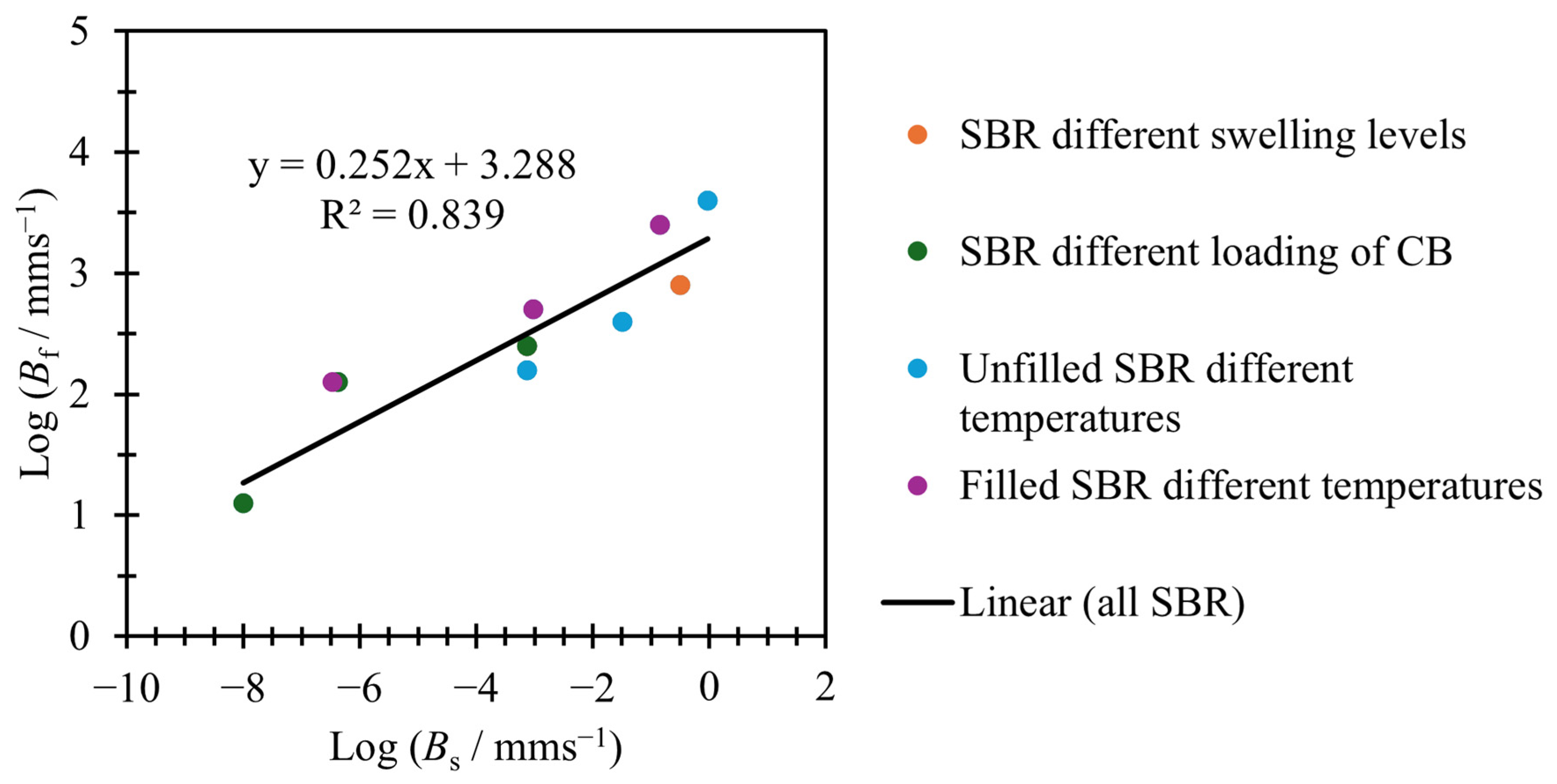
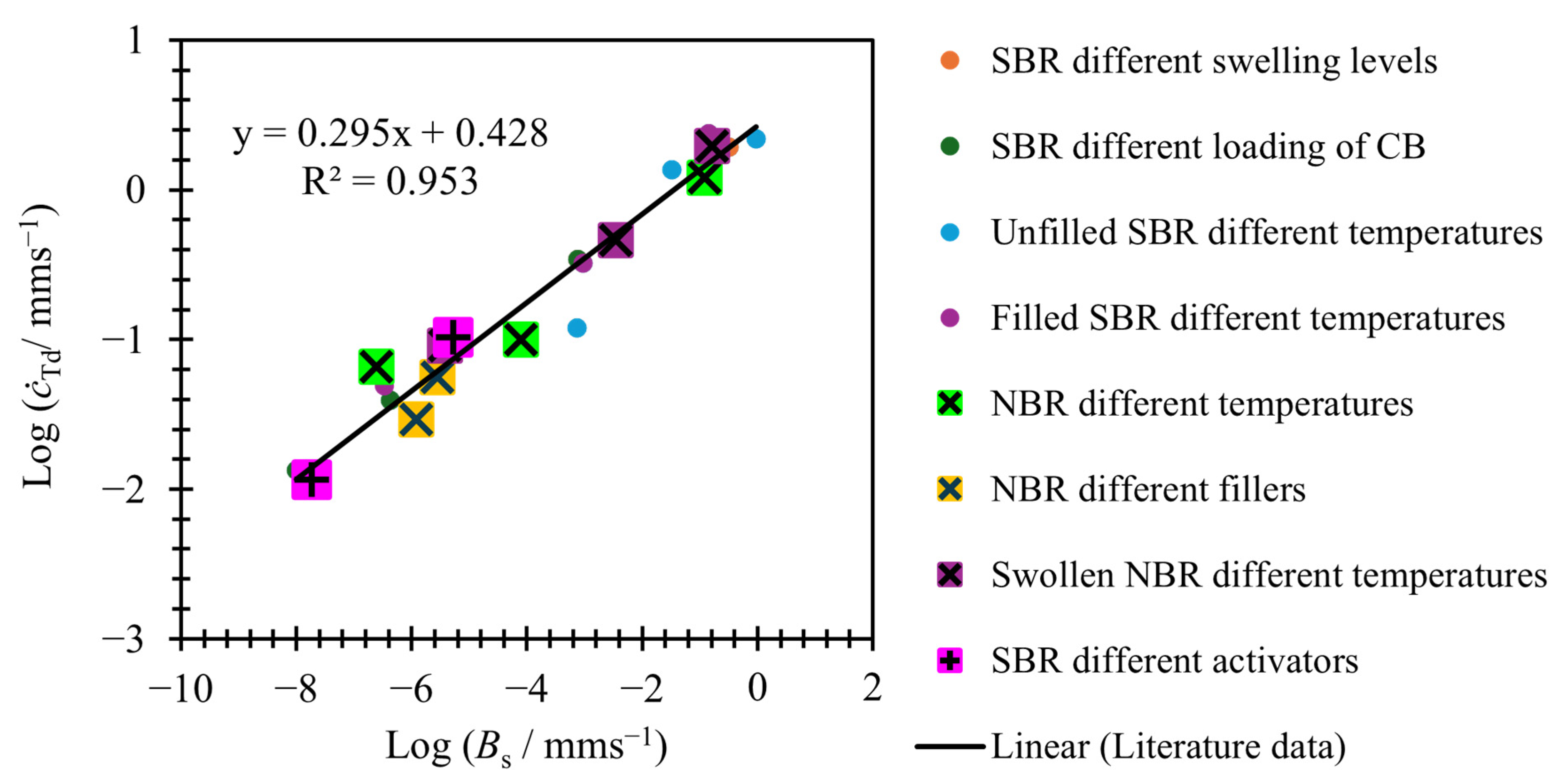

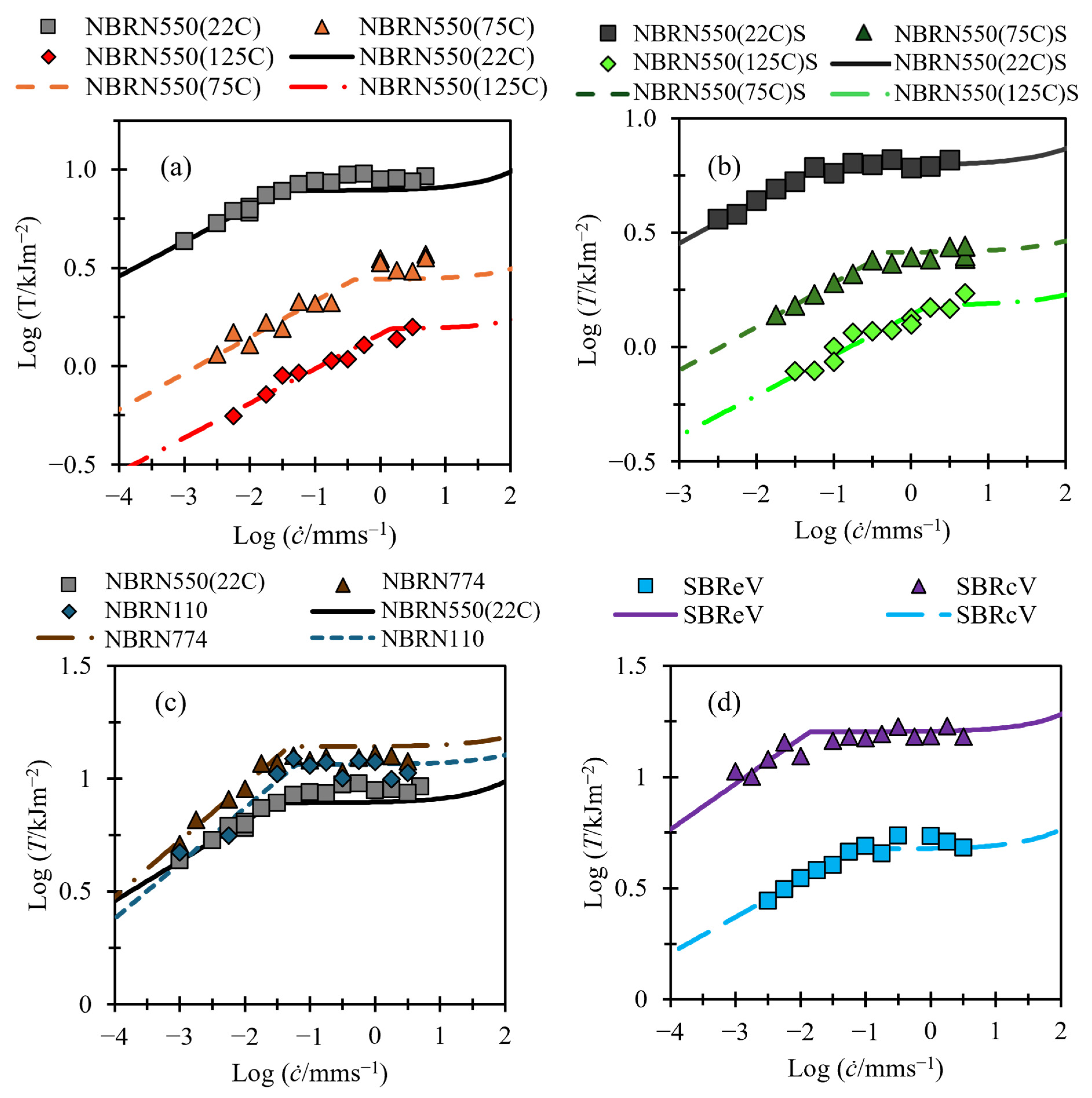
| Material Name | Rubber | Filler | Test Temperature/°C | Notes |
|---|---|---|---|---|
| SBR20C * | SBR | Unfilled | 20 | - |
| SBR60C * | SBR | Unfilled | 60 | - |
| SBR100C * | SBR | Unfilled | 100 | - |
| SBR10pph20C * | SBR | 10 pphr N220 | 20 | - |
| SBR10pph60C * | SBR | 10 pphr N220 | 60 | - |
| SBR10pph100C * | SBR | 10 pphr N220 | 100 | - |
| SBR50pph20C * | SBR | 50 pphr N220 | 20 | - |
| SBR0.8Vr * | SBR | Unfilled | 20 | Swollen to 80% rubber by volume in dibutyl adipate |
| SBR0.4Vr * | SBR | Unfilled | 20 | Swollen to 40% rubber by volume in dibutyl adipate |
| NBR_AT † | NBR | Unfilled | 20 | - |
| SBR_AT † | SBR | Unfilled | 20 | - |
| BR_AT † | BR | Unfilled | 20 | - |
| NBRN550(22C) | NBR | 60 pphr N550 | 22 | - |
| NBRN550(75C) | NBR | 60 pphr N550 | 75 | - |
| NBRN550(125C) | NBR | 60 pphr N550 | 125 | - |
| NBRN774 | NBR | 60 pphr NBRN774 | 22 | - |
| NBRN110 | NBR | 60 pphr NBRN110 | 22 | - |
| NBRN550(22C)S | NBR | 60 pphr N550 | 22 | - |
| NBRN550(75C)S | NBR | 60 pphr N550 | 75 | Swollen in ULTADRIL at 125 °C for 72 h |
| NBRN550(125C)S | NBR | 60 pphr N550 | 125 | Swollen in ULTADRIL at 125 °C for 72 h |
| SBReV | SBR | 50 pphr N220 | 22 | Efficient cure |
| SBRcV | SBR | 50 pphr N220 | 22 | Conventional cure |
| Material Name | /mms−1) | /kJm−2 | /mms−1) | ||
|---|---|---|---|---|---|
| SBR20C * | −3.13 | 7.35 | 6.0 | 2.20 | 4/3 |
| SBR60C * | −1.49 | 7.06 | 4.1 | 2.60 | 4/3 |
| SBR100C * | −0.023 | 3.20 | 2.0 | 3.60 | 4/3 |
| SBR10pph20C * | −6.47 | 6.51 | 2.2 | 2.05 | 4/3 |
| SBR10pph60C * | −3.03 | 4.22 | 1.9 | 2.70 | 4/3 |
| SBR10pph100C * | −0.85 | 4.05 | 1.3 | 3.40 | 4/3 |
| SBR50pph20C * | −8.00 | 8.25 | 10.0 | 1.10 | 4/3 |
| SBR0.8Vr * | −0.49 | 5.34 | 1.4 | 2.90 | 4/3 |
| SBR0.4Vr * | 3.42 | 4.20 | - | - | - |
| NBR_AT † | - | - | 4.1 | 0.9 | 4/3 |
| SBR_AT † | −2.77 | 5.10 | 2.7 | 2.05 | 4/3 |
| BR_AT † | −0.48 | 3.40 | >>10 | 3.40 | 4/3 |
| NBRN550(22C) | −6.61 | 5.69 | 9.0 | - | - |
| NBRN550(75C) | −2.80 | 5.45 | 3.1 | - | - |
| NBRN550(125C) | −0.92 | 5.69 | 2.1 | - | - |
| NBRN774 | −5.92 | 4.02 | 12.3 | - | - |
| NBRN110 | −5.55 | 4.08 | 11.3 | - | - |
| NBRN550(22C)S | −5.43 | 5.36 | 6.1 | - | - |
| NBRN550(75C)S | −2.46 | 5.23 | 2.55 | - | - |
| NBRN550(125C)S | −0.79 | 5.70 | 1.55 | - | - |
| SBReV | −5.27 | 6.13 | 5.0 | - | - |
| SBRcV | −7.73 | 4.88 | 15.4 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duncan, A.M.; Akutagawa, K.; Papageorgiou, D.G.; Ramier, J.L.; Busfield, J.J.C. A Unified Equation for Predicting Crack Growth in Rubber Composites Across All Crack Growth Rates. Polymers 2025, 17, 1357. https://doi.org/10.3390/polym17101357
Duncan AM, Akutagawa K, Papageorgiou DG, Ramier JL, Busfield JJC. A Unified Equation for Predicting Crack Growth in Rubber Composites Across All Crack Growth Rates. Polymers. 2025; 17(10):1357. https://doi.org/10.3390/polym17101357
Chicago/Turabian StyleDuncan, Aaron M., Keizo Akutagawa, Dimitrios G. Papageorgiou, Julien L. Ramier, and James J. C. Busfield. 2025. "A Unified Equation for Predicting Crack Growth in Rubber Composites Across All Crack Growth Rates" Polymers 17, no. 10: 1357. https://doi.org/10.3390/polym17101357
APA StyleDuncan, A. M., Akutagawa, K., Papageorgiou, D. G., Ramier, J. L., & Busfield, J. J. C. (2025). A Unified Equation for Predicting Crack Growth in Rubber Composites Across All Crack Growth Rates. Polymers, 17(10), 1357. https://doi.org/10.3390/polym17101357










