Hybrid Fabrics for Ohmic Heating Applications
Abstract
1. Introduction
2. Principle of Ohmic Heating
3. Materials and Methods
3.1. Materials
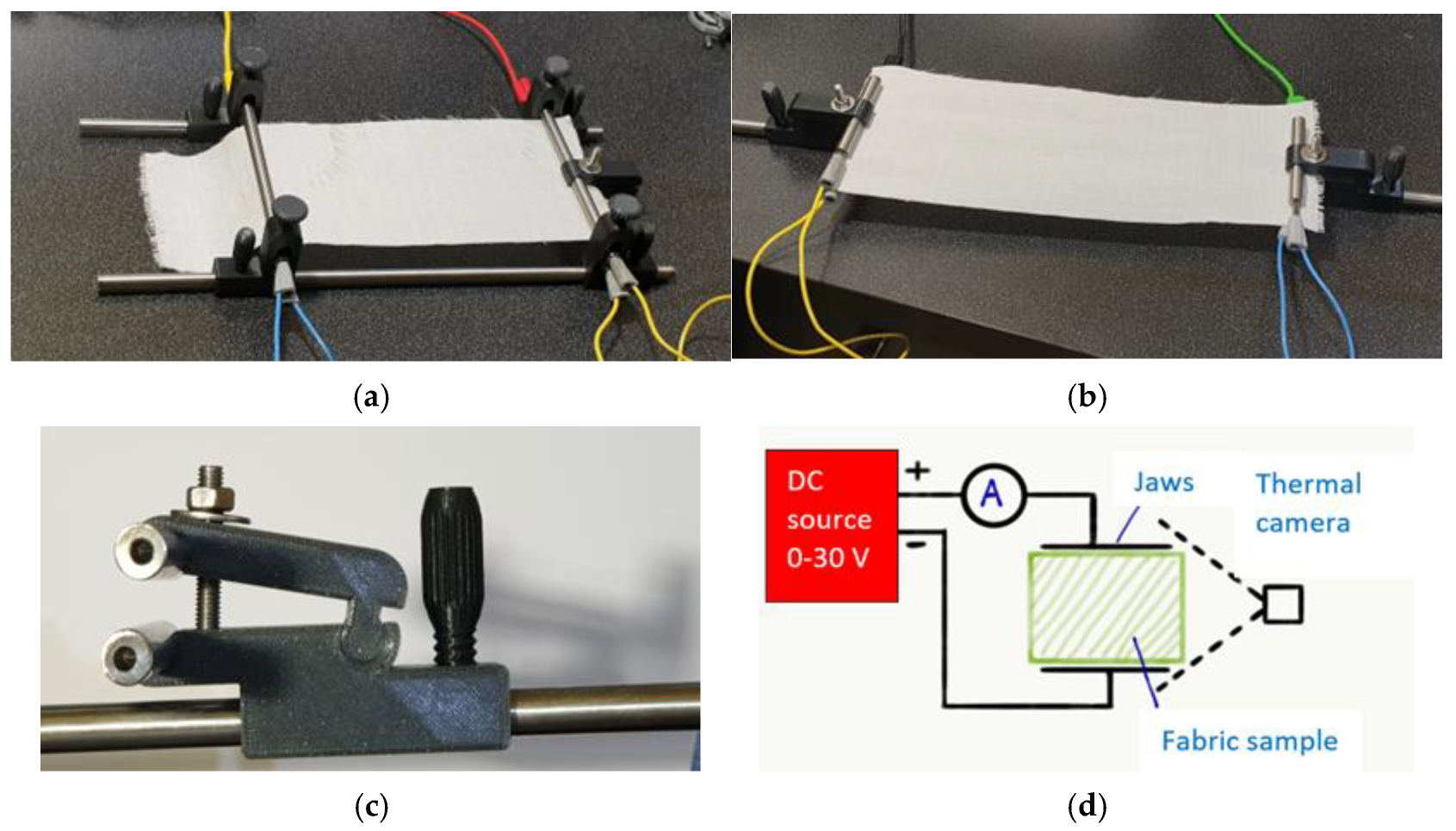
3.2. Measurements
4. Results and Discussion
4.1. Characterization of Materials
4.2. Electrical Properties of Hybrid Fabrics
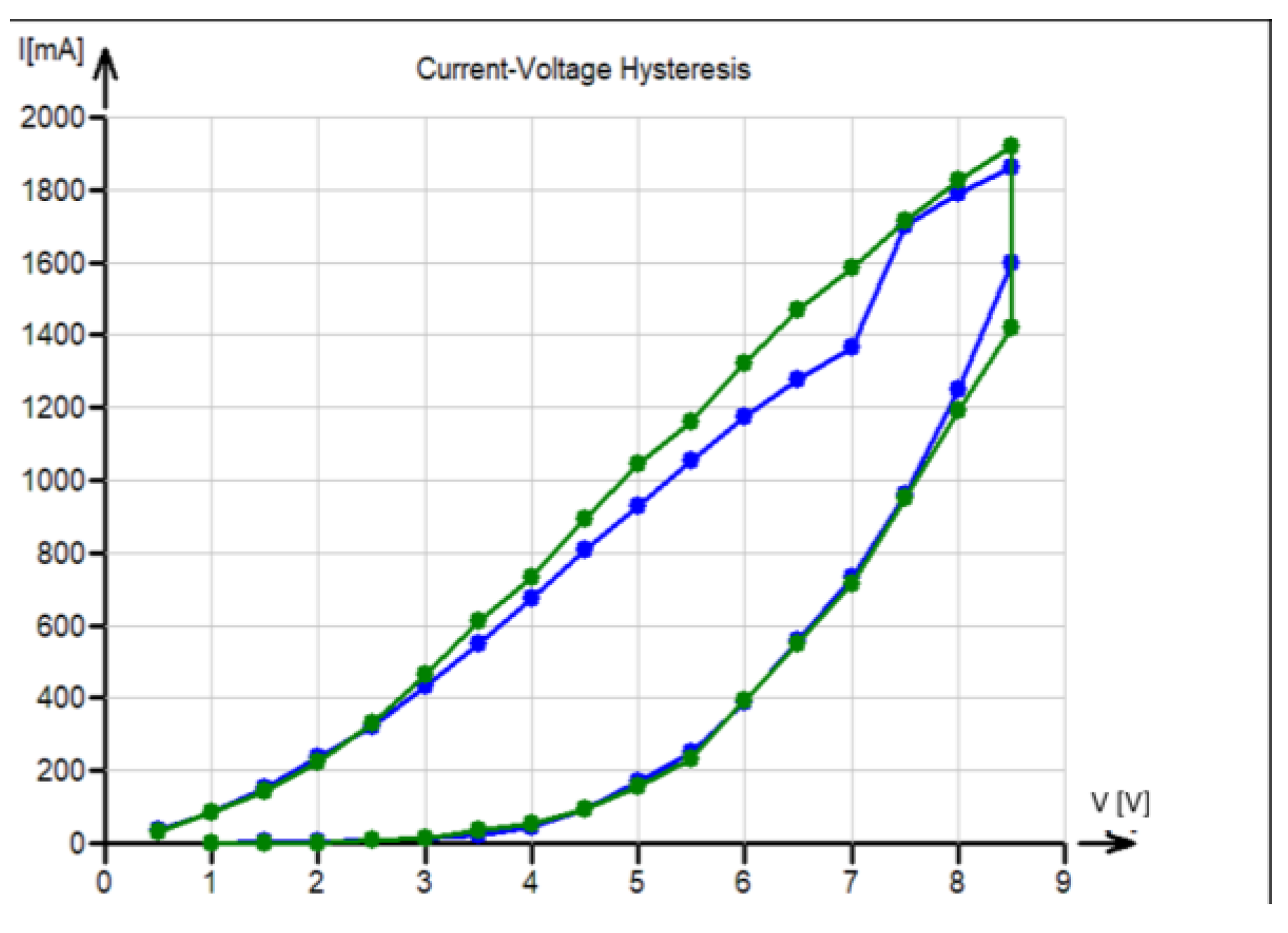
4.2.1. Current–Voltage Measurement
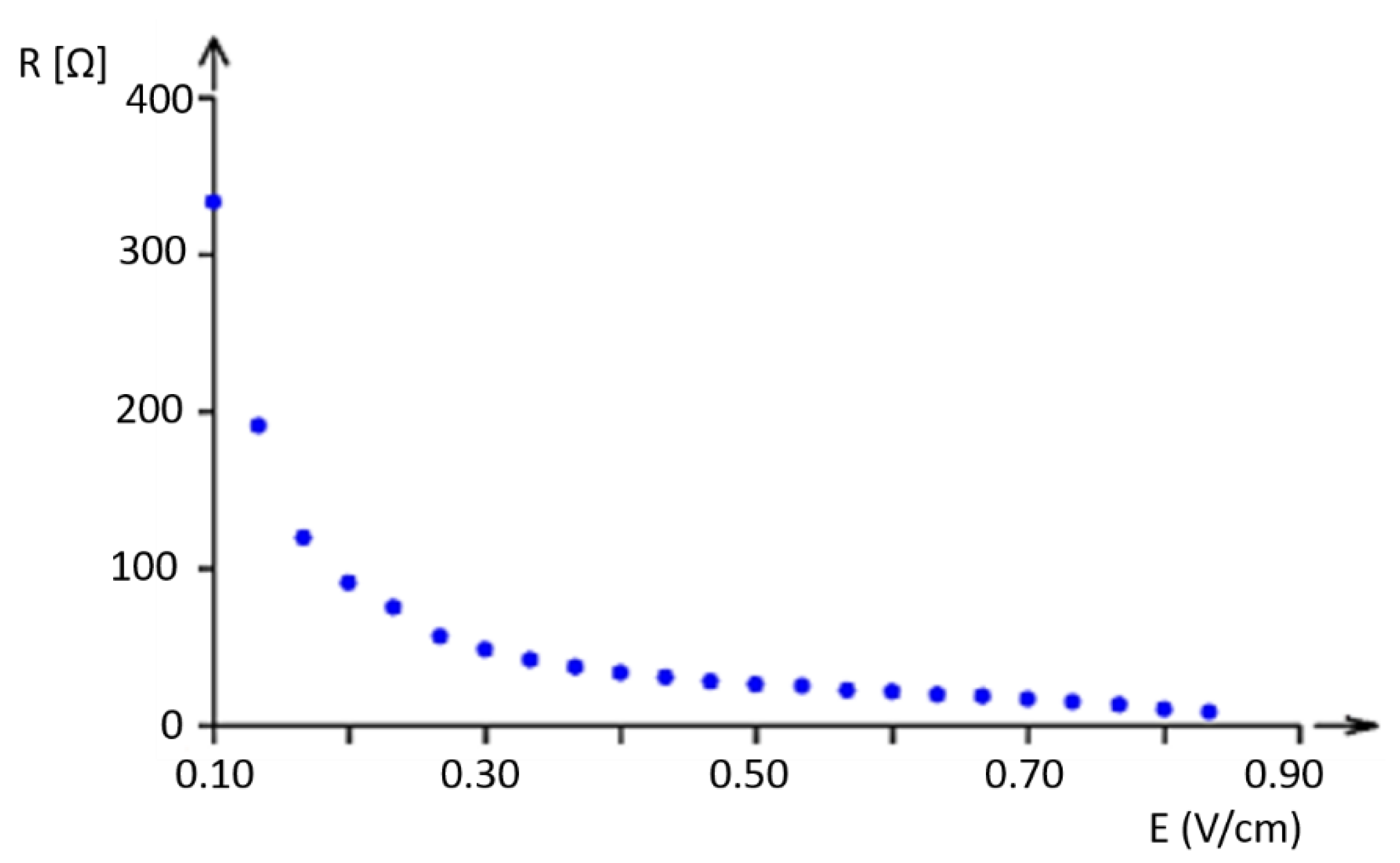
4.2.2. Resistance–Electrical Field Measurement
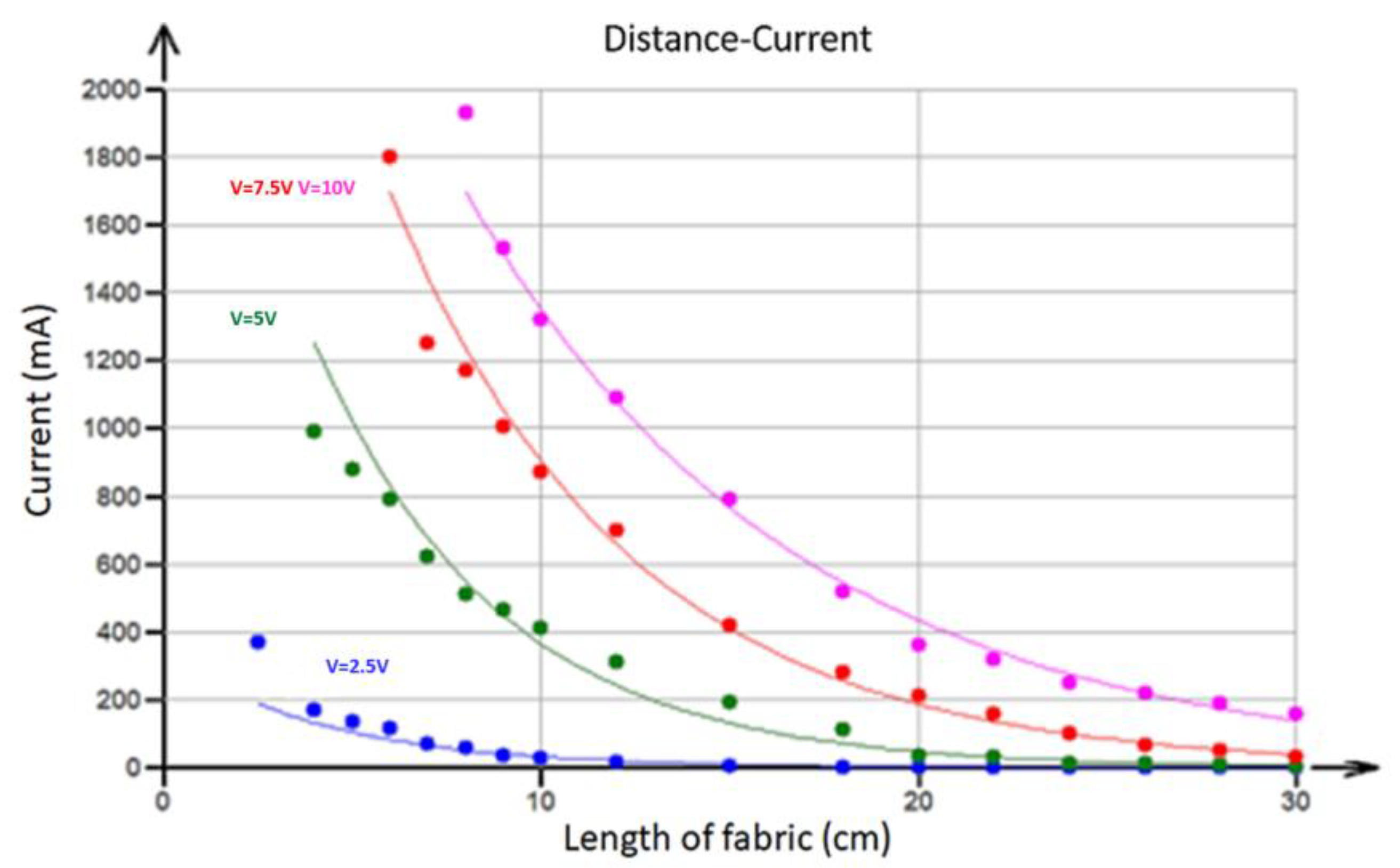
4.2.3. Influence of Distance on Electrical Properties
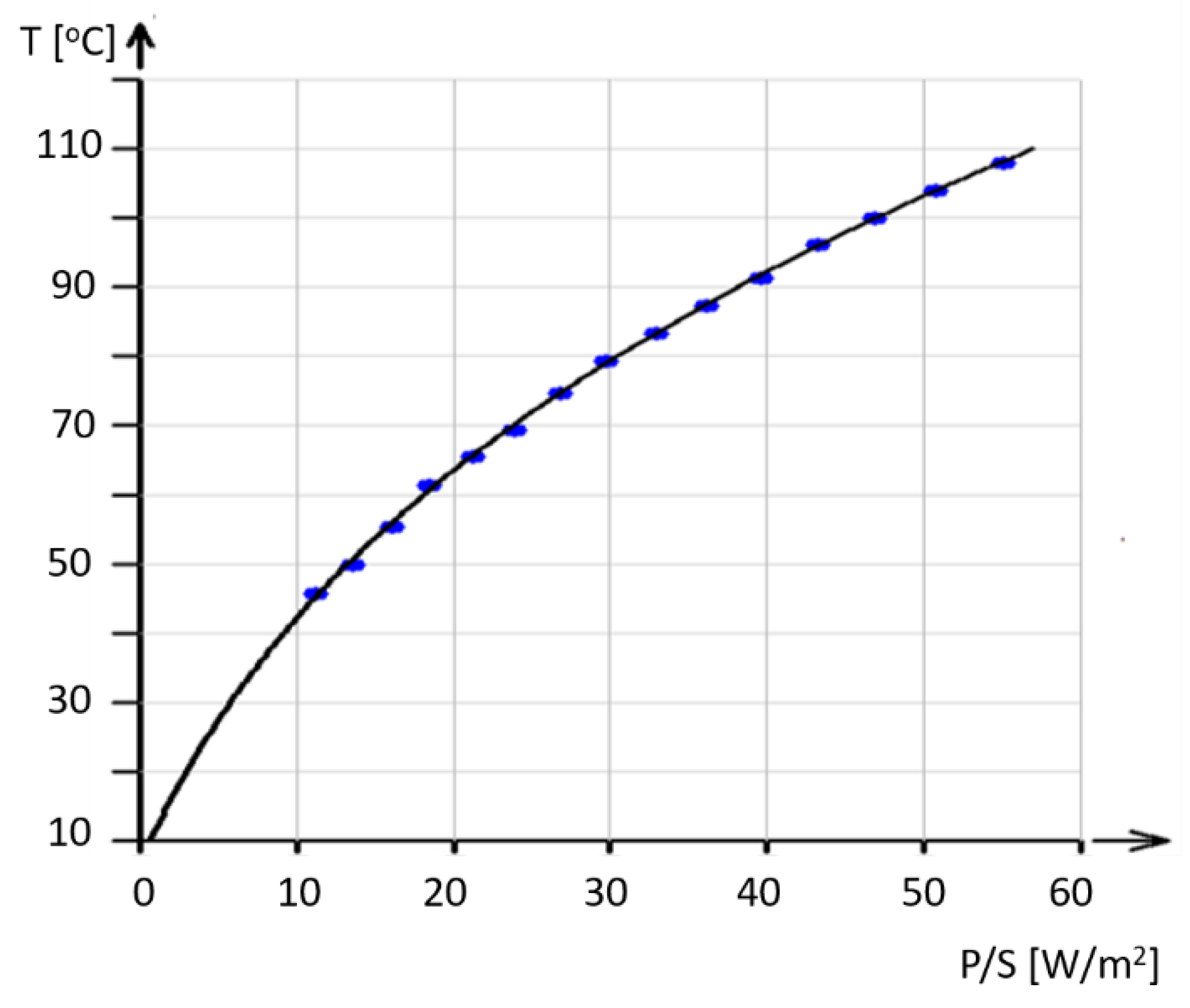
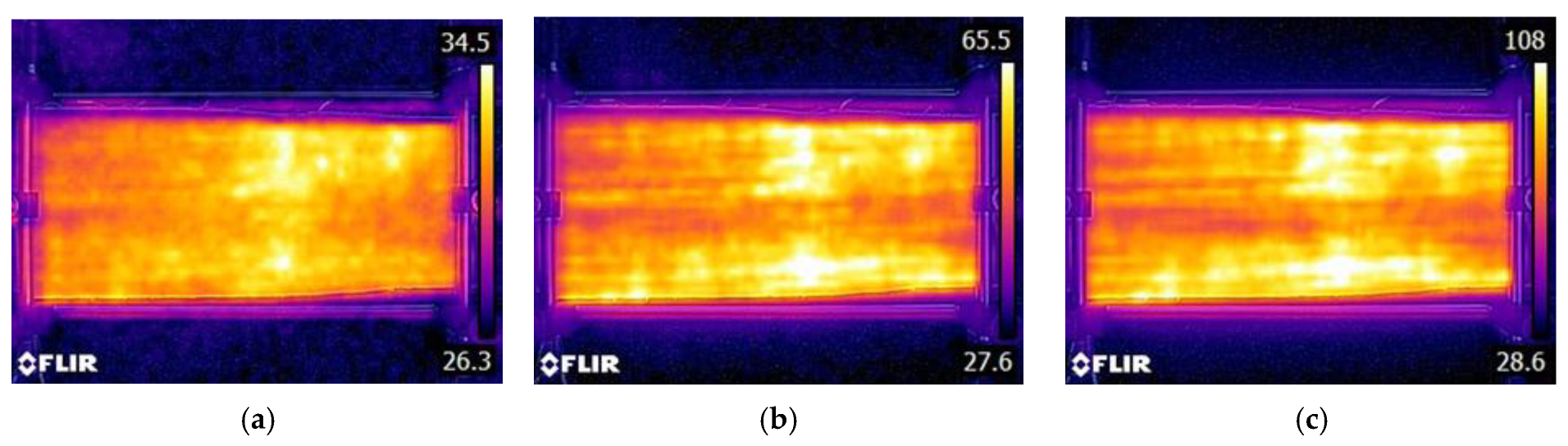
4.3. Surface Temperature Due to Ohmic Heating
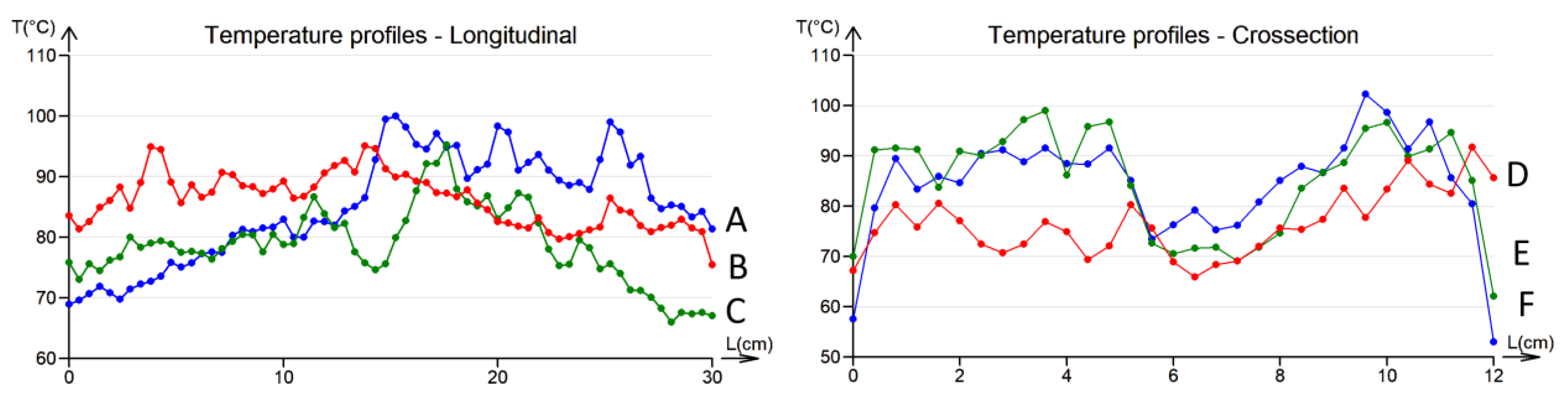
4.4. Heat Profiles
- ✓
- The structure of the fabric (twill 2/1 weave) and the structure of the staple hybrid yarns, which are responsible for the large total porosity.
- ✓
- The random variations in the electrical properties (apparent electrical resistance) of hybrid yarns.
5. Conclusions
- The evaluation of nonlinear dependence between current and voltage;
- The predicted dependence of current and voltage on the distance between electrodes;
- An evaluation of the surface temperature of ohmically heated hybrid fabrics as a function of input electrical power.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Nalwa, H.S. (Ed.) Handbook of Organic Conductive Molecules and Polymers, Volume, 4, Conductive Polymers: Photophysics and Application; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Wan, M. Conducting Polymers with Micro or Nanometer Structure; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Militký, J.; Venkataraman, M.; Periyasamy, A.P. (Eds.) Fibrous Structures and Their Impact on Textile Design; Springer: Singapore, 2023. [Google Scholar]
- Shyr, T.W.; Shie, J.W. Electromagnetic shielding mechanism using soft magnetic stainless steel fiber enabled polyester textiles. J. Magn. Magn. Mater. 2012, 324, 4127–4132. [Google Scholar] [CrossRef]
- Naeem, S.; Baheti, V.; Tunakova, V.; Militky, J.; Karthik, D.; Tomkova, B. Development of porous and electrically conductive activated carbon web for effective EMI shielding applications. Carbon 2017, 111, 439–444. [Google Scholar] [CrossRef]
- Xue, P.; Tao, X.; Kwok, K.W.; Leung, M.; Yu, T. Electromechanical behavior of fibers coated with an electrically conductive polymer. Text. Res. J. 2004, 74, 929–936. [Google Scholar] [CrossRef]
- Heisey, C.; Wightman, J.; Pittman, E.; Kuhn, H. Surface and Adhesion Properties of Polypyrrole-Coated Textiles. Text. Res. J. 1993, 63, 247–256. [Google Scholar] [CrossRef]
- Bowman, D.; Mattes, B.R. Conductive Fiber Prepared from Ultra-High Molecular Weight Polyaniline for Smart Fabric and Interactive Textile Applications. Synth. Metals 2005, 154, 29–32. [Google Scholar] [CrossRef]
- Eichhoff, J.; Hehl, A.; Jockenhoevel, S.; Grie, T. Multidisciplinary Know-How for Smart-Textiles Developers; Kristen, T., Ed.; Woodhead Publishing: Philadelphia, PA, USA, 2013; Chapter 7; pp. 191–226. [Google Scholar]
- Park, J. Functional Fibers, Composites and Textiles Utilizing Photothermal and Joule Heating. Polymers 2020, 12, 189. [Google Scholar] [CrossRef]
- Mamunya, Y.; Davydenko, V.; Pissis, P.; Lebedev, E. Electrical and thermal conductivity of polymers filled with metal powders. Eur. Polym. J. 2002, 38, 1887–1897. [Google Scholar] [CrossRef]
- Smith, W.C. Metallized Fabrics: Techniques and Applications. J. Coat. Fabr. 1988, 17, 242–253. [Google Scholar] [CrossRef]
- Gradenwitz, A. Electric heating fabrics. Sci. Am. 1906, 95, 96–98. [Google Scholar] [CrossRef]
- Safarova, V.; Militký, J. Multifunctional metal composite textile shields against electromagnetic radiation—Effect of various parameters on electromagnetic shielding effectiveness. Polym. Compos. 2017, 38, 309–323. [Google Scholar] [CrossRef]
- Repon, M.R.; Mikučioniené, D. Progress in Flexible Electronic Textile for Heating Application: A Critical Review. Materials 2021, 14, 6540. [Google Scholar] [CrossRef] [PubMed]
- Šafárová, V.; Malachová, K.; Militký, J. Electromechanical analysis of textile structures designed for wearable sensors. In Proceedings of the 16th International Conference on Mechatronics—Mechatronika, Brno, Czech Republic, 3–5 December 2014; pp. 416–422. [Google Scholar] [CrossRef]
- Bai, Y.; Li, H.; Gan, S.; Li, Y.; Liu, H.; Chen, L. Flexible heating fabrics with temperature perception based on fine copper wire and fusible interlining fabrics. Measurement 2018, 122, 192–200. [Google Scholar] [CrossRef]
- Sakr, M.; Liu, S. A comprehensive review on applications of ohmic heating (OH), Renew. Sustain. Energy Rev. 2014, 39, 262–269. [Google Scholar]
- Zhang, M.; Wang, C.; Liang, X.; Yin, Z.; Xia, K.; Wang, H.; Jian, M.; Zhang, Y. Weft-Knitted Fabric for a Highly Stretchable and Low-Voltage Wearable Heater. Adv. Electron. Mater. 2017, 3, 1700193. [Google Scholar] [CrossRef]
- Ge, F.; Yu, W.; Tan, J.; Sun, J.; Yin, Y.; Wang, C. Gradient Response Color-Changing Joule Heating Fabric for Visual Temperature Detection. Adv. Mater. Interfaces 2022, 9, 2201013. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Z.; Zhang, W.; Huang, H.; Zhang, J.; Gan, Y.; He, X.; Wang, B.; Han, Y.; Xia, Y. Glass fiber reinforced graphite/carbon black@PES composite films for high temperature electric heaters. J. Ind. Eng. Chem. 2022, 107, 401–409. [Google Scholar] [CrossRef]
- Joo, H.G.; Jang, Y.H.; Choi, H.S. Electrical contact resistance for a conductive Velcro system. Tribol. Int. 2014, 80, 115–121. [Google Scholar] [CrossRef]
- Banaszczyk, J.; De Mey, G.; Anca, A.; Schwarz-Pfeiffer, A.; Van Langenhove, L. Contact resistance investigation between stainless steel electroconductive yarns. In Proceedings of the 2009 MIXDES-16th International Conference Mixed Design of Integrated Circuits & Systems, Lodz, Poland, 25–27 June 2009; pp. 417–419. [Google Scholar]
- Meloun, M.; Militký, J. Statistical Data Analysis; Woodhead Publisher: New Delhi, India, 2011. [Google Scholar]
- Holm, R. Electric Contacts Theory and Application; Springer: Berlin, Germany, 1981. [Google Scholar]
- Morton, W.E.; Hearle, J.W.S. Physical Properties of Textile Fibres; Heinemann the Textile Institute: Manchester, UK, 1975. [Google Scholar]
- Šafářová, V.; Hes, L.; Militký, J. An approach to electrical resistance measurement eliminating contact resistance problem. In Proceedings of the 2014 International Conference on Applied Electronics, Pilsen, Czech Republic, 9–10 September 2014; pp. 259–262. [Google Scholar] [CrossRef]
- Neruda, M.; Vojtech, L. Heating Ability of Electrically Conductive Textile Materials. In Proceedings of the 16th International Conference on Mechatronics–Mechatronika 2014, Brno, Czech Republic, 3–5 December 2014; pp. 631–634. [Google Scholar] [CrossRef]
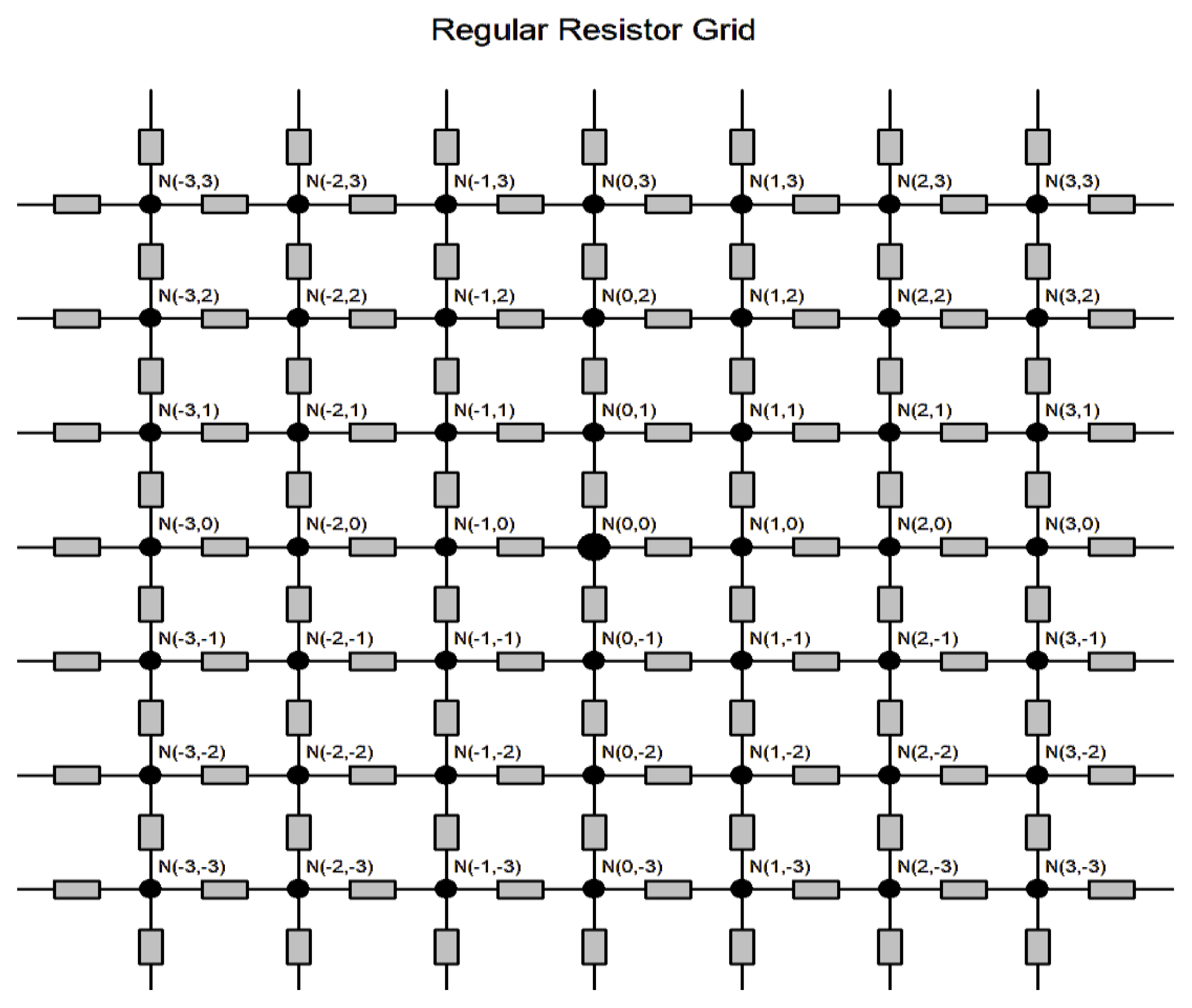
- Spivak-Lavrov, I. About Calculation the Resistance of Two-dimensional Infinite Grid Systems. J. Electr. Electron. 2021, 9, 194–199. [Google Scholar] [CrossRef]
- Asad, J.H.; Sakaji, A.; Hijjawi, R.S.; Khalifeh, J.M. On the resistance of an infinite square network of identical resistors—Theoretical and experimental comparison. Eur. Phys. J. 2006, 52, 365–370. [Google Scholar] [CrossRef][Green Version]
- Atkinson, D.; van Steenwijk, F.J. Infinite resistive lattices. Am. J. Phys. 1999, 67, 486–492. [Google Scholar] [CrossRef]
- Cserti, J. Application of the lattice Green’s function for calculating the resistance of an infinite network of resistors. Am. J. Phys. 2000, 68, 896. [Google Scholar] [CrossRef]
- Newbury, D.E.; Echlin, P.; Joy, D.C.; Lyman, C.E.; Lifshin, E.; Sawyer, L.; Michael, J.R. Scanning Electron Microscopy and X-Ray Microanalysis, 3rd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Vojtech, L.; Neruda, M.; Reichl, T.; Dusek, K.; Megías, C.D.L.T. Surface Area Evaluation of Electrically Conductive Polymer-Based Textiles. Materials 2018, 11, 1931. [Google Scholar] [CrossRef] [PubMed]






| Voltage (V) | Parameter a | Parameter b |
|---|---|---|
| 2.5 | 337 | 0.7907 |
| 5 | 2854 | 0.8139 |
| 7.5 | 4371 | 0.8540 |
| 10 | 4211 | 0.8925 |
| Voltage (V) | Parameter c | Parameter d |
|---|---|---|
| 2.5 | 2.68 | 0.364 |
| 5 | 1.67 | 0.211 |
| 7.5 | 1.70 | 0.158 |
| 10 | 2.36 | 0.113 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Militký, J.; Kupka, K.; Tunáková, V.; Venkataraman, M. Hybrid Fabrics for Ohmic Heating Applications. Polymers 2025, 17, 1339. https://doi.org/10.3390/polym17101339
Militký J, Kupka K, Tunáková V, Venkataraman M. Hybrid Fabrics for Ohmic Heating Applications. Polymers. 2025; 17(10):1339. https://doi.org/10.3390/polym17101339
Chicago/Turabian StyleMilitký, Jiří, Karel Kupka, Veronika Tunáková, and Mohanapriya Venkataraman. 2025. "Hybrid Fabrics for Ohmic Heating Applications" Polymers 17, no. 10: 1339. https://doi.org/10.3390/polym17101339
APA StyleMilitký, J., Kupka, K., Tunáková, V., & Venkataraman, M. (2025). Hybrid Fabrics for Ohmic Heating Applications. Polymers, 17(10), 1339. https://doi.org/10.3390/polym17101339








