Process Optimization of the Morphological Properties of Epoxy Resin Molding Compounds Using Response Surface Design
Abstract
1. Introduction
2. Materials and Methods
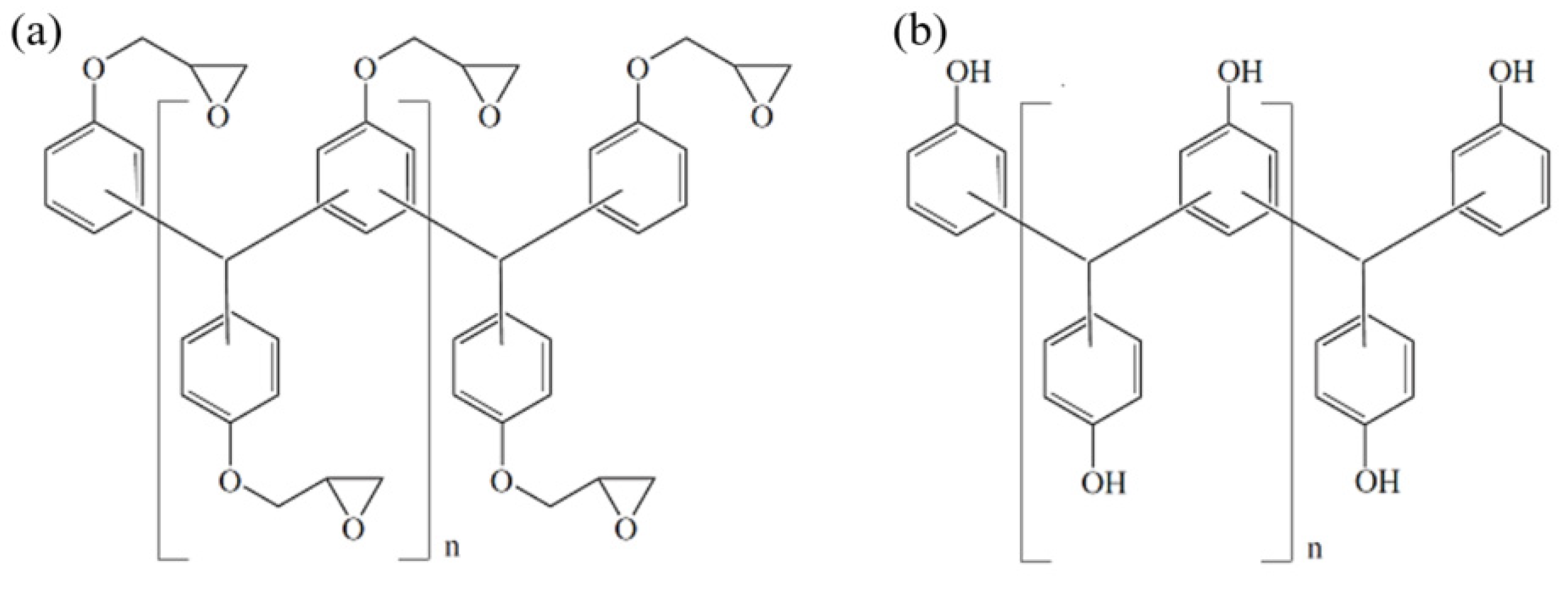
2.1. Materials
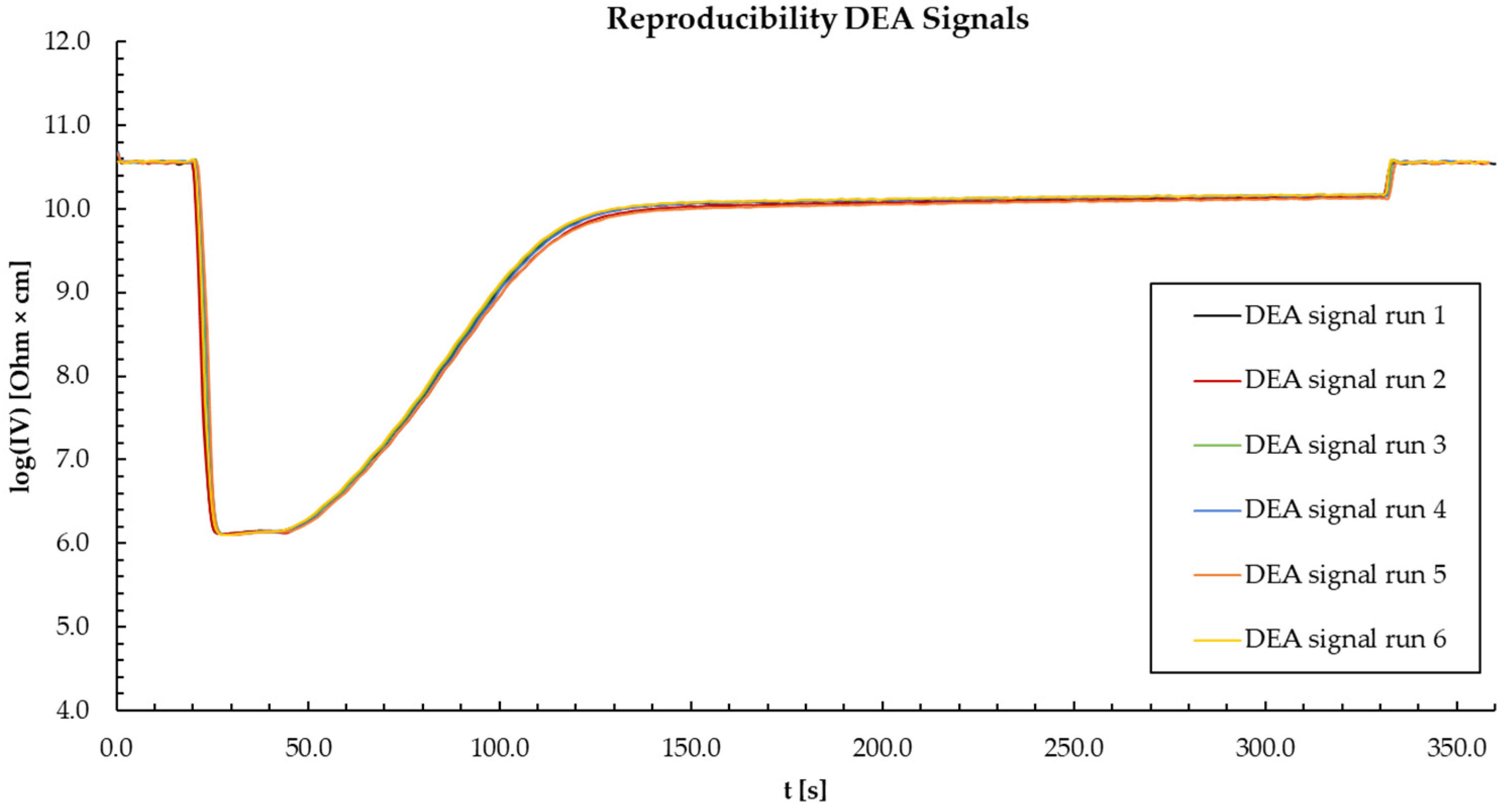
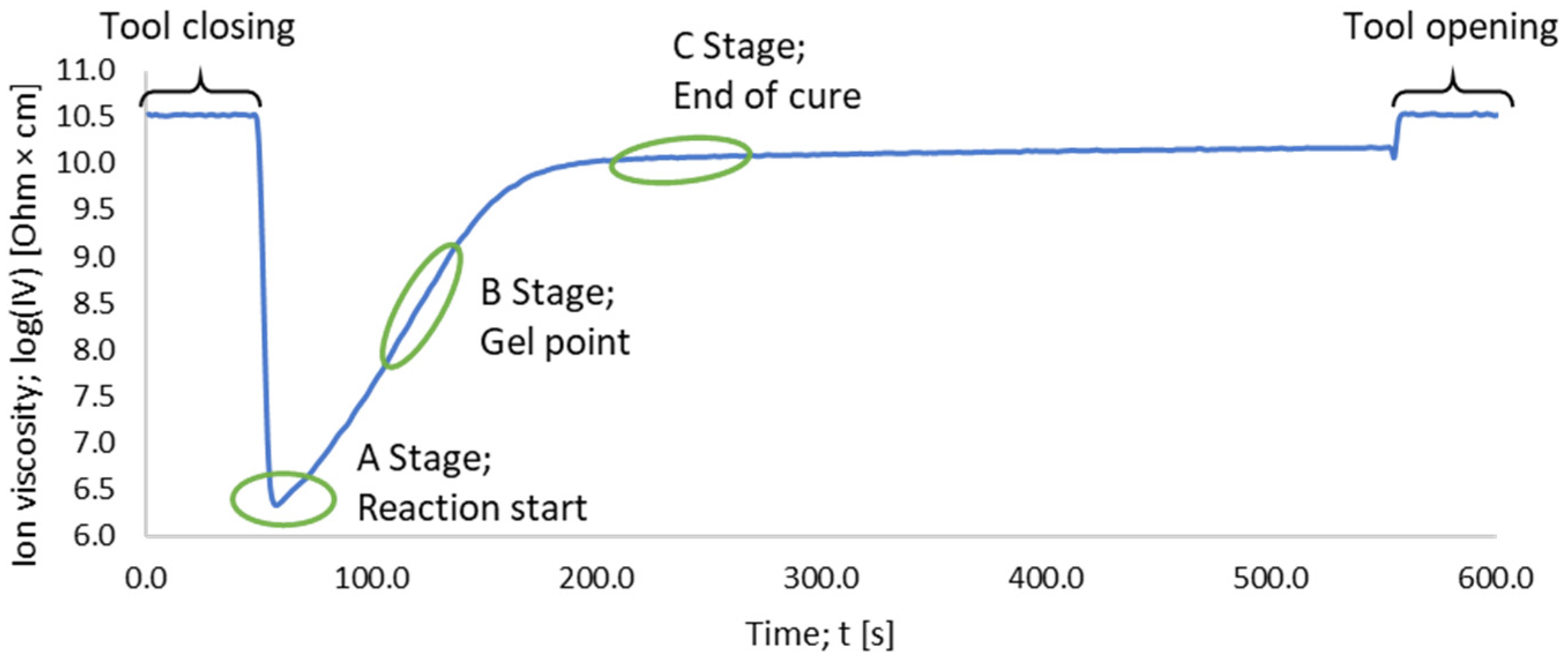
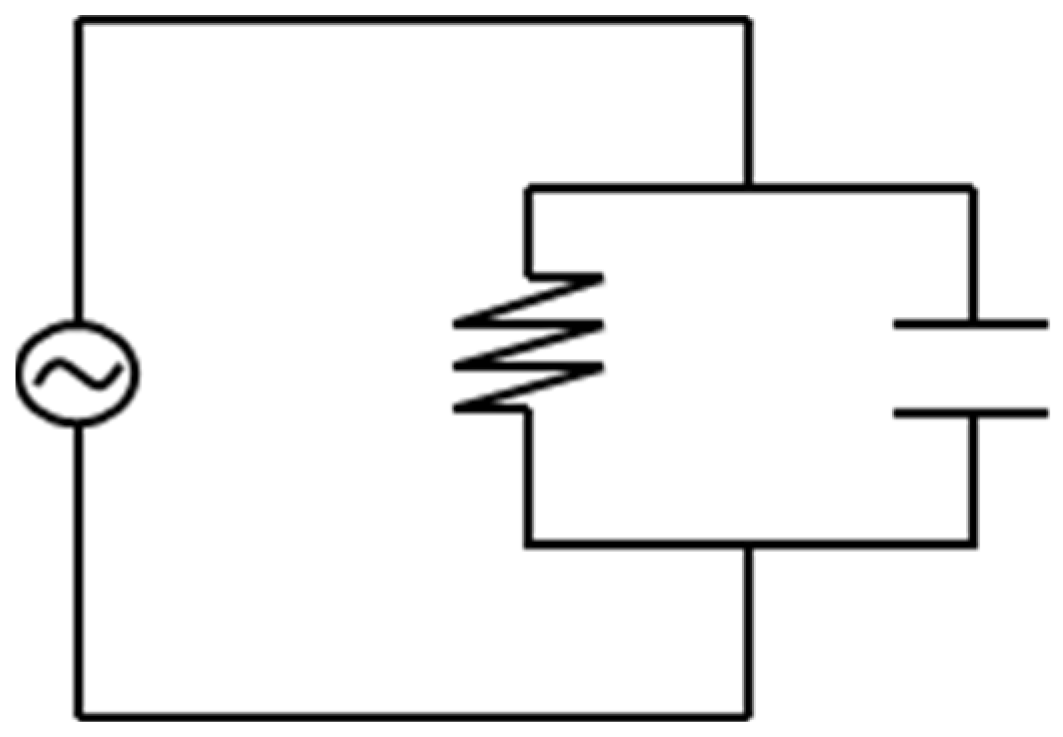
2.2. Dielectric Analysis (DEA) in Transfermold
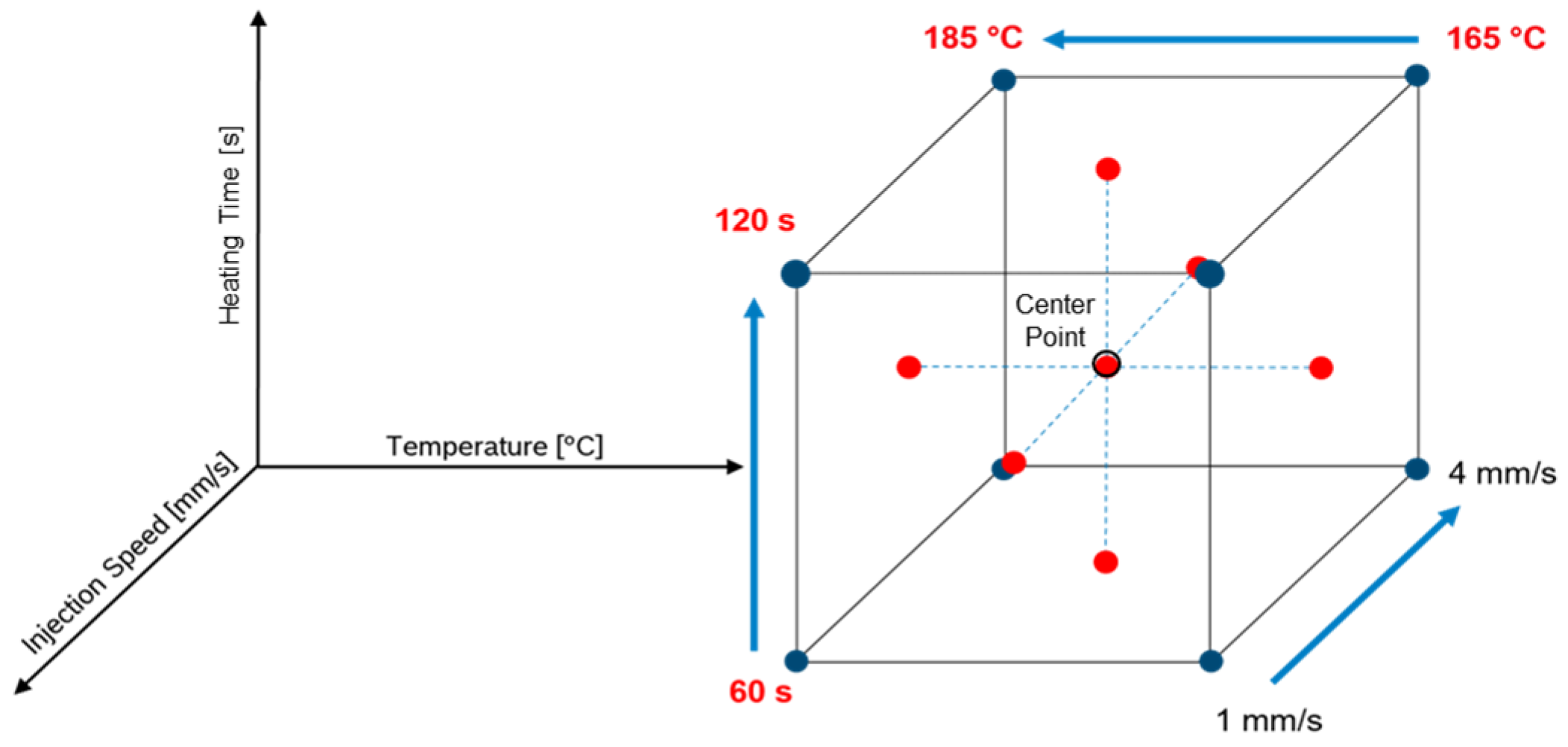
2.3. Design of Experiment—Face-Centered Design
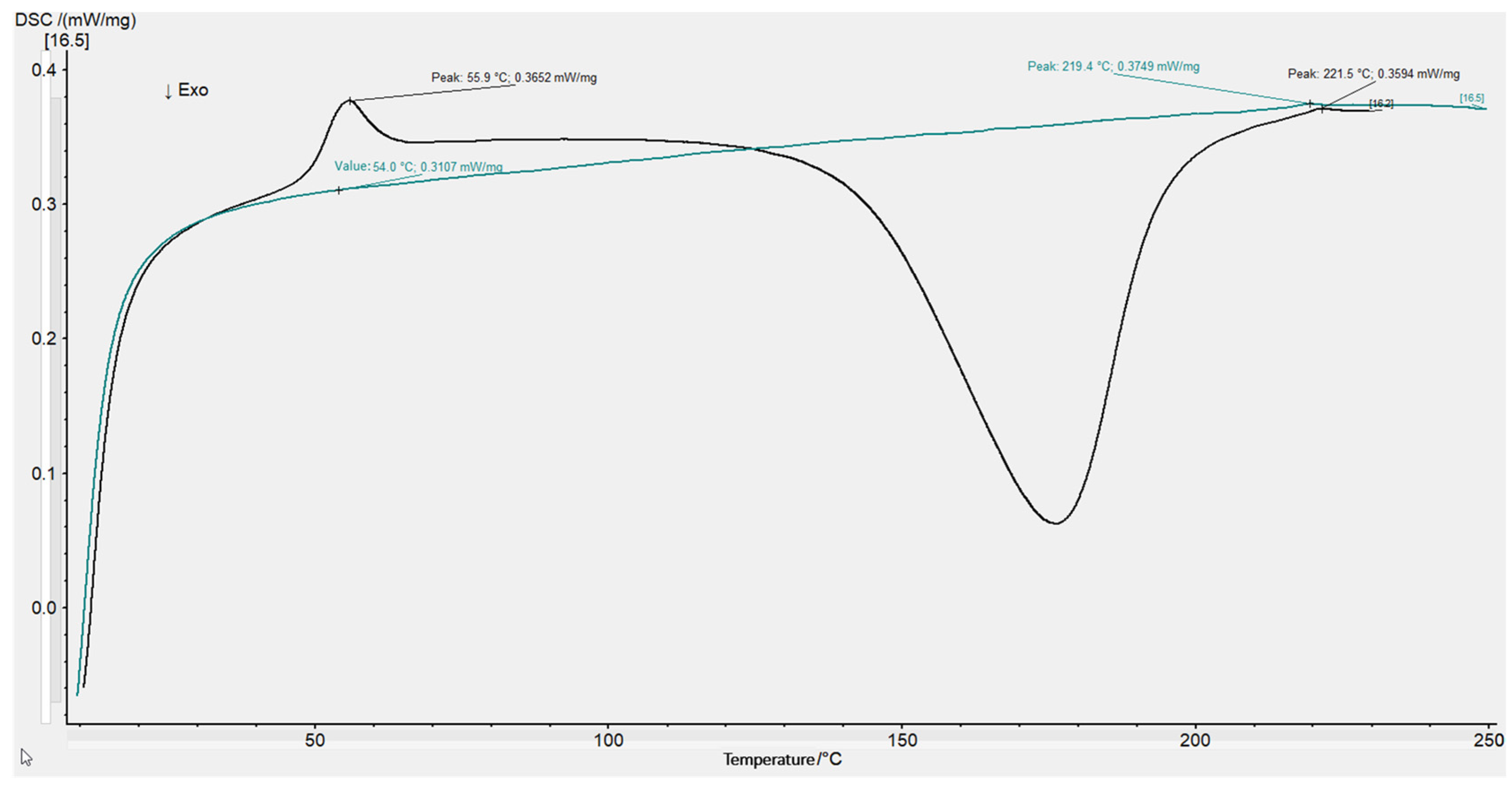
2.4. Residual Enthalpy Measurements via Differential Scanning Calorimetry (DSC)
2.5. Determination of the Glass Transition Temperature via Warpage Analysis
3. Results and Discussion
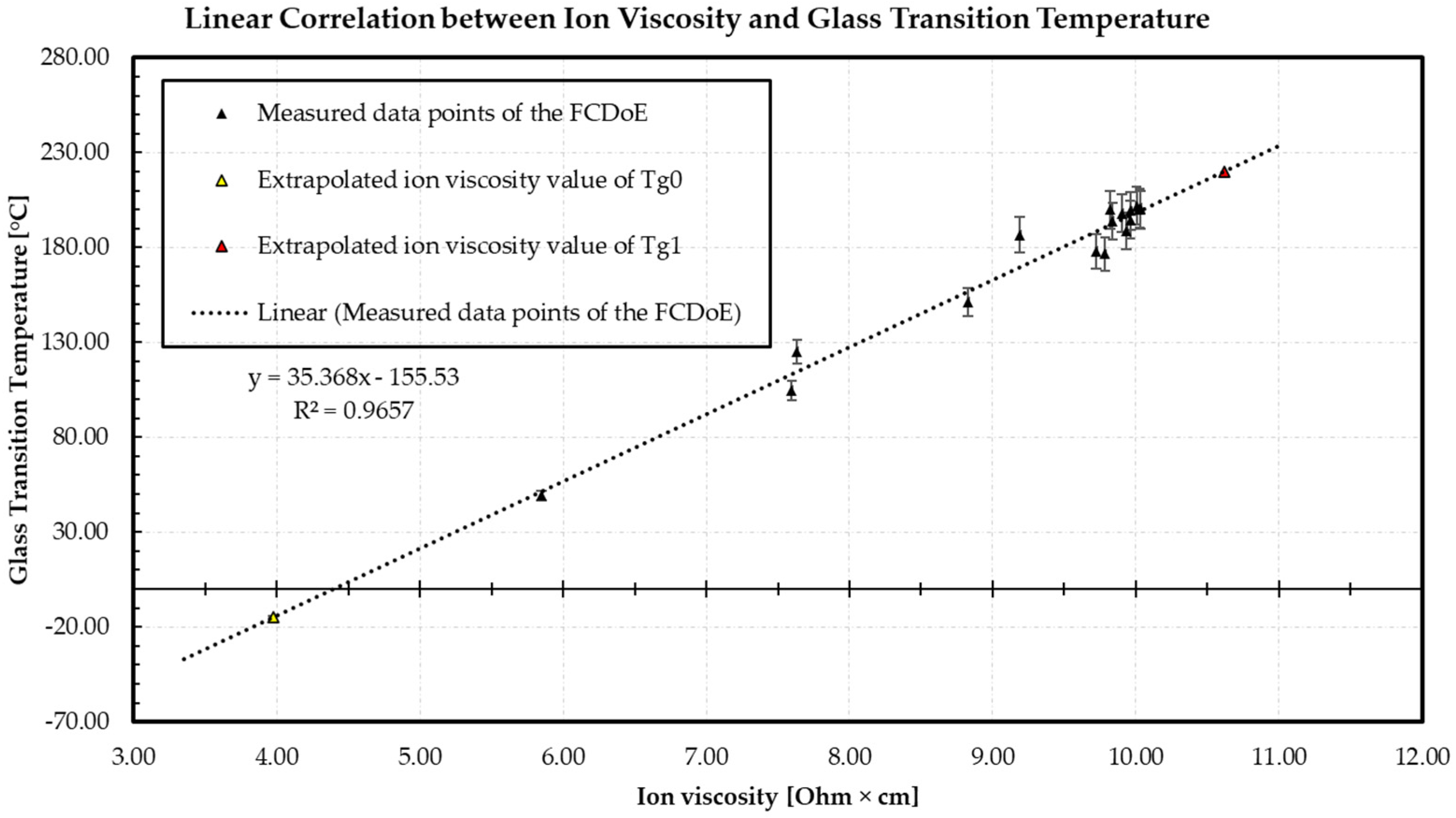
3.1. Correlation between Ion Viscosity and Glass Transition Temperature
3.2. DiBenedetto—Glass Transition Temperature vs. Conversion
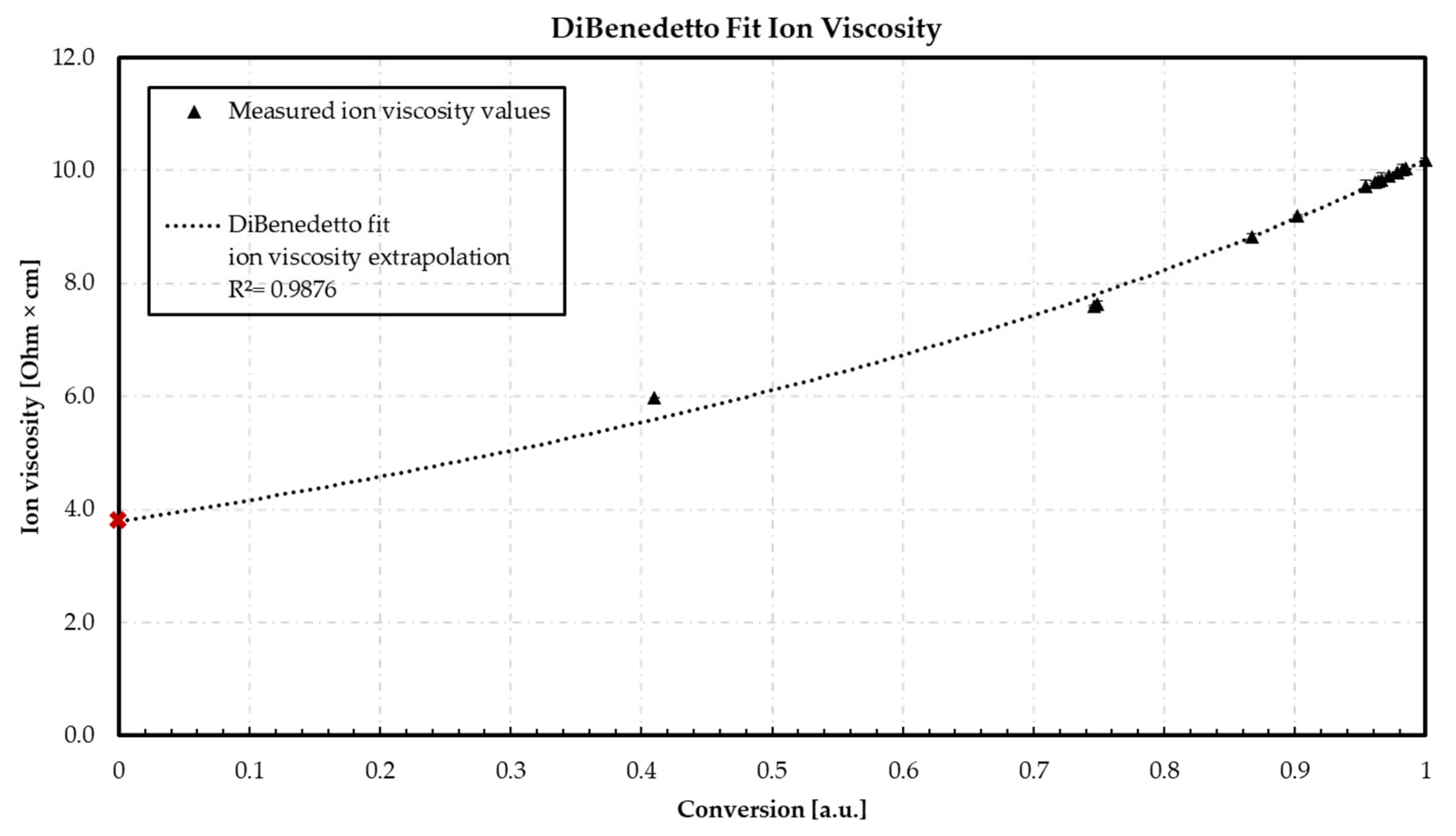
3.3. DiBenedetto—Ion Viscosity vs. Conversion
3.4. Results of the Design of Experiment (DoE)
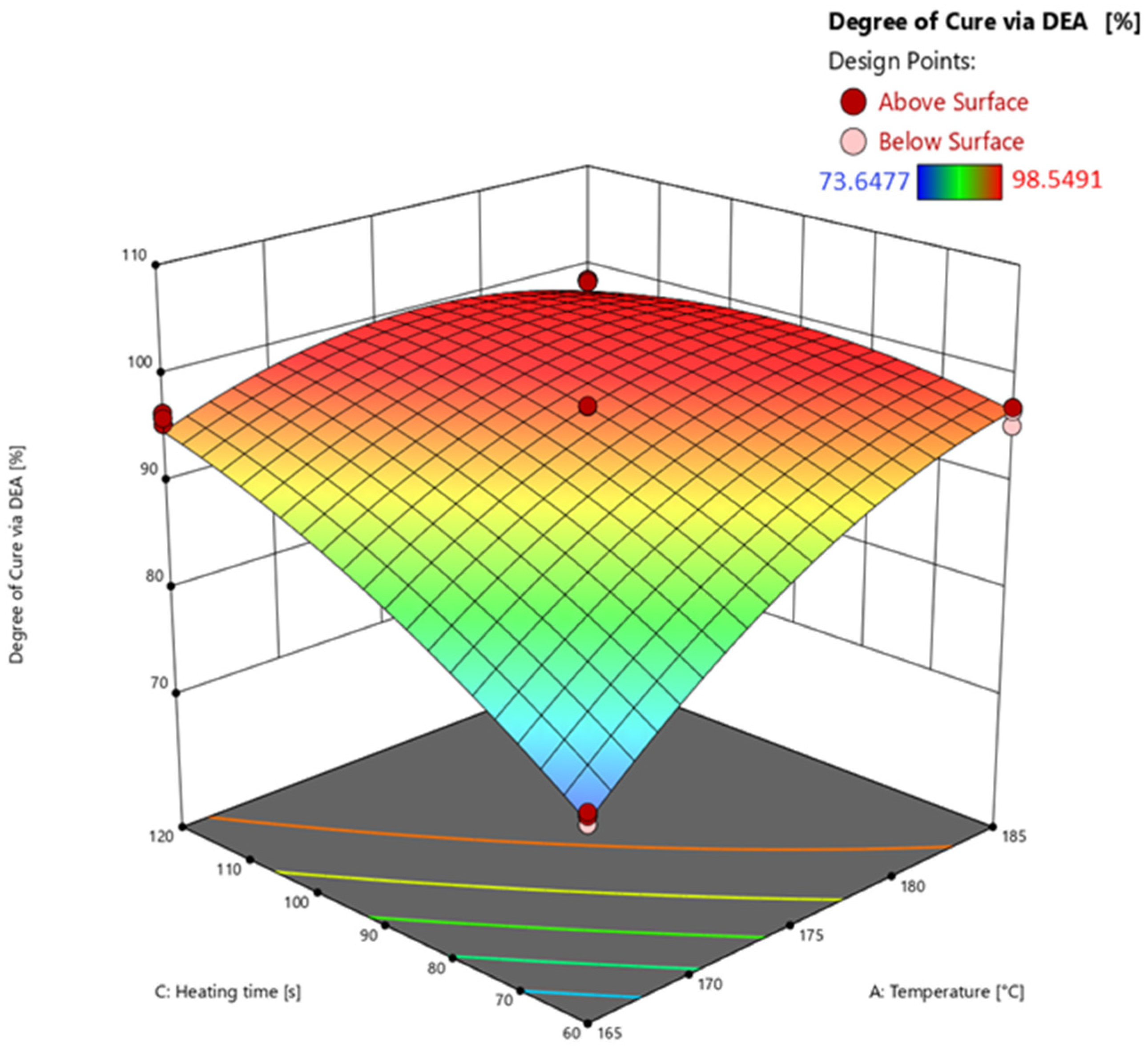
3.4.1. Response Surface of Degree of Cure Calculated via Dielectric Analysis (DEA)
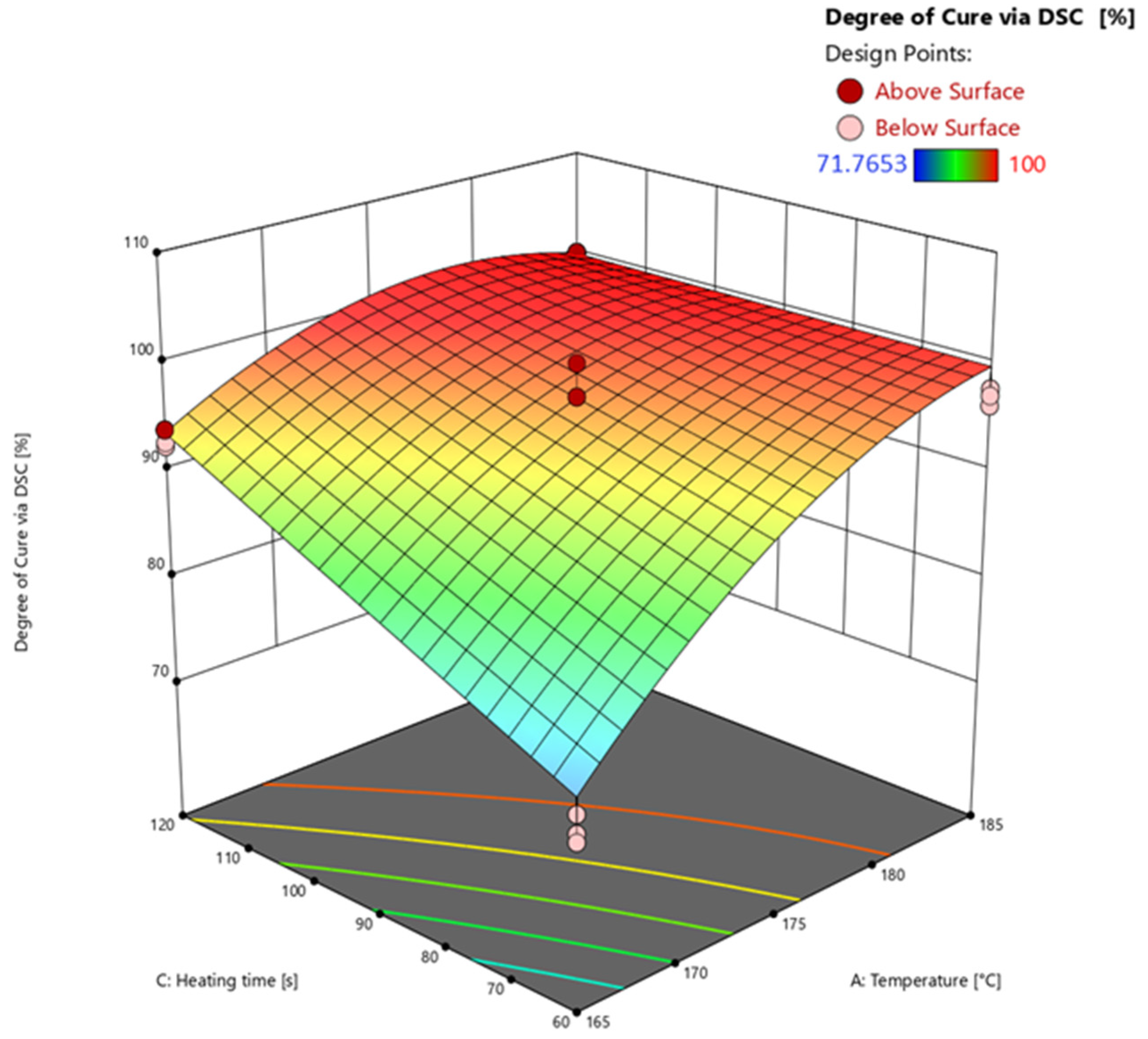
3.4.2. Degree of Cure via Differential Scanning Calorimetry (DSC)
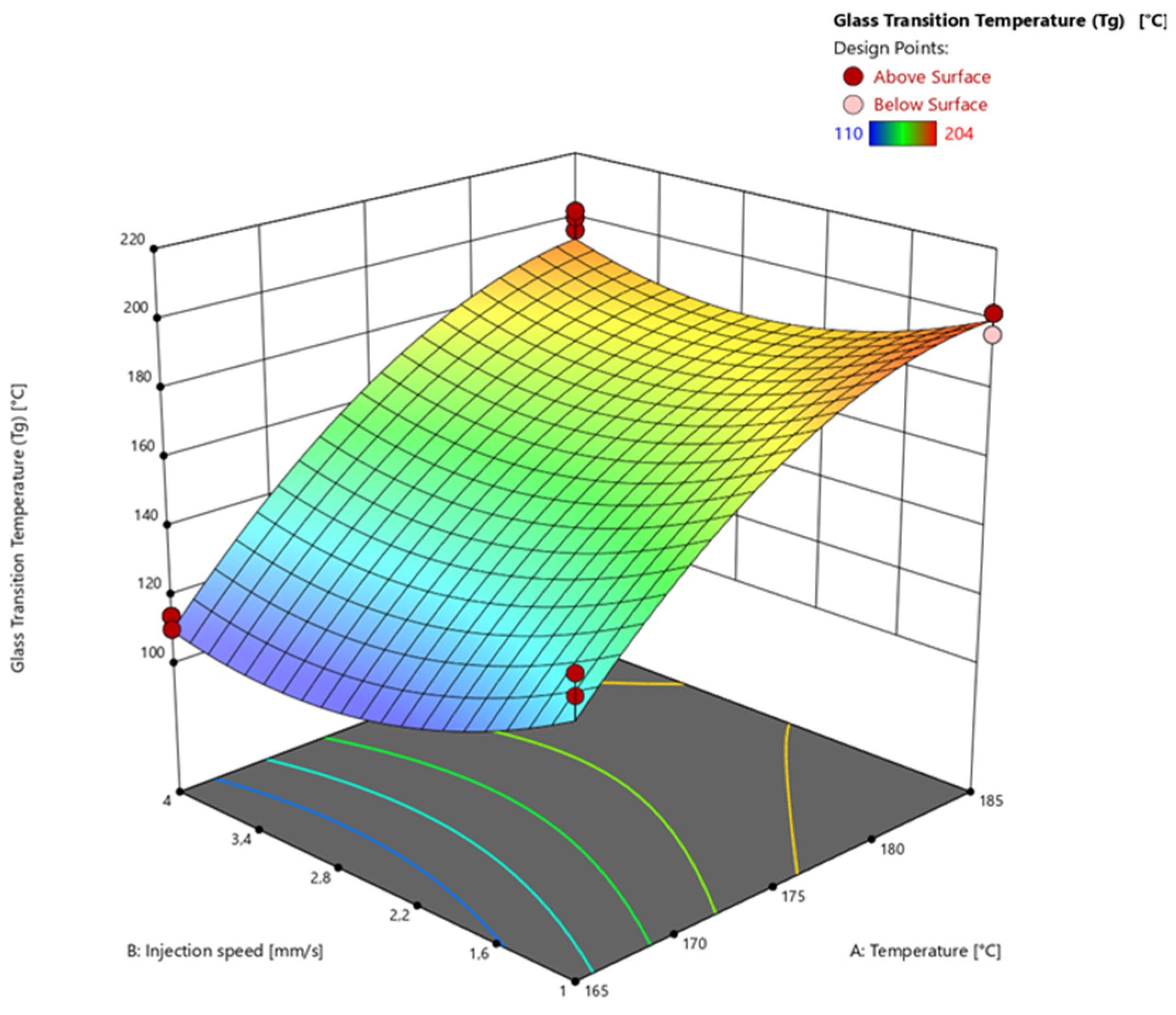
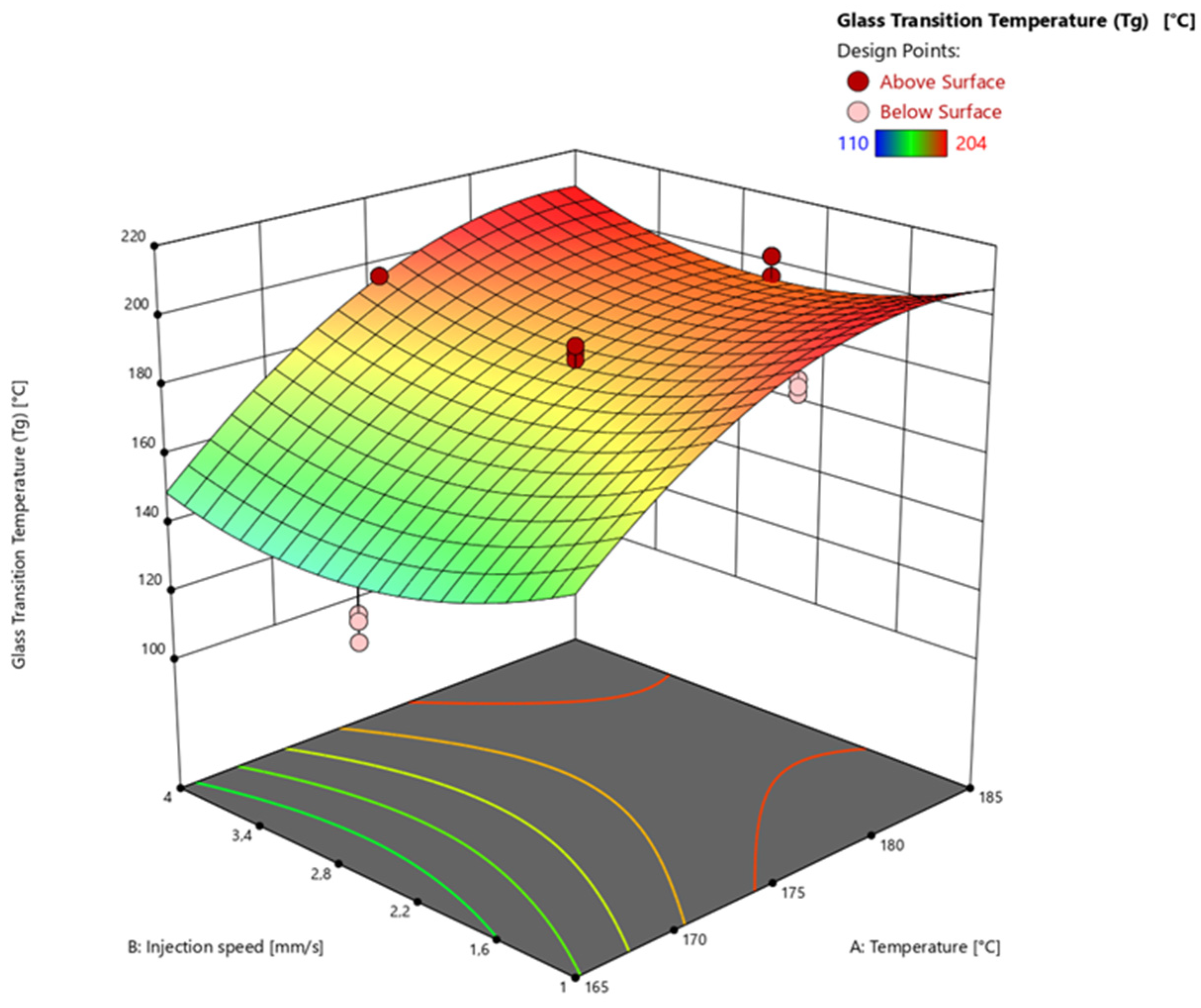
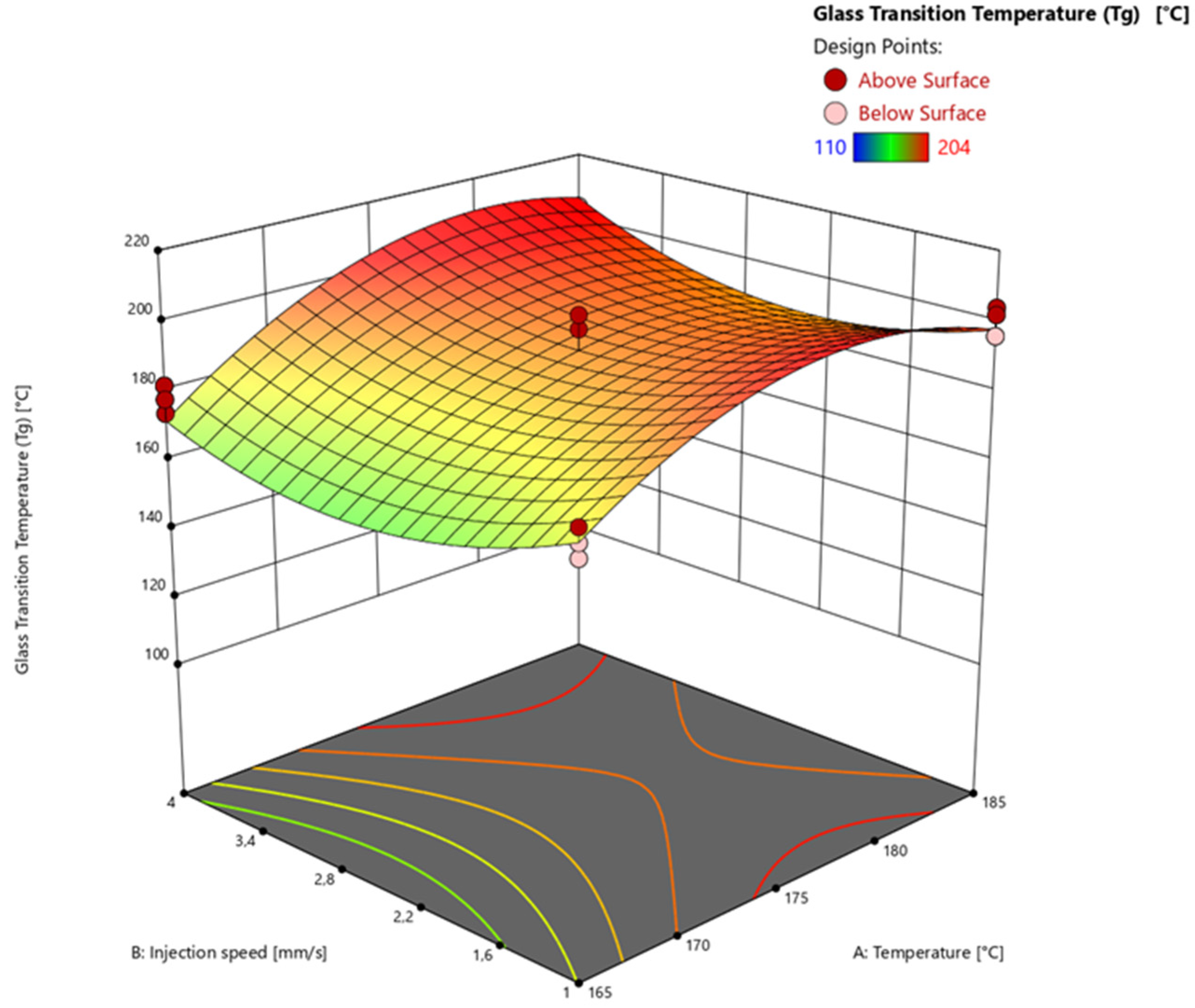
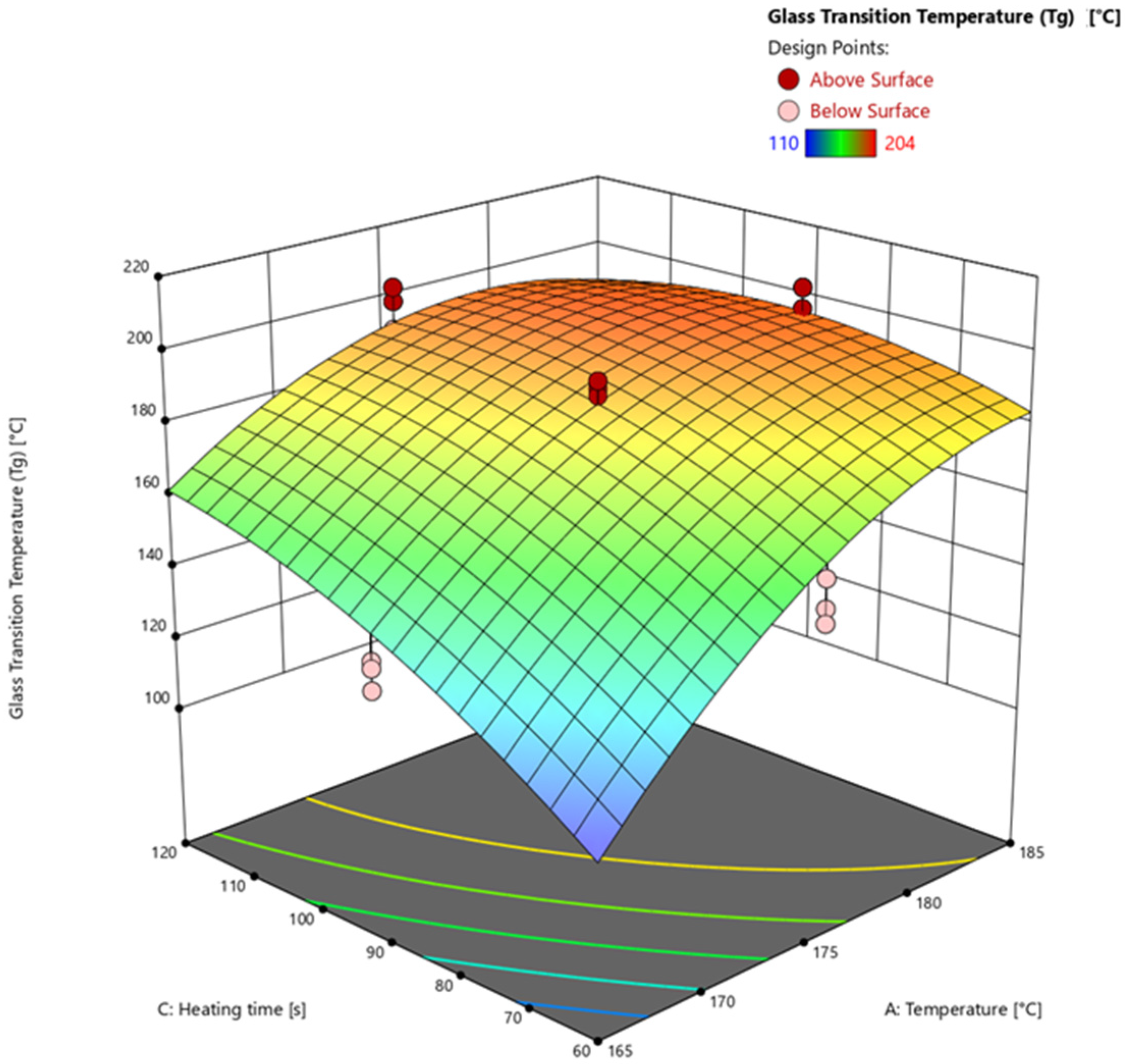
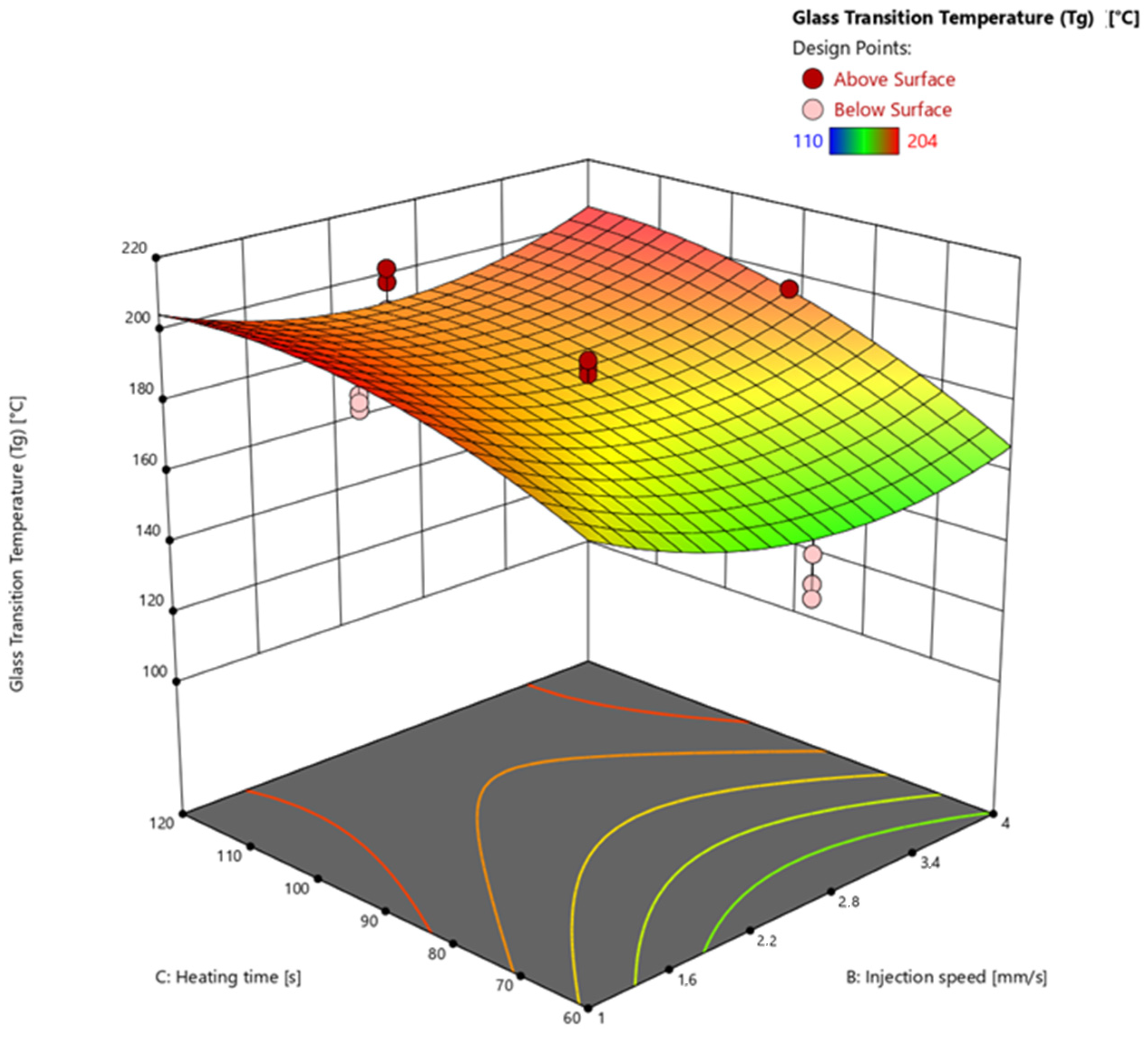
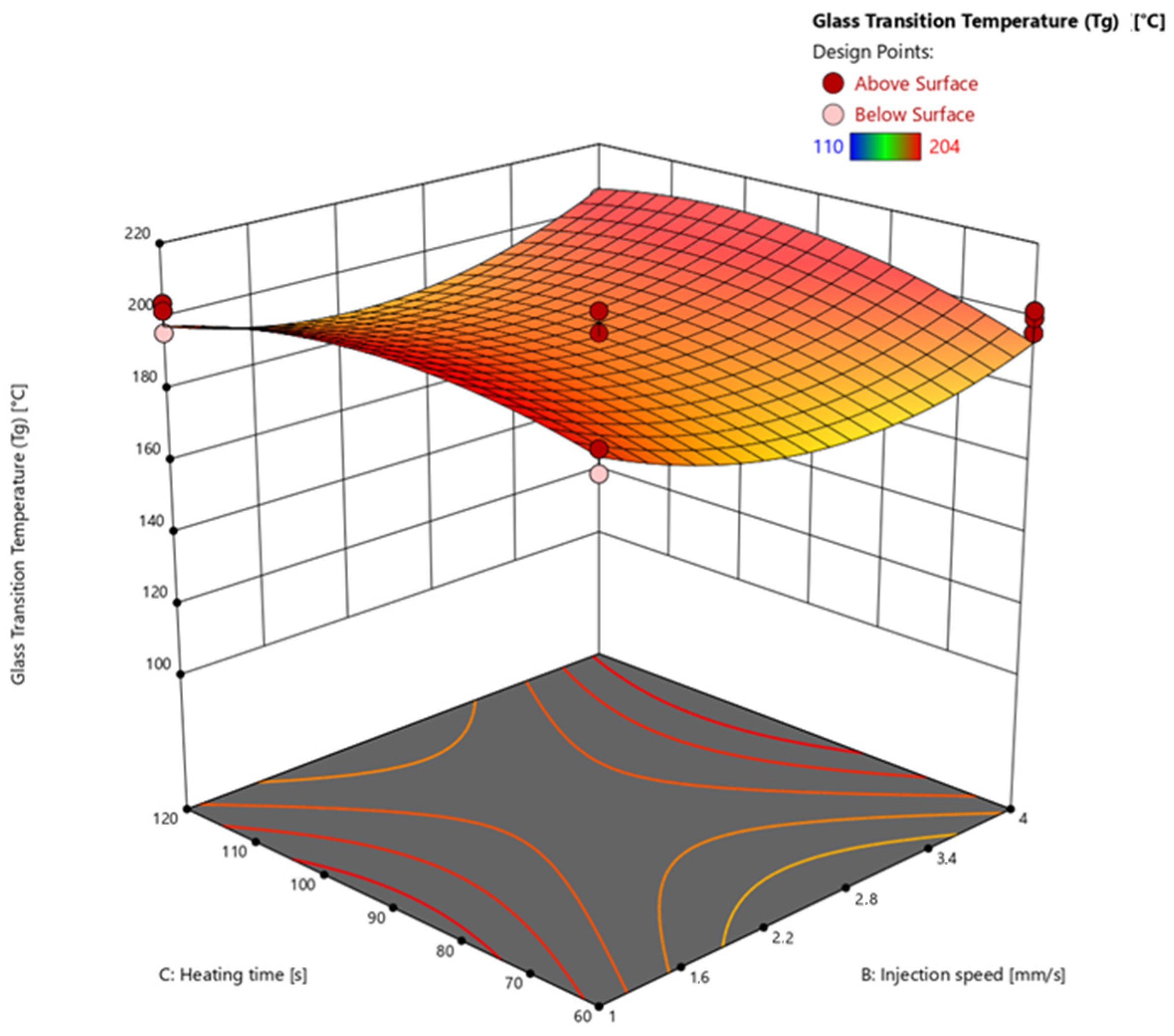
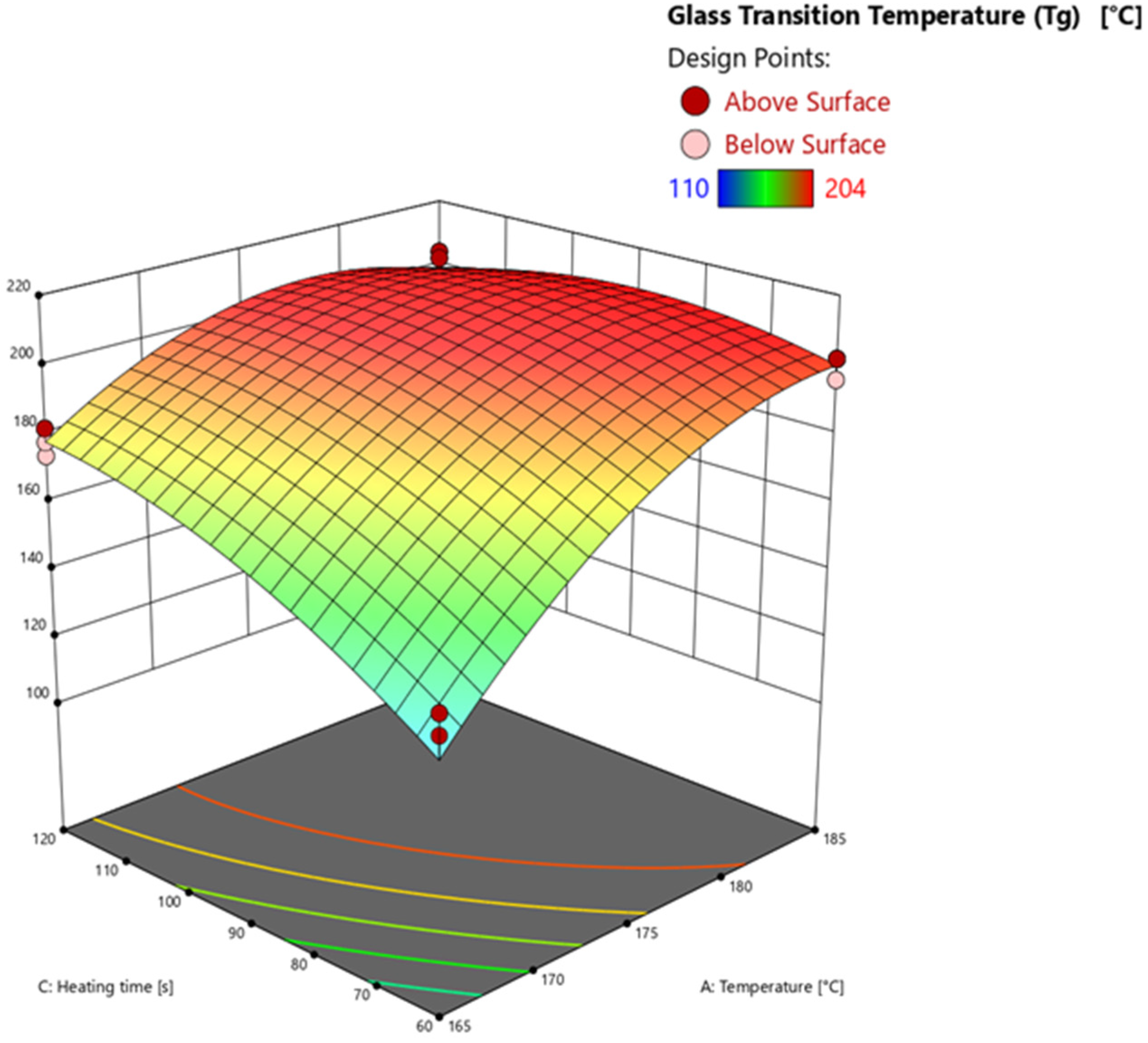
3.4.3. Glass Transition Temperature via Warpage Analyzer
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A






References
- Komori, S.; Sakamoto, Y. Development trend of epoxy molding compound for encapsulating semiconductor chips. In Materials for Advanced Packaging; Springer: Berlin/Heidelberg, Germany, 2009; pp. 339–363. [Google Scholar]
- Kinjo, N.; Ogata, M.; Nishi, K.; Kaneda, A.; Dušek, K. Epoxy molding compounds as encapsulation materials for microelectronic devices. In Speciality Polymers/Polymer Physics; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–48. [Google Scholar]
- Hakim, E.B.; Nguyen, L.T.; Pecht, M.G. Plastic-Encapsulated Microelectronics: Materials, Processes, Quality, Reliability, and Applications; Wiley-Interscience: Hoboken, NJ, USA, 1995. [Google Scholar]
- Ardebili, H.; Zhang, J.; Pecht, M. Encapsulation Technologies for Electronic Applications; William Andrew: Oxford, UK, 2018. [Google Scholar]
- Ardebili, H.; Pecht, M.G. Chapter 3—Encapsulation Process Technology. In Encapsulation Technologies for Electronic Applications; Ardebili, H., Pecht, M.G., Eds.; William Andrew Publishing: Oxford, UK, 2009; pp. 129–179. [Google Scholar]
- Tummala, R.R.; Rymaszewski, E.J.; Klopfenstein, A.G. Microelectronics Packaging Handbook: Technology Drivers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kandelbauer, A. Processing and process control. In Handbook of Thermoset Plastics; Elsevier: Amsterdam, The Netherlands, 2022; pp. 1045–1070. [Google Scholar]
- Tong, K.; Kwong, C.; Ip, K. Optimization of process conditions for the transfer molding of electronic packages. J. Mater. Process. Technol. 2003, 138, 361–365. [Google Scholar] [CrossRef]
- Yang, Y.; Plovie, B.; Chiesura, G.; Vervust, T.; Daelemans, L.; Mogosanu, D.-E.; Wuytens, P.; De Clerck, K.; Vanfleteren, J. Fully Integrated Flexible Dielectric Monitoring Sensor System for Real-Time In Situ Prediction of the Degree of Cure and Glass Transition Temperature of an Epoxy Resin. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Lee, C.-L.; Wei, K.-H. Curing kinetics and viscosity change of a two-part epoxy resin during mold filling in resin-transfer molding process. J. Appl. Polym. Sci. 2000, 77, 2139–2148. [Google Scholar] [CrossRef]
- Soares, L.L.; Amico, S.C.; Isoldi, L.A.; Souza, J.A. Modeling of the resin transfer molding process including viscosity dependence with time and temperature. Polym. Compos. 2021, 42, 2795–2807. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, X.; Lu, N.; Gao, F. Injection Molding Process Control, Monitoring, and Optimization; Carl Hanser Verlag GmbH: Munich, Germany, 2016. [Google Scholar]
- Lechner, M.D.; Gehrke, K.; Nordmeier, E.H. Makromolekulare Chemie: Ein Lehrbuch für Chemiker, Physiker, Materialwissenschaftler und Verfahrenstechniker, 4. Überarbeitete und Erweiterte Auflage; Birkhäuser Verlag: Basel, Switzerland, 2003. [Google Scholar]
- Weiss, S.; Seidl, R.; Kessler, W.; Kessler, R.W.; Zikulnig-Rusch, E.M.; Kandelbauer, A. Unravelling the phases of melamine formaldehyde resin cure by infrared spectroscopy (FTIR) and multivariate curve resolution (MCR). Polymers 2020, 12, 2569. [Google Scholar] [CrossRef] [PubMed]
- Kessler, W. Multivariate Datenanalyse: Für die Pharma, Bio-und Prozessanalytik; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Kaya, B. Concept Development and Implementation of Online Monitoring Methods in the Transfer Molding Process for Electronic Packages. Master’s Thesis, Technische Universität Berlin, Berlin, Germany, 2018. [Google Scholar]
- Demleitner, M.; Sanchez-Vazquez, S.A.; Raps, D.; Bakis, G.; Pflock, T.; Chaloupka, A.; Schmölzer, S.; Altstädt, V. Dielectric analysis monitoring of thermoset curing with ionic liquids: From modeling to the prediction in the resin transfer molding process. Polym. Compos. 2019, 40, 4500–4509. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Nasseri, L.; Rosenfeld, C.; Solt-Rindler, P.; Mitter, R.; Moser, J.; Kandelbauer, A.; Konnerth, J.; Van Herwijnen, H.W. Comparison between cure kinetics by means of dynamic rheology and DSC of formaldehyde-based wood adhesives. J. Adhes. 2024, 1–22. [Google Scholar] [CrossRef]
- Nasseri, L.; Rosenfeld, C.; Solt, P.; Mihalic, M.; Kandelbauer, A.; Konnerth, J.; Van Herwijnen, H.W. Determination of the gel point of formaldehyde-based wood adhesives by using a multiwave technique. ACS Appl. Polym. Mater. 2023, 5, 6354–6363. [Google Scholar] [CrossRef]
- Mahendran, A.R.; Wuzella, G.; Kandelbauer, A. Thermal characterization of kraft lignin phenol-formaldehyde resin for paper impregnation. J. Adhes. Sci. Technol. 2010, 24, 1553–1565. [Google Scholar] [CrossRef]
- Bilyeu, B.; Brostow, W.; Menard, K.P. Epoxy thermosets and their applications II. Thermal analysis. J. Mater. Educ. 2000, 22, 107–130. [Google Scholar]
- Kamal, M.R.; Sourour, S. Kinetics and thermal characterization of thermoset cure. Polym. Eng. Sci. 1973, 13, 59–64. [Google Scholar] [CrossRef]
- Kim, W.G.; Lee, J.Y. Contributions of the network structure to the cure kinetics of epoxy resin systems according to the change of hardeners. Polymer 2002, 43, 5713–5722. [Google Scholar] [CrossRef]
- Lee, H.L. The Handbook of Dielectric Analysis and Cure Monitoring; Lambient Technologies LLC: Cambridge, MA, USA, 2017. [Google Scholar]
- Weiss, S.; Seidl, R.; Kessler, W.; Kessler, R.W.; Zikulnig-Rusch, E.M.; Kandelbauer, A. Multivariate Curve Resolution (MCR) of real-time infrared spectra for analyzing the curing behavior of solid MF thermosetting resin. Int. J. Adhes. Adhes. 2021, 110, 102956. [Google Scholar] [CrossRef]
- Achilias, D.S.; Karabela, M.M.; Varkopoulou, E.A.; Sideridou, I.D. Cure Kinetics Study of Two Epoxy Systems with Fourier Tranform Infrared Spectroscopy (FTIR) and Differential Scanning Calorimetry (DSC). J. Macromol. Sci. Part A 2012, 49, 630–638. [Google Scholar] [CrossRef]
- Alig, I.; Fischer, D.; Lellinger, D.; Steinhoff, B. Combination of NIR, Raman, ultrasonic and dielectric spectroscopy for in-line monitoring of the extrusion process. Macromol. Symp. 2005, 230, 51–58. [Google Scholar] [CrossRef]
- Hardis, R.; Jessop, J.L.; Peters, F.E.; Kessler, M.R. Cure kinetics characterization and monitoring of an epoxy resin using DSC, Raman spectroscopy, and DEA. Compos. Part Appl. Sci. Manuf. 2013, 49, 100–108. [Google Scholar] [CrossRef]
- Weiss, S.; Urdl, K.; Mayer, H.A.; Zikulnig-Rusch, E.M.; Kandelbauer, A. IR spectroscopy: Suitable method for determination of curing degree and crosslinking type in melamine–formaldehyde resins. J. Appl. Polym. Sci. 2019, 136, 47691. [Google Scholar] [CrossRef]
- Franieck, E.; Fleischmann, M.; Hölck, O.; Schneider-Ramelow, M. Inline cure monitoring of epoxy resin by dielectric analysis. In Proceedings of the 2021 23rd European Microelectronics and Packaging Conference Exhibition (EMPC), Online, 13–16 September 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Franieck, E.; Fleischmann, M.; Hölck, O.; Kutuzova, L.; Kandelbauer, A. Cure Kinetics Modeling of a High Glass Transition Temperature Epoxy Molding Compound (EMC) Based on Inline Dielectric Analysis. Polymers 2021, 13, 1734. [Google Scholar] [CrossRef]
- Vassilikou-Dova, A.; Kalogeras, I.M. Dielectric analysis (DEA). In Thermal Analysis of Polymers: Fundamentals and Applications; Wiley: Hoboken, NJ, USA, 2009; pp. 497–613. [Google Scholar]
- Shigue, C.Y.; Dos Santos, R.G.S.; De Abreu, M.M.S.P.; Baldan, C.A.; Robin, A.L.M.; Ruppert-Filho, E. Dielectric Thermal Analysis as a Tool for Quantitative Evaluation of the Viscosity and the Kinetics of Epoxy Resin Cure. IEEE Trans. Appl. Supercond. 2006, 16, 1786–1789. [Google Scholar] [CrossRef]
- Pascault, J.-P.; Williams, R.J.J. Glass transition temperature versus conversion relationships for thermosetting polymers. J. Polym. Sci. Part B Polym. Phys. 1990, 28, 85–95. [Google Scholar] [CrossRef]
- Vogelwaid, J.; Hampel, F.; Bayer, M.; Walz, D.M.; Kutuzova, L.; Kandelbauer, A.; Lorenz, G.; Jacob, T. In Situ Monitoring of the Curing of Highly Filled Epoxy Molding Compounds: The Influence of Reaction Type and Silica Content on Cure Kinetic Models. Polymers 2024, 16, 1056. [Google Scholar] [CrossRef]
- DiBenedetto, A.T. Prediction of the glass transition temperature of polymers: A model based on the principle of corresponding states. J. Polym. Sci. Part B Polym. Phys. 1987, 25, 1949–1969. [Google Scholar] [CrossRef]
- Stutz, H.; Illers, K.-H.; Mertes, J. A generalized theory for the glass transition temperature of crosslinked and uncrosslinked polymers. J. Polym. Sci. Part B Polym. Phys. 1990, 28, 1483–1498. [Google Scholar] [CrossRef]
- Bellucci, F.; Valentino, M.; Monetta, T.; Nicodemo, L.; Kenny, J.; Nicolais, L.; Mijovic, J. Impedance spectroscopy of reactive polymers. 1. J. Polym. Sci. Part B Polym. Phys. 1994, 32, 2519–2527. [Google Scholar] [CrossRef]
- Gotro, J. Dielectric Cure Monitoring Part Six: Cure Index and Degree of Cure. Polymer Innovation Blog. 5 June 2019. Available online: https://polymerinnovationblog.com/dielectric-cure-monitoring-part-six-cure-index-and-degree-of-cure/ (accessed on 24 February 2024).
- Bidstrup, S.A.; Sheppard, N.F., Jr.; Senturia, S.D. Dielectric analysis of the cure of thermosetting epoxy/amine systems. Polym. Eng. Sci. 1989, 29, 325–328. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of Thermal Degradation of Char-Forming Plastics from Thermogravimetry. Application to a Phenolic Plastic. J. Polym. Sci. Part C Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Vyazovkin, S. Isoconversional Kinetics of Thermally Stimulated Processes; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]




| Factor 1 | Factor 2 | Factor 3 | Response 1 | Response 2 | Response 3 | |
|---|---|---|---|---|---|---|
| Run | A: Temperature [°C] | B: Injection speed [mm/s] | C: Heating time [s] | Degree of Cure via DEA [%] | Degree of Cure via DSC [%] | Glass Transition Temperature (Tg) [°C] |
| 1 | 165 | 1 | 60 | 75.08 | 74.21 | 144 |
| 2 | 165 | 1 | 60 | 75.43 | 72.51 | 138 |
| 3 | 165 | 1 | 60 | 74.34 | 71.77 | 144 |
| 4 | 185 | 1 | 60 | 95.38 | 97.67 | 202 |
| 5 | 185 | 1 | 60 | 97.08 | 96.12 | 202 |
| 6 | 185 | 1 | 60 | 96.75 | 97.04 | 196 |
| 7 | 165 | 4 | 60 | 74.22 | 74.99 | 114 |
| 8 | 165 | 4 | 60 | 73.65 | 72.31 | 114 |
| 9 | 165 | 4 | 60 | 75.83 | 78.27 | 110 |
| 10 | 185 | 4 | 60 | 97.87 | 100.00 | 196 |
| 11 | 185 | 4 | 60 | 97.47 | 100.00 | 200 |
| 12 | 185 | 4 | 60 | 98.11 | 100.00 | 202 |
| 13 | 165 | 1 | 120 | 95.56 | 92.37 | 174 |
| 14 | 165 | 1 | 120 | 96.56 | 92.72 | 182 |
| 15 | 165 | 1 | 120 | 96.11 | 93.90 | 178 |
| 16 | 185 | 1 | 120 | 98.55 | 100.00 | 204 |
| 17 | 185 | 1 | 120 | 98.53 | 100.00 | 196 |
| 18 | 185 | 1 | 120 | 98.30 | 100.00 | 202 |
| 19 | 165 | 4 | 120 | 95.34 | 93.58 | 174 |
| 20 | 165 | 4 | 120 | 95.58 | 93.25 | 182 |
| 21 | 165 | 4 | 120 | 95.40 | 93.47 | 178 |
| 22 | 185 | 4 | 120 | 98.29 | 100.00 | 200 |
| 23 | 185 | 4 | 120 | 98.34 | 100.00 | 202 |
| 24 | 185 | 4 | 120 | 98.06 | 100.00 | 204 |
| 25 | 175 | 2.5 | 90 | 97.55 | 96.67 | 190 |
| 26 | 175 | 2.5 | 90 | 97.69 | 97.64 | 188 |
| 27 | 175 | 2.5 | 90 | 97.66 | 97.49 | 192 |
| 28 | 175 | 2.5 | 90 | 97.55 | 94.83 | 192 |
| 29 | 175 | 2.5 | 90 | 97.18 | 96.83 | 182 |
| 30 | 165 | 2.5 | 90 | 86.69 | 86.54 | 136 |
| 31 | 165 | 2.5 | 90 | 86.83 | 87.09 | 128 |
| 32 | 165 | 2.5 | 90 | 86.49 | 86.86 | 134 |
| 33 | 185 | 2.5 | 90 | 98.55 | 100.00 | 202 |
| 34 | 185 | 2.5 | 90 | 98.38 | 100.00 | 196 |
| 35 | 185 | 2.5 | 90 | 98.54 | 100.00 | 202 |
| 36 | 175 | 1 | 90 | 97.23 | 96.92 | 196 |
| 37 | 175 | 1 | 90 | 97.17 | 100.00 | 200 |
| 38 | 175 | 1 | 90 | 97.29 | 96.94 | 198 |
| 39 | 175 | 4 | 90 | 96.42 | 100.00 | 190 |
| 40 | 175 | 4 | 90 | 96.56 | 96.96 | 196 |
| 41 | 175 | 4 | 90 | 96.77 | 96.48 | 196 |
| 42 | 175 | 2.5 | 60 | 91.20 | 94.91 | 150 |
| 43 | 175 | 2.5 | 60 | 88.99 | 94.28 | 146 |
| 44 | 175 | 2.5 | 60 | 90.43 | 95.43 | 158 |
| 45 | 175 | 2.5 | 120 | 97.72 | 98.54 | 198 |
| 46 | 175 | 2.5 | 120 | 97.76 | 98.45 | 202 |
| 47 | 175 | 2.5 | 120 | 97.88 | 98.70 | 190 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Block | 42.72 | 1 | 42.72 | ||
| Model | 2748.42 | 5 | 549.68 | 741.31 | <0.0001 |
| A-Temperature | 1141.70 | 1 | 1141.70 | 1539.71 | <0.0001 |
| C-Heating time | 812.67 | 1 | 812.67 | 1095.98 | <0.0001 |
| AC | 586.13 | 1 | 586.13 | 790.46 | <0.0001 |
| A2 | 111.87 | 1 | 111.87 | 150.87 | <0.0001 |
| C2 | 44.59 | 1 | 44.59 | 60.13 | <0.0001 |
| Residual | 29.66 | 40 | 0.7415 | ||
| Lack of Fit | 21.22 | 8 | 2.65 | 10.05 | <0.0001 |
| Pure Error | 8.44 | 32 | 0.2639 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Block | 149.84 | 1 | 149.84 | ||
| Model | 2969.13 | 4 | 742.28 | 226.44 | <0.0001 |
| A-Temperature | 1717.32 | 1 | 1717.32 | 523.87 | <0.0001 |
| C-Heating time | 611.78 | 1 | 611.78 | 186.63 | <0.0001 |
| AC | 468.66 | 1 | 468.66 | 142.97 | <0.0001 |
| A2 | 171.37 | 1 | 171.37 | 52.28 | <0.0001 |
| Residual | 134.40 | 41 | 3.28 | ||
| Lack of Fit | 91.43 | 9 | 10.16 | 7.57 | <0.0001 |
| Pure Error | 42.97 | 32 | 1.34 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Block | 0.0862 | 1 | 0.0862 | ||
| Model | 34,913.18 | 9 | 3879.24 | 83.02 | <0.0001 |
| A-Temperature | 20,072.53 | 1 | 20,072.53 | 429.58 | <0.0001 |
| B-Injection speed | 320.13 | 1 | 320.13 | 6.85 | 0.0129 |
| C-Heating time | 6750.00 | 1 | 6750.00 | 144.46 | <0.0001 |
| AB | 337.50 | 1 | 337.50 | 7.22 | 0.0108 |
| AC | 3601.50 | 1 | 3601.50 | 77.08 | <0.0001 |
| BC | 368.17 | 1 | 368.17 | 7.88 | 0.0080 |
| A2 | 1977.34 | 1 | 1977.34 | 42.32 | <0.0001 |
| B2 | 1253.40 | 1 | 1253.40 | 26.82 | <0.0001 |
| C2 | 567.71 | 1 | 567.71 | 12.15 | 0.0013 |
| Residual | 1682.13 | 36 | 46.73 | ||
| Lack of Fit | 1189.33 | 4 | 297.33 | 19.31 | <0.0001 |
| Pure Error | 492.80 | 32 | 15.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vogelwaid, J.; Bayer, M.; Walz, M.; Kutuzova, L.; Kandelbauer, A.; Jacob, T. Process Optimization of the Morphological Properties of Epoxy Resin Molding Compounds Using Response Surface Design. Polymers 2024, 16, 1102. https://doi.org/10.3390/polym16081102
Vogelwaid J, Bayer M, Walz M, Kutuzova L, Kandelbauer A, Jacob T. Process Optimization of the Morphological Properties of Epoxy Resin Molding Compounds Using Response Surface Design. Polymers. 2024; 16(8):1102. https://doi.org/10.3390/polym16081102
Chicago/Turabian StyleVogelwaid, Julian, Martin Bayer, Michael Walz, Larysa Kutuzova, Andreas Kandelbauer, and Timo Jacob. 2024. "Process Optimization of the Morphological Properties of Epoxy Resin Molding Compounds Using Response Surface Design" Polymers 16, no. 8: 1102. https://doi.org/10.3390/polym16081102
APA StyleVogelwaid, J., Bayer, M., Walz, M., Kutuzova, L., Kandelbauer, A., & Jacob, T. (2024). Process Optimization of the Morphological Properties of Epoxy Resin Molding Compounds Using Response Surface Design. Polymers, 16(8), 1102. https://doi.org/10.3390/polym16081102







