Abstract
Carbon fiber-reinforced composites are popular due to their high strength and light weight; thus, the structures demonstrate high performance and specific strength. However, these composites are susceptible to impact damage. The objective of this research was to study the behavior of carbon fiber-reinforced laminates based on a polyetheretherketone (PEEK) matrix with six stacking sequences under static and impact loading. Four-point bending, short-beam bending, drop weight impact, and compression after impact tests were carried out. The results were complemented with digital shearography to estimate the damaged areas. Finite element modeling served to assess the failure mechanisms, such as fiber and matrix failure, in different layers due to tension of compression. Three behavior pattern of layups under drop-weight impact were found: (i)—energy redistribution due to mostly linear behavior (like a trampoline) and thus lower kinetic energy absorption for damage initiation, (ii)—moderate absorption of energy with initiation and propagation of concentrated damage with depressed redistribution of energy in the material, (iii)—moderate energy absorption with good redistribution due to initiation of small, dispersed damage. The results can be used to predict the mechanical behavior of composites with different stacking sequences in materials for proper structural design.
1. Introduction
In structural design, not only the properties in static loads but also the dynamic behavior of the material plays great importance. Polymer fiber reinforced laminates, which are especially used in sports equipment, cars, or aircrafts, must be resistant to impacts and maintain high residual strength in the presence of damage. One of the widespread high-strength composites is epoxy reinforced with carbon fibers (CFs). It has excellent specific strength; however, its fracture toughness is quite low, making it prone to impact damaging and delamination. One of the approaches to enhance the material is to additionally reinforce the matrix using dispersed fillers [1]. This increases mechanical properties, particularly interlaminar and impact toughness. Another way is to make a three-dimensional composite by stitching the layers of fabric perpendicular to the plane of the laminate [2]. To solve the problem of low impact resistance, one may look for other matrix materials or reinforcing fibers. For example, implementing aramid fibers instead of carbon ones or using tougher thermoplastic matrices versus more brittle thermosets.
Polyetheretherketone (PEEK) is a promising thermoplastic polymer with high strength, low density, and ability to operate at elevated temperatures. A number of advantages of PEEK over epoxy resin have been demonstrated in the past [3,4]. Thus, residual compressive strength after impact for carbon-fiber reinforced laminates is significantly greater for PEEK than epoxy because delamination is less extensive. PEEK attracts quite a lot of attention from researchers. A study of its properties is being carried out for both states: unreinforced and reinforced with fibers. Mechanical properties were studied under various types of static loading as well as under impact. For example, Hu et al. [5] studied mechanical responses and damage behaviors of PEEK composites reinforced with carbon fiber fabric that were subjected to low-velocity impacts (LVIs).
An option to increase impact strength is to add additional layers such as polyetherimide (PEI) films between CF/PEEK layers [6]. The addition of PEI film was found to improve Mode I and Mode II interlaminar fracture toughness. For low-energy impacts (10 J), PEI-reinforced panels were found to perform well. However, the improvement of properties minimized as the impact energy increased. Compression after impact (CAI) and combined load compression (CLC) tests showed that although the PEI inserts reduced the laminate intact compressive strength, they exhibited higher relative residual strength than other laminates tested.
Another approach for improving the properties of laminated composites is to vary the stacking sequence. Strait et al. [7] conducted impact tests to characterize carbon fiber-reinforced polymer (CFRP) laminates. No significant effect of layup was found in terms of the energy required to cause damage. However, the maximum load is highly dependent on the stacking sequence. Replacing the woven fabric with unidirectional tape in a quasi-isotropic layup resulted in a significant reduction in energy to maximum load. The authors conclude that stacking sequence and shape of the reinforcement can have significant impact on toughness, especially at high impact energies.
Alhayek et al. [8] studied the effects of different layups of glass fibers on the flexural strength of pultruded polymers. At four-point bending, the layups—(±45/0/90/0/90/0) and (±45/90/0/±45)—showed a flexural strength of 399.9 MPa and 242.5 MPa, respectively.
The effects of layups on the properties of the composites was also studied using numerical calculations by Pradhan et al. [9]. It was observed that the available stiffness of a laminate with a crack was largely dependent on orientation angle of the outer layers, number of cracked cross-layers, and number of unbroken outer layers ±θ in the laminate.
It is obvious that layup affects bending and impact strength, since the distance of a certain layer from the middle plane makes a different contribution resulting in a non-uniform distribution of stresses and strains throughout the thickness of the laminate.
A number of investigations have been carried out by scientific teams varying CF/PEEK laminate layups in addition to those already mentioned earlier [3,4]. In a series of works by Morita et al. [10,11,12,13], several layups of carbon fiber-reinforced PEEK, namely (0/+30/0/−30)S, (0/+60/0/−60)S, and (0/+45/90/−45)S, have been studied. It was found that the damage area depends linearly on the impact energy. Moreover, the ratio of the damaged area to the impact energy is smaller the less the difference in the angles of rotation of the fibers in neighboring layers.
Liu et al. [14] compared the effects of two different stacking sequences ([0°/90°]8S and [0 °/45°/90°/−45°]4S) at four impact energies. The peak impact force with an increase in impact energies ranged from 7.8 kN/8.3 kN to 11.4 kN/13.7 kN, and the CAI strength ranged from 370.5 MPa/419.3 MPa to 212.8 MPa/232.5 MPa. At the same time, the relative change in residual strength at impact energies of 0, 15, and 30 J for the second layup is minimal, while for the first it ranges up to 30%. At higher impact energies (45 and 60 J), the relative drop in strength becomes approximately the same.
The paper by Wang et al. [15] presents the investigation on the properties of CF/PEEK laminates with cross-ply layups: A [05/905/05], B [03/903/03/903/03] and C [0/90]15. In A and B laminates, transverse cracks occurred at very low impact energies (~0.5–1 J). Delamination initiated at approximately 3 J and fiber rupture began to occur after 10 J. Laminate C exhibited very limited transverse cracking and delamination until penetration occurred at 13 J.
Simulations can be an important part of understanding the fracture processes of composites. In addition, a correctly designed model makes it possible to predict the behavior of a material under new conditions or with changed properties of the material itself. To model layered composite materials, the finite element method is often used in modern research. Layers are specified individually, considering the anisotropy of the properties of each layer. The interaction of layers can specified using the cohesive behavior of the contact planes without increasing the number of nodes or elements [14].
The important point in the simulation is the selection of fracture criterion for matrix and fibers or a composite as a whole. One of the possible criterion in the literature is the Puck criterion [16]. The Puck failure theory is a stress-based criterion applicable for unidirectional composite lamina developed for both matrix and fiber failure modes. In [14], Liu et al. used the Puck criterion to model matrix failure under compression. Numerical simulation errors for peak impact force, impact energy absorption, and CAI strength were 3.8–14.8%, 3.7–6.9%, and 2.2–6.7%, respectively.
Probably, the most popular way for simulate failure is the implementation of the Hashin criterion [17]. Liu et al. [18] describes a detailed experimental and numerical study of the behavior of composite laminates under a low-velocity impact with energy of 15 J and different geometry of the impactor. A three-dimensional finite element (FE) model with the damage initiation mechanisms defined in the Hashin damage criteria, which was implemented as a subroutine for Abaqus/Explicit, was employed to simulate the impact event and to investigate the effects of the impactor’s geometry. The numerical predictions, including those for the loading response and the damage maps, provided good agreement with the experimental results. Thus, for a hemispherical steel impactor, the maximum load, displacement, and area damage for experimental studies were 4.7 kN, 6.0 mm, and 1180 mm2, while for simulation, they amounted to 4.5 kN, 5.9 mm, and 1090 mm2, respectively. The same parameters for a flat impactor for the experiment are 7.1 kN, 4.7 mm, 1060 mm2, and 7.0 kN, 4.6 mm, and 980 mm2 for the simulation.
Ouyang et al. [19] simulated low-velocity impact and compression after the impact experiments of two composite materials at different energy levels with the Hashin criterion and virtual crack-closure technique, respectively. The predicted failure modes and CAI strengths of laminates are in good agreement with the experiment results from this paper and the literature at various impact energies, which proves the validity of the model. The predicted compression strengths after different impact energies of laminates had the errors relative to the average experiment values of 2.2%, 8.4%, 1.3%, 0.5%, 3.4%, and 3.6%, depending on testing conditions. For the studied M21 epoxy resin laminates in the impact energy range from 6.5 J to 29.5 J, the errors between the experimental and numerical results of CAI strength were 4.3%, 12.3%, 6.5%, and 5.3%.
Based on the results of the literature review, it can be seen that a sufficient number of works, including ones from recent years, deal with the influence of layups on the impact properties of laminated composites. However, most of them consider layups that do not meet the requirements described in [20] or the number of layups in the study is limited to two or three types.
The paper is aimed to estimate the effects of six different layups of PEEK/CF composites on their mechanical properties during static and impact tests. Furthermore, this work is directed to evaluate layups with higher properties and reveal the mechanics of the failure process.
2. Materials and Methods
2.1. Manufacturing Procedure
Toray TC1200 PEEK prepregs were chosen for laminate preparation. The layers of prepregs were stacked in the required layup and molded using hot pressing. The laminates had a rectangular shape of 215 × 150 mm, and the specimens for testing were cut out using CNC milling machine with polycrystalline diamond mill.
For the selection of the layups in the experiment, the basic rules and restrictions for the design and production of composites provided by Ntourmas et al. [20]:
- Symmetry. In order to avoid coupling between bending and extension symmetric laminates are usually preferred.
- Balance. Balanced laminates can be used to remove coupling between shear and extension. Balanced laminates are formed by an equal number of layers with +θ and −θ orientations (θ ≠ 0°, 90°).
- Damage tolerance. Plies placed on the external part of the laminate should not be in the direction of the principal load path. In most cases, a layer oriented at +45° or −45° is placed on the outer part of the laminate.
- Minimum percentage. In favor of minimizing matrix degradation and encouraging a fiber-dominated failure mode, a minimum percentage of all fiber orientations might be desirable in a laminate. The minimum percentage rule makes sense for laminates which use the four standard fiber orientations (0, 90, 45, −45). This design rule is commonly used in conjunction with a maximum allowed percentage.
- Grouping. In order to decrease the coupling between bending and twist, +θ and −θ layers may be grouped together.
- Contiguity. According to the contiguity design rule, the maximum number of consecutive layers placed in the same orientation is limited. This is carried out in order to minimize interlaminar stresses and encourage a more uniform stress distribution.
- Disorientation. To minimize interlaminar shear effects, the absolute difference between the fiber orientations of adjacent laminae might be limited to a maximum of 45°.
Although all the proposed rules may be desirable in the design process, they cannot be applied simultaneously as they conflict with each other and may lead to an unsolvable optimization problem.
The molded and tested layups were symmetrical, balanced, and quasi-isotropic. Some of the rules presented here (above) were violated in order to assess the changes in mechanical behavior. There were six types of stacking sequences, as follows:
- [−45/0/45/90]4S—quasi-isotropic layup proposed in [21,22] for testing of impact toughness of fiber reinforced laminates. The layup has a 45°-oriented fiber layer on the surface and 45° interface between any layers.
- [0/−45/90/45]4S—the layup with layers swapped in each pair (−45/0 and 45/90), resulting in a layup with 0°-oriented surface layer and 45° interface.
- [−45/45/0/90]4S—the layup with 0 and 45 swapped, resulting in an interface of 90° between layers in −45/45 and 0/90 pairs. The interface between these pairs is 45°.
- [0/90/45/−45]4S—the same as layup #3, but the −45/45 and 0/90 pairs are swapped. Thus, the surface layer is 0°-oriented.
- [(−45/45)2/(0/90)2]2S—the same as #3, but each layer pair is repeated two times. The 90° interface is between the layers in (−45/45)2 and (0/90)2 groups and 90° between groups. In the resulting layup, −45/45 layers are located closer to the surface while 0/90 s are shifted towards midplane.
- [(0/90)2/(−45/45)2]2S—the same as layup #5, but the (−45/45)2 and (0/90)2 groups are swapped.
2.2. Mechanical Tests
There were four mechanical tests performed to characterize the effects of layup on mechanical behavior. Flexural properties of laminates were assessed according to four-point bending procedure B of [23]. The rate of crosshead movement was 1 mm/min. The specimen thickness was ~4.4 mm, and the span was set to 88 mm, resulting in a span-to-thickness ratio of 20:1.
Stress at the outer surface in the midpoint of span and strain in bending test can be calculated using the following equations:
σ = 3PL/(4bh2); ε = 4.36δh/L2; δ = 11/8 dl,
- —stress at the outer surface at mid-span, MPa;
- —applied force, N;
- —support span, mm;
- —width of beam, mm;
- —thickness of beam, mm;
- —maximum strain at the outer surface, mm/mm (or × 100%);
- —mid-span deflection, mm;
- dl—displacement of the load points of movable grip, mm.
The second testing was performed according to [24] to determine short-beam strength (SBS), which may be related to interlaminar shear strength. SBS is less affected by the layup than flexural strength, and these properties together can be used to characterize CFRPs. The test is included herein mostly for quality control.
Specimen sizes are calculated relative to thickness t, which is ~4.4 mm. Width is 2 × t, while span is 4 × t. SBS is calculated as follows:
FSBS = 0.75 Pm/bh,
- FSBS—short-beam strength, MPa;
- Pm—maximum load observed during the test, N;
- b—measured specimen width, mm;
- h—measured specimen thickness, mm.
The third and fourth tests are jointly performed. The impact properties of the laminate might be divided into two parts: impact damaging via drop weight test and resistance to impact damage tested under compression of the impacted laminate.
The composite laminate is subjected to a drop-weight impact event according to [21], and then [22] determines the residual compressive strength after impact. Kinetic energy of the impact was 30 J. According to the thickness of 4.4 mm, the specific energy was 6.7 J/mm.
The specimens for testing are rectangular shaped with the dimensions of 100 × 150 mm. The cylindrical impactor with a hemispherical nose had a weight of 5.4 kg and a diameter of 16 mm. The specimens are clamped in a fixture with a window of 75 × 125 mm. The impactor falls down to the center of the plate with a velocity prior to collision of ~3.3 m/s. The impact with the level of kinetic energy used in the test results in the formation of damage in the CFRP.
Behavior of composites under impact loading might be estimated using several parameters:
- Peak load—maximum force obtained in the loading diagram (Figure 1a);
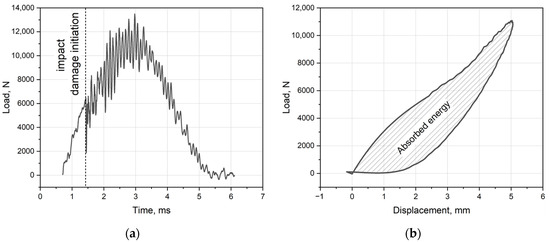 Figure 1. Results obtained after impact test: (a) “Load–time” diagram with impact damage initiation. (b) “Load–displacement” diagram and the area for calculation of absorbed energy.
Figure 1. Results obtained after impact test: (a) “Load–time” diagram with impact damage initiation. (b) “Load–displacement” diagram and the area for calculation of absorbed energy. - Damage load—force when the load drops in the diagram, indicating the origin of damage (dotted line in Figure 1a);
- Damage energy—energy lost by the impactor and transferred to the specimen at the moment of damage origin;
- Absorbed energy—calculated as an area delineated by a “load–displacement” diagram, as illustrated in Figure 1b. Absorbed energy also might be calculated as a difference between kinetic energy of impactor before and after impact. However, it includes energy loss via friction, heating, etc. Energy obtained from hysteresis area is slightly less than difference of kinetic energies.
2.3. Inspection Using Digital Shearography
Digital shearography was used to estimate the damage size after impact event. The technique implements a very sensitive optical analysis of a deformation pattern on the specimen’s surface. The surface was illuminated with a 532 nm (green) Nd:YAG laser to generate a speckle pattern. The specimen was heated with an IR lamp and during cooling; the photos of the speckle pattern for shearography were obtained.
During cooling, thermal flows provide deformation gradients in the composite, which also changes the laser speckle pattern on the surface. So, the post processing of speckle pattern images could derive the strain pattern on the specimen surface. When the plate is free of damage, the strain pattern is homogenous; however, in presence of any damage, it becomes irregular. The larger the damage, the larger the inhomogeneity observed in the processed image.
2.4. Finite Element Modelling of Impact Behavior
A full-scale simulation was carried out using ABAQUS 2019/Explicit. Material properties were obtained from the manufacturer’s datasheet and with preliminary experiments. Longitudinal and transverse Young’s moduli were E11 = 135 GPa and E22 = E33 = 10 GPa; shear moduli were G12 = G13 = 5.2 GPa and G23 = 3.8 GPa. Poisson ratios were υ12 = υ13 = 0.301 and υ23 = 0.396. Tensile and compressive strengths in the fiber direction were Xt = 2410 MPa and Xc = 1300 MPa; in the transverse direction, they were Yt = 86 MPa and Yc = 189 MPa, respectively. Longitudinal and transverse shear strengths were S12 = S13 = 152 MPa and S23 = 81 MPa. Material density was ρ = 1600 kg/m3.
The Hashin criterion [17] was used to simulate elements’ failure, including four different damage initiation mechanisms. Hashin criteria comprehensively consider various damage modes, such as fiber failure in tension, matrix cracking due to transverse tension and shear, fiber compressive damage (buckling or kinking) and matrix crushing under transverse compression, and shear effects. The Hashin theory is based on the separation of different failure modes and has been proven to be effective for the study of the onset and the evolution of fiber and matrix failures [25,26,27]. The Hashin criterion works quite correctly when assessing the fracture of fibers, but is not very effective in the failure of the matrix, especially during compression [14].
Failure energies for the Hashin criterion are as follows: longitudinal tensile and compressive fracture energy GXT = 90,000 J/m2 and GXC = 60,000 J/m2; transverse tensile and compressive fracture energy GYT = 1500 J/m2 and GYC = 5000 J/m2. This criterion was chosen for models because it allows us to determine the most critical damage process after impact and was already implemented in Abaqus Explicit.
The laminate was modeled as deformable solid. The interaction between layers was described by cohesive behavior with the following parameters of damage initiation, propagation, and stabilization. Fracture energies were GIC = 1.6 kJ/m2 and GIIC = 2.3 kJ/m2, linear degradation law based on the mixed mode law of the Benzeggagh–Kenane criterion was equal to 1.5, and the viscosity coefficient was 0.007. The Benzeggagh–Kenane criterion was used as the fracture criterion [28], which demonstrates high efficiency for composite materials with the use of identical critical fracture energies along the two shear directions. The Benzeggagh–Kenane fracture criterion is particularly useful when the critical fracture energies during deformation, purely along the first and the second shear directions, are the same.
All laminate layers were modeled using SC8R continuum shell elements. Metal impactors were modeled as 3D rigid (discretely rigid) elements. The interaction between a composite laminate and impactor was defined as a rigid contact with a friction coefficient of 0.3.
The boundary conditions reproduce real test conditions—the rectangular plate was positioned in the rectangular frame and pressed with supports. The weight, shape, and size of the impactor complied with the [21]. The impactor motion was determined by the initial velocity, measured in experiment before it struck the specimen.
3. Results
3.1. Flexural Tests and Short-Beam Strength
The diagrams of the calculated strain on the outer surface vs. flexural stress were plotted in Figure 2 for [23] tests. Table 1 presents the results on mechanical properties obtained according to [24]: strength, strain at failure, flexural modulus, and short-beam strength.
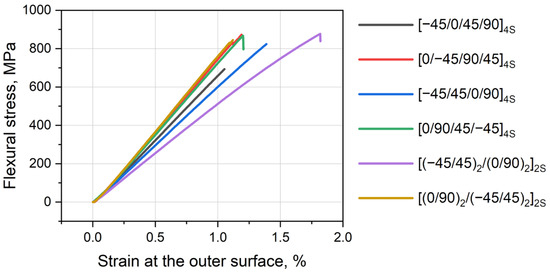
Figure 2.
Stress–strain diagram of flexural tests of PEEK composites with various layups.

Table 1.
Flexural properties of tested PEEK composites with various layups.
The diagram demonstrates that most stacking sequences have linear behavior under bending loads and have abrupt failure. Nonlinearity is visually observed for [(−45/45)2/(0/90)2]2S. According to Figure 2 and Table 1, various layups result in various flexural moduli and strengths. The highest flexural moduli were observed for layups where 0 layers were on the outer surfaces of the laminate ([(0/90)2/(−45/45)2]2S, [0/−45/90/45]4S and [0/90/45/−45]4S), while 45/−45 layers on the outer surface of composite reduced flexural stiffness, e.g., [(−45/45)2/(0/90)2]2S. Moderate moduli were observed for [−45/0/45/90]4S and [−45/45/0/90]4S. When fiber direction coincides with tension and compression forces (0° layer), it provides higher stiffness. The 45° layer had less longitudinal stiffness than 0° one. The 90° layer was even weaker than 45°. e.g., [0/90/45/−45]4S had a slightly lower modulus than [0/−45/90/45]4S (50.6 ± 1.2 vs. 53.1 ± 1.9 GPa). Thus, to obtain a higher flexural modulus, it is preferred to place 0° layers at the outer surface of the laminate.
However, high modulus does not guarantee high failure stress. The leaders in strength are [0/−45/90/45]4S and [0/90/45/−45]4S, while [(0/90)2/(−45/45)2]2S takes only 4th place, being adrift by approximately 65 MPa (or 7%). This layup is too stiff and thus has a lower ability to redistribute stresses, resulting in brittle failure. Surprisingly, the [(−45/45)2/(0/90)2]2S layup, having ±45 fiber on the outer space and the lowest flexural modulus, demonstrated good flexural strength. It should be noted that in most cases, failure occurs at the inner surface due to fiber compression and buckling of the layer.
Short-beam strength is mostly related to the interlaminar properties under in-plane shear loading (close to mode II interlaminar fracture toughness). So, the results are nearly the same for almost all layups, showing sufficient adhesion between layers. It should be noted that a lower SBS was observed for layups where a 90 interface was in the midplane of the specimen (where shear stresses are the highest).
3.2. Low-Velocity Impact and Compression after Impact
The testing machine is able to measure impactor displacement, velocity, and contact load in the impactor head. The key results measured in drop-weight tests are presented in Table 2, which include peak load, damage load, damage energy, and absorbed energy.

Table 2.
Summary of the properties of PEEK composites with various layups for impact and compression after impact tests.
Kinetic energy absorbed by the laminate can be estimated via the difference in kinetic energy of an impactor at the beginning of impact and after rebound from a laminate surface. It should be considered that this difference includes the loss of energy due to inertia and the friction in guide bearings. So, it is better to directly derive the energy from the loading diagrams.
The typical smoothed load–displacement curves for each laminate layup can be obtained and are plotted in Figure 3. The diagram shows loading and unloading of a specimen; thus, the area delineated by the curve characterizes absorbed energy, which is spent mostly on damage nucleation and propagation. Of course, some minor portion of energy is dissipated on internal and contact friction or heating. The key parameters of the loading and absorbed energy (as curve delineated area) are presented in Table 2. In should be noted that a higher maximum load does not mean higher absorbed energy.
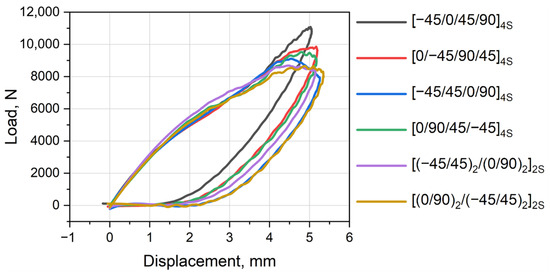
Figure 3.
Load–displacement diagram (namely mechanical hysteresis loops) of impact tests of PEEK composites with various layups.
The subsequent step for testing the damaged laminate is compression after impact. This is performed to estimate residual strength, which greatly depends on damage size and interlaminar strength. The results are also presented in Table 2.
The lowest absorbed energy had specimen of a [−45/0/45/90]4S layup, which resulted in the highest CAI strength and peak load. The composite demonstrated higher energy absorption by elastic straining and reduced the damage nucleation process. The energy for the first damage initiation was rather low—7.3 J (last but one); however, during further loading, this laminate was damaged less. It should be noted that the laminate at impact loading was clamped on the perimeter, which resulted in combined bending around two axes. Thus, it was difficult to easily use the flexural modulus and strength of the exact layup in comparison to the CAI strength. However, at CAI, the specimens were loaded along 0° axis via compression; thus, the layup should have determined the residual strength. It should be important what fiber layers are most damaged. For example, 0°-oriented plies dominate in resistance to compression, and their damage should probably decrease CAI strength. During the analysis of CAI for various layups, it was difficult to establish any regularity depending on the layup as the process of impact loading and subsequent compression is too complex in nature. The next section with the results of the shearography damage evaluation can assist with this.
Nevertheless, some minor points can be noted. Two layups—[0/−45/90/45]4S and [−45/45/0/90]4S—demonstrated high absorbed energies and thus a low CAI strength. The absorbed energy for [−45/0/45/90]4S was the lowest one, resulting in the highest CAI strength. Both layups—[(−45/45)2/(0/90)2]2S and [(0/90)2/(−45/45)2]2S—where the 0/90 and −45/45 layer pairs were grouped twice, demonstrated the lowest peak loads during impact and the highest damage energy, resulting in good residual CAI strength.
3.3. Digital Shearography
Figure 4 represents the examples of impact damage visualized using digital shearography, which are seen as inhomogeneities in the central parts of the photos. Images are presented with their front and back sides for each specimen type. The edges of the images correspond to the edges of the specimens, so the relative size of the damage might be compared to the total area of the laminate.

Figure 4.
Front and back images of impacted PEEK composites with various layups obtained via digital shearography (a–f).
Damage area estimated using digital shearography is presented in Table 3. It can be seen that smaller damage with a moderate scatter is in the front side of the impacted panel and almost twice-as-large damage with more significant scatter is on the back side. The results are consistent with the standard impact theory. This theory states that for thick laminates based on brittle fiber–matrix systems (like CFRPs), the cross-sectional damage profile looks like a “pine tree”. The damage in this case was caused by normal in-plane stress, which exceeded the transverse tensile stress. It initiated matrix failure at the back side, developing into delamination and fiber breakage.

Table 3.
Damage area of PEEK composites with various layups estimated via digital shearography.
Due to the visual analysis, some general results might be drawn. The damage to the front surface was smaller than that at the back surface. The layup had a minor effect on the damage shape at the front, while at the back, the top layer delaminated more extensively and thus affected the shape of damage. The shape of damage at the back surface was elongated in the horizontal direction for layups with a 0°-orientate direction of fiber on the outer layer (Figure 4b,d,f). On the contrary, for layups with 90° at outer layers, the damage at the back surface was elongated in a diagonal direction: from upper left to bottom right.
It can be observed that area of damage on the back surface had a good correlation with CAI residual strength for nearly all layups. The impact damage in the laminate was mainly located in the half opposed to the impact surface, and it dominated the residual bearing capacity.
3.4. Damage Modelled via Finite Element Technique
Figure 5 demonstrates damaged elements in the laminate after impact obtained via an ABAQUS simulation. There are several failure criteria presented. HFC is the Hashin criterion for fibers that fail due to compression, and HFT is the Hashin criterion for the tension of fibers. The DMG criterion demonstrates overall failure of the cohesive surface (literally matrix failure and delamination). All these criteria take values from 0 to 1, where 0 represents the absence of damage and 1 represents a fully failed element. For visualization purposes, the Hashin and DMG criteria have an index equal to 0.5, so their images include failed and partially damaged elements.
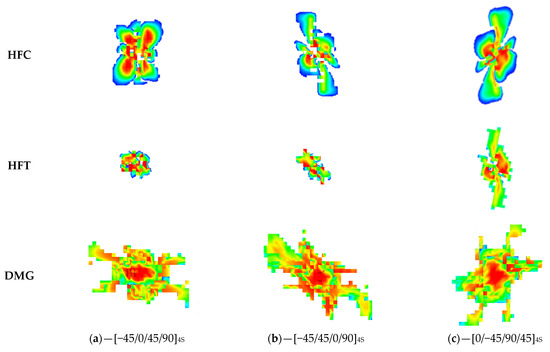
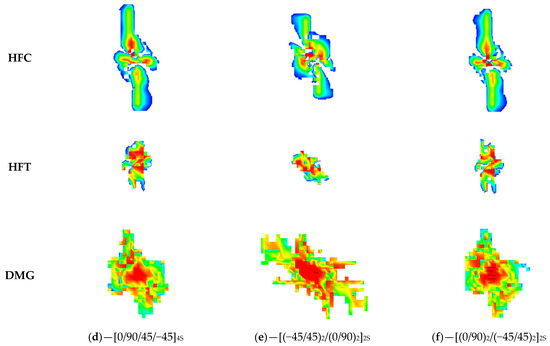
Figure 5.
Damage in various layups according to different failure criteria. HFC—Hashin failure criterion for fiber compression, HFT—Hashin failure criterion for fiber tension, DMG—overall damage index for cohesive surfaces (denoted in ABAQUS as CSDMG). Blue-green-red color scale depicts damage index from 0.5 to 1.
Results show that large, elongated damage originates mostly from fiber compression along the shorter side of the panel. Tensile damage has a more uniform shape, depending on the direction, and also has a lower size than failure due to compression. Matrix (delamination) failure is mostly concentrated along the −45/45 directions.
In general, it might be noted that the presence of 0/90 layers at the front outer surface leads to dominant damage in the 90 direction, which is seen for the HFC criterion in Figure 5d,e when compared to the other layups. However, this layup reduces matrix failure, especially in the −45/45 directions (DMG criterion in Figure 5d,e). Compression failure in the 90° direction has a minor effect on compression properties in the 0 direction when the compression after impact test is performed because these broken fibers are perpendicular to the loading axis. However, a non-damaged matrix is beneficial for preventing the longitudinal delamination of layers.
4. Discussion on Layup Selection
After the results were obtained and analyzed, it was found that, similar to [7], maximum load is highly dependent on the stacking sequence with variations of nearly 20%. The peak load in this paper was in the range of 10.26 to 12.19 kN, resulting in a difference of 19%. Individual properties might have variations. The [(0/90)2/(−45/45)2]2S layup has good compression strength after impact, high energy to initiate damage under impact, a significant flexural modulus, and moderate flexural strength. Peak load and absorbed energy are more complicated parameters which could not be directly evaluated. Not every higher value leads to a better performance. The [(0/90)2/(−45/45)2]2S specimens have a low peak load (10.26 kN) and high residual strength (268 MPa), while the specimens with the [0/−45/90/45]4S layup demonstrate a high peak load (11.80 kN) and low strength after impact (253.2 MPa). Moreover, [−45/0/45/90]4S shows high strength (272.6 MPa) and peak load (12.19 kN) but the lowest absorbed energy (17.64 J).
There are several ways how material may sustain an impact event:
A high peak load and low absorbed energy result in globally linear behavior, like a trampoline. Thus, the high flexural modulus is not required to reach a high peak load. Small damage energy might be attributed to early fracture initiation but without significant propagation. An example can be made of the [−45/0/45/90]4S layup, which demonstrates good resistance to impact loading. Similar findings can be found in [10,11,12,13], supporting the finding that the damaged area of the laminate is smaller the lower the difference in the angles of rotation of the fibers is in the neighboring layers. The abovementioned layup has all the interfaces of 45 degrees between its adjacent layers, and its good impact resistance and residual strength were confirmed with tests. However, such a rule cannot be generally used in all instances, and some layups demonstrate high absorbed energy but small damage, resulting in high CAI strength.
A high peak load and high absorbed energy with small damage energy result in the early initiation of damage, large damage propagation to absorb kinetic energy, and high stiffness to demonstrate a high peak load. However, this leads to small strength after impact. At the same time, some specimens demonstrate a low peak load, high absorbed energy, and low damage energy. The difference between low and high peak loads is the result of a difference in the flexural modulus. The lower the modulus, the lower the peak load. So, [0/−45/90/45]4S and [−45/45/0/90]4S demonstrate low resistance to impact loading.
Sufficiently high damage energy and good strength after impact accompanied with good CAI strength are connected with a later initiation of damage; thus, small damages are distributed on a large area for the absorption of kinetic energy. However, these damages should be small enough to have minor effects on deformation behavior. This redistribution of energy results in high strength. The [0/90/45/−45]4S, [(0/90)2/(−45/45)2]2S, and [(−45/45)2/(0/90)2]2S layups demonstrate good resistance to impact and the difference in peak load attributed to the flexural modulus.
Mechanical properties are dependent on the layup, but their effects are not obvious. The selection of the optimal layup which possesses the best combination of impact and flexural properties might be challenging. The authors would like to propose a simple estimation for selecting them. Firstly, the most valuable properties were determined with a condition that a higher value equates to better properties. The list of properties chosen for comparison is as follows:
- Flexural strength, MPa;
- Flexural modulus, GPa;
- SBS, MPa;
- Damage energy, J;
- CAI strength, MPa.
The chosen properties for each layup were divided by the max to normalize values. The results are summarized in Table 4. The value which equals to 1.00 means that this layup has the highest value compared to other layups. A five-axis radar diagram was plotted based on normalized values (Figure 6). Each axis is representative of each mechanical property in the normalized values. The radar diagram may help with visually comparing all the stacking sequences.

Table 4.
Summary for valuable mechanical properties of composites with various layups.
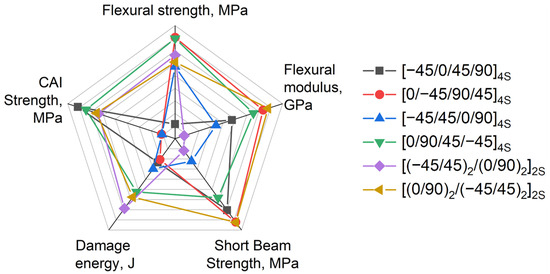
Figure 6.
Normalized (divided by max) radar diagram of valuable mechanical properties for various layups.
The question of “what layup is better?” might be answered via an analysis of the area delineated by the diagram for each layup or simply by calculating the sum of the normalized values for each layup. As far as the diagram is normalized, the contribution of each property is equal and does not depend on an absolute value. The sums are presented in Table 4.
According to described procedure, the best layups according to the aforementioned properties are the [(0/90)2/(−45/45)2]2S and [0/90/45/−45]4S layups. These layups have very close normalized sums—4.85 and 4.82. The worst layups also have similar overall properties. The third place is taken by the [0/−45/90/45]4S layup, which has a sum of 4.65 due to having significantly less damage energy. The fourth place is taken by the [(−45/45)2/(0/90)2]2S layup, which has a sum of 4.55 and a reduced flexural modulus. The last two places go to the [−45/45/0/90]4S and [−45/0/45/90]4S layups, which have very similar summarized values—4.93 and 4.37. These layups showed decreased properties; however, the [−45/0/45/90]4S layup demonstrated the highest CAI strength.
5. Conclusions
This manuscript presented the results of PEEK/CF composites that were impact tested with different layups. Preliminary flexural tests according to [23] (long beam) showed different strengths and flexural moduli for various layups. Stiffness was determined by fibers with the [0°] direction at the outer surface. Strength is not always associated with [0°] fibers only as fractures occur mostly due to compression at the inner surface. The short-beam strength test (according to [24]) showed nearly the same interlaminar properties for different layups, and showed sufficient adhesion between layers.
The effects of layups on the impact properties of composites were estimated according to [21] for low-velocity impacts and then in accordance with [22] for compression tests to determine their strengths after various impacts. The three ways of how the different layups may behave under and after impact are described in detail in the “Discussion” section: (i)—energy redistribution due to linear behavior (like a trampoline), which causes kinetic energy absorption for damage initiation, (ii)—moderate absorption of energy with initiation and propagation of concentrated damage with depressed redistribution of energy in the material, (iii)—moderate energy absorption with good redistribution due to initiation of small dispersed damage.
Modelling results show the contribution of several failure mechanisms to the overall damage that occurs and their dominant behavior depending on the layup. Layers with 0/90 fibers at the front outer surface result in dominant compression damage in the 90° direction; moreover, they reduce matrix failure, especially in the −45/45 directions.
To answer the question of what layup is better, five of the most valuable parameters were chosen—flexural strength, flexural modulus, short-beam strength, damage energy, and compression strength after impact. The higher the parameter value, the higher performance of the layup. In summary, the best layups in relation to the most of properties are the [(0/90)2/(−45/45)2]2S and [0/90/45/−45]4S layups.
Author Contributions
Conceptualization, A.V.E. and M.V.B.; methodology, A.V.E. and M.V.B.; validation, M.V.B. and A.A.K.; formal analysis, A.V.E., M.V.B., and P.S.L.; investigation, A.V.E., A.A.B., and A.A.K.; writing—original draft preparation, A.V.E. and M.V.B.; writing—review and editing, A.V.E. and A.A.B. All authors have read and agreed to the published version of the manuscript.
Funding
The work was performed according to the research assignment for the Russian Science Foundation, project # 21-79-10385.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data are contained within this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ji, C.; Hu, J.; Sadighi, M.; Alderliesten, R.; Wang, B.; Sun, Y. Experimental and Theoretical Study on Residual Ultimate Strength after Impact of CF/PEEK-Titanium Hybrid Laminates with Nano-Interfacial Enhancement. Compos. Sci. Technol. 2023, 232, 109871. [Google Scholar] [CrossRef]
- Lai, J.; Peng, Z.; Huang, Z.; Li, M.; Mo, M.; Liu, B. Effect of Stitching, Stitch Density, Stacking Sequences on Low-Velocity Edge Impact and Compression after Edge Impact (CAEI) Behavior of Stitched CFRP Laminates. Materials 2022, 15, 8822. [Google Scholar] [CrossRef] [PubMed]
- Bishop, S.M. The Mechanical Performance and Impact Behaviour of Carbon-Fibre Reinforced PEEK. Compos. Struct. 1985, 3, 295–318. [Google Scholar] [CrossRef]
- Dorey, G.; Bishop, S.M.; Curtis, P.T. On the Impact Performance of Carbon Fibre Laminates with Epoxy and PEEK Matrices. Compos. Sci. Technol. 1985, 23, 221–237. [Google Scholar] [CrossRef]
- Hu, J.; Ji, C.; Chen, S.; Li, S.; Zou, Y.; Zhou, Z.; Wang, B. Two-Position Impact Behavior and Interference Mechanism of CFF/PEEK Thermoplastic Composites. Int. J. Mech. Sci. 2022, 232, 107644. [Google Scholar] [CrossRef]
- McLaughlin, J.W.; Tobin, E.; O’Higgins, R.M. An Investigation of Polyether Imide (PEI) Toughening of Carbon Fibre-Reinforced Polyether Ether Ketone (PEEK) Laminates. Mater. Des. 2021, 212, 110189. [Google Scholar] [CrossRef]
- Strait, L.H.; Karasek, M.L.; Amateau, M.F. Effects of Stacking Sequence on the Impact Resistance of Carbon Fiber Reinforced Thermoplastic Toughened Epoxy Laminates. J. Compos. Mater. 1992, 26, 1725–1740. [Google Scholar] [CrossRef]
- Alhayek, A.; Syamsir, A.; Supian, A.B.M.; Usman, F.; Asyraf, M.R.M.; Atiqah, M.A. Flexural Creep Behaviour of Pultruded GFRP Composites Cross-Arm: A Comparative Study on the Effects of Stacking Sequence. Polymers 2022, 14, 1330. [Google Scholar] [CrossRef]
- Pradhan, B.; Venu Kumar, N.; Rao, N. Stiffness Degradation Resulting from 90° Ply Cracking in Angle-Ply Composite Laminates. Compos. Sci. Technol. 1999, 59, 1543–1552. [Google Scholar] [CrossRef]
- Thompson, D.O.; Chimenti, D.E. (Eds.) Review of Progress in Quantitative Nondestructive Evaluation; Springer: Boston, MA, USA, 1997; ISBN 978-1-4613-7725-2. [Google Scholar]
- Morita, H.; Hamamoto, A.; Adachi, T.; Matsumoto, K. Influence of Impact Velocity and Lay-up Parameter on Impact Damage Resistance of CF/PEEK Laminates. In Proceedings of the 36th Structures, Structural Dynamics and Materials Conference, New Orleans, LA, USA, 10–13 April 1995; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1995. [Google Scholar]
- Morita, H.; Tsang, P.H.W. Soft Body Impact Damage on CF/PEEK Laminates Using Gelatin Projectile. J. Reinf. Plast. Compos. 1997, 16, 1330–1341. [Google Scholar] [CrossRef]
- Morita, H.; Adachi, T.; Tateishi, Y.; Matsumot, H. Characterization of Impact Damage Resistance of CF/PEEK and CF/Toughened Epoxy Laminates under Low and High Velocity Impact Tests. J. Reinf. Plast. Compos. 1997, 16, 131–143. [Google Scholar] [CrossRef]
- Liu, A.; Chen, Y.; Hu, J.; Wang, B.; Ma, L. Low-velocity Impact Damage and Compression after Impact Behavior of CF/PEEK Thermoplastic Composite Laminates. Polym. Compos. 2022, 43, 8136–8151. [Google Scholar] [CrossRef]
- Wang, H.; vu-Khanh, T. Damage Extension in Carbon Fiber/PEEK Crossply Laminates under Low Velocity Impact. J. Compos. Mater. 1994, 28, 684–707. [Google Scholar] [CrossRef]
- Puck, A.; Schürmann, H. Failure Analysis of FRP Laminates by Means of Physically Based Phenomenological Models. Compos. Sci. Technol. 2002, 62, 1633–1662. [Google Scholar] [CrossRef]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. Trans. ASME 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.; Ding, Y.; Zhou, J.; Kong, X.; Blackman, B.R.K.; Kinloch, A.J.; Falzon, B.G.; Dear, J.P. Effects of Impactor Geometry on the Low-Velocity Impact Behaviour of Fibre-Reinforced Composites: An Experimental and Theoretical Investigation. Appl. Compos. Mater. 2020, 27, 533–553. [Google Scholar] [CrossRef]
- Ouyang, T.; Bao, R.; Sun, W.; Guan, Z.; Tan, R. A Fast and Efficient Numerical Prediction of Compression after Impact (CAI) Strength of Composite Laminates and Structures. Thin-Walled Struct. 2020, 148, 106588. [Google Scholar] [CrossRef]
- Ntourmas, G.; Glock, F.; Deinert, S.; Daoud, F.; Schuhmacher, G.; Chronopoulos, D.; Özcan, E.; Ninić, J. Stacking Sequence Optimisation of an Aircraft Wing Skin. Struct. Multidiscip. Optim. 2023, 66, 31. [Google Scholar] [CrossRef]
- ASTM Standard D7136/D7136M; Standard Test Method for Measuring the Damage Resistance of a Fiber-Reinforced Polymer Matrix Composite to a Drop-Weight Impact Event. ASTM International: West Conshohocken, PA, USA, 2015.
- ASTM Standard D7137/D7137M; Standard Test Method for Compressive Residual Strength Properties of Damaged Polymer Matrix Composite Plates. ASTM International: West Conshohocken, PA, USA, 2012.
- ASTM Standard D7264/D7264M; Standard Test Method for Flexural Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2015.
- ASTM Standard D2344/D2344M; Standard Test Method for Short-Beam Strength of Polymer Matrix Composite Materials and Their Laminates. ASTM International: West Conshohocken, PA, USA, 2016.
- Torabizadeh, M.A.; Fereidoon, A. Low-Velocity Impact Behavior of Foam Core Sandwich Panels with Different Face Sheet Layers: Numerical and Experimental Study. Mech. Adv. Compos. Struct. 2023, 10, 111–122. [Google Scholar] [CrossRef]
- Caputo, F.; De Luca, A.; Lamanna, G.; Borrelli, R.; Mercurio, U. Numerical Study for the Structural Analysis of Composite Laminates Subjected to Low Velocity Impact. Compos. Part B Eng. 2014, 67, 296–302. [Google Scholar] [CrossRef]
- Caputo, F.; De Luca, A.; Sepe, R. Numerical Study of the Structural Behaviour of Impacted Composite Laminates Subjected to Compression Load. Compos. Part B Eng. 2015, 79, 456–465. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of Mixed-Mode Delamination Fracture Toughness of Unidirectional Glass/Epoxy Composites with Mixed-Mode Bending Apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).