Experimental Study of the Airflow Field and Fiber Motion in the Melt-Blowing Process
Abstract
1. Introduction
2. Experiment and Materials
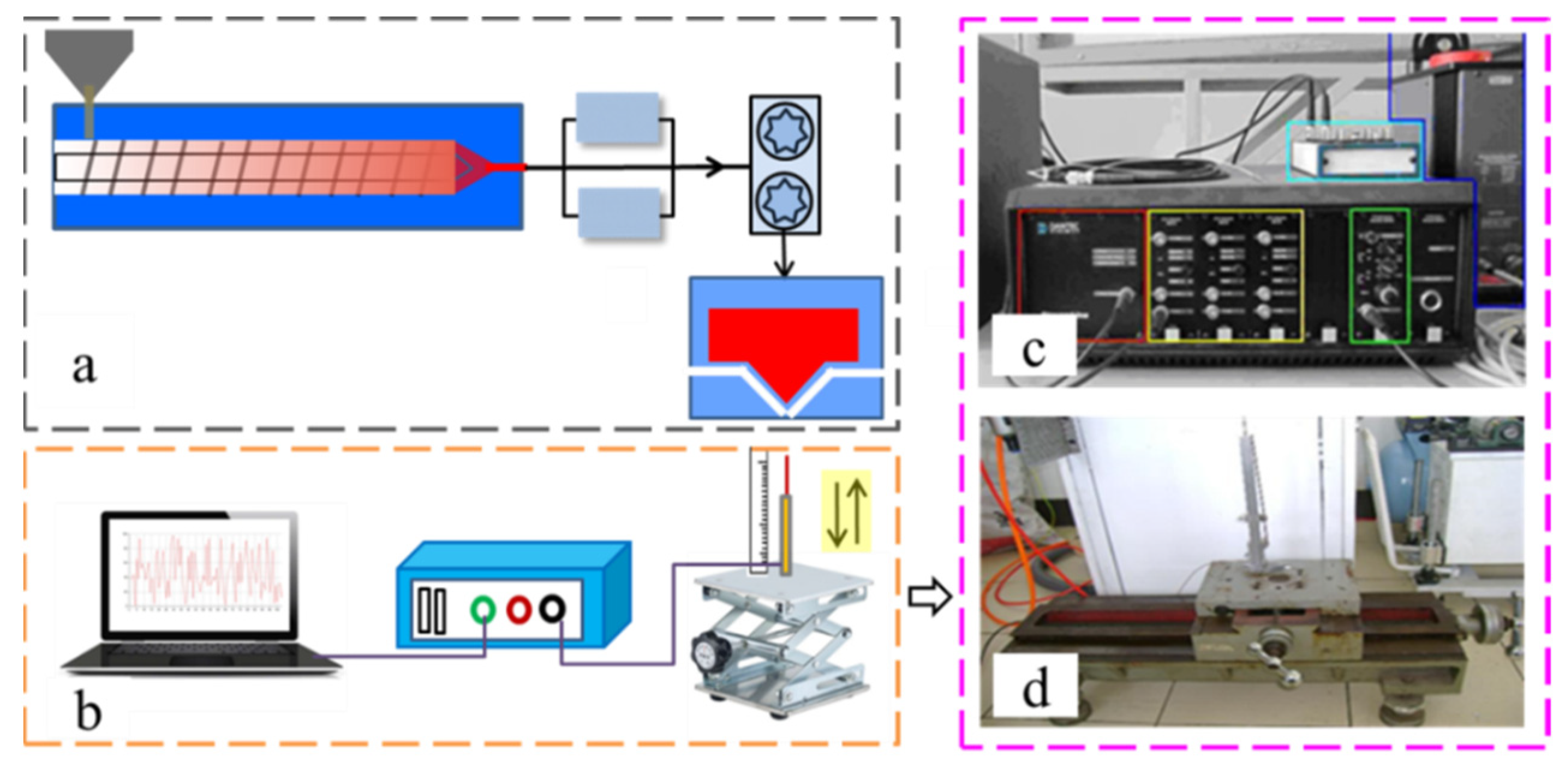
2.1. Experimental Setup
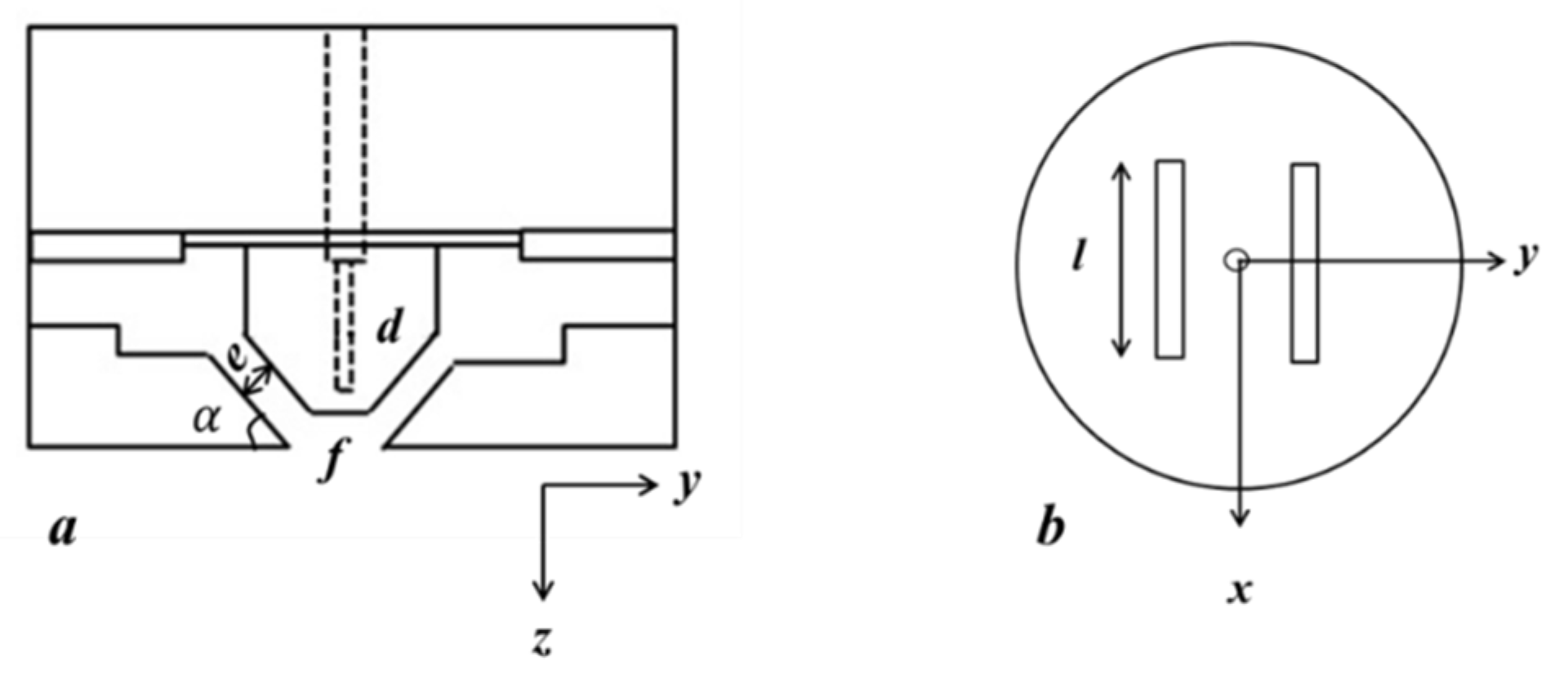
2.2. Melt-Blowing Die and Airflow Measure Parameter
2.3. Hot-Wire Anemometer Calibrations
2.4. Process Parameter and Material
3. Results and Discussion
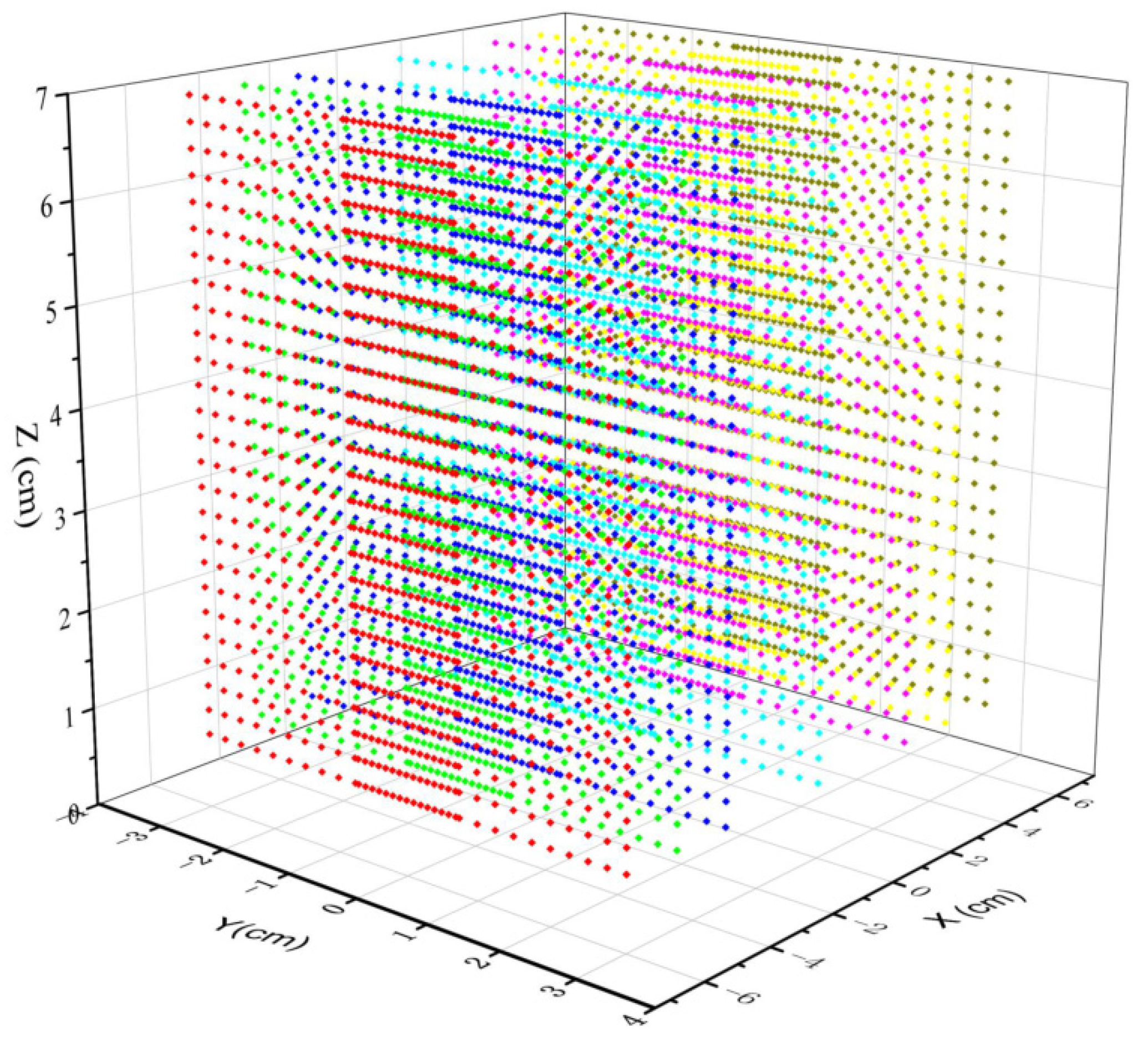
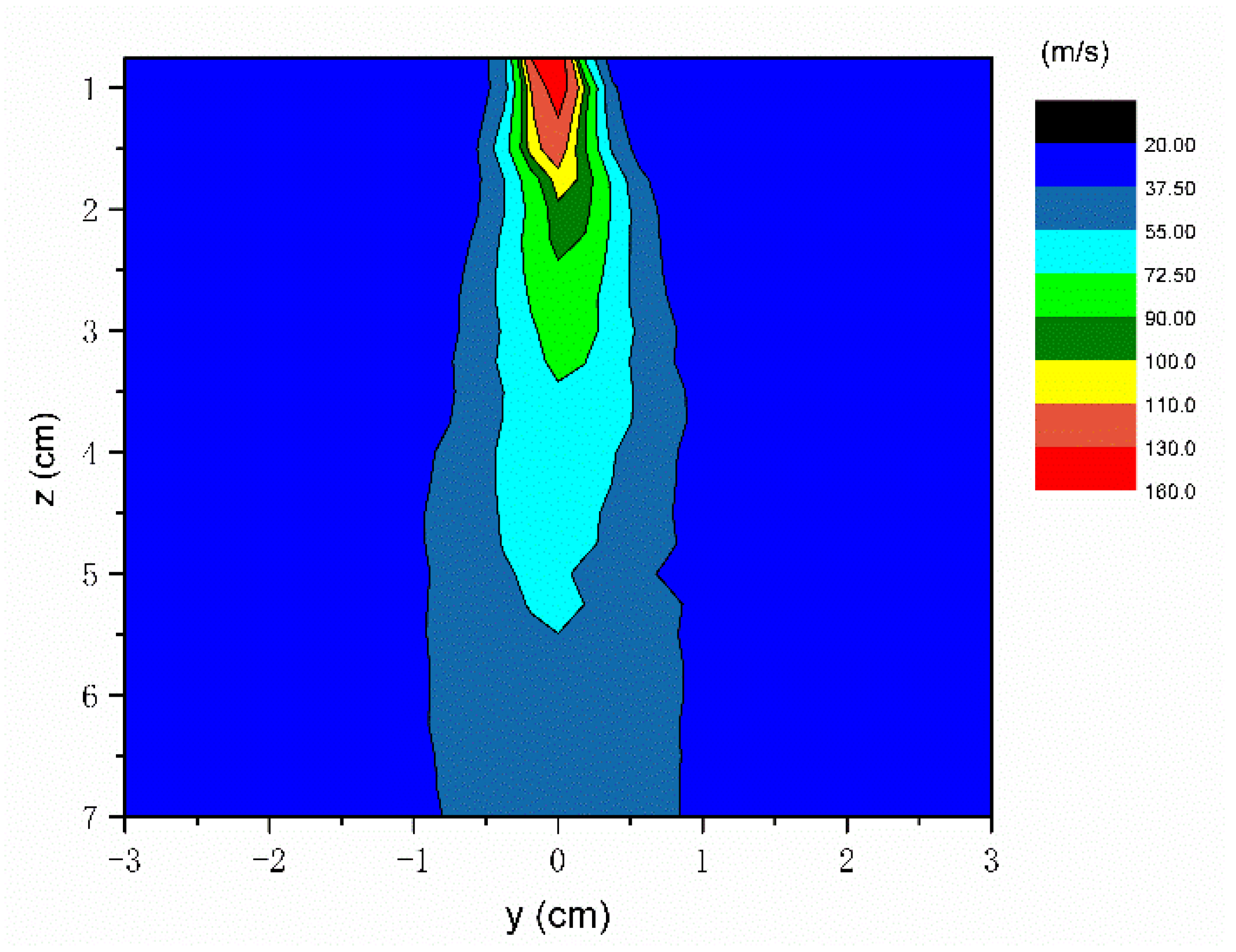
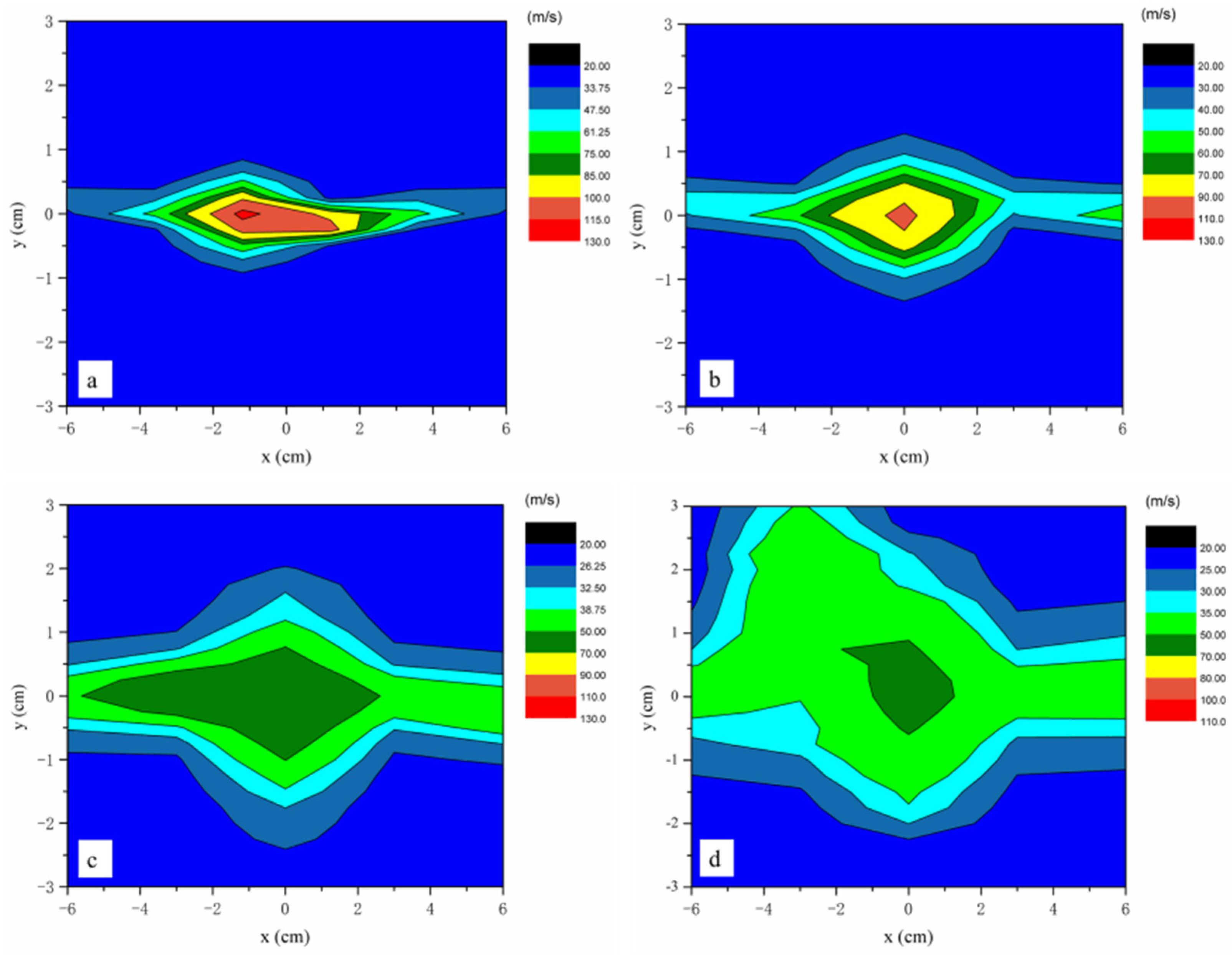
3.1. The Melt-Blowing Airflow Field Distribution
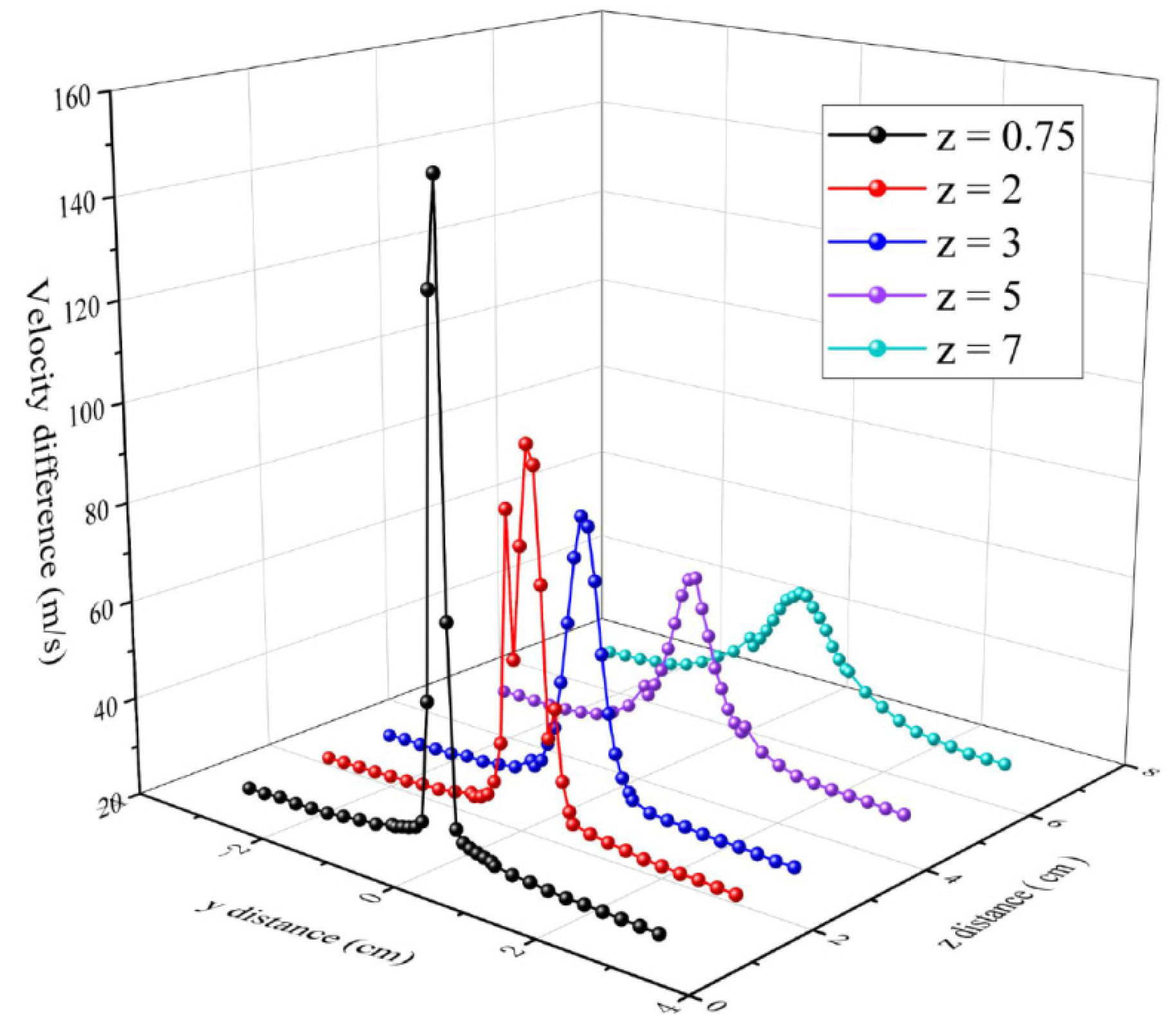
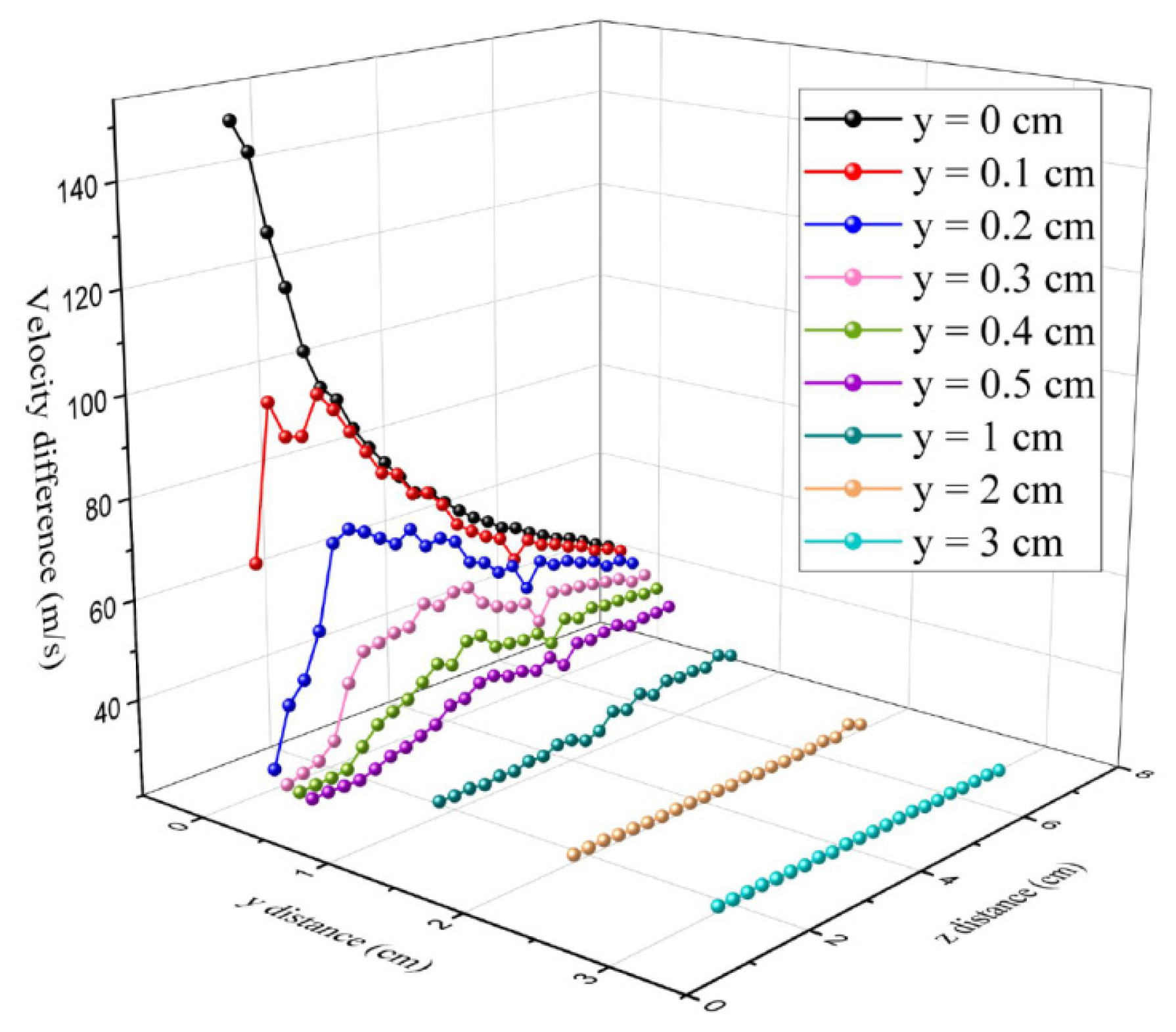
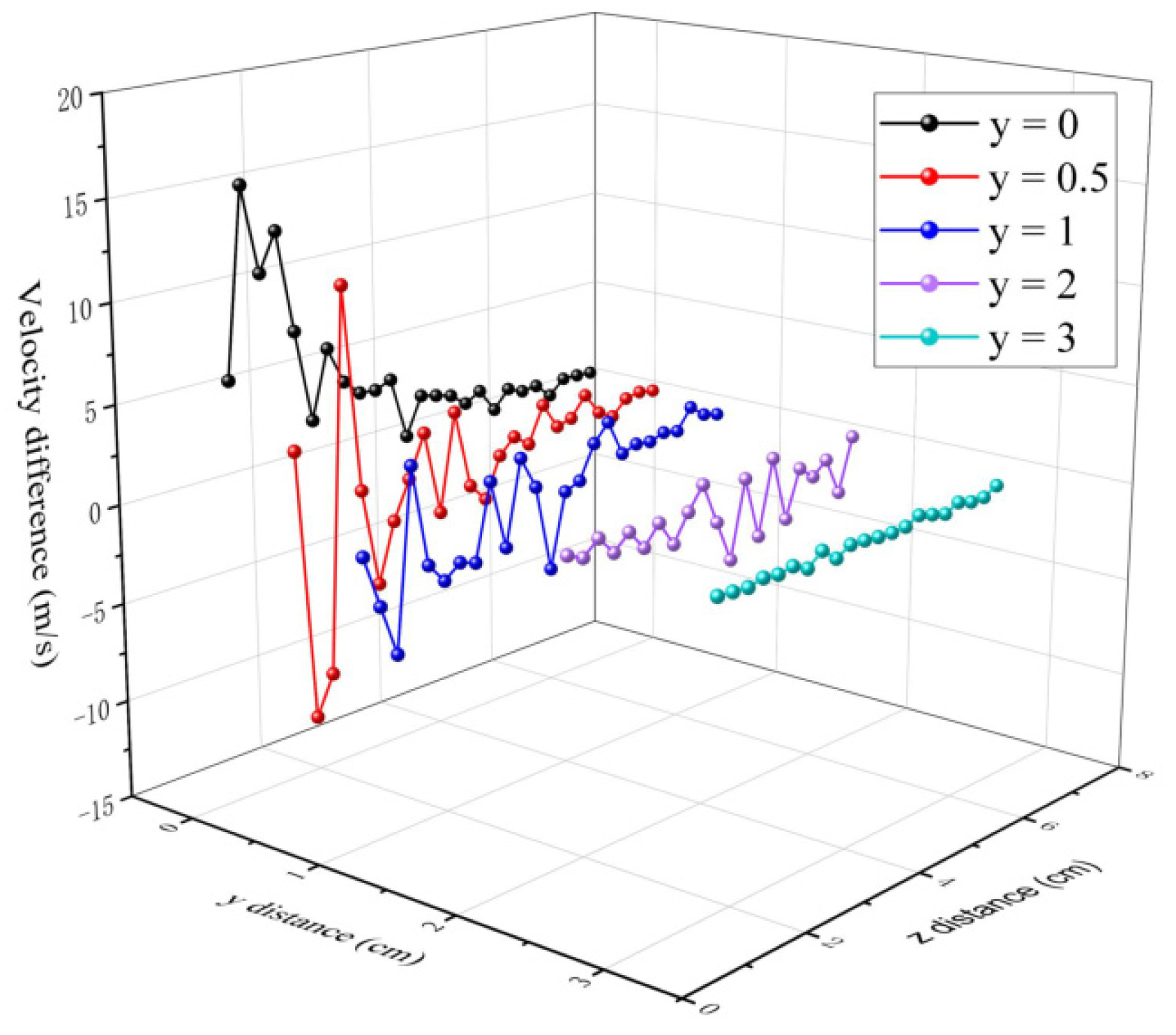
3.2. The Air Velocity Distribution in the Melt-Blowing Process
3.3. Fiber Motion in the Melt-Blowing Airflow Field
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Banerji, A.; Jin, K.; Mahanthappa, M.K.; Bates, F.S.; Ellison, C.J. Porous fibers templated by melt blowing cocontinuous immiscible polymer blends. ACS Macro Lett. 2021, 10, 1196–1203. [Google Scholar] [CrossRef]
- Nayak, R.; Kyratzis, I.L.; Truong, Y.B.; Padhye, R.; Arnold, L. Structural and mechanical properties of poly Structural and mechanical properties of polypropylene nanofibres fabricated by melt blowing. J. Text. Inst. 2014, 106, 629–640. [Google Scholar] [CrossRef]
- Ellison, C.J.; Phatak, A.; Giles, D.W.; Macosko, C.W.; Bates, F.S. Melt blown nanofibers: Fiber diameter distributions and onset of fiber breakup. Polymer 2007, 48, 3306–3316. [Google Scholar] [CrossRef]
- Wente, V.A. Superfine Thermoplastic Fibers. Ind. Eng. Chem. 1956, 48, 1342–1346. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Zhang, X.; Huang, C.; Jin, X. Design of electret polypropylene melt blown air filtration material containing nucleating agent for effective PM2.5 capture. RSC Adv. 2018, 8, 7932–7941. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhen, Q.; Cui, J.-Q.; Liu, R.-T.; Zhang, Y.-F.; Qian, X.-M.; Liu, Y. Groove-shaped polypropylene/polyester micro/nanofibrous nonwoven with enhanced oil wetting capability for high oil/water separation. Polymer 2020, 193, 122356. [Google Scholar] [CrossRef]
- Luiso, S.; Henry, J.J.; Pourdeyhimi, B.; Fedkiw, P.S. Meltblown polyvinylidene difluoride as a Li-Ion battery separator. ACS Appl. Polym. Mater. 2021, 3, 3038–3048. [Google Scholar] [CrossRef]
- Yesil, Y.; Bhat, G.S. Porosity and barrier properties of polyethylene meltblown nonwovens. J. Text. Inst. 2017, 108, 1035–1040. [Google Scholar] [CrossRef]
- Yang, C.; Jiang, X.; Gao, X.; Wang, H.; Li, L.; Hussain, N.; Xie, J.; Cheng, Z.; Li, Z.; Yan, J.; et al. Saving 80% Polypropylene in facemasks by laser-assisted melt-blown nanofibers. Nano Lett. 2022, 22, 7212–7219. [Google Scholar] [CrossRef]
- Hegde, R.R.; Bhat, G.S. Nanoparticle effects on structure and properties of polypropylene meltblown webs. J. Appl. Polym. Sci. 2010, 115, 1062–1072. [Google Scholar] [CrossRef]
- Kara, Y.; Molnar, K. A review of processing strategies to generate melt-blown nano/microfiber mats for high-efficiency filtration applications. J. Ind. Text. 2022, 51, 137S–180S. [Google Scholar] [CrossRef]
- Lee, Y.; Wadsworth, L.C. Effects of melt-blowing process conditions on morphological and mechanical properties of polypropylene webs. Polymer 1992, 33, 1200–1209. [Google Scholar] [CrossRef]
- Schmidt, J.; Usgaonkar, S.S.; Kumar, S.; Lozano, K.; Ellison, C.J. Advances in melt blowing process simulations. Ind. Eng. Chem. Res. 2022, 61, 65–85. [Google Scholar] [CrossRef]
- Hao, X.; Zeng, Y. A Review on the studies of air flow field and fiber formation process during melt blowing. Ind. Eng. Chem. Res. 2019, 58, 11624–11637. [Google Scholar] [CrossRef]
- Han, W.; Wang, X. Optimal geometry design of double coat-hanger die for melt blowing process. Fibers Polym. 2014, 15, 1190–1196. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, D. Analysis and simulation of non-Newtonian flow in the coat-hanger die of a meltblown process. J. Appl. Polym. Science. 1998, 67, 193–200. [Google Scholar] [CrossRef]
- Marla, V.T.; Shambaugh, R.L. Three-dimensional model of the melt-blowing process. Ind. Eng. Chem. Res. 2003, 42, 6993–7005. [Google Scholar] [CrossRef]
- Takarada, W.; Hatano, S.; Kikutani, T. Experimental and numerical analysis of unstable behavior of melt blowing process. J. Fiber Sci. Technol. 2020, 76, 208–216. [Google Scholar] [CrossRef]
- Hassan, M.A.; Anantharamaiah, N.; Khan, S.A.; Pourdeyhimi, B. Computational fluid dynamics simulations and experiments of meltblown fibrous media: New die designs to enhance fiber attenuation and filtration Quality. Ind. Eng. Chem. Res. 2016, 55, 2049–2058. [Google Scholar] [CrossRef]
- Han, W.; Xie, S.; Shi, J.; Wang, X. Study on airflow field and fiber motion with new melt blowing die. Polym. Eng. Sci. 2019, 59, 1182–1189. [Google Scholar] [CrossRef]
- Formoso, I.; Rivas, A.; Beltrame, G.; Larraona, G.S.; Ramos, J.C.; Antón, R.; Salterain, A. Experimental study of fiber breakup and shot formation in melt blowing nozzle designs. J. Ind. Text. 2020, 51, 3895–3922. [Google Scholar] [CrossRef]
- Wang, X.; Ke, Q. Computational simulation of the fiber movement in the melt-blowing process. Ind. Eng. Chem. Res. 2005, 44, 3912–3917. [Google Scholar] [CrossRef]
- Krutka, H.M.; Shambaugh, R.L.; Papavassiliou, D.V. Analysis of multiple jets in the schwarz melt-blowing die using computational fluid dynamics. Ind. Eng. Chem. Res. 2005, 44, 8922–8932. [Google Scholar] [CrossRef]
- Krutka, H.M.; Shambaugh, R.L.; Papavassiliou, D.V. Analysis of a melt-blowing die: Comparison of CFD and experiments. Ind. Eng. Chem. Res. 2002, 41, 5125–5138. [Google Scholar] [CrossRef]
- Shambaugh, B.R.; Papavassiliou, D.V.; Shambaugh, R.L. Modifying air fields to improve melt blowing. Ind. Eng. Chem. Res. 2012, 51, 3472–3482. [Google Scholar] [CrossRef]
- Chelikani, S.; Sparrow, E.M. Numerical simulations of plane-wall coanda effects for control of fiber trajectories in the melt-blown process. Ind. Eng. Chem. Res. 2013, 52, 11639–11645. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, Y.; Ji, C.; Wang, X.; Guan, F. The effect of the geometric structure of the modified slot die on the air field distribution in the meltblowing process. Text. Res. J. 2021, 92, 423–433. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X. Investigation on a new annular melt-blowing die using numerical simulation. Ind. Eng. Chem. Res. 2013, 52, 4597–4605. [Google Scholar] [CrossRef]
- Majumdar, B.; Shambaugh, R.L. Velocity and temperature fields of annular jets. Ind. Eng. Chem. Res. 1991, 30, 1300–1306. [Google Scholar] [CrossRef]
- Harpham, A.S.; Shambaugh, R.L. Flow field of practical dual rectangular jets. Ind. Eng. Chem. Res. 1996, 35, 3776–3781. [Google Scholar] [CrossRef]
- Harpham, A.S.; Shambaugh, R.L. Velocity and temperature fields of dual rectangular jets. Ind. Eng. Chem. Res. 1997, 36, 3937–3943. [Google Scholar] [CrossRef]
- Xie, S.; Zeng, Y. Turbulent air flow field and fiber whipping motion in the melt blowing process: Experimental study. Ind. Eng. Chem. Res. 2012, 51, 5346–5352. [Google Scholar] [CrossRef]
- Yang, Y.; Zeng, Y.C. Measurement and comparison of melt-blowing airflow fields: Nozzle modifications to reduce turbulence and fibre whipping. Polymers 2021, 13, 719. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.; Jiang, G.; Ye, B.; Shentu, B. Particle image velocimetry (PIV) investigation of the turbulent airflow in slot-die melt blowing. Polymers 2020, 12, 279. [Google Scholar] [CrossRef]
- Uyttendaele, M.A.J.; Shambaugh, R.L. The flow field of annular jets at moderate Reynolds numbers. Ind. Eng. Chem. Res. 1989, 28, 1735–1740. [Google Scholar] [CrossRef]
- Mohammed, A.; Shambaugh, R.L. Three-dimensional temperature field of a rectangular array of practical air jets. Ind. Eng. Chem. Res. 1994, 33, 730–735. [Google Scholar] [CrossRef]
- Tate, B.D.; Shambaugh, R.L. Temperature fields below melt-blowing dies of various geometries. Ind. Eng. Chem. Res. 2004, 43, 5405–5410. [Google Scholar] [CrossRef]
- Moore, E.M.; Shambaugh, R.L.; Papavassiliou, D.V. Analysis of isothermal annular jets: Comparison of computational fluid dynamics and experimental data. J. Appl. Polym. Sci. 2004, 94, 909–922. [Google Scholar] [CrossRef]
- Tan, D.H.; Herman, P.K.; Janakiraman, A.; Bates, F.S.; Kumar, S.; Macosko, C.W. Influence of Laval nozzles on the air flow field in melt blowing apparatus. Ind. Eng. Chem. Res. 2012, 80, 342–348. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, H.; Zeng, Y. Turbulence of melt-blowing airflow field: Comparison of a convergent jet and a typical free jet. Phys. Fluids 2021, 33, 751071–7510710. [Google Scholar] [CrossRef]
- Xie, S.; Zeng, Y. Online measurement of fiber whipping in the melt-blowing process. Ind. Eng. Chem. Res. 2013, 52, 2116–2122. [Google Scholar] [CrossRef]
- Entov, V.M.; Yarin, A.L. The dynamics of thin liquid jets in air. J. Fluid Mech. 1984, 140, 91–111. [Google Scholar] [CrossRef]
- Drabek, J.; Zatloukal, M. Meltblown technology for production of polymeric microfibers/nanofibers: A review. Phys. Fluids 2019, 31, 91301. [Google Scholar] [CrossRef]
- Wieland, M.; Arne, W.; Marheineke, N.; Wegener, R. Melt-blowing of viscoelastic jets in turbulent airflows: Stochastic modeling and simulation. Appl. Math. Model. 2019, 76, 558–577. [Google Scholar] [CrossRef]
- Benavides, R.E.; Jana, S.C.; Reneker, D.H. Role of liquid jet stretching and bending instability in nanofiber formation by gas jet method. Macromolecules 2013, 46, 6081–6090. [Google Scholar] [CrossRef]
- Sinha-Ray, S.; Yarin, A.L.; Pourdeyhimi, B. Prediction of angular and mass distribution in meltblown polymer lay-down. Polymer 2013, 54, 860–872. [Google Scholar] [CrossRef]


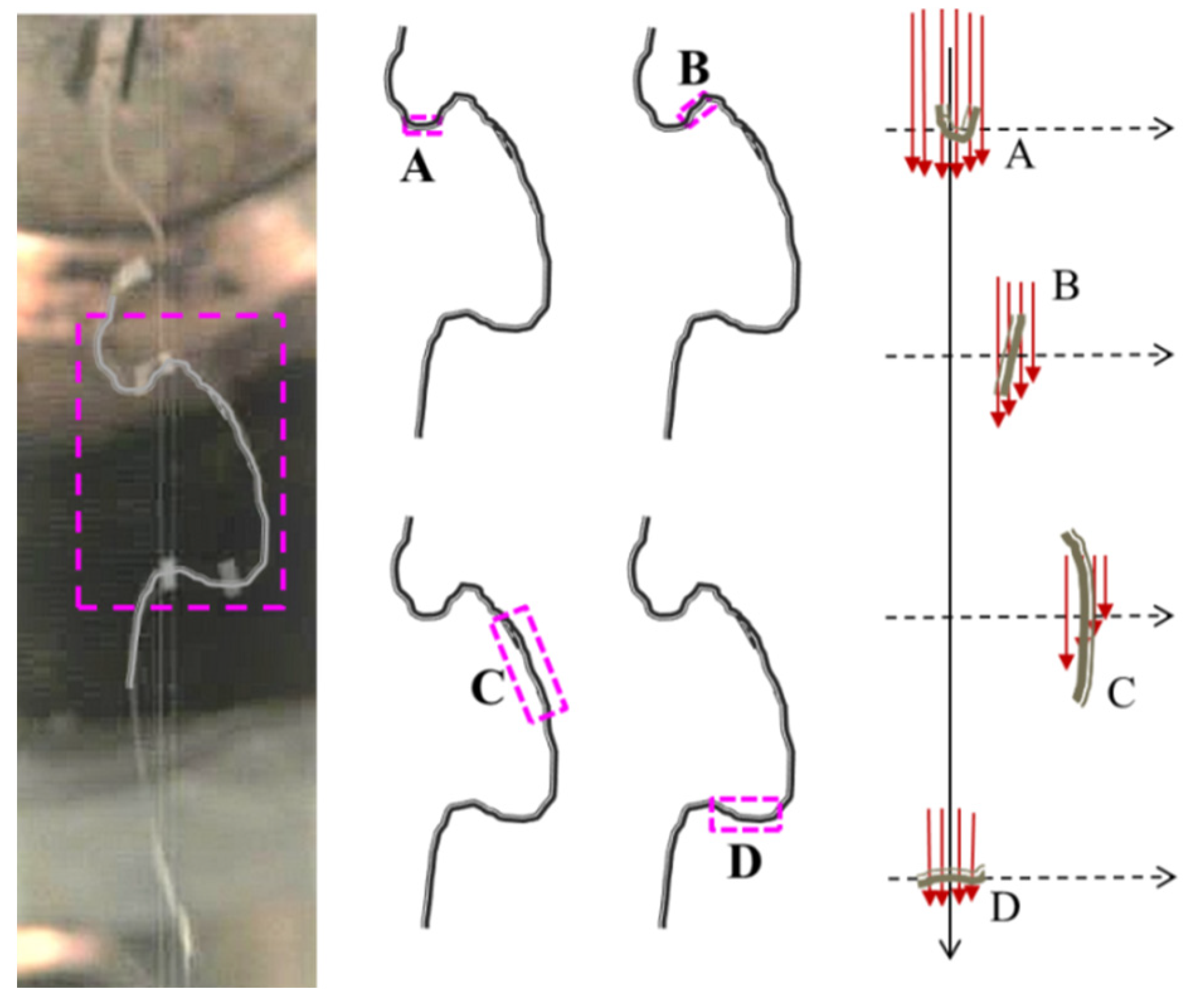
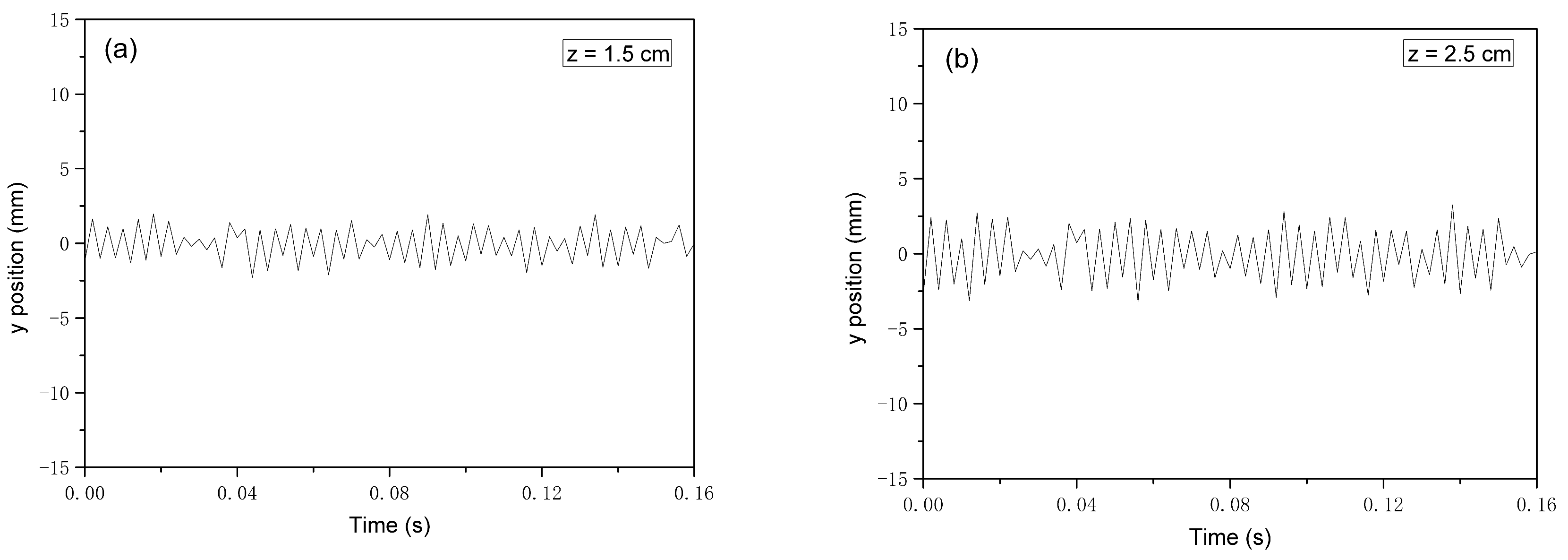
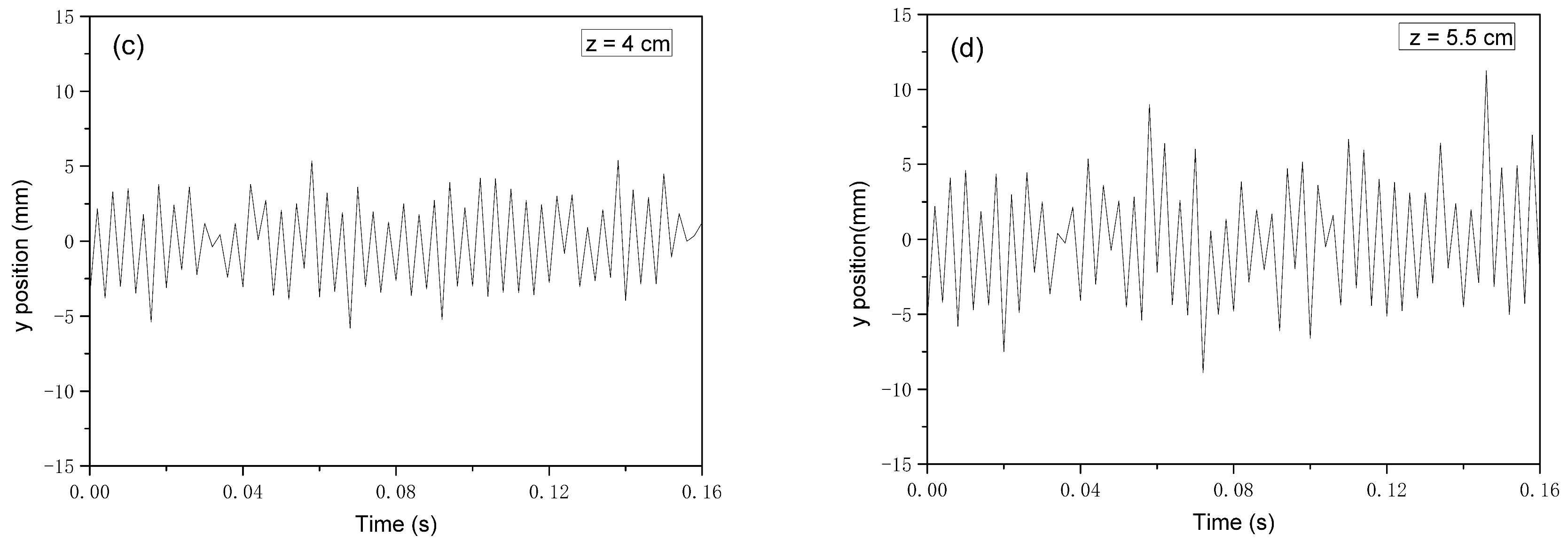

| Authors | Year | Measurement Instrument | Condition | Measurement Content |
|---|---|---|---|---|
| Uyttendaele and Shambaugh [36] | 1989 | Pitot tube | Isothermal | Velocity under an annular die |
| Majumda and Shambaugh [30] | 1991 | Pitot tube and thermocouple | Nonisothermal | Velocity and temperature under an annular die |
| Mohammed and Shambaugh [37] | 1993 | Pitot tube and thermocouple | Nonisothermal | Velocity and temperature under a multiorifice annular die |
| Harpham and Shambaugh [31] | 1996 | Pitot tube | Isothermal | Velocity under a slot die |
| Harpham and Shambaugh [32] | 1997 | Pitot tube and thermocouple | Nonisothermal | Velocity and temperature under a slot die |
| Tate and Shambaugh [38] | 2004 | Pitot tube and thermocouple | Nonisothermal | Effects of geometry parameters of slot dies on the air velocity and temperature |
| Moore [39] | 2004 | Pitot tube and thermocouple | Nonisothermal | Air velocity and temperature under a multiorifice slot die |
| Tan [40] | 2012 | Schlieren visualization | Nonisothermal | Air density oscillation |
| Xie [35] | 2020 | Particle Image Velocimetry | Nonisothermal | The turbulent Airflow in Slot die |
| The Nose-Piece Width (f) | The Slot Angle (α) | The Slot Width (e) | The Slot Length (l) | The Orifice Diameter (d) |
|---|---|---|---|---|
| 1.28 | 30° | 0.65 | 6 | 0.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.; Han, W.; Sun, Y.; Yi, H.; Wang, X. Experimental Study of the Airflow Field and Fiber Motion in the Melt-Blowing Process. Polymers 2024, 16, 469. https://doi.org/10.3390/polym16040469
Wu W, Han W, Sun Y, Yi H, Wang X. Experimental Study of the Airflow Field and Fiber Motion in the Melt-Blowing Process. Polymers. 2024; 16(4):469. https://doi.org/10.3390/polym16040469
Chicago/Turabian StyleWu, Wenhan, Wanli Han, Yafeng Sun, Honglei Yi, and Xinhou Wang. 2024. "Experimental Study of the Airflow Field and Fiber Motion in the Melt-Blowing Process" Polymers 16, no. 4: 469. https://doi.org/10.3390/polym16040469
APA StyleWu, W., Han, W., Sun, Y., Yi, H., & Wang, X. (2024). Experimental Study of the Airflow Field and Fiber Motion in the Melt-Blowing Process. Polymers, 16(4), 469. https://doi.org/10.3390/polym16040469






