Evaluation and Characterization of Functionally Graded Adhesive Joints: Experimental and Numerical Analyses
Abstract
1. Introduction
2. Materials and Methods
2.1. Selection of Materials
2.2. Thermal Characterization of Adhesives
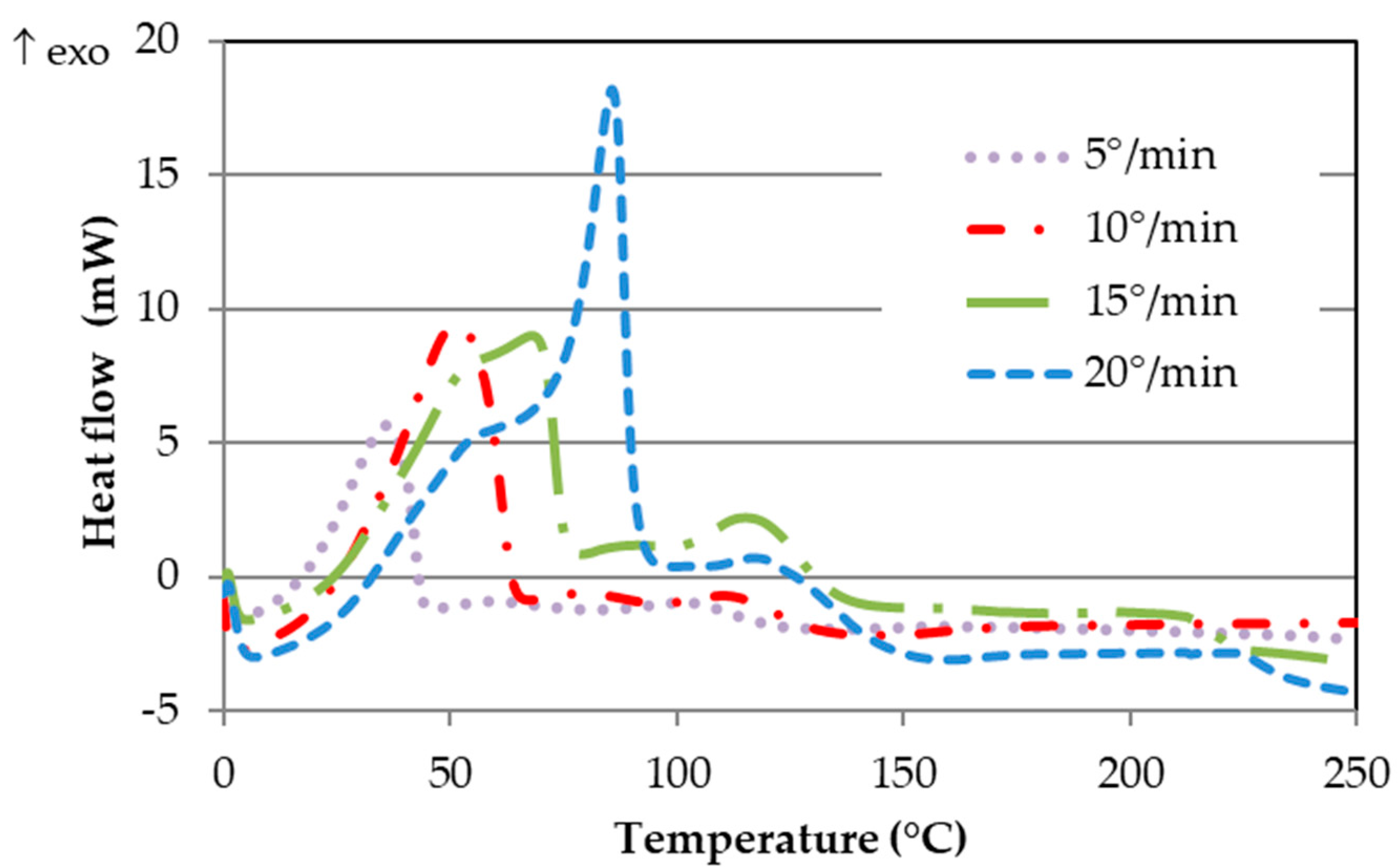
2.2.1. Differential Scanning Calorimetry
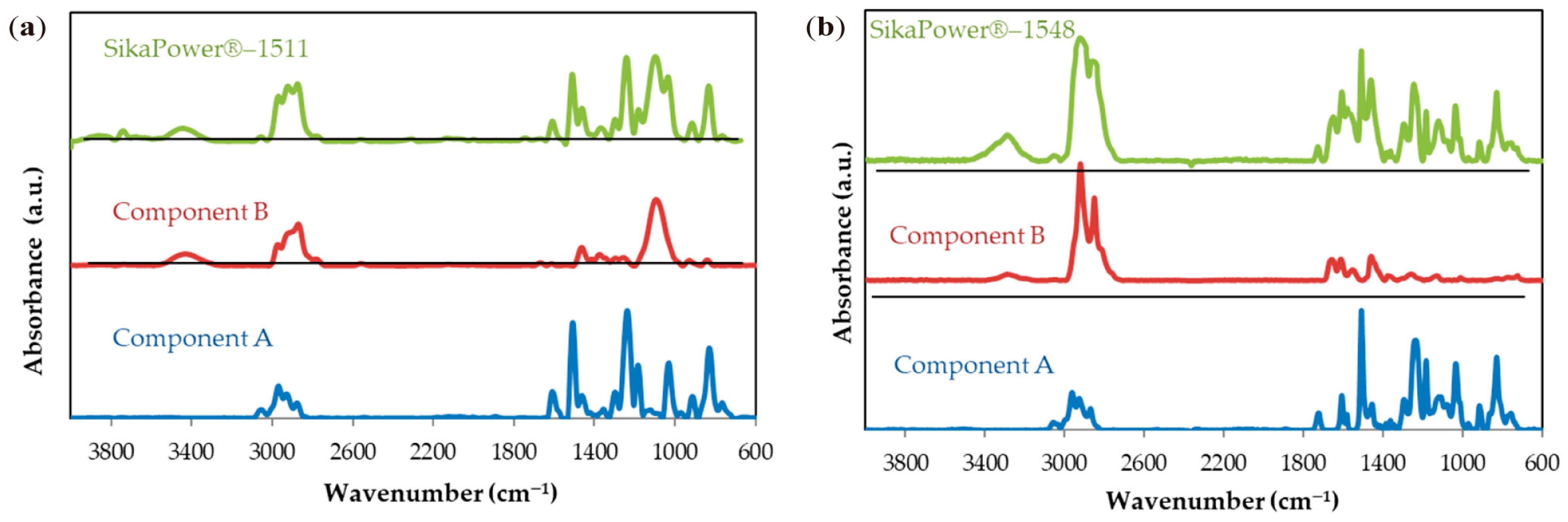
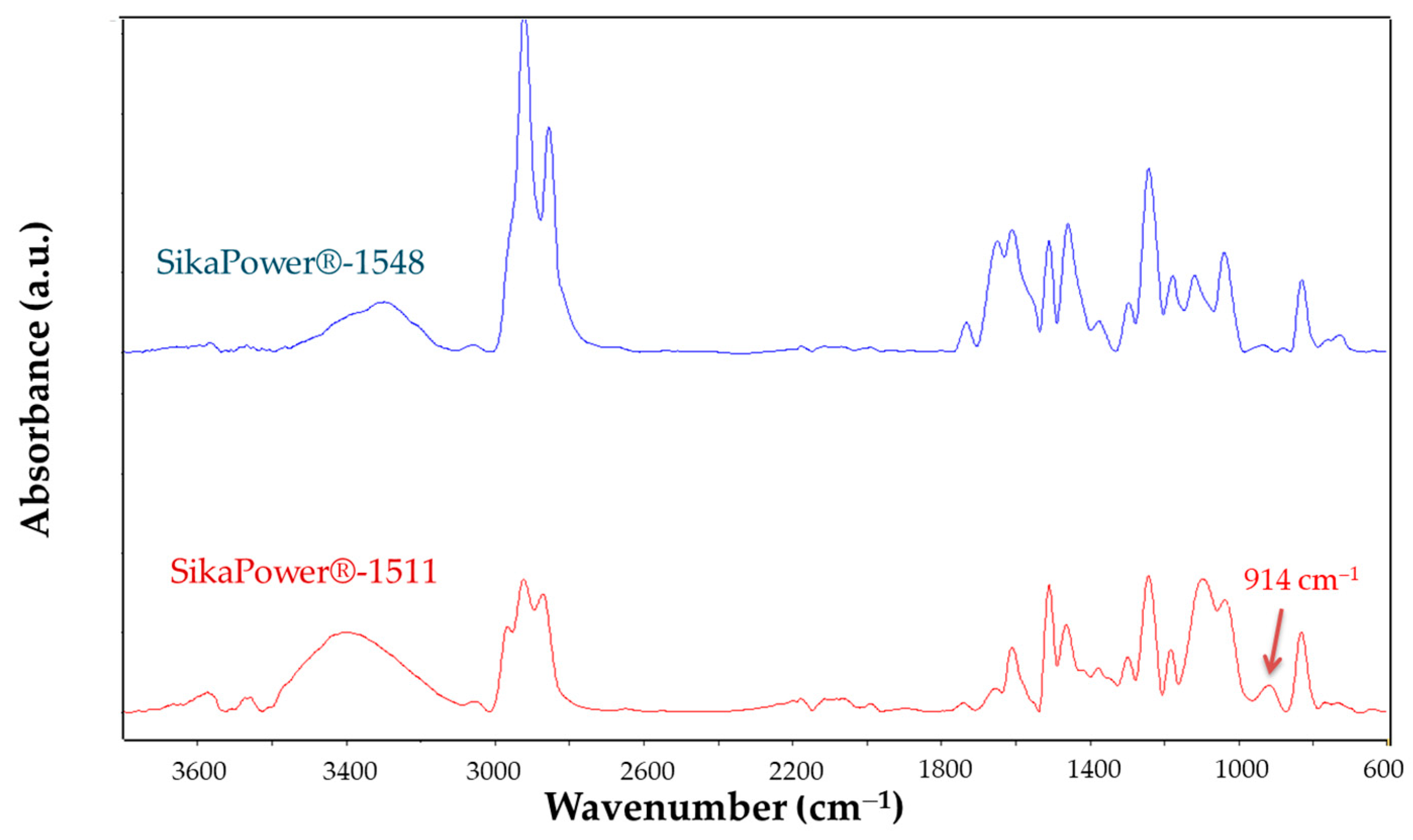
2.2.2. FTIR Spectroscopy
2.3. Mechanical Characteristics of Adhesives
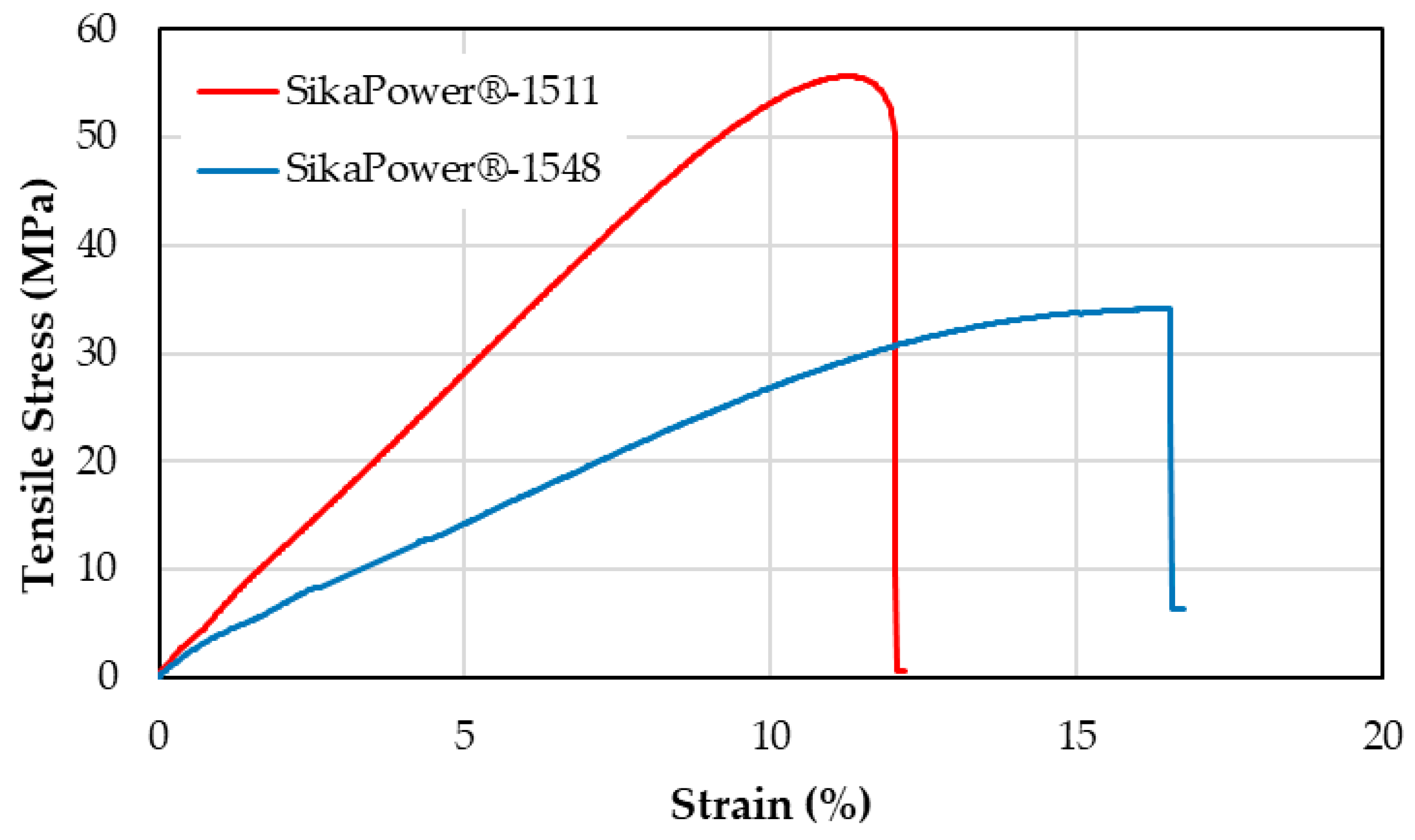
2.3.1. Tensile Test
2.3.2. Hardness Test
2.4. Surface Treatment of Steel
2.5. Shear Tests
3. Results
3.1. Curing Kinetic of the Selected Adhesives
3.2. Glass Transaction Temperature
3.3. Mechanical Properties of the Selected Adhesives
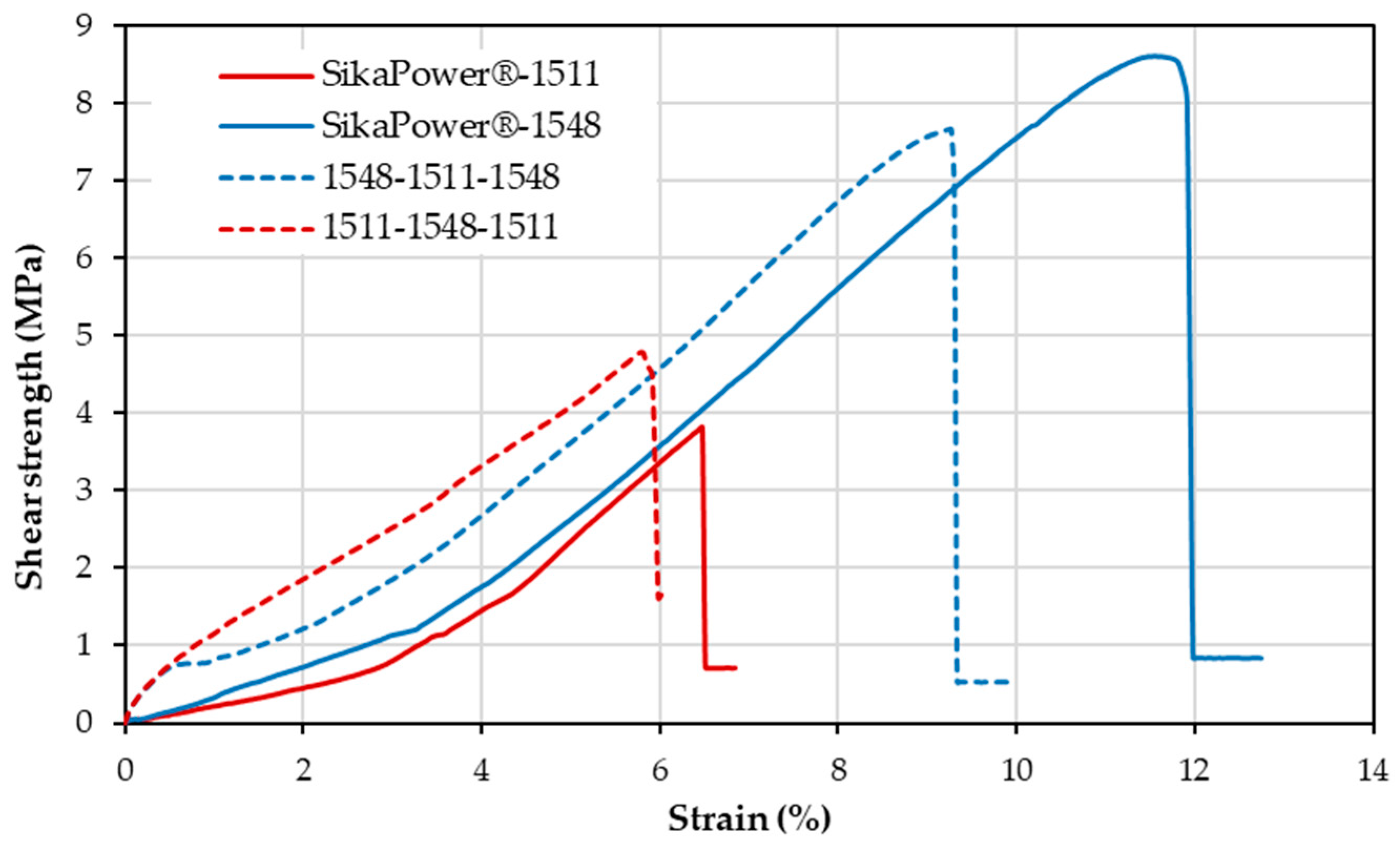
3.4. Shear Behavior and Graduated Joints
4. Numerical Analysis
4.1. Model Development
4.1.1. Material Properties
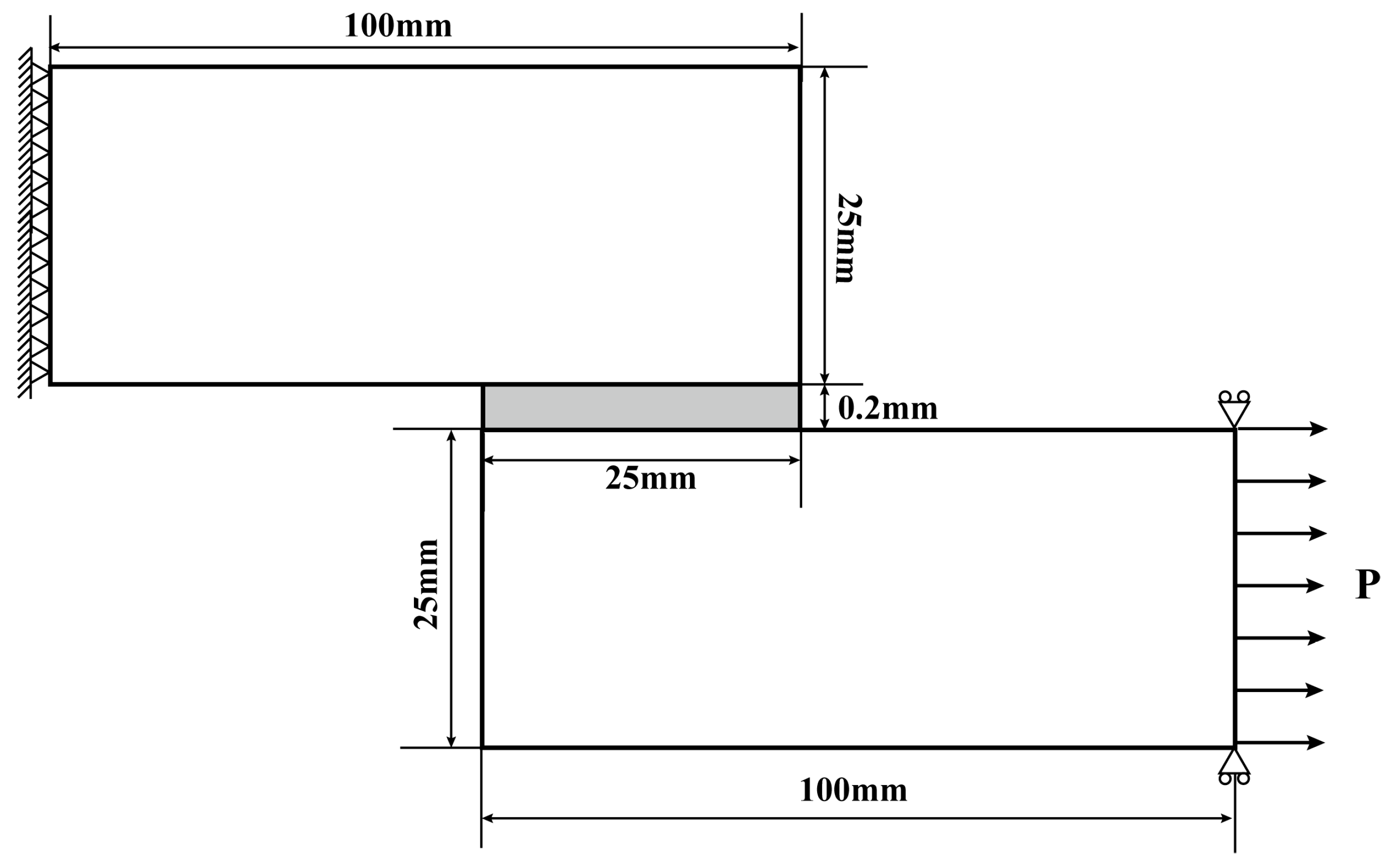
4.1.2. Joint Geometries and Conditions
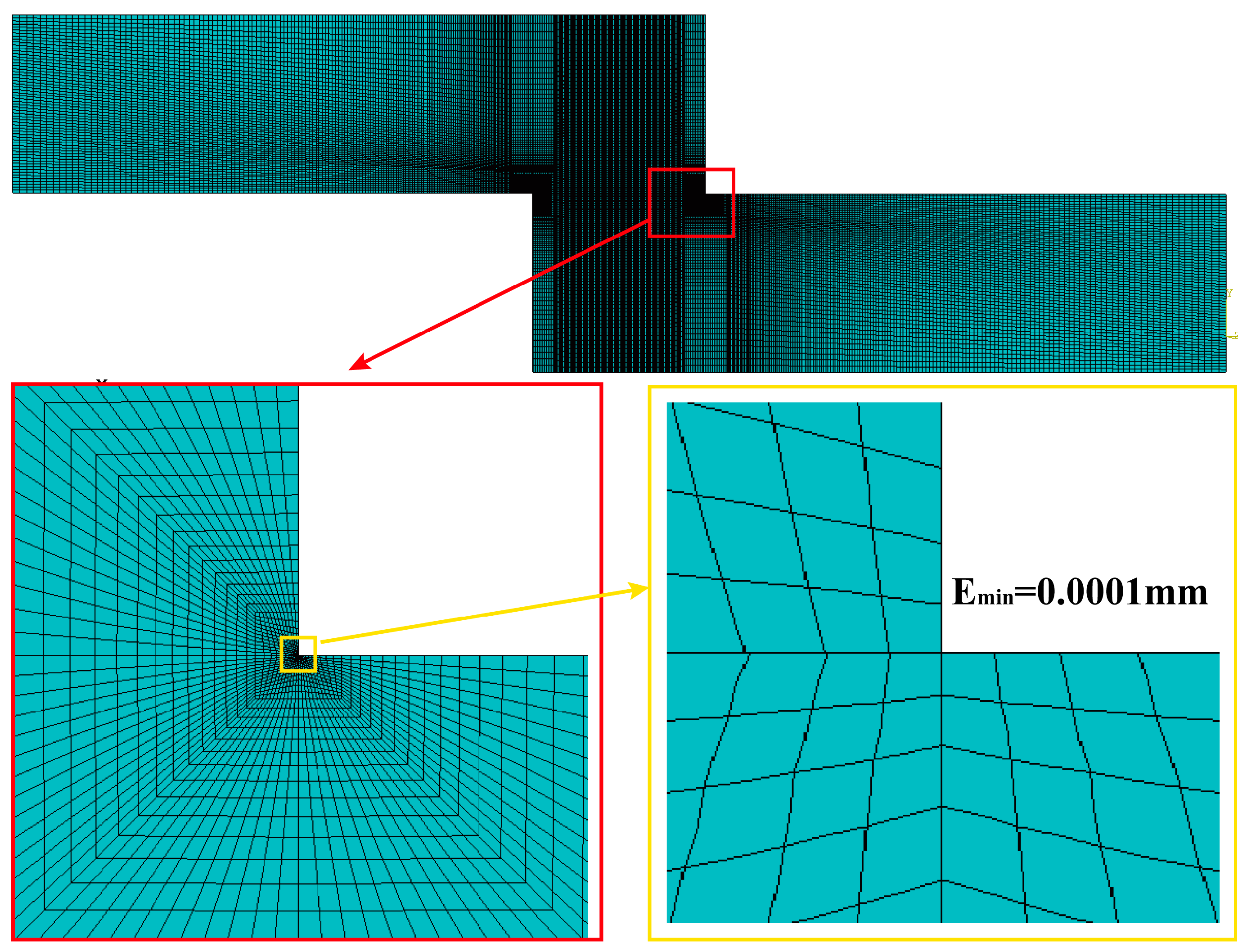
4.1.3. Meshing
4.2. Simulation Process
4.2.1. Functionally Graded Adhesive Joints
4.2.2. Simulation Analysis
4.3. Numerical Results
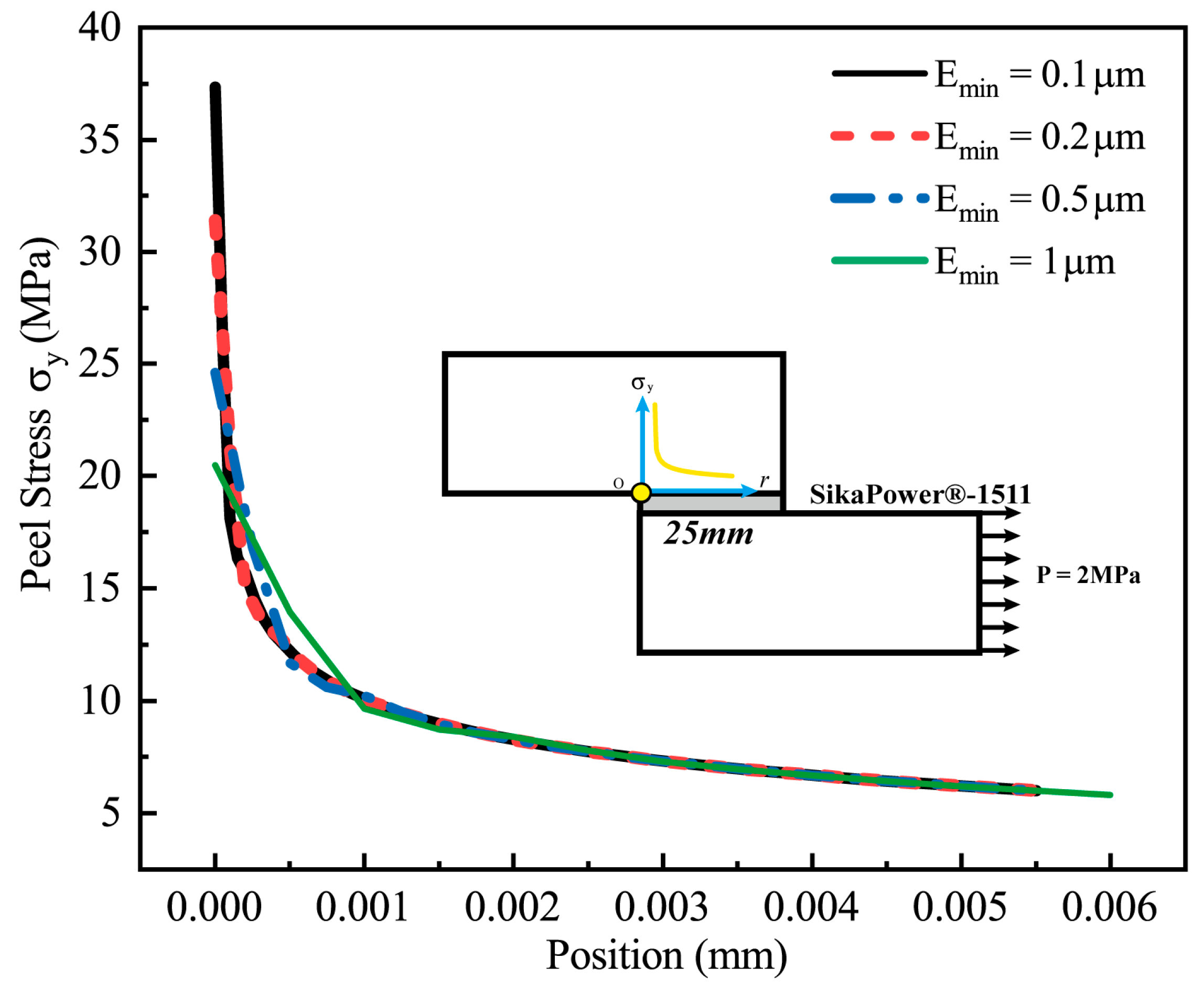
4.3.1. Mesh Sensitivity Analysis
4.3.2. Experimental and Numerical Failure Strength
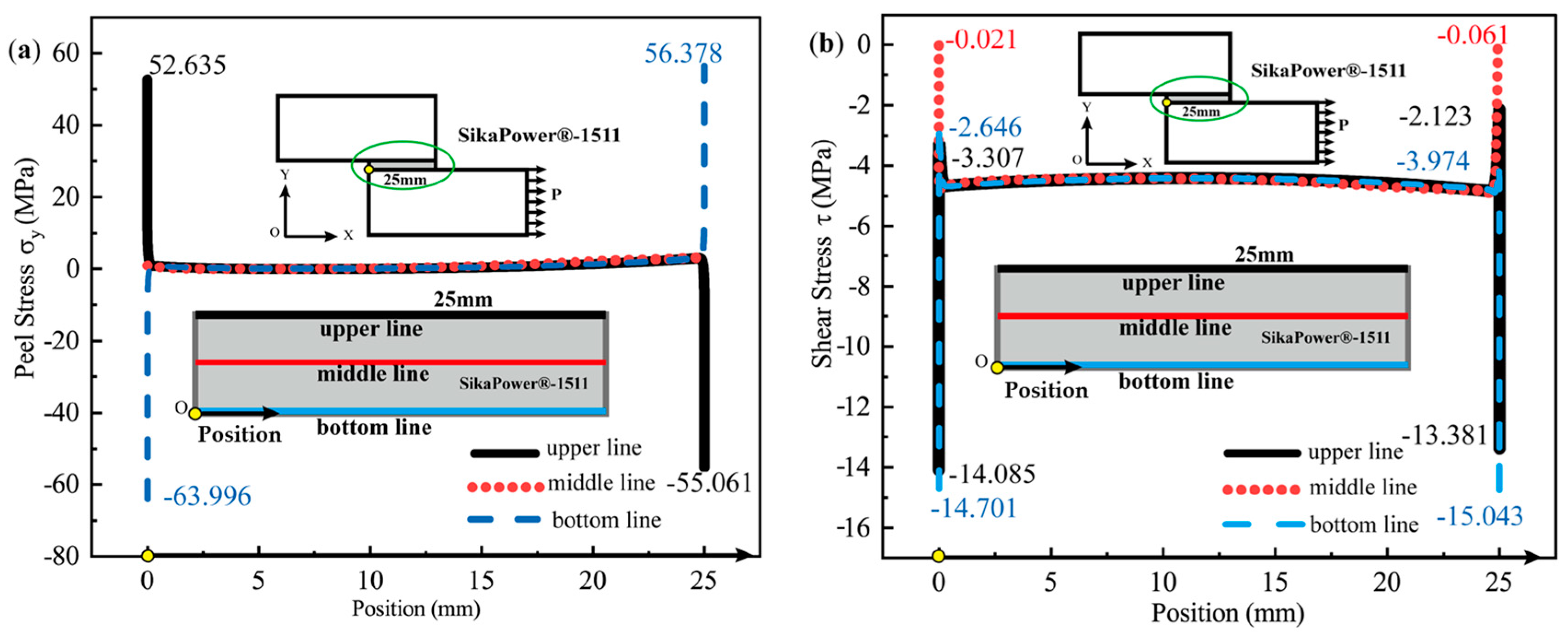
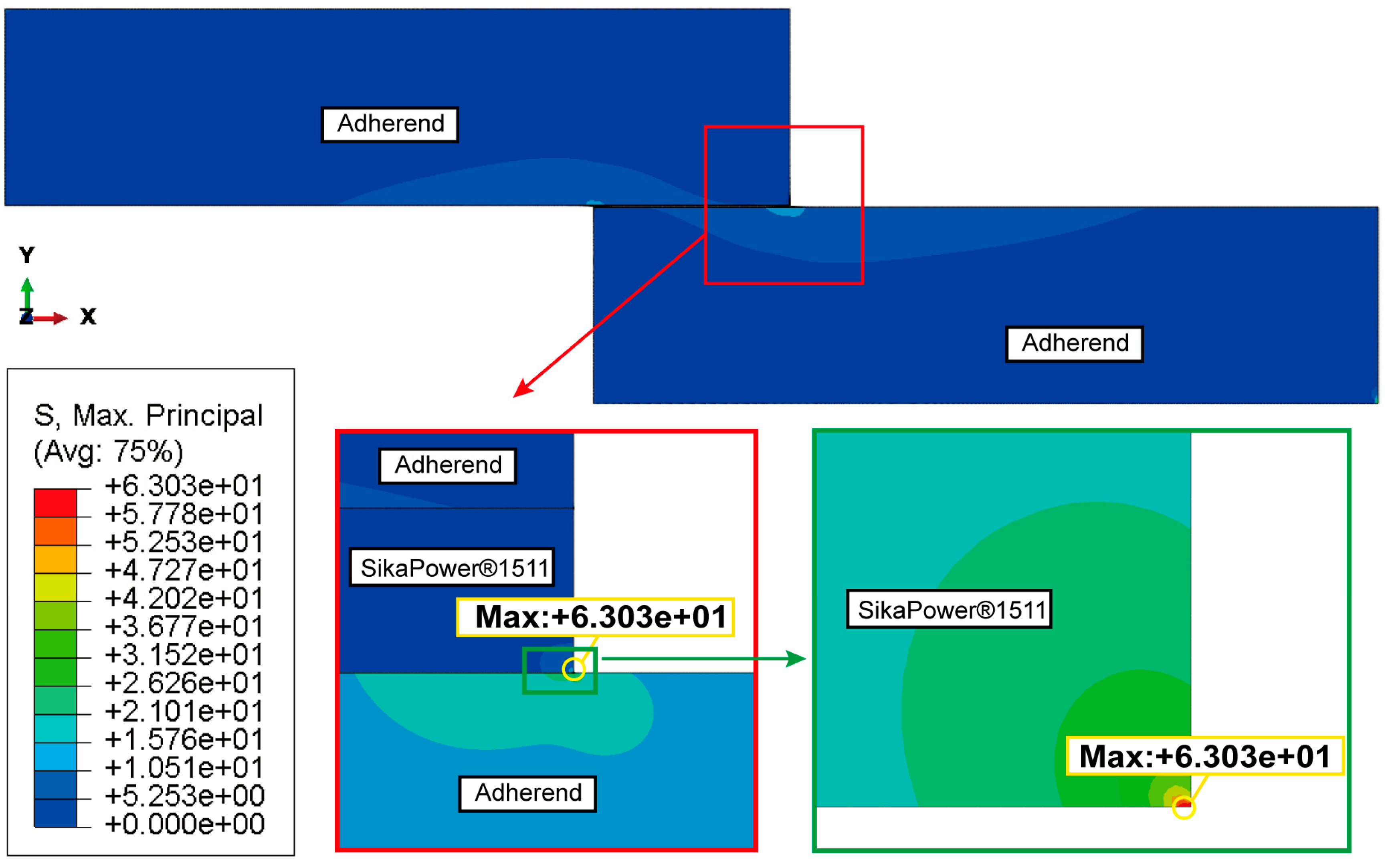
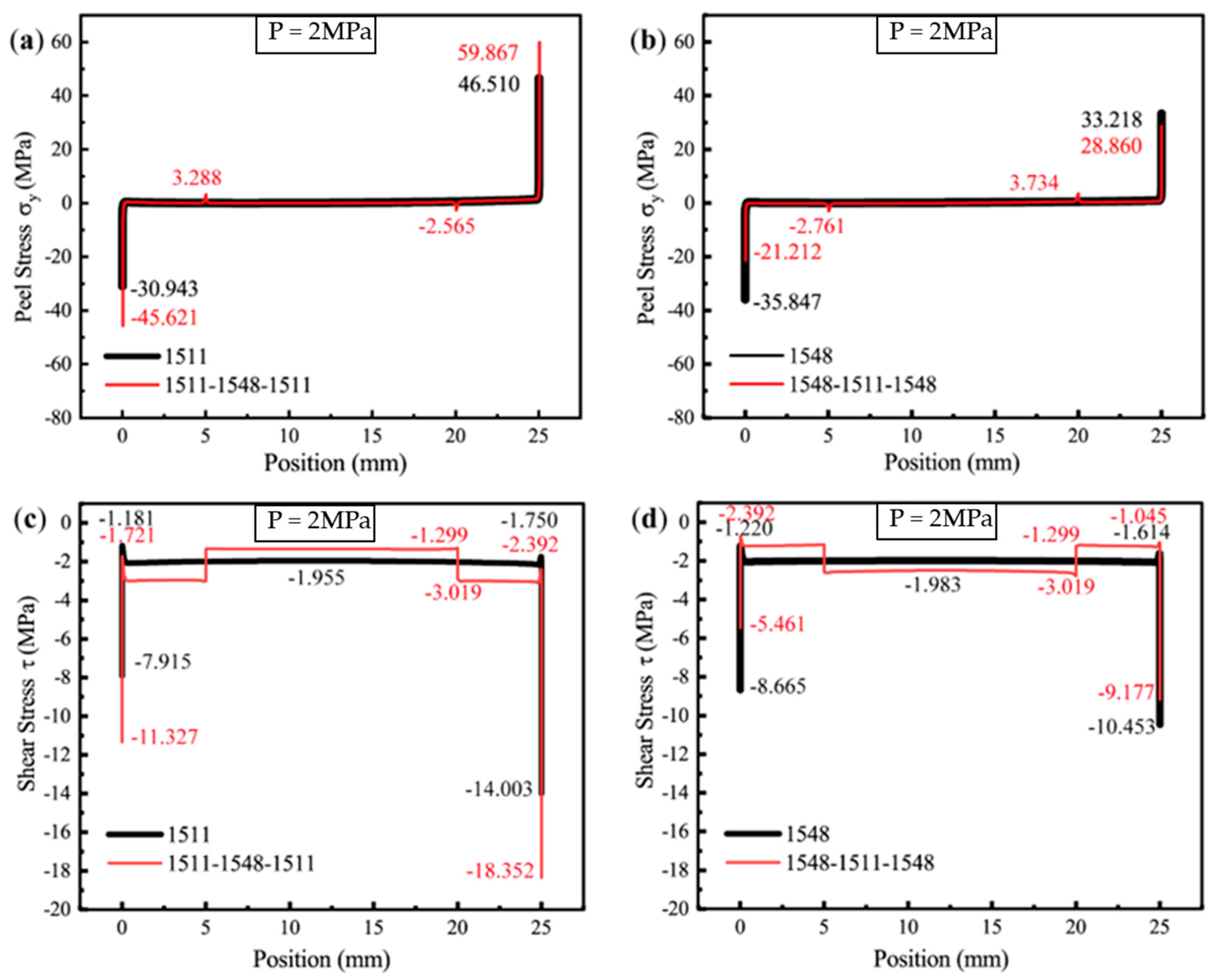
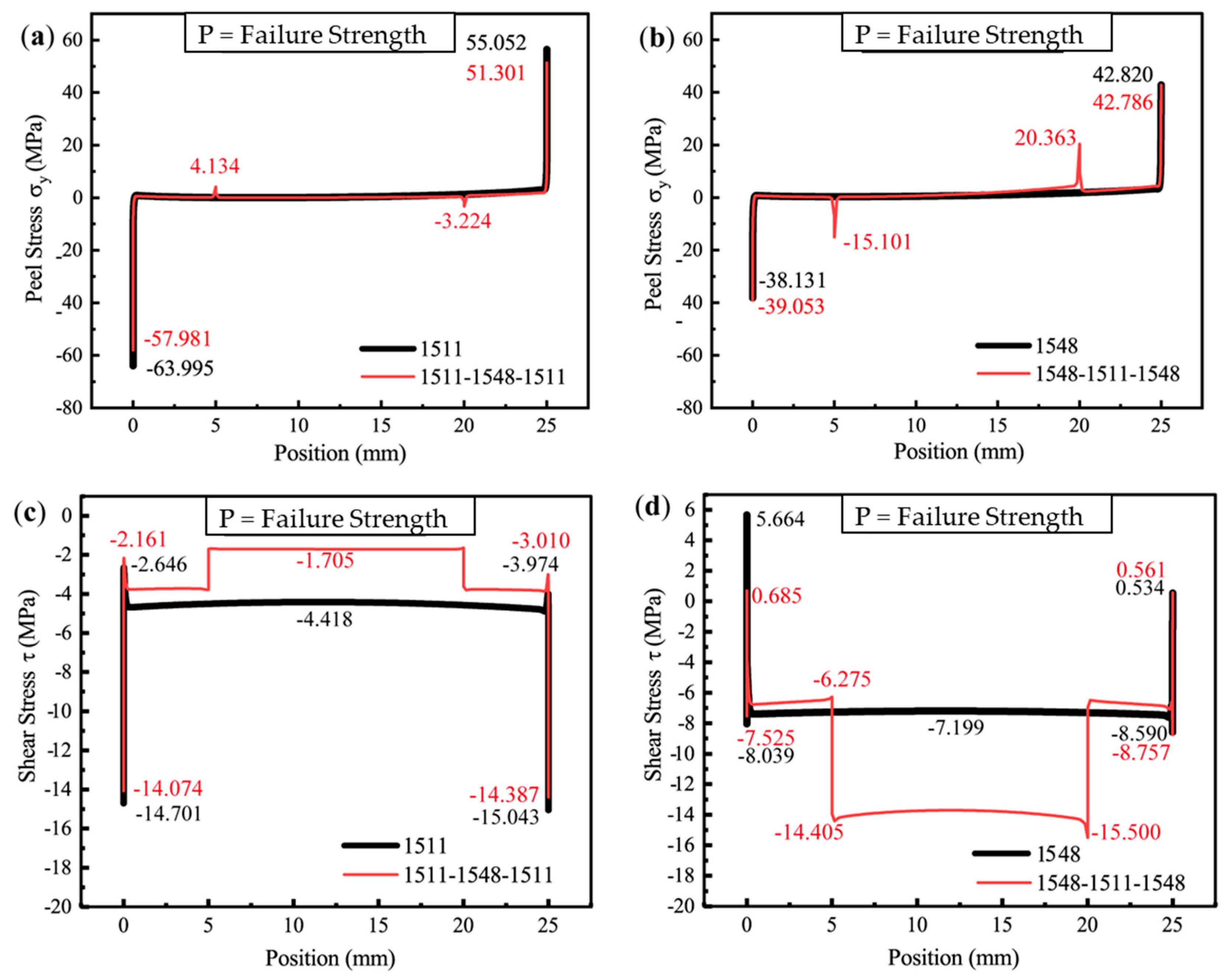
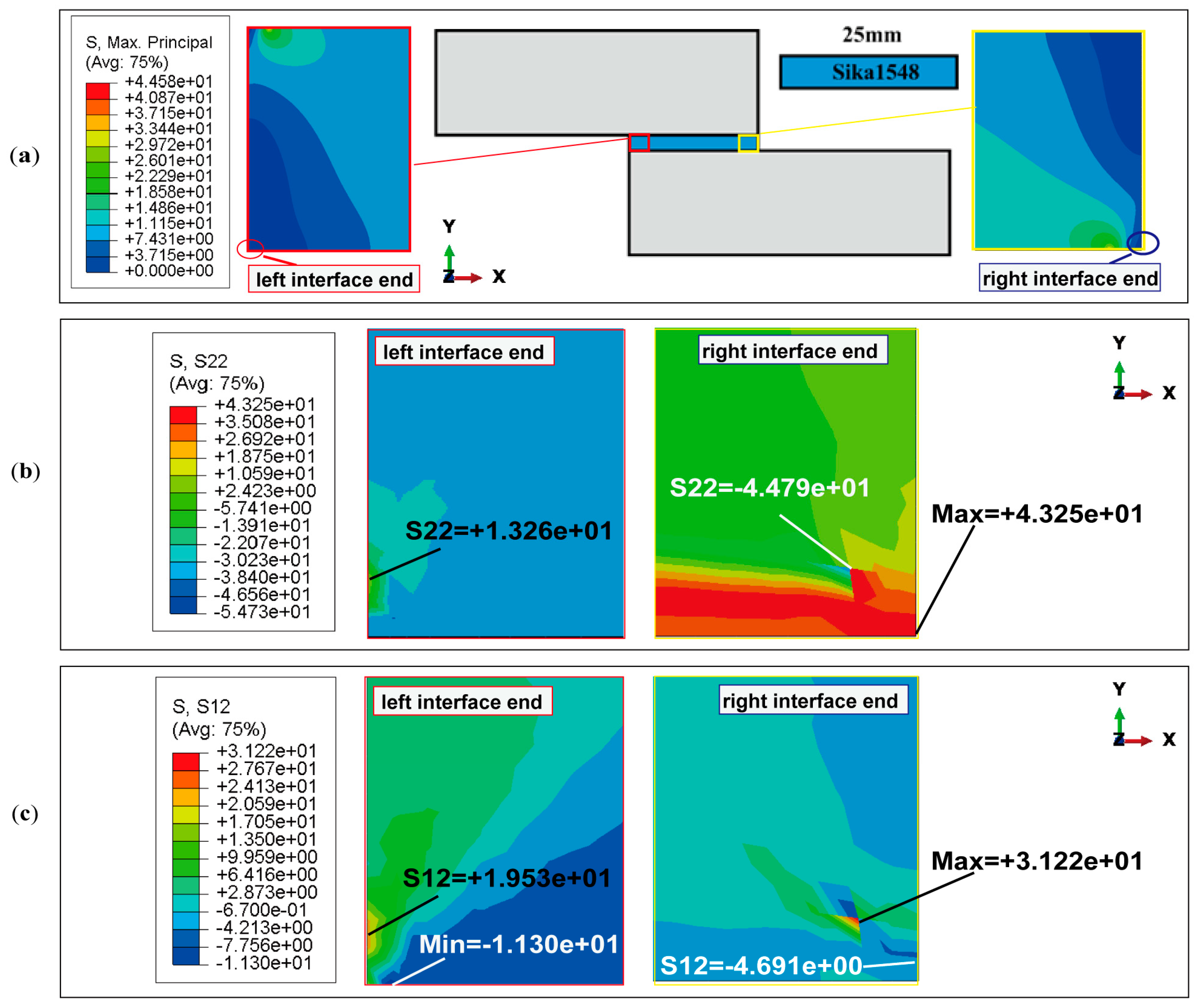
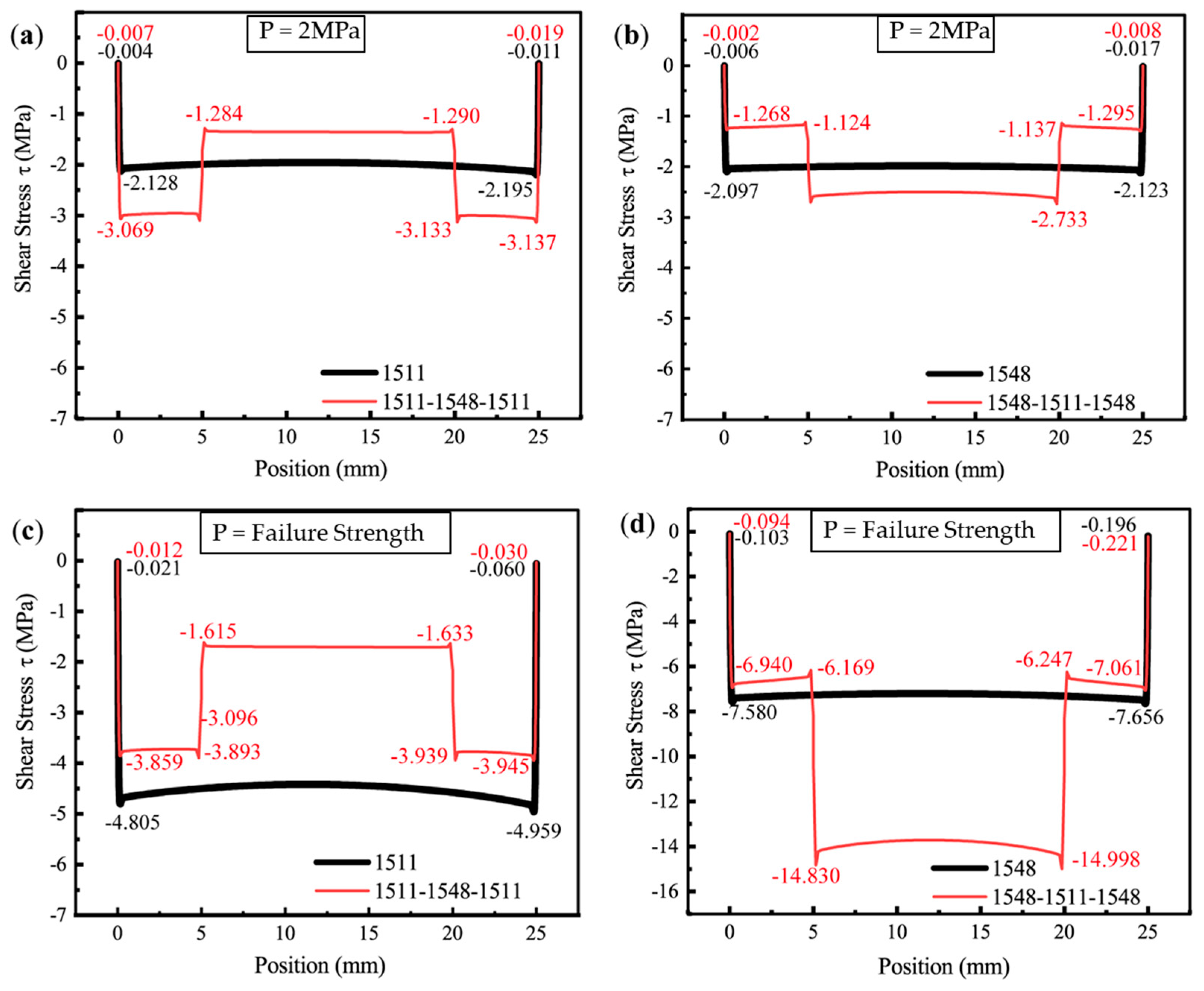
4.3.3. Stress Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karthikeyan, N.; Naveen, J. Progress in adhesive-bonded composite joints: A comprehensive review. J. Reinf. Plast. Compos. 2024. [Google Scholar] [CrossRef]
- Wei, Y.; Jin, X.; Luo, Q.; Li, Q.; Sun, G. Adhesively bonded joints–A review on design, manufacturing, experiments, modeling and challenges. Compos. Part B 2024, 276, 111225. [Google Scholar] [CrossRef]
- Borges, C.S.P.; Akhavan-Safar, A.; Tsokanas, P.; Carbas, R.J.C.; Marques, E.A.S.; da Silva, L.F.M. From fundamental concepts to recent developments in the adhesive bonding technology: A general view. Discov. Mech. Eng. 2023, 2, 8. [Google Scholar] [CrossRef]
- Desai, C.R.; Patel, D.C.; Desai, C.K. Investigations of joint strength & fracture parameter of adhesive joint: A review. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Jeevi, G.; Nayak, S.K.; Abdul Kader, M. Review on adhesive joints and their application in hybrid composite structures. J. Adhes. Sci. Technol. 2019, 33, 1497–1520. [Google Scholar] [CrossRef]
- Schlechte, J.S. Advances in Structural Adhesive Bonding; Woodhead Publishing: Cambridge, UK, 2023; pp. 3–67. [Google Scholar] [CrossRef]
- Zhou, M.-H.; Yin, G.-Z.; Prolongo, S.G. Review of thermal conductivity in epoxy thermosets and composites: Mechanisms, parameters, and filler influences. Adv. Ind. Eng. Polym. Res. 2024, 7, 295–308. [Google Scholar] [CrossRef]
- Sun, S.; Yu, Q.; Yu, B.; Zhou, F. New Progress in the Application of Flame-Retardant Modified Epoxy Resins and Fire-Retardant Coatings. Coatings 2023, 13, 1663. [Google Scholar] [CrossRef]
- Makhmetova, A.; Negim, E.-S.; Ainakulova, D.; Yeligbayeva, G.; Khatib, J. An Overview of Epoxy Resins as coating to protect metals from corrosion. Complex Use Miner. Resour. 2024, 328, 20–32. [Google Scholar] [CrossRef]
- Faggio, N.; Marotta, A.; Ambrogi, V.; Cerruti, P.; Gentile, G. Fully bio-based furan/maleic anhydride epoxy resin with enhanced adhesive properties. J. Mater. Sci. 2023, 58, 7195–7208. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Z.; Luo, Y. One-component epoxy resin adhesive featured with high storage stability based on microencapsulation. Colloids Surf. Physicochem. Eng. Asp. 2024, 683, 133045. [Google Scholar] [CrossRef]
- La, L.B.T.; Nguyen, H.; Tran, L.C.; Su, X.; Meng, Q.; Kuan, H.-C.; Ma, J. Exfoliation and dispersion of graphene nanoplatelets for epoxy nanocomposites. Adv. Nanocompos. 2024, 1, 39–51. [Google Scholar] [CrossRef]
- Khalid, M.Y.; Kamal, A.; Otabil, A.; Mamoun, O.; Liao, K. Graphene/epoxy nanocomposites for improved fracture toughness: A focused review on toughening mechanism. Chem. Eng. J. Adv. 2023, 16, 100537. [Google Scholar] [CrossRef]
- Białkowska, A.; Bakar, M.; Kucharczyk, W.; Zarzyka, I. Hybrid epoxy nanocomposites: Improvement in mechanical properties and toughening mechanisms—A review. Polymers 2023, 15, 1398. [Google Scholar] [CrossRef] [PubMed]
- Ba, H.; Guo, L.; Huan, H.; Zhang, S.; Lin, Z. Multi-objective optimization of epoxy resin adhesive for pavement toughened by self-made toughening agent. Polymers 2023, 15, 1946. [Google Scholar] [CrossRef]
- Huo, M.; Chen, J.; Jin, C.; Huo, S.; Liu, G.; Kong, Z. Preparation, characterization, and application of waterborne lignin-based epoxy resin as eco-friendly wood adhesive. Int. J. Biol. Macromol. 2024, 259, 129327. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; He, H.; Shen, Y.; Li, Q. High peel strength and excellent solder heat-resistance epoxy adhesive for flexible copper clad laminate. J. Appl. Polym. Sci. 2023, 140, e54596. [Google Scholar] [CrossRef]
- Cherian, R.M.; Unnikrishnan, T.G.; Cherian, M.; Joy, J.; Chirayil, C.J.; Panneerselvam, K.; Thomas, S. Chapter 11—Epoxy resins: Synthesis, structure, and properties. In Handbook of Thermosetting Foams, Aerogels, and Hydrogels; Elservier: Amsterdam, The Netherlands, 2024; pp. 251–286. [Google Scholar] [CrossRef]
- Huang, C.; Sun, X.; Yuan, H.; Song, C.; Meng, Y.; Li, X. Study on the reactivity and kinetics of primary and secondary amines during epoxy curing by NIR spectroscopy combined with multivariate analysis. Vib. Spectrosc. 2020, 106, 102993. [Google Scholar] [CrossRef]
- Puhurcuoğlu, N.; Arman, Y. Parameter estimation of epoxy resin cure kinetics by dynamics DSC data. Polym. Adv. Technol. 2024, 35, e6498. [Google Scholar] [CrossRef]
- Chu, C.-W.; Cheng, C.-H.; Obayashi, K.; Bayomi, R.A.H.; Takahara, A.; Kojio, K. Effects of curing conditions on adhesive and fatigue properties of hydrogenated epoxy resins in bulk state and single-lap-joint configuration. Int. J. Adhes. Adhes. 2024, 132, 103690. [Google Scholar] [CrossRef]
- Achilias, D.S.; Karabela, M.M.; Varkopoulou, E.A.; Sideridou, I.D. Cure kinetics study of two epoxy systems with fourier tranform infrared spectroscopy (FTIR) and differential scanning calorimetry (DSC). J. Macromol. Sci. Part A 2012, 49, 630–638. [Google Scholar] [CrossRef]
- Prime, R.B.; Bair, H.E.; Vyazovkin, S.; Gallagher, P.K.; Riga, A. Thermogravimetric analysis (TGA). In Thermal Analysis of Polymers: Fundamentals and Applications; Menczel, J.D., Prime, R.B., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 241–317. [Google Scholar] [CrossRef]
- Senturia, S.D.; Sheppard, N.F., Jr. Epoxy Resins and Composites IV; Springer: Heidelberg, Germany, 2005; pp. 1–47. [Google Scholar] [CrossRef]
- Fraga, F.; Vazquez, E.C.; Rodríguez-Núñez, E.; Martínez-Ageitos, J.M. Curing kinetics of the epoxy system diglycidyl ether of bisphenol A/isophoronediamine by Fourier transform infrared spectroscopy. Polym. Adv. Technol. 2008, 19, 1623–1628. [Google Scholar] [CrossRef]
- Rothenhäusler, F.; Kettenbach, M.; Ruckdaeschel, H. Influence of the Stoichiometric Ratio on the Curing Kinetics and Mechanical Properties of Epoxy Resin Cured with a Rosin-Based Anhydride. Macromol. Mater. Eng. 2023, 308, 2300122. [Google Scholar] [CrossRef]
- Gupta, N.; Mahendran, A.R.; Weiss, S.; Khalifa, M. Thermal curing behavior of phenol formaldehyde resin-impregnated paper evaluated using DSC and dielectric analysis. J. Therm. Anal. Calorim. 2024, 149, 2609–2618. [Google Scholar] [CrossRef]
- Okeola, A.A.; Hernandez-Limon, J.E.; Tatar, J. Core-Shell Rubber Nanoparticle-Modified CFRP/Steel Ambient-Cured Adhesive Joints: Curing Kinetics and Mechanical Behavior. Materials 2024, 17, 749. [Google Scholar] [CrossRef]
- El-Aouni, N.; Dagdag, O.; Haldhar, R.; Kim, S.-C.; Azogagh, M.; Berisha, A.; Sherif, E.-S.M.; Hsissou, R.; Elbachiri, A.; Ebenso, E.E.; et al. One-pot synthesis of epoxy resin composite: Thermal, rheological and Monte Carlo investigations. Iran. Polym. J. 2023, 33, 435–445. [Google Scholar] [CrossRef]
- Deriszadeh, A.; Shahraki, F.; Mostafa, L.; Ali, A.B.M.; Mohebbi-Kalhori, D.; Salahshour, S.; Alizad, A. Epoxy/phenolic nanocomposite based adhesives: Non-isothermal cure kinetic study. Results Eng. 2024, 24, 103312. [Google Scholar] [CrossRef]
- Şengül, B.; Tüzün, F.N. Investigation and assessment of epoxy resin adhesives using Fourier-transform infrared spectrometry. Mater. Werkst. 2023, 54, 345–358. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, L.; Guo, X.; Cai, Z.; Huang, K. Study on curing kinetics of epoxy system and DFT simulation. J. Therm. Anal. Calorim. 2023, 148, 11069–11079. [Google Scholar] [CrossRef]
- Duller, M.; Mahendran, A.R.; Zikulnig-Rusch, E.M. Investigating the thermal cure behavior of sorbitol-derived biobased melamine–formaldehyde impregnation resins using DSC and FTIR analysis. J. Therm. Anal. Calorim. 2024, 149, 10865–10884. [Google Scholar] [CrossRef]
- Jouenne, J.-B.; Barbier, D.; Hounkpati, V.; Cauret, L.; Vivet, A. Influence of flax fibers on the curing kinetics of bio-based epoxy resin. J. Mater. Sci. 2024, 59, 12418–12432. [Google Scholar] [CrossRef]
- YÜKsel, O.; Yildirim, E.; YÜCel, O.; EmİK, S. Synthesis and Investigation of Thermal and Dynamic Mechanical Properties of Urethane-Containing Epoxy Resins. J. Turk. Chem. Soc. Sect. B Chem. Eng. 2023, 6, 95–106. [Google Scholar] [CrossRef]
- Singh, S.K.; Kandpal, S.; Rajpoot, M.S.; Chandra, P. Investigating the Mechanical and Thermal Properties of PDMS-Toughened Epoxy Resins for Advanced Adhesive Solutions. J. Mater. Sci. Chem. Eng. 2024, 12, 18–29. [Google Scholar] [CrossRef]
- Aliakbari, M.; Moini Jazani, O.; Moghadam, M.; Martín-Martínez, J.M. Manipulating a novel epoxy-based composite with core–shell rubber particles for designing a structural adhesive in aluminum–aluminum bonded joints. Polym. Adv. Technol. 2024, 35, 6564. [Google Scholar] [CrossRef]
- Wang, Y.; Nian, G.; Yang, X.; Suo, Z. Lap shear of a soft and elastic adhesive. Mech. Mater. 2021, 158, 103845. [Google Scholar] [CrossRef]
- Cui, J.; Wang, S.; Wang, S.; Chen, S.; Li, G. Strength and failure analysis of adhesive single-lap joints under shear loading: Effects of surface morphologies and overlap zone parameters. J. Manuf. Process. 2020, 56, 238–247. [Google Scholar] [CrossRef]
- Naat, N.; Boutar, Y.; Naïmi, S.; Mezlini, S.; Da Silva, L.F.M. Effect of surface texture on the mechanical performance of bonded joints: A review. J. Adhes. 2023, 99, 166–258. [Google Scholar] [CrossRef]
- Kanani, A.Y.; Hou, X.; Laidlaw, R.; Ye, J. The effect of joint configuration on the strength and stress distributions of dissimilar adhesively bonded joints. Eng. Struct. 2021, 226, 111322. [Google Scholar] [CrossRef]
- Sousa, F.C.; Akhavan-Safar, A.; Carbas, R.J.C.; Marques, E.A.S.; Goyal, R.; Jennings, J.; da Silva, L.F.M. Investigation of geometric and material effects on the fatigue performance of composite and steel adhesive joints. Compos. Struct. 2024, 344, 118313. [Google Scholar] [CrossRef]
- Guo, L.; Liu, J.; Xia, H.; Li, X.; Zhang, X.; Yang, H.; Yang, Y. Effects of loading rate, temperature, and thickness on the tensile strength of precision adhesive joints. Polym. Test. 2022, 109, 107528. [Google Scholar] [CrossRef]
- dos Reis, M.Q.; Marques, E.A.S.; Carbas, R.J.C.; da Silva, L.F.M. Functionally graded adherends in adhesive joints: An overview. J. Adv. Join. Process. 2020, 2, 100033. [Google Scholar] [CrossRef]
- Marques, J.B.; Barbosa, A.Q.; da Silva, C.I.; Carbas, R.J.C.; da Silva, L.F.M. An overview of manufacturing functionally graded adhesives–Challenges and prospects. J. Adhes. 2019, 97, 172–206. [Google Scholar] [CrossRef]
- Boulenouar, A.; Bouchelarm, M.A.; Chafi, M. Numerical investigation of cracked metal/ceramic FGM plates repaired with bonded composite patch. Int. J. Interact. Des. Manuf. (IJIDeM) 2024, 18, 649–658. [Google Scholar] [CrossRef]
- Benali, A.; Cellard, C.; Sohier, L.; Moretti, A.; Créac’hcadec, R. Modelling edge effects at the interface in bonded joints using gradient functions in the mechanical properties of the adhesive: Application of the method to the Arcan test loaded in tension and shear. Int. J. Adhes. Adhes. 2023, 120, 103294. [Google Scholar] [CrossRef]
- Jia, Z.; Yu, J.; Liu, Q.; Yu, S.; Wang, Z. Functionally graded adhesive joints with exceptional strength and toughness by graphene nanoplatelets reinforced epoxy adhesives. Int. J. Adhes. Adhes. 2023, 125, 103402. [Google Scholar] [CrossRef]
- Ferreira, C.; Campilho, R.; Moreira, R. Bonded structures improvement by the dual adhesive technique. Procedia Struct. Integr. 2020, 28, 1116–1124. [Google Scholar] [CrossRef]
- Khan, M.A.; Tipireddy, R.; Dattaguru, B.; Kumar, S. Stochastic modeling of functionally graded double lap adhesive joints. Mech. Mater. 2023, 177, 104553. [Google Scholar] [CrossRef]
- Akhavan-Safar, A.; Ramezani, F.; Delzendehrooy, F.; Ayatollahi, M.R.; da Silva, L.F.M. A review on bi-adhesive joints: Benefits and challenges. Int. J. Adhes. Adhes. 2022, 114, 103098. [Google Scholar] [CrossRef]
- da Silva, C.I.; Cunha, M.R.O.; Barbosa, A.Q.; Carbas, R.J.C.; Marques, E.A.S.; da Silva, L.F.M. Functionally graded adhesive joints using magnetic microparticles with a polyurethane adhesive. J. Adv. Join. Process. 2021, 3, 100048. [Google Scholar] [CrossRef]
- Ramalho, L.D.C.; Campilho, R.D.S.G.; Belinha, J.; da Silva, L.F.M. Static strength prediction of adhesive joints: A review. Int. J. Adhes. Adhes. 2020, 96, 102451. [Google Scholar] [CrossRef]
- Hasheminia, S.M.; Park, B.C.; Chun, H.-J.; Park, J.-C.; Chang, H.S. Failure mechanism of bonded joints with similar and dissimilar material. Compos. Part B Eng. 2019, 161, 702–709. [Google Scholar] [CrossRef]
- Kim, M.-H.; Hong, H.-S.; Kim, Y.-C. Determination of failure envelope of functionally graded adhesive bonded joints by using mixed mode continuum damage model and response surface method. Int. J. Adhes. Adhes. 2021, 106, 102815. [Google Scholar] [CrossRef]
- Nimje, S.V.; Panigrahi, S.K. Damage behaviour in functionally graded structural adhesive joints with double lap joint configuration. In Structural Adhesive Joints; Mittal, K.L., Panigrahi, S.K., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020; pp. 221–245. [Google Scholar]
- Dadian, A.; Rahnama, S. Experimental and numerical study of optimum functionally graded Aluminum/GFRP adhesive lap shear joints using Epoxy/CTBN. Int. J. Adhes. Adhes. 2021, 107, 102854. [Google Scholar] [CrossRef]
- Li, R.; Noda, N.-A.; Takaki, R.; Sano, Y.; Takase, Y.; Miyazaki, T. Most suitable evaluation method for adhesive strength to minimize bend effect in lap joints in terms of the intensity of singular stress field. Int. J. Adhes. Adhes. 2018, 86, 45–58. [Google Scholar] [CrossRef]
- Sika Hellas. Product Data Sheet: SikaPower®-1511. 2020. Available online: https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://grc.sika.com/dms/getdocument.get/435e3071-7a94-43be-ad05-8e30be6f6020/013106155110001000_SikaPower_1511_eng.pdf&ved=2ahUKEwj9qcOp6bOKAxUiVqQEHX8BKvoQFnoECBgQAQ&usg=AOvVaw0TMBeaDYUIqOP3nQMaDZIG (accessed on 20 November 2024).
- Sika Hellas. Product Data Sheet: SikaPower®-1548. 2019. Available online: https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://ita.sika.com/dms/getdocument.get/7df29c35-3696-4966-b08a-816759f38da5/sikapower_-1548.pdf&ved=2ahUKEwj0xMTz6bOKAxWHTaQEHXMNHK0QFnoECBwQAQ&usg=AOvVaw11Aah0oPy0BpnfuoHK3D3Q (accessed on 20 November 2024).
- Vyazovkin, S.; Wight, C.A. Isothermal and non-isothermal kinetics of thermally stimulated reactions of solids. Int. Rev. Phys. Chem. 1998, 17, 407–433. [Google Scholar] [CrossRef]
- Barbosa, A.Q.; da Silva, L.F.M.; Abenojar, J.; Figueiredo, M.; Öchsner, A. Toughness of a brittle epoxy resin reinforced with micro cork particles: Effect of size, amount and surface treatment. Compos. Part B Eng. 2017, 114, 299–310. [Google Scholar] [CrossRef]
- UNE-EN ISO 527-1:2020; Plastics-Determination of Tensile Properties-Part 1: General Principles. UNE, the Spanish Association for Standardization: Madrid, Spain, 2020.
- ASTM D2240-15(2021); Standard Test Method for Rubber Property—Durometer Hardness. ASTM International: Conshohocken, PA, USA, 2021.
- da Silva, L.F.M.; Rodrigues, T.N.S.S.; Figueiredo, M.A.V.; de Moura, M.F.S.F.; Chousal, J.A.G. Effect of Adhesive Type and Thickness on the Lap Shear Strength. J. Adhes. 2006, 82, 1091–1115. [Google Scholar] [CrossRef]
- Socrates, G. Infrared and Raman Characteristic Group Frequencies: Tables and Charts, 3rd ed.; John Wiley & Sons LTD: West Sussex, UK, 2004. [Google Scholar] [CrossRef]
- Saleh, T.A. Surface Science of Adsorbents and Nanoadsorbents. In Interface Science and Technology; Saleh, T.A., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; Volume 34, pp. 1–38. [Google Scholar]
- Noda, N.-A.; Chen, D.; Zhang, G.; Sano, Y. Single-fiber pull-out analysis comparing the intensities of singular stress fields (ISSFs) at fiber end/entry points. Int. J. Mol. Sci. 2020, 165, 105196. [Google Scholar] [CrossRef]
- Noda, N.-A.; Takaki, R.; Sano, Y.; Wang, B. ISSF method to evaluate adhesive strength when two distinct singular stress fields appear along the interface. Indones. J. For. Res. 2023, 241, 95–114. [Google Scholar] [CrossRef]
- Dundurs, J. Discussion:“Edge-bonded dissimilar orthogonal elastic wedges under normal and shear loading”(Bogy, DB, 1968, ASME J. Appl. Mech., 35, pp. 460–466). J. Appl. Mech. 1969, 36, 650–652. [Google Scholar] [CrossRef]
- Noda, N.-A.; Miyazaki, T.; Li, R.; Uchikoba, T.; Sano, Y.; Takase, Y. Debonding strength evaluation in terms of the intensity of singular stress at the interface corner with and without fictitious crack. Int. J. Adhes. Adhes. 2015, 61, 46–64. [Google Scholar] [CrossRef]
- Noda, N.-A.; Li, R.; Miyazaki, T.; Takaki, R.; Sano, Y. Convenient adhesive strength evaluation method in terms of the intensity of singular stress field. Int. J. Comput. Methods 2019, 16, 1850085. [Google Scholar] [CrossRef]
- Kamal, M.; Sourour, S. Kinetics and thermal characterization of thermoset cure. Polym. Eng. Sci. 1973, 13, 59–64. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction kinetics in differential thermal analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Wight, C.A. Model-free and model-fitting approaches to kinetic analysis of isothermal and nonisothermal data. Thermochim. Acta 1999, 340, 53–68. [Google Scholar] [CrossRef]
- Abenojar, J.; Enciso, B.; Pantoja, M.; Velasco, F.; Martínez, M.-A. Thermal characterization and diffusivity of two mono-component epoxies for transformer insulation. Int. J. Adhes. Adhes. 2020, 103, 102726. [Google Scholar] [CrossRef]
- Abenojar, J.; Lopez de Armentia, S.; Barbosa, A.Q.; Martinez, M.A.; del Real, J.C.; da Silva, L.F.M.; Velasco, F. Magnetic cork particles as reinforcement in an epoxy resin: Effect of size and amount on thermal properties. J. Therm. Anal. Calorim. 2022, 148, 1981–1995. [Google Scholar] [CrossRef]
- Abenojar, J.; Tutor, J.; Ballesteros, Y.; del Real, J.C.; Martínez, M.A. Erosion-wear, mechanical and thermal properties of silica filled epoxy nanocomposites. Compos. Part B Eng. 2017, 120, 42–53. [Google Scholar] [CrossRef]
- Polymer Innovation Blog: Epoxy Curing Agents–Mercaptans, The Ultimate Quick Ambient Cure. Available online: https://polymerinnovationblog.com/epoxy-curing-agents-mercaptans-the-ultimate-quick-ambient-cure/ (accessed on 10 November 2024).
- Tsuji, Y. Molecular Understanding of the Distinction between Adhesive Failure and Cohesive Failure in Adhesive Bonds with Epoxy Resin Adhesives. Langmuir 2024, 40, 7479–7491. [Google Scholar] [CrossRef] [PubMed]
- Miyata, T.; Sato, Y.K.; Kawagoe, Y.; Shirasu, K.; Wang, H.F.; Kumagai, A.; Kinoshita, S.; Mizukami, M.; Yoshida, K.; Huang, H.H.; et al. Effect of inorganic material surface chemistry on structures and fracture behaviours of epoxy resin. Nat. Commun. 2024, 15, 1898. [Google Scholar] [CrossRef]
- Jairaja, R.; Naik, G.N. Single and dual adhesive bond strength analysis of single lap joint between dissimilar adherends. Int. J. Adhes. Adhes. 2019, 92, 142–153. [Google Scholar] [CrossRef]








| Composition | C | Si (≤) | Mn (≤) | P (≤) | S (≤) | Cr | Mo |
| 0.38–0.43 | 0.15–0.35 | 0.75–1.00 | 0.035 | 0.04 | 0.80–1.10 | 0.15–0.25 | |
| Mechanical Properties | Tensile strength (MPa) ≥ | Yield strength (MPa) ≥ | Elongation in 50 mm, %, ≥ | Reduction in area, % ≥ | Hardness (HB) | ||
| 1020 | 655 | 17.7 | 46.8 | 302 | |||
| SikaPower®-1511 | SikaPower®-1548 | ||||
|---|---|---|---|---|---|
| Heating Rate (°/min) | Peak Temperature (°C) | DHc (J/g) | Peak Temperature (°C) | DHc (J/g) | |
| 1st Peak | 2nd Peak | ||||
| 5 | 36 ± 1 | 102 ± 1 | 202 ± 1 | 101 ± 2 | 300 ± 2 |
| 10 | 51 ± 1 | 112 ± 2 | 203 ± 3 | 116 ± 1 | 295 ± 4 |
| 15 | 68 ± 1 | 117± 1 | 205 ± 2 | 123 ± 1 | 299 ± 2 |
| 20 | 86 ± 1 | 120 ± 1 | 203± 2 | 129 ± 3 | 297 ± 3 |
| Adhesive | Degree of Conversion (%) | Temperature (°C) | ||||
|---|---|---|---|---|---|---|
| 25 | 30 | 50 | 75 | 100 | ||
| Time (min) | ||||||
| SikaPower®-1511 | 5 | 1.8 | 1.4 | 0.5 | 0.2 | 0.1 |
| 20 | 4.0 | 3.2 | 1.5 | 0.6 | 0.3 | |
| 40 | 6.1 | 5.2 | 2.8 | 1.5 | 0.8 | |
| 70 | 8.5 | 7.4 | 4.3 | 2.4 | 1.5 | |
| 90 | 41.1 | 33.0 | 14.6 | 6.1 | 2.8 | |
| 99 | 750.3 | 523.0 | 123.4 | 25.4 | 6.4 | |
| SikaPower®-1548 | 5 | 67.0 | 39.1 | 5.4 | 0.6 | 0.3 |
| 20 | 136.8 | 92.5 | 21.8 | 4.5 | 1.2 | |
| 40 | 229.3 | 159.3 | 41.6 | 9.7 | 2.7 | |
| 70 | 323.8 | 232.8 | 68.9 | 18.3 | 5.8 | |
| 90 | 423.2 | 311.9 | 101.1 | 29.7 | 10.3 | |
| 99 | 715.4 | 533.4 | 180.5 | 55.5 | 20.0 | |
| Wavenumber (cm−1) | Functional Groups/Vibration | Components | |
|---|---|---|---|
| A | B | ||
| 723 | C-H out of plane deformation/bending | 1548 | |
| 765 | 1548/1511 | ||
| 827 | 1548/1511 | 1511 | |
| 914 | C-O-C oxirane | 1548/1511 | |
| 1014 | Primary amine C-N | 1548 | |
| 1030 | C-O-C stretching (aromatic) | 1548/1511 | |
| 1080 | 1511 | ||
| 1100 | C-H deformation—phenols | 1511 | |
| 1120 | H-C-H Bending | 1548 | 1548 |
| 1182 | 1548/1511 | ||
| 1245 | C-O-C stretching/ N-H deformation | 1548/1511 | 1548 |
| 1290 | 1548/1511 | ||
| 1367 | CH-S deformation | 1511 | |
| 1450 | C-O stretching | 1458/1511 | |
| 1456 | Tertiary amines | 1548/1511 | |
| 1508 | C-C aromatic ring | 1548/1511 | |
| 1556 | N-H secondary deformation | 1548 | |
| 1606 | C=C stretching Phenols C=C | 1548/1511 | 1548 |
| 1650 | 1548/1511 | ||
| 1730 | C=O stretching | 1548 | |
| 2750–3000 | C-H stretching | 1548/1511 | 1548/1511 |
| 3000–3400 | NH stretching | 1548/1511 | 1548/1511 |
| 3000–4000 | C=N/C=N-OH | 1511 | |
| Adhesive | 1st Scan | 2nd Scan | ||
|---|---|---|---|---|
| Tg1 (°C) | Tg2 (°C) | Tg1 (°C) | Tg2 (°C) | |
| SikaPower®-1511 | 38 ± 2 | 94 ± 1 | 37 ± 1 | 140 ± 1 |
| SikaPower®-1548 | 70 ± 1 | 127 ± 1 | 72 ± 1 | 129 ± 1 |
| Adhesive | σmax (MPa) | ε (%) in σmax | Young’s Modulus (MPa) | Hardness (SDH) |
|---|---|---|---|---|
| SikaPower®-1511 | 51 ± 10 | 11 ± 1 | 490 ± 60 | 80 ± 1 |
| SikaPower®-1548 | 33 ± 3 | 16 ± 3 | 270 ± 50 | 72 ± 2 |
| Adhesives | Shear Strength (MPa) | Strain (%) |
|---|---|---|
| SikaPower®-1511 | 4 ± 2 | 6 ± 2 |
| SikaPower®-1548 | 9 ± 3 | 11 ± 2 |
| 1548-1511-1548 | 8 ± 2 | 9 ± 1 |
| 1511-1548-1511 | 5 ± 1 | 6 ± 2 |
| Property | SikaPower®-1511 | SikaPower®-1548 |
|---|---|---|
| Young’s modulus, [MPa] | 490 | 270 |
| Poisson’s ratio, | 0.367 | 0.396 |
| Tensile strength, [MPa] | 51 | 33 |
| Elongation at break, [%] | 3 | 9 |
| Plastic hardening modulus, [MPa] | 165 | 50 |
| Shear Modulus, G [MPa] | 179.3 | 96.7 |
| Node | Position (mm) | Peel Stress σy (MPa) | Ratio = σ0.2/σ0.1 | |||
|---|---|---|---|---|---|---|
| Emin = 0.1 μm | Emin = 0.2 μm | Emin = 0.5 μm | Emin = 1 μm | |||
| 1 | 0 | 37.346 | 31.413 | 24.598 | 20.483 | 0.8411 |
| 2 | 0.0005 | 12.214 | 12.343 | 11.770 | 13.939 | 1.0106 |
| 3 | 0.001 | 10.087 | 10.081 | 10.234 | 9.649 | 0.9995 |
| 4 | 0.0015 | 8.989 | 8.990 | 8.961 | 8.721 | 1.0002 |
| 5 | 0.002 | 8.275 | 8.272 | 8.271 | 8.400 | 0.9996 |
| 6 | 0.0025 | 7.742 | 7.743 | 7.737 | 7.775 | 1.0002 |
| 7 | 0.003 | 7.325 | 7.328 | 7.320 | 7.295 | 1.0004 |
| 8 | 0.0035 | 6.979 | 6.982 | 6.976 | 6.956 | 1.0004 |
| 9 | 0.004 | 6.685 | 6.687 | 6.684 | 6.682 | 1.0002 |
| 10 | 0.0045 | 6.432 | 6.433 | 6.430 | 6.424 | 1.0002 |
| 11 | 0.005 | 6.205 | 6.205 | 6.206 | 6.200 | 0.9999 |
| Adhesives | Simulation Failure load (KN) | Simulation Strength (MPa) | Experimental Strength (MPa) |
|---|---|---|---|
| SikaPower®-1511 | 2.82 | 4.515 | 4 ± 2 |
| SikaPower®-1548 | 5.17 | 8.274 | 9 ± 3 |
| 1511-1548-1511 | 2.57 | 4.115 | 5 ± 1 |
| 1548-1511-1548 | 6.84 | 10.941 | 8 ± 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Gálvez, P.; Martínez, M.A.; Abenojar, J.; Wahab, M.A. Evaluation and Characterization of Functionally Graded Adhesive Joints: Experimental and Numerical Analyses. Polymers 2024, 16, 3561. https://doi.org/10.3390/polym16243561
Zhang Y, Gálvez P, Martínez MA, Abenojar J, Wahab MA. Evaluation and Characterization of Functionally Graded Adhesive Joints: Experimental and Numerical Analyses. Polymers. 2024; 16(24):3561. https://doi.org/10.3390/polym16243561
Chicago/Turabian StyleZhang, Yanan, Pedro Gálvez, Miguel Angel Martínez, Juana Abenojar, and Magd Abdel Wahab. 2024. "Evaluation and Characterization of Functionally Graded Adhesive Joints: Experimental and Numerical Analyses" Polymers 16, no. 24: 3561. https://doi.org/10.3390/polym16243561
APA StyleZhang, Y., Gálvez, P., Martínez, M. A., Abenojar, J., & Wahab, M. A. (2024). Evaluation and Characterization of Functionally Graded Adhesive Joints: Experimental and Numerical Analyses. Polymers, 16(24), 3561. https://doi.org/10.3390/polym16243561






