Damage and Failure Monitoring of Aerospace Insulation Layers Based on Embedded Fiber Bragg Grating Sensors
Abstract
1. Introduction
2. Principle
2.1. Fiber Bragg Grating Sensor Principle
2.2. Failure Criteria for CFRP Laminates
- Fiber tensile failure ( > 0)
- Fiber compression failure ( < 0)
- Matrix tensile failure ( > 0)
- Substrate compression failure ( < 0)
- Tensile delamination failure (σ33 > 0):
- Compressive delamination failure (σ33 < 0):where , , and are positive stresses; , , and are shear stresses; and are the longitudinal tensile and compressive strengths of the single-layer plate; and are the transverse tensile and compressive strengths of the single-layer plate; and are the tensile and compressive strengths perpendicular to the direction of the single-layer plate; and , , and are the longitudinal and the two transverse shear strengths, respectively.
3. Finite Element Simulation Analysis
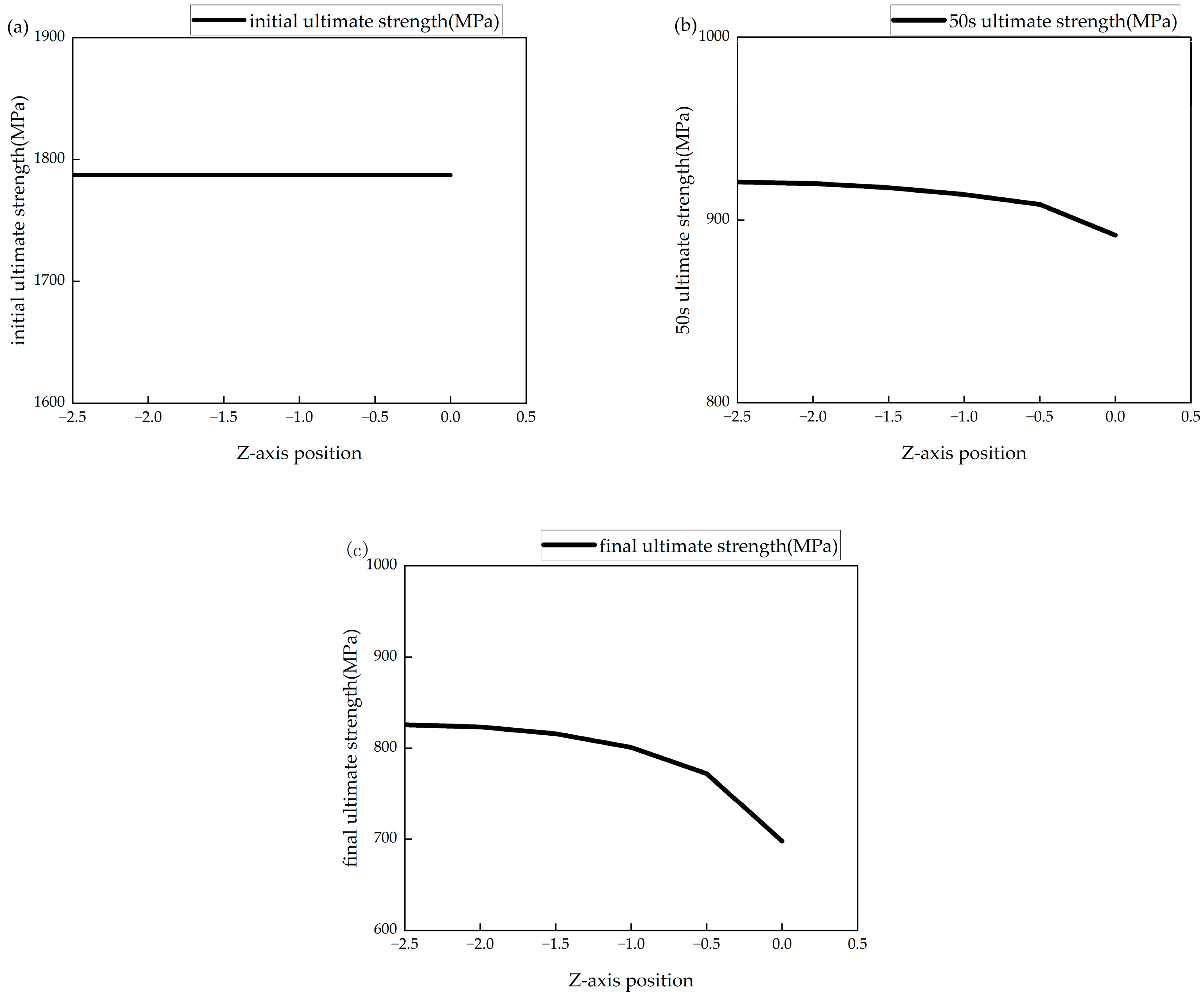
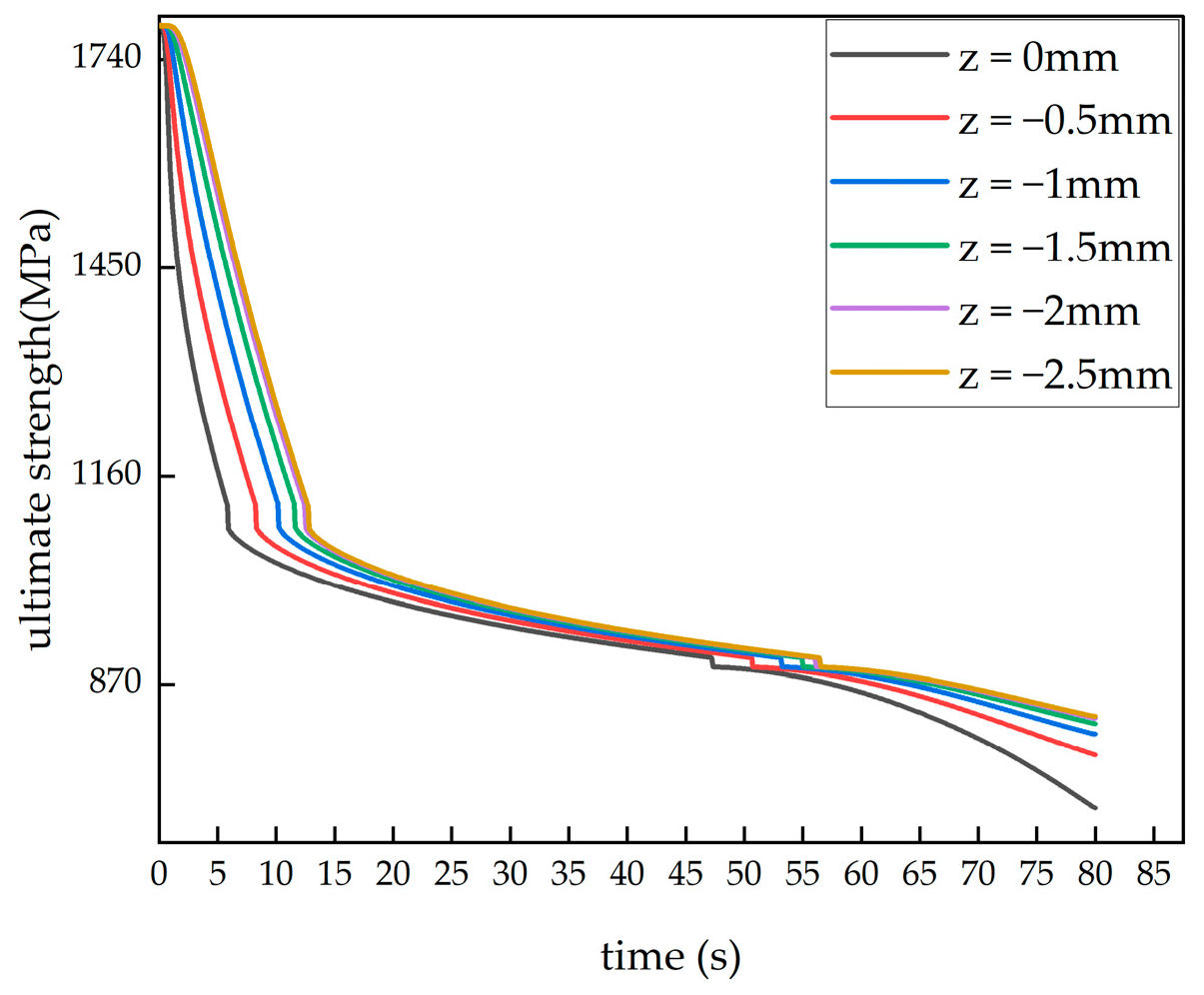
3.1. Finite Element Simulation of CFRP Laminated Plate Strength
3.2. Tensile Load Damage Study of the Model
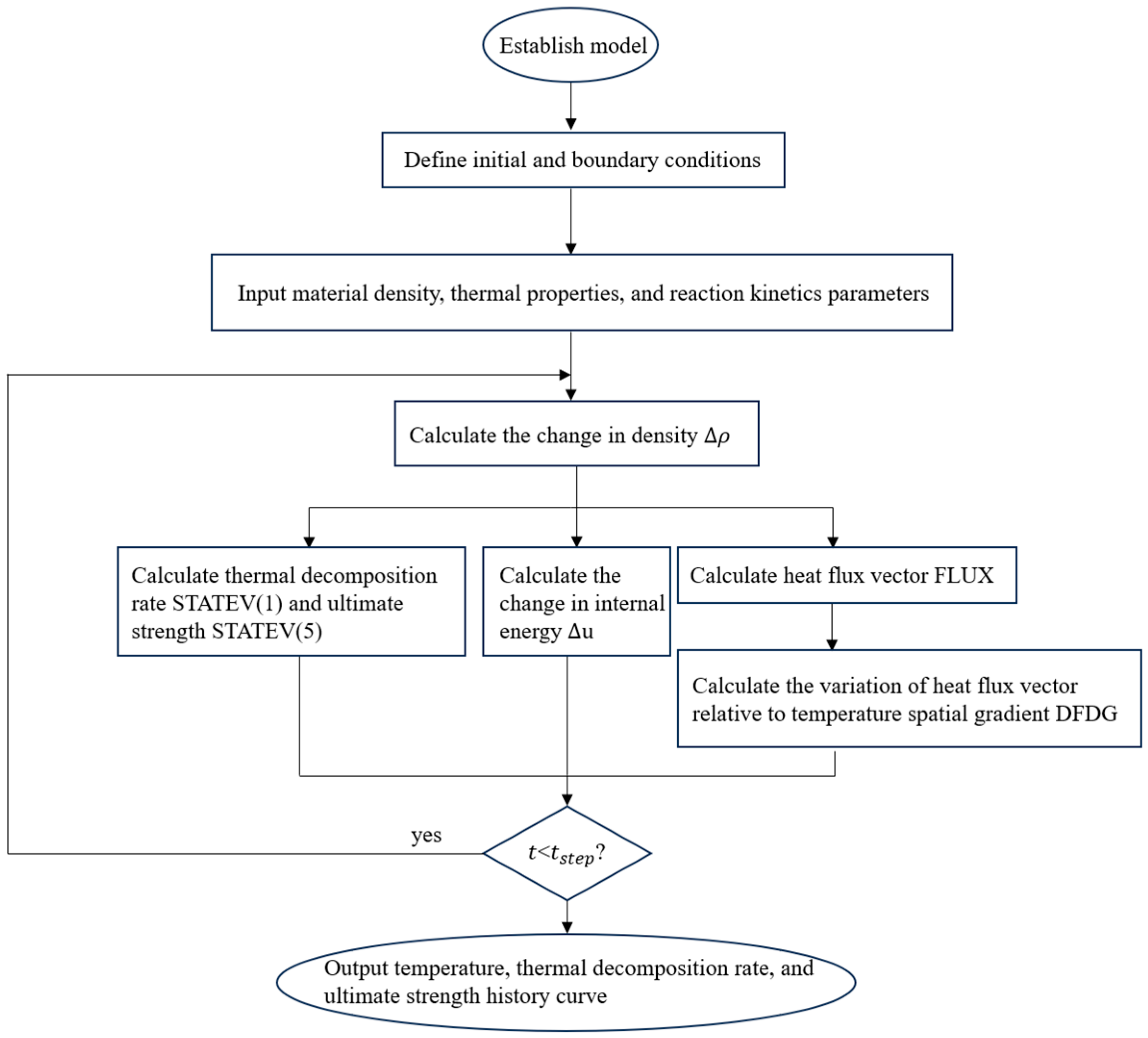
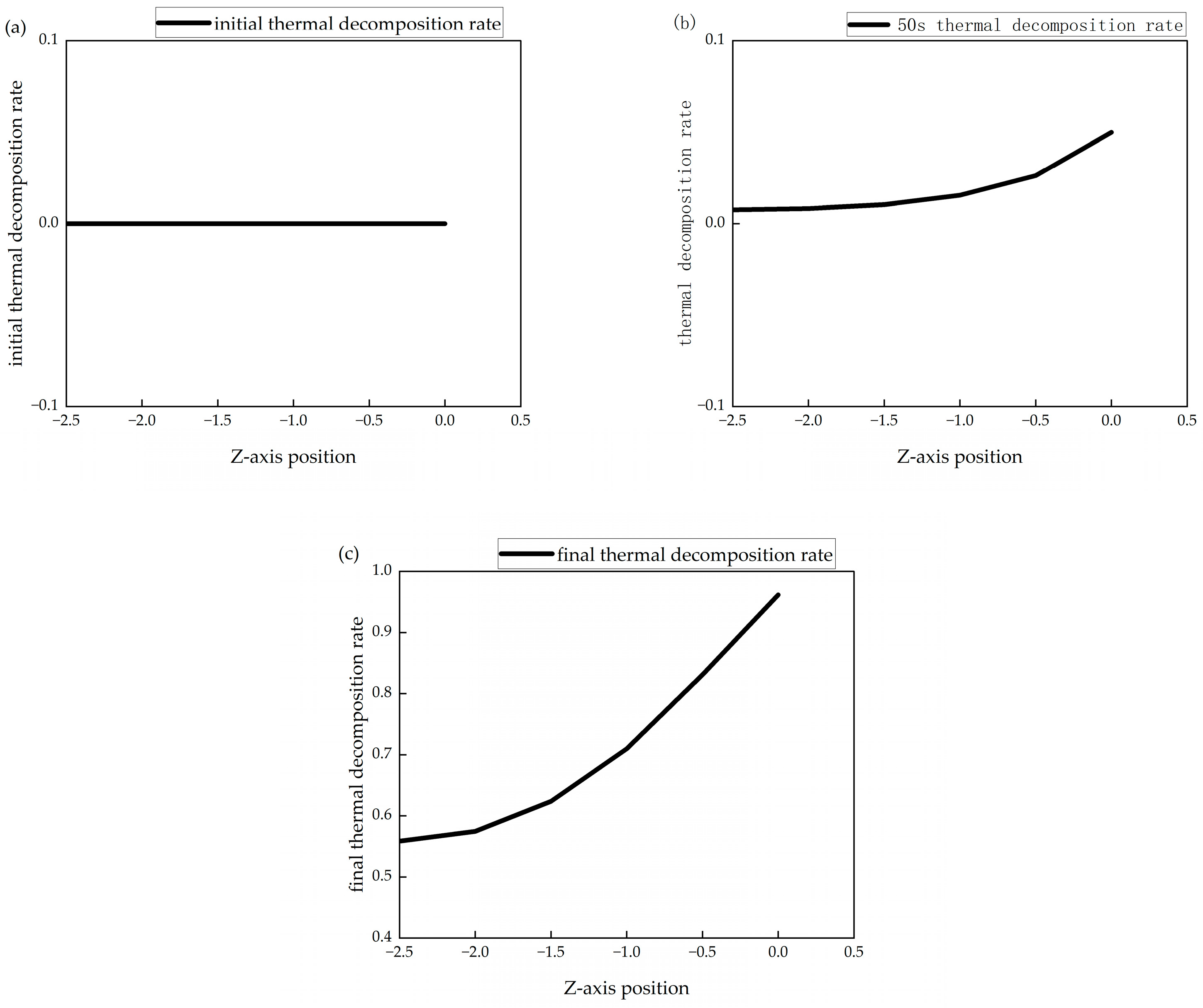
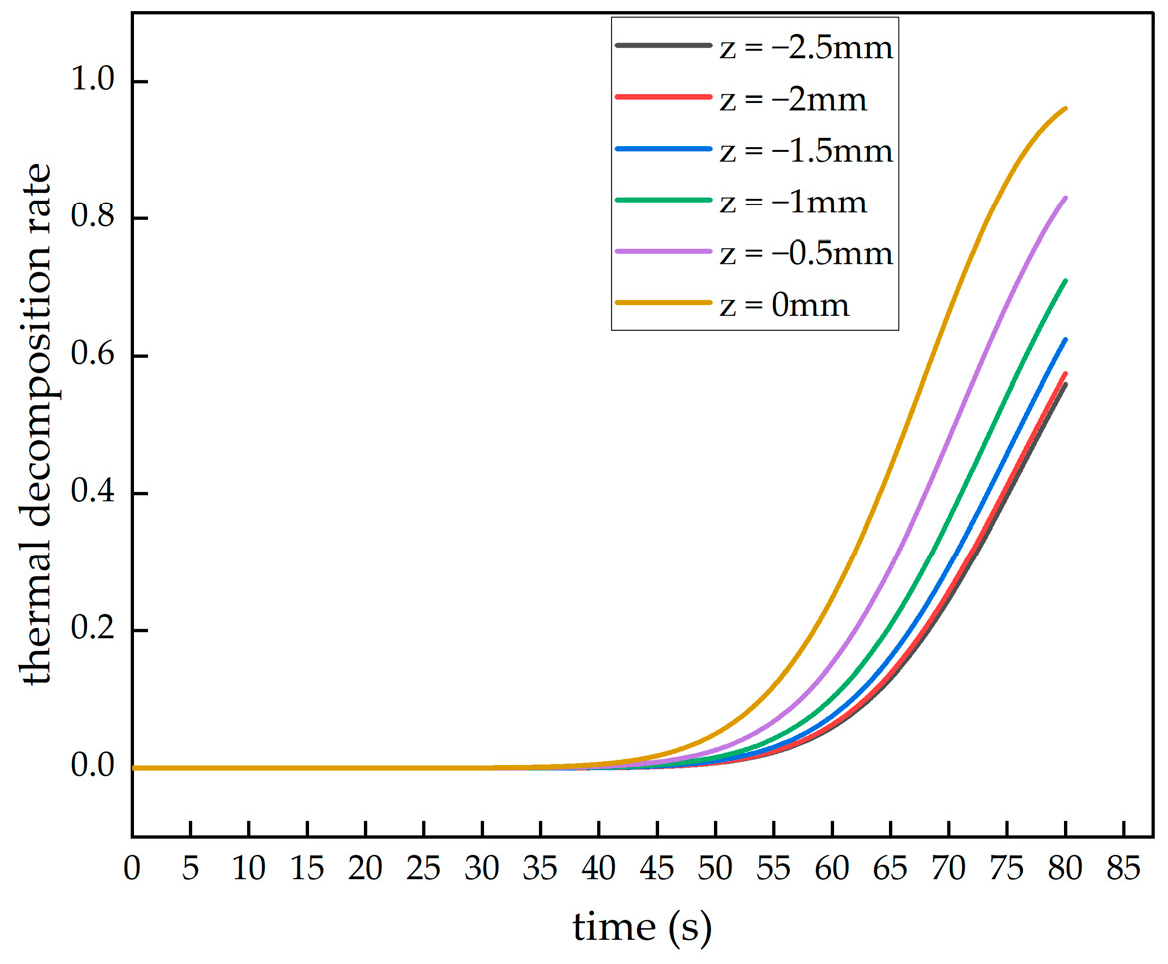
3.3. Finite Element Simulation Analysis of High-Temperature Decomposition
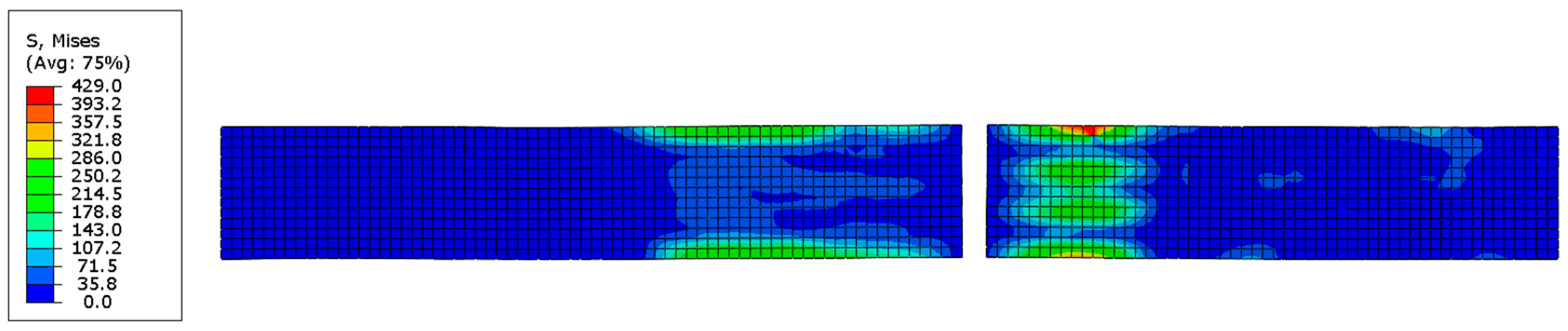
3.4. Simulation Results and Analysis
4. Experiment and Analysis
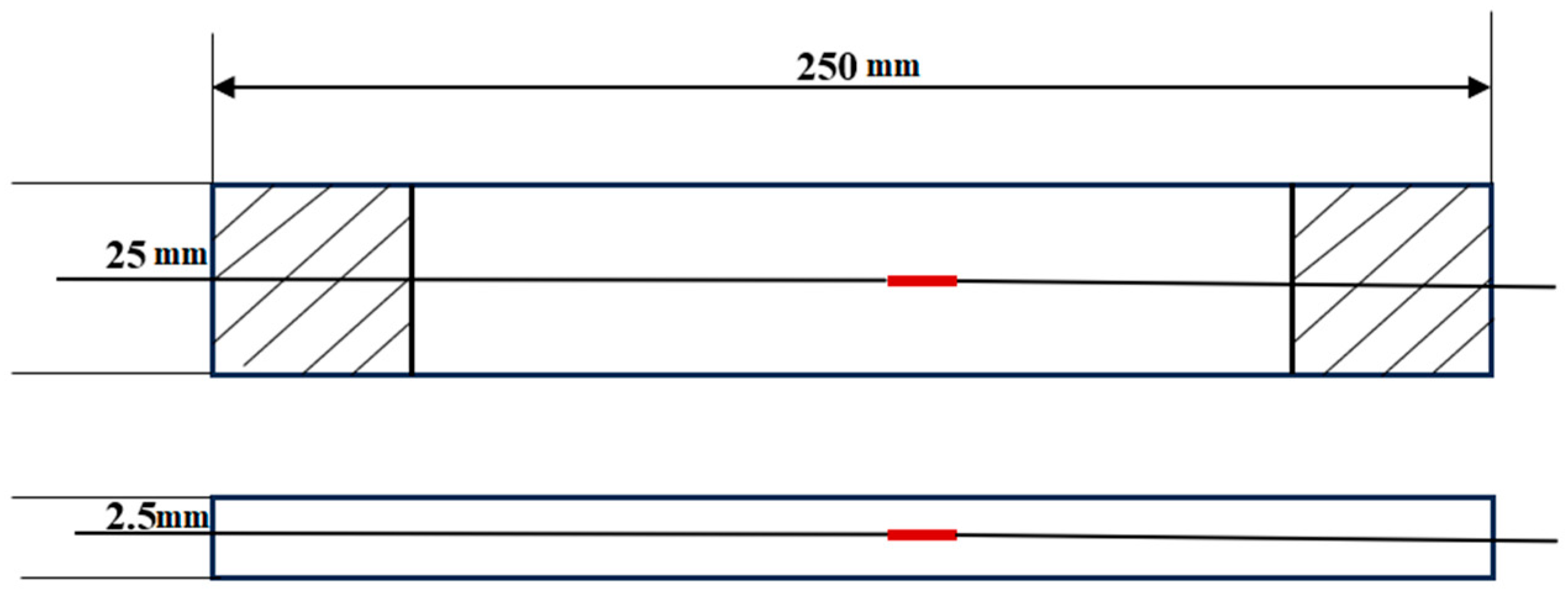
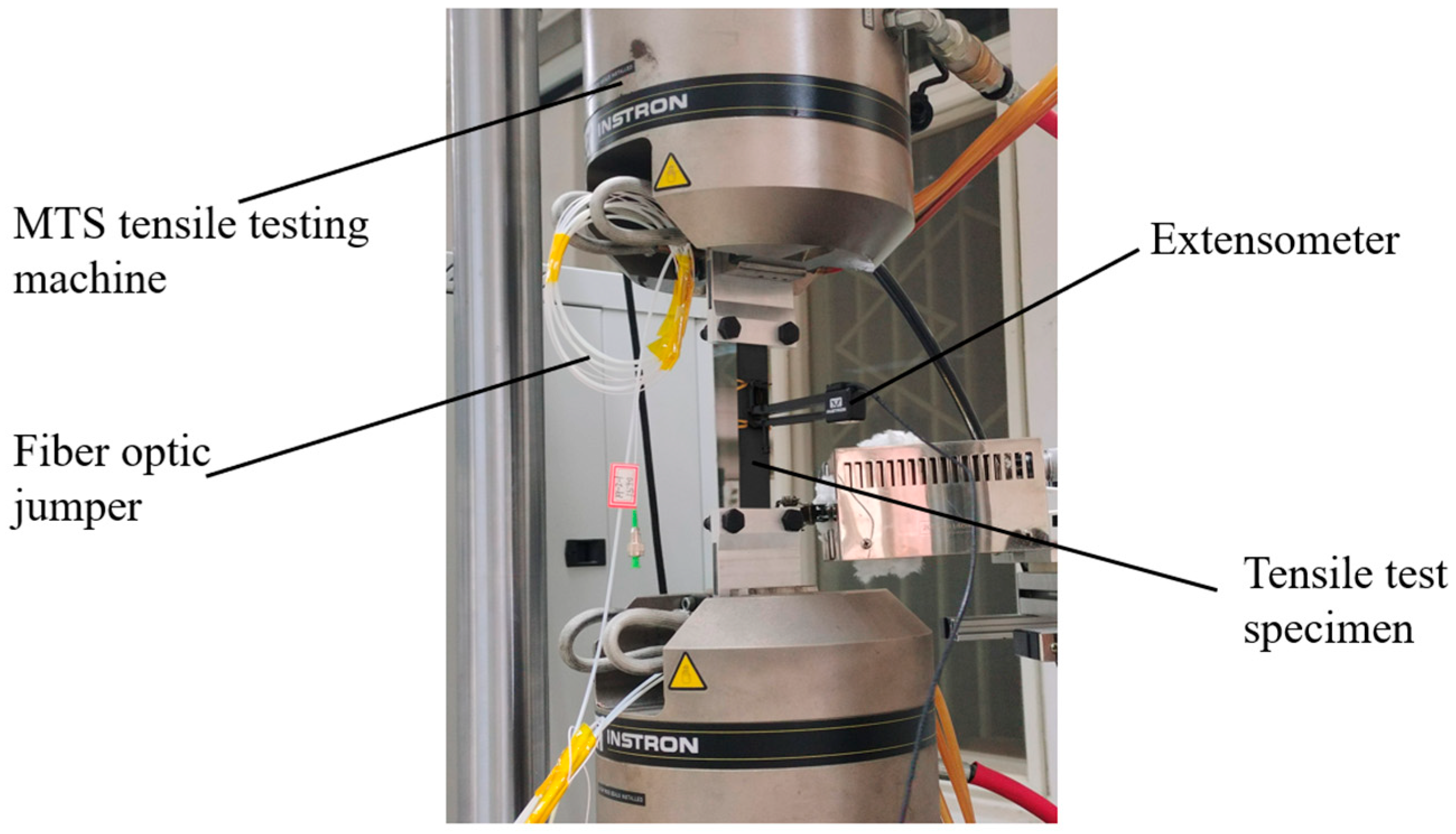
4.1. Tensile Fracture Test for Specimen 1
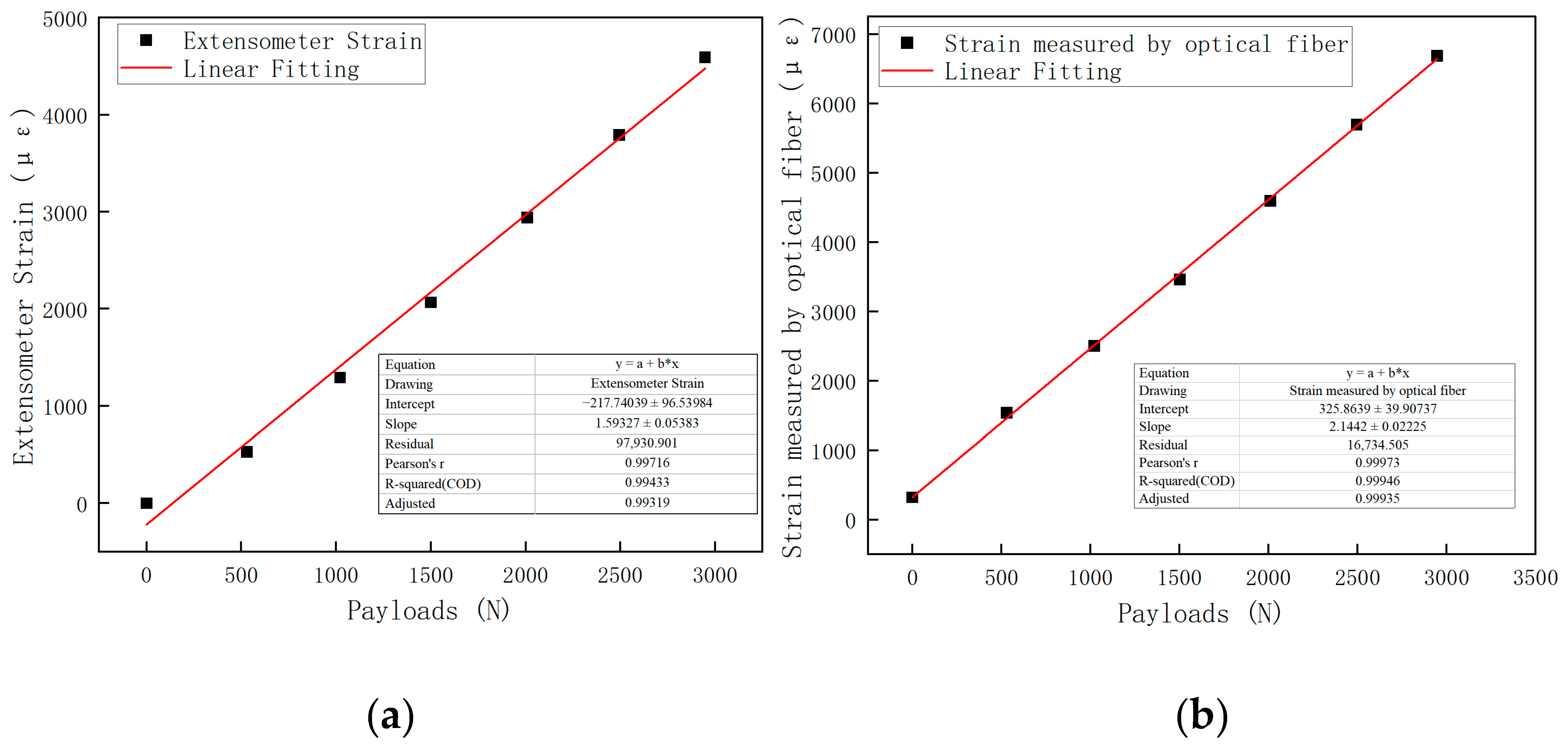
4.1.1. Calibration Data Processing for Specimen 1
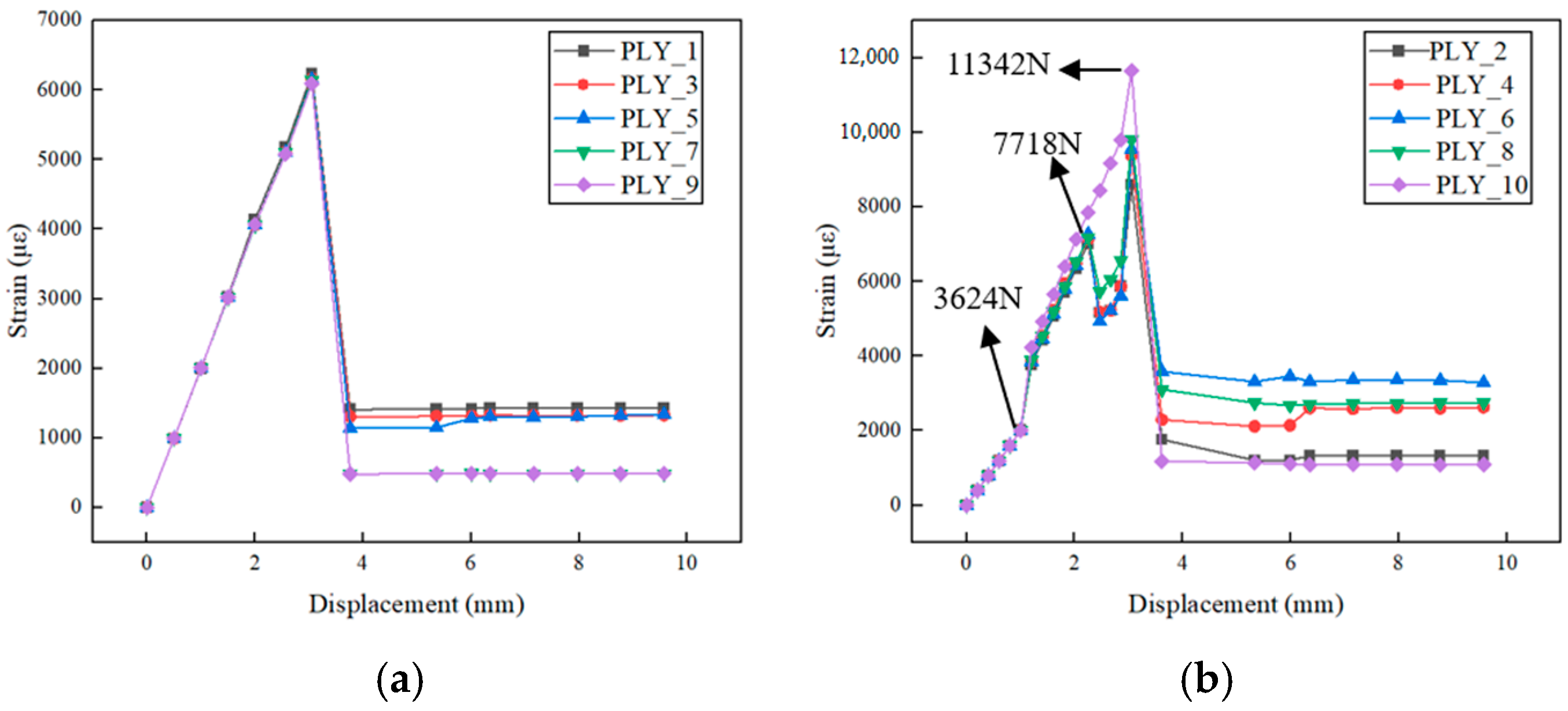
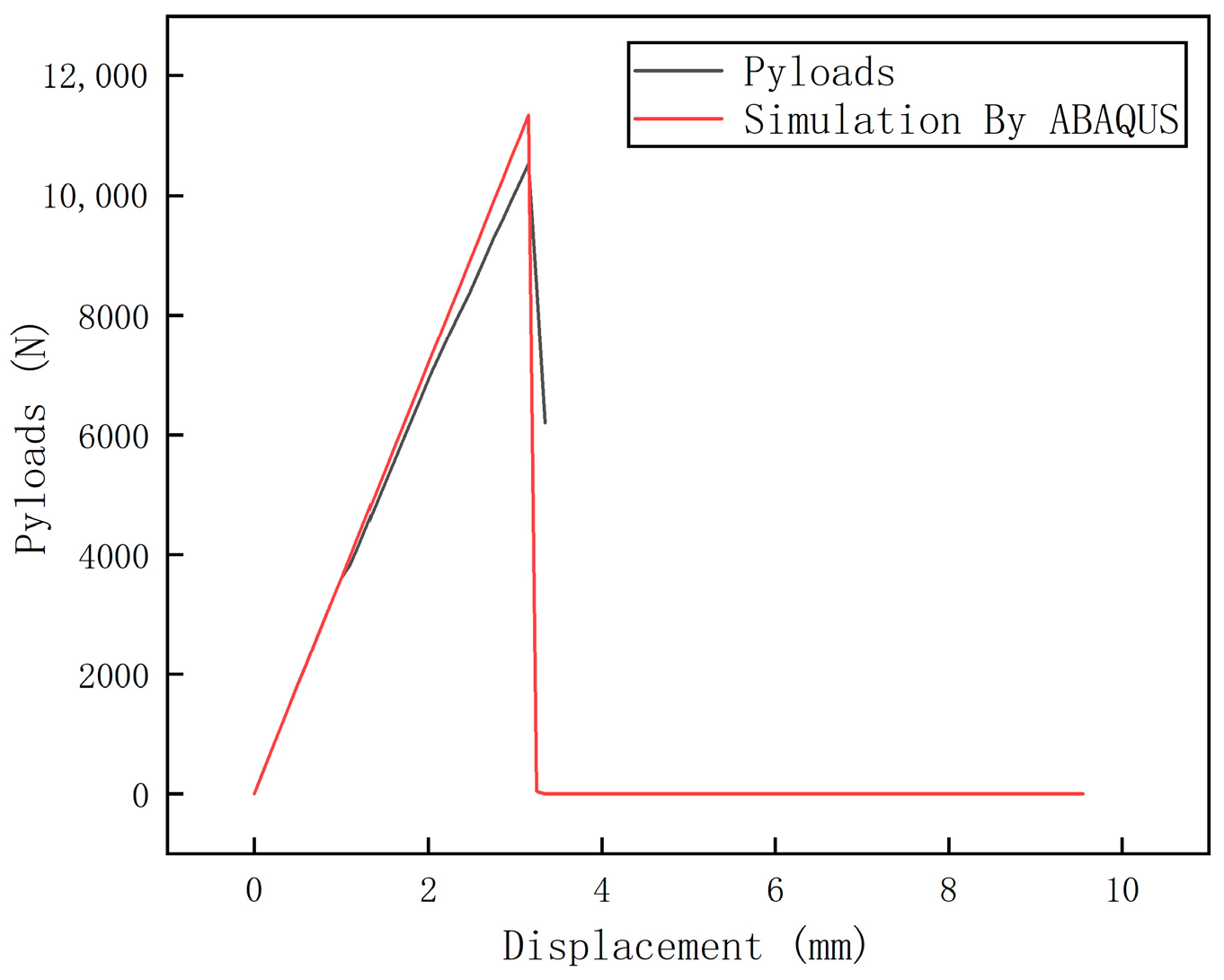
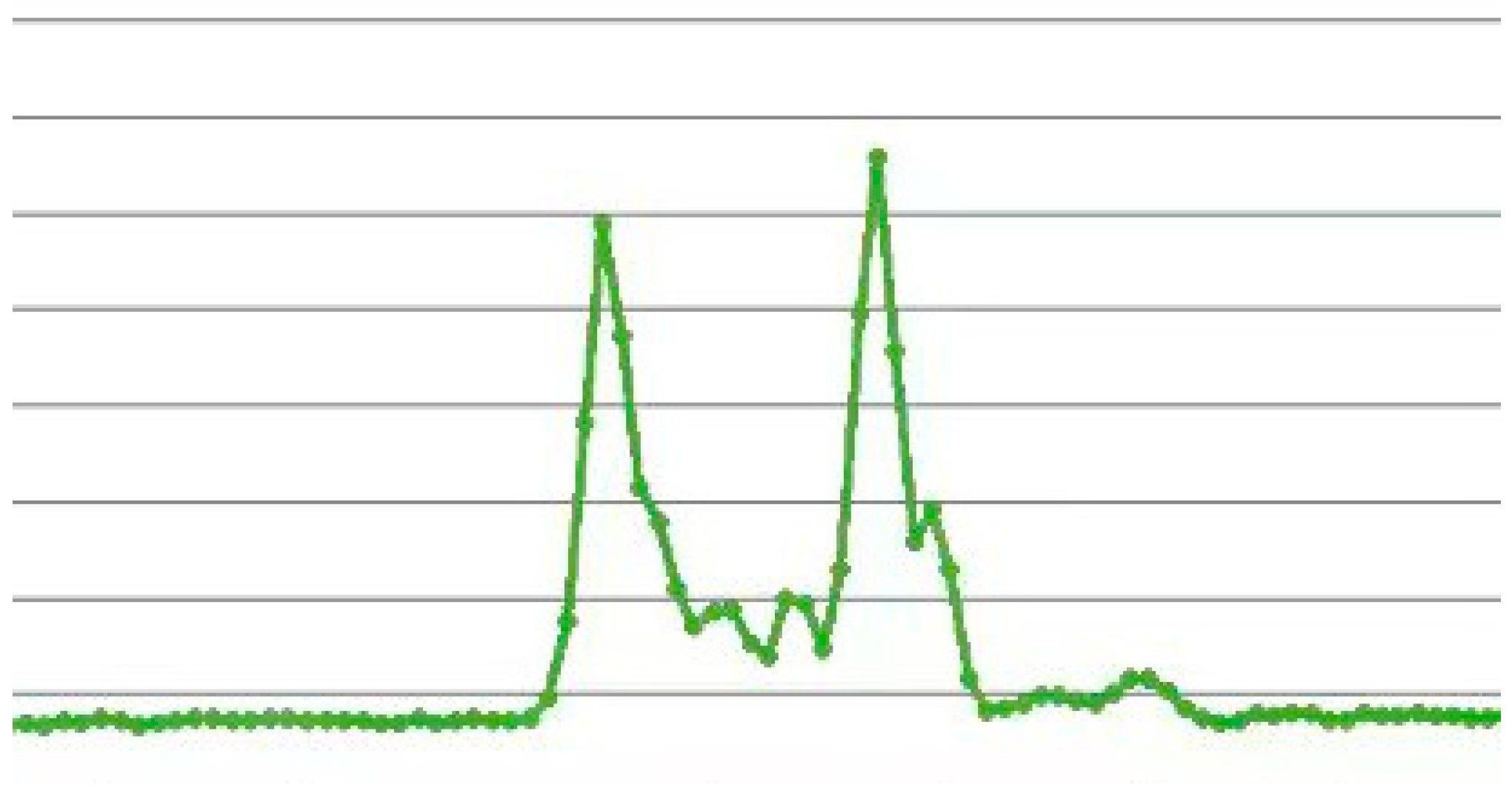
4.1.2. Tensile Fracture Test Data Processing for Specimen 1
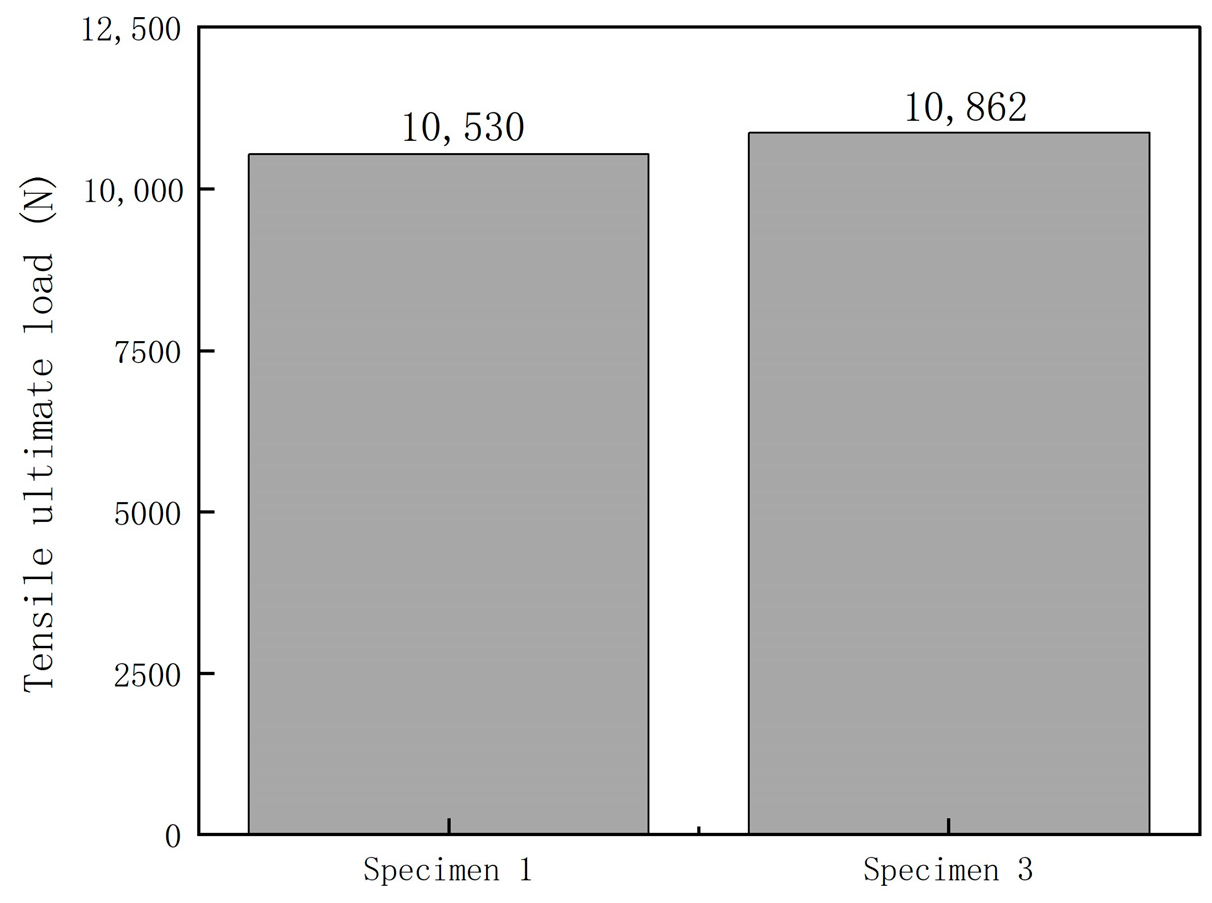
4.1.3. Comparison of Ultimate Strength Between Specimen 3 and Specimen 1
4.2. High-Temperature Sintering Experiment of Specimen 2
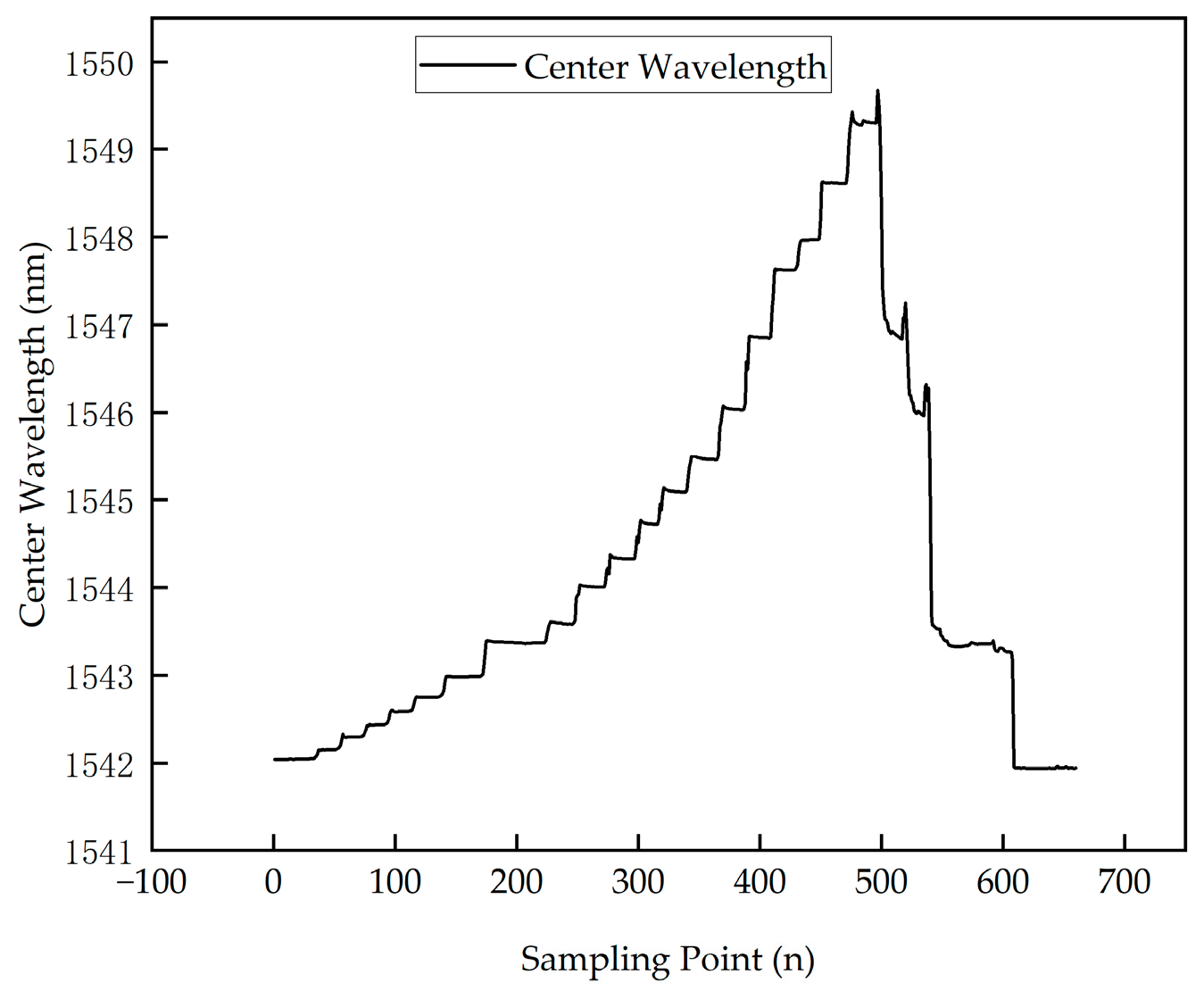
High-Temperature Sintering Experimental Data Processing
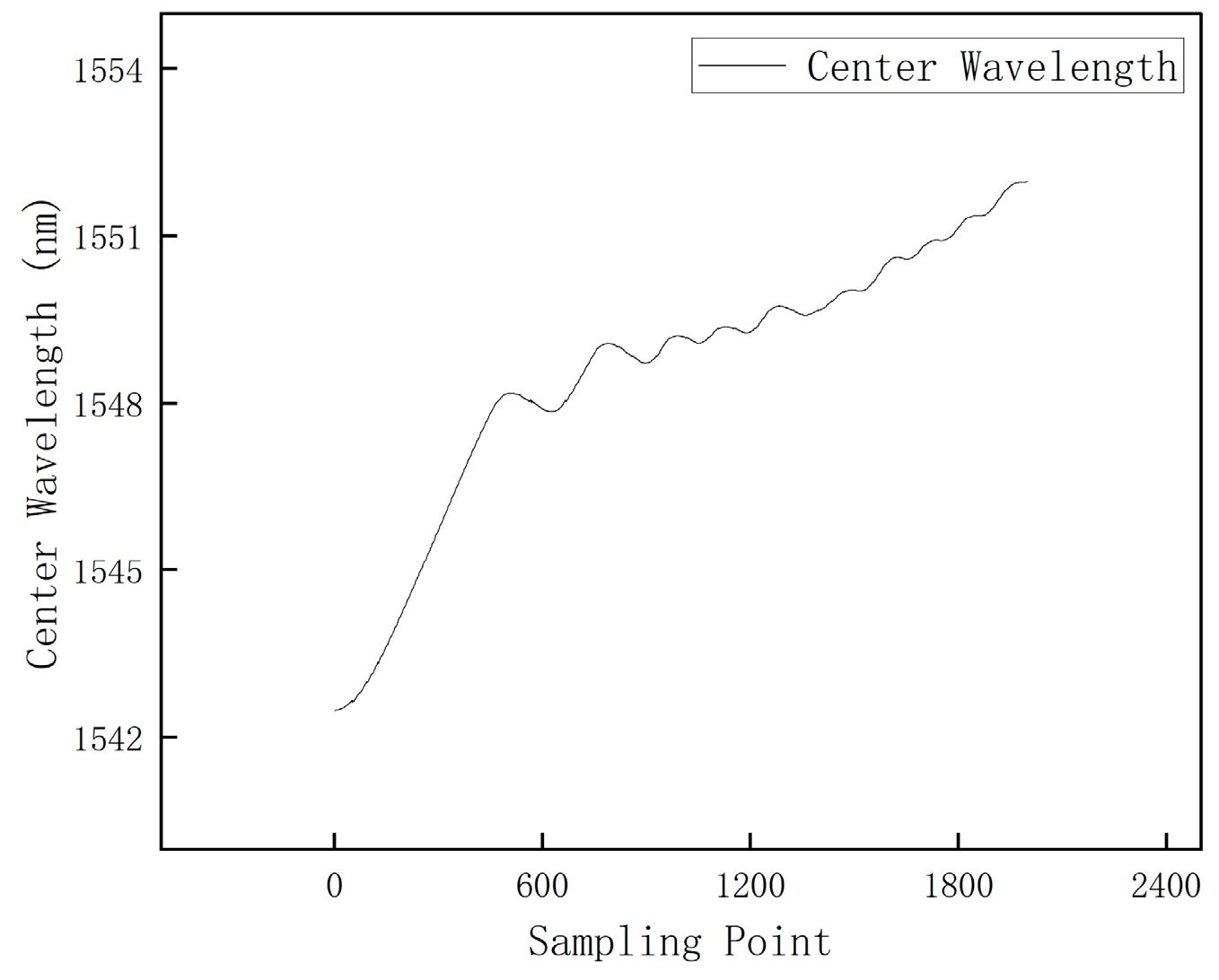
4.3. Tensile Fracture Test for Specimen 2 After High-Temperature Treatment
5. Conclusions
- In CFRP laminated plates without high-temperature treatment, FBG sensors accurately captured the entire process from elastic deformation to final failure and provided preliminary identification of damage types. The damage evolution process, dynamically tracked through wavelength changes, was highly consistent with the finite element simulation results, validating the reliability of FBG sensors in complex stress environments.
- In CFRP laminated plates subjected to 650 °C high-temperature treatment, although the mechanical properties significantly deteriorated, with a 75% reduction in tensile strength, FBG sensors continued to effectively monitor internal strain changes, recording the entire progression from damage accumulation to final failure. This demonstrates the stability and durability of FBG sensors in high-temperature environments.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Congdon, E.; Mehoke, D.; Buchta, M.; Nagle, D.; Zhang, D. Development of a high-temperature optical coating for thermal managemnt on Solar Probe Plus. In Proceedings of the 10th AIAA/ASME Joint Thermphysics Heat Transfer Conference, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar]
- Reynolds, E.L.; Driesman, A.; Kinnison, J.; Lockwood, M.K. Solar probe plus mission overview. In Proceedings of the AIAA Guidance, Navigation and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Dombrovsky, L.A.; Reviznikov, D.L.; Kryukov, A.P.; Levashov, V.Y. Self-generated clouds of micron-sized particles as a promsing way of a Solar Probe shielding from intense thermal radiation of the Sun. J. Quant. Sprectroscopy Radiat. Transf. 2017, 200, 234–243. [Google Scholar] [CrossRef]
- Pramanik, A.; Basak, A.K.; Dong, Y.; Sarker, P.K.; Uddin, M.S.; Littlefair, G.; Dixit, A.R.; Chattopadhyaya, S. Joining of carbon fibre reinforced polymer (CFRP) composites and aluminium alloys—A review. J. Compos. Part A Appl. Sci. Manuf. 2017, 101, 1–29. [Google Scholar] [CrossRef]
- Wang, F.F. Study on the application of carbon fiber composite materials in high-speed trains. Mater. Sci. Forum 2017, 893, 31–34. [Google Scholar] [CrossRef]
- Rajak, D.K.; Wagh, P.H.; Linul, E. Manufacturing technologies of carbon/glass fiber-reinforced polymer composites and their properties: A review. J. Polym. 2021, 13, 3721. [Google Scholar] [CrossRef] [PubMed]
- Scheel, I.; Udd, E. Fiber gratings strain sensor systems for composites and adhesive joints. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Portland, OR, USA, 25–29 March 2017; Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems. SPIE: Bellingham, WA, USA, 2017; Volume 10168, pp. 448–455. [Google Scholar]
- Kahandawa, G.C.; Epaarachchi, J.; Wang, H.; Lau, K.T. Use of FBG sensors for SHM in aerospace structures. J. Photonic Sens. 2012, 2, 203–214. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, H.; Jin, L.; Liu, B.; Zhao, J.; Tu, Q.; Kai, G.; Dong, X. An embedded FBG sensor for simultaneous measurement of stress and temperature. J. IEEE Photonics Technol. Lett. 2005, 18, 154–156. [Google Scholar]
- Leng, J.; Asundi, A. Structural health monitoring of smart composite materials by using EFPI and FBG sensors. J. Sens. Actuators A Phys. 2003, 103, 330–340. [Google Scholar] [CrossRef]
- Torres, B.; Payá-Zaforteza, I.; Calderón, P.A.; Adam, J.M. Analysis of the strain transfer in a new FBG sensor for structural health monitoring. J. Eng. Struct. 2011, 33, 539–548. [Google Scholar] [CrossRef]
- Takeda, S.; Yokozeki, T.; Ogasawara, T. Damage monitoring of polymer-lined carbon fibre-reinforced plastic using small-diameter fibre Bragg grating sensors. J. Reinf. Plast. Compos. 2015, 34, 454–462. [Google Scholar] [CrossRef]
- Shin, C.-S.; Lin, T.-C. Adhesive Joint Integrity Monitoring Using the Full Spectral Response of Fiber Bragg Grating Sensors. J. Polym. 2021, 13, 2954. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Xu, C.; Yang, G. Experimental research on damage detecting in composite materials with FBG sensors under low frequency cycling. J. Int. J. Fatigue 2017, 101, 61–66. [Google Scholar] [CrossRef]
- Yin, W.; Hu, Y.; Ding, G.; Fan, Z.; Jiang, N. Damage identification of CFRP laminate based on finite element analysis and FBG sensor network. J. Opt. Fiber Technol. 2022, 73, 103057. [Google Scholar] [CrossRef]
- Zhan, Y.; Feng, C.; Shen, Z.; Xie, N.; Liu, H.; Xiong, F.; Wang, S.; Sun, Z.; Yu, M. Fiber Bragg grating monitoring for composites in the out-of-autoclave curing process. J. Opt. Technol. 2018, 85, 371–376. [Google Scholar] [CrossRef]
- Ma, K.-P.; Wu, C.-W.; Tsai, Y.-T.; Hsu, Y.-C.; Chiang, C.-C. Internal residual strain measurements in carbon fiber-reinforced polymer laminates curing process using embedded tilted fiber bragg grating sensor. J. Polym. 2020, 12, 1479. [Google Scholar] [CrossRef] [PubMed]
- Hashin, Z. Failure criteria for unidirectional fiber composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Henderson, J.B.; Wiebelt, J.A.; Tant, M.R. A model for the thermal response of polymer composite materials with experimental verification. J. Compos. Mater. 1985, 19, 579–595. [Google Scholar] [CrossRef]
- Wang, K.; Young, B.; Smith, S.T. Mechanical properties of pultruded carbon fibre-reinforced polymer (CFRP) plates at elevated temperatures. J. Eng. Struct. 2011, 33, 2154–2161. [Google Scholar] [CrossRef]
- Chen, J.; Young, B. Stress–strain curves for stainless steel at elevated temperatures. Eng. Struct. 2006, 28, 229–239. [Google Scholar] [CrossRef]
- Zhou, Y.-J.; Song, H.; Liu, G.; Wang, W.-J.; Li, X.Q. Tensile strain of composite laminates using embedded fiber bragg grating sensors. J. Mater. Eng. 2012, 9, 58–61+65. [Google Scholar]
- ASTM D3039/D3039M-17; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2017.





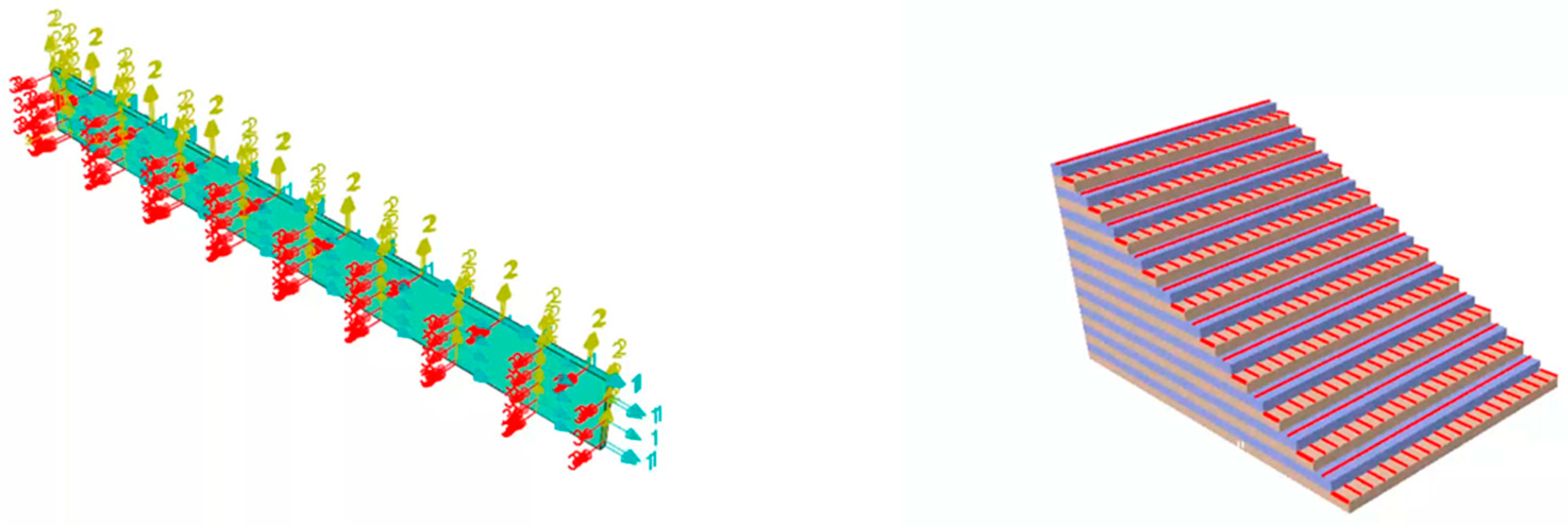





| Parameter | Value |
|---|---|
| (kg/m3) | 1700 |
| E1/GPa | 132 |
| E2, E3/GPa | 9.2 |
| G12, G13/GPa | 4.68 |
| G23/GPa | 3.35 |
| μ12, μ13 | 0.312 |
| μ23 | 0.32 |
| XT/MPa | 1622 |
| XC/MPa | 1270 |
| YT, ZT/MPa | 46.2 |
| YC/ZC/MPa | 179 |
| S12, S13, S23/MPa | 69 |
| Payloads/N | 0 | 530 | 1021.800 | 1500.500 | 2009.390 | 2494.136 | 2946.701 |
| Extensometer strain/με | 0 | 529 | 1292.325 | 2066.714 | 2940.667 | 3790.483 | 4590.015 |
| Strain measured by optical fiber/με | 321.824 | 1538.721 | 2504.193 | 3459.608 | 4596.049 | 5692.262 | 6687.905 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, G.; Wan, B.; Huang, H.; Li, W. Damage and Failure Monitoring of Aerospace Insulation Layers Based on Embedded Fiber Bragg Grating Sensors. Polymers 2024, 16, 3543. https://doi.org/10.3390/polym16243543
Yan G, Wan B, Huang H, Li W. Damage and Failure Monitoring of Aerospace Insulation Layers Based on Embedded Fiber Bragg Grating Sensors. Polymers. 2024; 16(24):3543. https://doi.org/10.3390/polym16243543
Chicago/Turabian StyleYan, Guang, Boli Wan, Heng Huang, and Wuyi Li. 2024. "Damage and Failure Monitoring of Aerospace Insulation Layers Based on Embedded Fiber Bragg Grating Sensors" Polymers 16, no. 24: 3543. https://doi.org/10.3390/polym16243543
APA StyleYan, G., Wan, B., Huang, H., & Li, W. (2024). Damage and Failure Monitoring of Aerospace Insulation Layers Based on Embedded Fiber Bragg Grating Sensors. Polymers, 16(24), 3543. https://doi.org/10.3390/polym16243543





