Reduction in Floor Impact Noise Using Resilient Pads Composed of Machining Scraps
Abstract
1. Introduction
2. Properties and Performance Analysis of Recycled Metal Scrap Pads
2.1. Scrap Pads Made of Metal Recycled Materials
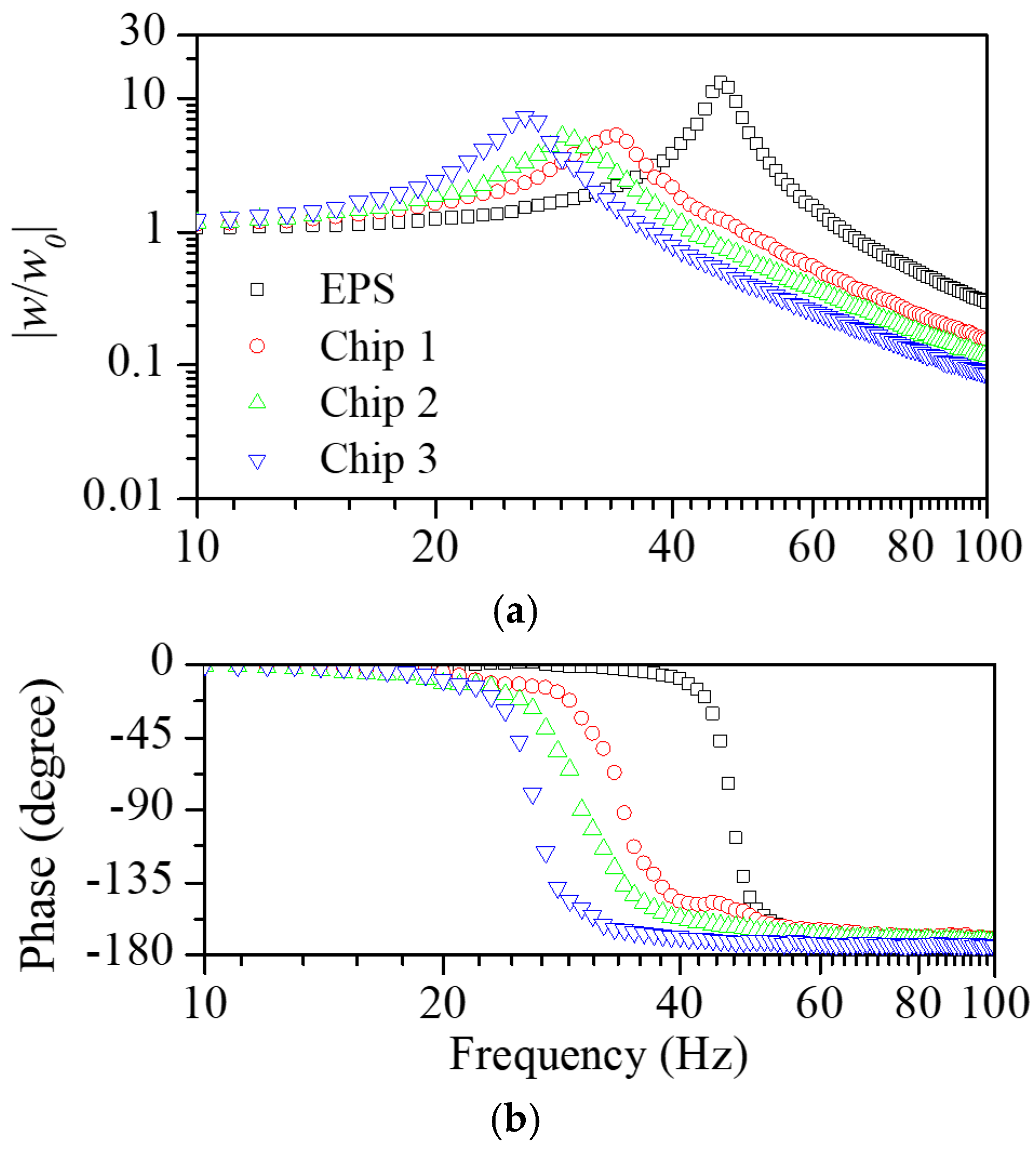
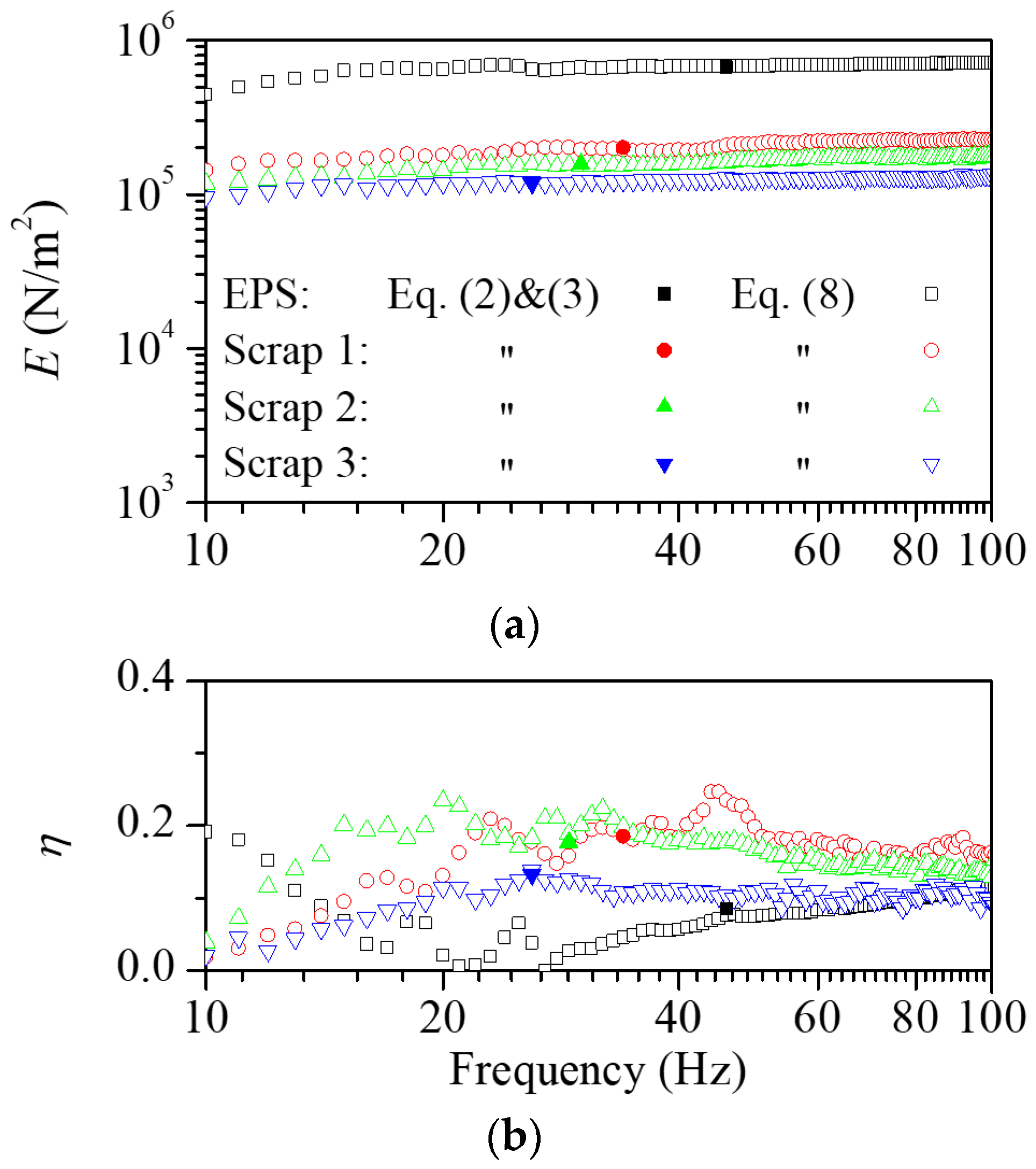
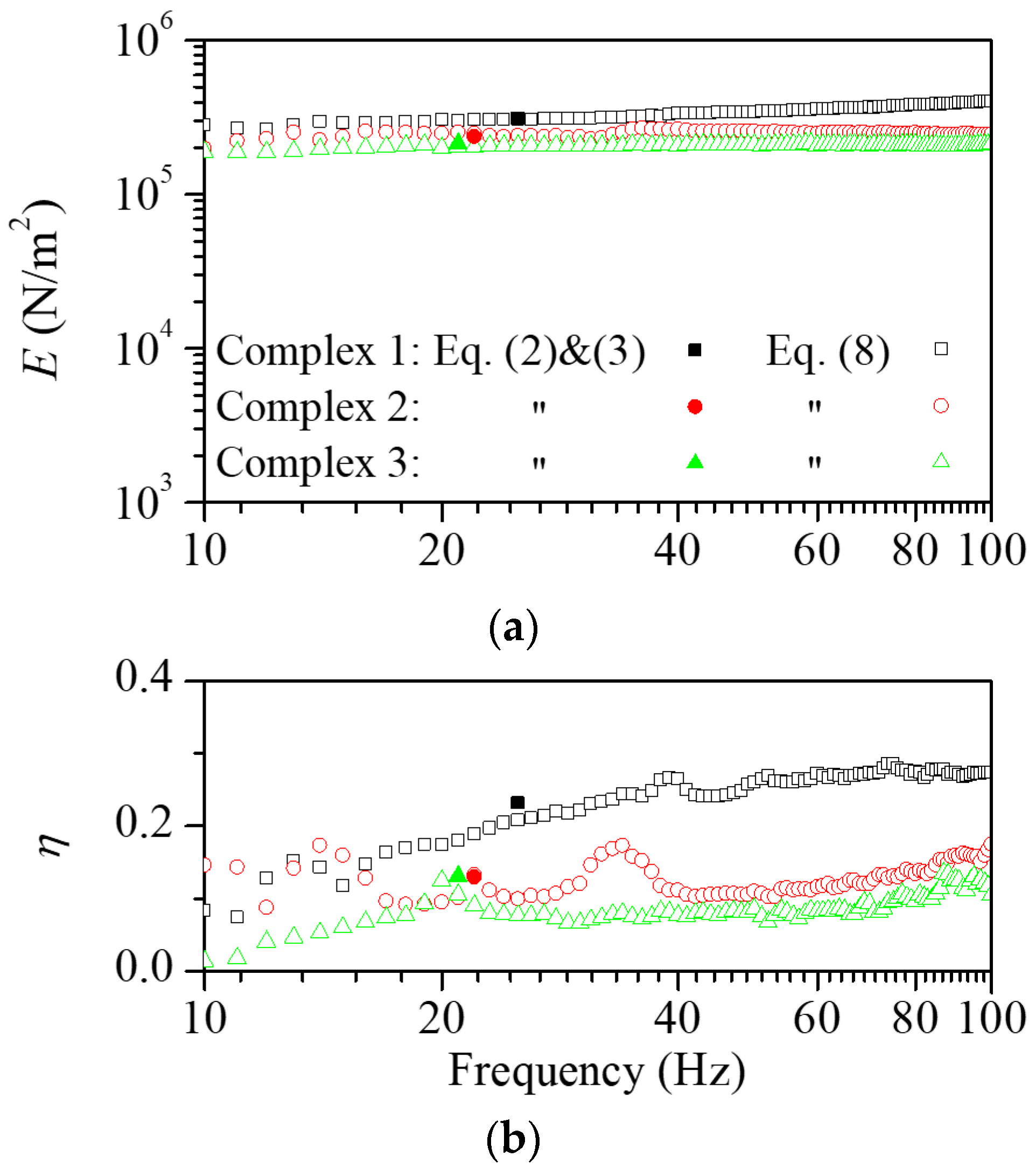
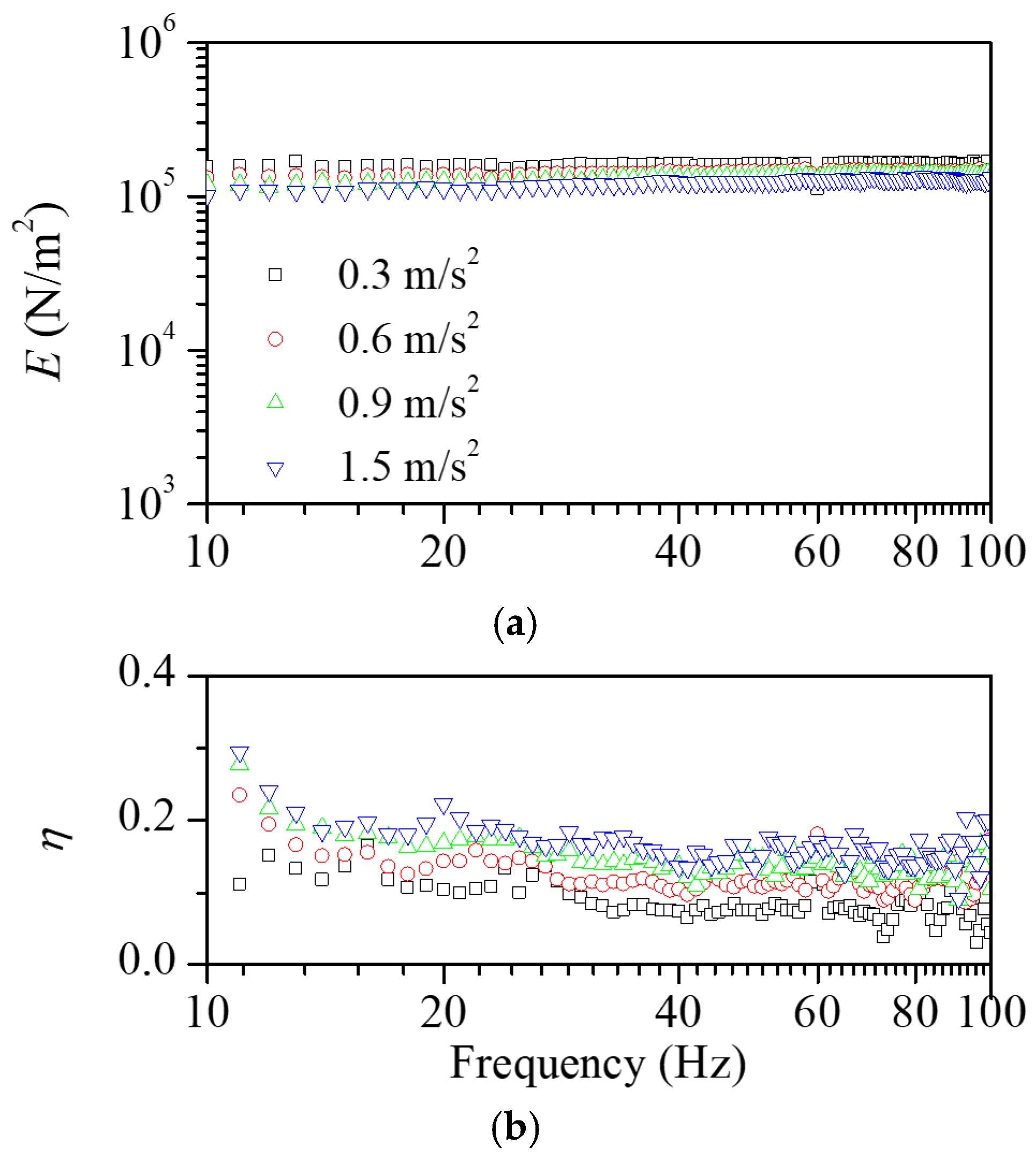
2.2. Viscoelastic Properties of Scrap Pads
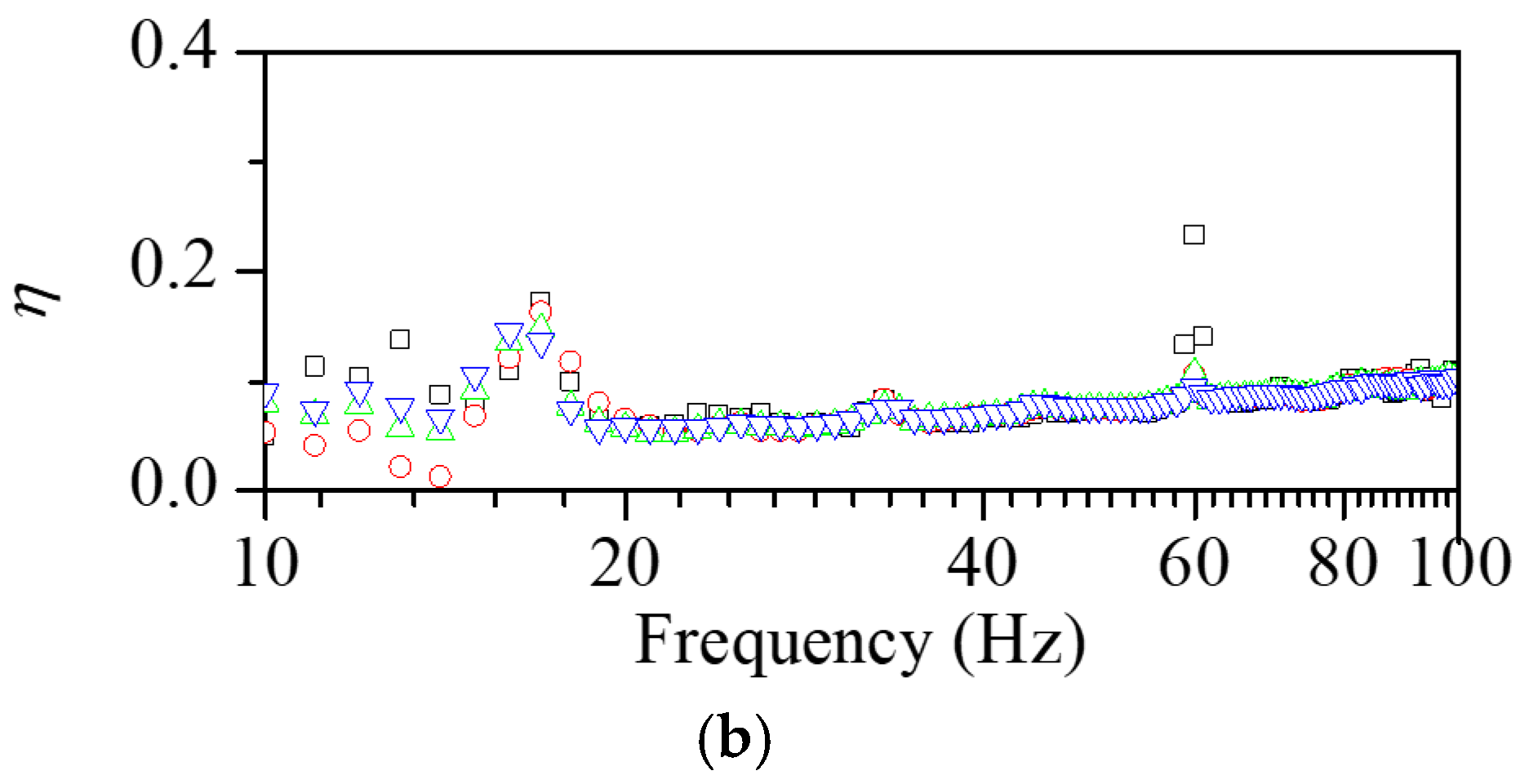
2.3. Quantification of Practical Damping Performance of Scrap Pads
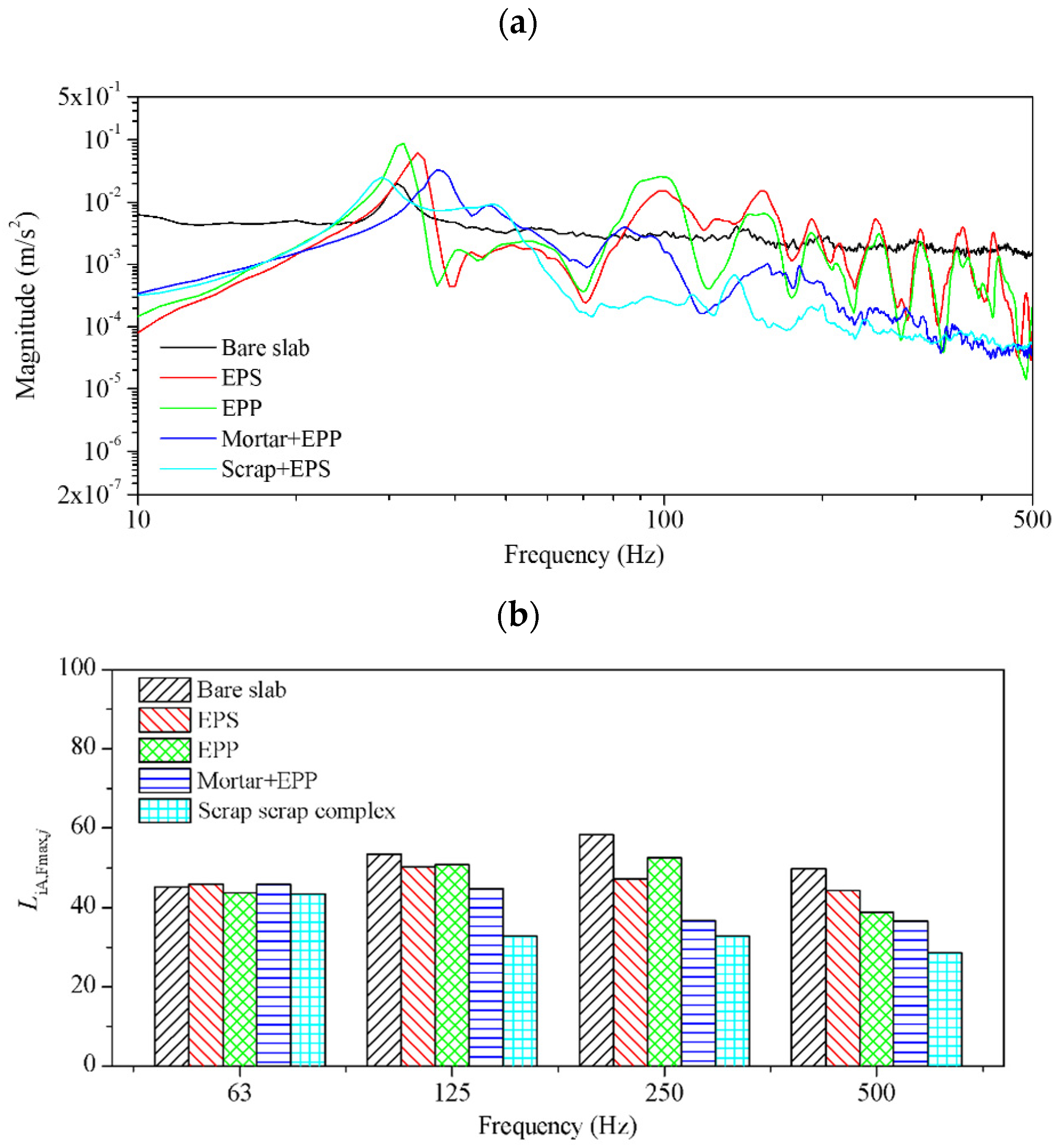
3. Floor Impact Noise Reduction by Scrap Pads
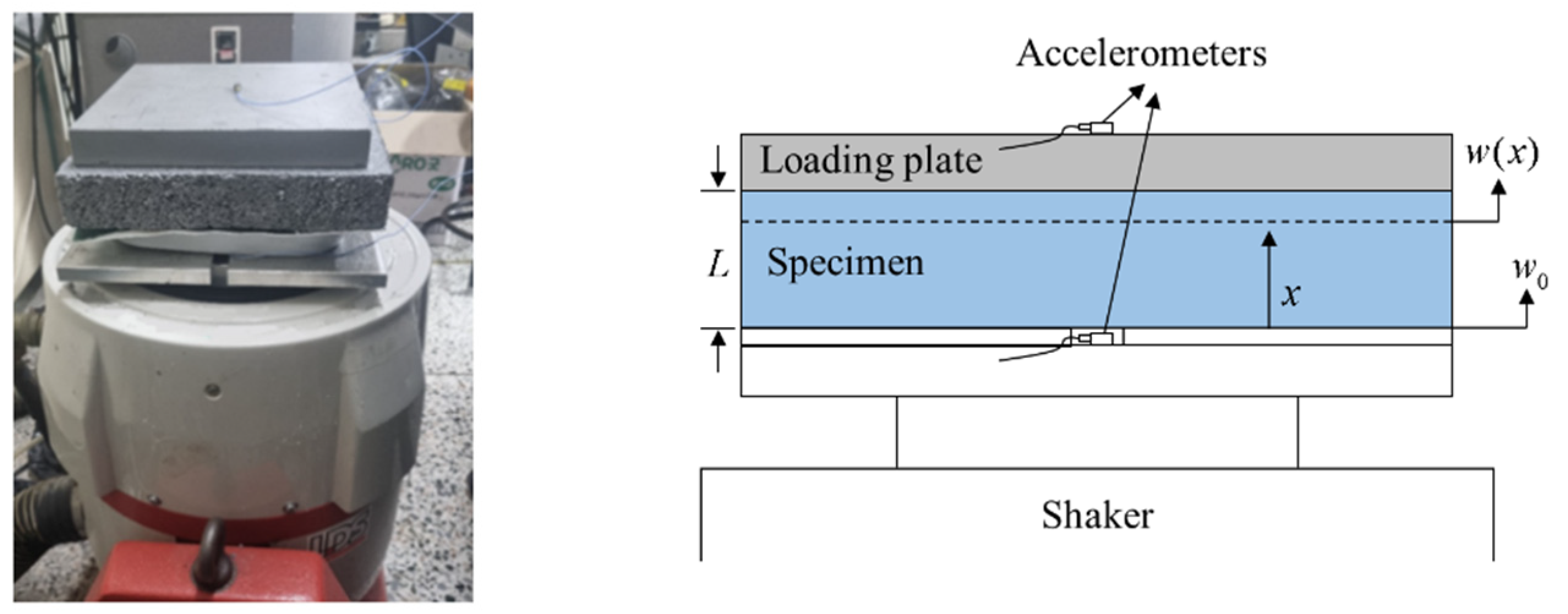
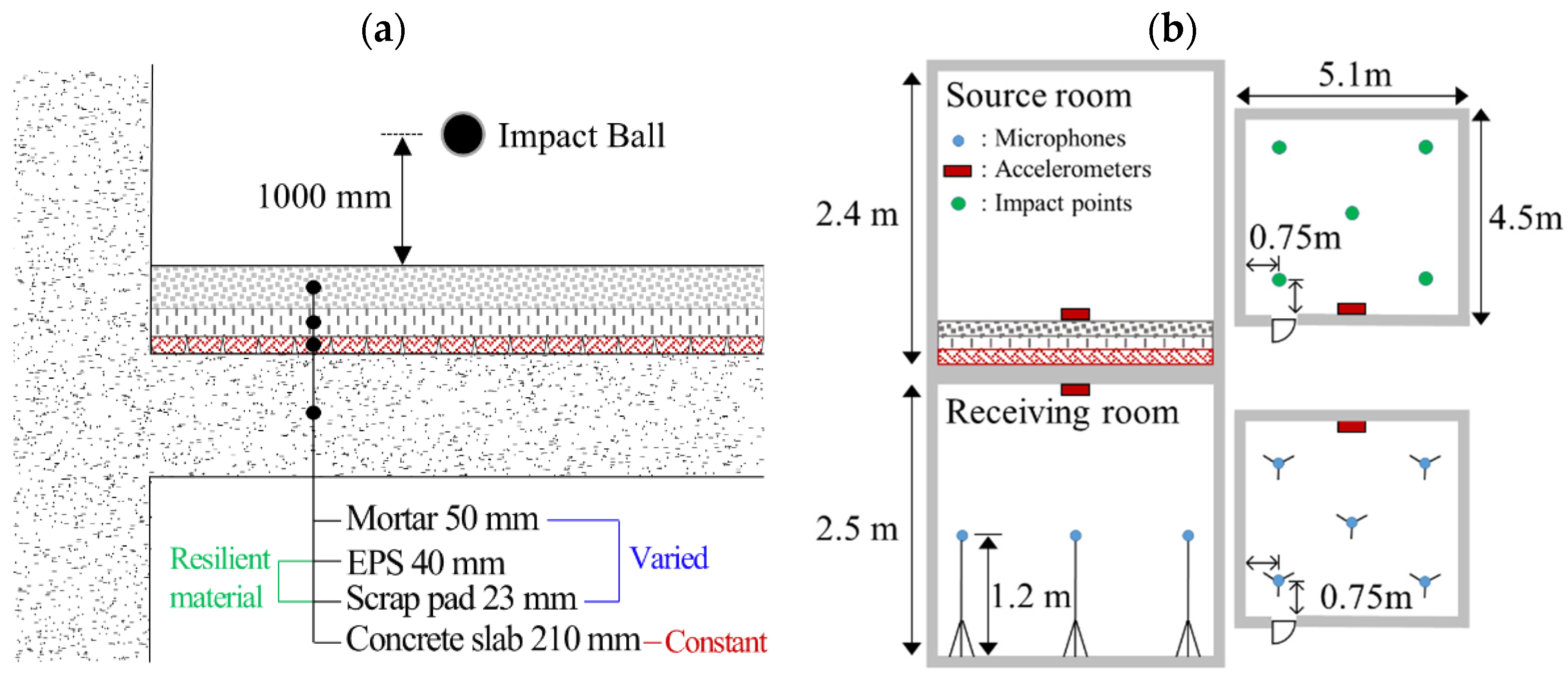
3.1. Experimental Setup to Measure Floor Impact Noise in Building Structures
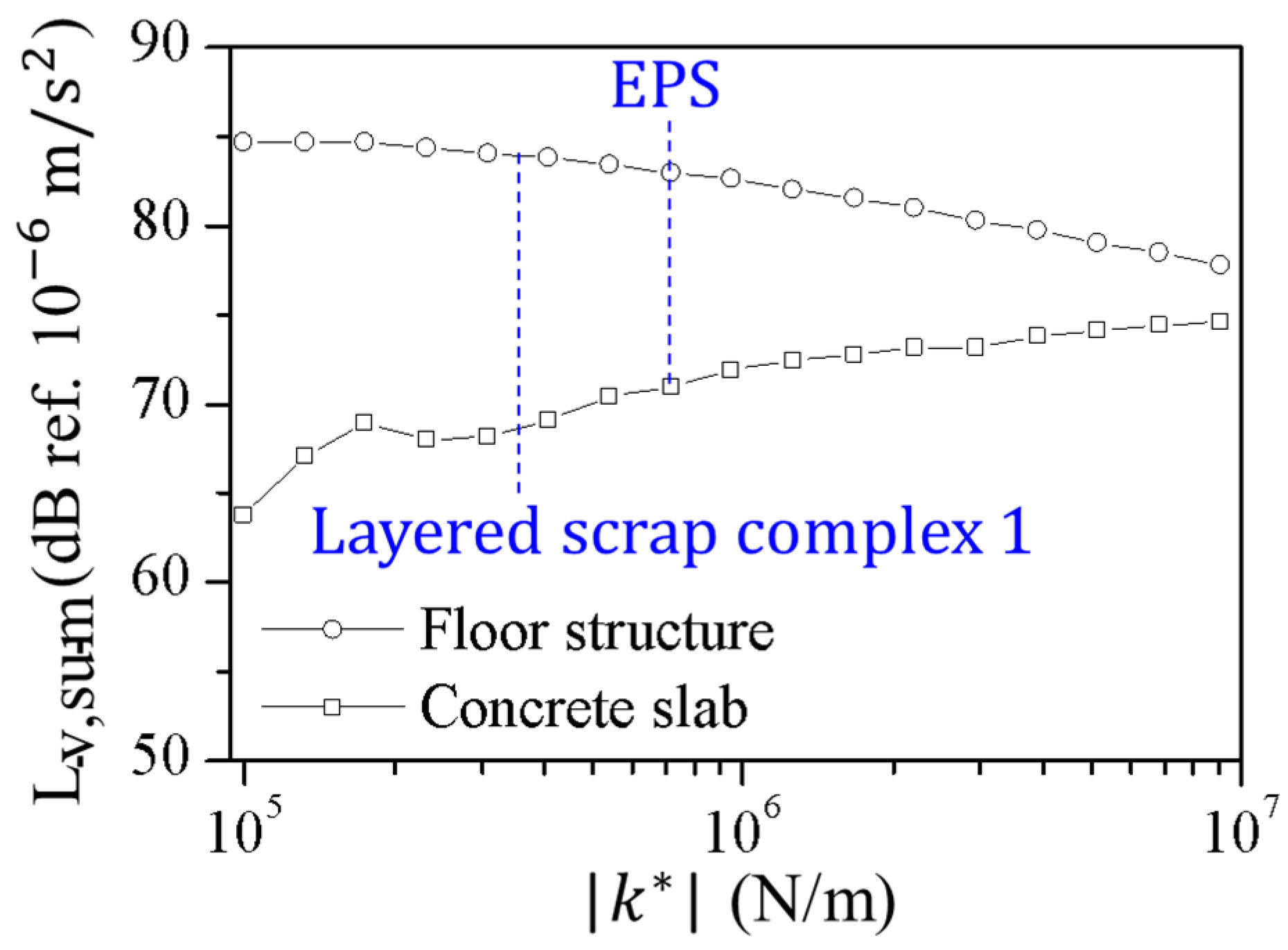
3.2. Floor Impact Sound Insulation Performance
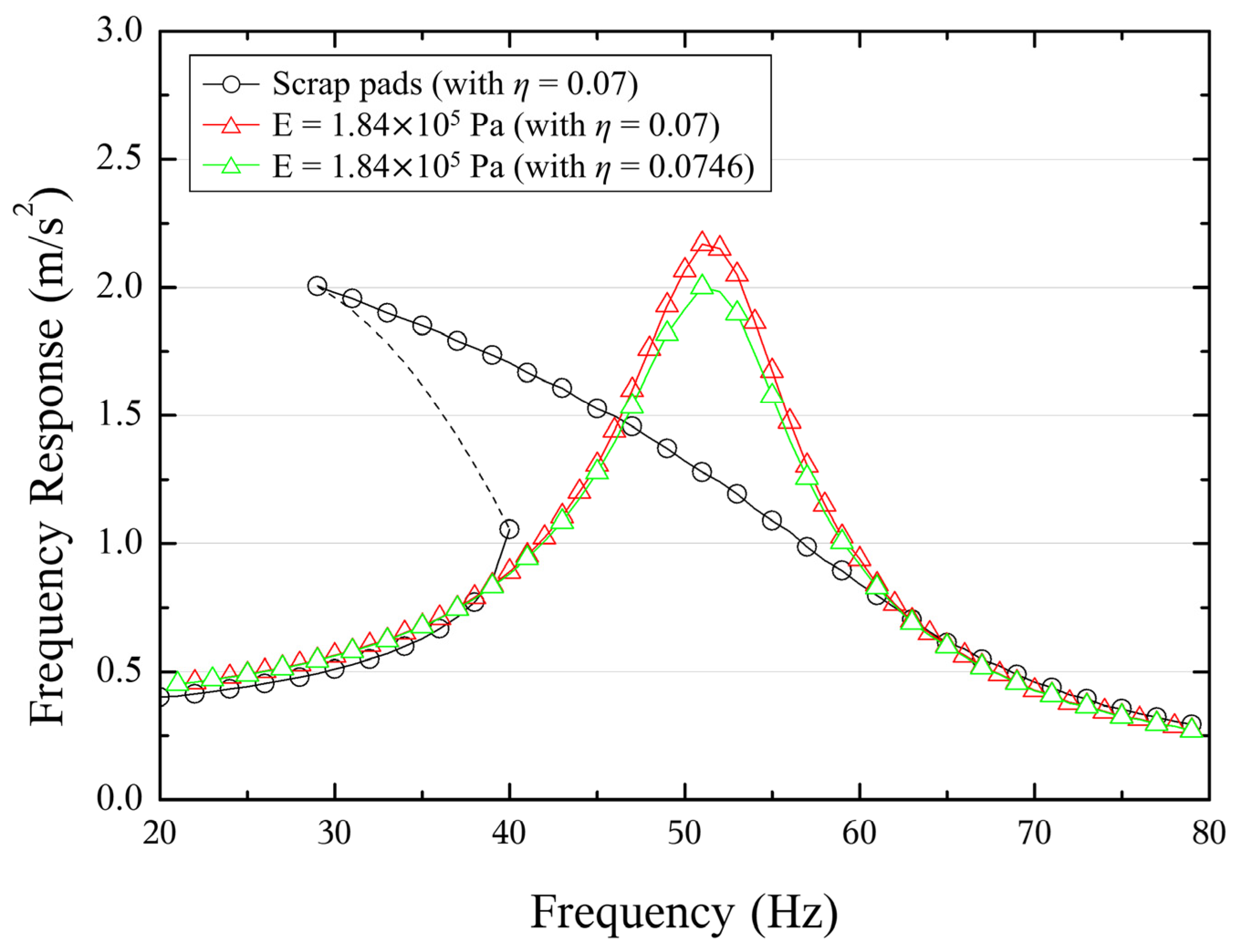
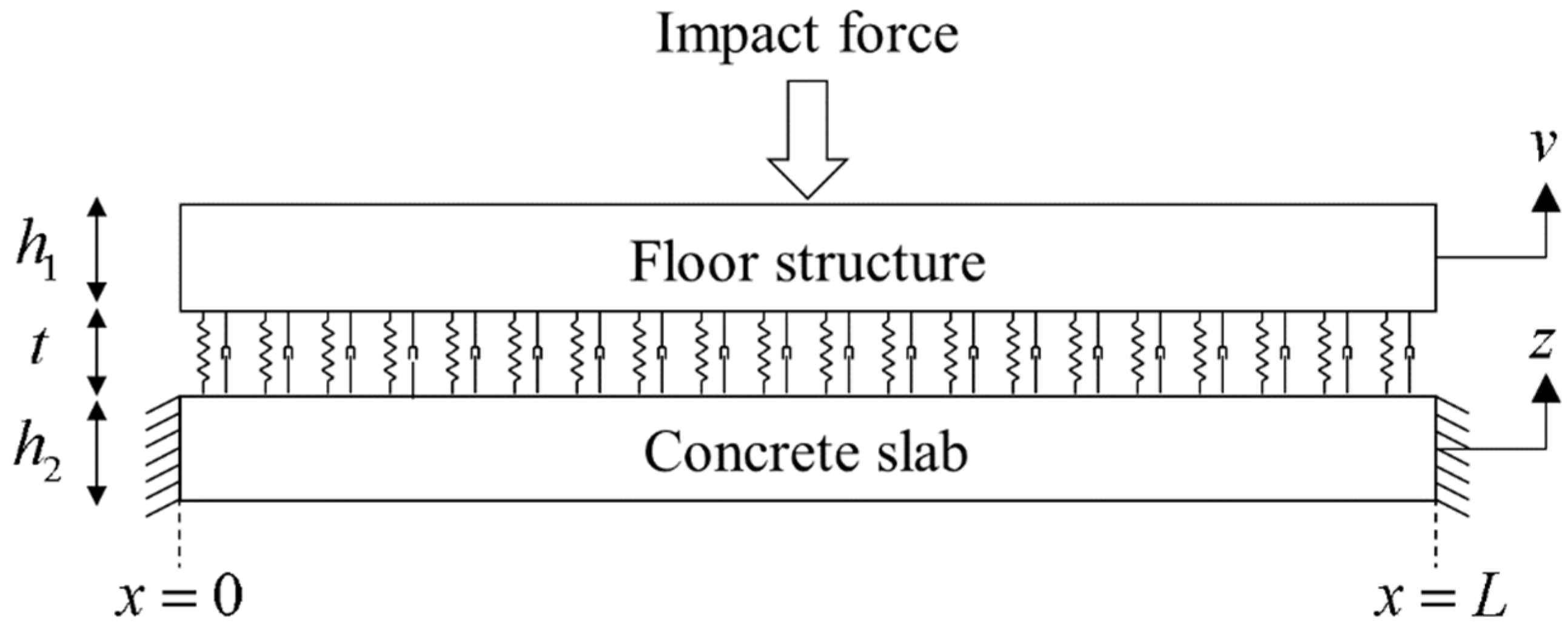
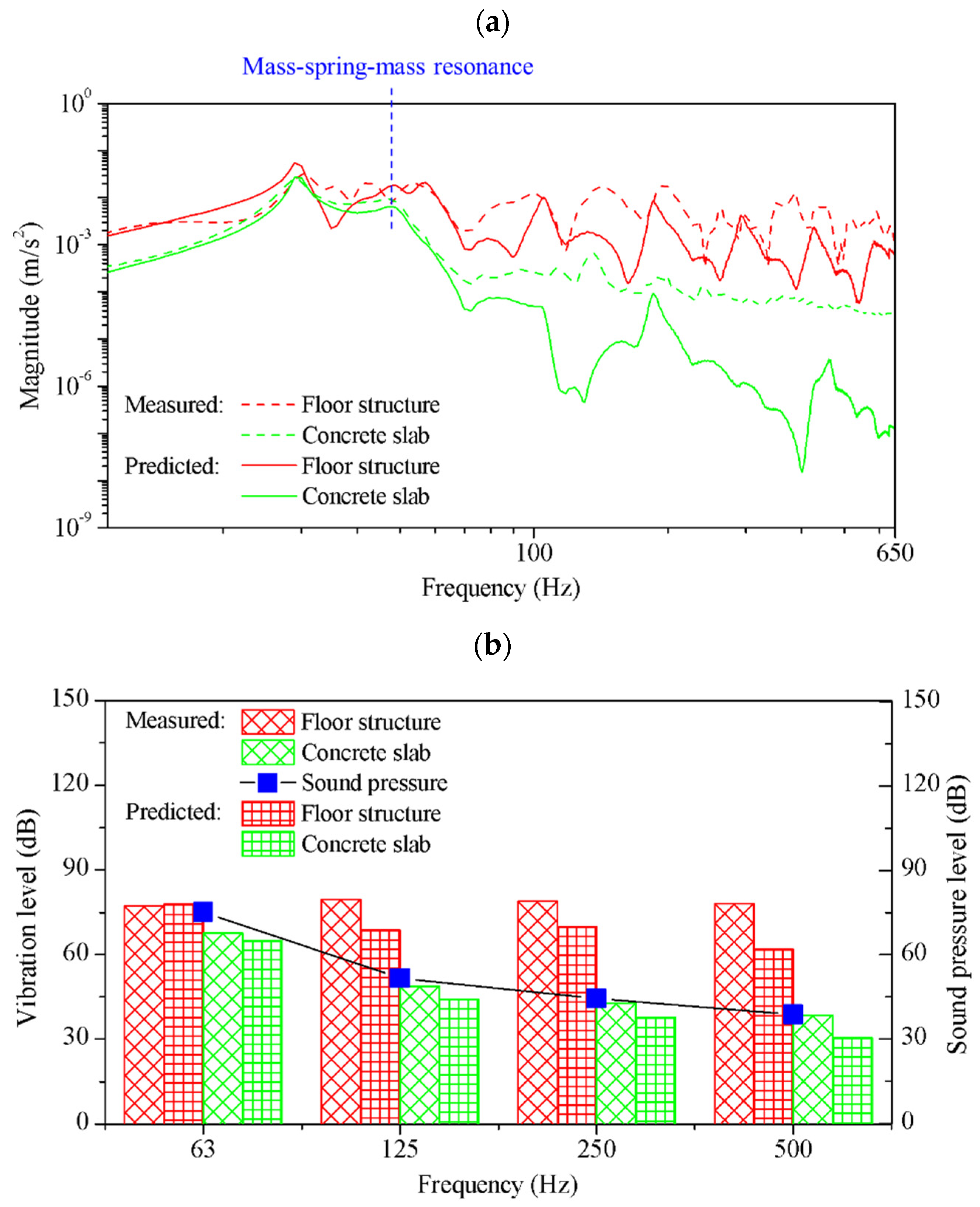
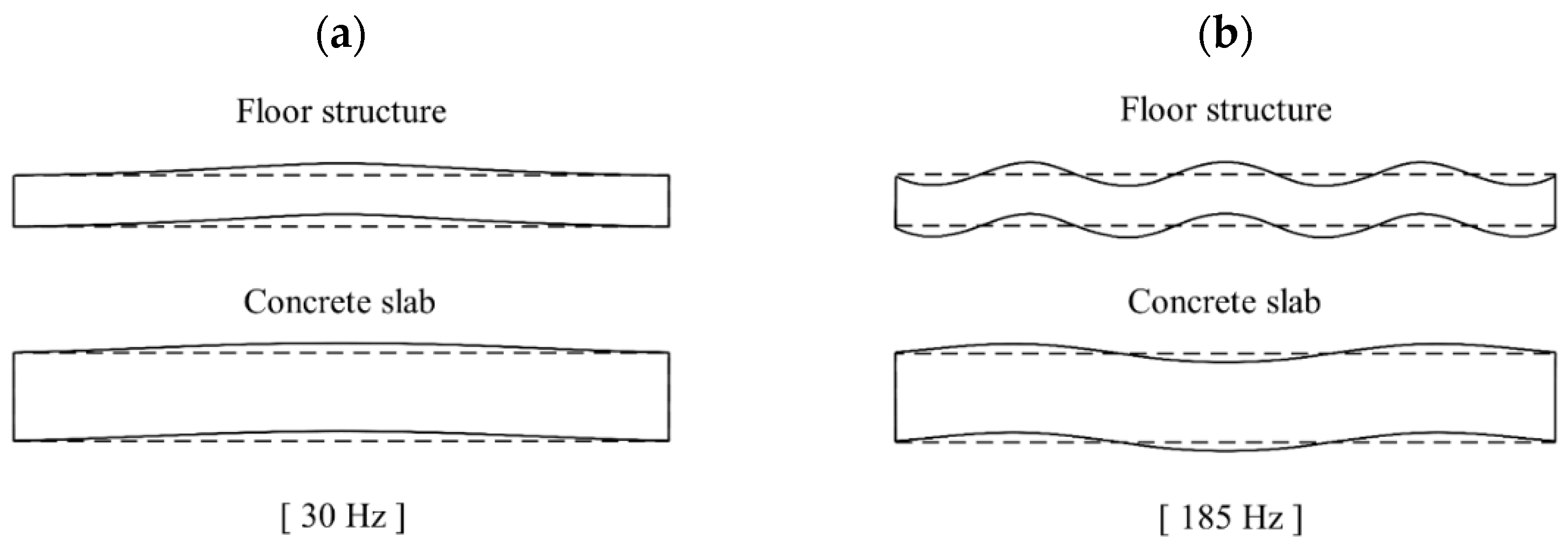
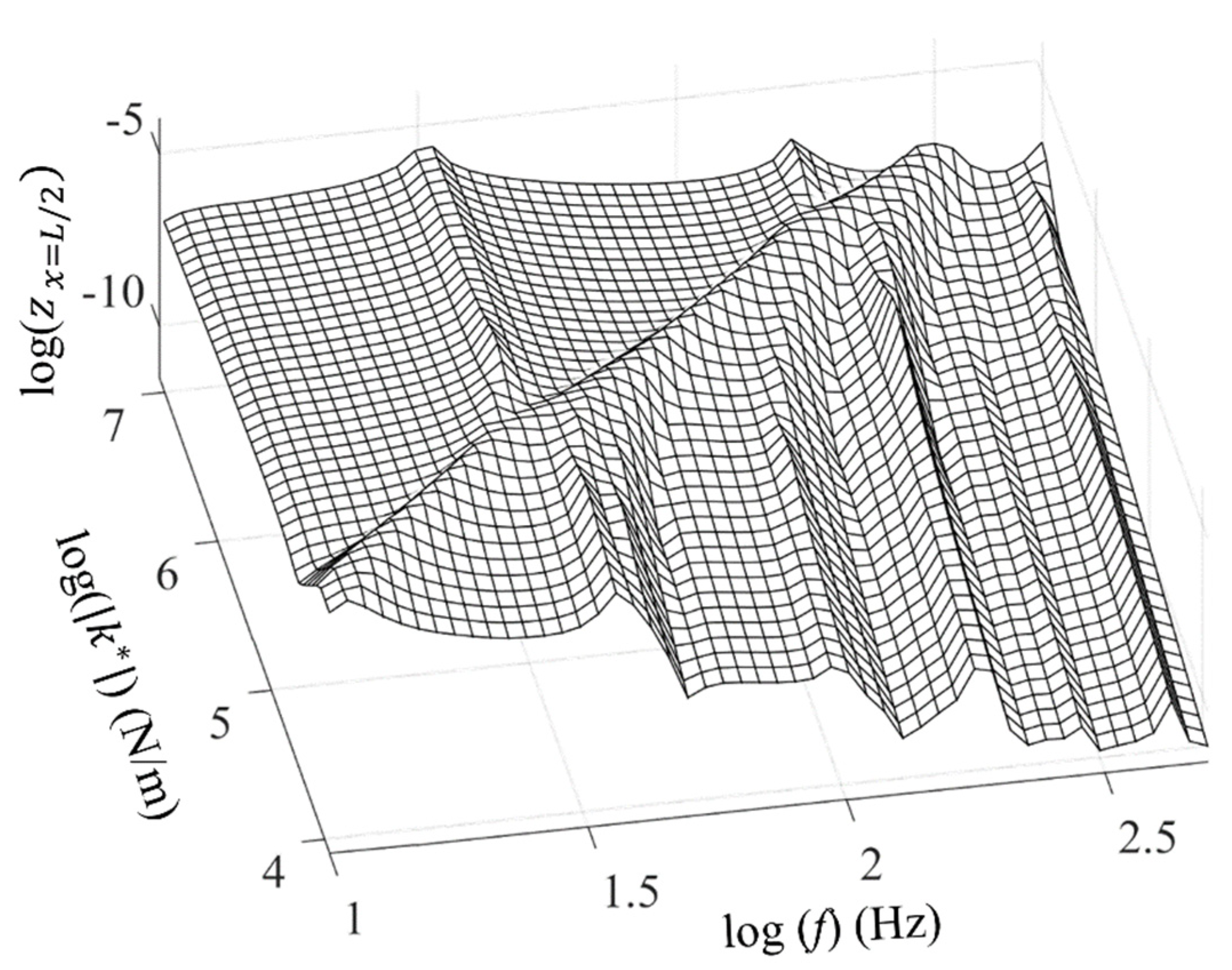
4. Prediction of Floor Impact Noise Reduction Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Gerretsen, E. A new system for rating impact sound insulation. Appl. Acoust. 1976, 9, 247–263. [Google Scholar] [CrossRef]
- Jeon, J. Subjective evaluation of floor impact noise based on the model of ACF/IACF. J. Sound Vib. 2001, 241, 147–155. [Google Scholar] [CrossRef]
- Ryu, J.; Sato, H.; Kurakata, K.; Hiramitsu, A.; Tanaka, M.; Hirota, T. Relation between annoyance and single-number quantities for rating heavy-weight floor impact sound insulation in wooden houses. J. Acoust. Soc. Am. 2011, 129, 3047–3055. [Google Scholar] [CrossRef] [PubMed]
- Sousa, A.N.; Gibbs, B. Low frequency impact sound transmission in dwellings through homogeneous concrete floors and floating floors. Appl. Acoust. 2011, 72, 177–189. [Google Scholar] [CrossRef]
- Park, H.S.; Oh, B.K.; Kim, Y.; Cho, T. Low-frequency impact sound transmission of floating floor: Case study of mortar bed on concrete slab with continuous interlayer. Build. Environ. 2015, 94, 793–801. [Google Scholar] [CrossRef]
- Sylwan, O. Shear and compressional damping effects of constrained layered beams. J. Sound Vib. 1987, 118, 35–45. [Google Scholar] [CrossRef]
- Sisemore, C.; Darvennes, C. Transverse Vibration of Elastic-Viscoelastic-Elastic Sandwich Beams: Compression-Experimental and Analytical Study. J. Sound Vib. 2002, 252, 155–167. [Google Scholar] [CrossRef]
- Kim, D.-K.; Kim, J.-H.; Jeon, J.-Y.; Park, J.-H. An Analysis of Vibration and Sound Radiation of Sandwich Panels Using the Rayleigh-Ritz Method. Trans. Korean Soc. Noise Vib. Eng. 2011, 21, 430–436. [Google Scholar] [CrossRef]
- Schiavi, A. Improvement of impact sound insulation: A constitutive model for floating floors. Appl. Acoust. 2018, 129, 64–71. [Google Scholar] [CrossRef]
- Branco, F.G.; Godinho, L. On the use of lightweight mortars for the minimization of impact sound transmission. Constr. Build. Mater. 2013, 45, 184–191. [Google Scholar] [CrossRef]
- Caniato, M.; Bettarello, F.; Marsich, L.; Ferluga, A.; Sbaizero, O.; Schmid, C. Time-depending performance of resilient layers under floating floors. Constr. Build. Mater. 2016, 102, 226–232. [Google Scholar] [CrossRef]
- Madigosky, W.M.; Lee, G.F. Automated dynamic Young’s modulus and loss factor measurements. J. Acoust. Soc. Am. 1979, 66, 345–349. [Google Scholar] [CrossRef]
- Pritz, T. Transfer function method for investigating the complex modulus of acoustic materials: Rod-like specimen. J. Sound Vib. 1982, 81, 359–376. [Google Scholar] [CrossRef]
- American National Standards Institute. Resonance Method for Measuring the Dynamic Mechanical Properties of Viscoelastic Materials; Acoustical Society of America, American National Standards Institute: New York, NY, USA, 1998; Available online: https://webstore.ansi.org/preview-pages/ASA/preview_ANSI+ASA+S2.22-1998+(R2012).pdf?srsltid=AfmBOopHlMiFP2qDY2QjhXPZg-syYM7kPv7XLKXneyxEiU_Fy7DZIPEx (accessed on 19 September 2024).
- Lee, J.-Y.; Kim, J.-M.; Kim, J.; Kim, J. Evaluation of the Long-Term Sound Reduction Performance of Resilient Materials in Floating Floor Systems. J. Sound Vib. 2016, 366, 199–210. [Google Scholar] [CrossRef]
- Kim, C.; Hong, Y.-K.; Lee, J.-Y. Long-term dynamic stiffness of resilient materials in floating floor systems. Constr. Build. Mater. 2017, 133, 27–38. [Google Scholar] [CrossRef]
- Rahman, M.; Al-Ghalib, A.; Mohammad, F. Anti-vibration characteristics of rubberised reinforced concrete beams. Mater. Struct. 2013, 47, 1807–1815. [Google Scholar] [CrossRef]
- Tiuc, A.-E.; Vermeşan, H.; Gabor, T.; Vasile, O. Improved Sound Absorption Properties of Polyurethane Foam Mixed with Textile Waste. Energy Procedia 2016, 85, 559–565. [Google Scholar] [CrossRef]
- Ribeiro, R.S.; Henneberg, F.; Catai, R.; Arnela, M.; Avelar, M.; Amarilla, R.S.D.; Wille, V. Assessing impact sound insulation in floating floors assembled from Construction and Demolition Waste. Constr. Build. Mater. 2024, 416, 135196. [Google Scholar] [CrossRef]
- Zhang, J.; Pang, X.; Chen, H.; Shi, G.; Deng, W. Process and forming performance of ploughing extrusion cutting for recycling of metal chips. J. Mech. Work. Technol. 2019, 274, 116283. [Google Scholar] [CrossRef]
- Simon, L.; Moraes, C.A.; Modolo, R.C.; Vargas, M.; Calheiro, D.; Brehm, F.A. Recycling of contaminated metallic chip based on eco-efficiency and eco-effectiveness approaches. J. Clean. Prod. 2017, 153, 417–424. [Google Scholar] [CrossRef]
- Lotfi, M.; Farid, A.A.; Soleimanimehr, H. The Effect of Chip Breaker Geometry on Chip Shape, Bending Moment, and Cutting Force: FE Analysis and Experimental Study. J. Adv. Manuf. Technol. 2014, 78, 917–925. [Google Scholar] [CrossRef]
- Aslan, A.; Salur, E.; Gunes, A.; Sahin, O.S.; Karadag, H.B.; Akdemir, A. The mechanical properties of composite materials recycled from waste metallic chips under different pressures. Int. J. Environ. Sci. Technol. 2019, 16, 5259–5266. [Google Scholar] [CrossRef]
- Abbas, H.; Hai, H.; Rongong, J.; Xing, Y. Damping performance of metal swarfs in a horizontal hollow structure. J. Mech. Sci. Technol. 2014, 28, 9–13. [Google Scholar] [CrossRef]
- Tang, N.; Rongong, J.A.; Tomlinson, G.R. Nonlinear Behaviour of Tangled Metal Wire Particle Dampers. In Proceedings of the International Conference on Structural Engineering Dynamics, Lagos, Portugal, 22–24 June 2015. [Google Scholar]
- ISO 9052-1; Acoustics. Determination of Dynamic Stiffness. Part 1: Materials Used under Floating Floors in Dwellings. International Organization for Standardization: Geneva, Switzerland, 1989.
- Inman, D.J.; Singh, R.C. Engineering Vibration (Vol. 3); Prentice Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Ward, I.M.; Sweeney, J. Mechanical Properties of Solid Polymers; John Wiley & Sons: Hoboken, NJ, USA, 2013; Available online: https://www.eng.uc.edu/~beaucag/Classes/Properties/Books/Mechanical%20Properties%20of%20Solid%20Polymers-Ward.pdf (accessed on 19 September 2024).
- Park, J. Measurements of the frame acoustic properties of porous and granular materials. J. Acoust. Soc. Am. 2005, 118, 3483–3490. [Google Scholar] [CrossRef]
- ISO 10140-5; Acoustics. Laboratory Measurement of Sound Insulation of Building Elements. Part 5: Requirements for Test Facilities and Equipment. International Organization for Standardization: Geneva, Switzerland, 2021.
- ISO 10140-3; Acoustics. Laboratory Measurement of Sound Insulation of Building Elements. Part 3: Measurement of Impact Sound Insulation. International Organization for Standardization: Geneva, Switzerland, 2021.
- ISO 717-2; Acoustics. Rating of Sound Insulation in Buildings and of Building Elements. Part 2: Impact Sound Insulation. International Organization for Standardization: Geneva, Switzerland, 2020.
- Douglas, B.E.; Yang, J.C.S. Transverse compressional damping in the vibratory response of elastic-viscoelastic-elastic beams. AIAA J. 1978, 16, 925–930. [Google Scholar] [CrossRef]




| Resilient Pad | Scrap Length (mm) | Pad Thickness (mm) | Mass (g/m2) |
|---|---|---|---|
| EPS | - | 40 | 875 |
| Scrap 1 | 60 | 23 | 4550 |
| Scrap 2 | 90 | 23 | 4600 |
| Scrap 3 | 120 | 23 | 4650 |
| Layered scrap complex 1 | 60 | 63 (Scrap 1 + EPS) | 5425 |
| Layered scrap complex 2 | 90 | 63 (Scrap 2 + EPS) | 5475 |
| Layered scrap complex 3 | 120 | 63 (Scrap 3 + EPS) | 5525 |
| Vibration Level (m/s2/kg) | Practical Loss Factor, η* |
|---|---|
| 0.3 | 0.0807 |
| 0.6 | 0.0812 |
| 0.9 | 0.0824 |
| 1.2 | 0.0812 |
| 1.5 | 0.0746 |
| Resilient Pad | Mortar Thickness (mm) | Total Thickness (mm) | (dBA) |
|---|---|---|---|
| - (Bare slab) | - | 60.2 | |
| EPS (40 mm) | 70 | 110 | 53.5 |
| EPP (40 mm) | 70 | 110 | 55.2 |
| Mortar (30 mm) + EPP (40 mm) | 50 | 120 | 48.9 |
| Scrap complex: Scrap (23 mm) + EPS (40 mm) | 50 | 113 | 44.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.; Jeon, J.; Kim, W.; Kim, N.; Lee, M.; Park, J. Reduction in Floor Impact Noise Using Resilient Pads Composed of Machining Scraps. Polymers 2024, 16, 2912. https://doi.org/10.3390/polym16202912
Lee D, Jeon J, Kim W, Kim N, Lee M, Park J. Reduction in Floor Impact Noise Using Resilient Pads Composed of Machining Scraps. Polymers. 2024; 16(20):2912. https://doi.org/10.3390/polym16202912
Chicago/Turabian StyleLee, Donghyeon, Jonghoon Jeon, Wanseung Kim, Narae Kim, Minjung Lee, and Junhong Park. 2024. "Reduction in Floor Impact Noise Using Resilient Pads Composed of Machining Scraps" Polymers 16, no. 20: 2912. https://doi.org/10.3390/polym16202912
APA StyleLee, D., Jeon, J., Kim, W., Kim, N., Lee, M., & Park, J. (2024). Reduction in Floor Impact Noise Using Resilient Pads Composed of Machining Scraps. Polymers, 16(20), 2912. https://doi.org/10.3390/polym16202912







