Structure Design on Thermoplastic Composites Considering Forming Effects
Abstract
1. Introduction
2. Stamping–Bending Coupled FEM Development and Validation
2.1. Experimental Procedure for Stamping–Bending Process
2.2. Strategy for Stamping–Bending Coupled FEM Development
2.3. Stamping–Bending Coupled FEM and Validation
3. Influence of Stamping Condition on Bending Performance
3.1. Cross-Sectional Shape (CSS)
3.2. Blank Holding Ring Shape (BHRS)
3.3. Blank Holding Ring Length (BHRL)
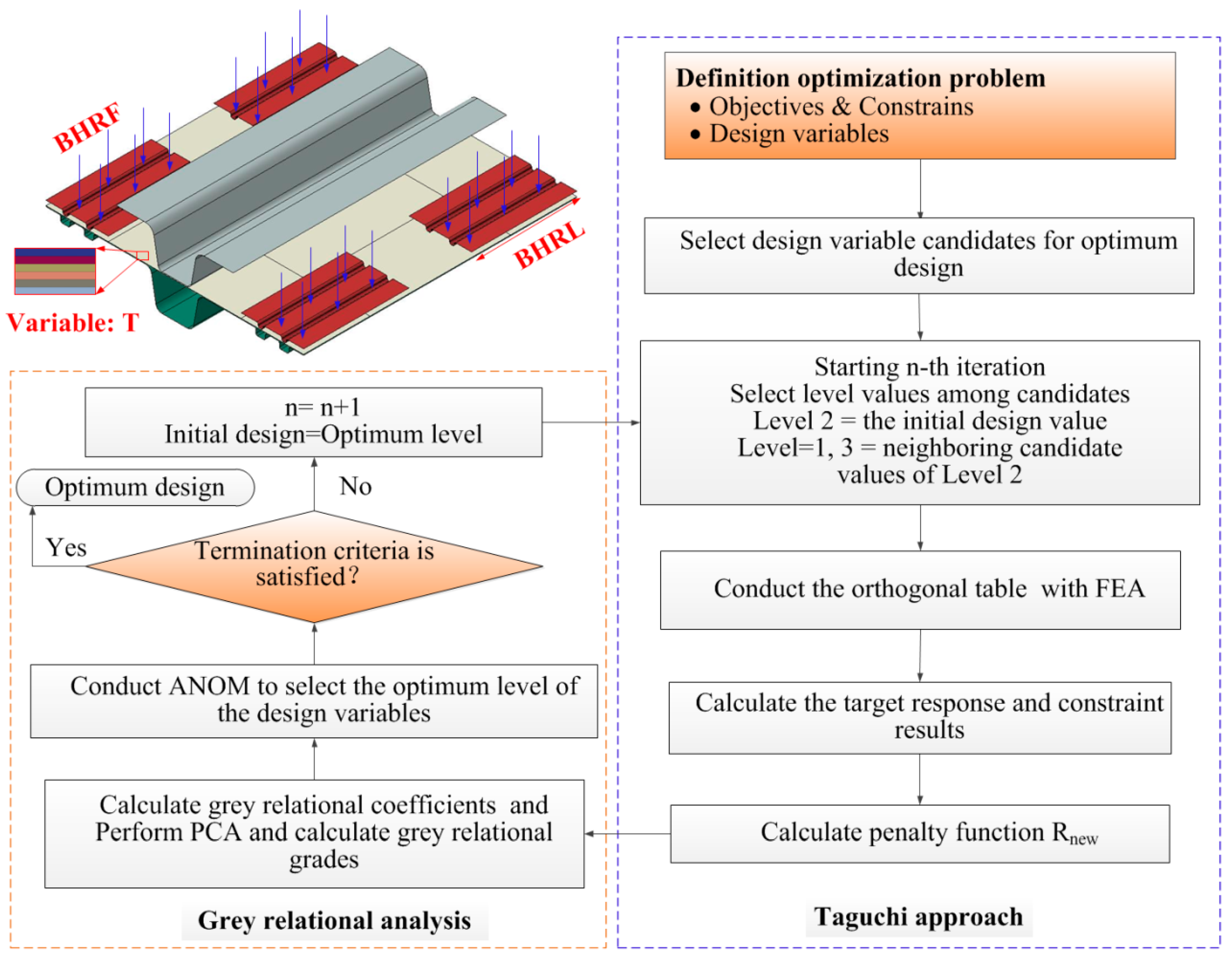
4. Multi-Objective Discrete Optimization Design
4.1. Optimization Problem Definition
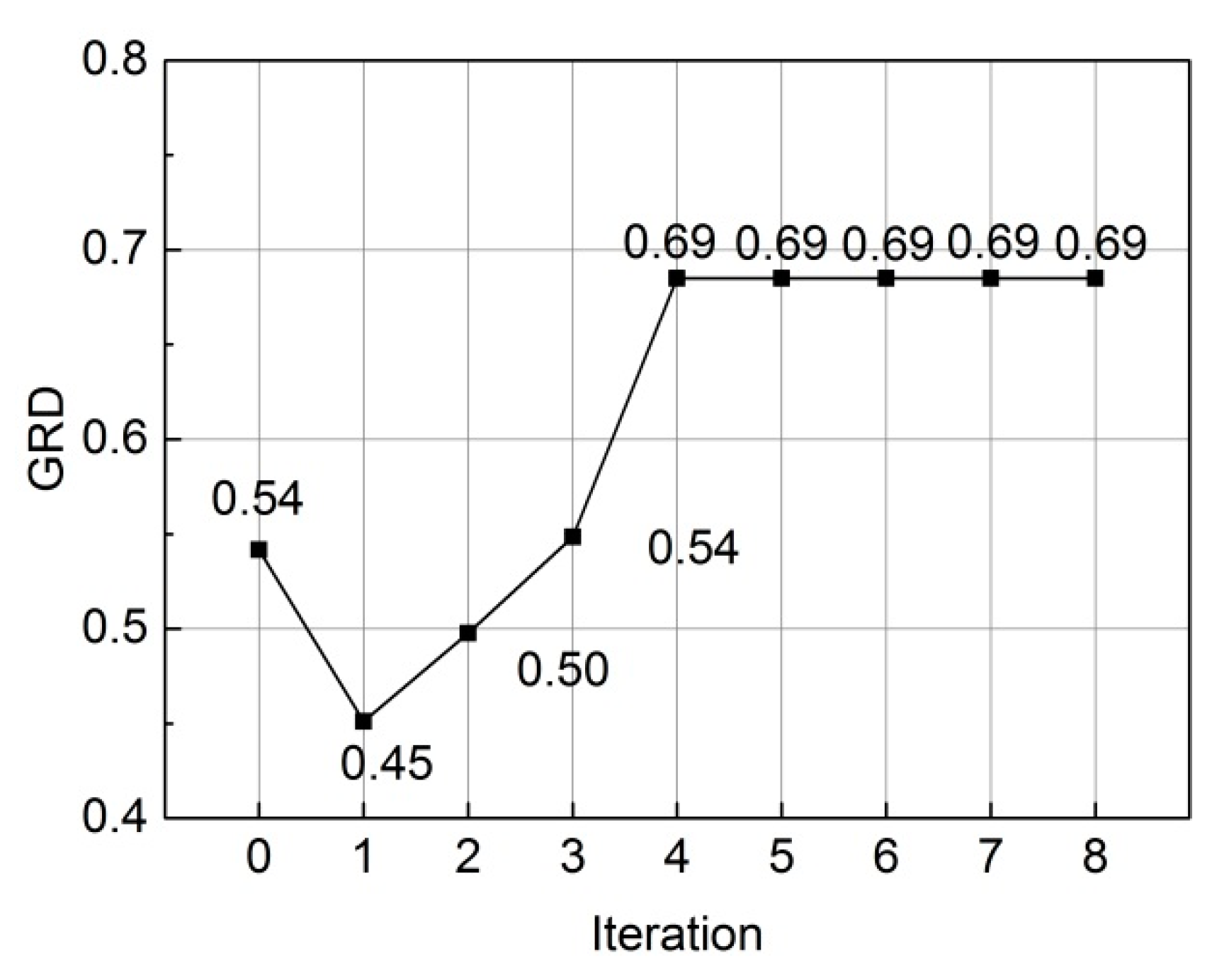
4.2. Optimization Design Result
5. Conclusions
- (1)
- The orthogonal configuration of the fabric in CF/PP prepreg was altered to the non-orthogonal configuration due to the constraints imposed by the blank holder. In off-axis tensile tests, laminates with a larger non-orthogonal fiber yarn angle exhibited an increased failure strain, albeit with a reduced failure strength. Furthermore, in the three-point bending test, the non-orthogonal CF/PP hollow specimen exhibited significant shear plastic deformations, with the maximum plastic strain reaching approximately 63.4% at the failure point.
- (2)
- The influences of the blank holding ring shape (BHRS) on the shear angle characteristics and bending responses of the CF/PP hollow specimens were not significant. In contrast, the cross-sectional shape (CSS) and blank holding ring length (BHRL) displayed significant variations in shear angle distributions.
- (3)
- The multi-objective discrete optimization for the three-point bending performance of CF/PP structures accounting for the influences of the stamping process was successfully implemented. The optimized design achieved an improvement of 17.5% while simultaneously reducing mass by 14%, and the maximum shear angle only increased by 1.4% compared to the baseline design, remaining below the specified limit shear angle.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Design Variables | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| T4 | T5 | T6 | |
| F4 | F5 | F6 | |
| L4 | L5 | L6 | |
| No. | Design Variables | Objective Functions | |||
|---|---|---|---|---|---|
| 1 | T4 | F4 | L4 | 0.528 | −0.090 |
| 2 | T4 | F5 | L5 | 0.529 | −0.090 |
| 3 | T4 | F6 | L6 | 0.500 | −0.090 |
| 4 | T5 | F4 | L6 | 0.570 | −0.101 |
| 5 | T5 | F5 | L5 | 0.544 | −0.101 |
| 6 | T5 | F6 | L4 | 0.513 | −0.101 |
| 7 | T6 | F4 | L5 | 0.691 | −0.112 |
| 8 | T6 | F5 | L6 | 0.700 | −0.112 |
| 9 | T6 | F6 | L4 | 0.691 | −0.112 |
| No. | Sequence after Normalizing | Gray Relational Coefficient | GRD | ||||
|---|---|---|---|---|---|---|---|
| 1 | 0.528 | −0.090 | 0.140 | 1.000 | 0.368 | 1.000 | 0.684 |
| 2 | 0.529 | −0.090 | 0.146 | 1.000 | 0.369 | 1.000 | 0.685 |
| 3 | 0.500 | −0.090 | 0.000 | 1.000 | 0.333 | 1.000 | 0.667 |
| 4 | 0.570 | −0.101 | 0.351 | 0.500 | 0.435 | 0.500 | 0.468 |
| 5 | 0.544 | −0.101 | 0.222 | 0.500 | 0.391 | 0.500 | 0.446 |
| 6 | 0.513 | −0.101 | 0.068 | 0.500 | 0.349 | 0.500 | 0.425 |
| 7 | 0.691 | −0.112 | 0.956 | 0.000 | 0.920 | 0.333 | 0.626 |
| 8 | 0.700 | −0.112 | 1.000 | 0.000 | 1.000 | 0.333 | 0.667 |
| 9 | 0.691 | −0.112 | 0.956 | 0.000 | 0.920 | 0.333 | 0.627 |
| Design Variables | Levels | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| 0.672 | 0.441 | 0.633 | |
| 0.587 | 0.593 | 0.567 | |
| 0.586 | 0.587 | 0.574 | |
| Design Variables | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| T4 | T5 | T6 | |
| F4 | F5 | F6 | |
| L4 | L5 | L6 | |
| Design Variables | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| T3 | T4 | T5 | |
| F4 | F5 | F6 | |
| L4 | L5 | L6 | |
| No. | Design Variables | Objective Functions | |||
|---|---|---|---|---|---|
| 1 | T3 | F4 | L4 | 0.350 | −0.078 |
| 2 | T3 | F5 | L5 | 0.388 | −0.078 |
| 3 | T3 | F6 | L6 | 0.385 | −0.078 |
| 4 | T4 | F4 | L6 | 0.534 | −0.090 |
| 5 | T4 | F5 | L5 | 0.529 | −0.090 |
| 6 | T4 | F6 | L4 | 0.482 | −0.090 |
| 7 | T5 | F4 | L5 | 0.474 | −0.101 |
| 8 | T5 | F5 | L6 | 0.550 | −0.101 |
| 9 | T5 | F6 | L4 | 0.513 | −0.101 |
| No. | The Sequence after Normalizing | Gray Relational Coefficient | GRD | ||||
|---|---|---|---|---|---|---|---|
| f1(x) | f2(x) | f1(x) | f2(x) | f1(x) | f2(x) | ||
| 1 | 0.350 | −0.078 | 0.000 | 1.000 | 0.333 | 1.000 | 0.667 |
| 2 | 0.388 | −0.078 | 0.193 | 1.000 | 0.382 | 1.000 | 0.691 |
| 3 | 0.385 | −0.078 | 0.174 | 1.000 | 0.377 | 1.000 | 0.689 |
| 4 | 0.534 | −0.090 | 0.919 | 0.500 | 0.861 | 0.500 | 0.680 |
| 5 | 0.529 | −0.090 | 0.894 | 0.500 | 0.826 | 0.500 | 0.663 |
| 6 | 0.482 | −0.090 | 0.662 | 0.500 | 0.597 | 0.500 | 0.548 |
| 7 | 0.474 | −0.101 | 0.618 | 0.000 | 0.567 | 0.333 | 0.450 |
| 8 | 0.550 | −0.101 | 1.000 | 0.000 | 1.000 | 0.333 | 0.667 |
| 9 | 0.513 | −0.101 | 0.817 | 0.000 | 0.732 | 0.333 | 0.533 |
| Design Variables | Levels | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| 0.675 | 0.624 | 0.544 | |
| 0.593 | 0.667 | 0.584 | |
| 0.621 | 0.628 | 0.595 | |
| Design Variables | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| T3 | T4 | T5 | |
| F4 | F5 | F6 | |
| L4 | L5 | L6 | |
| Design Variables | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| T2 | T3 | T4 | |
| F4 | F5 | F6 | |
| L4 | L5 | L6 | |
| No. | Design Variables | Objective Functions | |||
|---|---|---|---|---|---|
| 1 | T2 | F4 | L4 | 0.314 | −0.067 |
| 2 | T2 | F5 | L5 | 0.352 | −0.067 |
| 3 | T2 | F6 | L6 | 0.344 | −0.082 |
| 4 | T3 | F4 | L6 | 0.418 | −0.078 |
| 5 | T3 | F5 | L5 | 0.388 | −0.078 |
| 6 | T3 | F6 | L4 | 0.396 | −0.082 |
| 7 | T4 | F4 | L5 | 0.487 | −0.090 |
| 8 | T4 | F5 | L6 | 0.497 | −0.090 |
| 9 | T4 | F6 | L4 | 0.482 | −0.090 |
| No. | The Sequence after Normalizing | Gray Relational Coefficient | GRD | ||||
|---|---|---|---|---|---|---|---|
| f1(x) | f2(x) | f1(x) | f2(x) | f1(x) | f2(x) | ||
| 1 | 0.314 | −0.067 | 0.000 | 1.000 | 0.333 | 1.000 | 0.667 |
| 2 | 0.352 | −0.067 | 0.210 | 1.000 | 0.388 | 1.000 | 0.694 |
| 3 | 0.344 | −0.082 | 0.164 | 0.330 | 0.374 | 0.427 | 0.401 |
| 4 | 0.418 | −0.078 | 0.571 | 0.500 | 0.538 | 0.500 | 0.519 |
| 5 | 0.388 | −0.078 | 0.407 | 0.500 | 0.457 | 0.500 | 0.479 |
| 6 | 0.396 | −0.082 | 0.451 | 0.321 | 0.477 | 0.424 | 0.450 |
| 7 | 0.487 | −0.090 | 0.947 | 0.000 | 0.903 | 0.333 | 0.618 |
| 8 | 0.497 | −0.090 | 1.000 | 0.000 | 1.000 | 0.333 | 0.667 |
| 9 | 0.482 | −0.090 | 0.920 | 0.000 | 0.862 | 0.333 | 0.598 |
| Design Variables | Levels | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| 0.581 | 0.478 | 0.621 | |
| 0.595 | 0.607 | 0.478 | |
| 0.589 | 0.597 | 0.494 | |
| Design Variables | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| T2 | T3 | T4 | |
| F4 | F5 | F6 | |
| L4 | L5 | L6 | |
| Design Variables | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| T1 | T2 | T3 | |
| F4 | F5 | F6 | |
| L4 | L5 | L6 | |
| No. | Design Variables | Objective Functions | |||
|---|---|---|---|---|---|
| 1 | T1 | F4 | L4 | 0.276 | −0.069 |
| 2 | T1 | F5 | L5 | 0.304 | −0.071 |
| 3 | T1 | F6 | L6 | 0.230 | −0.076 |
| 4 | T2 | F4 | L6 | 0.307 | −0.067 |
| 5 | T2 | F5 | L5 | 0.352 | −0.067 |
| 6 | T2 | F6 | L4 | 0.306 | −0.078 |
| 7 | T3 | F4 | L5 | 0.389 | −0.078 |
| 8 | T3 | F5 | L6 | 0.410 | −0.078 |
| 9 | T3 | F6 | L4 | 0.396 | −0.082 |
| No. | The Sequence after Normalizing | Gray Relational Coefficient | GRD | ||||
|---|---|---|---|---|---|---|---|
| f1(x) | f2(x) | f1(x) | f2(x) | f1(x) | f2(x) | ||
| 1 | 0.276 | −0.069 | 0.257 | 0.862 | 0.402 | 0.784 | 0.593 |
| 2 | 0.304 | −0.071 | 0.410 | 0.783 | 0.459 | 0.697 | 0.578 |
| 3 | 0.230 | −0.076 | 0.000 | 0.421 | 0.333 | 0.463 | 0.398 |
| 4 | 0.307 | −0.067 | 0.428 | 1.000 | 0.466 | 1.000 | 0.733 |
| 5 | 0.352 | −0.067 | 0.678 | 1.000 | 0.609 | 1.000 | 0.804 |
| 6 | 0.306 | −0.078 | 0.424 | 0.270 | 0.465 | 0.406 | 0.436 |
| 7 | 0.389 | −0.078 | 0.884 | 0.263 | 0.812 | 0.404 | 0.608 |
| 8 | 0.410 | −0.078 | 1.000 | 0.263 | 1.000 | 0.404 | 0.702 |
| 9 | 0.396 | −0.082 | 0.924 | 0.000 | 0.868 | 0.333 | 0.601 |
| Design Variables | Levels | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| 0.518 | 0.651 | 0.631 | |
| 0.638 | 0.688 | 0.473 | |
| 0.571 | 0.631 | 0.597 | |
| Design Variables | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| T1 | T2 | T3 | |
| F4 | F5 | F6 | |
| L4 | L5 | L6 | |
References
- Najafi, A.; Rais-Rohani, M. Sequential coupled process-performance simulation and multi-objective optimization of thin-walled tubes. Mater. Des. 2012, 41, 89–98. [Google Scholar] [CrossRef]
- Najafi, A.; Marin, E.B.; Rais-Rohani, M. Concurrent multi-scale crush simulations with a crystal plasticity model. Thin-Walled Struct. 2012, 53, 176–187. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, H.; Wang, R.; Lv, X.; Li, Q. Multiobjective reliability-based optimization for crashworthy structures coupled with metal forming process. Struct. Multidiscip. Optim. 2017, 56, 1571–1587. [Google Scholar] [CrossRef]
- Najafi, A.; Acar, E.; Rais-Rohani, M. Multi-objective robust design of energy-absorbing components using coupled process–performance simulations. Eng. Optim. 2014, 46, 146–164. [Google Scholar] [CrossRef]
- Cheng, W.; Zhang, H.; Fu, S.; Xie, H.; Tang, Z.; Zhu, Z. A process-performance coupled design method for hot-stamped tailor rolled blank structure. Thin-Walled Struct. 2019, 140, 132–143. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, H.; Huang, B.; Zhou, H.; Peng, X. Characterization of tool-ply friction behavior for treated jute/PLA biocomposite prepregs in thermoforming. Compos. Part A Appl. Sci. Manuf. 2024, 177, 107875. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Zhang, H.; Ding, S.; Yang, T.; Pang, J.; Zhang, H.; Zhang, J.; Zhang, Y.; Jiang, Z. Study on the Preparation and Process Parameter-Mechanical Property Relationships of Carbon Fiber Fabric Reinforced Poly(Ether Ether Ketone) Thermoplastic Composites. Polymers 2024, 16, 897. [Google Scholar] [CrossRef]
- Jeong, E.; Kim, Y.; Hong, S.; Yoon, K.; Lee, S. Innovative Injection Molding Process for the Fabrication of Woven Fabric Reinforced Thermoplastic Composites. Polymers 2022, 14, 1577. [Google Scholar] [CrossRef]
- Shahinur, S.; Sayeed, M.M.A.; Hasan, M.; Sayem, A.S.M.; Haider, J.; Ura, S. Current Development and Future Perspective on Natural Jute Fibers and Their Biocomposites. Polymers 2022, 14, 1445. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, G. Development of the temperature-dependent constitutive model of glass fiber reinforced polypropylene composites. Mater. Manuf. Process. 2023, 38, 295–305. [Google Scholar] [CrossRef]
- Chen, S.; Harper, L.T.; Endruweit, A.; Warrior, N.A. Formability optimisation of fabric preforms by controlling material draw-in through in-plane constraints. Compos. Part A Appl. Sci. Manuf. 2015, 76, 10–19. [Google Scholar] [CrossRef]
- Harrison, P.; Camacho, L.F.G. Deep draw induced wrinkling of engineering fabrics. Int. J. Solids Struct. 2021, 212, 220–236. [Google Scholar] [CrossRef]
- Liang, B.; Hamila, N.; Peillon, M.; Boisse, P. Analysis of thermoplastic prepreg bending stiffness during manufacturing and of its influence on wrinkling simulations. Compos. Part A Appl. Sci. Manuf. 2014, 67, 111–122. [Google Scholar] [CrossRef]
- Studer, J.; Dransfeld, C.; Cano, J.J.; Keller, A.; Wink, M.; Masania, K.; Fiedler, B. Effect of fabric architecture, compaction and permeability on through thickness thermoplastic melt impregnation. Compos. Part A Appl. Sci. Manuf. 2019, 122, 45–53. [Google Scholar] [CrossRef]
- Wang, Z.; Ren, H.; Cao, X.A.; Mei, X.; Zhu, G.; Chen, Y.; Guo, Y. Compressive Failure Analysis of Thin-Walled Thermosetting Composite Structures Accounting for the Preforming Effects. Fiber. Polym. 2024, 25, 317–329. [Google Scholar] [CrossRef]
- Gong, Y.; Xu, P.; Peng, X.; Wei, R.; Yao, Y.; Zhao, K. A lamination model for forming simulation of woven fabric reinforced thermoplastic prepregs. Compos. Struct. 2018, 196, 89–95. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Fang, G.; Zhang, J.; Zhou, Z.; Wang, S. Influence of temperature on the impact behavior of woven-ply carbon fiber reinforced thermoplastic composites. Compos. Struct. 2018, 185, 435–445. [Google Scholar] [CrossRef]
- Karakuzu, R.; Aslan, Z.; Okutan, B. The effect of ply number, orientation angle and bonding type on residual stresses of woven steel fiber reinforced thermoplastic laminated composite plates subjected to transverse uniform load. Compos. Sci. Technol. 2004, 64, 1049–1056. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, W.; Wang, Z.; Yin, H.; Zheng, G.; Li, Q. A novel specimen design to establish the forming limit diagram (FLD) for GFRP through stamping test. Compos. Part A Appl. Sci. Manuf. 2020, 130, 105737. [Google Scholar] [CrossRef]
- Holmes, J.; Das, R.; Stachurski, Z.; Compston, P.; Kalyanasundaram, S. Development of an S-specimen geometry for shear testing of woven thermoplastic composites. Compos. Part B Eng. 2020, 203, 108485. [Google Scholar] [CrossRef]
- Kärger, L.; Bernath, A.; Fritz, F.; Galkin, S.; Magagnato, D.; Oeckerath, A.; Schön, A.; Henning, F. Development and validation of a CAE chain for unidirectional fibre reinforced composite components. Compos. Struct. 2015, 132, 350–358. [Google Scholar] [CrossRef]
- Sun, Q.; Zhou, G.; Meng, Z.; Jain, M.; Su, X. An integrated computational materials engineering framework to analyze the failure behaviors of carbon fiber reinforced polymer composites for lightweight vehicle applications. Compos. Sci. Technol. 2021, 202, 108560. [Google Scholar] [CrossRef] [PubMed]
- Liang, B.; Zhang, W.; Fenner, J.S.; Gao, J.; Shi, Y.; Zeng, D.; Cao, J. Multi-scale modeling of mechanical behavior of cured woven textile composites accounting for the influence of yarn angle variation. Compos. Part A Appl. Sci. Manuf. 2019, 124, 105460. [Google Scholar] [CrossRef]
- Kim, D.J.; Yu, M.H.; Lim, J.; Nam, B.; Kim, H.S. Prediction of the mechanical behavior of fiber-reinforced composite structure considering its shear angle distribution generated during thermo-compression molding process. Compos. Struct. 2019, 220, 441–450. [Google Scholar] [CrossRef]
- Han, M.G.; Chang, S.H. Draping simulation of carbon/epoxy plain weave fabrics with non-orthogonal constitutive model and material behavior analysis of the cured structure. Compos. Part A Appl. Sci. Manuf. 2018, 110, 172–182. [Google Scholar] [CrossRef]
- Aridhi, A.; Arfaoui, M.; Mabrouki, T.; Naouar, N.; Denis, Y.; Zarroug, M.; Boisse, P. Textile composite structural analysis taking into account the forming process. Compos. Part B Eng. 2019, 166, 773–784. [Google Scholar] [CrossRef]
- Jayasree, N.A.; Airale, A.G.; Ferraris, A.; Messana, A.; Sisca, L.; Carello, M. Process analysis for structural optimisation of thermoplastic composite component using the building block approach. Compos. Part B Eng. 2017, 126, 119–132. [Google Scholar] [CrossRef]
- Kärger, L.; Galkin, S.; Zimmerling, C.; Dörr, D.; Linden, J.; Oeckerath, A.; Wolf, K. Forming optimisation embedded in a CAE chain to assess and enhance the structural performance of composite components. Compos. Struct. 2018, 192, 143–152. [Google Scholar] [CrossRef]
- Cao, J.; Akkerman, R.; Boisse, P.; Chen, J.; Cheng, H.; de Graaf, E.; Gorczyca, J.; Harrison, P.; Hivet, G.; Launay, J.; et al. Characterization of mechanical behavior of woven fabrics: Experimental methods and benchmark results. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1037–1053. [Google Scholar] [CrossRef]
- Rashidi, A.; Milani, A.S. A multi-step biaxial bias extension test for wrinkling/de-wrinkling characterization of woven fabrics: Towards optimum forming design guidelines. Mater. Des. 2018, 146, 273–285. [Google Scholar] [CrossRef]
- Harrison, P.; Taylor, E.; Alsayednoor, J. Improving the Accuracy of the Uniaxial Bias Extension Test on Engineering Fabrics Using a Simple Wrinkle Mitigation Technique. Compos. Part A Appl. Sci. Manuf. 2018, 108, 53–61. [Google Scholar] [CrossRef]
- Mei, M.; He, Y.; Yang, X.; Wei, K.; Mo, F. Meso/macro scale response of the comingled glass polypropylene 2-2 twill woven fabric under shear pre-tension coupling. Compos. Struct. 2020, 236, 111854. [Google Scholar] [CrossRef]
- Badel, P.; Gauthier, S.; Vidal-Sallé, E.; Boisse, P. Rate constitutive equations for computational analyses of textile composite reinforcement mechanical behaviour during forming. Compos. Part A Appl. Sci. Manuf. 2009, 40, 997–1007. [Google Scholar] [CrossRef]
- Khan, M.A.; Mabrouki, T.; Vidal-Sallé, E.; Boisse, P. Numerical and experimental analyses of woven composite reinforcement forming using a hypoelastic behaviour. Application to the double dome benchmark. J. Mater. Process. Technol. 2010, 210, 378–388. [Google Scholar] [CrossRef]
- Truesdell, C. The simplest rate theory of pure elasticity. Comm. Pure. Appl. Math. 1955, 8, 123–132. [Google Scholar] [CrossRef]
- Truesdell, C. Hypo-elasticity. J. Rat. Mech. Anal. 1955, 4, 83–133. [Google Scholar] [CrossRef]
- Truesdell, C. Hypo-elastic shear. J. Appl. Phys. 1956, 27, 441–447. [Google Scholar] [CrossRef]
- Wang, Z.; Jin, X.; Li, Q.; Sun, G. On crashworthiness design of hybrid metal-composite structures. Int. J. Mech. Sci. 2020, 171, 105380. [Google Scholar] [CrossRef]
- Zhu, G.; Liao, J.; Sun, G.; Li, Q. Comparative study on metal/CFRP hybrid structures under static and dynamic loading. Int. J. Impact Eng. 2020, 141, 103509. [Google Scholar] [CrossRef]
- Zhu, G.; Zhao, Z.; Cao, X.A.; Wei, L.; Wang, Z.; Zhao, X. On crushing behavior of square aluminum/CFRP hybrid structures subjected to quasi-static loading. Thin-Walled Struct. 2023, 184, 110486. [Google Scholar] [CrossRef]
- Xiao, J.R.; Gama, B.A.; Gillespie, J.W., Jr. Progressive damage and delamination in plain weave S-2 glass/SC-15 composites under quasi-static punch-shear loading. Compos. Struct. 2007, 78, 182–196. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, Q.; Li, Q.; Sun, G. Design optimization of bioinspired helicoidal CFRPP/GFRPP hybrid composites for multiple low-velocity impact loads. Int. J. Mech. Sci. 2022, 219, 107064. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, W.; Luo, Q.; Zheng, G.; Li, Q.; Sun, G. A novel failure criterion based upon forming limit curve for thermoplastic composites. Compos. Part B Eng. 2020, 202, 108320. [Google Scholar] [CrossRef]
- Kim, N.H. Introduction to Nonlinear Finite Element Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2014; pp. 241–255. [Google Scholar]
- Boria, S.; Scattina, A.; Belingardi, G. Experimental evaluation of a fully recyclable thermoplastic composite. Compos. Struct. 2016, 140, 21–35. [Google Scholar] [CrossRef]
- Fang, J.; Sun, G.; Qiu, N.; Kim, N.H.; Li, Q. On design optimization for structural crashworthiness and its state of the art. Struct. Multidiscip. Optim. 2017, 55, 1091–1119. [Google Scholar] [CrossRef]
- Lee, K.H.; Yi, J.W.; Park, J.S.; Park, G.J. An optimization algorithm using orthogonal arrays in discrete design space for structures. Finite Elem. Anal. Des. 2003, 40, 121–135. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z.; Zhu, G. Structural design of multimaterial columns accounting for multiple loads. Int. J. Mech. Sci. 2022, 227, 107427. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Z.; Chen, Y.; Wu, Y.; Song, K.; Zhu, G. Structure design of aluminum/CFRP hybrid stringers accounting for multiple impact angles. Compos. Struct. 2023, 305, 116554. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, H.; Fang, J.; Li, G.; Li, Q. A new multi-objective discrete robust optimization algorithm for engineering design. Appl. Math. Model. 2017, 53, 602–621. [Google Scholar] [CrossRef]
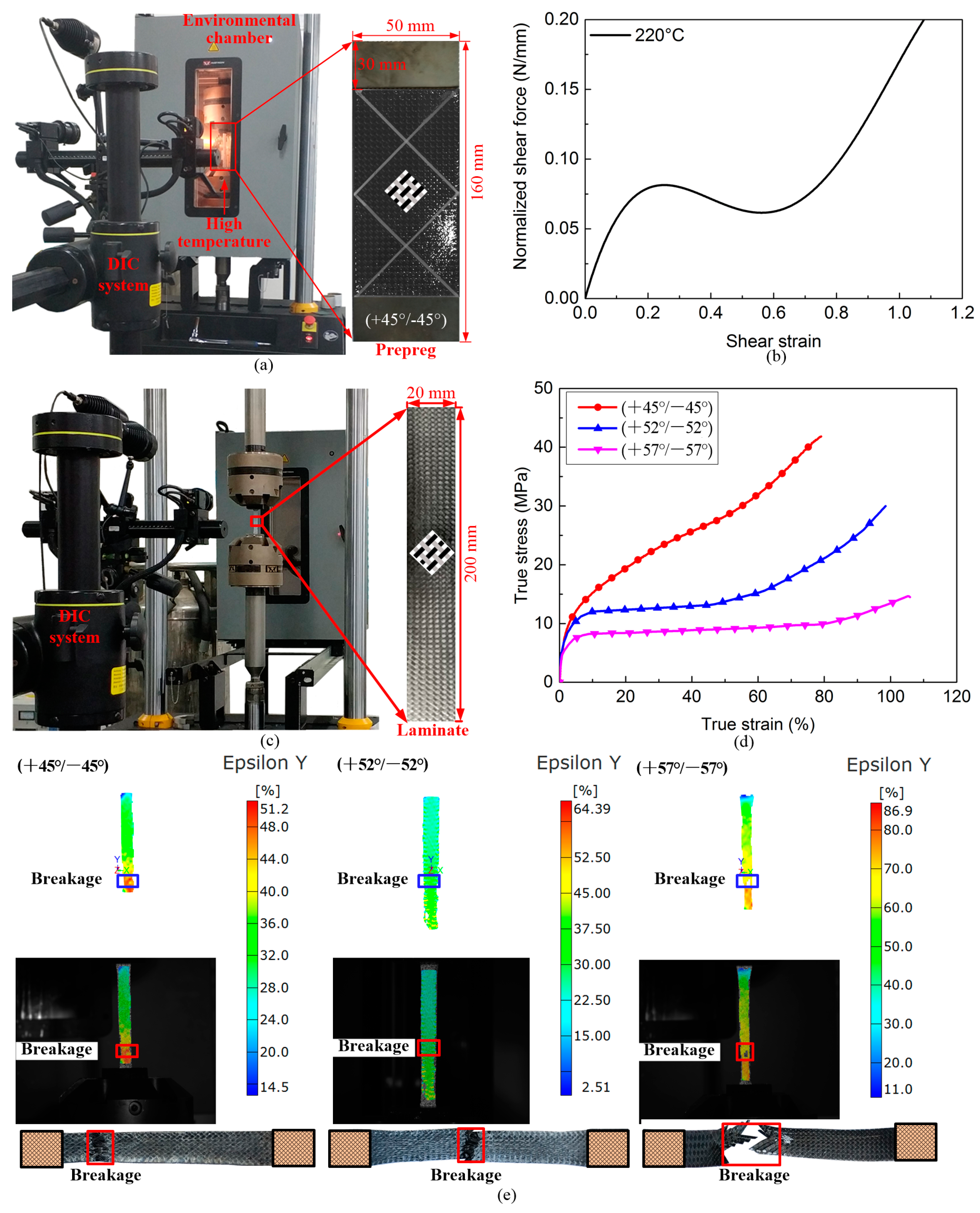
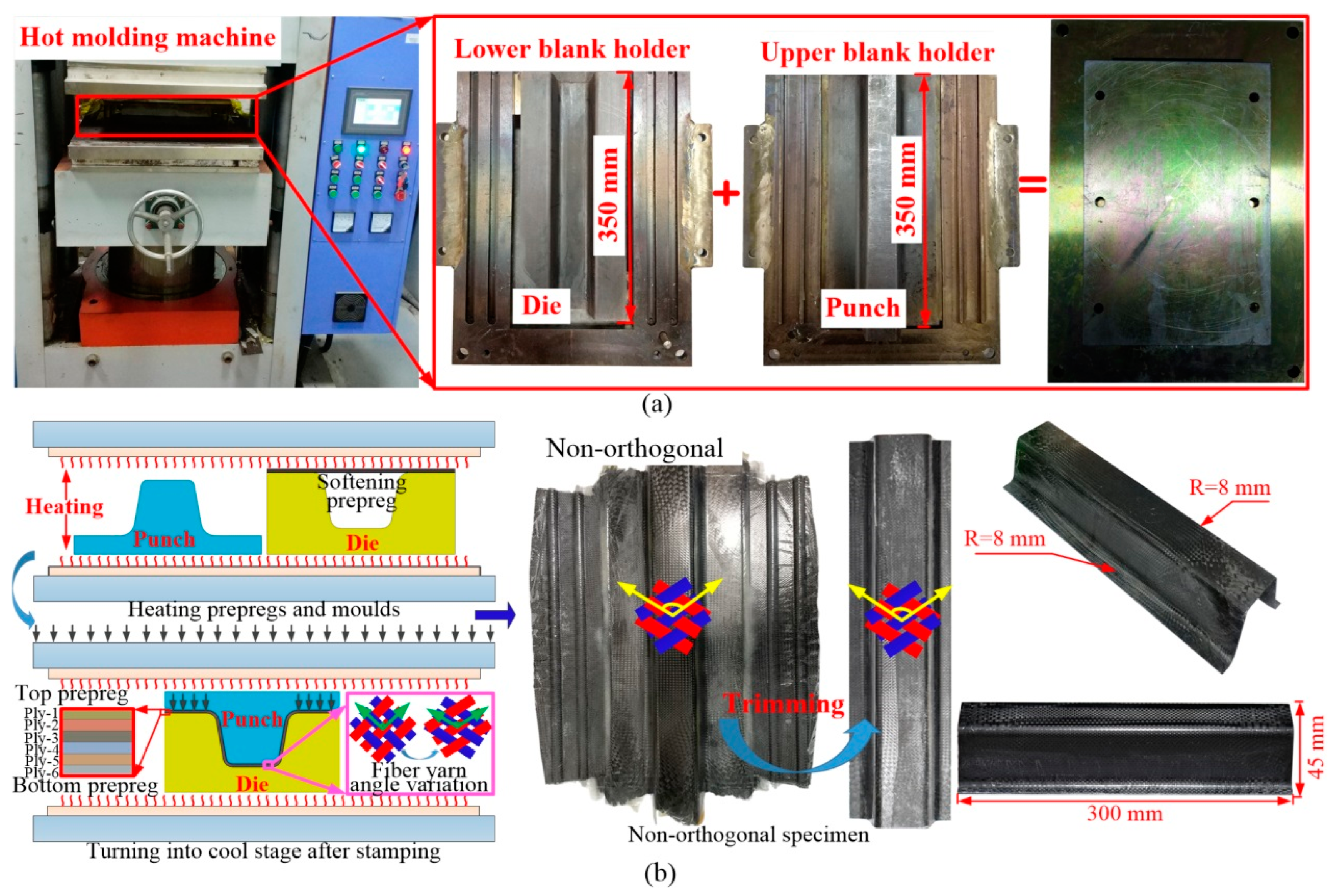



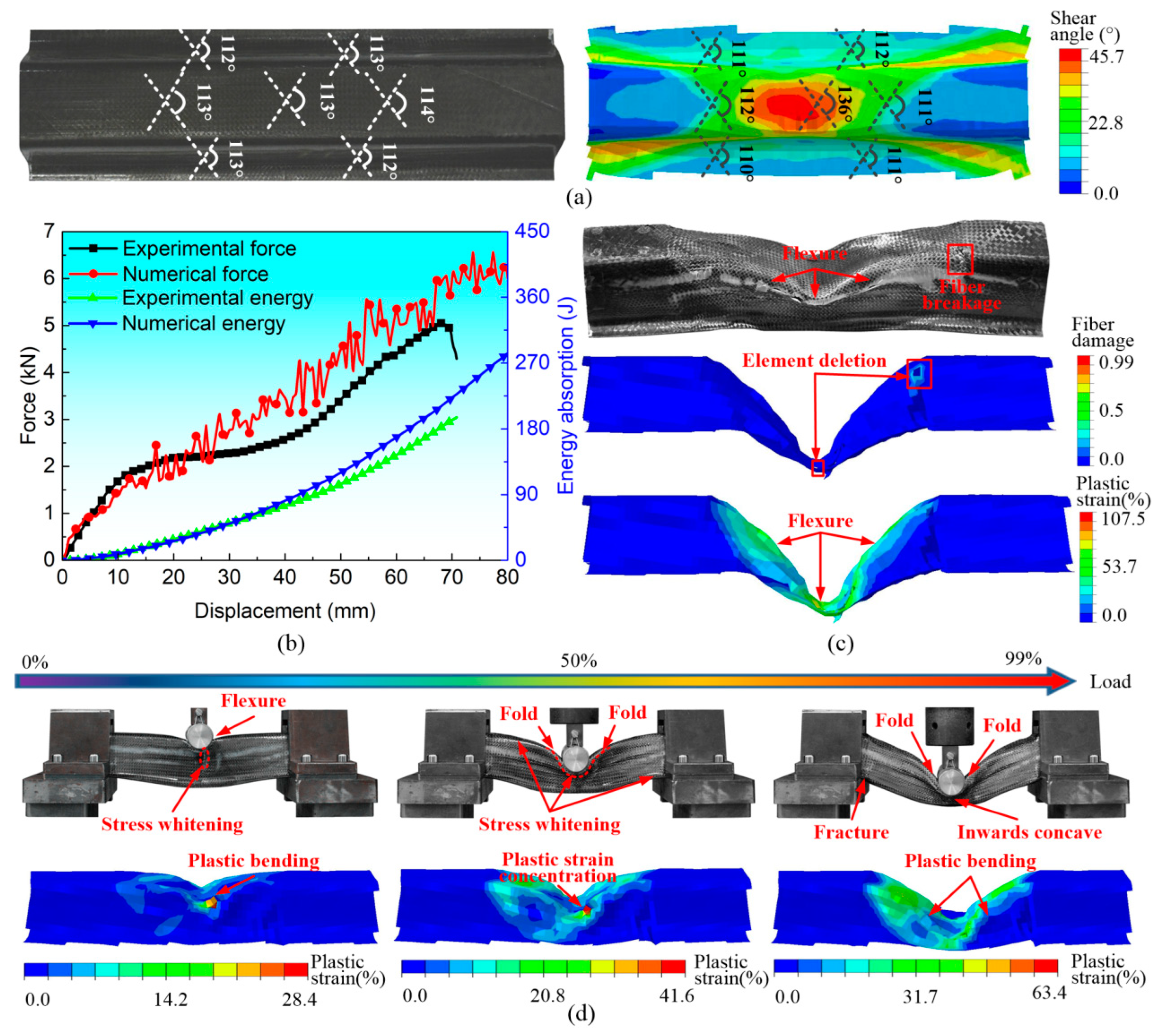



| Samples | Strength (Mpa) | Modulus (Mpa) | Failure Strain (%) | Yield Strength (Mpa) |
|---|---|---|---|---|
| (+45°/−45°)6 | 41 | 550 | 79.1 | 11.0 |
| (+52°/−52°)6 | 22 | 475 | 98.5 | 9.5 |
| (+57°/−57°)6 | 9 | 435 | 105.6 | 6.5 |
| T | Description | BHRF | Description | BHRL | Description |
|---|---|---|---|---|---|
| T1 | 5-ply | F1 | 700 N | L1 | 85 mm |
| T2 | 6-ply | F2 | 900 N | L2 | 95 mm |
| T3 | 7-ply | F3 | 1100 N | L3 | 105 mm |
| T4 | 8-ply | F4 | 1300 N | L4 | 115 mm |
| T5 | 9-ply | F5 | 1500 N | L5 | 125 mm |
| T6 | 10-ply | F6 | 1700 N | L6 | 135 mm |
| T7 | 11-ply | F7 | 1900 N | L7 | 145 mm |
| T8 | 12-ply | F8 | 2100 N | L8 | 155 mm |
| T9 | 13-ply | F9 | 2300 N | L9 | 165 mm |
| T10 | 14-ply | F10 | 2500 N | L10 | 175 mm |
| Design Variables | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| T5 | T6 | T7 | |
| F5 | F6 | F7 | |
| L5 | L6 | L7 | |
| No. | Design Variables | Objective Functions | |||
|---|---|---|---|---|---|
| 1 | T5 | F5 | L5 | 0.544 | −0.101 |
| 2 | T5 | F6 | L6 | 0.529 | −0.101 |
| 3 | T5 | F7 | L7 | 0.615 | −0.103 |
| 4 | T6 | F5 | L7 | 0.795 | −0.112 |
| 5 | T6 | F6 | L6 | 0.615 | −0.115 |
| 6 | T6 | F7 | L5 | 0.737 | −0.112 |
| 7 | T7 | F5 | L6 | 1.049 | −0.123 |
| 8 | T7 | F6 | L7 | 1.034 | −0.123 |
| 9 | T7 | F7 | L5 | 1.014 | −0.123 |
| No. | Sequence after Normalizing | Gray Relational Coefficient | GRD | ||||
|---|---|---|---|---|---|---|---|
| 1 | 0.544 | −0.101 | 0.029 | 1.000 | 0.340 | 1.000 | 0.670 |
| 2 | 0.529 | −0.101 | 0.000 | 1.000 | 0.333 | 1.000 | 0.667 |
| 3 | 0.615 | −0.103 | 0.165 | 0.911 | 0.375 | 0.848 | 0.612 |
| 4 | 0.795 | −0.112 | 0.511 | 0.500 | 0.506 | 0.500 | 0.503 |
| 5 | 0.615 | −0.115 | 0.165 | 0.366 | 0.375 | 0.441 | 0.408 |
| 6 | 0.737 | −0.112 | 0.401 | 0.500 | 0.455 | 0.500 | 0.477 |
| 7 | 1.049 | −0.123 | 1.000 | 0.000 | 1.000 | 0.333 | 0.667 |
| 8 | 1.034 | −0.123 | 0.970 | 0.000 | 0.944 | 0.333 | 0.639 |
| 9 | 1.014 | −0.123 | 0.933 | 0.000 | 0.881 | 0.333 | 0.607 |
| Design Variables | Levels | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| 0.643 | 0.458 | 0.631 | |
| 0.607 | 0.565 | 0.560 | |
| 0.589 | 0.586 | 0.556 | |
| Design Variables | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| T5 | T6 | T7 | |
| F5 | F6 | F7 | |
| L5 | L6 | L7 | |
| Comparison | (g) | (J) | (J/g) | (rad) | |
|---|---|---|---|---|---|
| Baseline design | T3F4L4 | 78.4 | 349.63 | 4.46 | 0.84 |
| Optimum design | T2F5L5 | 67.2 | 352.18 | 5.24 | 0.85 |
| Improvement | −14.3% | +0.7% | +17.5% | +1.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, W.; Song, K.; Yang, J.; Wang, F.; Dong, L.; Jin, S.; Zhu, G.; Wang, Z. Structure Design on Thermoplastic Composites Considering Forming Effects. Polymers 2024, 16, 2905. https://doi.org/10.3390/polym16202905
Xie W, Song K, Yang J, Wang F, Dong L, Jin S, Zhu G, Wang Z. Structure Design on Thermoplastic Composites Considering Forming Effects. Polymers. 2024; 16(20):2905. https://doi.org/10.3390/polym16202905
Chicago/Turabian StyleXie, Wei, Kai Song, Ju Yang, Fengyu Wang, Linjie Dong, Shengjie Jin, Guohua Zhu, and Zhen Wang. 2024. "Structure Design on Thermoplastic Composites Considering Forming Effects" Polymers 16, no. 20: 2905. https://doi.org/10.3390/polym16202905
APA StyleXie, W., Song, K., Yang, J., Wang, F., Dong, L., Jin, S., Zhu, G., & Wang, Z. (2024). Structure Design on Thermoplastic Composites Considering Forming Effects. Polymers, 16(20), 2905. https://doi.org/10.3390/polym16202905








