Modeling and Experimental Validation of Cell Morphology in Microcellular-Foamed Polycaprolactone
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Microcellular Foaming Process
2.3. Modeling
2.3.1. Thermodynamic Analysis to Predict Weight Fraction of CO2
2.3.2. Nucleation Theory
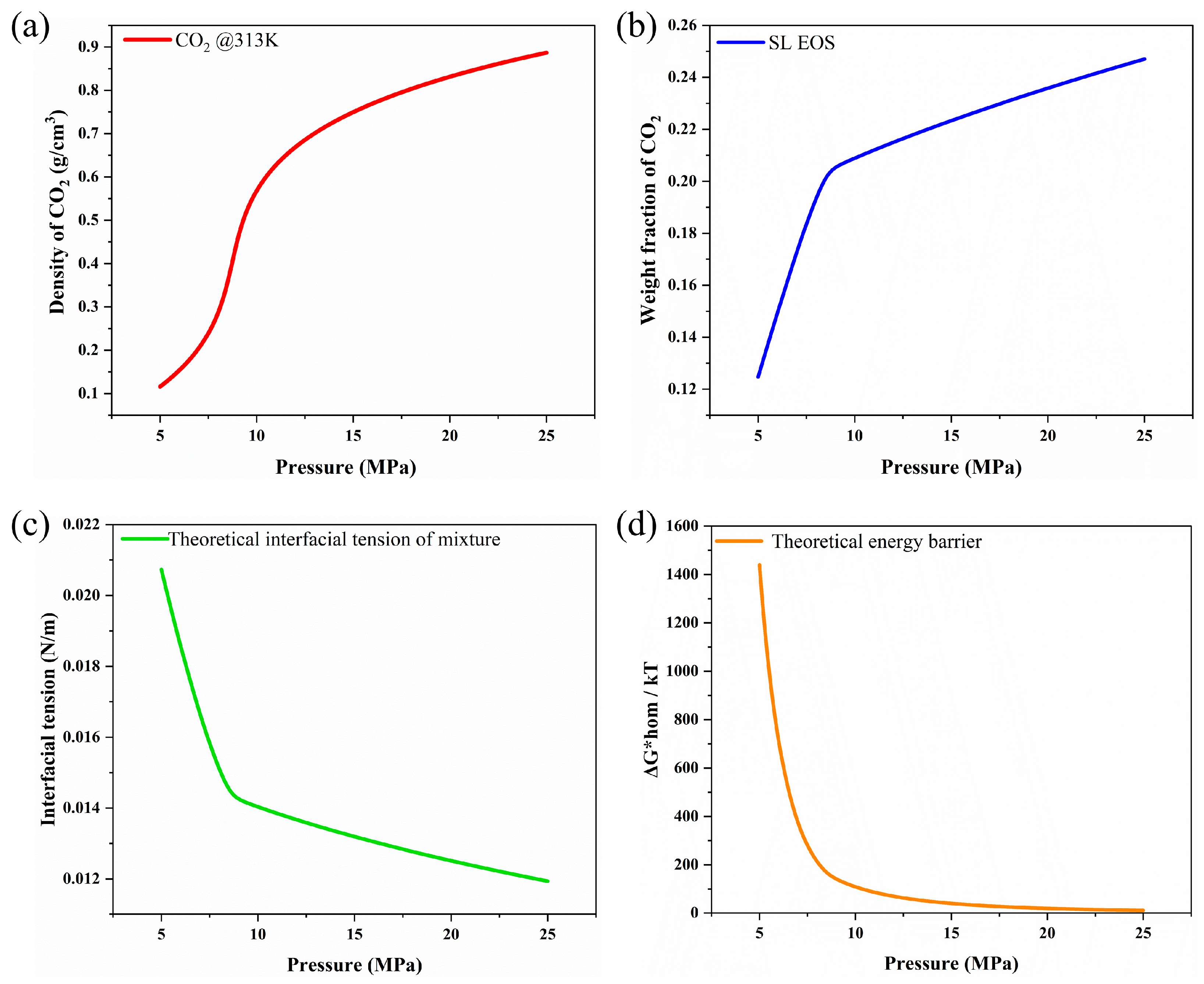
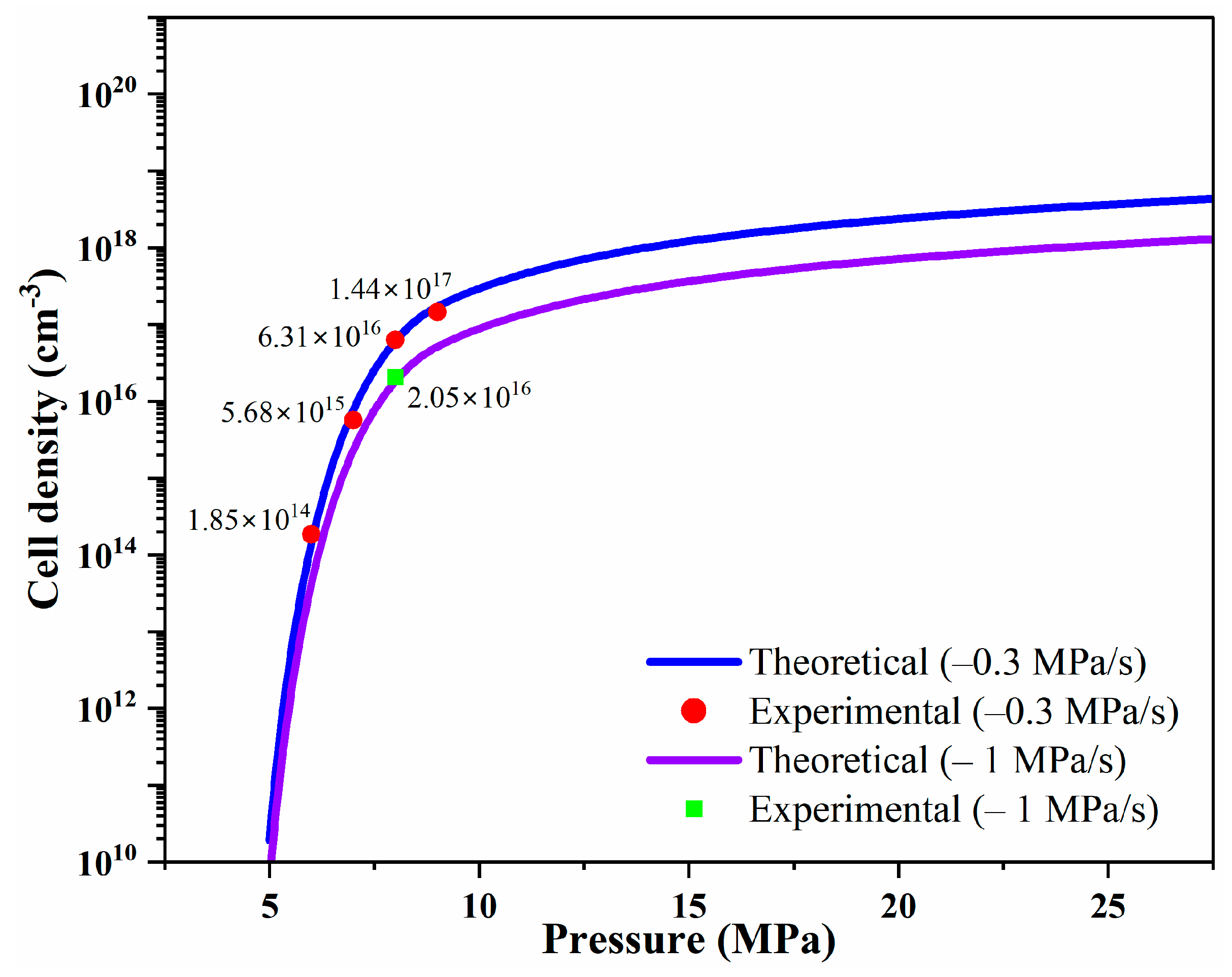
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, V.; Suh, N.P. A process for making microcellular thermoplastic parts. Polym. Eng. Sci. 1990, 30, 1323–1329. [Google Scholar] [CrossRef]
- Sorrentino, L.; Aurilia, M.; Iannace, S. Polymeric foams from high-performance thermoplastics. Adv. Polym. Technol. 2011, 30, 234–243. [Google Scholar] [CrossRef]
- Roberts, R.D.; Kwok, J.C. Styrene-maleic anhydride copolymer foam for heat resistant packaging. J. Cell. Plast. 2007, 43, 135–143. [Google Scholar] [CrossRef]
- Okolieocha, C.; Raps, D.; Subramaniam, K.; Altstädt, V. Microcellular to nanocellular polymer foams: Progress (2004–2015) and future directions—A review. Eur. Polym. J. 2015, 73, 500–519. [Google Scholar] [CrossRef]
- Colton, J.S.; Suh, N.P. The nucleation of microcellular thermoplastic foam with additives: Part I: Theoretical considerations. Polym. Eng. Sci. 1987, 27, 485–492. [Google Scholar] [CrossRef]
- Cha, S.W. A Microcellular Foaming/Forming Process Performed at Ambient Temperature and a Super-Microcellular Foaming Process. Ph.D Thesis, Mechanical Engineering Department, Massachusetts Institute of Technology, Cambridge, MA, USA, 1994. [Google Scholar]
- Dugad, R.; Radhakrishna, G.; Gandhi, A. Recent advancements in manufacturing technologies of microcellular polymers: A review. J. Polym. Res. 2020, 27, 182. [Google Scholar] [CrossRef]
- Kazarian, S.G.; Martirosyan, G.G. Spectroscopy of Polymer/Drug Formulations Processed with Supercritical Fluids: In situ ATR-IR and Raman study of impregnation of ibuprofen into PVP. Int. J. Pharm. 2002, 232, 81–90. [Google Scholar] [CrossRef]
- Woods, H.M.; Silva, M.M.C.G.; Nouvel, C.; Shakesheff, K.M.; Howdle, S.M. Materials processing in supercritical carbon dioxide: Surfactants, polymers and biomaterials. J. Mater. Chem. 2004, 14, 1663–1678. [Google Scholar] [CrossRef]
- Cao, G.P.; Liu, T.; Roberts, G.W. Predicting the effect of dissolved carbon dioxide on the glass transition temperature of poly (acrylic acid). J. Appl. Polym. Sci. 2010, 115, 2136–2143. [Google Scholar] [CrossRef]
- Jenkins, M.J.; Harrison, K.L.; Silva, M.M.C.G.; Whitaker, M.J.; Shakesheff, K.M.; Howdle, S.M. Characterisation of microcellular foams produced from semi-crystalline PCL using supercritical carbon dioxide. Eur. Polym. J. 2006, 42, 3145–3151. [Google Scholar] [CrossRef]
- Woodruff, M.A.; Hutmacher, D.W. The return of a forgotten polymer—Polycaprolactone in the 21st century. Prog. Polym. Sci. 2010, 35, 1217–1256. [Google Scholar] [CrossRef]
- Malikmammadov, E.; Tanir, T.E.; Kiziltay, A.; Hasirci, V.; Hasirci, N. PCL and PCL-based materials in biomedical applications. J. Biomater. Sci. Polym. Ed. 2018, 29, 863–893. [Google Scholar] [CrossRef] [PubMed]
- Lim, D.; Yoon, D.; Kim, J.; Sung, K.; Choi, Y.; Sheen, H.; Shin, H.B.; Cha, S.W. Development of a biocompatible radiotherapy spacer using 3D printing and microcellular foaming process for enhanced prostate cancer treatment. Int. J. Bioprint. 2024, 4252. [Google Scholar] [CrossRef]
- Mohamed, R.M.; Yusoh, K. A Review on the Recent Research of Polycaprolactone (PCL). Adv. Mater. Res. 2015, 1134, 249–255. [Google Scholar] [CrossRef]
- Akki, A.J.; Patil, S.A.; Hungund, S.; Sahana, R.; Patil, M.M.; Kulkarni, R.V.; Reddy, K.R.; Zameer, F.; Raghu, A.V. Advances in Parkinson’s disease research—A computational network pharmacological approach. Int. Immunopharmacol. 2024, 139, 112758. [Google Scholar] [CrossRef] [PubMed]
- Patil, S.A.; Akki, A.J.; Raghu, A.V.; Kulkarni, R.V.; Akamanchi, K.G. Sugarcane polyphenol oxidase: Structural elucidation using molecular modeling and docking analyses. Process Biochem. 2023, 134, 243–249. [Google Scholar] [CrossRef]
- Colton, J.S. The Nucleation of Thermoplastic Microcellular Foam. Ph.D Thesis, Mechanical Engineering Department, Massachusetts Institute of Technology, Cambridge, MA, USA, 1985. [Google Scholar]
- Cotugno, S.; Di Maio, E.; Mensitieri, G.; Iannace, S.; Roberts, G.W.; Carbonell, R.G.; Hopfenberg, H.B. Characterization of microcellular biodegradable polymeric foams produced from supercritical carbon dioxide solutions. Ind. Eng. Chem. Res. 2005, 44, 1795–1803. [Google Scholar] [CrossRef]
- Karimi, M.; Heuchel, M.; Weigel, T.; Schossig, M.; Hofmann, D.; Lendlein, A. Formation and size distribution of pores in poly (ε-caprolactone) foams prepared by pressure quenching using supercritical CO2. J. Supercrit. Fluids 2012, 61, 175–190. [Google Scholar] [CrossRef]
- Alhanish, A.; Ali, G.A.M. Biodegradable Polymers. In Handbook of Biodegradable Materials; Springer International Publishing: Cham, Switzerland, 2022; pp. 1–29. [Google Scholar] [CrossRef]
- Ma, Q.; Shi, K.; Su, T.; Wang, Z. Biodegradation of Polycaprolactone (PCL) with Different Molecular Weights by Candida antarctica Lipase. J. Polym. Env. 2020, 28, 2947–2955. [Google Scholar] [CrossRef]
- Wang, H.; Li, W.; Kumar, V. Solid-State Foaming of Polycaprolactone (PCL). ASME Int. Mech. Eng. Congr. Expo. 2007, 42975, 61–66. [Google Scholar]
- Hatami, T.; Johner, J.C.F.; de Castro, K.C.; Mei, L.H.I.; Vieira, M.G.A.; Angela, M. New insight into a step-by-step modeling of supercritical CO2 foaming to fabricate poly(ε-caprolactone) scaffold. Ind. Eng. Chem. Res. 2020, 59, 20033–20044. [Google Scholar] [CrossRef]
- Kosowska, K.; Krzysztoforski, J.; Henczka, M. Foaming of PCL-Based Composites Using scCO2: Structure and Physical Properties. Materials 2022, 15, 1169. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, I.C.; Lacombe, R.H. An elementary equation of state for polymer liquids. J. Polym. Sci. Polym. Lett. Ed. 1977, 15, 71–75. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. Statistical thermodynamics of polymer solutions. Macromolecules 1978, 11, 1145–1156. [Google Scholar] [CrossRef]
- Stryjek, R.; Vera, J.H. PRSV2: A cubic equation of state for accurate vapor—Liquid equilibria calculations. Can. J. Chem. Eng. 1986, 64, 820–826. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, H.; Wang, X.; Mi, J. Mechanism of bubble nucleation in poly(ε-caprolactone) foaming at low temperature. Polymer 2015, 79, 47–55. [Google Scholar] [CrossRef]
- Abbard, R.G.G. The Development of a Homogeneous Nucleation Rate Model for Thermoplastic Foams Based on a Molecular Partition Function and Fickian Diffusion; New Jersey Institute of Technology: Newark, NJ, USA, 2002. [Google Scholar]
- Goel, S.K.; Beckman, E.J. Generation of microcellular polymeric foams using supercritical carbon dioxide. I: Effect of pressure and temperature on nucleation. Polym. Eng. Sci. 1994, 34, 1137–1147. [Google Scholar] [CrossRef]
- Kumar, V.; Weller, J. Production of Microcellular Polycarbonate Using Carbon Dioxide for Bubble Nucleation. J. Eng. Ind. 1994, 116, 413–420. [Google Scholar] [CrossRef]
- Colton, J.S.; Suh, N.P. Nucleation of microcellular foam: Theory and practice. Polym. Eng. Sci. 1987, 27, 500–503. [Google Scholar] [CrossRef]
- Mahieu, A.; Terrié, C.; Agoulon, A.; Leblanc, N.; Youssef, B. Thermoplastic starch and poly(ε-caprolactone) blends: Morphology and mechanical properties as a function of relative humidity. J. Polym. Res. 2013, 20, 1–13. [Google Scholar] [CrossRef]
- Markočič, E.; Škerget, M.; Knez, Ž. Effect of temperature and pressure on the behavior of poly (ε-caprolactone) in the presence of supercritical carbon dioxide. Ind. Eng. Chem. Res. 2013, 52, 15594–15601. [Google Scholar] [CrossRef]
- Macleod, D.B. On a relation between surface tension and density. Trans. Faraday Soc. 1923, 19, 38–41. [Google Scholar] [CrossRef]



| Property | Value |
|---|---|
| Saturation pressure (MPa) | 6, 7, 8, 9 ± 0.2 |
| Saturation temperature (K) | 313 ± 2 |
| Saturation time (min) | 15 |
| Depressurization rate (MPa/s) | −0.3, −1 |
| (K) | |||
|---|---|---|---|
| 7.382 | 304.2 | 0.225 | 0.04285 |
| Subscript | Component | |||||
|---|---|---|---|---|---|---|
| 1 | CO2 | 574.5 | 305.3 | 1.510 | 4.42 | 6.6 |
| 2 | PCL | 548.6 | 637.7 | 1.158 | 9.66 | 9.5 |
| None | PCL–CO2 | Can be calculated using Equations (1)–(13) | - | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, D.; Lee, S.; Jung, S.; Kim, K.; Hong, J.; Cha, S.W. Modeling and Experimental Validation of Cell Morphology in Microcellular-Foamed Polycaprolactone. Polymers 2024, 16, 2723. https://doi.org/10.3390/polym16192723
Lim D, Lee S, Jung S, Kim K, Hong J, Cha SW. Modeling and Experimental Validation of Cell Morphology in Microcellular-Foamed Polycaprolactone. Polymers. 2024; 16(19):2723. https://doi.org/10.3390/polym16192723
Chicago/Turabian StyleLim, Donghwan, Sanghyun Lee, Seungho Jung, Kwanhoon Kim, Jin Hong, and Sung Woon Cha. 2024. "Modeling and Experimental Validation of Cell Morphology in Microcellular-Foamed Polycaprolactone" Polymers 16, no. 19: 2723. https://doi.org/10.3390/polym16192723
APA StyleLim, D., Lee, S., Jung, S., Kim, K., Hong, J., & Cha, S. W. (2024). Modeling and Experimental Validation of Cell Morphology in Microcellular-Foamed Polycaprolactone. Polymers, 16(19), 2723. https://doi.org/10.3390/polym16192723






