Scaling-Up for the Counter-Rotating Twin Screw Extrusion of Polymers
Abstract
1. Introduction
- optimization parameters are not processed directly (they are encoded);
- the search for a solution takes place in a randomly generated population, which allows for avoiding local extrema;
- selection rules are probabilistic in nature;
- a new search surface is specified based on previous experience;
- the objective function is used, not its derivatives.
- may cover only single scaling criteria (for example, the polymer melting rate or polymer pumping rate) and single steps of the extrusion process (for example, melting or melt transport);
- may consider only a few geometrical or operational data, e.g., the screw speed or screw dimensions;
- are based on the very simplified models of the process.
- taking into account several scaling criteria simultaneously;
- the selection of single quantities (for example, the melting rate) or functions (for example, polymer solid bed distribution over the screw) as scaling criteria.
- simulating an extrusion to obtain the response parameters of a reference machine with a given set of process data (input data ≥ modeling ≥ results);
- indication of scaling-up criteria (results ≥ scaling criteria);
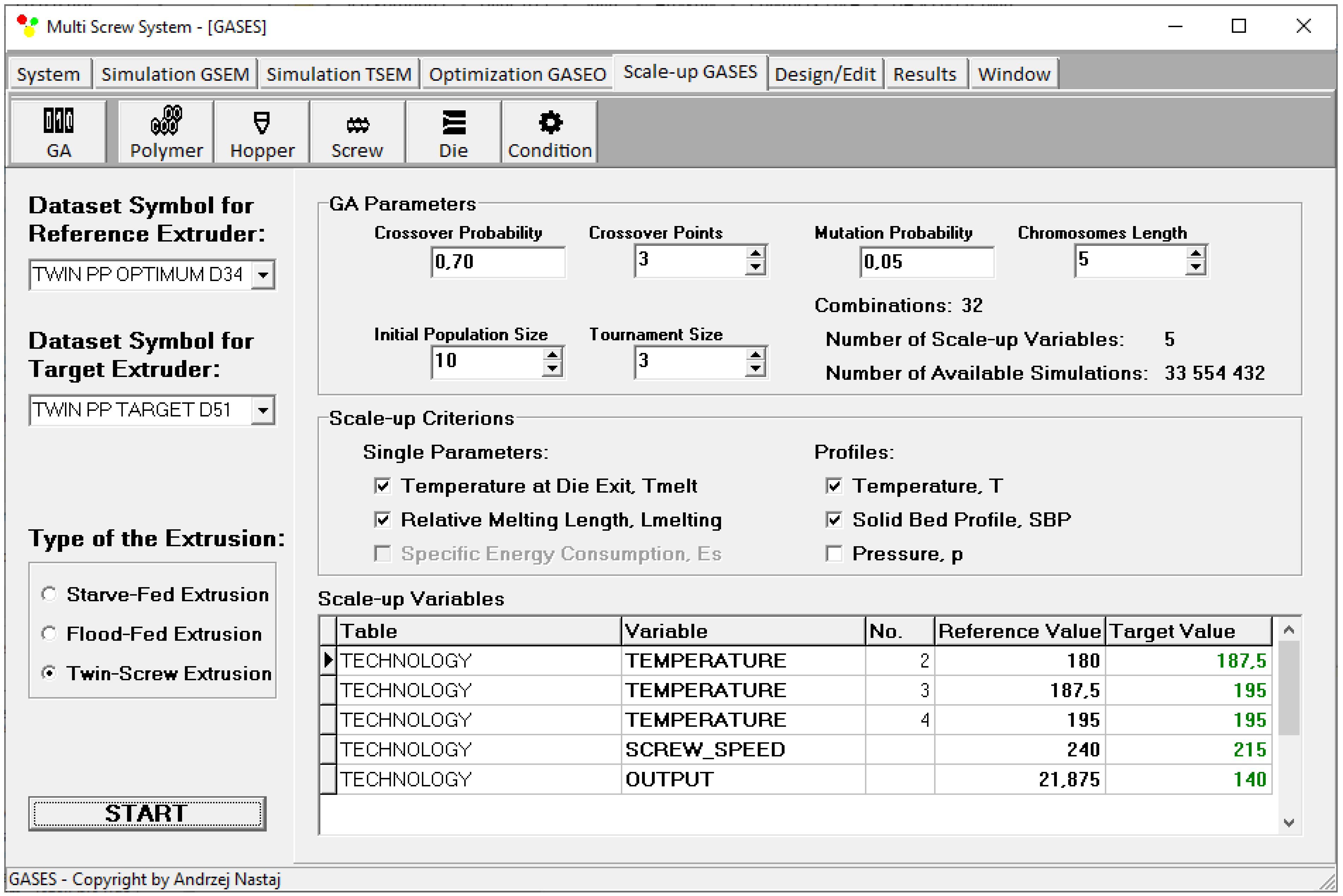
- determining the fixed parameters of the target machine; for example, the screw diameter Dscrew and the ratio of the screw length to the screw diameter Lscrew/Dscrew;
- carrying out the scaling-up procedure by minimizing the differences between the specified data of the target machine and reference machine (optimization ≥ geometry/operational parameters).
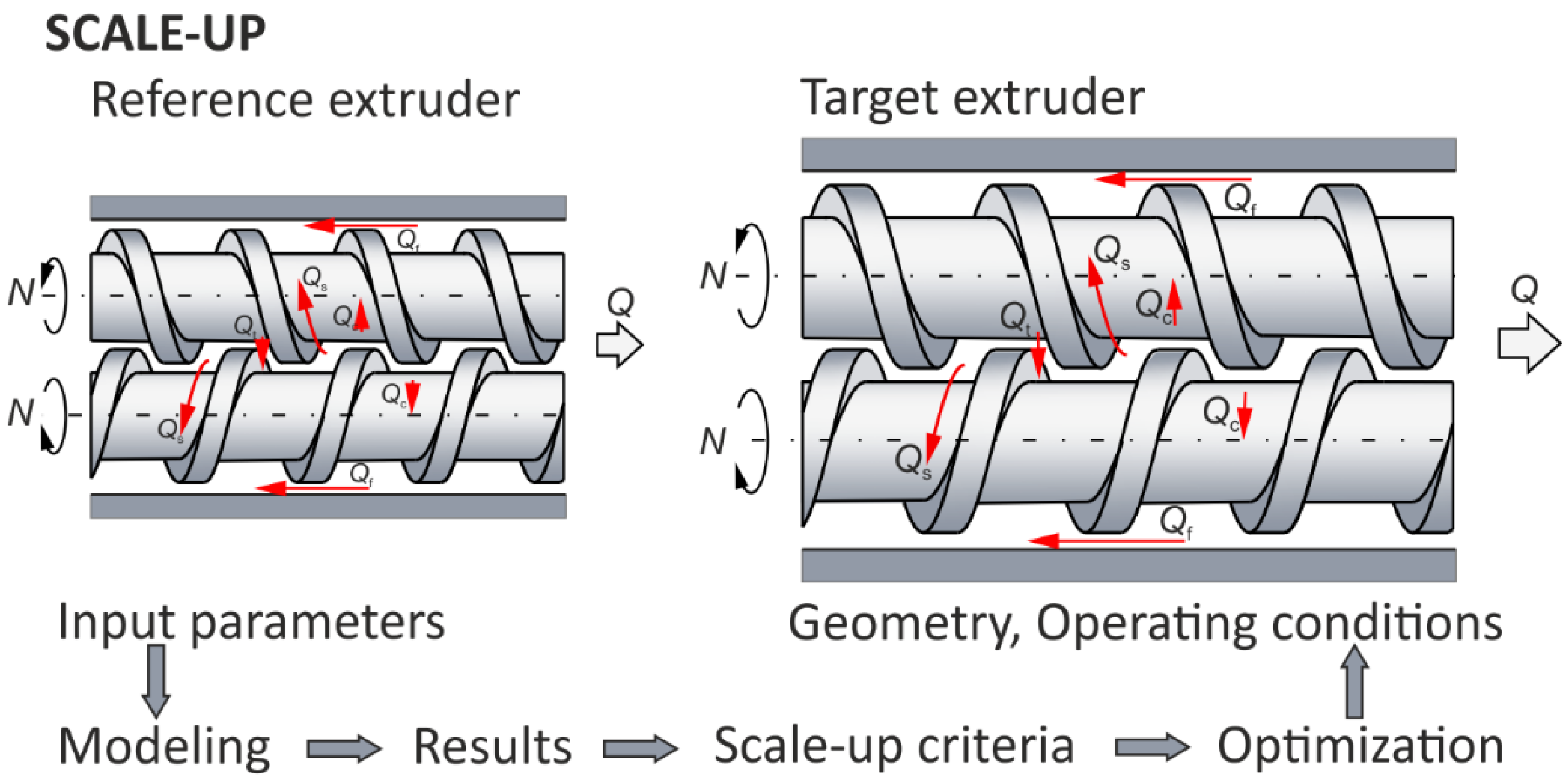
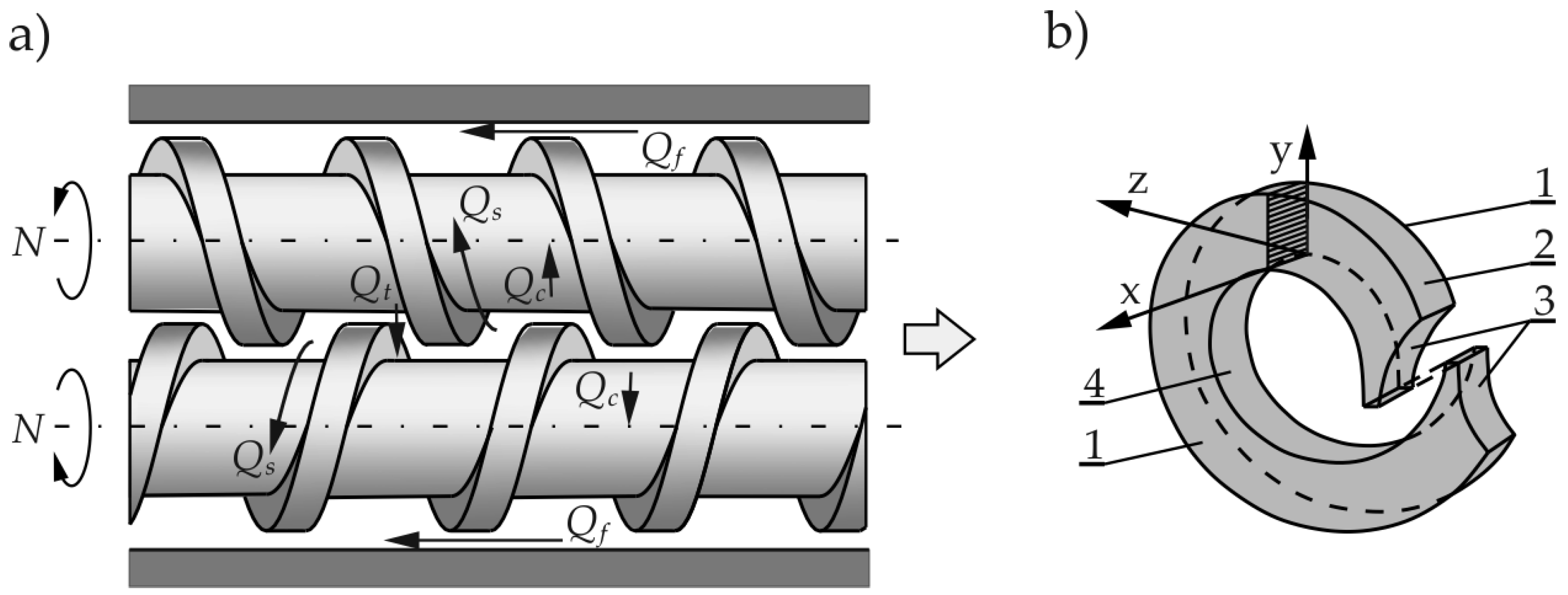
2. Counter-Rotating Twin-Screw Extrusion
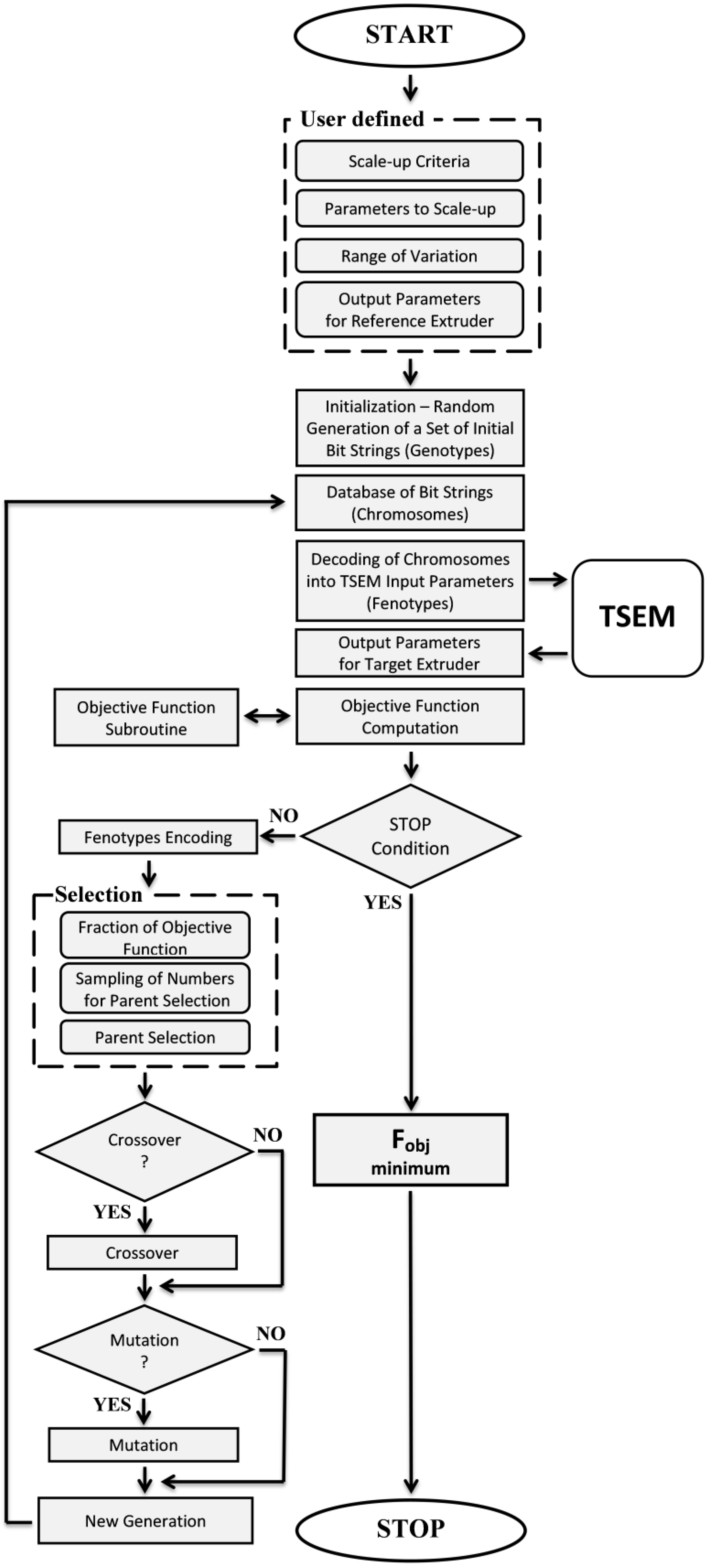
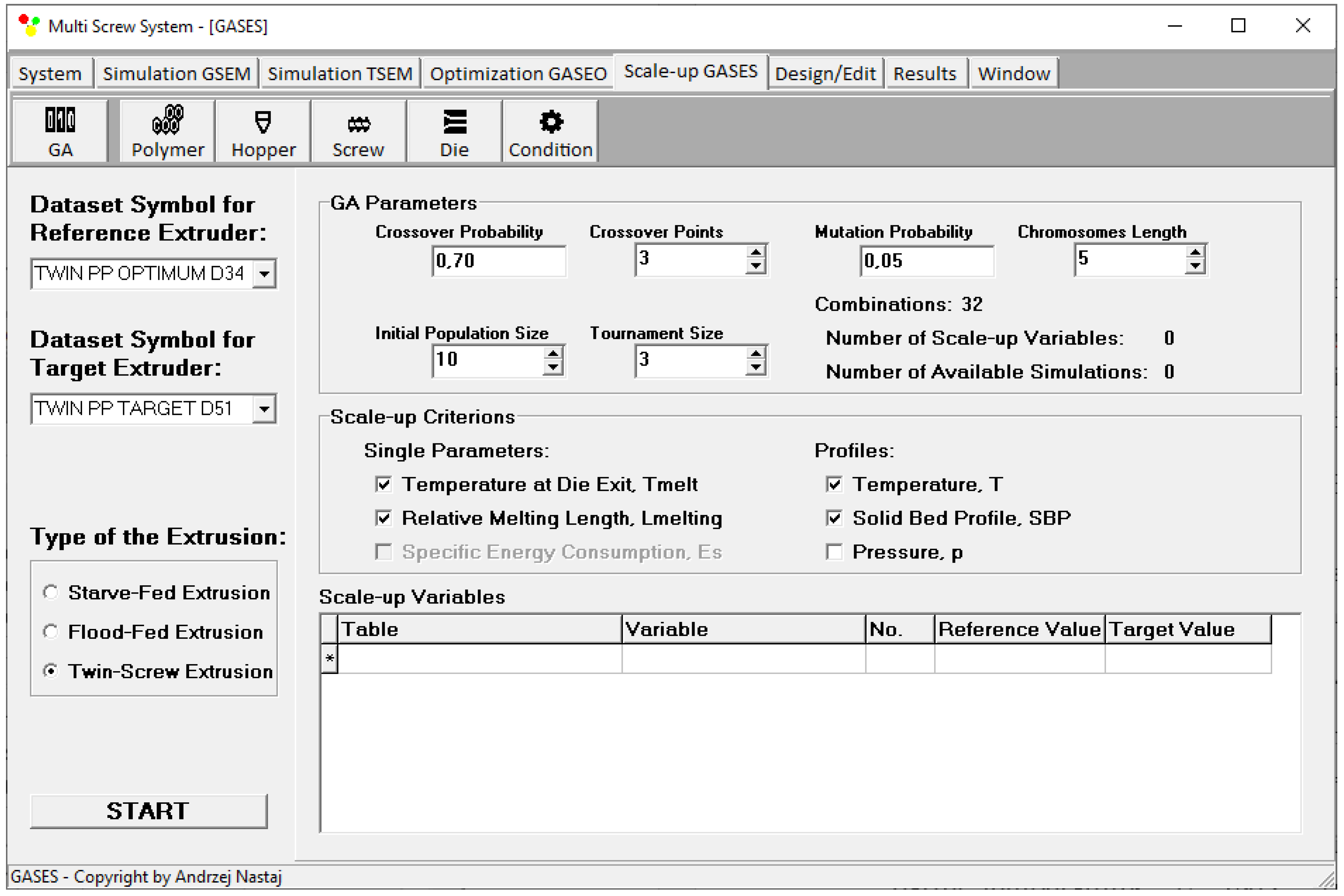
3. Scaling-Up Procedure
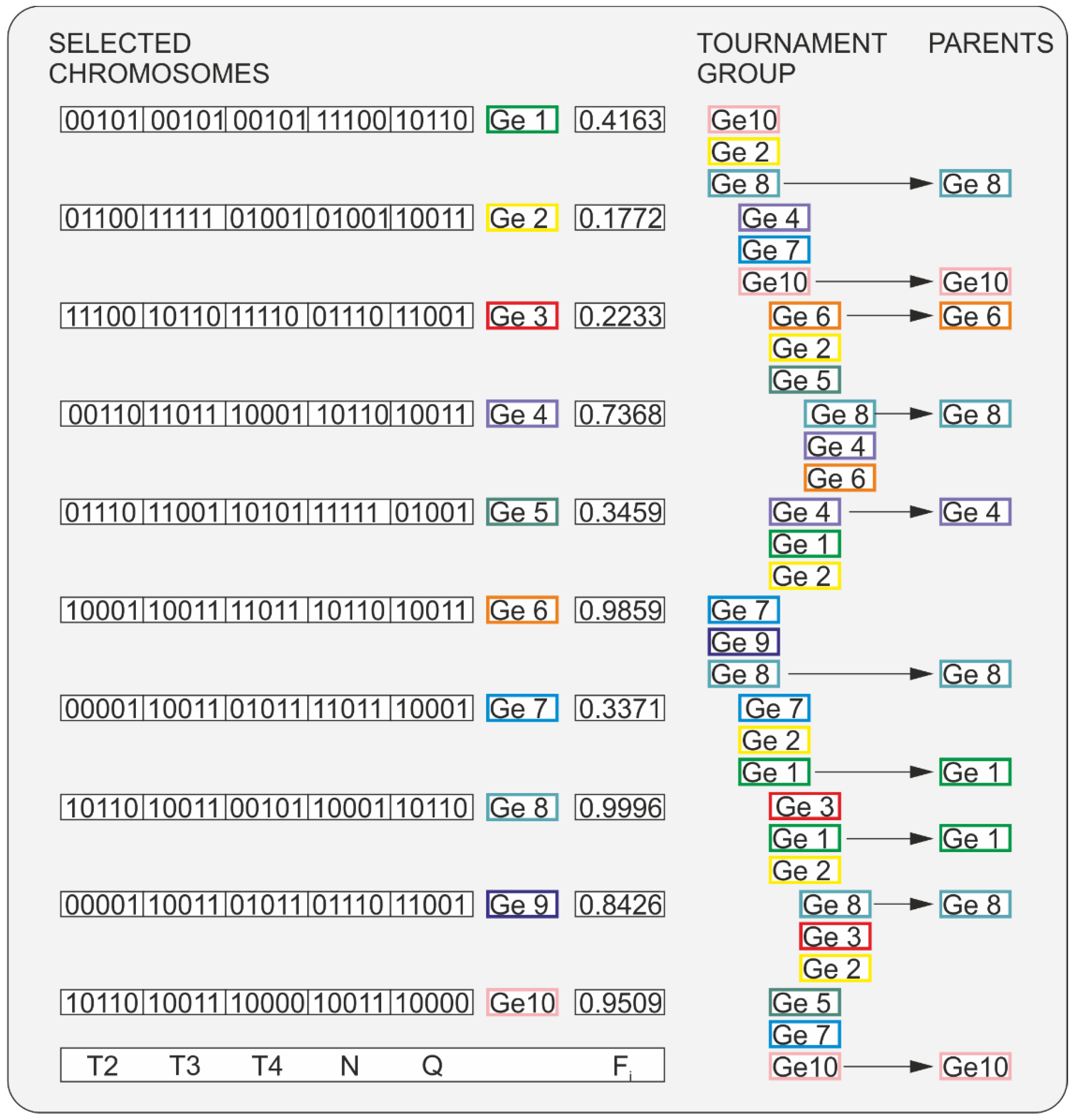
- Define Tournament Size: specify the number of individuals that will compete in each mini-competition (tournament).
- Determine Selection Count: set the total number of individuals you need to select for the next generation.
- Random Subset Selection: randomly choose a group of individuals from the population; each individual has an equal chance of being selected.
- Fitness Evaluation: evaluate the fitness of each individual within this randomly chosen subset.
- Winner Selection: identify the individual with the highest fitness score in the subset; this individual becomes a parent for the next generation.
- Repeat: repeat steps 3–5 until the desired number of individuals (as defined in step 2) have been chosen for the next generation.
4. Scaling Up
4.1. Research Program
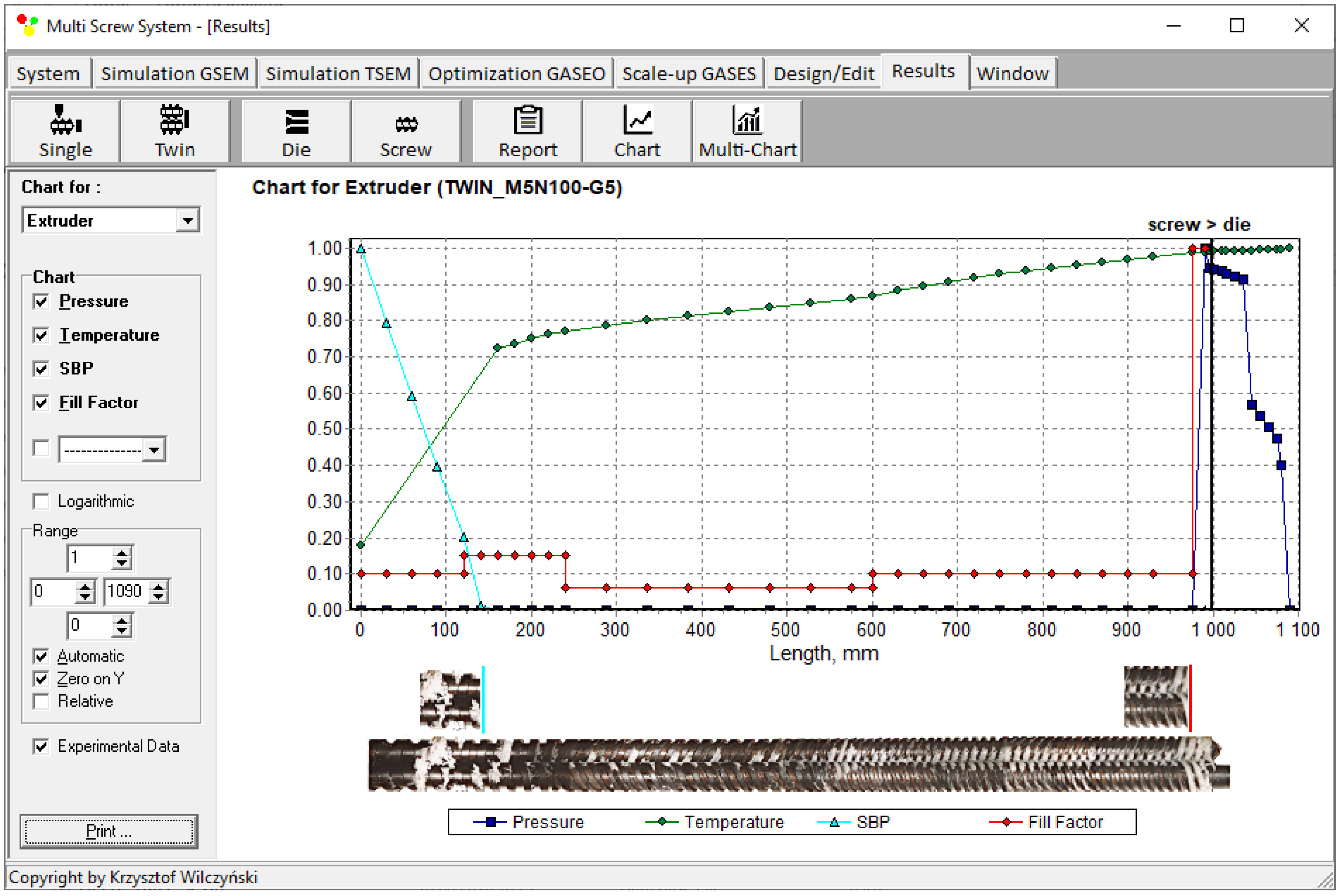
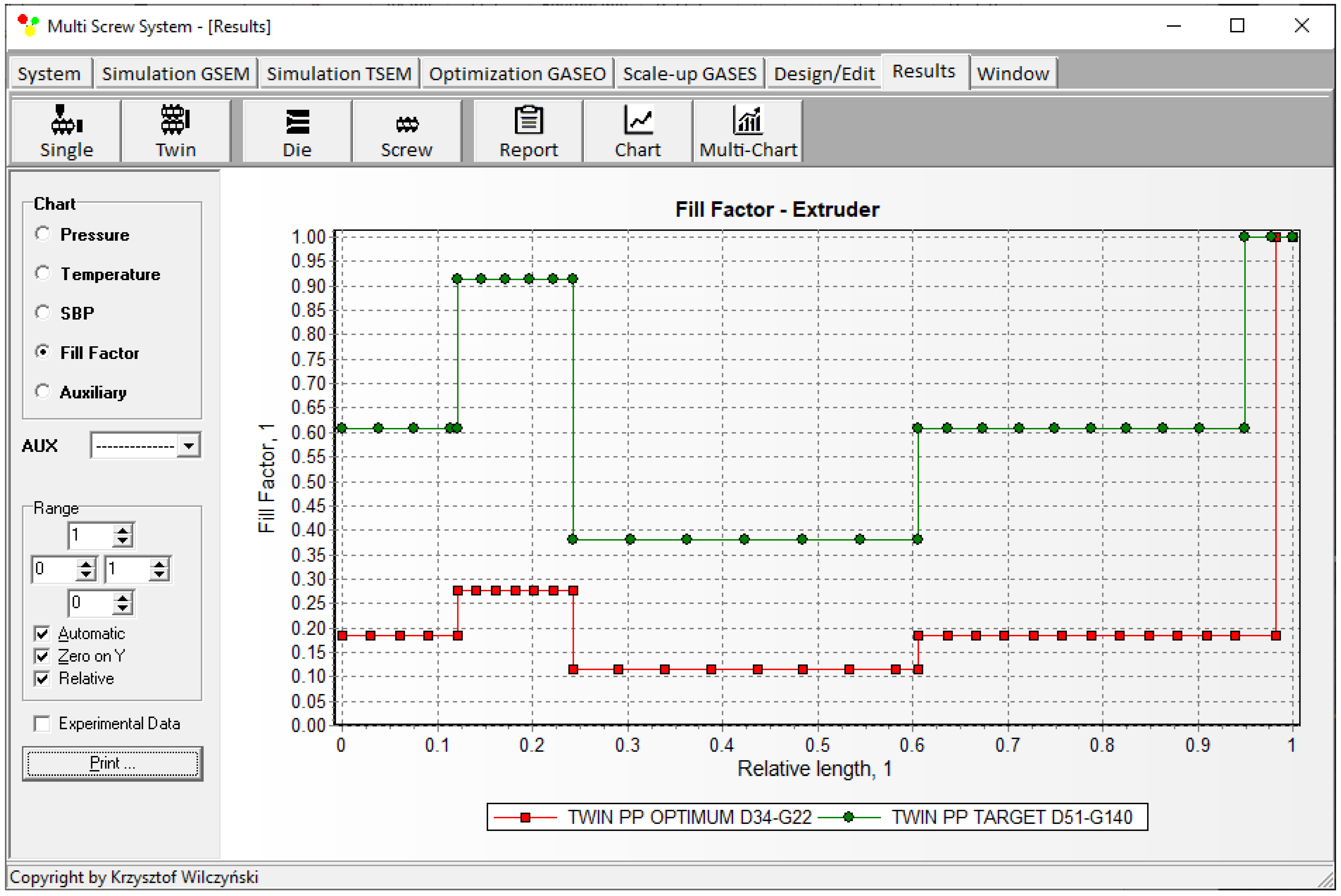
4.2. Scale-Up of Counter-Rotating Twin-Screw Extrusion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Covas, J.A.; Cunha, A.G.; Oliveira, P. An Optimization Approach to Practical Problems in Plasticating Single Screw Extrusion. Polym. Eng. Sci. 1999, 39, 443–456. [Google Scholar] [CrossRef]
- Covas, J.A.; Gaspar-Cunha, A. The Use of an Optimization Approach to the Design of Extrusion Screw. In Proceedings of the Polymer Processing Society 16th Annual Meeting (PPS-16), Shanghai, China, 18–23 June 2000. [Google Scholar]
- Gaspar-Cunha, A.; Covas, J.A. The Design of Extrusion Screw: An Optimization Approach. Int. Polym. Proc. 2001, 16, 229–240. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Costa, P.; Delbem, A.; Monaco, F.; Ferreira, M.J.; Covas, J. Evolutionary Multi-Objective Optimization of Extrusion Barrier Screws: Data Mining and Decision Making. Polymers 2023, 15, 2212. [Google Scholar] [CrossRef]
- Nastaj, A.; Wilczyński, K. Optimization for Single Screw Extrusion of Polymeric Materials—Experimental Studies. Polimery 2018, 1, 38–44. [Google Scholar] [CrossRef]
- Nastaj, A.; Wilczyński, K. Process Optimization for Single Screw Extrusion of Polymeric Materials—Simulation Studies. Polimery 2018, 4, 297–304. [Google Scholar] [CrossRef]
- Nastaj, A. Optimization for Starve Fed Single Screw Extrusion of Polymeric Materials—Simulations. Polimery 2020, 6, 468–477. [Google Scholar] [CrossRef]
- Nastaj, A.; Wilczyński, K. Optimization for Starve Fed/Flood Fed Single Screw Extrusion of Polymeric Materials. Polymers 2020, 12, 149. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Poulesquen, A.; Vergnes, B.; Covas, J.A. Optimization of Processing Conditions for Polymer Twin-Screw Extrusion. Int. Polym. Proc. 2002, 17, 201–213. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Covas, J.A.; Vergnes, B. An Optimization Methodology for Setting the Operating Conditions in Twin-Screw Extrusion. In Proceedings of the Materiały konferencyjne The Polymer Processing Society Eighteenth Annual Meeting (PPS-18), Guimaraes, Portugalia, 16–20 June 2002. [Google Scholar]
- Gaspar-Cunha, A.; Covas, J.; Vergnes, B. Defining the Configuration of Co-Rotating Twin-Screw Extruders with Multiobjective Evolutionary Algorithms. Polym. Eng. Sci. 2005, 45, 1159–1173. [Google Scholar] [CrossRef]
- Covas, J.A.; Gaspar-Cunha, A. Polymer Extrusion—Setting the Operating Conditions and Defining the Screw Geometry. In Optimization in Polymer Processing; Gaspar-Cunha, A., Covas, J.A., Eds.; Nova Science Publishers Inc.: Hauppauge, NY, USA, 2011; Chapter 5; pp. 1–35. ISBN 978-1-61122-818-2. [Google Scholar]
- Nastaj, A.; Wilczyński, K. Optimization for the Contrary-Rotating Double-Screw Extrusion of Plastics. Polymers 2023, 15, 1489. [Google Scholar] [CrossRef]
- Rauwendaal, C. Polymer Extrusion, 5th ed.; Carl Hanser Verlag: Munich, Germany, 2014; ISBN 978-1-56990-516-6. [Google Scholar]
- Hensen, F.; Knappe, W.; Potente, H. Handbuch der Kunststoff-Extrusiontechnik. Grundlagen; Carl Hanser Verlag: Munich, Germany, 1989; ISBN 978-3446143395. [Google Scholar]
- McKelvey, J.M. Polymer Processing; John Wiley & Sons Inc.: New York, NY, USA, 1962; ISBN 978-0471584438. [Google Scholar]
- Stevens, M.J.; Covas, J.A. Extruder Principles and Operation; Springer: Berlin/Heidelberg, Germany, 1995; ISBN 978-94-010-4247-5. [Google Scholar]
- Campbell, G.A.; Spalding, M.A. Analyzing and Troubleshooting Single-Screw Extruders; Carl Hanser Verlag: Munich, Germany, 2013; ISBN 978-3-446-41371-9. [Google Scholar]
- Chung, C.I. Extrusion of Polymers. Theory and Practice, 3rd ed.; Carl Hanser Verlag: Munich, Germany, 2019; ISBN 978-1-569-907375. [Google Scholar]
- Chen, B.; Zhu, L.; Zhang, F.; Qiu, Y. Process Development and Scale-Up. In Developing Solid Oral Dosage Forms; Elsevier: Amsterdam, The Netherlands, 2017; pp. 821–868. [Google Scholar] [CrossRef]
- Carley, J.F.; McKelvey, J.M. Extruder Scale-Up Theory and Experiments. Ind. Eng. Chem. 1953, 45, 989–992. [Google Scholar] [CrossRef]
- Maddock, B.H. A Visual Analysis of Flow and Mixing in Extruder Screws. Soc. Plast. Eng. J. 1959, 15, 383–389. [Google Scholar]
- Maddock, B.H. Extruder Scale-up by Computer. Polym. Eng. Sci. 1974, 14, 853–858. [Google Scholar] [CrossRef]
- Fenner, R.T.; Williams, J.G. Some Melt Flow and Mechanical Design Aspects of Large Extruders. Polym. Eng. Sci. 1971, 11, 474–483. [Google Scholar] [CrossRef]
- Yi, B.; Fenner, R.T. Scaling-up Plasticating Screw Extruders on the Basis of Similar Melting Performances. Plast. Rubber Process. 1976, 1, 119–123. [Google Scholar]
- Pearson, J.R.A. Scale-up of Single Screw Extruders for Polymer Processing. Plast. Rubber Process. 1976, 1, 113–118. [Google Scholar]
- Potente, H.; Fischer, P. Model Laws for the Design of Single Screw Plasticating Extruders. Kunststoffe 1977, 67, 242–247. [Google Scholar]
- Schenkel, G. Extruder Series with Variable L/D Ratios. Kunststoffe 1978, 68, 155–162. [Google Scholar]
- Chung, C.I. On the Scale-up of Plasticating Extruder Screws. Polym. Eng. Sci. 1984, 24, 626–632. [Google Scholar] [CrossRef]
- Rauwendaal, C. Scale-up of Single Screw Extruders. Polym. Eng. Sci. 1987, 27, 1059–1068. [Google Scholar] [CrossRef]
- Potente, H. Existing Scale-Up Rules for Single-Screw Plasticating Extruders. Int. Polym. Proc. 1991, 6, 267–278. [Google Scholar] [CrossRef]
- Potente, H. Scale-up of Mixing Equipments. In Mixing and Compounding of Polymers, 2nd ed.; Manas-Zloczower, I., Ed.; Carl Hanser Verlag: Munich, Germany, 2009; pp. 577–643. ISBN 978-1-56990-660-6. [Google Scholar]
- Covas, J.A.; Gaspar-Cunha, A. Extrusion Scale-up: An Optimization-based Methodology. Int. Polym. Proc. 2009, 24, 67–82. [Google Scholar] [CrossRef]
- Wilczyński, K. Rheology in Polymer Processing. Modeling and Simulation; Carl Hanser Verlag: Munich, Germany, 2021; ISBN 978-1-56990-660-6. [Google Scholar]
- Berzin, F.; David, C.; Vergnes, B. Optimization and Scale-Up of Twin-Screw Reactive Extrusion: The Case of EVA Transesterification. Int. Polym. Proc. 2020, 35, 422–428. [Google Scholar] [CrossRef]
- Cegla, M.; Fage, A.; Kemmerling, S.; Engell, S. Optimal design and operation of reactive extrusion processes: Application to the production and scale-up of polyurethane rheology modifiers for paints. Polym. Eng. Sci. 2023, 63, 4220–4235. [Google Scholar] [CrossRef]
- Covas, J.A.; Gaspar-Cunha, A. A Scaling-up Methodology for Co-rotating Twin-Extruders. In Proceedings of the 27th Annual Meeting of the Polymer Processing Society (PPS-27), Marrakesh, Morocco, 10–14 May 2011; pp. 1–6. [Google Scholar]
- Gaspar-Cunha, A.; Covas, J.A. An Engineering Scale-Up Approach Using Multi-Objective Optimization. Intern. J. Nat. Comp. Res. 2014, 4, 17–30. [Google Scholar] [CrossRef]
- Denysiuk, R.; Recio, G.; Covas, J.A.; Gaspar-Cunha, A. Using Multi-objective Optimization Algorithms and Decision Making Support to Solve Polymer Extrusion Problems. Polym. Eng. Sci. 2018, 58, 493–502. [Google Scholar] [CrossRef]
- Nastaj, A. Scale-up for Single Screw Extrusion of Polymeric Materials. Polimery 2021, 6, 331–340. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A. Modeling and Optimization of Single Screw Extrusion. Ph.D. Dissertation, University of Minho, Guimarães, Portugal, 2000. [Google Scholar]
- Gaspar-Cunha, A.; Covas, J.A. The Plasticating Sequence in Barrier Extrusion Screws Part I: Modeling. Polym. Eng. Sci. 2014, 54, 1791–1803. [Google Scholar] [CrossRef]
- Wilczyński, K. Single Screw Extrusion Model for Plasticating Extruders. Polym. Plast. Technol. 1999, 38, 581–608. [Google Scholar] [CrossRef]
- Tayeb, J.; Vergnes, B.; Della Valle, G. A Basic Model for a Twin-Screw Extruder. J. Food Sci. 1989, 54, 1047–1056. [Google Scholar] [CrossRef]
- Vergnes, B.; Valle, G.D.; Delamare, L. A Global Computer Software for Polymer Flows in Corotating Twin Screw Extruders. Polym. Eng. Sci. 1998, 38, 1781–1792. [Google Scholar] [CrossRef]
- Vergnes, B.; Delacour, M.L.; Souveton, G.; Bouvier, J.M. A Study of Polymer Melting in a Co-Rotating Twin Screw Extruder. In Proceedings of the International Polymer Processing Society 15th Annual Meeting (PPS-15), Hertogenbosch, The Netherlands, 31 May–4 June 1999. [Google Scholar]
- Vergnes, B.; Souveton, G.; Delacour, M.L.; Ainser, A. Experimental and Theoretical Study of Polymer Melting in a Co-rotating Twin Screw Extruder. Int. Polym. Proc. 2001, 16, 351–362. [Google Scholar] [CrossRef]
- Teixeira, C.; Gaspar-Cunha, A.; Covas, J.A. Flow and Heat Transfer Along the Length of a Co-Rotating Twin Screw Extruder. Polym. Plast. Technol. 2012, 51, 1567–1577. [Google Scholar] [CrossRef]
- Cegla, M.; Engell, S. Optimal design and operation of reactive extrusion processes: Modeling, model validation, and optimization algorithm. Polym Eng Sci. 2023, 63, 4153–4173. [Google Scholar] [CrossRef]
- Nastaj, A.; Wilczyński, K. Optimization and Scale-Up for Polymer Extrusion. Polymers 2021, 13, 1547. [Google Scholar] [CrossRef]
- Nastaj, A.; Wilczyński, K. Computational Scale-Up for Flood Fed/Starve Fed Single Screw Extrusion of Polymers. Polymers 2022, 14, 240. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Nastaj, A.; Lewandowski, A.; Wilczyński, K. A Composite Model for Starve Fed Single Screw Extrusion of Thermoplastics. Polym. Eng. Sci. 2014, 54, 2362–2374. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Lewandowski, A.; Nastaj, A.; Wilczyński, K. Modeling for Starve Fed/Flood Fed Mixing Single-Screw Extruders. Int. Polym. Proc. 2016, 31, 82–91. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Lewandowski, A.; Nastaj, A.; Wilczyński, K. A Global Model for Starve-Fed Nonconventional Single-Screw Extrusion of Thermoplastics. Adv. Polym. Technol. 2017, 36, 23–35. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Nastaj, A.; Wilczyński, K. A Computer Model for Starve-Fed Single-Screw Extrusion of Polymer Blends. Adv. Polym. Technol. 2018, 37, 2142–2151. [Google Scholar] [CrossRef]
- White, J.L.; Potente, H. Screw Extrusion. In Science and Technology; Hanser Publishers: Munich, Germany, 2003; ISBN 978-3-446-19624-7. [Google Scholar]
- Tadmor, Z.; Gogos, C.G. Principles of Polymer Processing, 2nd ed.; John Wiley & Sons Inc.: New York, NY, USA, 2006; ISBN 978-0-471-38770-1. [Google Scholar]
- Osswald, T.; Hernandez-Ortiz, J.P. Polymer Processing. Modeling and Simulation; Carl Hanser Verlag: Munich, Germany, 2006; ISBN 978-3-446-40381-9. [Google Scholar]
- Agassant, J.F.; Avenas, P.; Carreau, P.J.; Vergnes, B.; Vincent, M. Polymer Processing. Principles and Modelling, 2nd ed.; Carl Hanser Verlag: Munich, Germany, 2017; ISBN 978-1-56990-605-7. [Google Scholar]
- Wong, A.C.-Y. Polymer Extrusion; Carl Hanser Verlag: Munich, Germany, 2024; ISBN 978-1-56990-917-1. [Google Scholar]
- Altinkaynak, A.; Gupta, M.; Spalding, M.A.; Crabtree, S.L. Melting in a Single Screw Extruder: Experiments and 3D Finite Element Simulations. Int. Polym. Proc. 2011, 26, 182–196. [Google Scholar] [CrossRef]
- Ariffin, A.; Ahmad, M.S.B. Review: Single Screw Extruder in Particulate Filler Composite. Polym.-Plast. Technol. 2011, 50, 395–403. [Google Scholar] [CrossRef]
- Malik, M.; Kalyon, D.M.; Golba, J.C., Jr. Simulation of Co-Rotating Twin Screw Extrusion Process Subject to Pressure-Dependent Wall Slip at Barrel and Screw Surfaces: 3D FEM Analysis for Combinations of Forward- and Reverse-Conveying Screw Elements. Int. Polym. Proc. 2014, 29, 51–62. [Google Scholar] [CrossRef]
- Hyvärinen, M.; Jabeen, R.; Kärki, T. The Modeling of Extrusion Processes for Polymers—A Review. Polymers 2020, 12, 1306. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J.; Buziak, K. Fundamentals of Global Modeling for Polymer Extrusion. Polymers 2019, 11, 2106. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K. Modeling of Twin Screw Extrusion of Polymeric Materials. Polymers 2022, 14, 274. [Google Scholar] [CrossRef]
- Leistritz, P.; Burghauser, F. German Patent. 1927; 453, 727. [Google Scholar]
- Kiesskalt, S. Untersuchungen an einer Kapsel Pumpe. VDI Zeitschr. 1927, 71, 453. [Google Scholar]
- Montelius, C.O.J. U.S. Patent 1 698 802, 1929.
- Montelius, C.O.J. Der Kogelige Danske Videnscabernes Selscabs Skrifter. Teknist Tidskaift. 1933, 6, 61–63. [Google Scholar]
- Schenkel, G. Kunststoffe Extrudertechnik; Hanser: Munich, Germany, 1963. [Google Scholar]
- White, J.L. Twin Screw Extrusion. In Technology and Principles; Hanser: Munich, Germany, 1990. [Google Scholar]
- Doboczky, Z. Theoretische and wirkliche Ausstoßleistung der Doppelschnecken Extruder. Plastverarbeiter 1965, 19, 395–400. [Google Scholar]
- Janssen, L.P.B.M. Twin Screw Extrusion; Elsevier: Amsterdam, The Netherlands, 1978. [Google Scholar]
- White, J.L.; Adewale, A. A Unified View of Modeling Flow in Counter-rotating Twin Screw Extruders. Int. Polym. Process. 1993, 8, 210–217. [Google Scholar] [CrossRef]
- Li, T.; Manas Zloczower, I. Flow Field Analysis of an Intermeshing Counter-Rotating Twin Screw Extruder. Polym. Eng. Sci. 1994, 34, 551–558. [Google Scholar] [CrossRef]
- Kajiwara, T.; Nagashima, Y.; Naakano, Y.; Funatsu, K. Numerical Study of Twin Screw Extruders by Three Dimensional Flow Analysis—Development of Analysis Technique and Evaluation of Mixing Performance for Full Flight Screws. Polym. Eng. Sci. 1996, 36, 2142–2152. [Google Scholar] [CrossRef]
- Hong, M.H.; White, J.L. Fluid Mechanics of Intermeshing Counter-Rotating Twin Screw Extruders. Int. Polym. Proc. 1998, 13, 342–346. [Google Scholar] [CrossRef]
- Hong, M.H.; White, J.L. Simulation of Flow in an Intermeshing Modular Counter-Rotating Twin Screw Extruder: Non-Newtonian and Non-Isothermal Behavior. Int. Polym. Proc. 1999, 14, 136–143. [Google Scholar] [CrossRef]
- Wilczyński, K.; Lewandowski, A. Study on the Polymer Melt Flow in a Closely Intermeshing Counter-Rotating Twin Screw Extruder. Int. Polym. Proc. 2014, 29, 649–659. [Google Scholar] [CrossRef]
- Wilczyński, K.; White, J.L. Experimental Study of Melting in an Intermeshing Counter-Rotating Twin Screw Extruder. Int. Polym. Proc. 2001, 16, 257–262. [Google Scholar] [CrossRef]
- Wilczyński, K.; White, J.L. Melting Model for Intermeshing Counter-Rotating Twin-Screw Extruders. Polym. Eng. Sci. 2003, 43, 1715–1726. [Google Scholar] [CrossRef]
- Wang, D.; Min, K. In-Line Monitoring and Analysis of Polymer Melting Behavior in an Intermeshing Counter-Rotating Twin-Screw Extruder by Ultrasound Waves. Polym. Eng. Sci. 2005, 45, 998–1010. [Google Scholar] [CrossRef]
- Wang, D.; Min, K. Experiments and Analysis of Effect of Calender Gaps on Melting of PVC Powders in an Intermeshing Counter-Rotating Twin-Screw Extruder. Int. Polym. Proc. 2006, 21, 17–23. [Google Scholar] [CrossRef]
- Wilczyński, K.; Lewandowski, A.; Wilczyński, K.J. Experimental Study of Melting of LDPE/PS Polyblend in an Intermeshing Counter-Rotating Twin Screw Extruder. Polym. Eng. Sci. 2012, 52, 449–458. [Google Scholar] [CrossRef]
- Wilczyński, K.; Jiang, Q.; White, J.L. A Composite Model for Melting, Pressure and Fill Factor Profiles in a Metered Fed Closely Intermeshing Counter-Rotating Twin Screw Extruder. Int. Polym. Proc. 2007, 22, 198–203. [Google Scholar] [CrossRef]
- Wilczyński, K.; White, J.L. Modeling of Twin Screw Extrusion. Part I. A Model of Counter-Rotating Extrusion. Polimery 2008, 53, 754–759. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J. Modeling of the Polymer Melt Flow in a Twin Screw Counter-Rotating Extrusion Process. Part II. Simulation and Experimental Studies—Verification of the Adopted Model. Polimery 2011, 56, 45–50. [Google Scholar] [CrossRef]
- Jiang, Q.; White, J.L.; Yang, J. A Global Model for Closely Intermeshing Counter-Rotating Twin Screw Extruders with Flood Feeding. Int. Polym. Proc. 2010, 25, 223–235. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K.J.; Nastaj, A.; Wilczyński, K. A Composite Model for an Intermeshing Counter-Rotating Twin-Screw Extruder and its Experimental Verification. Polym. Eng. Sci. 2015, 55, 2838–2848. [Google Scholar] [CrossRef]
- Wilczyński, K.; White, J.L. Modeling of Twin Screw Extrusion. Part II. Model Verification. Polimery 2009, 54, 51–56. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Longman Publishing Co.: Boston, MA, USA, 1989; ISBN 978-0-201-15767-3. [Google Scholar]
- Kramer, O. Genetic Algorithm Essentials; Springer: Cham, Switzerland, 2018; ISBN 978-3-319-52155-8. [Google Scholar] [CrossRef]
- Harmsen, J. Industrial Process Scale-Up; Elsevier B.V.: Amsterdam, The Netherlands, 2019; ISBN 978-0-444-64210-3. [Google Scholar] [CrossRef]
- Phan, H. Springer Handbook of Engineering Statistics; Springer: London, UK, 2023; ISBN 978-1-4471-7502-5. [Google Scholar] [CrossRef]
- Ganzeveld, K.J.; Janssen, L.P.B.M. Scale-up of counter-rotating closely intermeshing twin screw extruders without and with reactions. Polym. Eng. Sci. 1990, 30, 1529–1536. [Google Scholar] [CrossRef]
- Bigio, D.; Wang, K. Scale-up rules for mixing in a non-intermeshing twin-screw extruder. Polym. Eng. Sci. 1996, 36, 2832–2839. [Google Scholar] [CrossRef]
- Agur, E.E. Extruder scale-up in a corotating twin-screw extrusion compounding process. Adv. Polym. Technol. 2003, 6, 225–231. [Google Scholar] [CrossRef]
- Fukuda, G.; Chavez, D.; Bigio, D.I.; Wetzel, M.; Andersen, P. Investigation of scale-up methodologies in twin-screw compounding. Annu. Technol. Conf.—ANTEC Conf. Proc. 2014, 2, 1142–1150. [Google Scholar]
- Dryer, B.; Fukuda, G.; Webb, J.; Montemayor, K.; Bigio, D.I.; Anders, P.; Wetzel, M. Comparison of scale-up methods for dispersive mixing in twin-screw extruders. Polym. Eng. Sci. 2017, 57, 345–354. [Google Scholar] [CrossRef]

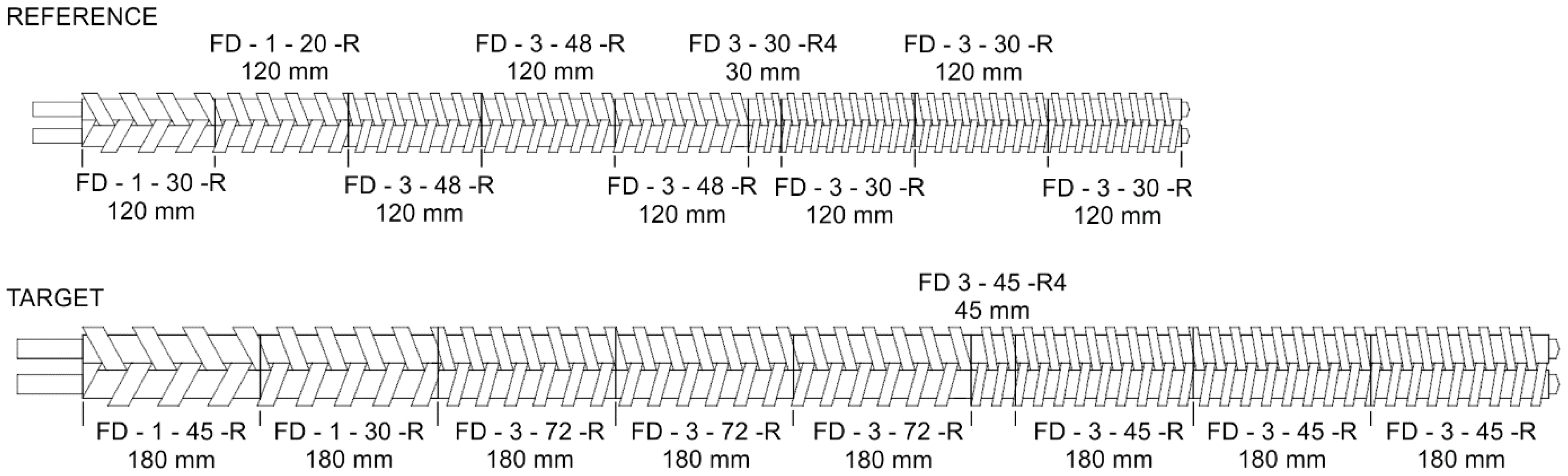




| Screws Configuration | |||||||
| Reference | |||||||
| Inside Barrel Diameter, mm | Distance between Centres of Screws, mm | ||||||
| 34 | 30 | ||||||
| Zone No. | Zone Length, mm | Screw Lead, mm | Cylindrical Clearance, mm | Clearance, mm | Number of Thread Starts | Flight Angle, ° | |
| 1. | 120.0 | 30.0 | 0.1 | 0.5 | 1 | 10.0 | |
| 2. | 120.0 | 20.0 | 0.1 | 0.5 | 1 | 10.0 | |
| 3. | 120.0 | 48.0 | 0.1 | 0.5 | 3 | 10.0 | |
| 4. | 120.0 | 48.0 | 0.1 | 0.5 | 3 | 10.0 | |
| 5. | 120.0 | 48.0 | 0.1 | 0.5 | 3 | 10.0 | |
| 6. | 30.0 | 30.0 | 0.1 | 0.5 | 3 | 10.0 | |
| 7. | 120.0 | 30.0 | 0.1 | 0.5 | 3 | 10.0 | |
| 8. | 120.0 | 30.0 | 0.1 | 0.5 | 3 | 10.0 | |
| 9. | 120.0 | 30.0 | 0.1 | 0.5 | 3 | 10.0 | |
| Target | |||||||
| Inside Barrel Diameter, mm | Distance between Centres of Screws, mm | ||||||
| 51 | 45 | ||||||
| Zone No. | Zone Length, mm | Screw Lead, mm | Cylindrical Clearance, mm | Clearance, mm | Number of Thread Starts | Flight Angle, ° | |
| 1. | 180.0 | 45.0 | 0.1 | 0.5 | 1 | 10.0 | |
| 2. | 180.0 | 30.0 | 0.1 | 0.5 | 1 | 10.0 | |
| 3. | 180.0 | 72.0 | 0.1 | 0.5 | 3 | 10.0 | |
| 4. | 180.0 | 72.0 | 0.1 | 0.5 | 3 | 10.0 | |
| 5. | 180.0 | 72.0 | 0.1 | 0.5 | 3 | 10.0 | |
| 6. | 45.0 | 45.0 | 0.1 | 0.5 | 3 | 10.0 | |
| 7. | 180.0 | 45.0 | 0.1 | 0.5 | 3 | 10.0 | |
| 8. | 180.0 | 45.0 | 0.1 | 0.5 | 3 | 10.0 | |
| 9. | 180.0 | 45.0 | 0.1 | 0.5 | 3 | 10.0 | |
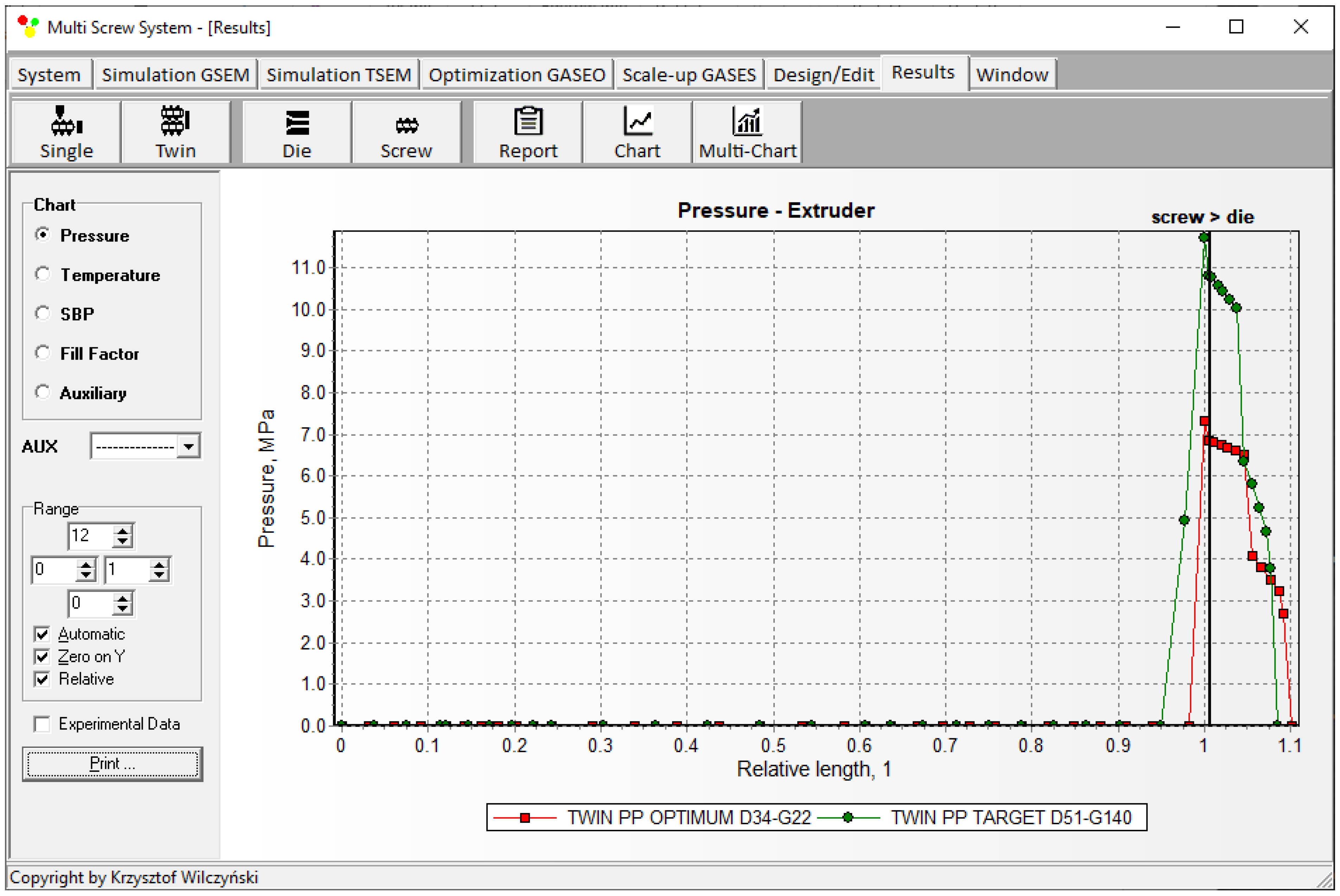
| Scaling-Up Results | |||
|---|---|---|---|
| Extruder | |||
| Single Parameters | Reference | Target | Deviation |
| Relative melting length | 0.242 | 0.242 | 0.0% |
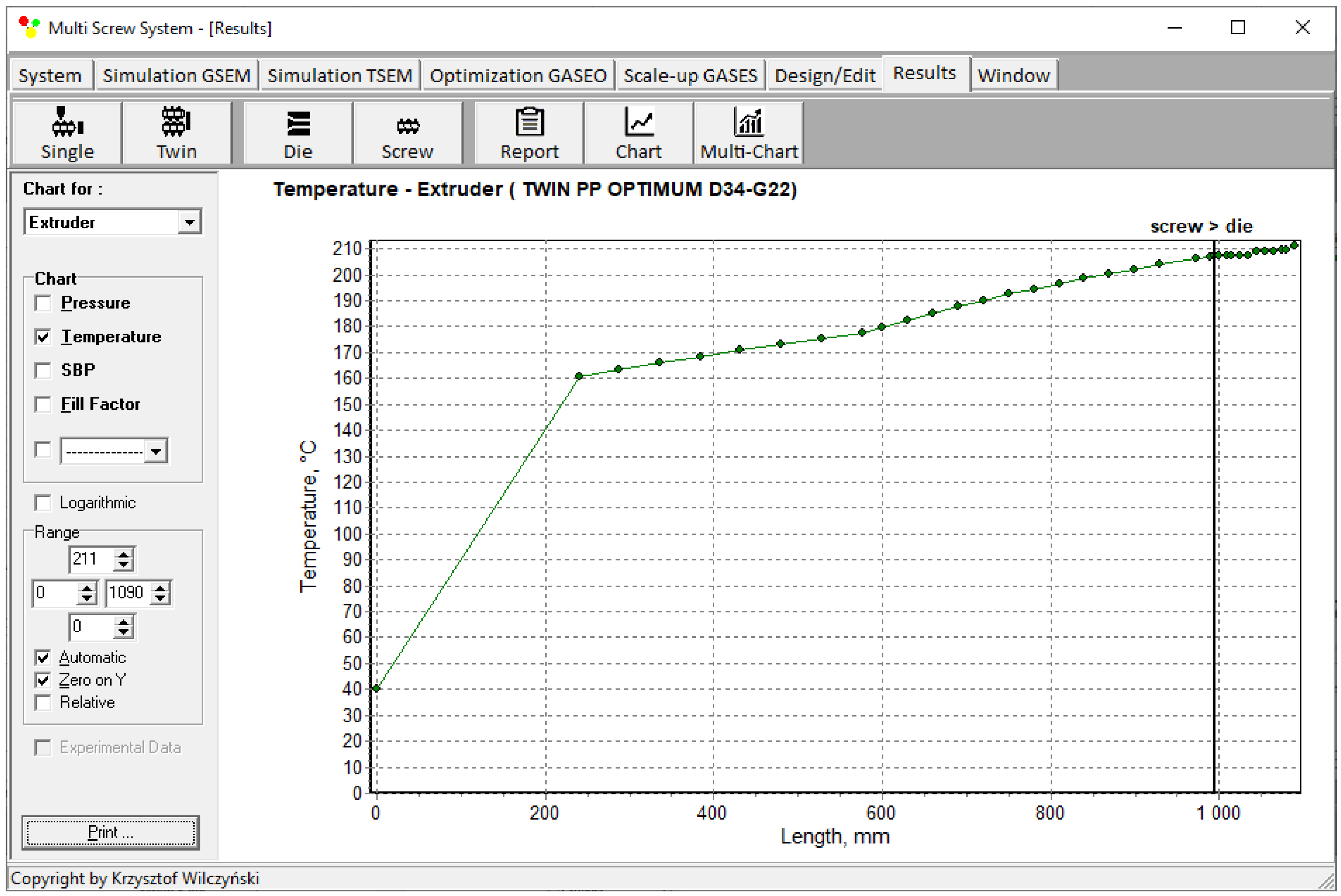
| Polymer melt temperature | 207 °C | 202 °C | 2.4% |
| Extrusion throughput/ Feeding flow rate | 21.88 kg/h | 140.0 kg/h | 539.9% |
| Functional parameters (profiles) | |||
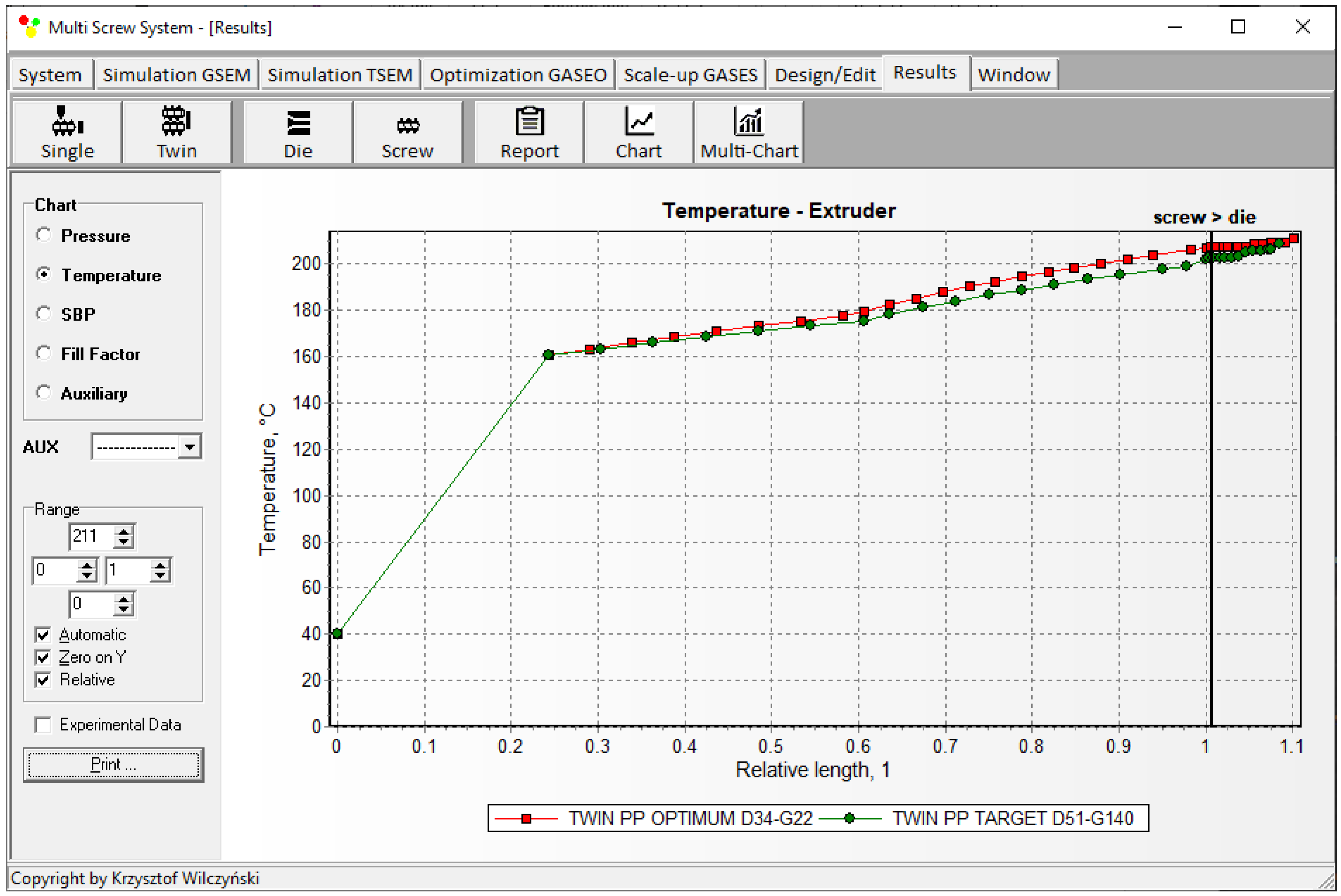
| Temperature | |||
| 1. | 20.00 °C | 20.00 °C | 0.00% |
| … | … | … | … |
| 10. | 163.26 °C | 163.37 °C | 0.07% |
| 11. | 165.95 °C | 166.04 °C | 0.05% |
| … | … | … | … |
| 24. | 206.10 °C | 199.20 °C | 3.35% |
| 25. | 207.00 °C | 202.02 °C | 2.41% |
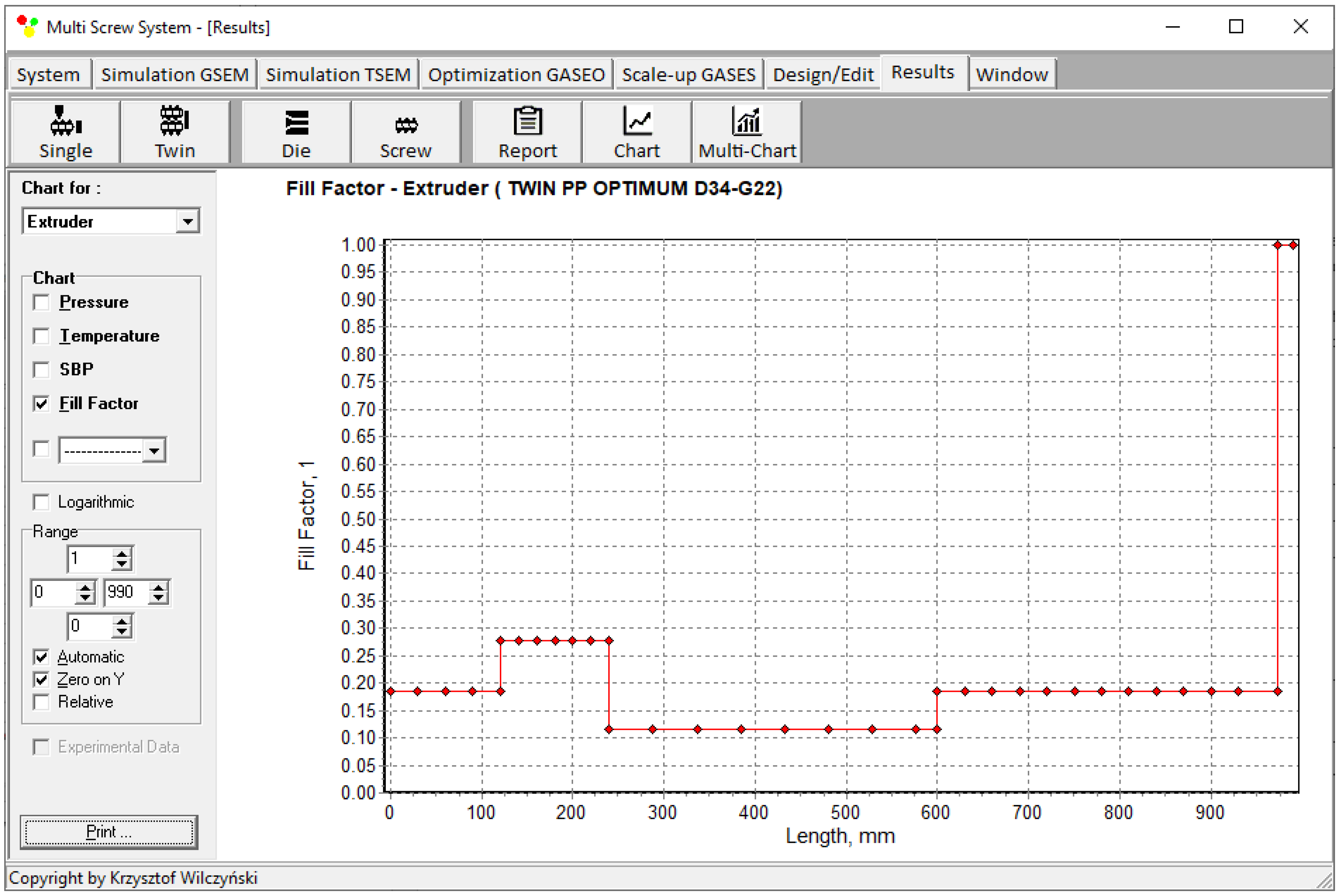
| Solid bed, SBP | |||
| 1. | 1.00 | 1.00 | 0.00% |
| … | … | … | … |
| 5. | 0.58 | 0.54 | 6.9% |
| 6. | 0.48 | 0.43 | 10.4% |
| … | … | … | … |
| 9. | 0.08 | 0.09 | 12.5% |
| 10. | 0.00 | 0.00 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nastaj, A.; Wilczyński, K. Scaling-Up for the Counter-Rotating Twin Screw Extrusion of Polymers. Polymers 2024, 16, 2720. https://doi.org/10.3390/polym16192720
Nastaj A, Wilczyński K. Scaling-Up for the Counter-Rotating Twin Screw Extrusion of Polymers. Polymers. 2024; 16(19):2720. https://doi.org/10.3390/polym16192720
Chicago/Turabian StyleNastaj, Andrzej, and Krzysztof Wilczyński. 2024. "Scaling-Up for the Counter-Rotating Twin Screw Extrusion of Polymers" Polymers 16, no. 19: 2720. https://doi.org/10.3390/polym16192720
APA StyleNastaj, A., & Wilczyński, K. (2024). Scaling-Up for the Counter-Rotating Twin Screw Extrusion of Polymers. Polymers, 16(19), 2720. https://doi.org/10.3390/polym16192720







