On the Piezomagnetism of Magnetoactive Elastomeric Cylinders in Uniform Magnetic Fields: Height Modulation in the Vicinity of an Operating Point by Time-Harmonic Fields
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis of MAE Cylinders
2.2. Experimental Setup
2.3. Image Processing
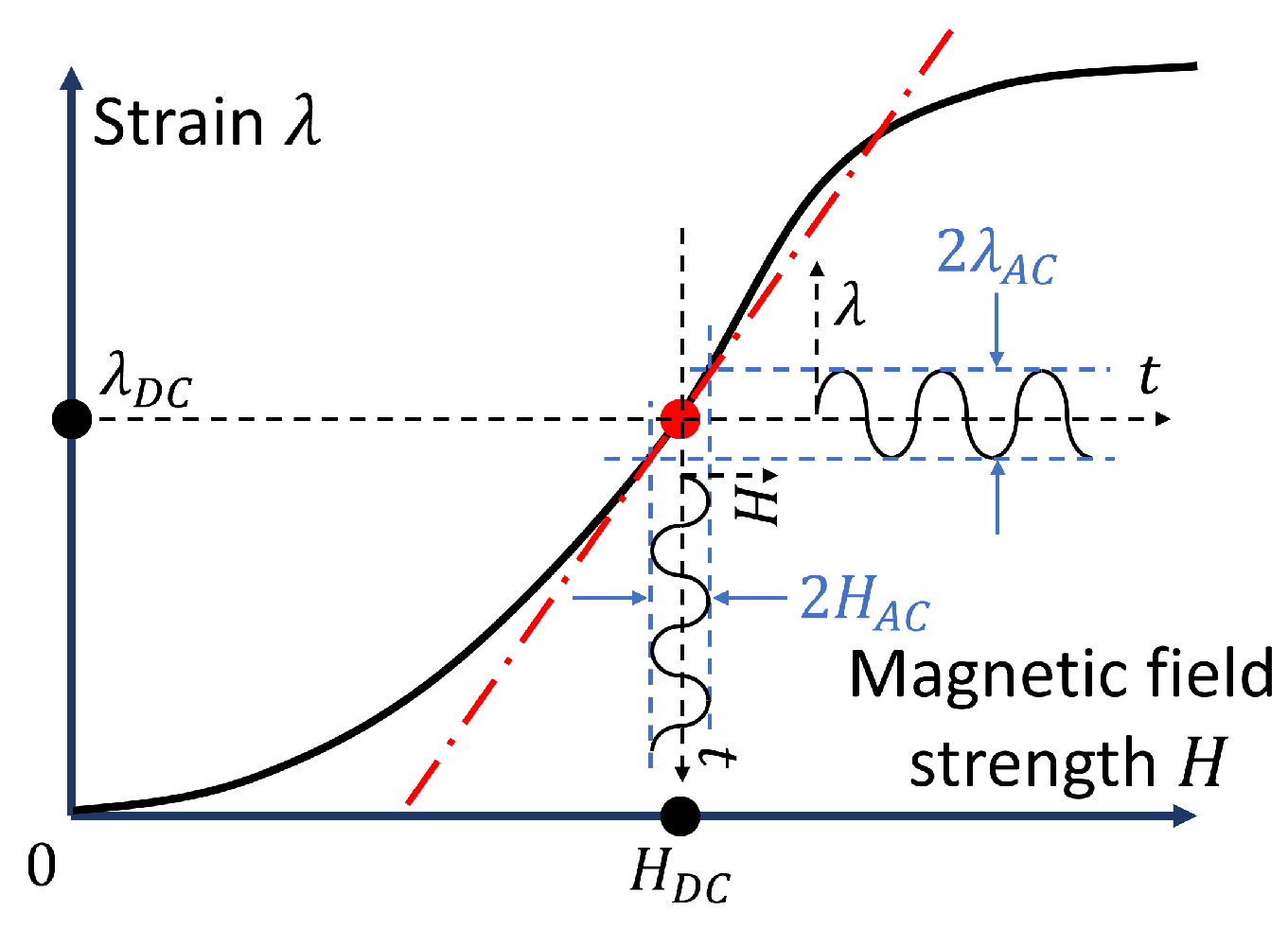
2.4. Measurement Protocol
3. Results and Discussion
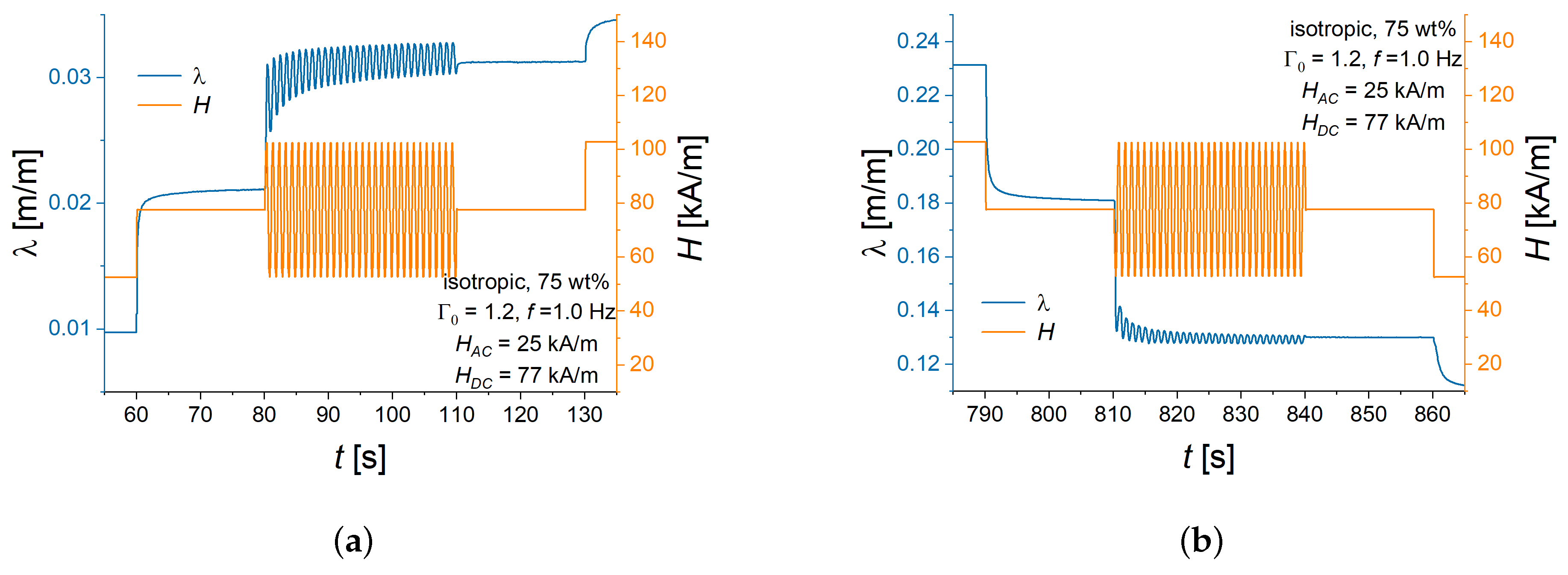
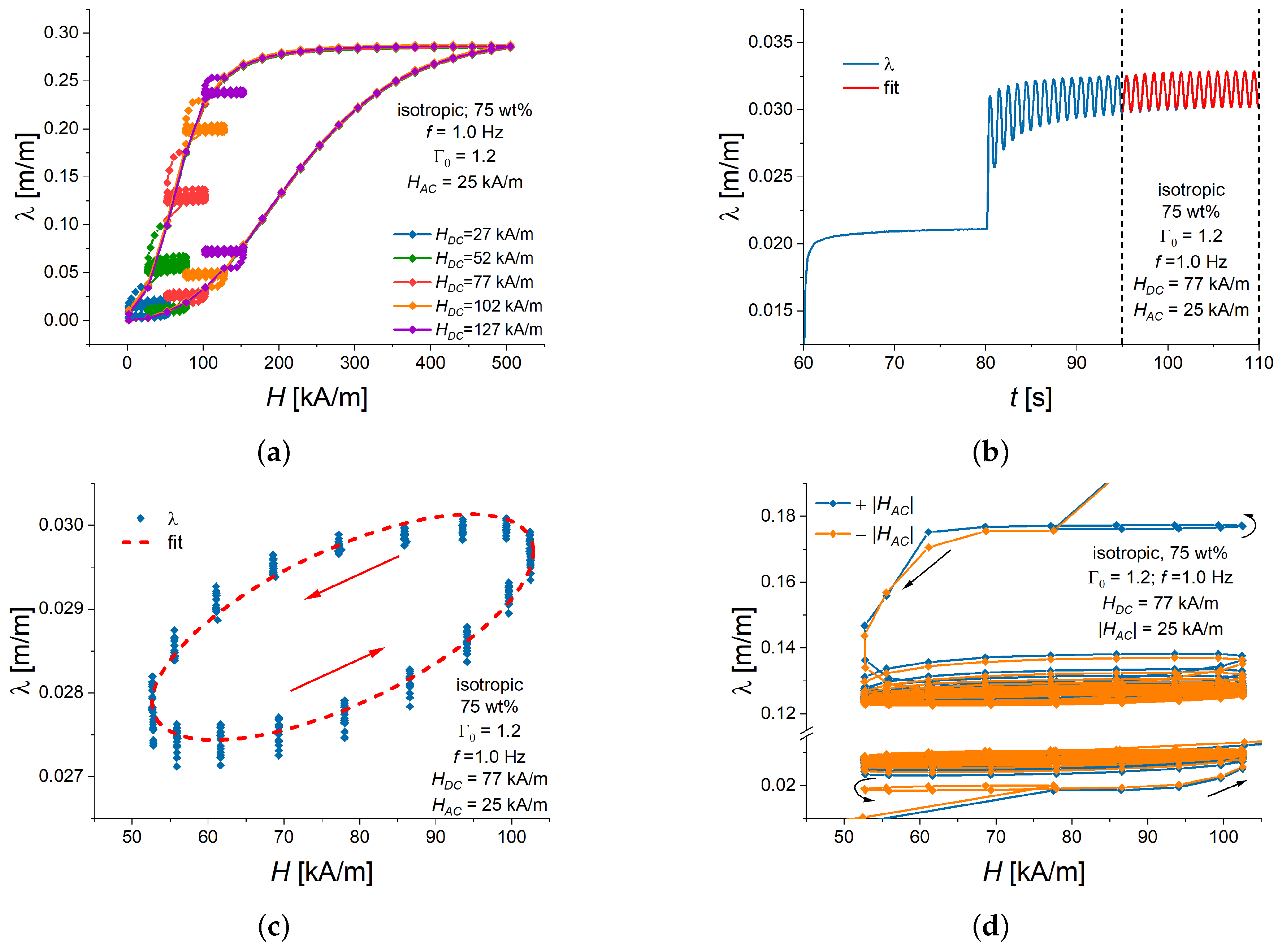
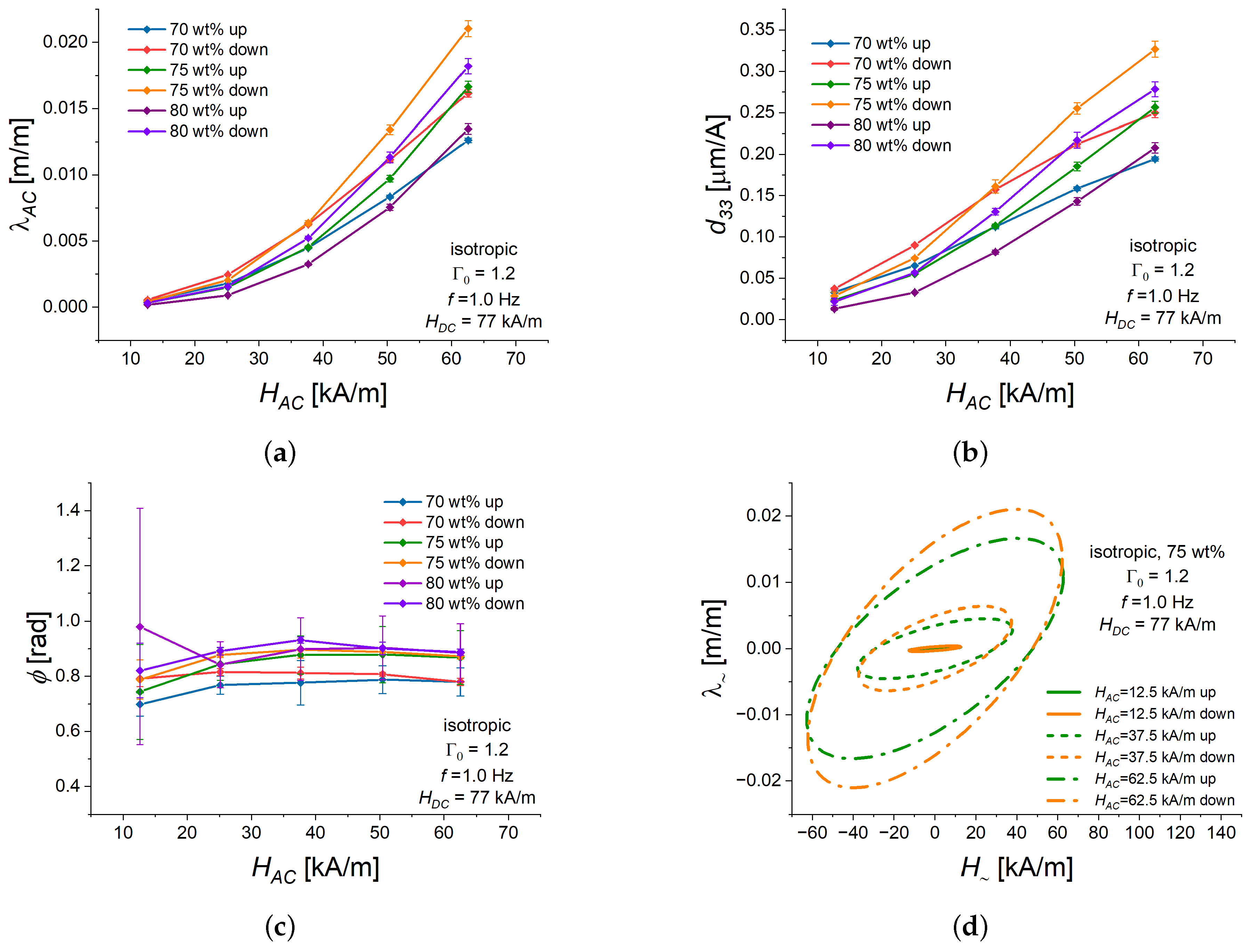
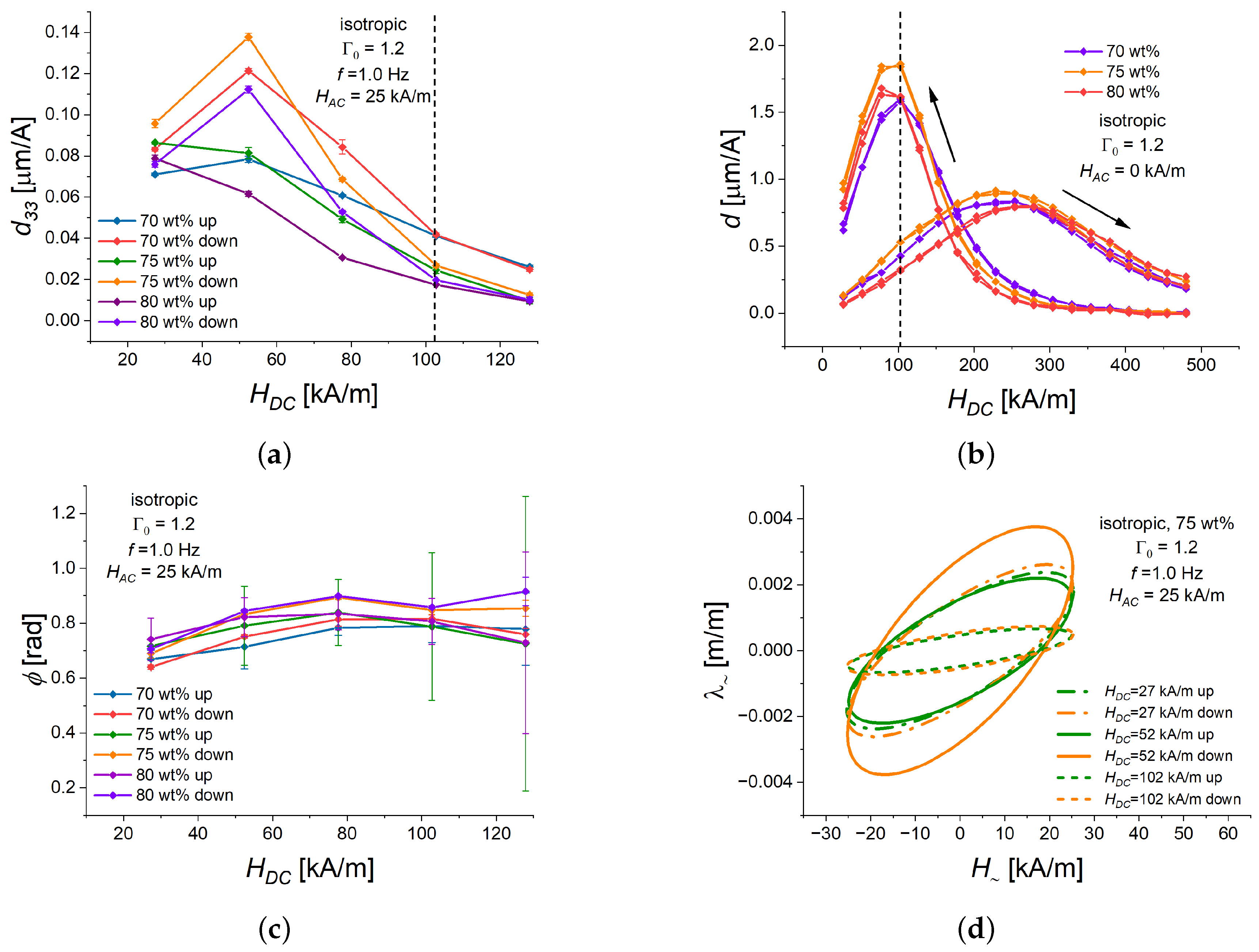
3.1. Dependence of the Alternating Strain on the Magnitude of
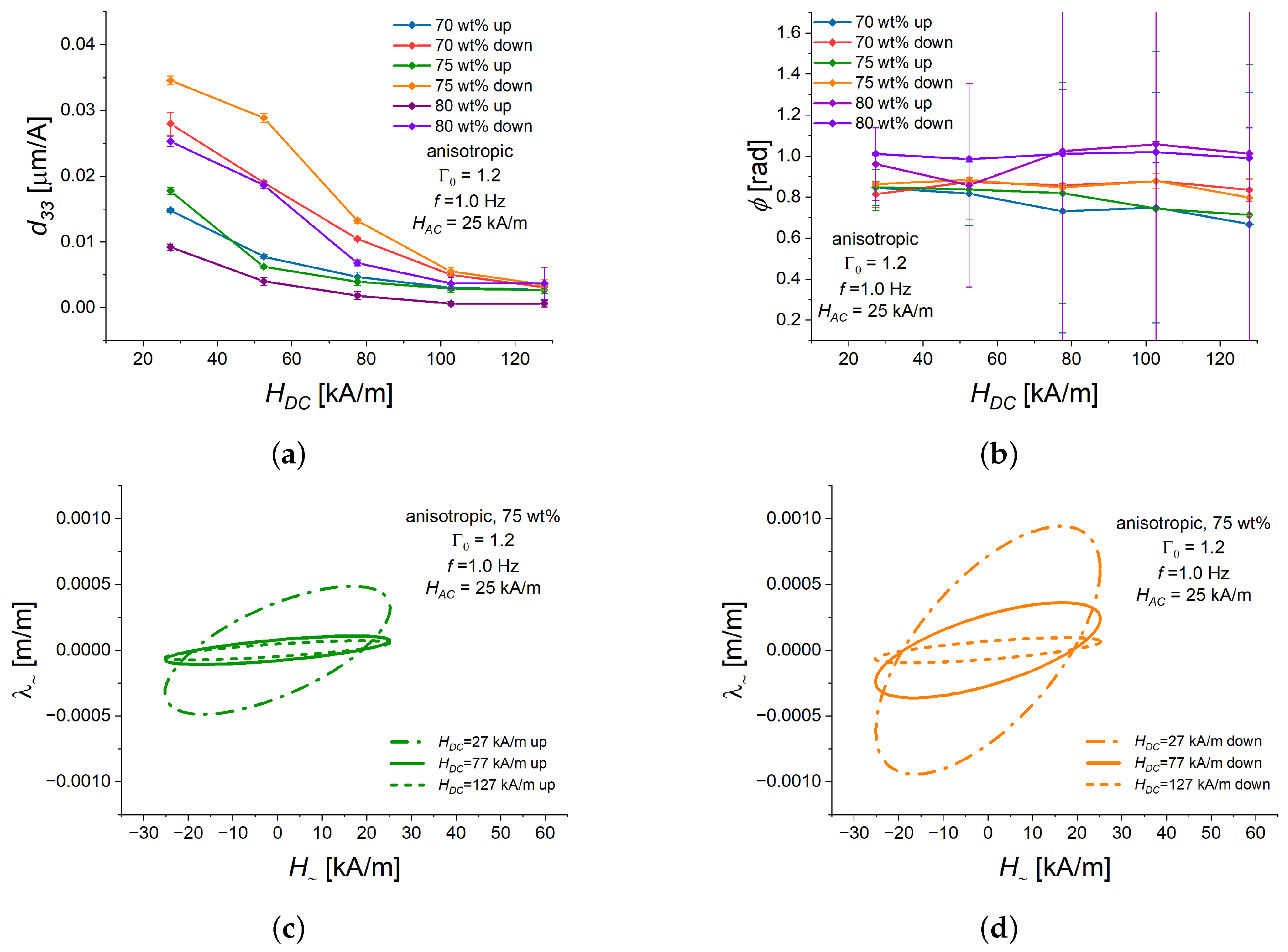
3.2. Dependence of the Alternating Strain on the Bias Magnetic Field
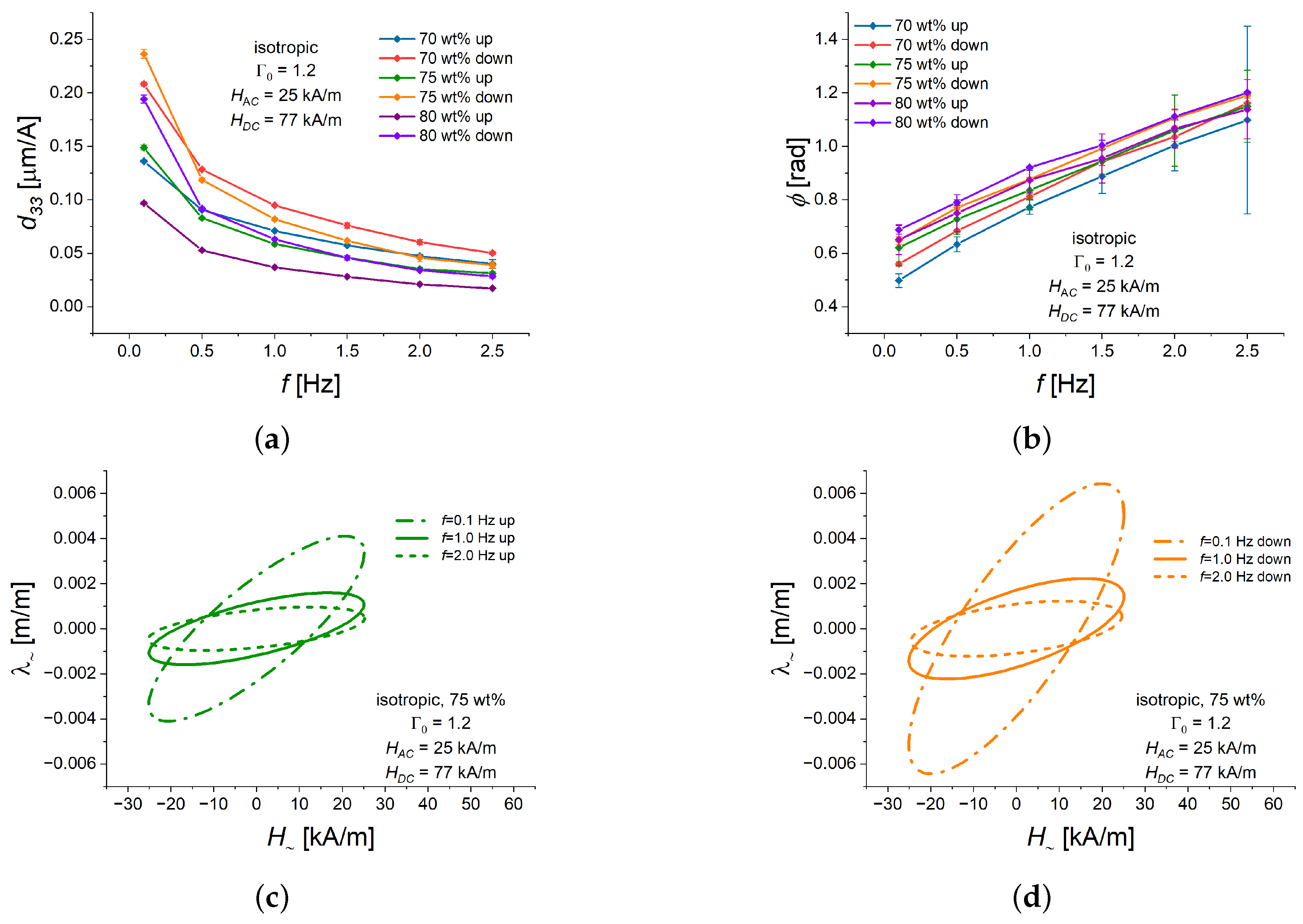
3.3. Frequency Dependence of the Alternating Strain
3.4. Dependence of the Alternating Strain on the Aspect Ratio
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B

References
- Borovik-Romanov, A.S. Piezomagnetism, linear magnetostriction and magnetooptic effect. Ferroelectrics 1994, 162, 153–159. [Google Scholar] [CrossRef]
- Piercy, A.R. The changing shape of magnetostriction. Phys. Educ. 1997, 32, 160. [Google Scholar] [CrossRef]
- Ekreem, N.; Olabi, A.; Prescott, T.; Rafferty, A.; Hashmi, M. An overview of magnetostriction, its use and methods to measure these properties. J. Mater. Process. Technol. 2007, 191, 96–101. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Lyshevski, S.E. Micromechatronics: Modeling, Analysis, and Design with MATLAB; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- IEEE Std 319-1990; IEEE Standard on Magnetostrictive Materials: Piezomagnetic Nomenclature. IEEE Standard Association: Piscataway, NJ, USA, 1991. [CrossRef]
- Magnetostriction and Piezomagnetism. Available online: https://doc.comsol.com/6.1/doc/com.comsol.help.sme/sme_ug_theory.06.041.html (accessed on 11 July 2024).
- Kim, Y.Y.; Kwon, Y.E. Review of magnetostrictive patch transducers and applications in ultrasonic nondestructive testing of waveguides. Ultrasonics 2015, 62, 3–19. [Google Scholar] [CrossRef]
- Nan, C.W.; Bichurin, M.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 1. [Google Scholar] [CrossRef]
- Srinivasan, G. Magnetoelectric composites. Annu. Rev. Mater. Res. 2010, 40, 153–178. [Google Scholar] [CrossRef]
- Zhou, Y.; Maurya, D.; Yan, Y.; Srinivasan, G.; Quandt, E.; Priya, S. Self-Biased Magnetoelectric Composites: An Overview and Future Perspectives. Energy Harvest. Syst. 2016, 3, 1–42. [Google Scholar] [CrossRef]
- Leung, C.M.; Li, J.; Viehland, D.; Zhuang, X. A review on applications of magnetoelectric composites: From heterostructural uncooled magnetic sensors, energy harvesters to highly efficient power converters. J. Phys. D Appl. Phys. 2018, 51, 263002. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Kumari, S.; Rack, P.D. Magnetoelectric Composites: Applications, Coupling Mechanisms, and Future Directions. Nanomaterials 2020, 10, 2072. [Google Scholar] [CrossRef]
- Liang, X.; Matyushov, A.; Hayes, P.; Schell, V.; Dong, C.; Chen, H.; He, Y.; Will-Cole, A.; Quandt, E.; Martins, P.; et al. Roadmap on Magnetoelectric Materials and Devices. IEEE Trans. Magn. 2021, 57, 1–57. [Google Scholar] [CrossRef]
- Feng, J.; Xuan, S.; Ding, L.; Gong, X. Magnetoactive elastomer/PVDF composite film based magnetically controllable actuator with real-time deformation feedback property. Compos. Part A Appl. Sci. Manuf. 2017, 103, 25–34. [Google Scholar] [CrossRef]
- Makarova, L.A.; Alekhina, Y.A.; Isaev, D.A.; Khairullin, M.F.; Perov, N.S. Tunable layered composites based on magnetoactive elastomers and piezopolymer for sensors and energy harvesting devices. J. Phys. D Appl. Phys. 2020, 54, 015003. [Google Scholar] [CrossRef]
- Saveliev, D.V.; Glavan, G.; Belan, V.O.; Belyaeva, I.A.; Fetisov, L.Y.; Shamonin, M. Resonant Magnetoelectric Effect at Low Frequencies in Layered Polymeric Cantilevers Containing a Magnetoactive Elastomer. Appl. Sci. 2022, 12, 2102. [Google Scholar] [CrossRef]
- Savelev, D.V.; Glavan, G.; Burdin, D.A.; Belyaeva, I.A.; Fetisov, L.Y.; Shamonin, M.; Fetisov, Y.K. Enhancement of magnetoelectric effect in polymer composites at low resonance frequencies by operation in the transverse-transverse mode. J. Magn. Magn. Mater. 2024, 598, 172020. [Google Scholar] [CrossRef]
- Ju, S.; Chae, S.H.; Choi, Y.; Lee, S.; Lee, H.W.; Ji, C.H. A low frequency vibration energy harvester using magnetoelectric laminate composite. Smart Mater. Struct. 2013, 22, 115037. [Google Scholar] [CrossRef]
- Marauska, S.; Jahns, R.; Greve, H.; Quandt, E.; Knöchel, R.; Wagner, B. MEMS magnetic field sensor based on magnetoelectric composites. J. Micromech. Microeng. 2012, 22, 065024. [Google Scholar] [CrossRef]
- Moreno, M.; Gonzalez-Rico, J.; Lopez-Donaire, M.; Arias, A.; Garcia-Gonzalez, D. New experimental insights into magneto-mechanical rate dependences of magnetorheological elastomers. Compos. Part B Eng. 2021, 224, 109148. [Google Scholar] [CrossRef]
- Ubaidillah; Sutrisno, J.; Purwanto, A.; Mazlan, S.A. Recent Progress on Magnetorheological Solids: Materials, Fabrication, Testing, and Applications. Adv. Eng. Mater. 2015, 17, 563–597. [Google Scholar] [CrossRef]
- Menzel, A.M. Tuned, driven, and active soft matter. Phys. Rep. 2015, 554, 1–45. [Google Scholar] [CrossRef]
- Lopez-Lopez, M.T.; Durán, J.D.G.; Iskakova, L.Y.; Zubarev, A.Y. Mechanics of Magnetopolymer Composites: A Review. J. Nanofluids 2016, 5, 479–495. [Google Scholar] [CrossRef]
- Weeber, R.; Hermes, M.; Schmidt, A.M.; Holm, C. Polymer architecture of magnetic gels: A review. J. Phys. Condens. Matter 2018, 30, 063002. [Google Scholar] [CrossRef] [PubMed]
- Bastola, A.K.; Paudel, M.; Li, L.; Li, W. Recent progress of magnetorheological elastomers: A review. Smart Mater. Struct. 2020, 29, 123002. [Google Scholar] [CrossRef]
- Odenbach, S. (Ed.) Magnetic Hybrid-Materials: Multi-Scale Modelling, Synthesis, and Applications; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2021. [Google Scholar]
- Nadzharyan, T.A.; Shamonin, M.; Kramarenko, E.Y. Theoretical Modeling of Magnetoactive Elastomers on Different Scales: A State-of-the-Art Review. Polymers 2022, 14, 4096. [Google Scholar] [CrossRef] [PubMed]
- Kostrov, S.A.; Marshall, J.H.; Maw, M.; Sheiko, S.S.; Kramarenko, E.Y. Programming and Reprogramming the Viscoelasticity and Magnetic Response of Magnetoactive Thermoplastic Elastomers. Polymers 2023, 15, 4607. [Google Scholar] [CrossRef] [PubMed]
- Boyraz, P.; Runge, G.; Raatz, A. An Overview of Novel Actuators for Soft Robotics. Actuators 2018, 7, 48. [Google Scholar] [CrossRef]
- Bernat, J.; Gajewski, P.; Kołota, J.; Marcinkowska, A. Review of Soft Actuators Controlled with Electrical Stimuli: IPMC, DEAP, and MRE. Appl. Sci. 2023, 13, 1651. [Google Scholar] [CrossRef]
- Domenjoud, M.; Berthelot, E.; Galopin, N.; Corcolle, R.; Bernard, Y.; Daniel, L. Characterization of giant magnetostrictive materials under static stress: Influence of loading boundary conditions. Smart Mater. Struct. 2019, 28, 095012. [Google Scholar] [CrossRef]
- Romeis, D.; Toshchevikov, V.; Saphiannikova, M. Effects of local rearrangement of magnetic particles on deformation in magneto-sensitive elastomers. Soft Matter 2019, 15, 3552–3564. [Google Scholar] [CrossRef]
- Stolbov, O.V.; Raikher, Y.L. Magnetostriction effect in soft magnetic elastomers. Arch. Appl. Mech. 2019, 89, 63–76. [Google Scholar] [CrossRef]
- Sánchez, P.A.; Stolbov, O.V.; Kantorovich, S.S.; Raikher, Y.L. Modeling the magnetostriction effect in elastomers with magnetically soft and hard particles. Soft Matter 2019, 15, 7145–7158. [Google Scholar] [CrossRef]
- Kalina, K.A.; Metsch, P.; Brummund, J.; Kästner, M. A macroscopic model for magnetorheological elastomers based on microscopic simulations. Int. J. Solids Struct. 2020, 193–194, 200–212. [Google Scholar] [CrossRef]
- Saveliev, D.V.; Belyaeva, I.A.; Chashin, D.V.; Fetisov, L.Y.; Romeis, D.; Kettl, W.; Kramarenko, E.Y.; Saphiannikova, M.; Stepanov, G.V.; Shamonin, M. Giant Extensional Strain of Magnetoactive Elastomeric Cylinders in Uniform Magnetic Fields. Materials 2020, 13, 3297. [Google Scholar] [CrossRef] [PubMed]
- Bastola, A.K.; Hossain, M. The shape—Morphing performance of magnetoactive soft materials. Mater. Des. 2021, 211, 110172. [Google Scholar] [CrossRef]
- Silva, J.; Gouveia, C.; Dinis, G.; Pinto, A.; Pereira, A. Giant magnetostriction in low-concentration magnetorheological elastomers. Compos. Part B Eng. 2022, 243, 110125. [Google Scholar] [CrossRef]
- Balogh, D.; Guba, S.; Horváth, B.; Szalai, I. Magnetic Field-Induced Deformation of Isotropic Magnetorheological Elastomers. Magnetochemistry 2022, 8, 146. [Google Scholar] [CrossRef]
- Tasin, M.A.; Aziz, S.A.A.; Mazlan, S.A.; Johari, M.A.F.; Nordin, N.A.; Yusuf, S.Y.M.; Choi, S.B.; Bahiuddin, I. Magnetostriction Enhancement in Midrange Modulus Magnetorheological Elastomers for Sensor Applications. Micromachines 2023, 14, 767. [Google Scholar] [CrossRef]
- Glavan, G.; Belyaeva, I.A.; Drevenšek-Olenik, I.; Shamonin, M. Experimental study of longitudinal, transverse and volume strains of magnetoactive elastomeric cylinders in uniform magnetic fields. J. Magn. Magn. Mater. 2023, 579, 170826. [Google Scholar] [CrossRef]
- Roghani, M.; Romeis, D.; Saphiannikova, M. Effect of microstructure evolution on the mechanical behavior of magneto-active elastomers with different matrix stiffness. Soft Matter 2023, 19, 6387–6398. [Google Scholar] [CrossRef]
- Goh, S.; Menzel, A.M.; Wittmann, R.; Löwen, H. Density functional approach to elastic properties of three-dimensional dipole-spring models for magnetic gels. J. Chem. Phys. 2023, 158, 054909. [Google Scholar] [CrossRef]
- Hogea, C.S.; Armstrong, W.D. The time-dependent magneto-visco-elastic behavior of a magnetostrictive fiber actuated viscoelastic polymer matrix composite. J. Acoust. Soc. Am. 2002, 112, 1928–1936. [Google Scholar] [CrossRef]
- Lin, C.h.; Lin, Y.Z. Analysis of non-linear piezomagnetism for magnetostrictive terfenol-D composites. J. Magn. Magn. Mater. 2021, 540, 168490. [Google Scholar] [CrossRef]
- Lin, C.h.; Lin, C.J. Effective magnetoelastic responses of hybrid fiber composites with viscoelastic matrices. Compos. Struct. 2024, 333, 117874. [Google Scholar] [CrossRef]
- Zubarev, A.; Chirikov, D.; Stepanov, G.; Borin, D.; Lopez-Lopez, M. On the theory of hysteretic magnetostriction of soft ferrogels. Phys. A Stat. Mech. Its Appl. 2018, 498, 86–95. [Google Scholar] [CrossRef]
- Belyaeva, I.A.; Klepp, J.; Lemmel, H.; Shamonin, M. Feasibility of Probing the Filler Restructuring in Magnetoactive Elastomers by Ultra-Small-Angle Neutron Scattering. Appl. Sci. 2021, 11, 4470. [Google Scholar] [CrossRef]
- Biller, A.M.; Stolbov, O.V.; Raikher, Y.L. Mesoscopic magnetomechanical hysteresis in a magnetorheological elastomer. Phys. Rev. E 2015, 92, 023202. [Google Scholar] [CrossRef]
- Wang, B.; Kari, L.; Pang, H.; Gong, X. Modelling the dynamic magnetic actuation of isotropic soft magnetorheological elastomers. Int. J. Mech. Sci. 2024, 266, 108908. [Google Scholar] [CrossRef]
- Fields, T.H.E. Time Harmonic Electromagnetic Fields; McGraw-Hill: New York City, NY, USA, 1961. [Google Scholar]
- Glavan, G.; Belyaeva, I.A.; Shamonin, M. Transient Response of Macroscopic Deformation of Magnetoactive Elastomeric Cylinders in Uniform Magnetic Fields. Polymers 2024, 16, 586. [Google Scholar] [CrossRef]
- Mazurek, P.; Vudayagiri, S.; Skov, A.L. How to tailor flexible silicone elastomers with mechanical integrity: A tutorial review. Chem. Soc. Rev. 2019, 48, 1448–1464. [Google Scholar] [CrossRef]
- Sorokin, V.V.; Belyaeva, I.A.; Shamonin, M.; Kramarenko, E.Y. Magnetorheological response of highly filled magnetoactive elastomers from perspective of mechanical energy density: Fractal aggregates above the nanometer scale? Phys. Rev. E 2017, 95, 062501. [Google Scholar] [CrossRef]
- Belyaeva, I.A.; Kramarenko, E.Y.; Shamonin, M. Magnetodielectric effect in magnetoactive elastomers: Transient response and hysteresis. Polymer 2017, 127, 119–128. [Google Scholar] [CrossRef]
- Glavan, G.; Belyaeva, I.A.; Ruwisch, K.; Wollschläger, J.; Shamonin, M. Magnetoelectric Response of Laminated Cantilevers Comprising a Magnetoactive Elastomer and a Piezoelectric Polymer, in Pulsed Uniform Magnetic Fields. Sensors 2021, 21, 6390. [Google Scholar] [CrossRef] [PubMed]
- Trujillo-Pino, A.; Krissian, K.; Alemán-Flores, M.; Santana-Cedrés, D. Accurate subpixel edge location based on partial area effect. Image Vis. Comput. 2013, 31, 72–90. [Google Scholar] [CrossRef]
- Schmusch, W. Elektronische Messtechnik: Prinzipien, Verfahren, Schaltungen; Vogel: Würzburg, Germany, 2001; p. 139. [Google Scholar]
- Elhajjar, R.; Law, C.T.; Pegoretti, A. Magnetostrictive polymer composites: Recent advances in materials, structures and properties. Prog. Mater. Sci. 2018, 97, 204–229. [Google Scholar] [CrossRef]
- Payne, A.R. The dynamic properties of carbon black-loaded natural rubber vulcanizates. Part I. J. Appl. Polym. Sci. 1962, 6, 57–63. [Google Scholar] [CrossRef]
- Ginder, J.; Clark, S.; Schlotter, W.; Nichols, M. Magnetostrictive phenomena in magnetorheological elastomers. Int. J. Mod. Phys. B 2002, 16, 2412–2418. [Google Scholar] [CrossRef]
- Sorokin, V.V.; Ecker, E.; Stepanov, G.V.; Shamonin, M.; Monkman, G.J.; Kramarenko, E.Y.; Khokhlov, A.R. Experimental study of the magnetic field enhanced Payne effect in magnetorheological elastomers. Soft Matter 2014, 10, 8765–8776. [Google Scholar] [CrossRef]
- Shamonin, M.; Kramarenko, E.Y. Chapter 7—Highly Responsive Magnetoactive Elastomers. In Novel Magnetic Nanostructures; Domracheva, N., Caporali, M., Rentschler, E., Eds.; Advanced Nanomaterials; Elsevier: Amsterdam, The Netherlands, 2018; pp. 221–245. [Google Scholar] [CrossRef]
- Diguet, G.; Beaugnon, E.; Cavaillé, J. Shape effect in the magnetostriction of ferromagnetic composite. J. Magn. Magn. Mater. 2010, 322, 3337–3341. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glavan, G.; Belyaeva, I.A.; Shamonin, M. On the Piezomagnetism of Magnetoactive Elastomeric Cylinders in Uniform Magnetic Fields: Height Modulation in the Vicinity of an Operating Point by Time-Harmonic Fields. Polymers 2024, 16, 2706. https://doi.org/10.3390/polym16192706
Glavan G, Belyaeva IA, Shamonin M. On the Piezomagnetism of Magnetoactive Elastomeric Cylinders in Uniform Magnetic Fields: Height Modulation in the Vicinity of an Operating Point by Time-Harmonic Fields. Polymers. 2024; 16(19):2706. https://doi.org/10.3390/polym16192706
Chicago/Turabian StyleGlavan, Gašper, Inna A. Belyaeva, and Mikhail Shamonin. 2024. "On the Piezomagnetism of Magnetoactive Elastomeric Cylinders in Uniform Magnetic Fields: Height Modulation in the Vicinity of an Operating Point by Time-Harmonic Fields" Polymers 16, no. 19: 2706. https://doi.org/10.3390/polym16192706
APA StyleGlavan, G., Belyaeva, I. A., & Shamonin, M. (2024). On the Piezomagnetism of Magnetoactive Elastomeric Cylinders in Uniform Magnetic Fields: Height Modulation in the Vicinity of an Operating Point by Time-Harmonic Fields. Polymers, 16(19), 2706. https://doi.org/10.3390/polym16192706







