Study on the Diffusion Characteristics of Polymer Grouting Materials Applied for Crack Filling in Underground Mines Based on Numerical Simulation and Experimental Methods
Abstract
1. Introduction
2. Numerical Models and Experimental Methods
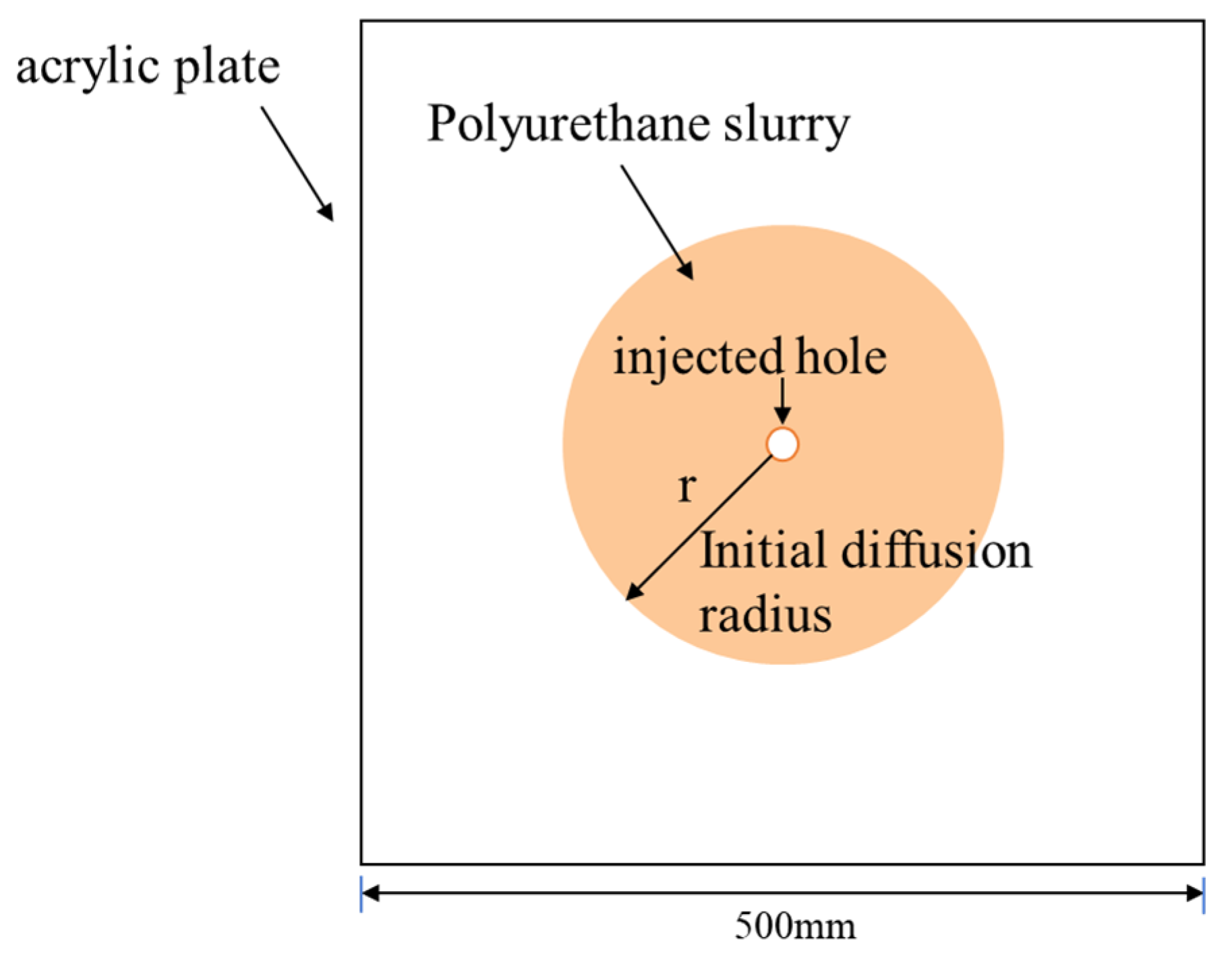
2.1. The Polymer Slurry’s Diffusion Process
2.2. Fundamental Assumption
2.3. Numerical Computation Method
2.4. Governing Equations
2.4.1. Continuity Equation
2.4.2. Momentum Equation
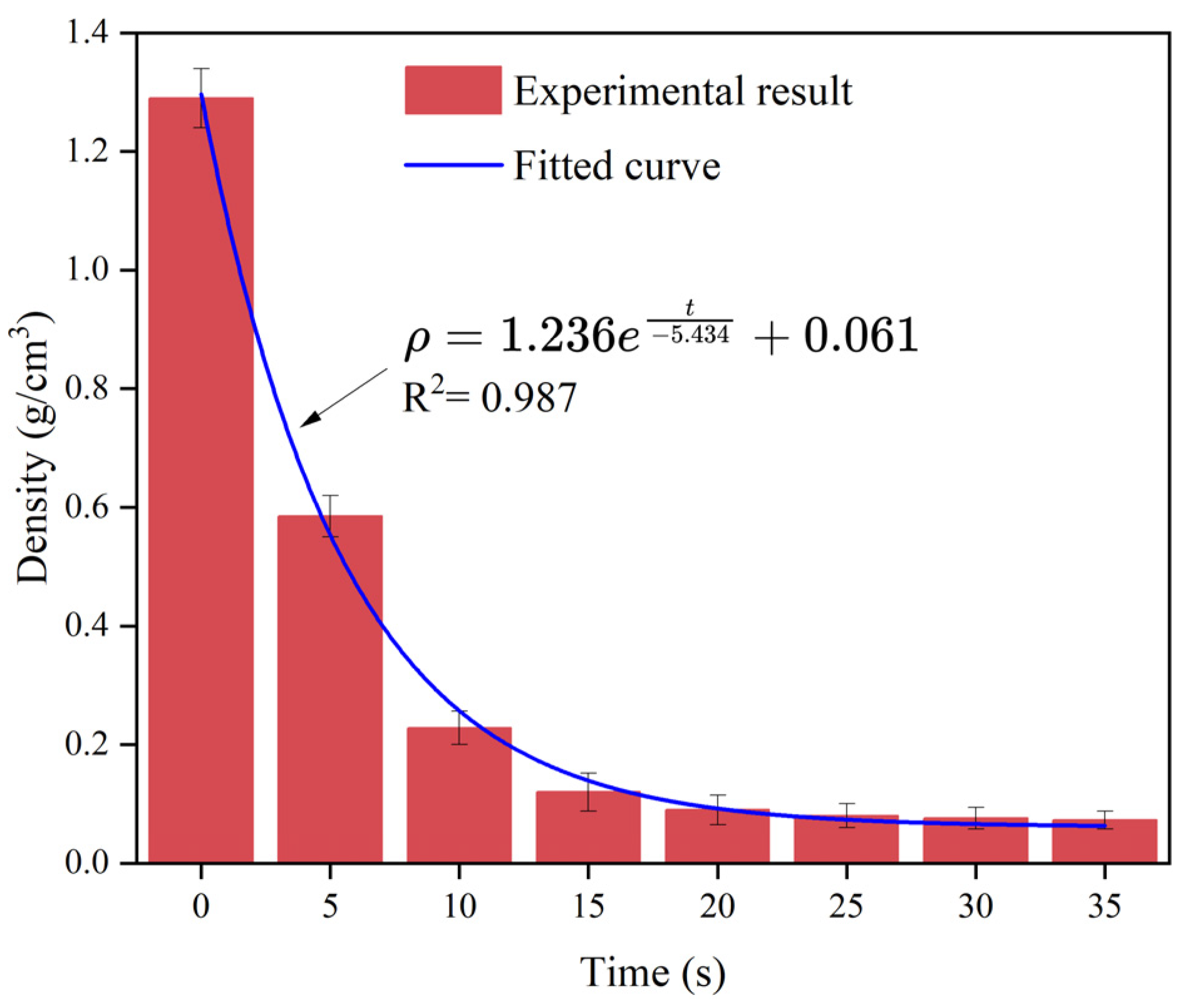
2.5. Density Function
- Fill a cylindrical container with a graduated scale with prepared homogeneous, uncured polyurethane.
- Record the time and volume at this point and start the timer. At the same time, make sure that the ambient temperature and humidity remain constant during the test.
- Record the volume of the slurry at 5 s intervals until the slurry is completely set, the volume no longer changes, and the test is stopped.
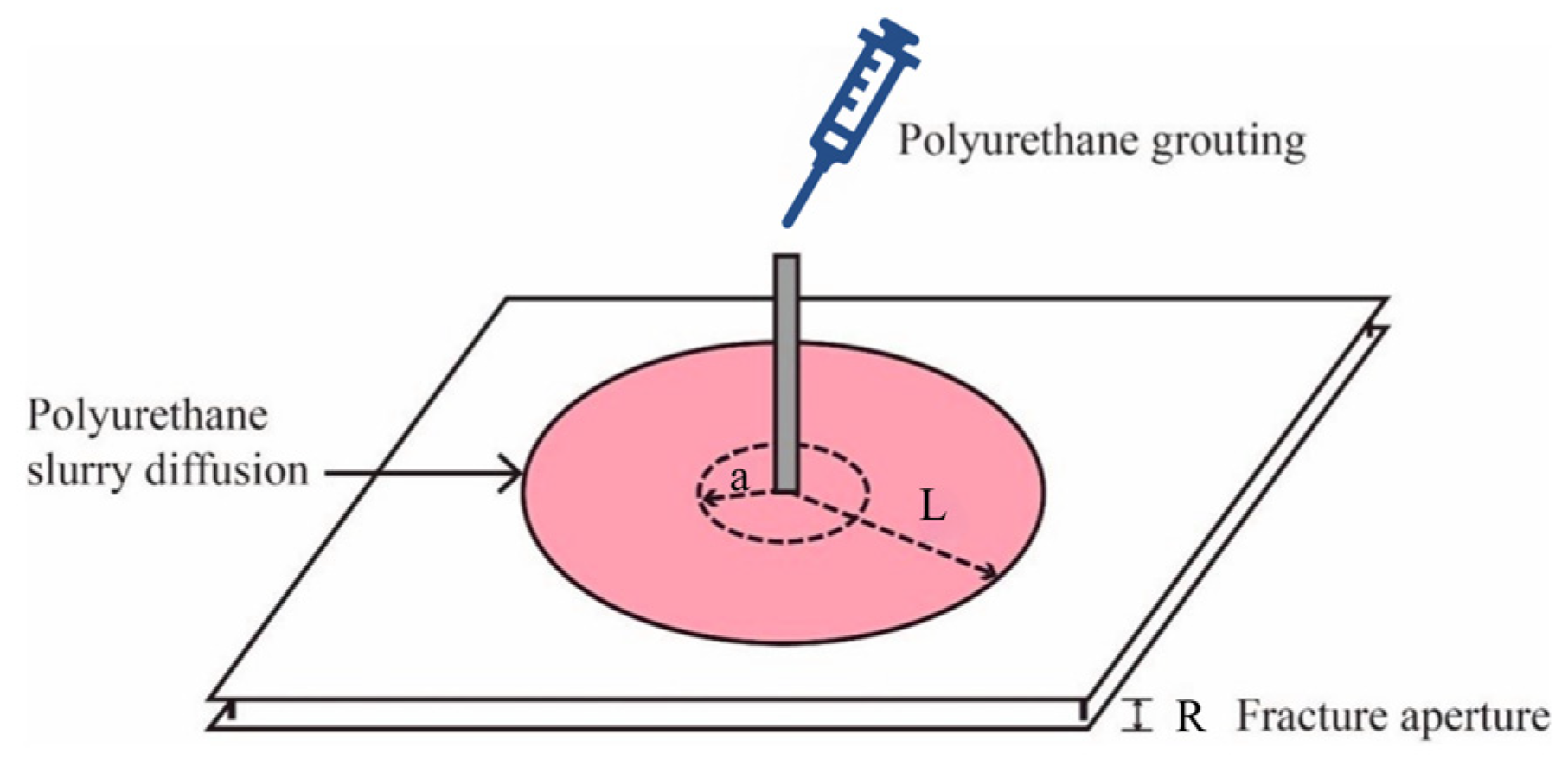
2.6. Simulated Crack Grouting Test
3. Numeric Calculations
3.1. Discretization
3.2. Initial and Boundary Conditions
4. Results and Discussion
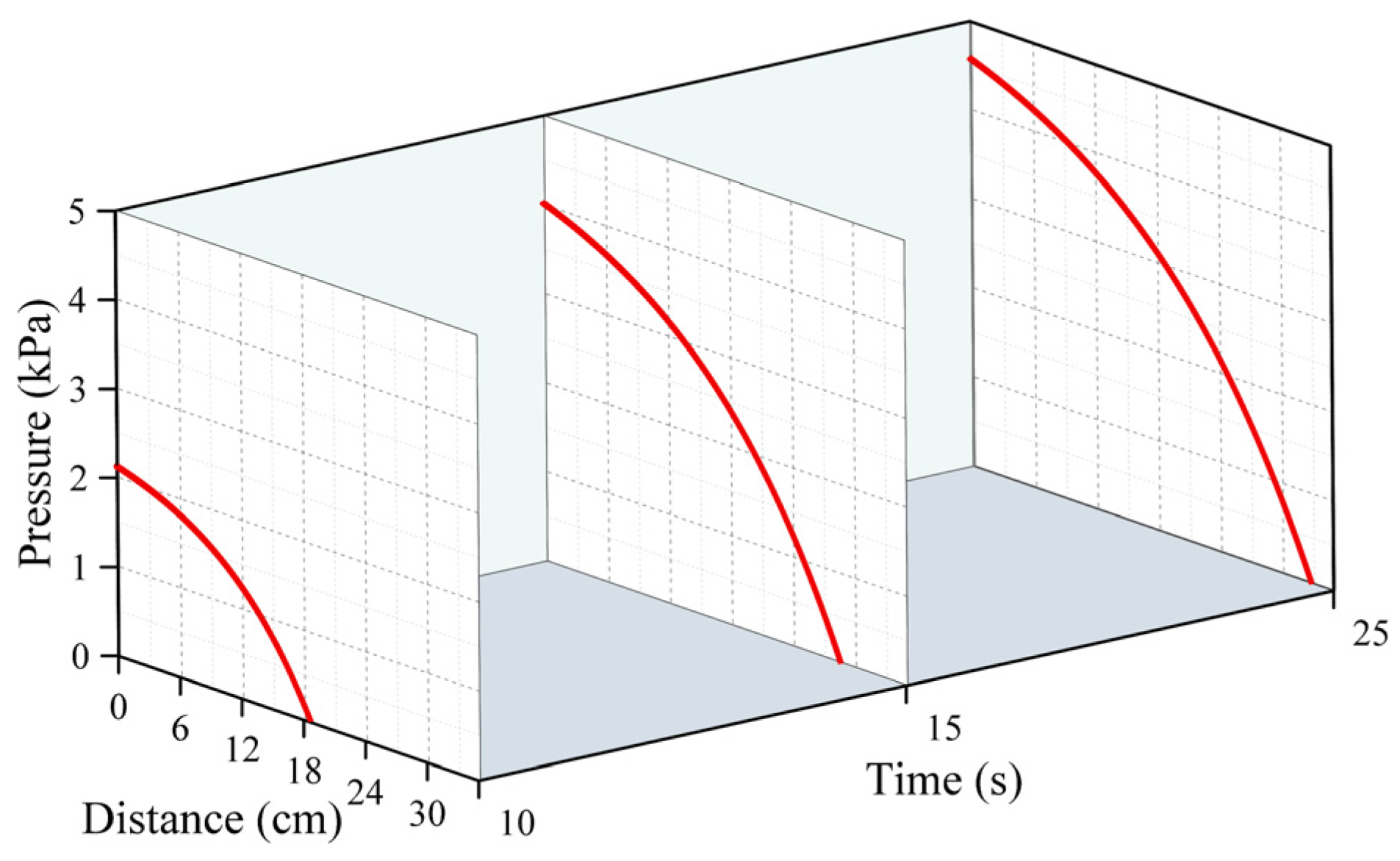
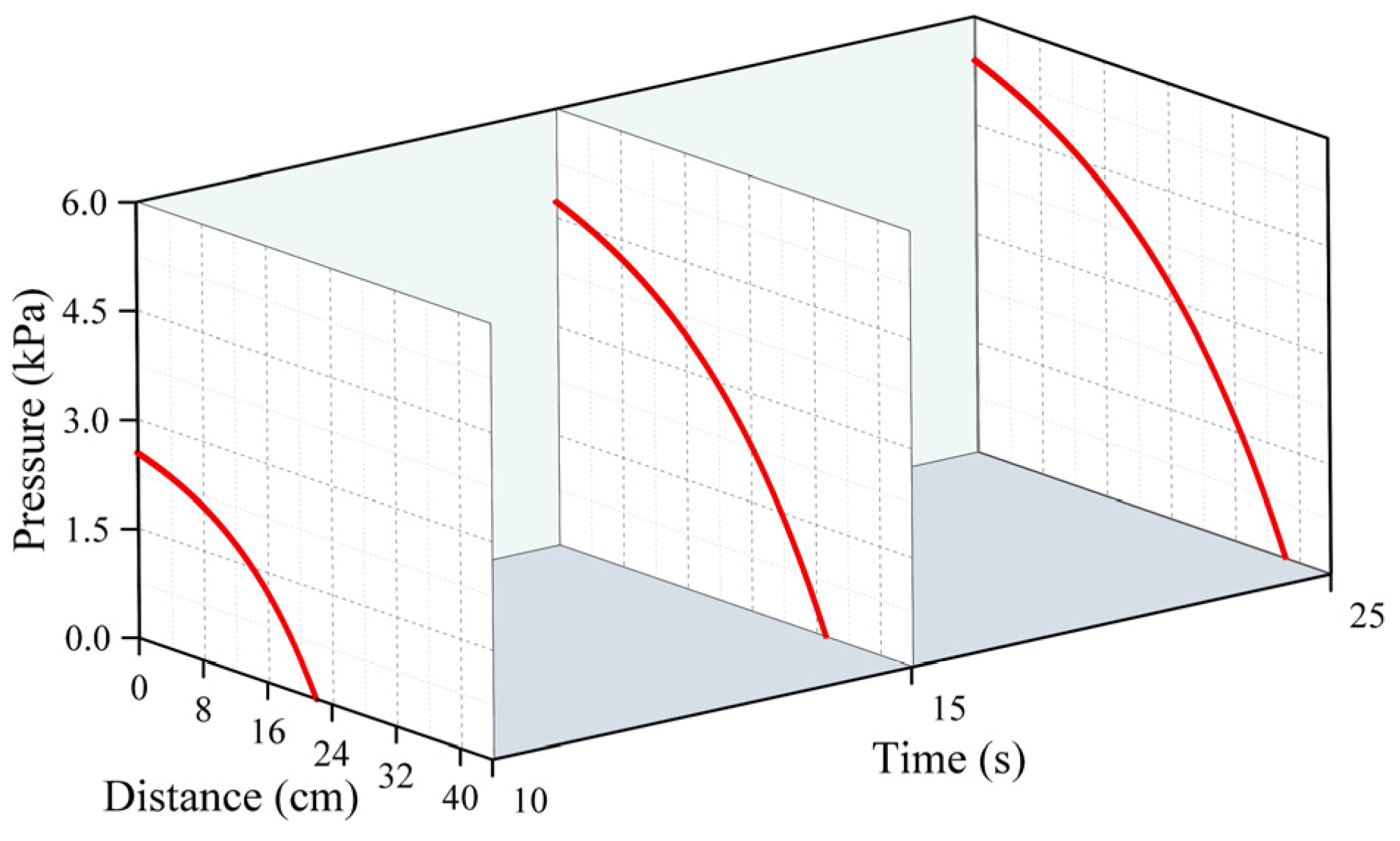
4.1. Distribution of the Pressure Field
4.1.1. Results of the Numerical Calculation of Pressure
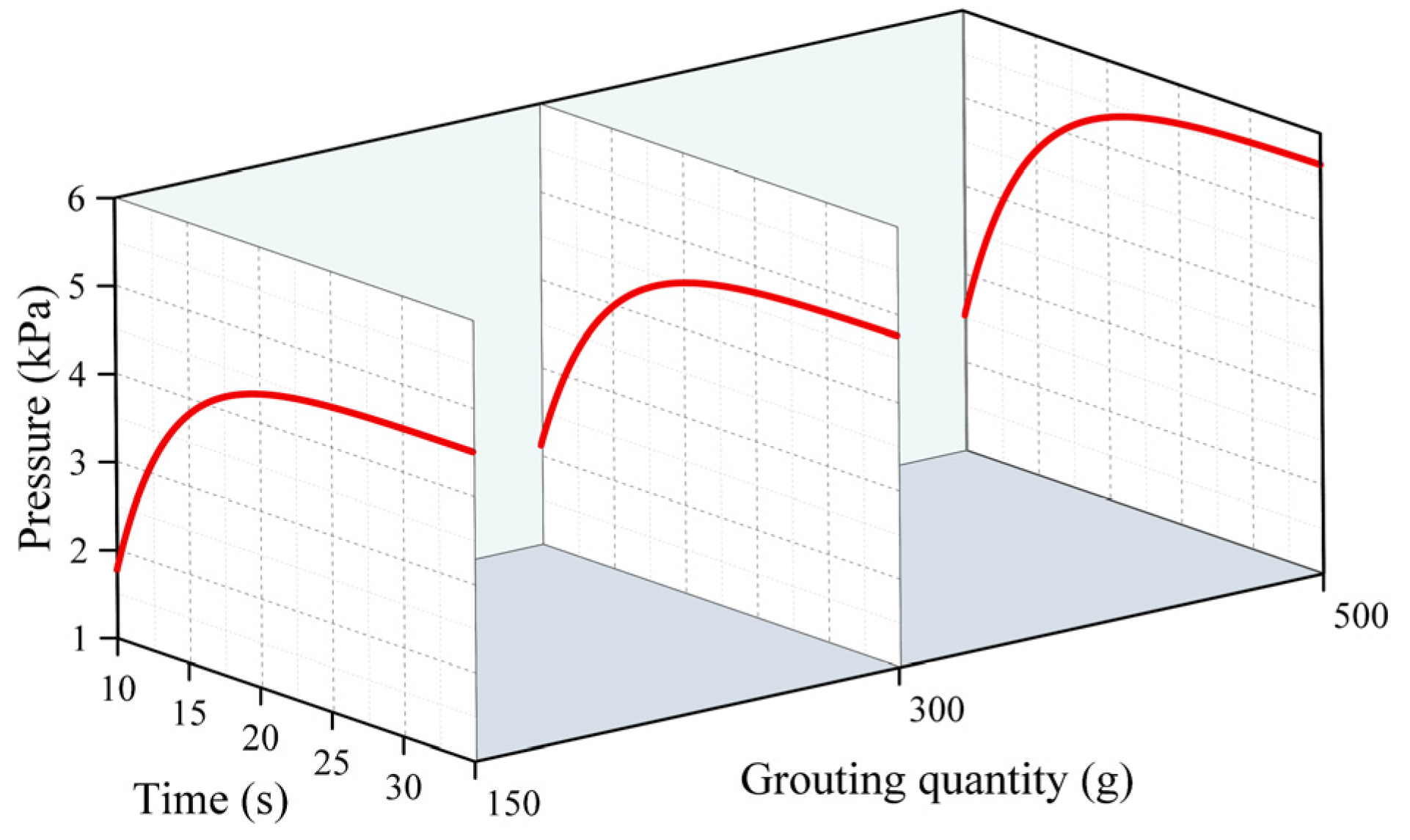
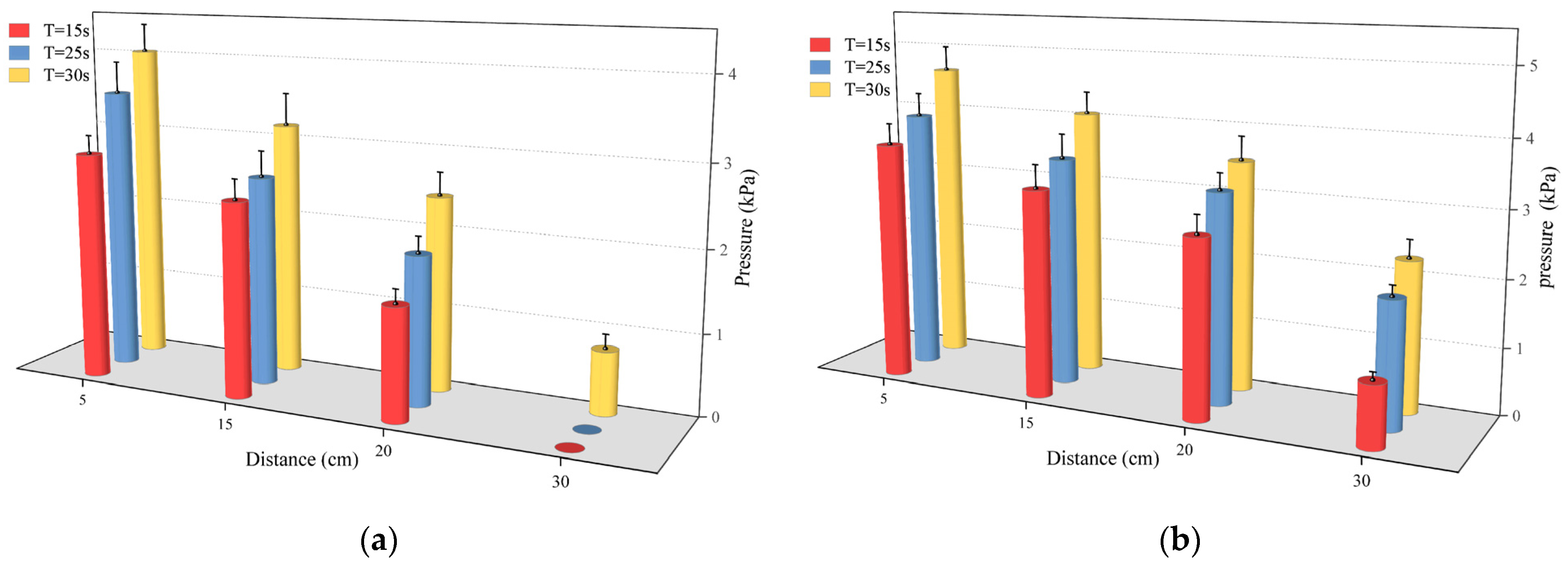
4.1.2. Experimental Analysis of Pressure Field
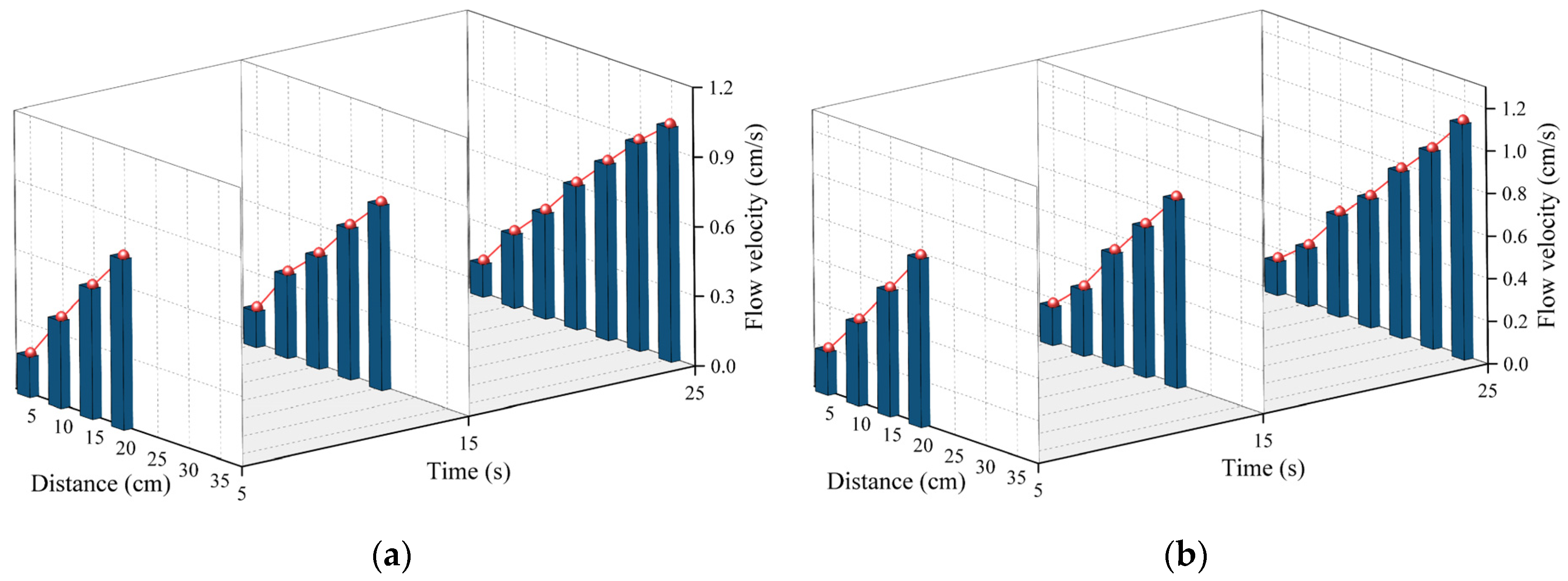
4.2. Distribution of Velocity
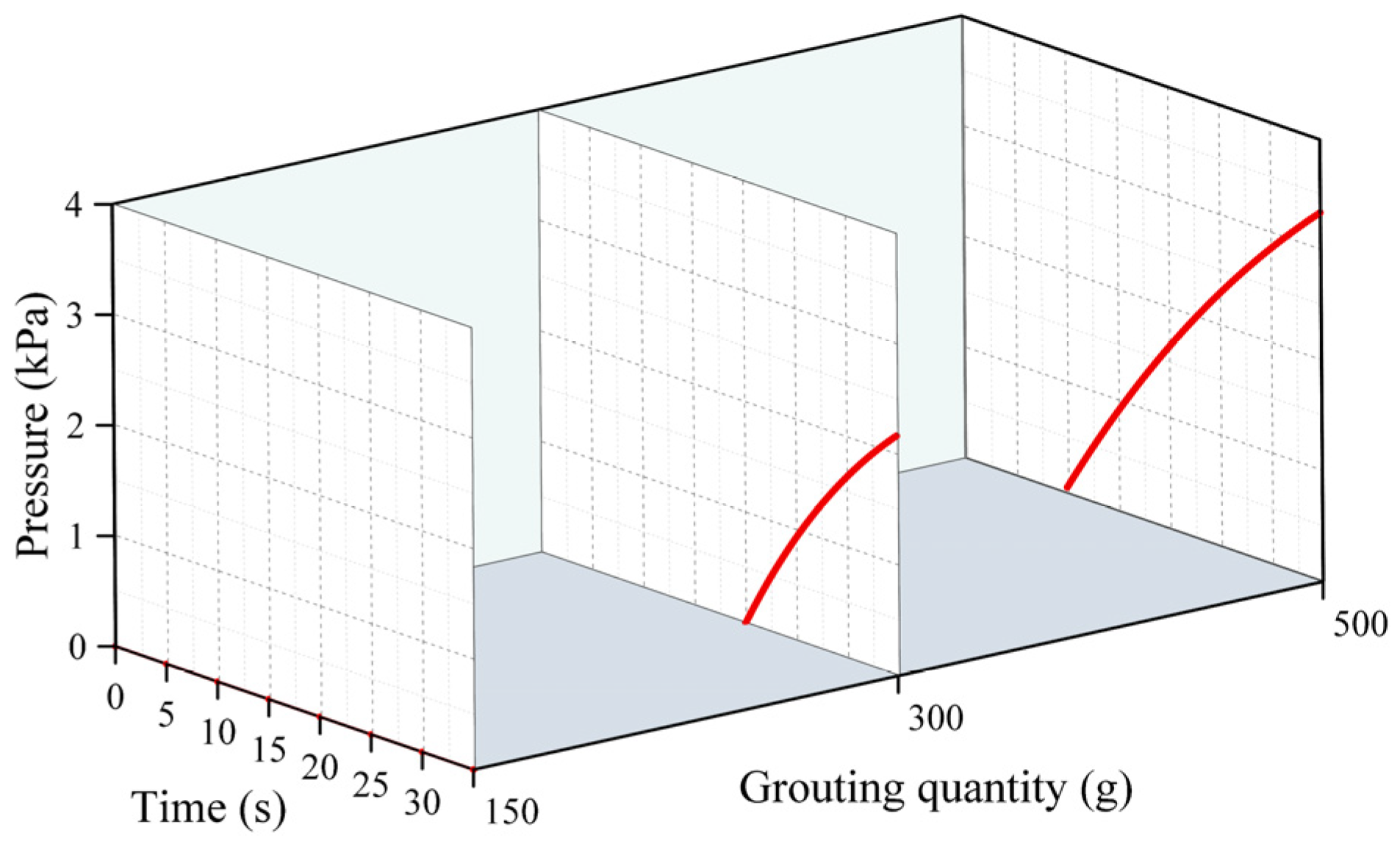
4.3. Movement Distance of the Polymer Slurry
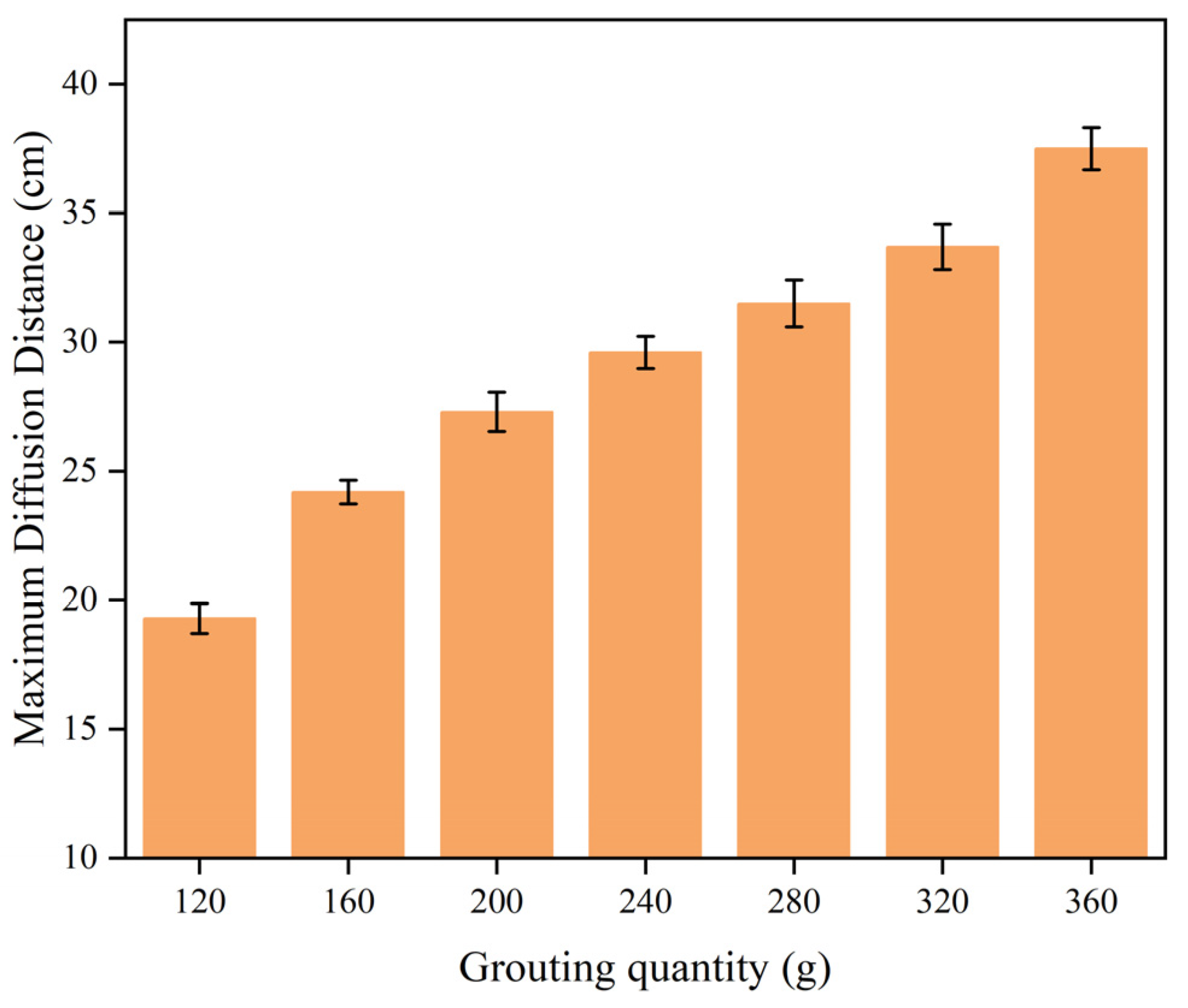
4.3.1. Results of the Numerical Calculation of Movement Distance
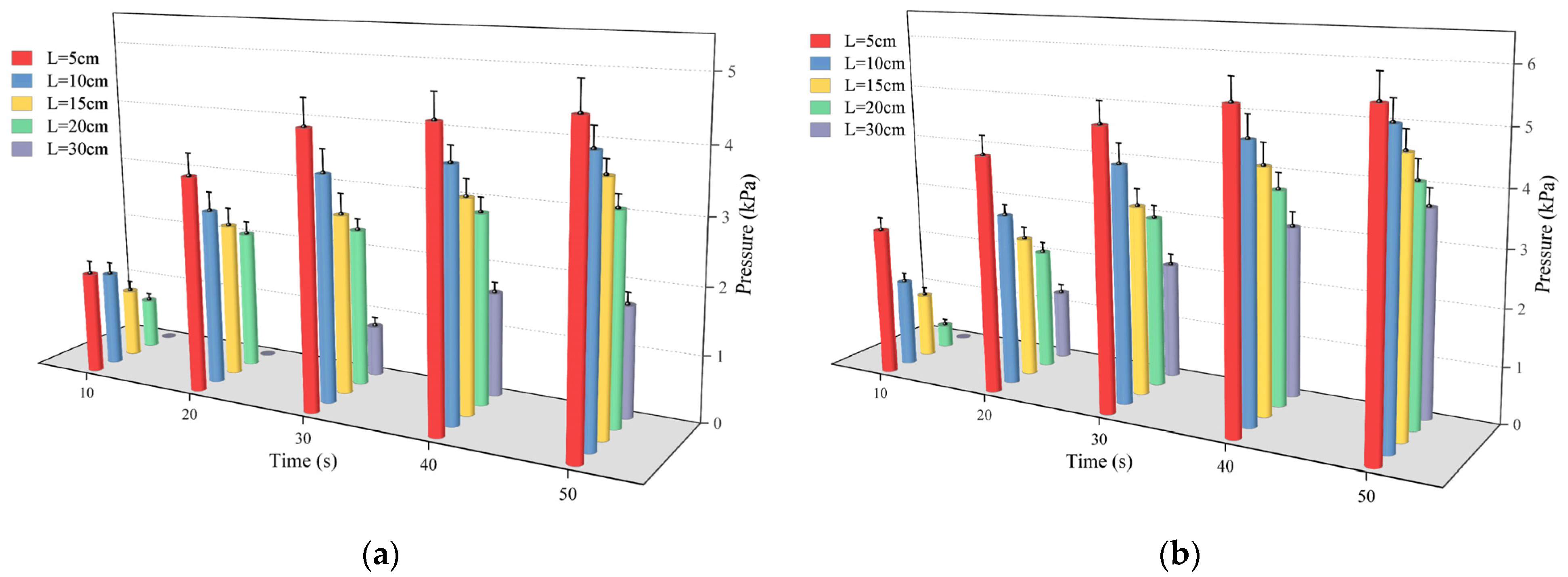
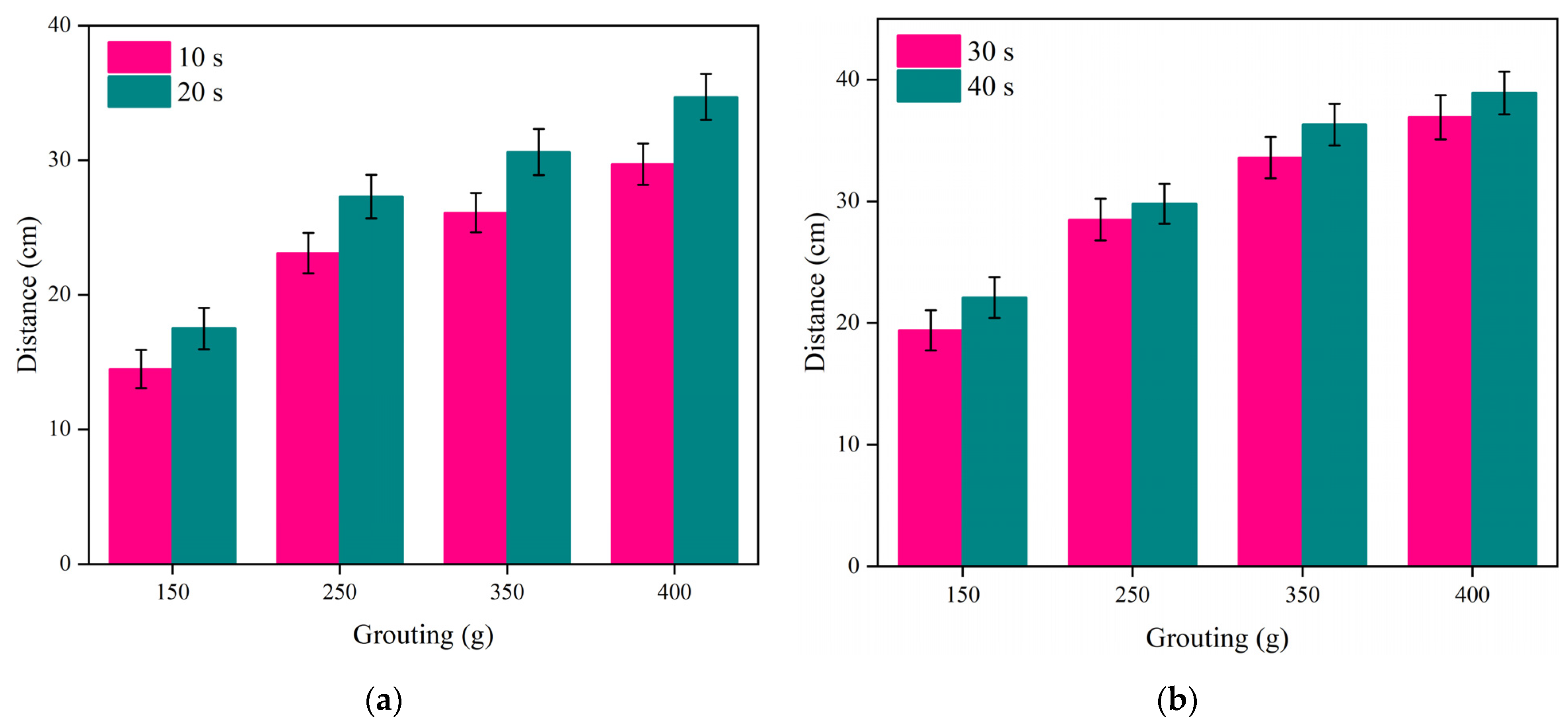
4.3.2. Experimental Analysis of Movement Distance
4.4. Comparison of Experimental and Numerical Results
5. Conclusions
- During the diffusion process of polymer slurry, accompanied by a foaming reaction, a large amount of carbon dioxide was generated, which led to the growth and expansion of bubbles. Therefore, the density of the slurry decreased exponentially with the occurrence of a chemical reaction, from about 1.29 g/cm3 to 0.073 g/cm3 in about half a minute. It was not until the chemical reaction had completed that the density of the polymer could stabilize.
- As the polymer slurry rapidly expanded in a brief timeframe, the pressure of the slurry decreased in a parabolic manner over time. The greater the amount of grouting, the greater the pressure. When the mass of the slurry was 500 g, the maximum pressure of the slurry was up to 5.7 kPa. As the slurry undergoes diffusion movement, the pressure decreases with increasing distance from the slurry injection holes. The location of the slurry’s minimum pressure is observed at the interface between the slurry and air. The slurry’s speed rose steadily as the distance of diffusion increased. Near the grouting hole, the slurry’s speed was low, staying around 0.2 cm/s. The speed was highest at the slurry–air interface, reaching a maximum of 1.1 cm/s.
- The diffusion behavior of polymer slurry in cracks could be divided into three stages: the static pressure injection stage, the slurry’s expansion stage, and the curing stage. The movement distance of polymer slurry was affected by the amount of grouting. With an increase in the amount of grouting, the movement distance of the slurry increased exponentially. When the amount of grouting increased from 120 g to 280 g, the maximum movement distance of the slurry increased by 77%.
- The comparison between the ANSYS FLUENT 2022 R1 simulation’s results and the fissure grouting test’s results revealed a close match in the spreading distance of the slurry, with only a 7% deviation. Additionally, the distribution trend of the pressure field aligned with the test results, validating the numerical simulation method proposed in this study. Although the predictive accuracy of the magnitude of pressure needs to be improved, these studies can still provide theoretical guidance for the application of polymer slurries in underground mine fissure-filling projects.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Izatt, R.M.; Izatt, S.R.; Bruening, R.L.; Izatt, N.E.; Moyer, B.A. Challenges to Achievement of Metal Sustainability in Our High-Tech Society. Chem. Soc. Rev. 2014, 43, 2451–2475. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y.; Cui, N.; Pan, D. Economic and Social Effects Analysis of Mineral Development in China and Policy Implications. Resour. Policy 2013, 38, 448–457. [Google Scholar] [CrossRef]
- Carvalho, F.P. Mining Industry and Sustainable Development: Time for Change. Food Energy Secur. 2017, 6, 61–77. [Google Scholar] [CrossRef]
- Dong, L.; Tong, X.; Li, X.; Zhou, J.; Wang, S.; Liu, B. Some Developments and New Insights of Environmental Problems and Deep Mining Strategy for Cleaner Production in Mines. J. Clean. Prod. 2019, 210, 1562–1578. [Google Scholar] [CrossRef]
- Wu, Q.; Fan, S.; Zhou, W.; Liu, S. Application of the Analytic Hierarchy Process to Assessment of Water Inrush: A Case Study for the No. 17 Coal Seam in the Sanhejian Coal Mine, China. Mine Water Environ. 2013, 32, 229–238. [Google Scholar] [CrossRef]
- Bo, L.; Yang, S.; Liu, Y.; Zhang, Z.; Wang, Y.; Wang, Y. Coal Mine Solid Waste Backfill Process in China: Current Status and Challenges. Sustainability 2023, 15, 13489. [Google Scholar] [CrossRef]
- Bai, E.; Guo, W.; Tan, Y. Negative Externalities of High-Intensity Mining and Disaster Prevention Technology in China. Bull. Eng. Geol. Environ. 2019, 78, 5219–5235. [Google Scholar] [CrossRef]
- Xue, Y.; Kong, F.; Li, S.; Qiu, D.; Su, M.; Li, Z.; Zhou, B. Water and Mud Inrush Hazard in Underground Engineering: Genesis, Evolution and Prevention. Tunn. Undergr. Space Technol. 2021, 114, 103987. [Google Scholar] [CrossRef]
- Fang, H.; Zhao, P.; Zhang, C.; Pan, W.; Yu, Z.; Cai, K.; Wang, C.; Wang, J.; Du, M.; He, W.; et al. A Cleaner Polyurethane Elastomer Grouting Material with High Hardening Strain for the Fundamental Rehabilitation: The Comprehensive Mechanical Properties Study. Constr. Build. Mater. 2022, 318, 125951. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, X.; Wu, M.; Zhao, Y.; Yu, C. Effects of Different Catalysts on the Structure and Properties of Polyurethane/Water Glass Grouting Materials. J. Appl. Polym. Sci. 2018, 135, 46460. [Google Scholar] [CrossRef]
- Wu, L.; Wu, Z.; Weng, L.; Liu, Y.; Liu, Q. Investigation on Basic Properties and Microscopic Mechanisms of Polyacrylate Latex Modified Cement Grouting Material for Water Blocking and Reinforcement. Constr. Build. Mater. 2023, 409, 133872. [Google Scholar] [CrossRef]
- Li, S.; Liu, R.; Zhang, Q.; Zhang, X. Protection against Water or Mud Inrush in Tunnels by Grouting: A Review. J. Rock Mech. Geotech. Eng. 2016, 8, 753–766. [Google Scholar] [CrossRef]
- Ramkumar, V.R.; Murali, G.; Asrani, N.P.; Karthikeyan, K. Development of a Novel Low Carbon Cementitious Two Stage Layered Fibrous Concrete with Superior Impact Strength. J. Build. Eng. 2019, 25, 100841. [Google Scholar] [CrossRef]
- He, Z.; Li, Q.; Wang, J.; Yin, N.; Jiang, S.; Kang, M. Effect of Silane Treatment on the Mechanical Properties of Polyurethane/Water Glass Grouting Materials. Constr. Build. Mater. 2016, 116, 110–120. [Google Scholar] [CrossRef]
- Lee, G.; Cui, M.; Yoon, Y.; Khim, J.; Jang, M. Passive Treatment of Arsenic and Heavy Metals Contaminated Circumneutral Mine Drainage Using Granular Polyurethane Impregnated by Coal Mine Drainage Sludge. J. Clean. Prod. 2018, 186, 282–292. [Google Scholar] [CrossRef]
- Wang, S.; Gong, R.; Li, Z.; Yuan, C.; Jiang, G.; Wang, J.; Chen, L.; Ye, C. Water-Blocking Nano-Composite Cement-Based Grouting Materials. Appl. Nanosci. 2019, 9, 1565–1578. [Google Scholar] [CrossRef]
- Jing, M.; Ni, G.; Zhu, C.; Li, Z.; Wang, G.; Wang, Z.; Huang, Q. Effect of New Modified Materials on the Microscopic Pore Structure and Hydration Characteristics of Sealing Materials in Coal Seam Boreholes. Constr. Build. Mater. 2023, 377, 131076. [Google Scholar] [CrossRef]
- Saleh, S.; Yunus, N.Z.M.; Ahmad, K.; Ali, N. Improving the Strength of Weak Soil Using Polyurethane Grouts: A Review. Constr. Build. Mater. 2019, 202, 738–752. [Google Scholar] [CrossRef]
- Peper, S.; Dohrn, R.; Konejung, K. Methods for the Prediction of Thermophysical Properties of Polyurethane Raw Material Mixtures. Fluid Phase Equilibria 2016, 424, 137–151. [Google Scholar] [CrossRef]
- Zhou, C.; Ren, F.; Wang, Z.; Chen, W.; Wang, W. Why Permeability to Water Is Anomalously Lower than That to Many Other Fluids for Cement-Based Material? Cem. Concr. Res. 2017, 100, 373–384. [Google Scholar] [CrossRef]
- Zhou, K.; Gong, K.; Zhou, Q.; Zhao, S.; Guo, H.; Qian, X. Estimating the Feasibility of Using Industrial Solid Wastes as Raw Material for Polyurethane Composites with Low Fire Hazards. J. Clean. Prod. 2020, 257, 120606. [Google Scholar] [CrossRef]
- Cui, Y.; Tan, Z.; Han, D.; Song, J. Investigation and Application of a High Performance Grouting Material in Water-Rich Silty Fine Sand Stratum. Constr. Build. Mater. 2022, 329, 127100. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, E. Study on the Gelation Process and Mechanical Properties of Organic Polymer Grouting Materials Applied to Fissure Sealing in Underground Mines. Polymers 2024, 16, 446. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zhang, X.; Liu, X.; Guan, X.; Zhang, C.; Niu, Y. Flexible and Stretchable Polyurethane/Waterglass Grouting Material. Constr. Build. Mater. 2017, 138, 240–246. [Google Scholar] [CrossRef]
- Liu, X.; Hu, C.; Liu, Q.; He, J. Grout Penetration Process Simulation and Grouting Parameters Analysis in Fractured Rock Mass Using Numerical Manifold Method. Eng. Anal. Bound. Elem. 2021, 123, 93–106. [Google Scholar] [CrossRef]
- Yan, C.; Tong, Y.; Luo, Z.; Ke, W.; Wang, G. A Two-Dimensional Grouting Model Considering Hydromechanical Coupling and Fracturing for Fractured Rock Mass. Eng. Anal. Bound. Elem. 2021, 133, 385–397. [Google Scholar] [CrossRef]
- Hässler, L.; Håkansson, U.; Stille, H. Computer-Simulated Flow of Grouts in Jointed Rock. Tunn. Undergr. Space Technol. 1992, 7, 441–446. [Google Scholar] [CrossRef]
- Li, X.; Hao, M.; Zhong, Y.; Zhang, B.; Wang, F.; Wang, L. A Quasi-3D Numerical Model for Grout Injection in a Parallel Fracture Based on Finite Volume Method. Complexity 2019, 2019, 4139616. [Google Scholar] [CrossRef]
- Saeidi, O.; Stille, H.; Torabi, S.R. Numerical and Analytical Analyses of the Effects of Different Joint and Grout Properties on the Rock Mass Groutability. Tunn. Undergr. Space Technol. 2013, 38, 11–25. [Google Scholar] [CrossRef]
- Yang, M.J.; Yue, Z.Q.; Lee, P.K.; Su, B.; Tham, L.G. Prediction of Grout Penetration in Fractured Rocks by Numerical Simulation. Can. Geotech. J. 2002, 39, 1384–1394. [Google Scholar] [CrossRef]
- Li, X. An Analytical Solution for the Radial Flow of Variable Density Grout in Rock Fractures. Constr. Build. Mater. 2019, 206, 630–640. [Google Scholar] [CrossRef]
- Li, X.; Hao, M.; Zhong, Y.; Zhang, B.; Wang, F.; Wang, L. Experimental Study on the Diffusion Characteristics of Polyurethane Grout in a Fracture. Constr. Build. Mater. 2021, 273, 121711. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, E. Study on the Diffusion Characteristics of Polymer Grouting Materials Applied for Crack Filling in Underground Mines Based on Numerical Simulation and Experimental Methods. Polymers 2024, 16, 2612. https://doi.org/10.3390/polym16182612
Zhang X, Wang E. Study on the Diffusion Characteristics of Polymer Grouting Materials Applied for Crack Filling in Underground Mines Based on Numerical Simulation and Experimental Methods. Polymers. 2024; 16(18):2612. https://doi.org/10.3390/polym16182612
Chicago/Turabian StyleZhang, Xuanning, and Ende Wang. 2024. "Study on the Diffusion Characteristics of Polymer Grouting Materials Applied for Crack Filling in Underground Mines Based on Numerical Simulation and Experimental Methods" Polymers 16, no. 18: 2612. https://doi.org/10.3390/polym16182612
APA StyleZhang, X., & Wang, E. (2024). Study on the Diffusion Characteristics of Polymer Grouting Materials Applied for Crack Filling in Underground Mines Based on Numerical Simulation and Experimental Methods. Polymers, 16(18), 2612. https://doi.org/10.3390/polym16182612




