Fabrication of Anti-Fatigue Double-Wrapped Yarns with Excellent Mechanical Properties for Generating Compression Fabrics
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Fabrication of Double-Wrapped Yarns
2.3. Fabrication of Weft-Lined Knitted Fabrics
2.4. Characterizations
2.5. Queueing Scoring Rule
2.6. Statistical Evaluation
3. Results and Discussion
3.1. Design of Double-Wrapped Yarns and Weft-Lined Knitted Fabric
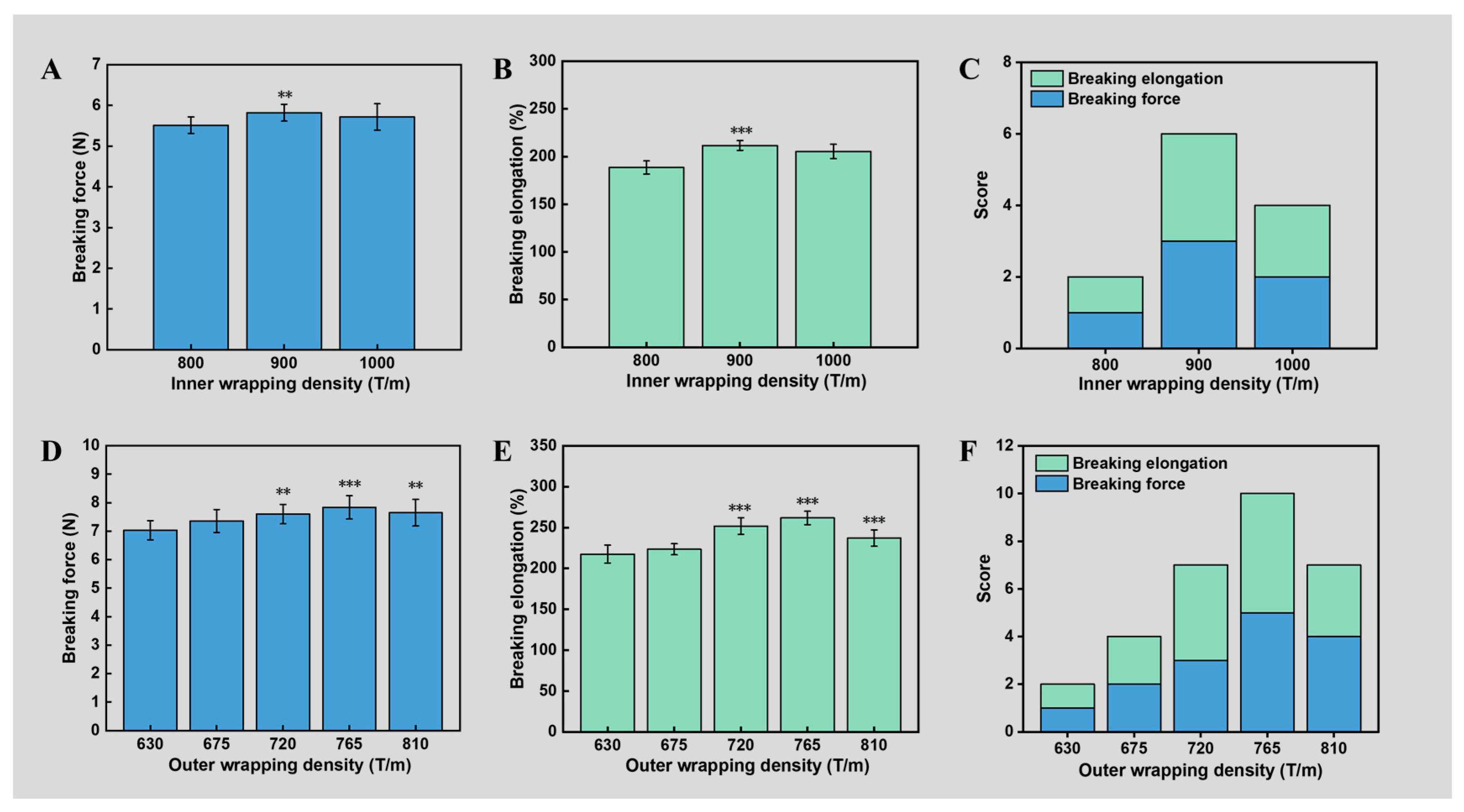
3.2. Effect of the Inner and Outer Wrapping Density on the Mechanical Properties of Double-Wrapped Yarns
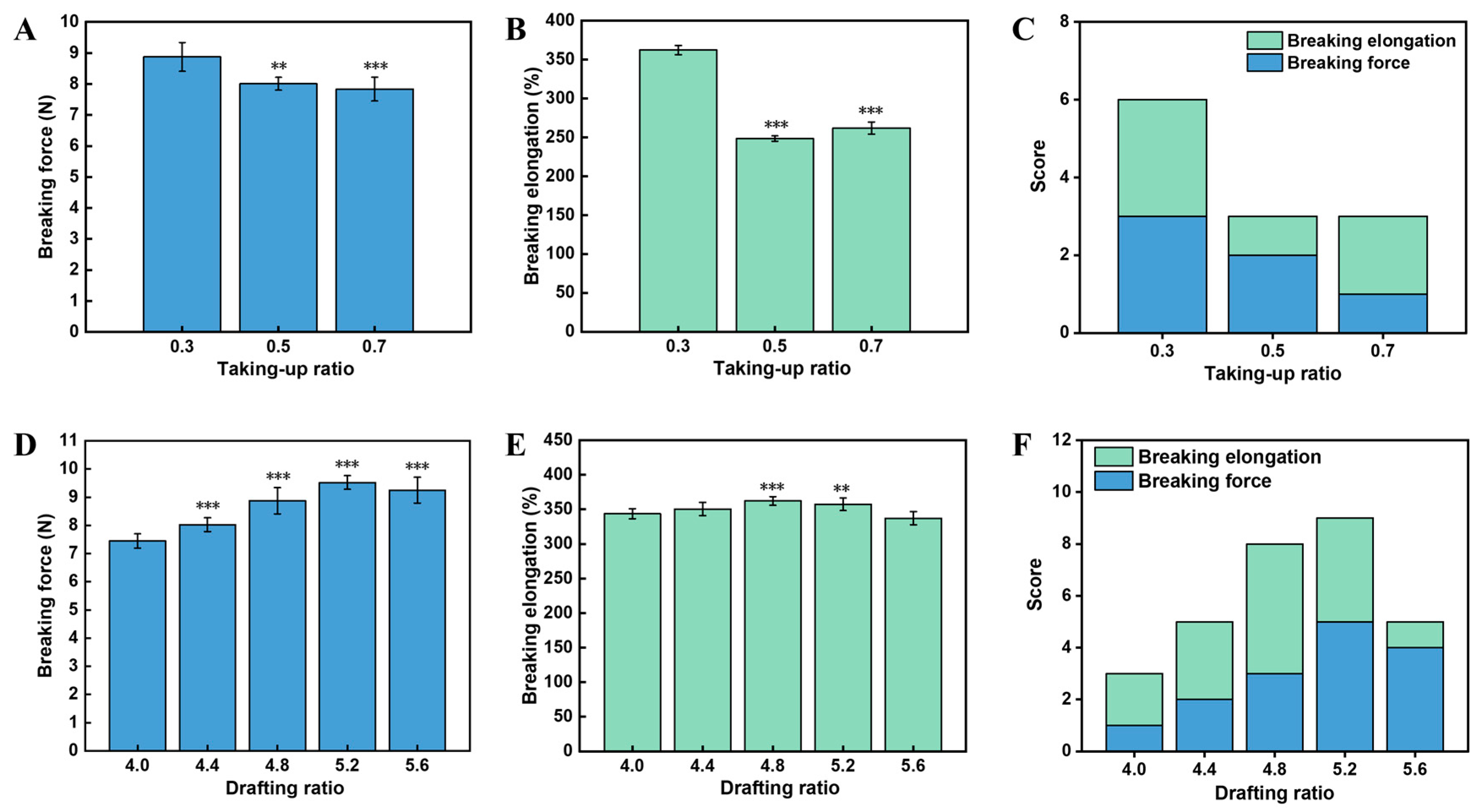
3.3. Effect of the Take-Up and Drafting Ratios on Mechanical Properties of Double-Wrapped Yarns
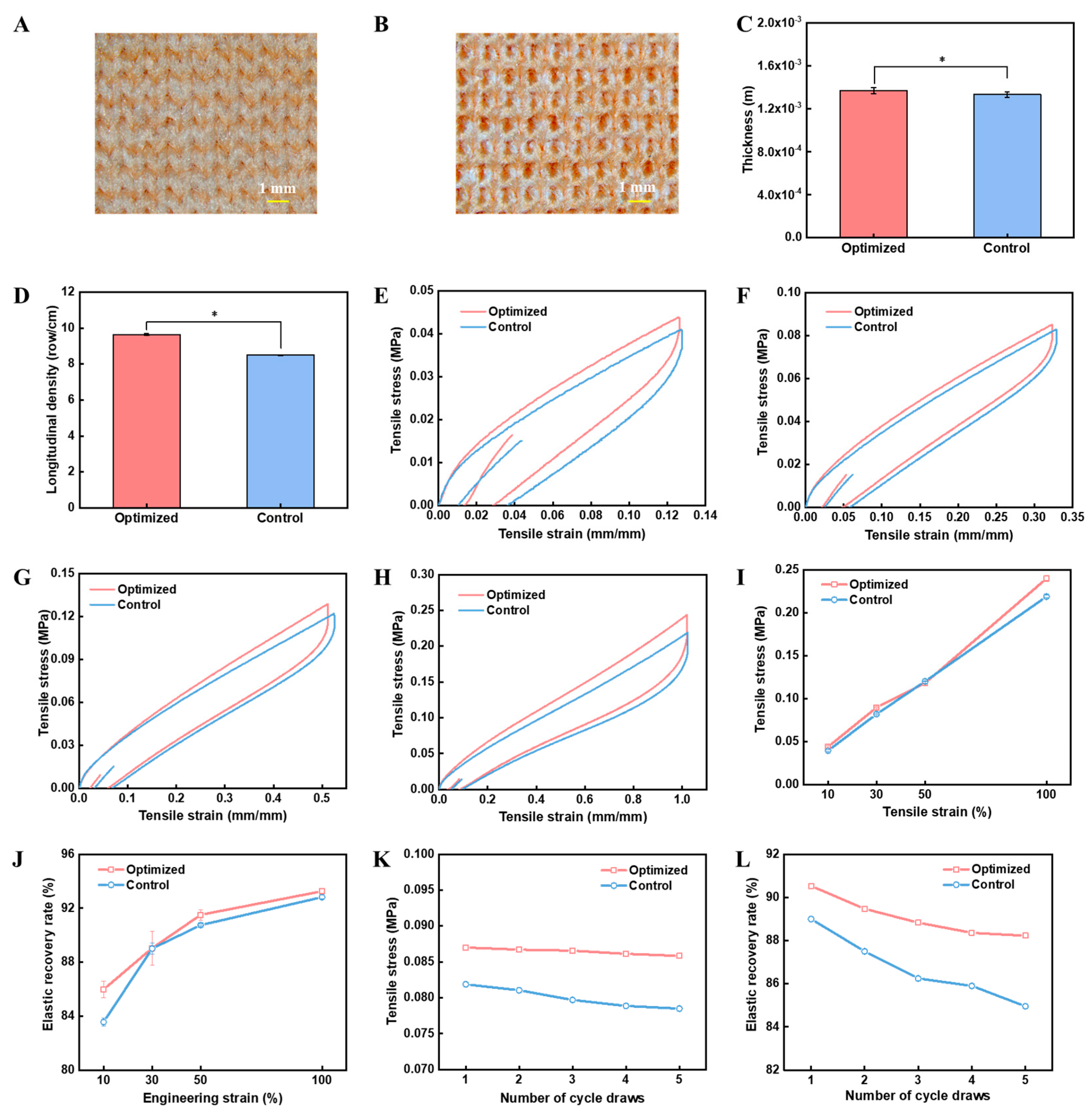
3.4. Comparison of Yarn Mechanical Properties and Knitted Fabrics
4. Conclusions
- (1)
- Yarns with excellent tensile stress (32.59 ± 0.82 MPa) and tensile strain (357.28% ± 9.10%) were obtained when inner and outer wrapping density, the take-up ratio, and drafting ratio of 900 T/m, 765 T/m, 0.3, and 5.2, respectively.
- (2)
- Compared to commercial wrapped yarns and reported data about core-spun and wrapped yarns, the optimized yarns exhibited a higher elastic recovery rate (89.6% ± 0.5%) and a much lower stress decay rate (12.0% ± 2.2%).
- (3)
- Notably, the elastic recovery rate of weft-lined fabrics based on optimized wrapped yarns can be maintained above 85.98% ± 0.62% at any elongation. The stress decay rate can be kept below 10.67% ± 0.15% after five cycles of stretching, indicating that the knitted fabrics are ideal candidates to meet the performance requirements of compression stockings and sleeves.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Mikucioniene, D.; Halavska, L.; Melnyk, L.; Milašius, R.; Laureckiene, G.; Arabuli, S. Classification, Structure and Construction of Functional Orthopaedic Compression Knits for Medical Application: A Review. Appl. Sci. 2024, 14, 4486. [Google Scholar] [CrossRef]
- Ghai, S.; Nilson, F.; Gustavsson, J.; Ghai, I. Influence of compression garments on proprioception: A systematic review and meta-analysis. Ann. N. Y. Acad. Sci. 2024, 1536, 60–81. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Liu, X.; Chen, F.; Zhang, H.; Xiao, X. Numerical Simulation on Crack–Inclusion Interaction for Rib-to-Deck Welded Joints in Orthotropic Steel Deck. Metals 2023, 13, 1402. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, H.; Li, Z.; Luo, Y.; Xiao, X.; Liu, Y. Residual stresses effects on fatigue crack growth behavior of rib-to-deck double-sided welded joints in orthotropic steel decks. Adv. Struct. Eng. 2023, 27, 35–50. [Google Scholar] [CrossRef]
- Weakley, J.; Broatch, J.; O’Riordan, S.; Morrison, M.; Maniar, N.; Halson, S.L. Putting the Squeeze on Compression Garments: Current Evidence and Recommendations for Future Research: A Systematic Scoping Review. Sports Med. 2022, 52, 1141–1160. [Google Scholar] [CrossRef]
- Ye, C.; Liu, R.; Ying, M.T.C.; Liang, F.; Shi, Y. Characterizing the biomechanical transmission effects of elastic compression stockings on lower limb tissues by using 3D finite element modelling. Mater. Des. 2023, 232, 112182. [Google Scholar] [CrossRef]
- Carman, T.L.; Al-Omari, A. Evaluation and Management of Chronic Venous Disease Using the Foundation of CEAP. Curr. Cardiol. Rep. 2019, 21, 114. [Google Scholar] [CrossRef] [PubMed]
- Kankariya, N. Material, structure, and design of textile-based compression devices for managing chronic edema. J. Ind. Text. 2022, 52, 1–35. [Google Scholar] [CrossRef]
- De Decker, I.; Beeckman, A.; Hoeksema, H.; De Mey, K.; Verbelen, J.; De Coninck, P.; Blondeel, P.; Speeckaert, M.M.; Monstrey, S.; Claes, K.E.Y. Pressure therapy for scars: Myth or reality? A systematic review. Burns 2023, 49, 741–756. [Google Scholar] [CrossRef]
- Powell, H.M.; Nedelec, B. Mechanomodulation of Burn Scarring Via Pressure Therapy. Adv. Wound Care 2021, 11, 179–191. [Google Scholar] [CrossRef]
- Play, M.-C.; Trama, R.; Millet, G.Y.; Hautier, C.; Giandolini, M.; Rossi, J. Soft Tissue Vibrations in Running: A Narrative Review. Sports Med. Open 2022, 8, 131. [Google Scholar] [CrossRef]
- Lee, H.; Kim, R.-K.; Chae, W.-S.; Kang, N. Compression Sportswear Improves Speed, Endurance, and Functional Motor Performances: A Meta-Analysis. Appl. Sci. 2023, 13, 13198. [Google Scholar] [CrossRef]
- Yang, C.; Yang, Y.; Xu, Y.; Zhang, Z.; Lake, M.; Fu, W. Whole leg compression garments influence lower limb kinematics and associated muscle synergies during running. Front. Bioeng. Biotechnol. 2024, 12, 1310464. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Tao, X. Compression Garments for Medical Therapy and Sports. Polymers 2018, 10, 663. [Google Scholar] [CrossRef]
- Hu, J.; Lu, J.; Zhu, Y. New Developments in Elastic Fibers. Polym. Rev. 2008, 48, 275–301. [Google Scholar] [CrossRef]
- Wu, J.; Jin, Z.; Jin, J.; Yan, Y.; Tao, J. Study on the tensile modulus of seamless fabric and tight compression finite element modeling. Text. Res. J. 2019, 90, 110–122. [Google Scholar] [CrossRef]
- Bhat, G.; Chand, S.; Yakopson, S. Thermal properties of elastic fibers. Thermochim. Acta 2001, 367–368, 161–164. [Google Scholar] [CrossRef]
- Bansal, P.; Maity, S.; Sinha, S.K. Elastic Recovery and Performance of Denim Fabric Prepared by Cotton/Lycra Core Spun Yarns. J. Nat. Fibers 2020, 17, 1184–1198. [Google Scholar] [CrossRef]
- Lin, J.-H.; Chang, C.-W.; Lou, C.-W.; Hsing, W.-H. Mechanical Properties of Highly Elastic Complex Yarns with Spandex Made by a Novel Rotor Twister. Text. Res. J. 2004, 74, 480–484. [Google Scholar] [CrossRef]
- Helali, H.; Babay, A.D.; Msahli, S. Effect of elastane draft on the rheological modelling of elastane core spun yarn. J. Text. Inst. 2012, 103, 451–457. [Google Scholar] [CrossRef]
- Waseem Ullah Khan, R.M.; Nawab, Y.; Mubeen Safdar, M.; Ayub Asghar, M.; Umair, M. Comparative Geometrical Analysis of In Situ Mechanical Performance of 2-D Woven In-Plane Auxetic Structures. J. Test. Eval. 2023, 51, JTE20230195. [Google Scholar] [CrossRef]
- Babaarslan, O.; Sarıoğlu, E.; Ertek Avcı, M. A comparative study on performance characteristics of multicomponent core-spun yarns containing cotton/PET/elastane. J. Text. Inst. 2020, 111, 775–784. [Google Scholar] [CrossRef]
- Babaarslan, O.; Shahid, M.A.; Doğan, F.B. Design of Hybrid Yarn with the Combination of Fiber and Filaments and Its Effect on the Denim Fabric Performance. Fibres Text. East. Eur. 2023, 31, 25–37. [Google Scholar] [CrossRef]
- Elrys, S.M.E.; Faheem El-Habiby, F.; Abd Elkhalek, R.; Eldeeb, A.S.; El-Hossiny, A.M. Investigation into the effects of yarn structure and yarn count on different types of core-spun yarns. Text. Res. J. 2021, 92, 2285–2297. [Google Scholar] [CrossRef]
- Lou, C.W.; Hu, J.-J.; Lu, P.C.; Lin, J.-H. Effect of twist coefficient and thermal treatment temperature on elasticity and tensile strength of wrapped yarns. Text. Res. J. 2015, 86, 24–33. [Google Scholar] [CrossRef]
- Jin, Z.M.; Ou, Y.; Xu, N.; Yan, Y.X. Pressure Analysis on Medical Compression Hosiery and Property Research of Lycra/Nylon Double Wrapped Yarn. Adv. Mater. Res. 2013, 821–822, 215–218. [Google Scholar] [CrossRef]
- Bera, M.; Chattopadhyay, R.; Gupta, D. Influence of linear density of elastic inlay yarn on pressure generation on human body. J. Ind. Text. 2015, 46, 1053–1066. [Google Scholar] [CrossRef]
- Coghlan, N.; Copley, J.; Aplin, T.; Strong, J. How to improve compression garment wear after burns: Patient and therapist perspectives. Burns 2019, 45, 1447–1455. [Google Scholar] [CrossRef]
- Maleki, H.; Aghajani, M.; Sadeghi, A.H.; Jeddi, A.A.A. On the Pressure Behavior of Tubular Weft Knitted Fabrics Constructed from Textured Polyester Yarns. J. Eng. Fibers Fabr. 2011, 6, 155892501100600204. [Google Scholar] [CrossRef]
- Senthilkumar, M.; Anbumani, N. Dynamics of Elastic Knitted Fabrics for Sports Wear. J. Ind. Text. 2010, 41, 13–24. [Google Scholar] [CrossRef]
- Halfaoui, R.; Chemani, B. The influence of cyclic deformation on the strength and elongation at break of carded and combed wool yarns. J. Text. Inst. 2013, 104, 1156–1163. [Google Scholar] [CrossRef]
- ISO 139:2005; Textiles—Standard Atmospheres for Conditioning and Testing. ISO: Geneva, Switzerland, 2005.
- FZ/T 50006-2013; Testing Method for Tencity of Spandex Filament Yarns. The Standardization Administration of the People’s Republic of China: Beijing, China, 2013.
- GB/T 3916-2013; Textiles—Yarns from Packages—Determination of Single-End Breaking Force and Elongation at Break Using Constant Rate of Extension(CRE) Tester. AQSIQ/SAC: Beijing, China, 2013.
- FZ/T 50007-2012; Testing Method for Elasticty of Spandex Filament Yarns. State Economic and Trade Commission: Beijing, China, 2012.
- FZ/T 70006-2004; Stretch and Recovery Testing Method for Knits. NDRC: Beijing, China, 2004.
- Knoth, S.; Amin, R. Autocorrelation and tolerance limits. J. Stat. Comput. Simul. 2003, 73, 467–489. [Google Scholar] [CrossRef]
- Bruniaux, P.; Crepin, D.; Lun, B. Modeling the mechanics of a medical compression stocking through its components behavior: Part 1—modeling at the yarn scale. Text. Res. J. 2012, 82, 1833–1845. [Google Scholar] [CrossRef]
- Lin, J.-H.; He, C.-H.; Huang, Y.-T.; Lou, C.-W. Functional Elastic Knits Made of Bamboo Charcoal and Quick-Dry Yarns: Manufacturing Techniques and Property Evaluations. Appl. Sci. 2017, 7, 1287. [Google Scholar] [CrossRef]
- Falkner, A.H. Bar Design for Length Compensation in Textile Winding. Text. Res. J. 1994, 64, 351–356. [Google Scholar] [CrossRef]
- Hossain, M.A.; Hossain, M.A.; Emon, J.H.; Islam, M.T. Effect of core material draft ratio and denier on core spun yarn and denim fabric properties pre and post washing. Heliyon 2024, 10, e24965. [Google Scholar] [CrossRef]
- Farajzadeh, Z.; Ghasemi, F.; Mousazadegan, F.; Ezazshahabi, N. Investigation of the Spike Penetration Resistance of the Weft-Knitted Fabrics with Different Elasticity Ratio. Fibers Polym. 2024, 25, 1543–1557. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y.; Yan, T.; Liu, X.; Cao, J.; Du, Z. Influence of re-entrant hexagonal structure and helical auxetic yarn on the tensile and auxetic behavior of parametric fabrics. Text. Res. J. 2021, 92, 2605–2615. [Google Scholar] [CrossRef]
- Yang, R.; Hu, A.; Zhang, X.; Liu, S.; Gao, J.; Lv, Z.; Zhang, H. Viscoelastic tensile model of core/wrapped composite yarn with double filament. Text. Res. J. 2023, 93, 3564–3572. [Google Scholar] [CrossRef]
- Wang, H.; Hazell, P.J.; Shankar, K.; Morozov, E.V.; Jovanoski, Z.; Brown, A.D.; Li, Z.; Escobedo-Diaz, J.P. Tensile properties of ultra-high-molecular-weight polyethylene single yarns at different strain rates. J. Compos. Mater. 2019, 54, 1453–1466. [Google Scholar] [CrossRef]
- Allaer, K.; De Baere, I.; Lava, P.; Van Paepegem, W.; Degrieck, J. On the in-plane mechanical properties of stainless steel fibre reinforced ductile composites. Compos. Sci. Technol. 2014, 100, 34–43. [Google Scholar] [CrossRef]
- Sohanaki, P.; Ahamadloo, E.; Gharehaghaji, A.A.; Malek, R.M.A. Fabrication and characterization of three-layer nanofibrous yarn (PA6/PU/PA6). Polym. Bull. 2022, 79, 7245–7264. [Google Scholar] [CrossRef]
- Liu, S.; Gao, Y.; Chen, X.; Du, Z. A Theoretical Study on the Effect of Structural Parameter on Tensile Properties of Helical Auxetic Yarns. Fibers Polym. 2019, 20, 1742–1748. [Google Scholar] [CrossRef]
- Peng, L.; Zheng, Q.; Li, Y.; Hu, X. Application of viscoelastic-plastic model in blended yarn. Text. Res. J. 2022, 93, 370–381. [Google Scholar] [CrossRef]
- Elrys, S.M.M.E.; El- Habiby, F.F.; Eldeeb, A.S.; El-Hossiny, A.M.; Abd Elkhalek, R. Influence of core yarn structure and yarn count on yarn elastic properties. Text. Res. J. 2022, 92, 3534–3544. [Google Scholar] [CrossRef]
- Jiang, L.; Zulifqar, A.; Hai, A.M.; Anwar, F.; Hu, H.; Liu, F.; Chen, H. Effect of using alternate elastic and non-elastic yarns in warp on shrinkage and stretch behavior of bi-stretch woven fabrics. J. Eng. Fibers Fabr. 2023, 18, 15589250221137897. [Google Scholar] [CrossRef]
- Jovanović, T.; Penava, Ž.; Vrljičak, Z. Impact of the Elastane Percentage on the Elastic Properties of Knitted Fabrics under Cyclic Loading. Materials 2022, 15, 6512. [Google Scholar] [CrossRef]


| Materials | Linear Density | Force (N) | Elongation | Elastic Recovery Rate | Stress Decay Rate | Role |
|---|---|---|---|---|---|---|
| Spandex filament | 560 D | 0.84 ± 0.03 (300%) | —— | 87.5% ± 3.2% | 10.0% ± 1.3% | Core |
| Nylon filament | 70 D/24 f | 3.87 ± 0.09 (Break) | 34.46% ± 2.30% | 21.8% ± 10.2% | 15.7% ± 1.4% | Sheath |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Chen, J.; He, Z.; Liu, W.; Kritchenkov, A.S.; Wang, L.; Liu, W.; Gao, J. Fabrication of Anti-Fatigue Double-Wrapped Yarns with Excellent Mechanical Properties for Generating Compression Fabrics. Polymers 2024, 16, 2476. https://doi.org/10.3390/polym16172476
Zhang Q, Chen J, He Z, Liu W, Kritchenkov AS, Wang L, Liu W, Gao J. Fabrication of Anti-Fatigue Double-Wrapped Yarns with Excellent Mechanical Properties for Generating Compression Fabrics. Polymers. 2024; 16(17):2476. https://doi.org/10.3390/polym16172476
Chicago/Turabian StyleZhang, Qian, Jiaqi Chen, Ziqin He, Wenfu Liu, Andreii S. Kritchenkov, Lu Wang, Wanjun Liu, and Jing Gao. 2024. "Fabrication of Anti-Fatigue Double-Wrapped Yarns with Excellent Mechanical Properties for Generating Compression Fabrics" Polymers 16, no. 17: 2476. https://doi.org/10.3390/polym16172476
APA StyleZhang, Q., Chen, J., He, Z., Liu, W., Kritchenkov, A. S., Wang, L., Liu, W., & Gao, J. (2024). Fabrication of Anti-Fatigue Double-Wrapped Yarns with Excellent Mechanical Properties for Generating Compression Fabrics. Polymers, 16(17), 2476. https://doi.org/10.3390/polym16172476








