A Light-Powered Self-Circling Slider on an Elliptical Track with a Liquid Crystal Elastomer Fiber
Abstract
1. Introduction
2. Theoretical Model and Formulation
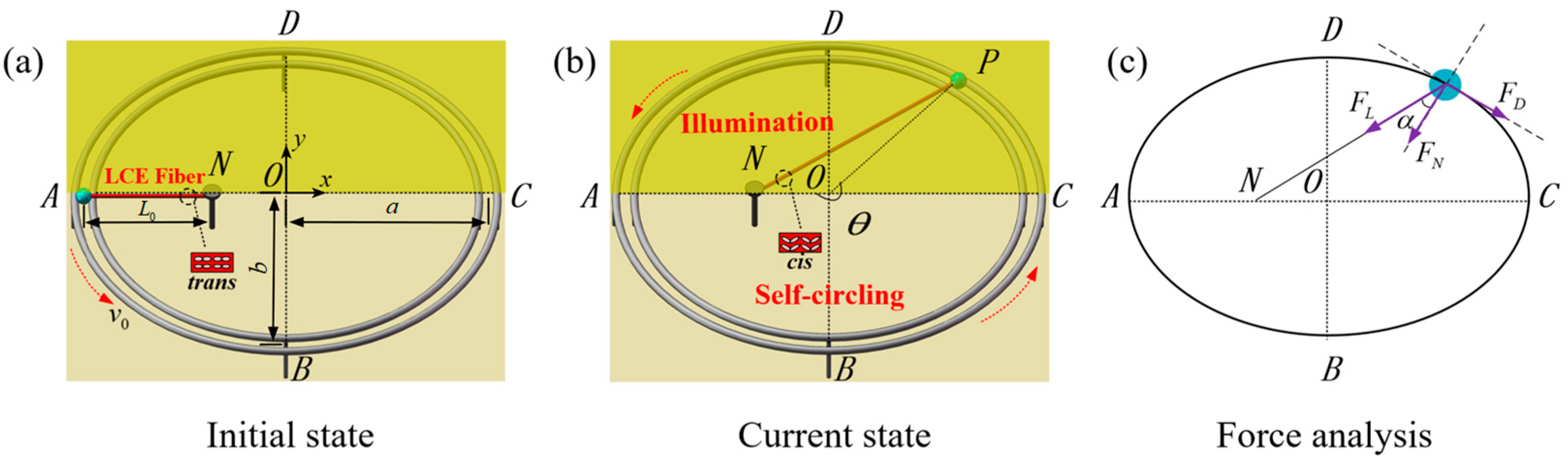
2.1. Dynamics of Self-Circling System
2.2. Dynamic Model of LCE Fiber
2.3. Nondimensionalization
3. Two Dynamic Regimes and Mechanism of Self-Circling
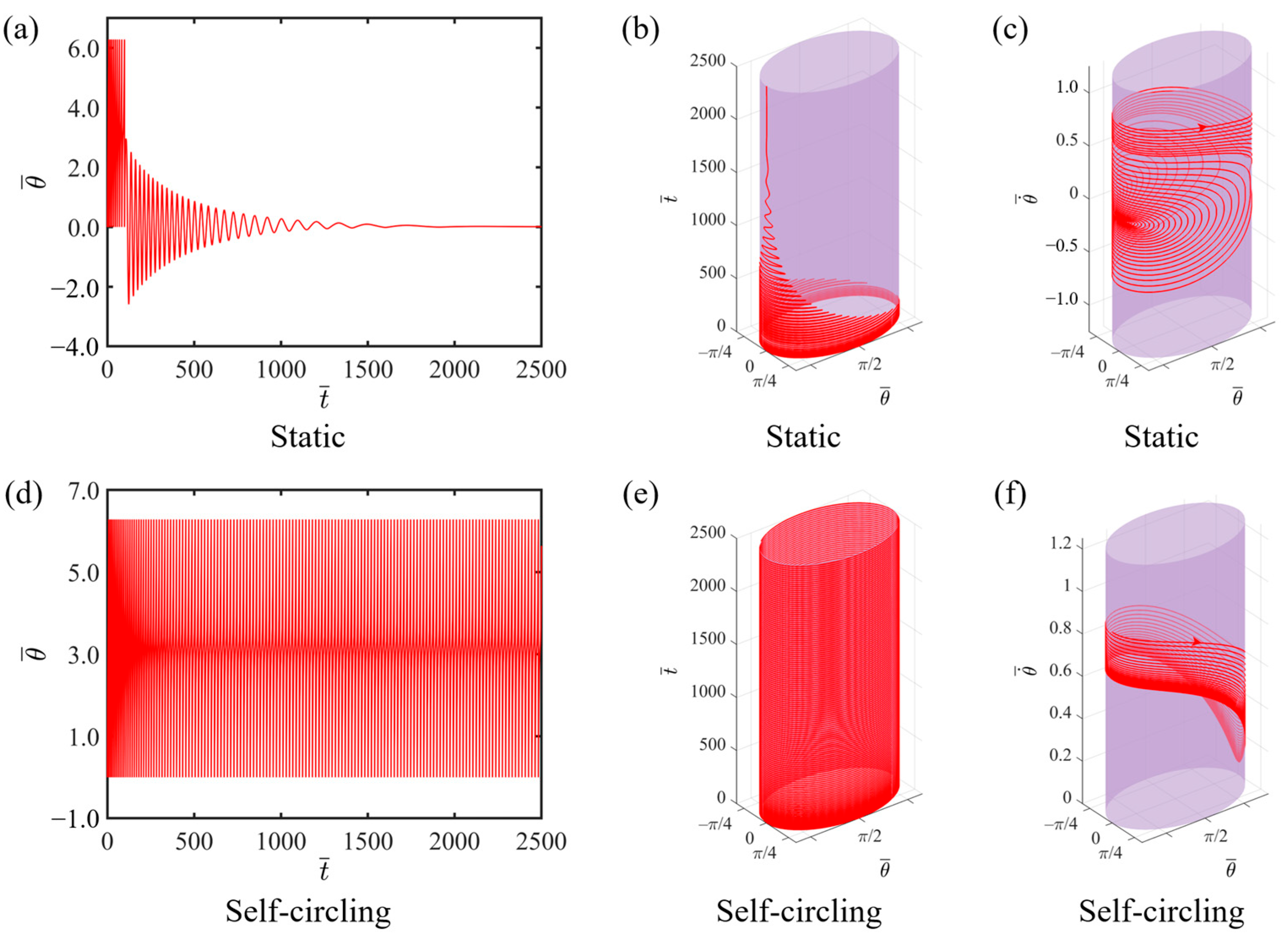
3.1. Two Motion Regimes
3.2. Mechanism of Self-Circling
4. Parameter Study
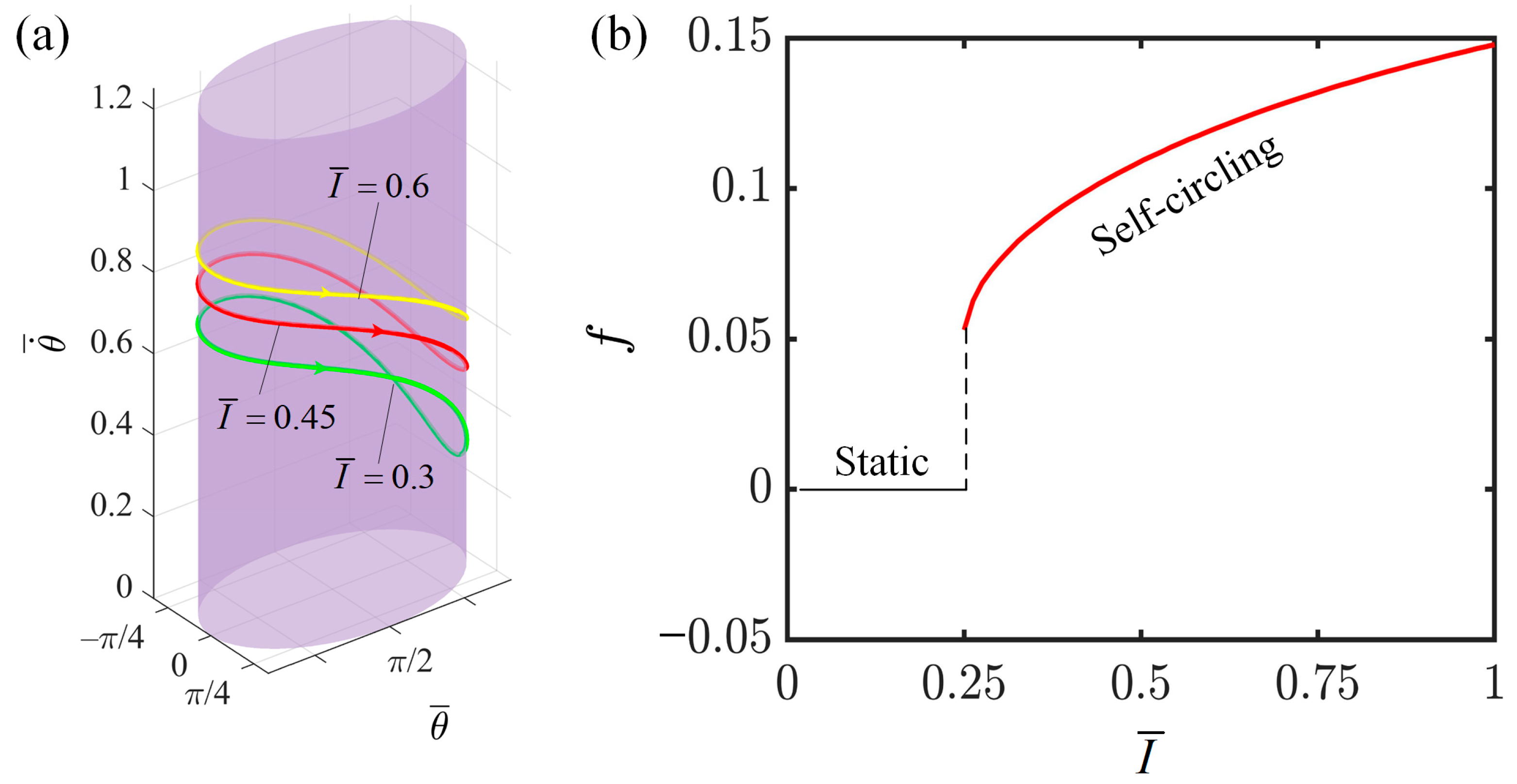
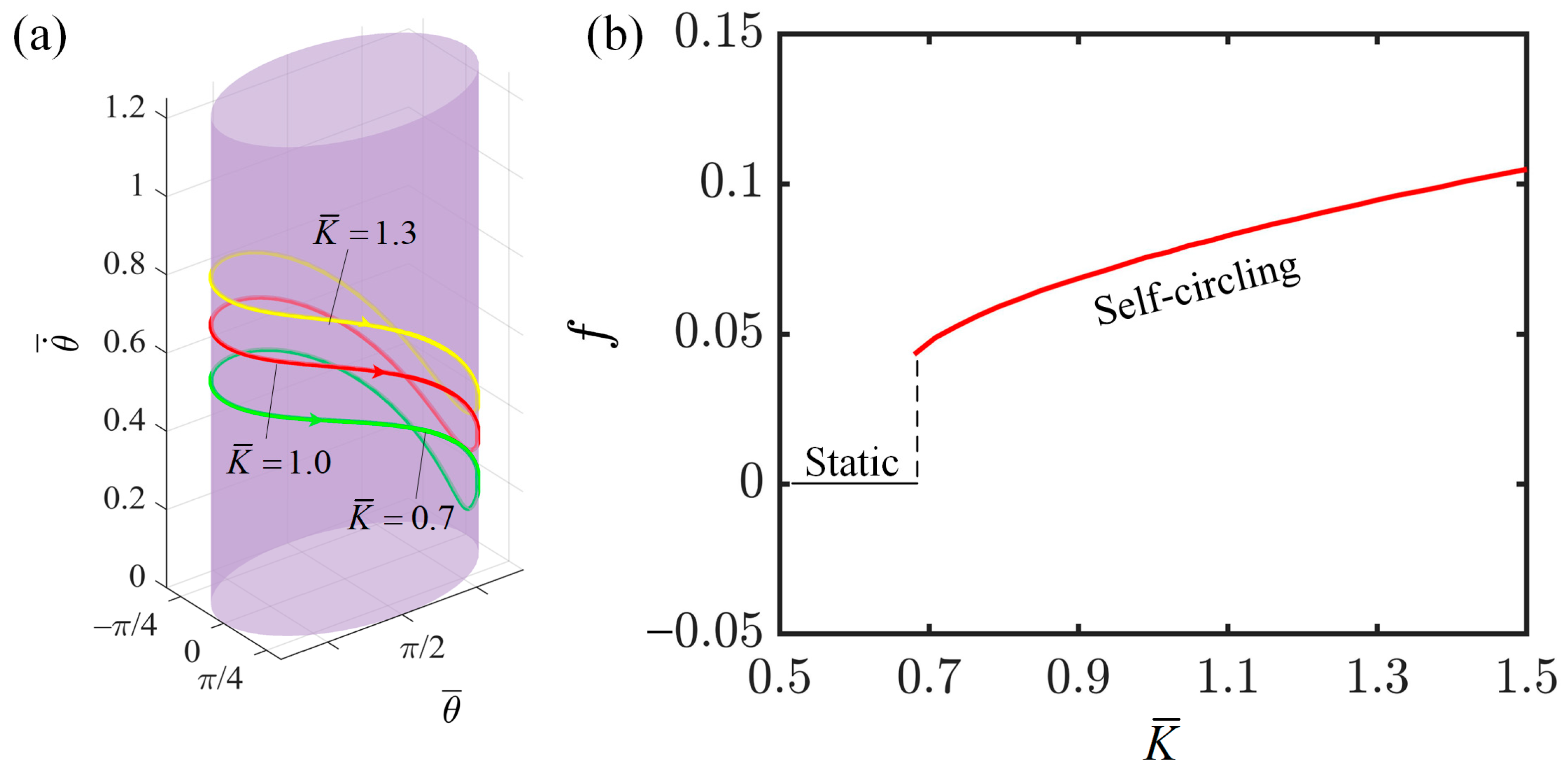
4.1. Effect of Light Intensity
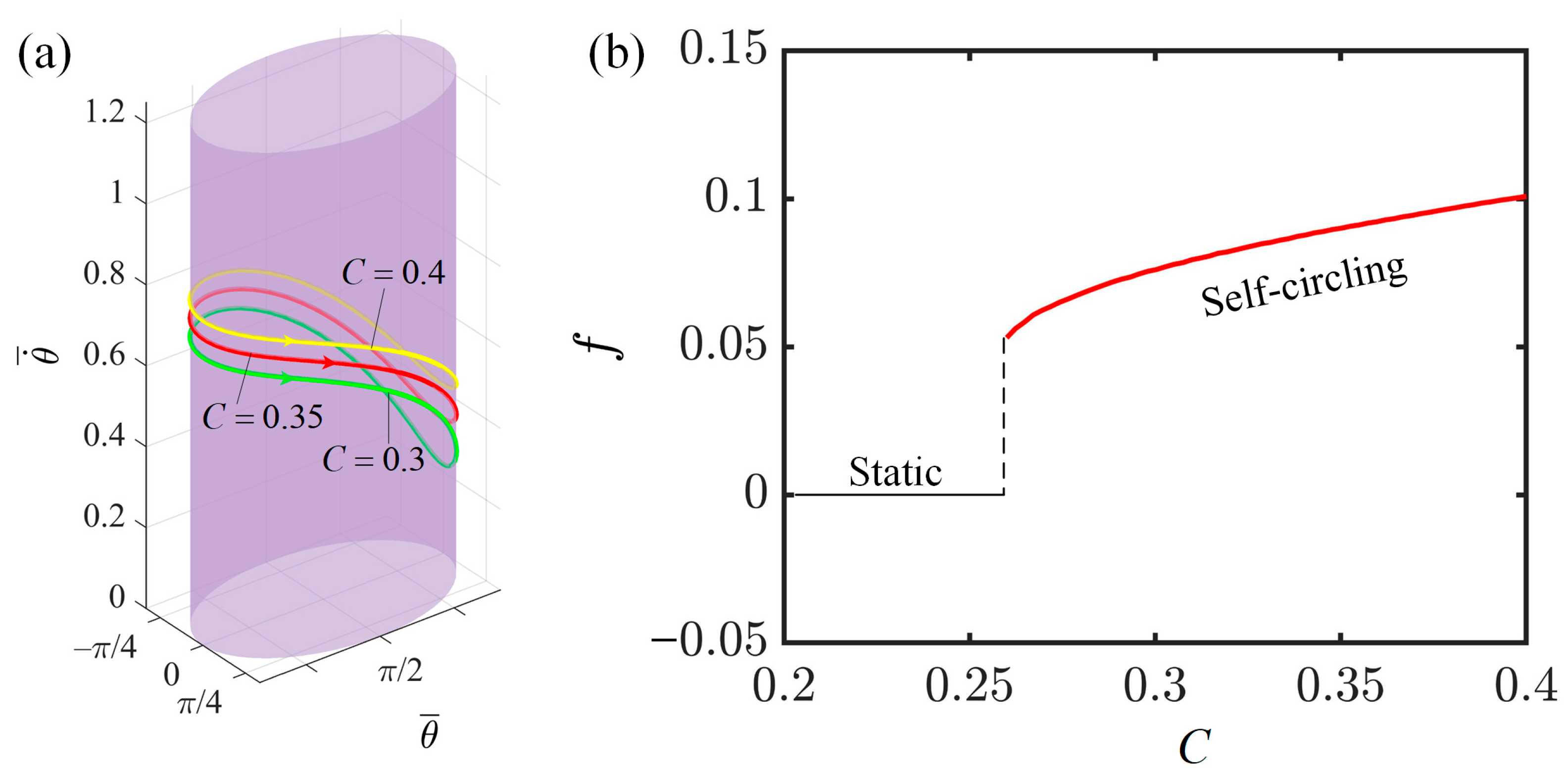
4.2. Effect of Contraction Coefficient of LCE
4.3. Effect of Elastic Coefficient of LCE
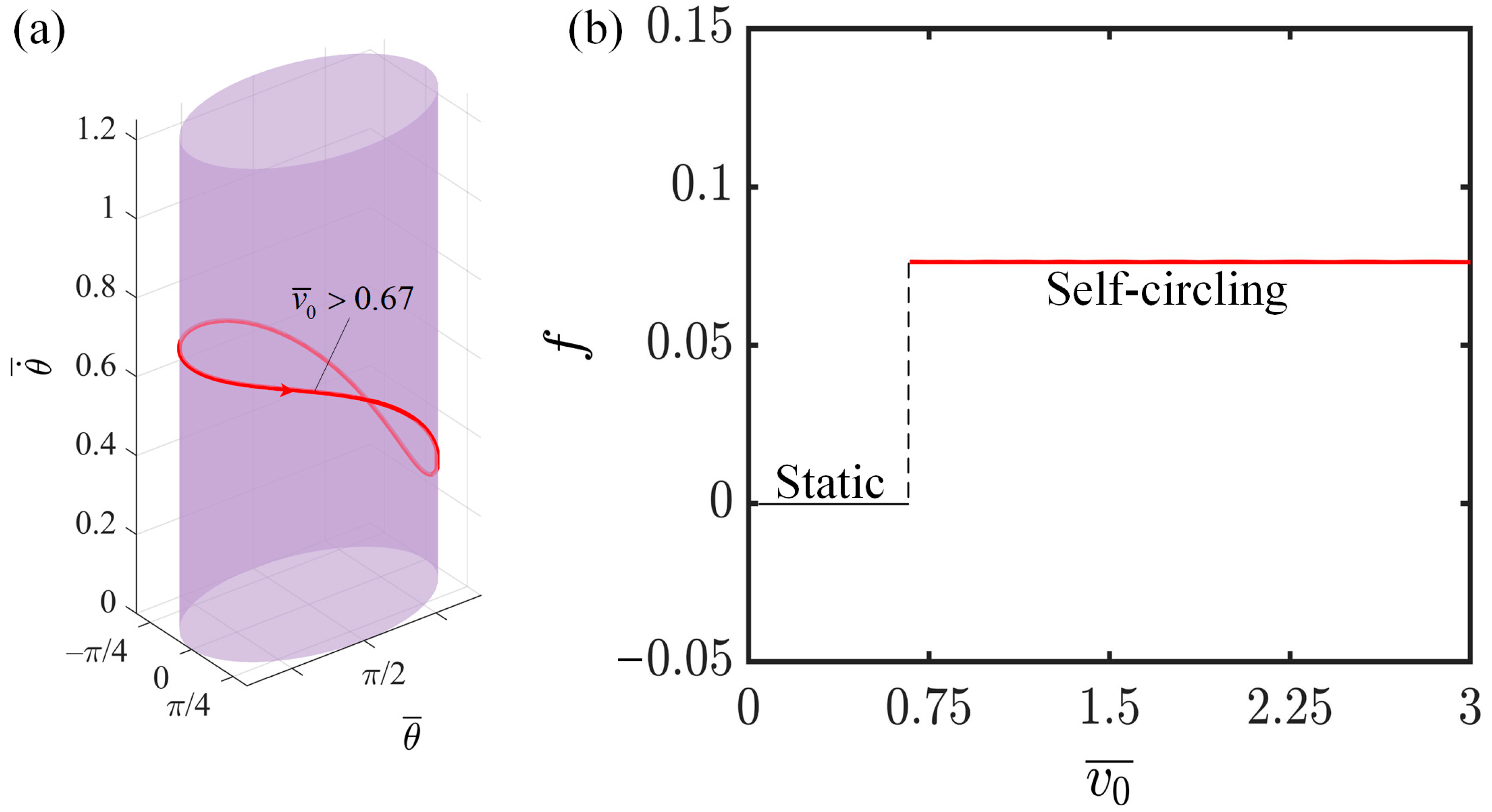
4.4. Effect of Initial Tangential Velocity
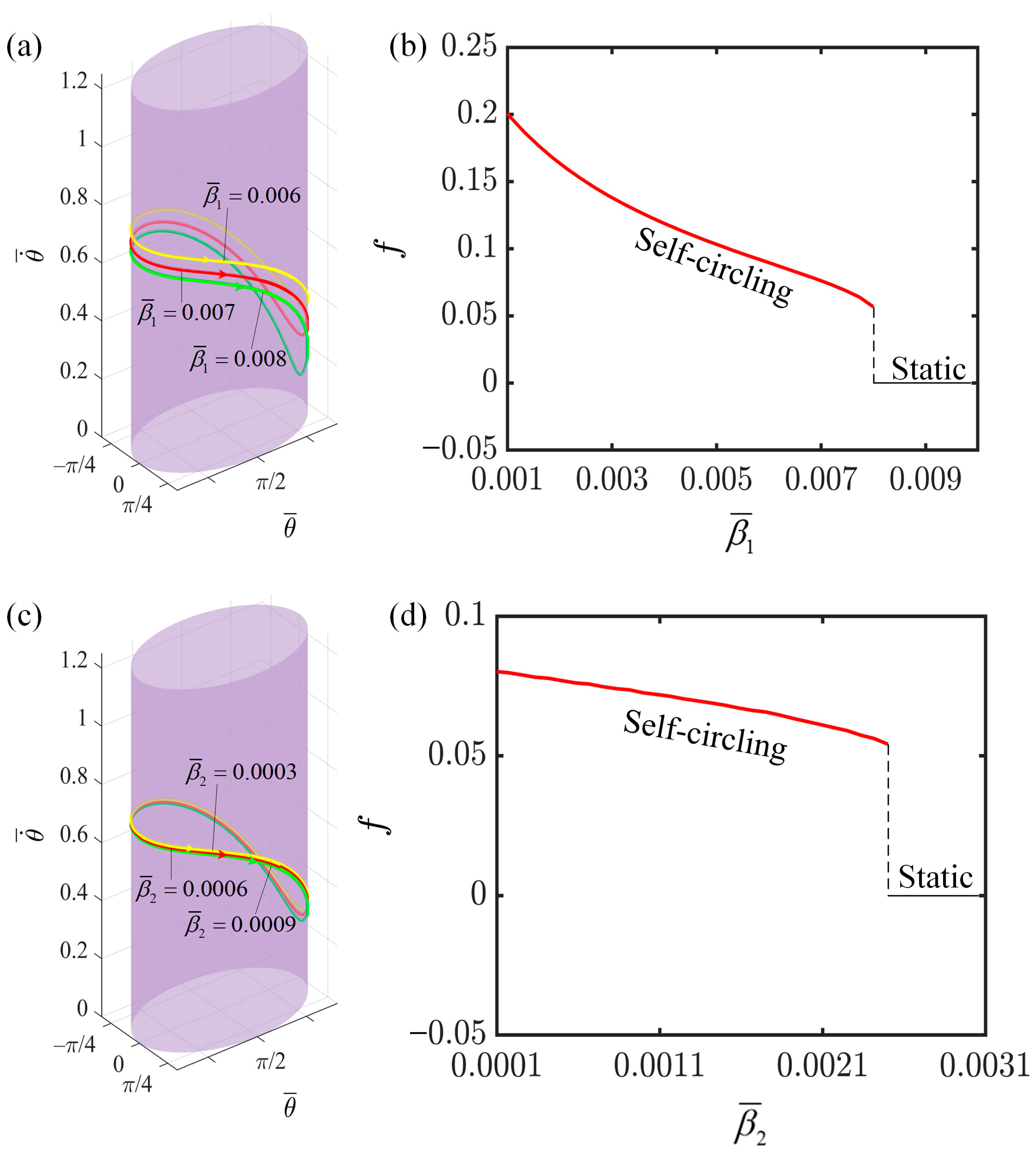
4.5. Effect of the First Damping Coefficient
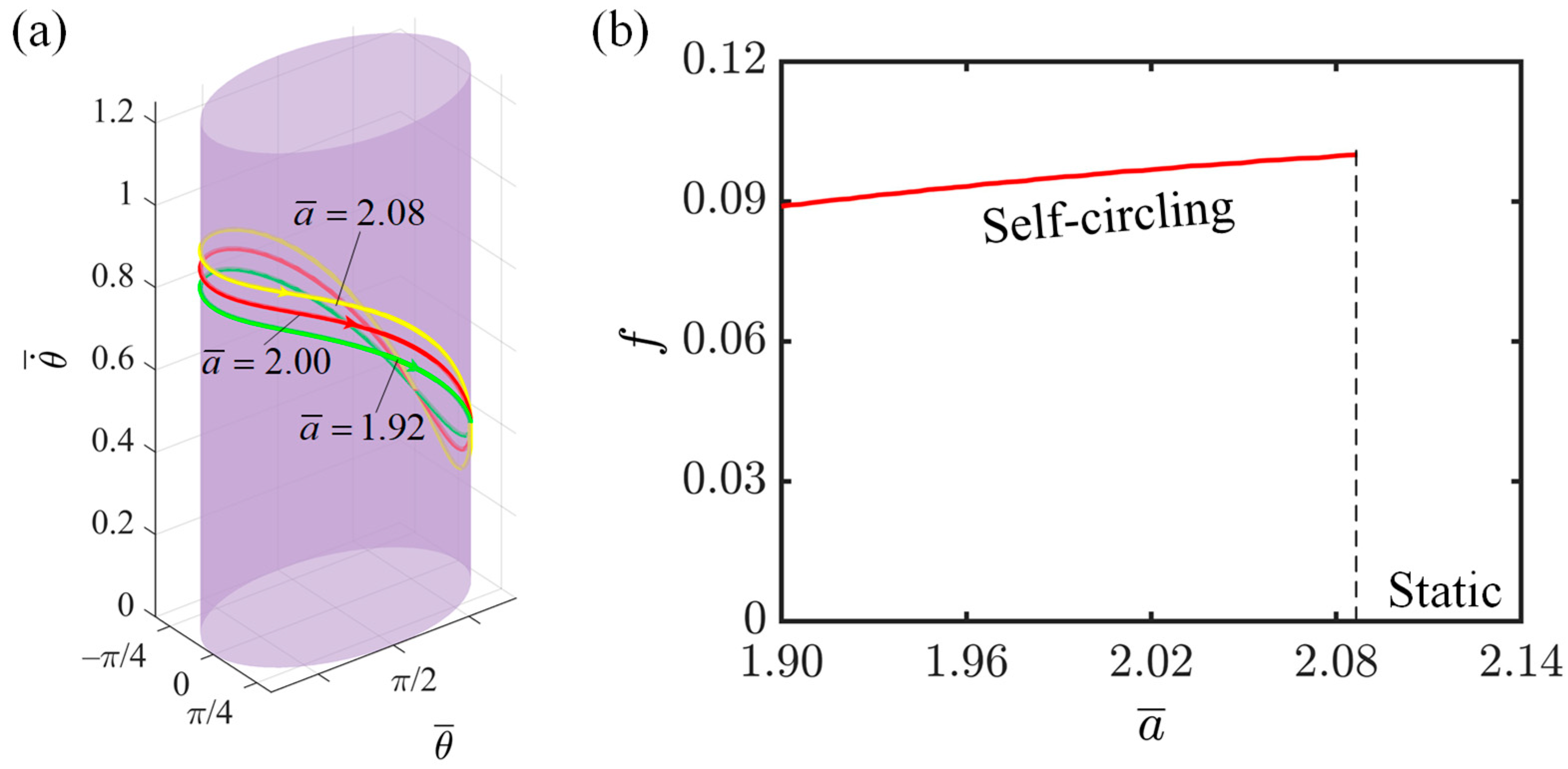
4.6. Effect of Semi-Major Axis
4.7. Effect of Semi-Minor Axis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ge, D.; Dai, Y.; Liang, H.; Li, K. Self-rolling and circling of a conical liquid crystal elastomer rod on a hot surface. Int. J. Mech. Sci. 2024, 263, 108780. [Google Scholar] [CrossRef]
- Ding, W. Self-Excited Vibration; Tsing-Hua University Press: Beijing, China, 2009. [Google Scholar]
- Zhang, Z.; Duan, N.; Lin, C.; Hua, H. Coupled dynamic analysis of a heavily-loaded propulsion shafting system with continuous bearing-shaft friction. Int. J. Mech. Sci. 2020, 172, 105431. [Google Scholar] [CrossRef]
- Kinoshita, S. Introduction to nonequilibrium phenomena. In Pattern Formations and Oscillatory Phenomena; Elsevier: Amsterdam, The Netherlands, 2013; pp. 1–59. [Google Scholar]
- Chakrabarti, A.; Choi, G.P.; Mahadevan, L. Self-excited motions of volatile drops on swellable sheets. Phys. Rev. Lett. 2020, 124, 258002. [Google Scholar] [CrossRef]
- Chun, S.; Pang, C.; Cho, S.B. A micropillar-assisted versatile strategy for highly sensitive and efficient triboelectric energy generation under in-plane stimuli. Adv. Mater. 2020, 32, 1905539. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Tan, C.F.; Chan, K.H.; Lu, X.; Zhu, L.; Kim, S.-W.; Ho, G.W. In-built thermo-mechanical cooperative feedback mechanism for self-propelled multimodal locomotion and electricity generation. Nat. Commun. 2018, 9, 3438. [Google Scholar] [CrossRef]
- Nocentini, S.; Parmeggiani, C.; Martella, D.; Wiersma, D.S. Optically driven soft micro robotics. Adv. Opt. Mater. 2018, 6, 1800207. [Google Scholar] [CrossRef]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Huang, H.; Aida, T. Towards molecular motors in unison. Nat. Nanotechnol. 2019, 14, 407. [Google Scholar] [CrossRef]
- White, T.J.; Broer, D.J. Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 2015, 14, 1087–1098. [Google Scholar] [CrossRef]
- Hines, L.; Petersen, K.; Lum, G.Z.; Sitti, M. Soft actuators for small-scale robotics. Adv. Mater. 2017, 29, 1603483. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Ho, G.W. Design of untethered soft material micromachine for life-like locomotion. Mater. Today 2022, 53, 197–216. [Google Scholar] [CrossRef]
- Graeber, G.; Regulagadda, K.; Hodel, P.; Küttel, C.; Landolf, D.; Schutzius, T.M.; Poulikakos, D. Leidenfrost droplet trampolining. Nat. Commun. 2021, 12, 1727. [Google Scholar] [CrossRef] [PubMed]
- Gelebart, A.H.; Jan Mulder, D.; Varga, M.; Konya, A.; Vantomme, G.; Meijer, E.; Selinger, R.L.; Broer, D.J. Making waves in a photoactive polymer film. Nature 2017, 546, 632–636. [Google Scholar] [CrossRef]
- Vick, D.; Friedrich, L.; Dew, S.; Brett, M.; Robbie, K.; Seto, M.; Smy, T. Self-shadowing and surface diffusion effects in obliquely deposited thin films. Thin Solid Film. 1999, 339, 88–94. [Google Scholar] [CrossRef]
- Lv, X.; Yu, M.; Wang, W.; Yu, H. Photothermal pneumatic wheel with high loadbearing capacity. Compos. Commun. 2021, 24, 100651. [Google Scholar] [CrossRef]
- Lendlein, A.; Jiang, H.; Jünger, O.; Langer, R. Light-induced shape-memory polymers. Nature 2005, 434, 879–882. [Google Scholar] [CrossRef]
- Bubnov, A.; Domenici, V.; Hamplová, V.; Kašpar, M.; Zalar, B. First liquid single crystal elastomer containing lactic acid derivative as chiral co-monomer: Synthesis and properties. Polymer 2011, 52, 4490–4497. [Google Scholar] [CrossRef]
- Kim, H.; Sundaram, S.; Kang, J.-H.; Tanjeem, N.; Emrick, T.; Hayward, R.C. Coupled oscillation and spinning of photothermal particles in Marangoni optical traps. Proc. Natl. Acad. Sci USA 2021, 118, e2024581118. [Google Scholar] [CrossRef]
- Fu, L.; Zhao, W.; Ma, J.; Yang, M.; Liu, X.; Zhang, L.; Chen, Y. A humidity-powered soft robot with fast rolling locomotion. Research 2022, 2022, 9832901. [Google Scholar] [CrossRef]
- Ge, D.; Liang, H.; Li, K. Self-oscillation of a liquid crystal elastomer string-mass system under constant gradient temperature. J. Appl. Mech. 2024, 91, 101001. [Google Scholar] [CrossRef]
- Ge, F.; Yang, R.; Tong, X.; Camerel, F.; Zhao, Y. A multifunctional dye-doped liquid crystal polymer actuator: Light-guided transportation, turning in locomotion, and autonomous motion. Angew. Chem. 2018, 130, 11932–11937. [Google Scholar] [CrossRef]
- Hara, Y. Function and autonomous behavior of self-oscillating polymer systems. Polymers 2014, 6, 1958–1971. [Google Scholar] [CrossRef]
- Shin, B.; Ha, J.; Lee, M.; Park, K.; Park, G.H.; Choi, T.H.; Cho, K.-J.; Kim, H.-Y. Hygrobot: A self-locomotive ratcheted actuator powered by environmental humidity. Sci. Robot. 2018, 3, eaar2629. [Google Scholar] [CrossRef]
- Liao, B.; Zang, H.; Chen, M.; Wang, Y.; Lang, X.; Zhu, N.; Yang, Z.; Yi, Y. Soft rod-climbing robot inspired by winding locomotion of snake. Soft Robot. 2020, 7, 500–511. [Google Scholar] [CrossRef]
- Yamada, M.; Kondo, M.; Mamiya, J.i.; Yu, Y.; Kinoshita, M.; Barrett, C.J.; Ikeda, T. Photomobile polymer materials: Towards light-driven plastic motors. Angew. Chem. Int. Ed. 2008, 47, 4986–4988. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, H.; Mao, J.; Chirarattananon, P.; Helbling, E.F.; Hyun, N.-s.P.; Clarke, D.R.; Wood, R.J. Controlled flight of a microrobot powered by soft artificial muscles. Nature 2019, 575, 324–329. [Google Scholar] [CrossRef]
- Wehner, M.; Truby, R.L.; Fitzgerald, D.J.; Mosadegh, B.; Whitesides, G.M.; Lewis, J.A.; Wood, R.J. An integrated design and fabrication strategy for entirely soft, autonomous robots. Nature 2016, 536, 451–455. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, Y. A prototype for light-electric harvester based on light sensitive liquid crystal elastomer cantilever. Energy 2020, 198, 117351. [Google Scholar] [CrossRef]
- Serak, S.; Tabiryan, N.; Vergara, R.; White, T.J.; Vaia, R.A.; Bunning, T.J. Liquid crystalline polymer cantilever oscillators fueled by light. Soft Matter 2010, 6, 779–783. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Lu, H.C.; Lee, X.; Zeng, H.; Priimagi, A. Kirigami-based light-induced shape-morphing and locomotion. Adv. Mater. 2020, 32, 1906233. [Google Scholar] [CrossRef]
- Castagna, R.; Riminesi, C.; Pianesi, M.S.; Sabbatini, S.; Di Donato, A.; Singh, G.; Francescangeli, O.; Cantisani, E.; Castellini, P.; Lucchetta, D.E. Development of a Quartz-Based Photo-Mobile Polymer Film for Controlled Motion Triggered by Light or Heat. Materials 2023, 16, 3046. [Google Scholar] [CrossRef]
- Lucchetta, D.E.; Castellini, P.; Martarelli, M.; Scalise, L.; Pandarese, G.; Riminesi, C.; Singh, G.; Di Donato, A.; Francescangeli, O.; Castagna, R. Light-Controlled Rotational Speed of an Acoustically Levitating Photomobile Polymer Film. Materials 2023, 16, 553. [Google Scholar] [CrossRef]
- Rothemund, P.; Ainla, A.; Belding, L.; Preston, D.J.; Kurihara, S.; Suo, Z.; Whitesides, G.M. A soft, bistable valve for autonomous control of soft actuators. Sci. Robot. 2018, 3, eaar7986. [Google Scholar] [CrossRef]
- Yang, L.; Miao, J.; Li, G.; Ren, H.; Zhang, T.; Guo, D.; Tang, Y.; Shang, W.; Shen, Y. Soft tunable gelatin robot with insect-like claw for grasping, transportation, and delivery. ACS Appl. Polym. Mater. 2022, 4, 5431–5440. [Google Scholar] [CrossRef]
- Li, M.H.; Keller, P.; Li, B.; Wang, X.; Brunet, M. Light-driven side-on nematic elastomer actuators. Adv. Mater. 2003, 15, 569–572. [Google Scholar] [CrossRef]
- Lahikainen, M.; Zeng, H.; Priimagi, A. Reconfigurable photoactuator through synergistic use of photochemical and photothermal effects. Nat. Commun. 2018, 9, 4148. [Google Scholar] [CrossRef]
- Yang, L.; Chang, L.; Hu, Y.; Huang, M.; Ji, Q.; Lu, P.; Liu, J.; Chen, W.; Wu, Y. An autonomous soft actuator with light-driven self-sustained wavelike oscillation for phototactic self-locomotion and power generation. Adv. Funct. Mater. 2020, 30, 1908842. [Google Scholar] [CrossRef]
- Chen, B.; Liu, C.; Xu, Z.; Wang, Z.; Xiao, R. Modeling the thermo-responsive behaviors of polydomain and monodomain nematic liquid crystal elastomers. Mech. Mater. 2024, 188, 104838. [Google Scholar] [CrossRef]
- Wang, Y.; Dang, A.; Zhang, Z.; Yin, R.; Gao, Y.; Feng, L.; Yang, S. Repeatable and reprogrammable shape morphing from photoresponsive gold nanorod/liquid crystal elastomers. Adv. Mater. 2020, 32, 2004270. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Guo, Y.; Hu, W.; Soon, R.H.; Davidson, Z.S.; Sitti, M. Liquid crystal elastomer-based magnetic composite films for reconfigurable shape-morphing soft miniature machines. Adv. Mater. 2021, 33, 2006191. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Liao, W.; Yang, Z. Ultrafast, high-contractile electrothermal-driven liquid crystal elastomer fibers towards artificial muscles. Small 2021, 17, 2103700. [Google Scholar] [CrossRef]
- Liao, W.; Yang, Z. The integration of sensing and actuating based on a simple design fiber actuator towards intelligent soft robots. Adv. Mater. Technol. 2022, 7, 2101260. [Google Scholar] [CrossRef]
- Lan, R.; Shen, W.; Yao, W.; Chen, J.; Chen, X.; Yang, H. Bioinspired humidity-responsive liquid crystalline materials: From adaptive soft actuators to visualized sensors and detectors. Mater. Horiz. 2023, 10, 2824–2844. [Google Scholar] [CrossRef]
- Shokrollahi, H.; Janghorban, K. Soft magnetic composite materials (SMCs). J. Mater. Process. Technol. 2007, 189, 1–12. [Google Scholar] [CrossRef]
- Le Bideau, J.; Viau, L.; Vioux, A. Ionogels, ionic liquid based hybrid materials. Chem. Soc. Rev. 2011, 40, 907–925. [Google Scholar] [CrossRef]
- Dai, L.; Wang, L.; Chen, B.; Xu, Z.; Wang, Z.; Xiao, R. Shape memory behaviors of 3D printed liquid crystal elastomers. Soft Sci. 2023, 3, 4. [Google Scholar] [CrossRef]
- Wang, L.; Wei, Z.; Xu, Z.; Yu, Q.; Wu, Z.; Wang, Z.; Qian, J.; Xiao, R. Shape morphing of 3D printed liquid crystal elastomer structures with precuts. ACS Appl. Polym. Mater. 2023, 5, 7477–7484. [Google Scholar] [CrossRef]
- Hager, M.D.; Bode, S.; Weber, C.; Schubert, U.S. Shape memory polymers: Past, present and future developments. Prog. Polym. Sci. 2015, 49, 3–33. [Google Scholar] [CrossRef]
- Yoshida, R. Self-oscillating gels driven by the Belousov–Zhabotinsky reaction as novel smart materials. Adv. Mater. 2010, 22, 3463–3483. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, C.; Chen, B.; Wang, Z.; Xu, Y.; Xiao, R. Bioinspired design of stimuli-responsive artificial muscles with multiple actuation modes. Smart Mater. Struct. 2023, 32, 085023. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, R.; Jin, L.; Liu, M.; Gao, Y.; Raney, J.; Yang, S. 3D-Printed Photoresponsive Liquid Crystal Elastomer Composites for Free-Form Actuation. Adv. Funct. Mater. 2023, 33, 2210614. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, Y. Light-induced spontaneous bending of a simply supported liquid crystal elastomer rectangular plate. Phys. Rev. E 2020, 101, 042701. [Google Scholar] [CrossRef]
- Yu, Y.; Li, L.; Liu, E.; Han, X.; Wang, J.; Xie, Y.-X.; Lu, C. Light-driven core-shell fiber actuator based on carbon nanotubes/liquid crystal elastomer for artificial muscle and phototropic locomotion. Carbon 2022, 187, 97–107. [Google Scholar] [CrossRef]
- He, Q.; Yin, R.; Hua, Y.; Jiao, W.; Mo, C.; Shu, H.; Raney, J.R. A modular strategy for distributed, embodied control of electronics-free soft robots. Sci. Adv. 2023, 9, eade9247. [Google Scholar] [CrossRef]
- Bartlett, N.W.; Tolley, M.T.; Overvelde, J.T.; Weaver, J.C.; Mosadegh, B.; Bertoldi, K.; Whitesides, G.M.; Wood, R.J. A 3D-printed, functionally graded soft robot powered by combustion. Science 2015, 349, 161–165. [Google Scholar] [CrossRef]
- Rodriguez, A.S.-M.; Hosseini, M.; Paik, J. Hybrid control strategy for force and precise end effector positioning of a twisted string actuator. IEEE/ASME Trans. Mechatron. 2020, 26, 2791–2802. [Google Scholar] [CrossRef]
- Dawson, N.J.; Kuzyk, M.G.; Neal, J.; Luchette, P.; Palffy-Muhoray, P. Cascading of liquid crystal elastomer photomechanical optical devices. Opt. Commun. 2011, 284, 991–993. [Google Scholar] [CrossRef]
- Zeng, W.; Shu, L.; Li, Q.; Chen, S.; Wang, F.; Tao, X.M. Fiber-based wearable electronics: A review of materials, fabrication, devices, and applications. Adv. Mater. 2014, 26, 5310–5336. [Google Scholar] [CrossRef]
- Kantaros, A.; Ganetsos, T. From static to dynamic: Smart materials pioneering additive manufacturing in regenerative medicine. Int. J. Mol. Sci. 2023, 24, 15748. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Yang, S. Multi-functional liquid crystal elastomer composites. Appl. Phys. Rev. 2022, 9, 011301. [Google Scholar] [CrossRef]
- Bai, C.; Kang, J.; Wang, Y. Light-induced motion of three-dimensional pendulum with liquid crystal elastomeric fiber. Int. J. Mech. Sci. 2024, 266, 108911. [Google Scholar] [CrossRef]
- Kuenstler, A.S.; Chen, Y.; Bui, P.; Kim, H.; DeSimone, A.; Jin, L.; Hayward, R.C. Blueprinting photothermal shape-morphing of liquid crystal elastomers. Adv. Mater. 2020, 32, 2000609. [Google Scholar] [CrossRef]
- Yu, Y.; Zhou, L.; Du, C.; Zhu, F.; Dai, Y.; Ge, D.; Li, K. Self-galloping of a liquid crystal elastomer catenary cable under a steady temperature field. Thin-Walled Struct. 2024, 202, 112071. [Google Scholar] [CrossRef]
- Xu, P.; Chen, Y.; Sun, X.; Dai, Y.; Li, K. Light-powered self-sustained chaotic motion of a liquid crystal elastomer-based pendulum. Chaos Solitons Fractals 2024, 184, 115027. [Google Scholar] [CrossRef]
- Wu, H.; Dai, Y.; Li, K.; Xu, P. Theoretical study of chaotic jumping of liquid crystal elastomer ball under periodic illumination. Nonlinear Dyn. 2024, 112, 7799–7815. [Google Scholar] [CrossRef]
- Baumann, A.; Sánchez-Ferrer, A.; Jacomine, L.; Martinoty, P.; Le Houerou, V.; Ziebert, F.; Kulić, I.M. Motorizing fibres with geometric zero-energy modes. Nat. Mater. 2018, 17, 523–527. [Google Scholar] [CrossRef]
- Qiu, Y.; Li, K. Self-rotation-eversion of an anisotropic-friction-surface torus. Int. J. Mech. Sci. 2024, 281, 109584. [Google Scholar] [CrossRef]
- Vantomme, G.; Elands, L.C.; Gelebart, A.H.; Meijer, E.; Pogromsky, A.Y.; Nijmeijer, H.; Broer, D.J. Coupled liquid crystalline oscillators in Huygens’ synchrony. Nat. Mater. 2021, 20, 1702–1706. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, H.; Li, K. Optically-responsive liquid crystal elastomer thin film motors in linear/nonlinear optical fields. Thin-Walled Struct. 2024, 202, 112082. [Google Scholar] [CrossRef]
- Zhao, J.; Dai, C.; Dai, Y.; Wu, J.; Li, K. Self-oscillation of cantilevered silicone oil paper sheet system driven by steam. Thin-Walled Struct. 2024, 203, 112270. [Google Scholar] [CrossRef]
- Liu, J.; Qian, G.; Dai, Y.; Yuan, Z.; Song, W.; Li, K. Nonlinear dynamics modeling of a light-powered liquid crystal elastomer-based perpetual motion machine. Chaos Solitons Fractals 2024, 184, 114957. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, C.; Dai, Y.; Li, K. Modeling of a light-fueled self-paddling boat with a liquid crystal elastomer-based motor. Phys. Rev. E 2024, 109, 044705. [Google Scholar] [CrossRef]
- Wu, H.; Ge, D.; Chen, J.; Xu, P.; Li, K. A light-fueled self-rolling unicycle with a liquid crystal elastomer rod engine. Chaos Solitons Fractals 2024, 186, 115327. [Google Scholar] [CrossRef]
- Qiu, Y.; Chen, J.; Dai, Y.; Zhou, L.; Yu, Y.; Li, K. Mathematical modeling of the displacement of a light-fuel self-moving automobile with an on-board liquid crystal elastomer propulsion device. Mathematics 2024, 12, 1322. [Google Scholar] [CrossRef]
- Soltani, M.; Raahemifar, K.; Nokhosteen, A.; Kashkooli, F.M.; Zoudani, E.L. Numerical methods in studies of liquid crystal elastomers. Polymers 2021, 13, 1650. [Google Scholar] [CrossRef]
- Bai, R.; Bhattacharya, K. Photomechanical coupling in photoactive nematic elastomers. J. Mech. Phys. Solids 2020, 144, 104115. [Google Scholar] [CrossRef]
- Jaramillo-Morales, M.F.; Dogru, S.; Gomez-Mendoza, J.B.; Marques, L. Energy estimation for differential drive mobile robots on straight and rotational trajectories. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420909654. [Google Scholar] [CrossRef]
- Yao, W.; Yuan, J.; Zhou, F.; Chen, Z.; Zhao, T.; Zhong, M. Trajectory analysis and experiments of both-sides cylindrical lapping in eccentric rotation. Int. J. Adv. Manuf. Technol. 2017, 88, 2849–2859. [Google Scholar] [CrossRef]
- Pourciau, B. Newton’s interpretation of newton’s second law. Arch. Hist. Exact Sci. 2006, 60, 157–207. [Google Scholar] [CrossRef]
- Warner, M.; Terentjev, E.M. Liquid Crystal Elastomers; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Yu, Y.; Nakano, M.; Ikeda, T. Directed bending of a polymer film by light. Nature 2003, 425, 145. [Google Scholar] [CrossRef]
- Herbert, K.M.; Fowler, H.E.; McCracken, J.M.; Schlafmann, K.R.; Koch, J.A.; White, T.J. Synthesis and alignment of liquid crystalline elastomers. Nat. Rev. Mater. 2022, 7, 23–38. [Google Scholar] [CrossRef]
- Nägele, T.; Hoche, R.; Zinth, W.; Wachtveitl, J. Femtosecond photoisomerization of cis-azobenzene. Chem. Phys. Lett. 1997, 272, 489–495. [Google Scholar] [CrossRef]
- Jampani, V.; Volpe, R.; Reguengo de Sousa, K.; Ferreira Machado, J.; Yakacki, C.; Lagerwall, J. Liquid crystal elastomer shell actuators with negative order parameter. Sci. Adv. 2019, 5, eaaw2476. [Google Scholar] [CrossRef]
- Lee, V.; Bhattacharya, K. Actuation of cylindrical nematic elastomer balloons. J. Appl. Phys. 2021, 129, 114701. [Google Scholar] [CrossRef]


| Parameter | Definition | Value | Unit |
|---|---|---|---|
| Light intensity | 0–80 | kW/m2 | |
| Contraction coefficient of LCE fiber | 0–0.4 | / | |
| Elastic coefficient of LCE fiber | 20–40 | N/m | |
| Cis to trans thermal relaxation time | 0.02–0.45 | s | |
| Light absorption constant | 0.002 | m2/(s W) | |
| Mass of the slider | 0–0.02 | kg | |
| Initial tangential velocity | 0–5 | m/s | |
| The first damping coefficient | 0–0.3 | kg/s | |
| The second damping coefficient | 0–0.15 | kg/s2 | |
| Range of the illuminated zone | [0, 2π] | rad | |
| Semi-major axis | 0.01–5 | m | |
| Semi-minor axis | 0.01–5 | m | |
| Original length of LCE fiber | 0.01–5 | m |
| Parameter | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Value | 0–1 | 0–0.4 | 0–10 | 0–3 | [π, 2π] | 0–0.2 | 0–0.1 | 0.01–3 | 0.01–2.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, L.; Chen, Y.; Hu, J.; Hu, X.; Wang, J.; Li, K. A Light-Powered Self-Circling Slider on an Elliptical Track with a Liquid Crystal Elastomer Fiber. Polymers 2024, 16, 2375. https://doi.org/10.3390/polym16162375
Wei L, Chen Y, Hu J, Hu X, Wang J, Li K. A Light-Powered Self-Circling Slider on an Elliptical Track with a Liquid Crystal Elastomer Fiber. Polymers. 2024; 16(16):2375. https://doi.org/10.3390/polym16162375
Chicago/Turabian StyleWei, Lu, Yanan Chen, Junjie Hu, Xueao Hu, Jiale Wang, and Kai Li. 2024. "A Light-Powered Self-Circling Slider on an Elliptical Track with a Liquid Crystal Elastomer Fiber" Polymers 16, no. 16: 2375. https://doi.org/10.3390/polym16162375
APA StyleWei, L., Chen, Y., Hu, J., Hu, X., Wang, J., & Li, K. (2024). A Light-Powered Self-Circling Slider on an Elliptical Track with a Liquid Crystal Elastomer Fiber. Polymers, 16(16), 2375. https://doi.org/10.3390/polym16162375








