An Investigation of the Energy-Absorption Characteristics of Thin-Walled Polymer Composite C-Channels: Experiment and Stacked Shell Simulation
Abstract
1. Introduction
2. Specimens and Experimental
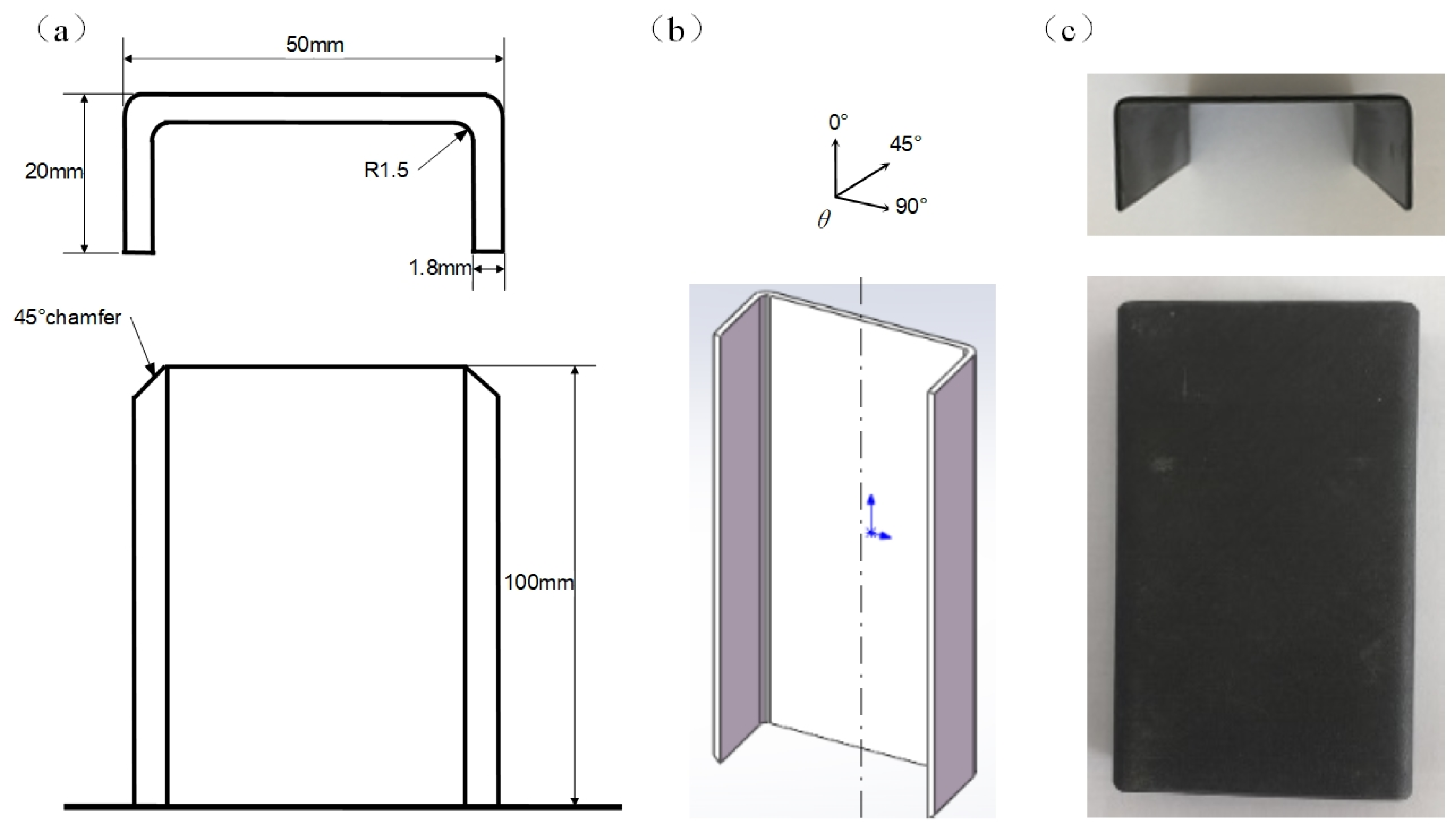
2.1. Specimens Design and Manufacture
2.2. Experimental Procedures
2.3. Energy-Absorbing Metrics
3. Numerical Study
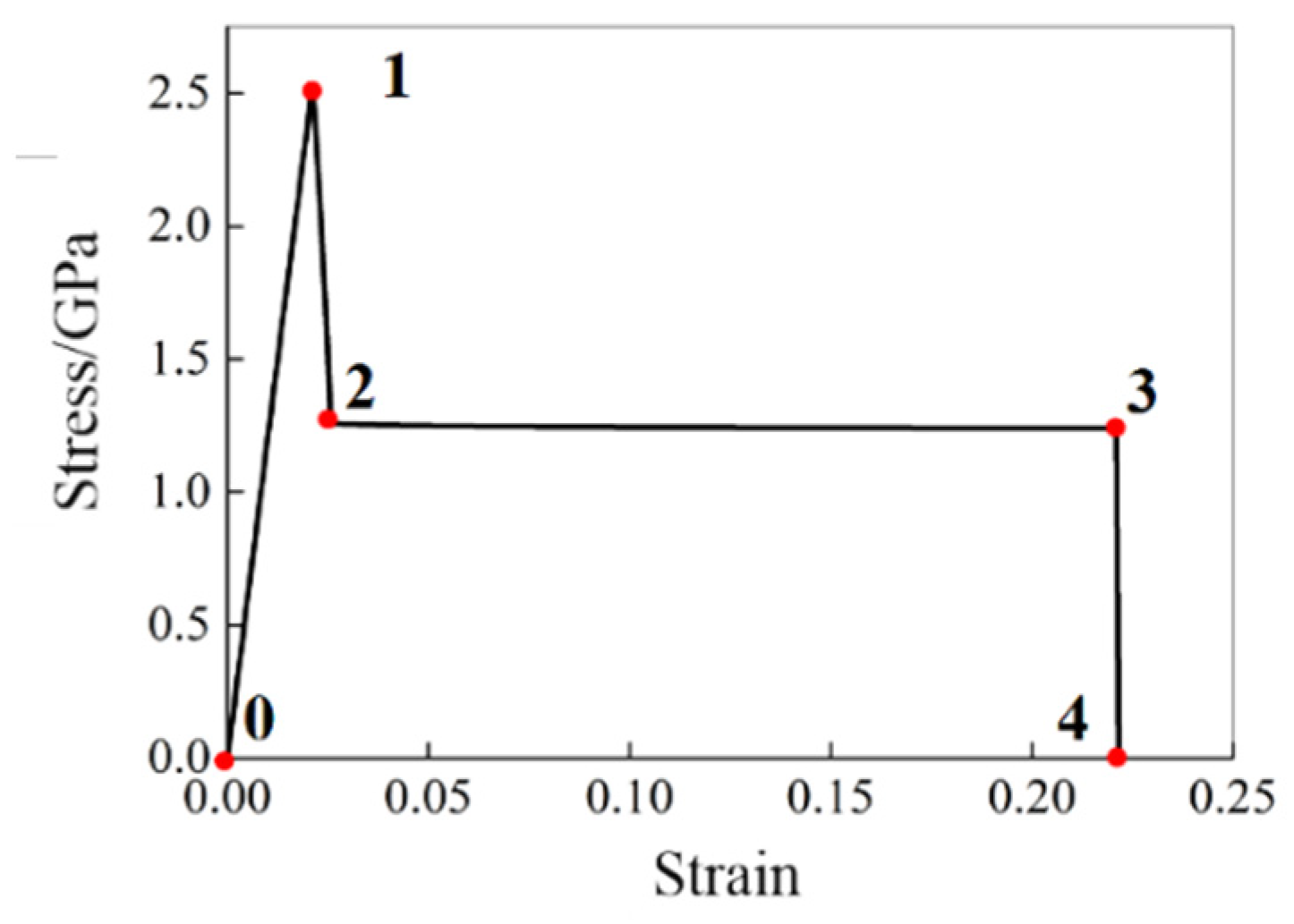
3.1. Constitutive Model
3.2. Failure Criteria
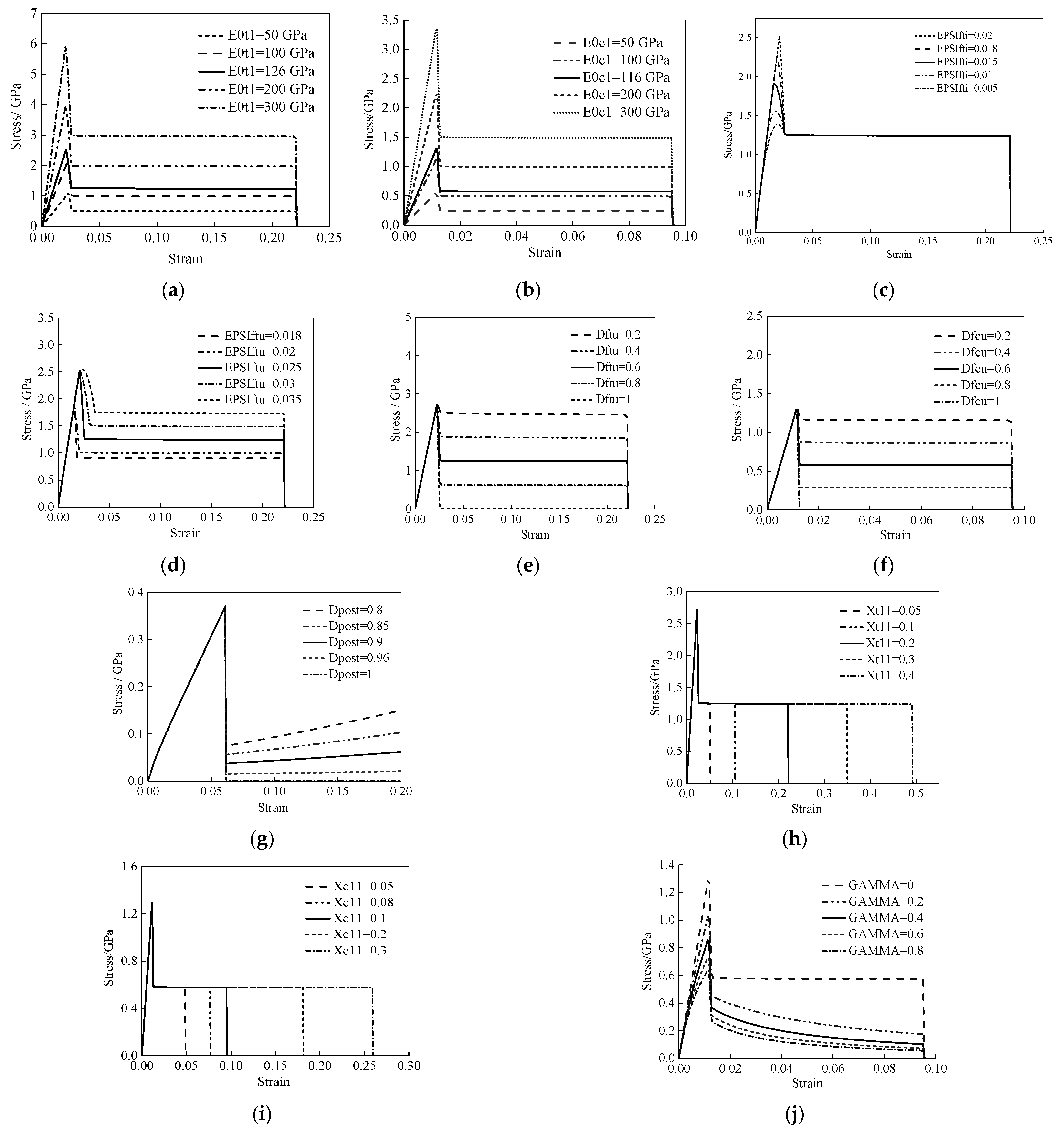
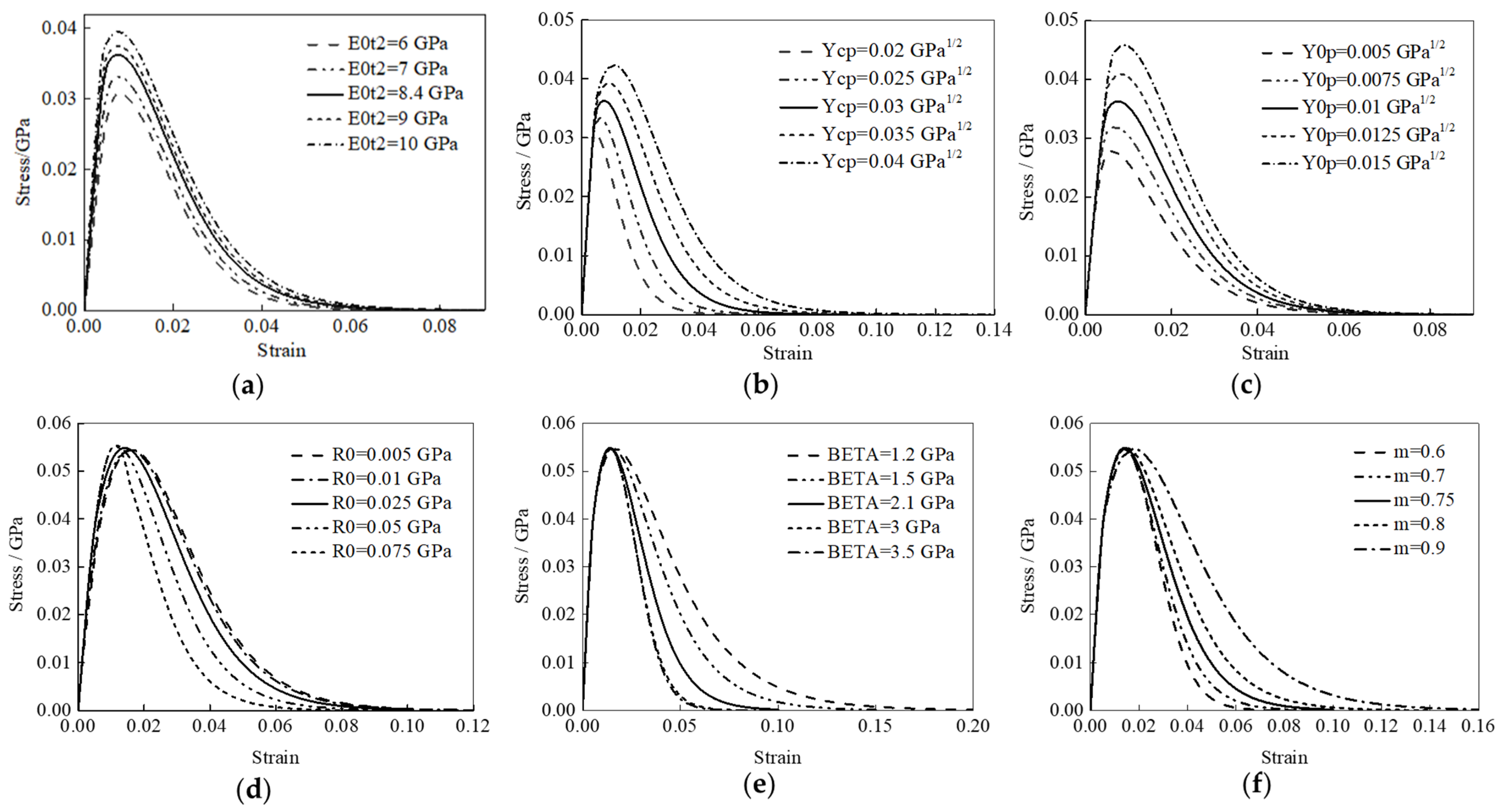
3.3. Parametric Analysis
3.3.1. [0] Single-Element Model
3.3.2. [90] Single-Element Model
3.3.3. Material Model Parameters
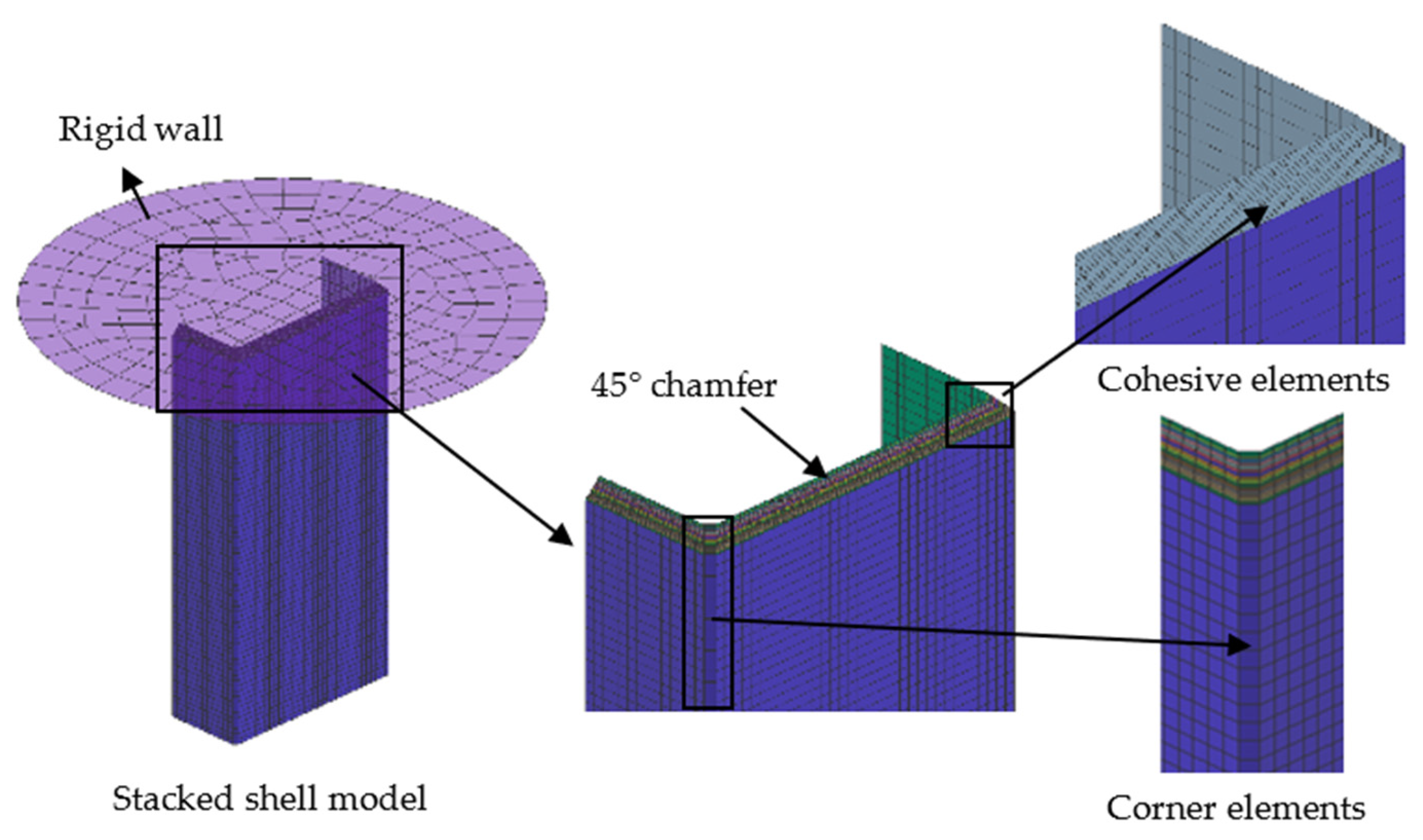
3.4. Stacked Shell Model
4. Results and Discussion
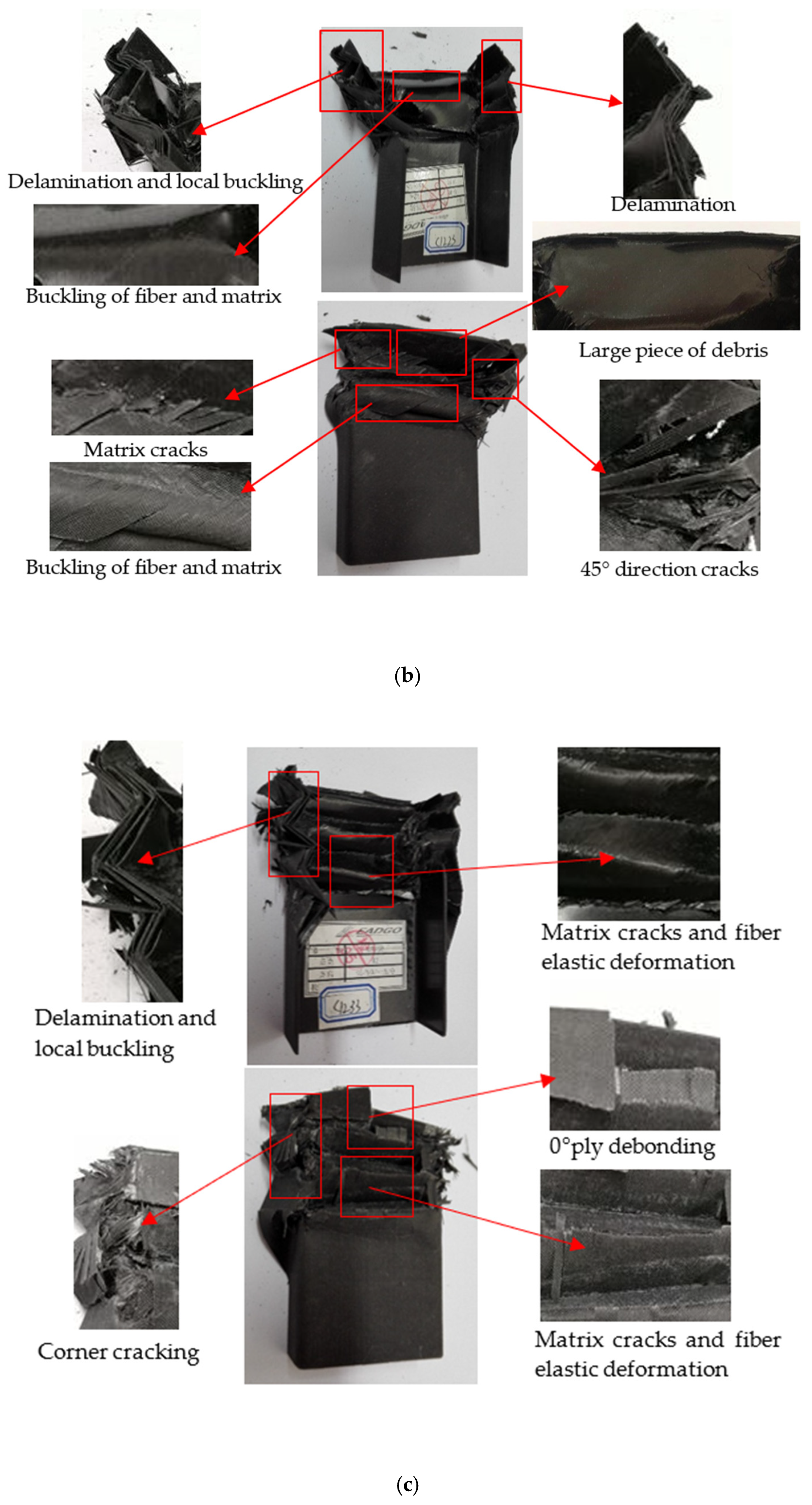
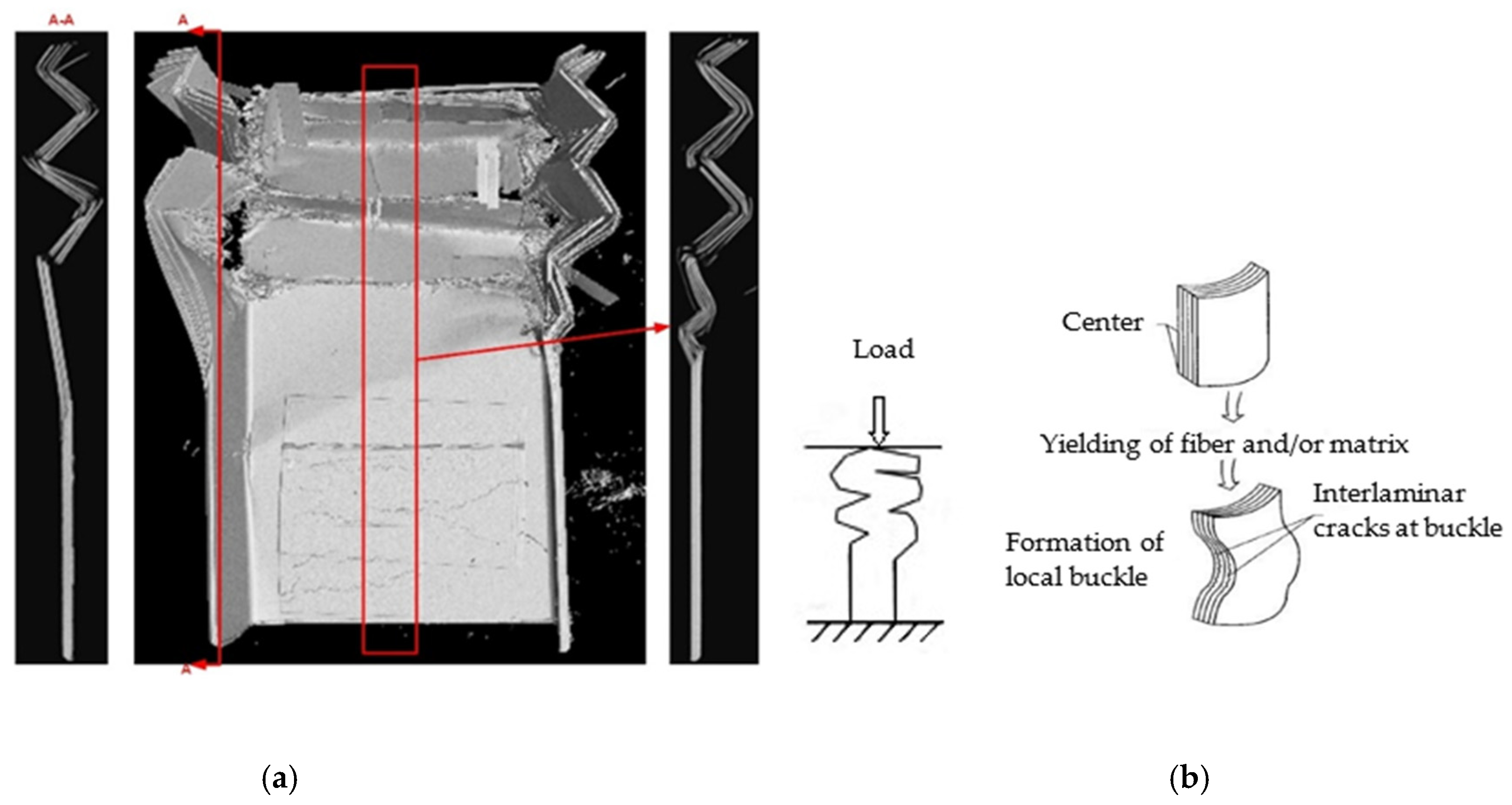
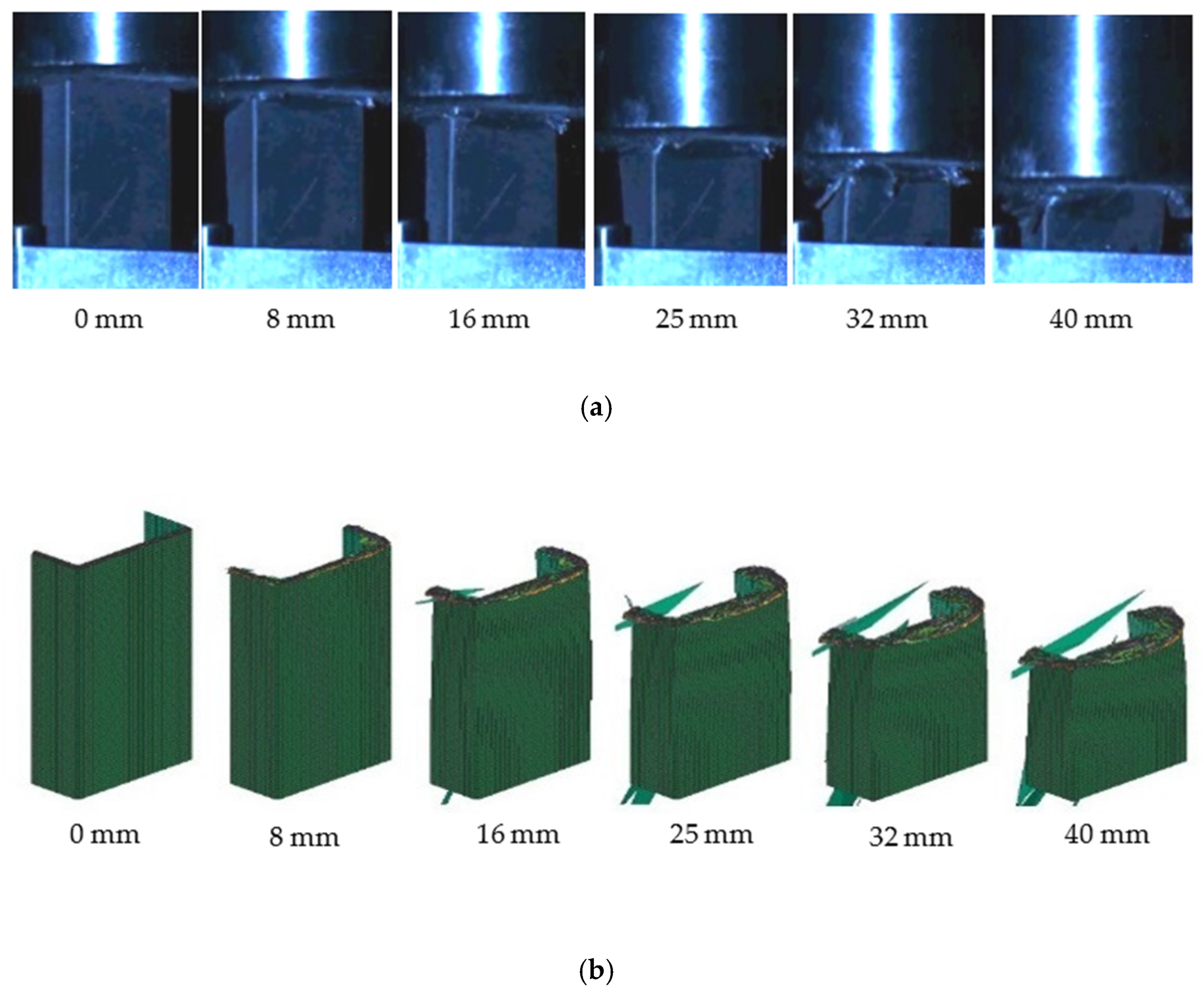
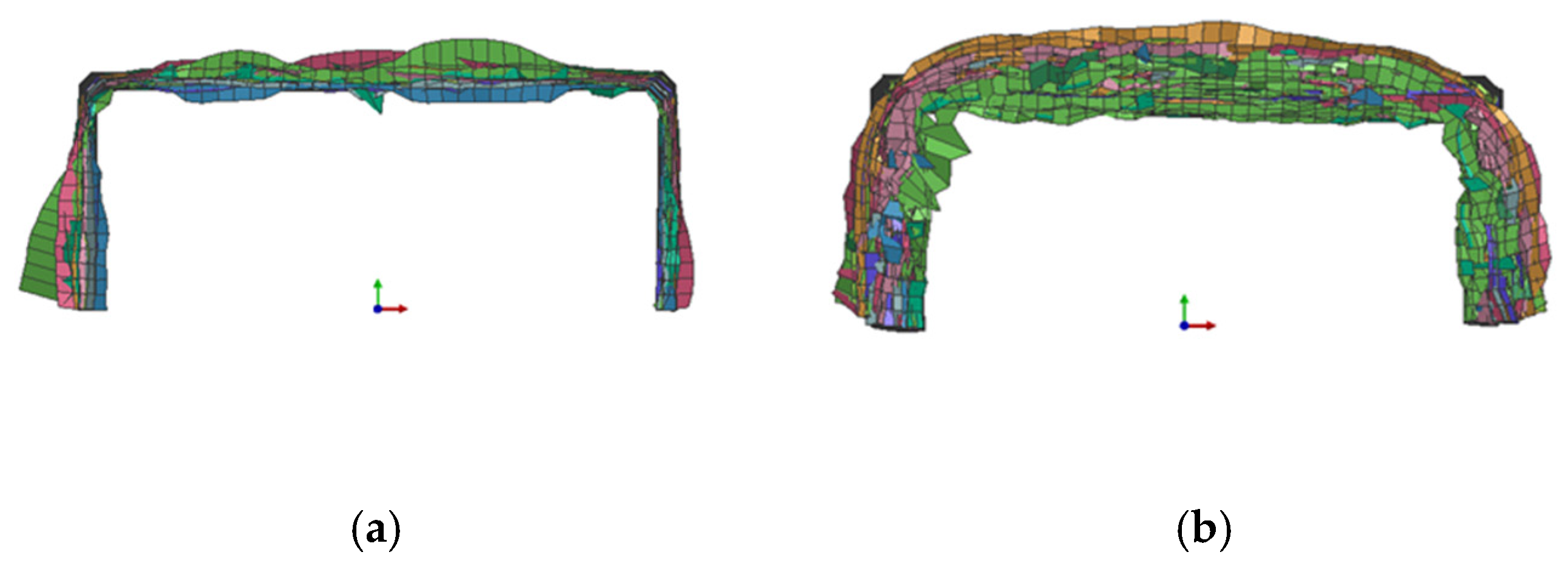
4.1. Failure Morphology and Mechanism Analysis
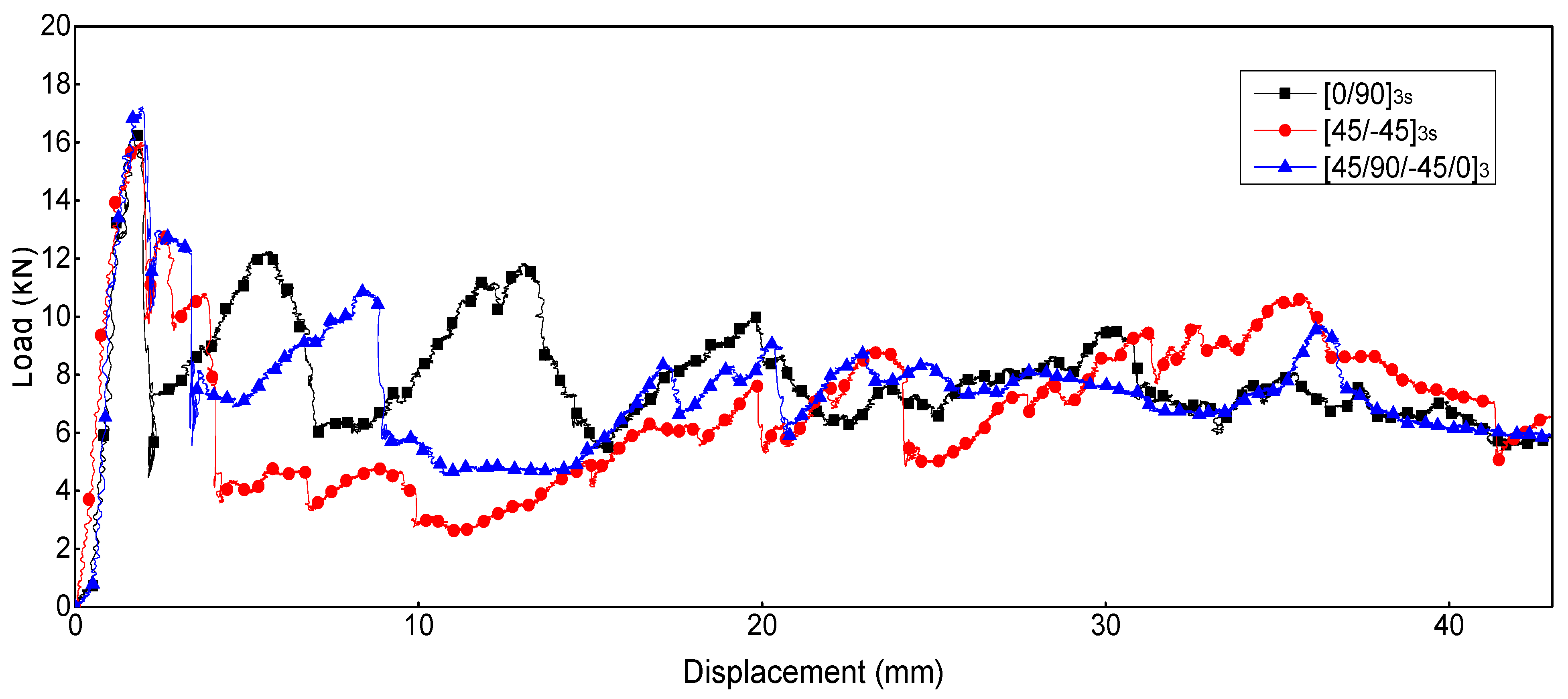
4.2. Energy-Absorbing Characteristics Analysis
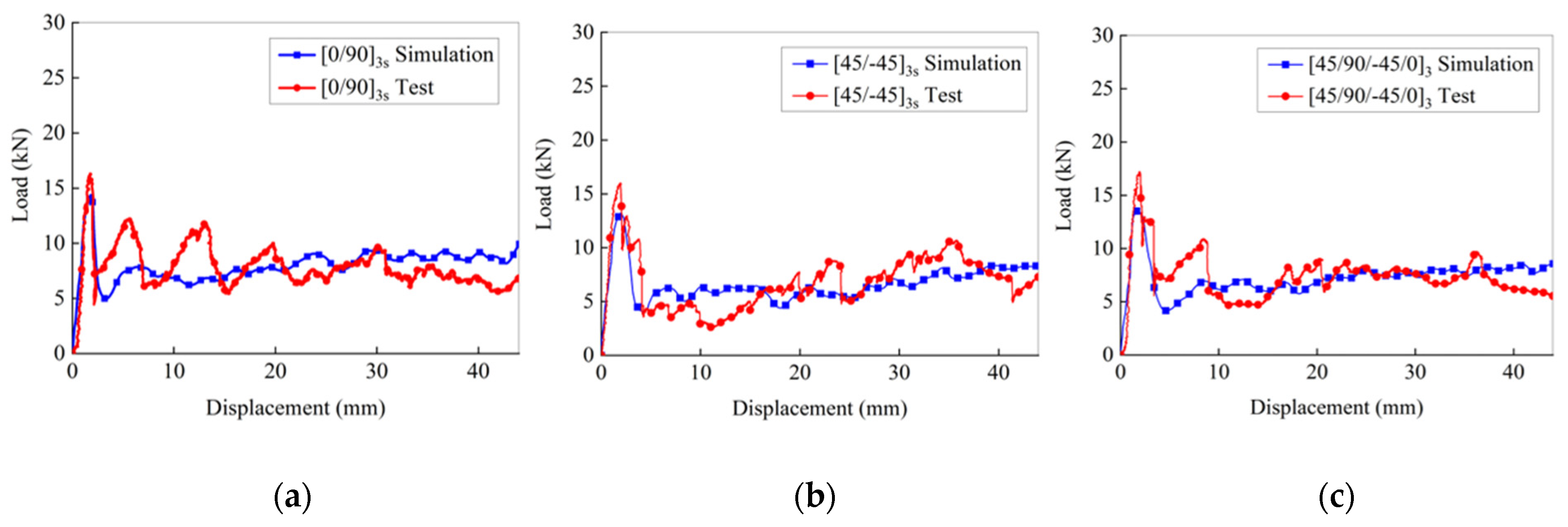
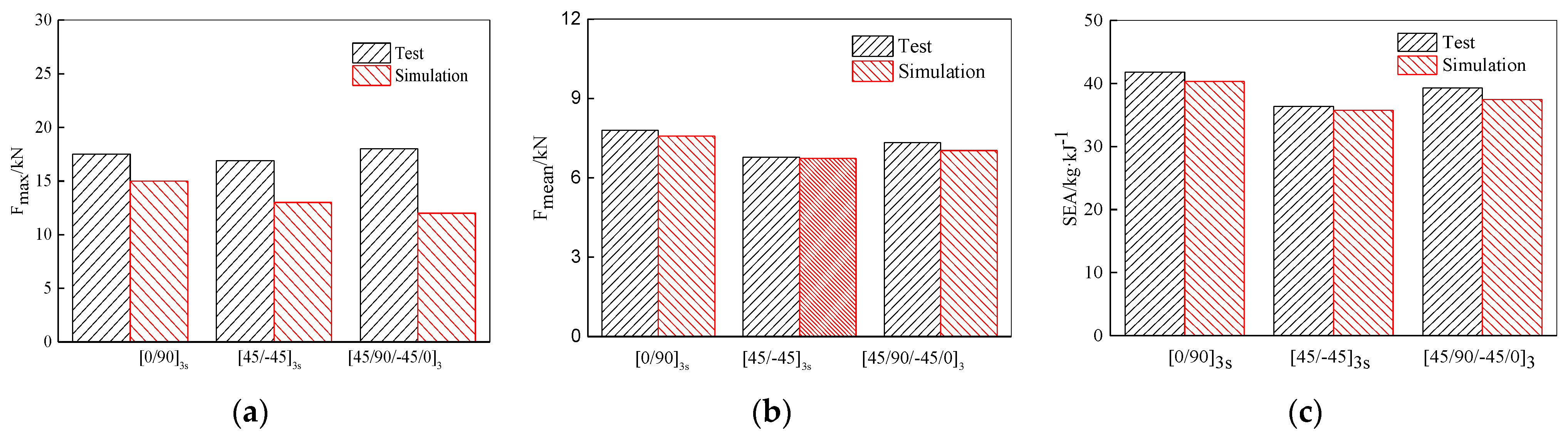
4.3. Simulation and Model Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Sharifah, R.; Ali, J.S.; Shaik, I.; Adib, R. Influence of Composite Skin on the Energy Absorption Characteristics of an Aircraft Fuselage. Int. J. Eng. Mater. Manuf. 2023, 8, 13–20. [Google Scholar] [CrossRef]
- Guida, M.; Marulo, F.; Abrate, S. Advances in crash dynamics for aircraft safety. Prog. Aerosp. Sci. 2018, 98, 106–123. [Google Scholar] [CrossRef]
- Jacob, G.C.; Fellers, J.F.; Simunovic, S.; Starbuck, J.M. Energy Absorption in Polymer Composites for Automotive Crashworthiness. J. Compos. Mater. 2016, 36, 813–850. [Google Scholar] [CrossRef]
- Di Palma, L.; Di Caprio, F.; Chiariello, A.; Ignarra, M.; Russo, S.; Riccio, A.; De Luca, A.; Caputo, F. Vertical Drop Test of Composite Fuselage Section of a Regional Aircraft. AIAA J. 2020, 58, 474–487. [Google Scholar] [CrossRef]
- Di Caprio, F.; Ignarra, M.; Marulo, F.; Guida, M.; Lamboglia, A.; Gambino, B. Design of Composite Stanchions for the Cargo Subfloor Structure of a Civil Aircraft. Procedia Eng. 2016, 167, 88–96. [Google Scholar] [CrossRef]
- Mou, H.; Xie, J.; Feng, Z. Research status and future development of crashworthiness of civil aircraft fuselage structures: An overview. Prog. Aerosp. Sci. 2020, 119, 100644. [Google Scholar] [CrossRef]
- David, M.; Johnson, A.F.; Voggenreiter, H. Analysis of Crushing Response of Composite Crashworthy Structures. Appl. Compos. Mater. 2012, 20, 773–787. [Google Scholar] [CrossRef]
- Elahi, S.A.; Rouzegar, J.; Niknejad, A.; Assaee, H. Theoretical study of absorbed energy by empty and foam-filled composite tubes under lateral compression. Thin-Walled Struct. 2017, 114, 1–10. [Google Scholar] [CrossRef]
- Reuter, C.; Tröster, T. Crashworthiness and numerical simulation of hybrid aluminium-CFRP tubes under axial impact. Thin-Walled Struct. 2017, 117, 1–9. [Google Scholar] [CrossRef]
- Bolukbasi, A.O.; Baxter, T.R.; Nguyen, T.A.; Rassaian, M.; Davis, K.R.; Koch, W.; Firth, L.C. Energy Absorbing Structure for Aircraft. USA. GB2444645A, 11 June 2008. [Google Scholar]
- FAA. Special Conditions: Boeing Model 787-8 Airplane. Crashworthiness. In 5-362-SC; Federal Aviation Administration: Washington, DC, USA, 2007. [Google Scholar]
- FAA. Special Conditions: Airbus A350-900 Airplane. Crashworthiness, Emergency Landing Conditions. In 25-537-SC; Federal Aviation Administration: Washington, DC, USA, 2014. [Google Scholar]
- Mahdi, E.; Sebaey, T.A. An experimental investigation into crushing behavior of radially stiffened GFRP composite tubes. Thin-Walled Struct. 2014, 76, 8–13. [Google Scholar] [CrossRef]
- Böhm, H.; Weck, D.; Hornig, A.; Langkamp, A.; Adam, F.; Gude, M. Experimental and Numerical Study on the Axial Crushing Behavior of Textile-Reinforced Thermoplastic Composite Tubes. Adv. Eng. Mater. 2016, 18, 437–443. [Google Scholar] [CrossRef]
- Wang, Z.; Jin, X.; Li, Q.; Sun, G. On crashworthiness design of hybrid metal-composite structures. Int. J. Mech. Sci. 2020, 171, 105380. [Google Scholar] [CrossRef]
- Rozylo, P.; Debski, H. Stability and load carrying capacity of thin-walled composite columns with square cross-section under axial compression. Compos. Struct. 2024, 329, 117795. [Google Scholar] [CrossRef]
- Bussadori, B.P.; Schuffenhauer, K.; Scattina, A. Modelling of CFRP crushing structures in explicit crash analysis. Compos. Part B: Eng. 2014, 60, 725–735. [Google Scholar] [CrossRef]
- Jiang, H.; Ren, Y.; Gao, B. Research on the progressive damage model and trigger geometry of composite waved beam to improve crashworthiness. Thin-Walled Struct. 2017, 119, 531–543. [Google Scholar] [CrossRef]
- Ren, Y.; Jiang, H.; Ji, W.; Zhang, H.; Xiang, J.; Yuan, F.-G. Improvement of Progressive Damage Model to Predicting Crashworthy Composite Corrugated Plate. Appl. Compos. Mater. 2017, 25, 45–66. [Google Scholar] [CrossRef]
- Mou, H.L.; Su, X.; Xie, J.; Feng, Z.Y. Parametric analysis of composite sinusoidal specimens under quasi-static crushing. Aeronaut. J. 2018, 122, 1244–1262. [Google Scholar] [CrossRef]
- Lin, J.S.; Wang, X.; Fang, C.Q.; Huang, X. Collapse loading and energy absorption of fiber-reinforced conical shells. Compos. Part B Eng. 2015, 74, 178–189. [Google Scholar] [CrossRef]
- Ying, L.W.; Yang, F.P.; Wang, X. Analytical method for the axial crushing force of fiber-reinforced tapered square metal tubes. Compos. Struct. 2016, 153, 222–233. [Google Scholar] [CrossRef]
- El-Hage, H.; Mallick, P.K.; Zamani, N. A numerical study on the quasi-static axial crush characteristics of square aluminum–composite hybrid tubes. Compos. Struct. 2006, 73, 505–514. [Google Scholar] [CrossRef]
- Paz, J.; Díaz, J.; Romera, L.; Costas, M. Crushing analysis and multi-objective crashworthiness optimization of GFRP honeycomb-filled energy absorption devices. Finite Elem. Anal. Des. 2014, 91, 30–39. [Google Scholar] [CrossRef]
- Bi, J.; Fang, H.; Wang, Q.; Ren, X. Modeling and optimization of foam-filled thin-walled columns for crashworthiness designs. Finite Elem. Anal. Des. 2010, 46, 698–709. [Google Scholar] [CrossRef]
- Siromani, D.; Henderson, G.; Mikita, D.; Mirarchi, K.; Park, R.; Smolko, J.; Awerbuch, J.; Tan, T.-M. An experimental study on the effect of failure trigger mechanisms on the energy absorption capability of CFRP tubes under axial compression. Compos. Part A Appl. Sci. Manuf. 2014, 64, 25–35. [Google Scholar] [CrossRef]
- Feraboli, P. Development of a Modified Flat-plate Test Specimen and Fixture for Composite Materials Crush Energy Absorption. J. Compos. Mater. 2009, 43, 1967–1990. [Google Scholar] [CrossRef]
- Palanivelu, S.; Paepegem, W.V.; Degrieck, J.; Kakogiannis, D.; Ackeren, J.V.; Hemelrijck, D.v.; Wastiels, J.; Vantomme, J. Comparative study of the quasi-static energy absorption of small-scale composite tubes with different geometrical shapes for use in sacrificial cladding structures. Polym. Test. 2010, 29, 381–396. [Google Scholar] [CrossRef]
- Tran, T.; Hou, S.; Han, X.; Chau, M. Crushing analysis and numerical optimization of angle element structures under axial impact loading. Compos. Struct. 2015, 119, 422–435. [Google Scholar] [CrossRef]
- Różyło, P. Experimental-numerical test of open section composite columns stability subjected to axial compression. Arch. Mater. Sci. Eng. 2017, 84, 58–64. [Google Scholar] [CrossRef]
- Wysmulski, P. Non-linear analysis of the postbuckling behaviour of eccentrically compressed composite channel-section columns. Compos. Struct. 2023, 305, 116446. [Google Scholar] [CrossRef]
- Wysmulski, P.; Debski, H.; Falkowicz, K. Sensitivity of Compressed Composite Channel Columns to Eccentric Loading. Materials 2022, 15, 6938. [Google Scholar] [CrossRef]
- Friedrich, L.; Loosen, S.; Liang, K.; Ruess, M.; Bisagni, C.; Schröder, K.-U. Stacking sequence influence on imperfection sensitivity of cylindrical composite shells under axial compression. Compos. Struct. 2015, 134, 750–761. [Google Scholar] [CrossRef]
- PAM-CRASH User Manual Version 2014; ESI Group Paris: Paris, France, 2014.
- LSDKU Manual. Version 971, Livermore Software Technology Corporation (LSTC); LSDKU Manual: Livermore, CA, USA, 2009. [Google Scholar]
- Abaqus Theory Guide, Version 6.14; Dassault Systèmes Simulia. Inc.: Providence, RI, USA, 2014.
- Rozylo, P.; Falkowicz, K.; Wysmulski, P.; Debski, H.; Pasnik, J.; Kral, J. Experimental-Numerical Failure Analysis of Thin-Walled Composite Columns Using Advanced Damage Models. Materials 2021, 14, 1506. [Google Scholar] [CrossRef]
- Debski, H.; Rozylo, P.; Teter, A. Buckling and limit states of thin-walled composite columns under eccentric load. Thin-Walled Struct. 2020, 149, 106627. [Google Scholar] [CrossRef]
- Wysmulski, P.; Debski, H. Post-buckling and limit states of composite channel-section profiles under eccentric compression. Compos. Struct. 2020, 245, 112356. [Google Scholar] [CrossRef]
- Vasiliev, V.; Lurie, S.; Salov, V. Estimation of the strength of plates with cracks based on the maximum stress criterion in a scale-dependent generalized theory of elasticity. Phys. Mesomech. 2019, 22, 456–462. [Google Scholar] [CrossRef]
- Zhao, L.; Qin, T.; Zhang, J.; Shenoi, R.A. Modified maximum stress failure criterion for composite π joints. J. Compos. Mater. 2013, 47, 2995–3008. [Google Scholar] [CrossRef]
- Mirsayar, M. Maximum principal strain criterion for fracture in orthotropic composites under combined tensile/shear loading. Theor. Appl. Fract. Mech. 2022, 118, 103291. [Google Scholar] [CrossRef]
- Rao, P.M.; Subba Rao, V. Degradation model based on Tsai-Hill factors to model the progressive failure of fiber metal laminates. J. Compos. Mater. 2011, 45, 1783–1792. [Google Scholar] [CrossRef]
- Hashin, Z. Finite thermoelastic fracture criterion with application to laminate cracking analysis. J. Mech. Phys. Solids 1996, 44, 1129–1145. [Google Scholar] [CrossRef]
- Lee, C.-S.; Kim, J.-H.; Kim, S.-k.; Ryu, D.-M.; Lee, J.-M. Initial and progressive failure analyses for composite laminates using Puck failure criterion and damage-coupled finite element method. Compos. Struct. 2015, 121, 406–419. [Google Scholar] [CrossRef]
- Zheng, J.; Maharaj, C.; Liu, J.; Chai, H.; Liu, H.; Dear, J.P. A comparative study on the failure criteria for predicting the damage initiation in fiber-reinforced composites. Mech. Compos. Mater. 2022, 58, 125–140. [Google Scholar] [CrossRef]
- Mohamadzadeh, M.; Haftkhani, A.R.; Ebrahimi, G.; Yoshihara, H. Numerical and experimental failure analysis of screwed single shear joints in wood plastic composite. Mater. Des. 2012, 35, 404–413. [Google Scholar] [CrossRef]
- Palanivelu, S.; Van Paepegem, W.; Degrieck, J.; Kakogiannis, D.; Van Ackeren, J.; Van Hemelrijck, D.; Wastiels, J.; Vantomme, J. Parametric study of crushing parameters and failure patterns of pultruded composite tubes using cohesive elements and seam, Part I: Central delamination and triggering modelling. Polym. Test. 2010, 29, 729–741. [Google Scholar] [CrossRef]
- Siromani, D.; Awerbuch, J.; Tan, T.-M. Finite element modeling of the crushing behavior of thin-walled CFRP tubes under axial compression. Compos. Part B Eng. 2014, 64, 50–58. [Google Scholar] [CrossRef]
- Johnson, A.F.; David, M. Failure mechanisms in energy-absorbing composite structures. Philos. Mag. 2010, 90, 4245–4261. [Google Scholar] [CrossRef]
- Feraboli, P.; Wade, B.; Deleo, F.; Rassaian, M.; Higgins, M.; Byar, A. LS-DYNA MAT54 modeling of the axial crushing of a composite tape sinusoidal specimen. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1809–1825. [Google Scholar] [CrossRef]
- Feraboli, P.; Wade, B. Simulating Laminated Composite Materials Using LS-DYNA Material Model MAT54: Single-Element Investigation. Federal Aviation Administration Technical Report. 2015. Available online: https://www.researchgate.net/publication/322152587_Simulating_Laminated_Composite_Materials_Using_LS-DYNA_Material_Model_MAT54_Single-Element_Investigation (accessed on 23 April 2024).
- Chang, F.-K.; Chang, K.-Y. Post-failure analysis of bolted composite joints in tension or shear-out mode failure. J. Compos. Mater. 1987, 21, 809–833. [Google Scholar] [CrossRef]
- Chang, F.-K.; Lessard, L.B. Damage tolerance of laminated composites containing an open hole and subjected to compressive loadings: Part I—Analysis. J. Compos. Mater. 1991, 25, 2–43. [Google Scholar] [CrossRef]
- DINENISO7822-2000; Textile Glass Reinforced Plastics—Determination of Void Content—Loss on Ignition, Mechanical Disintegration and statistical Counting Methods. German version 2000. Deutsches Institut für Normung e.V.: Berlin, Germany, 1990; pp. 1–8.
- ASTM D792-13; Standard Test Methods for Density and Specific Gravity (Relative Density) of Plastics by Displacement, American Society for Testing and Materials. ASTM: West Conshohocken, PA, USA, 2013.
- ASTM D3039/D3039M-17; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2015.
- ASTM D3410; Standard Test Method for Compressive Properties of Unidirectional or Crossply Fiber-Resin Composites. ASTM: West Conshohocken, PA, USA, 1987.
- ASTM D3518/D3518M-18; Standard Test Method for In-Plane Shear Response of Polymer Matrix Composite Materials by Tensile Test of a ±45° Laminate EUA. ASTM: West Conshohocken, PA, USA, 2010.
- ASTM D638; Standard Test Method for Tensile Properties of Plastics. ASTM: West Conshohocken, PA, USA, 2008.
- ASTM D695; Standard Test Method for Compressive Properties of Rigid Plastics. ASTM: West Conshohocken, PA, USA, 2010.
- ASTM D5379; Standard Test Method for Shear Properties of Composite Materials by the V-Notched Beam Method. ASTM: West Conshohocken, PA, USA, 2015.







| Parameter | Physical Significance | Unit | Parametric Variation | |||
|---|---|---|---|---|---|---|
| E0t1 | Young’s modulus in Direction 1 | GPa | 50 | 100 | 200 | 300 |
| EPSIfti | Tensile fiber initial strain | - | 0.005 | 0.01 | 0.018 | 0.02 |
| EPSIftu | Tensile fiber ultimate strain | - | 0.018 | 0.02 | 0.03 | 0.035 |
| Dftu | Tensile fiber ultimate damage | - | 0.2 | 0.4 | 0.8 | 1 |
| Xt11 | Tensile fiber strength/strain for failure | - | 0.05 | 0.1 | 0.3 | 0.4 |
| E0c1 | Compressive fiber Young’s modulus in Direction 1 | GPa | 50 | 100 | 200 | 300 |
| GAMMA | Compressive factor of modulus correction | - | 0 | 0.2 | 0.6 | 0.8 |
| Dfcu | Compressive fiber ultimate damage | - | 0.2 | 0.4 | 0.8 | 1 |
| Xc11 | Compressive tensile fiber strength/strain for failure | - | 0.05 | 0.08 | 0.2 | 0.3 |
| E0t2 | Young’s modulus in Direction 2 | GPa | 6 | 7 | 9 | 10 |
| Ycp | Critical transverse damage limit | GPa1/2 | 0.02 | 0.025 | 0.035 | 0.04 |
| Y0p | Initial transverse damage limit | GPa1/2 | 0.005 | 0.0075 | 0.0125 | 0.015 |
| R0 | Initial yield stress | GPa | 0.005 | 0.01 | 0.05 | 0.075 |
| BETA | Hardening law multiplier | GPa | 1.2 | 1.5 | 3 | 3.5 |
| m | Hardening law exponent | 0.6 | 0.7 | 0.8 | 0.9 | |
| DAMpost | Post damage of matrix | - | 1 | 0.9 | 0.85 | |
| Parameters | Definition | Unit | Value | Measurement |
|---|---|---|---|---|
| RHO | Mass density of ply material | g/cm3 | 1.52 | ASTM D792 [56] |
| E0t1 | Young’s modulus in Direction 1 of fiber | GPa | 126 | ASTM D3039 [57] |
| E0t2 | Young’s modulus in Direction 2 of fiber | GPa | 8.40 | ASTM D3039 |
| E0c1 | Compressive Young’s modulus of fiber | GPa | 116 | ASTM D3410 [58] |
| G012 | Shear modulus of 1,2-plane | GPa | 3.69 | ASTM D3518 [59] |
| NU12 | Poisson’s ratio in 1,2-plane | - | 0.3 | ASTM D3039 |
| R22+ | Matrix tensile transverse strength | GPa | 0.0554 | ASTM D638 [60] |
| R22- | Matrix compressive transverse strength | GPa | 0.225 | ASTM D695 [61] |
| R12 | Matrix shear strength | GPa | 0.2 | ASTM D5379 [62] |
| EPSIfti | Tensile fiber initial strain | - | 0.0217 | |
| Ycp | Critical transverse damage limit | GPa1/2 | 0.0596 | Calibrated by material coupon level test results. |
| Y0p | Initial transverse damage limit | GPa1/2 | 0.01 | |
| Dmax | Maximum allowed damage value for shear damage and transverse damage | - | 1 | |
| GAMMA | Compressive factor of modulus correction | - | 0 | |
| R0 | Initial yield stress | GPa | 0.025 | |
| BETA | Hardening law multiple | GPa | 2.1 | |
| m | Hardening law exponent | - | 0.75 | |
| Dpost | Post damage of matrix | - | 0.96 | |
| Dftu | Tensile fiber ultimate damage | 0.7~0.85 | ||
| Dfcu | Compressive fiber ultimate damage | 0.7~0.85 | ||
| EPSIftu | Tensile fiber ultimate strain | - | 0.025 | |
| Xt11 | Tensile fiber strain for failure | - | 0.52 | |
| Xc11 | Compressive tensile fiber strain for failure | - | 0.38 |
| Parameters | Definition | Unit | Values |
|---|---|---|---|
| hcont | Distance for kinematic computation | mm | 0.3 |
| E0 | Normal modulus | GPa | 4 |
| G0 | Shear modulus | GPa | 2.5 |
| SIGprpg | Normal stress to continue delamination | GPa | 0.098 |
| GAMAprpg | Shear stress to continue delamination | GPa | 0.094 |
| Mode I fracture energy | J/mm2 | 0.00047 | |
| Mode II fracture energy | J/mm2 | 0.002 | |
| SIGstrt | Normal stress to initiate delamination | GPa | 0.1 |
| GAMAstrt | Shear stress to initiate delamination | GPa | 0.1 |
| Ncycle | Stress reduction cycle number | 100 |
| Layups | Fmax/kN | Fmean/kN | EA/kJ | SEA/(kJ/kg) |
|---|---|---|---|---|
| [0/90]3s | 16.294 | 7.801 | 345.058 | 41.793 |
| [45/-45]3s | 16.006 | 6.776 | 300.236 | 36.364 |
| [45/90/-45/0]3 | 17.225 | 7.329 | 324.625 | 39.318 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Mou, H.; Song, S.; Feng, Z. An Investigation of the Energy-Absorption Characteristics of Thin-Walled Polymer Composite C-Channels: Experiment and Stacked Shell Simulation. Polymers 2024, 16, 2099. https://doi.org/10.3390/polym16152099
Zhang X, Mou H, Song S, Feng Z. An Investigation of the Energy-Absorption Characteristics of Thin-Walled Polymer Composite C-Channels: Experiment and Stacked Shell Simulation. Polymers. 2024; 16(15):2099. https://doi.org/10.3390/polym16152099
Chicago/Turabian StyleZhang, Xiaomin, Haolei Mou, Shanshan Song, and Zhenyu Feng. 2024. "An Investigation of the Energy-Absorption Characteristics of Thin-Walled Polymer Composite C-Channels: Experiment and Stacked Shell Simulation" Polymers 16, no. 15: 2099. https://doi.org/10.3390/polym16152099
APA StyleZhang, X., Mou, H., Song, S., & Feng, Z. (2024). An Investigation of the Energy-Absorption Characteristics of Thin-Walled Polymer Composite C-Channels: Experiment and Stacked Shell Simulation. Polymers, 16(15), 2099. https://doi.org/10.3390/polym16152099






