Validation of DOE Factorial/Taguchi/Surface Response Models of Mechanical Properties of Synthetic and Natural Fiber Reinforced Epoxy Matrix Hybrid Material
Abstract
1. Introduction
2. Materials and Methods
3. Results
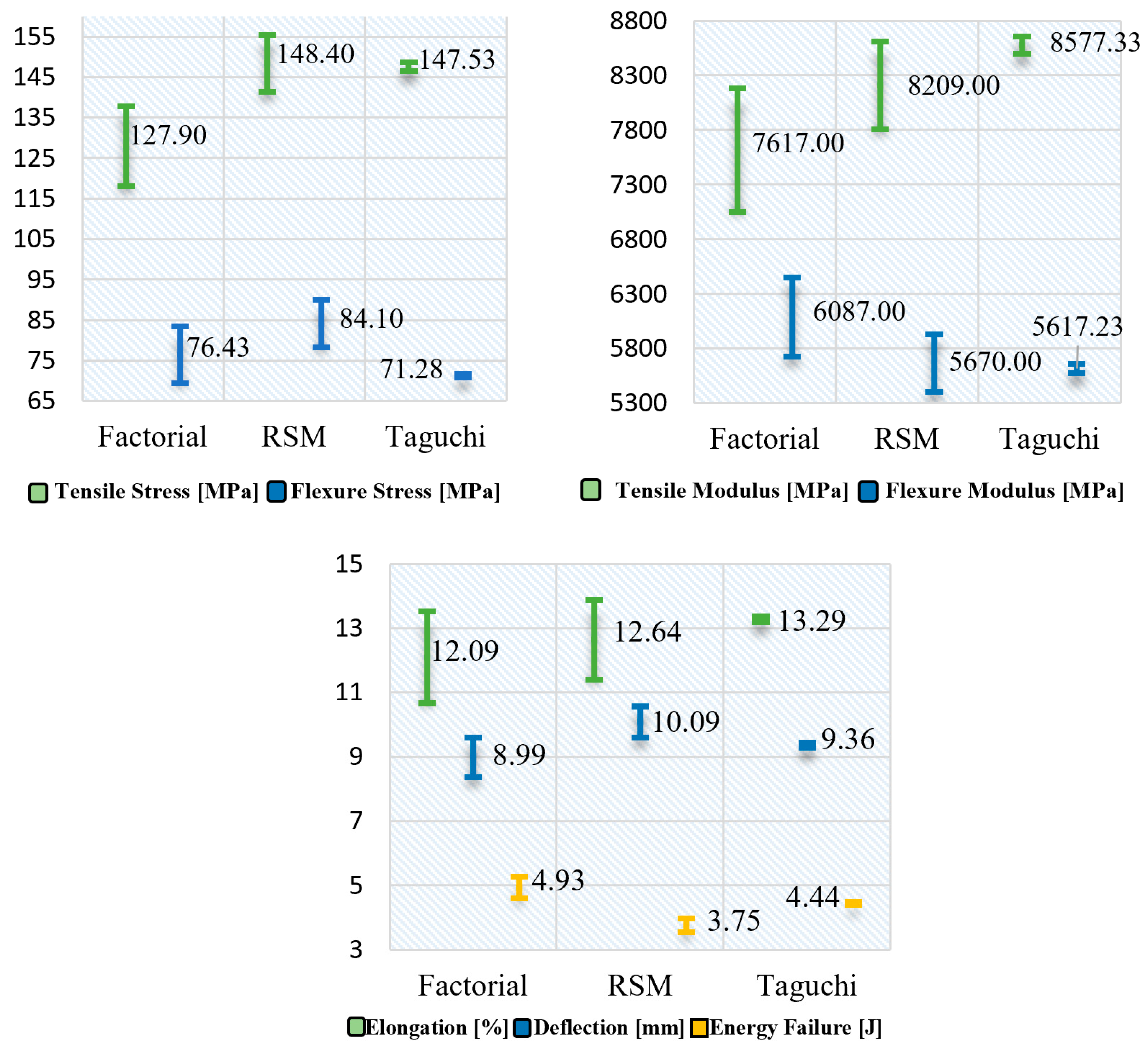
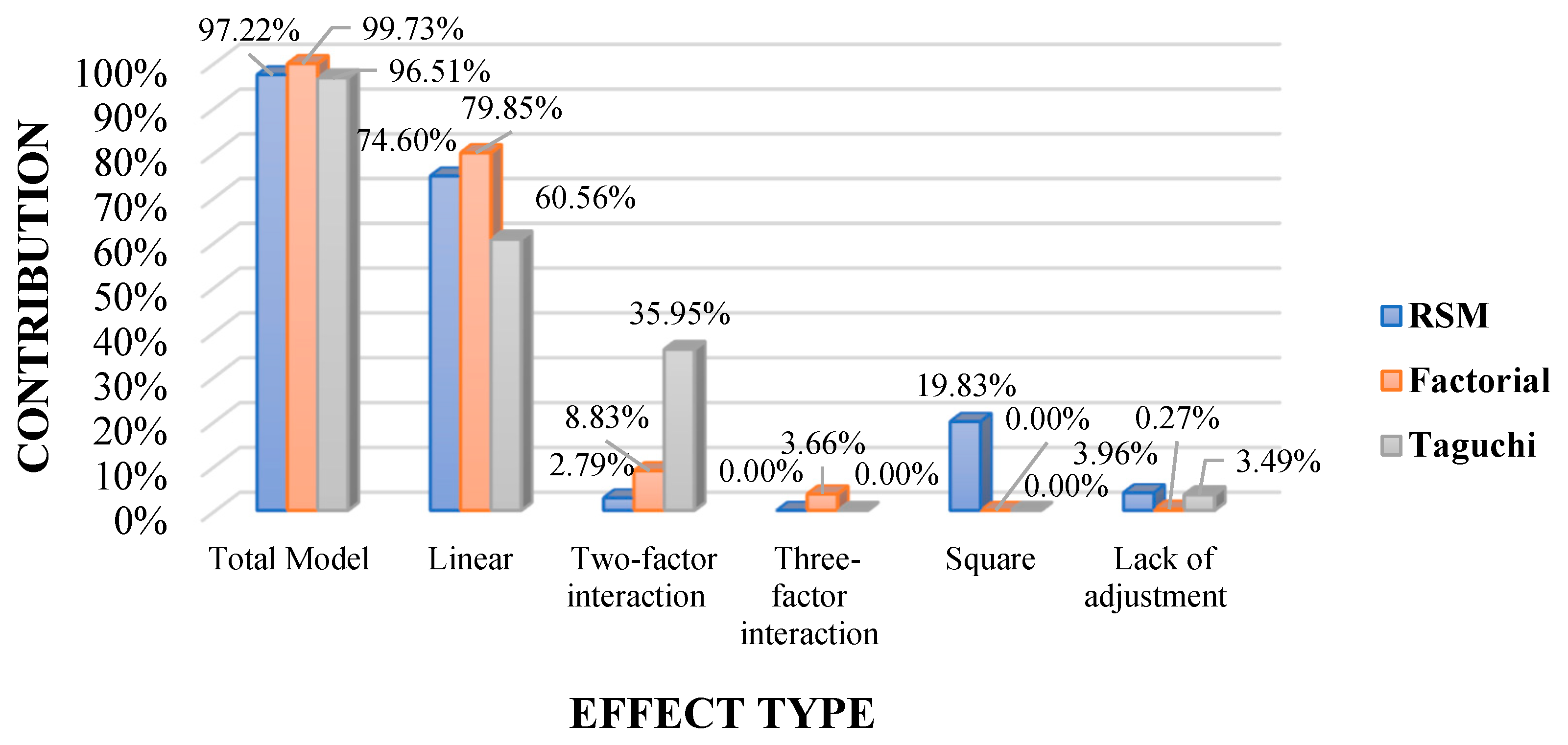
3.1. Comparative Analysis of Design of Experiments Models
3.1.1. Factorial Model
3.1.2. Taguchi Model
3.1.3. Response Surface Methodology Model (RSM)
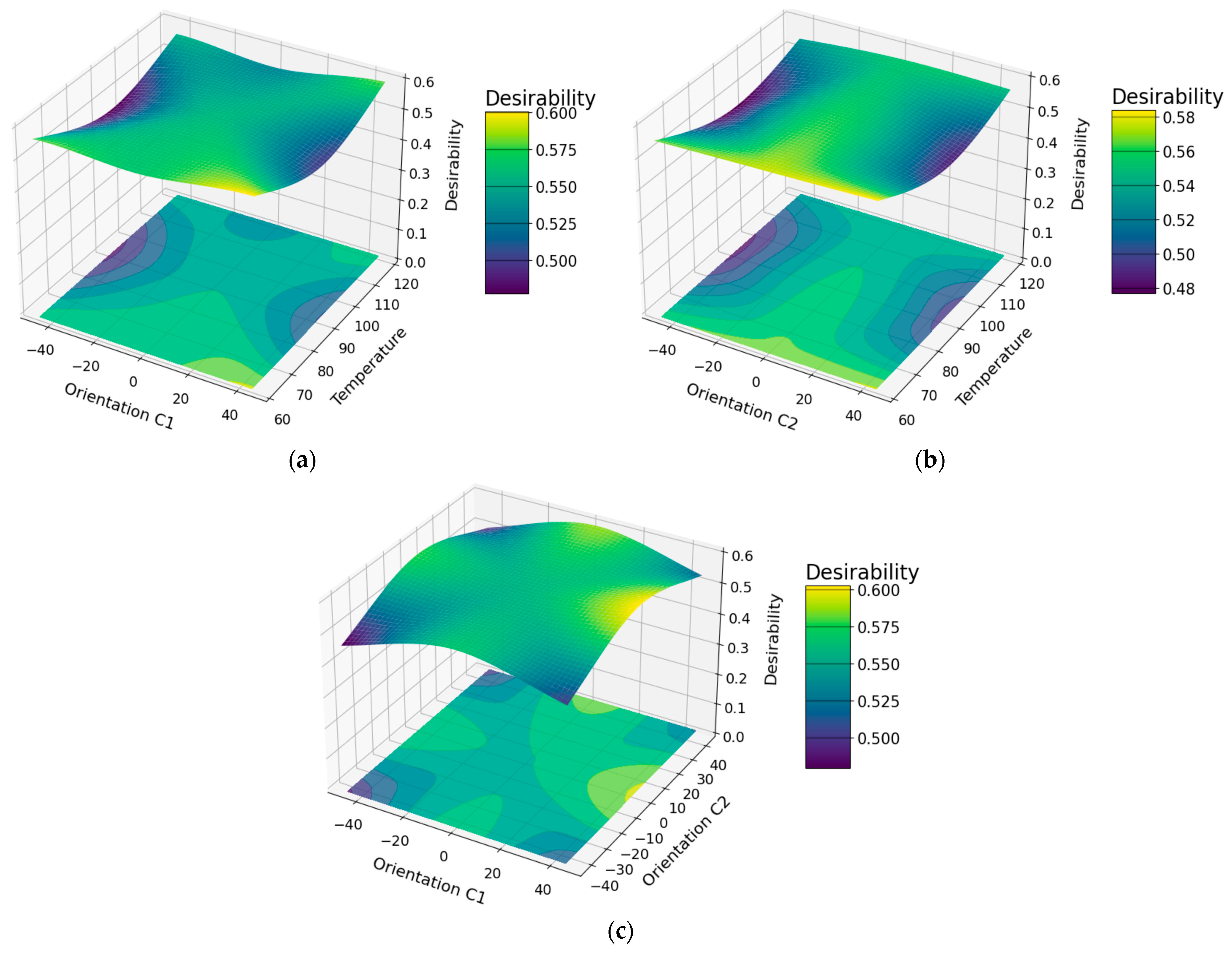
3.2. Optimization of the Mechanical Properties of Hybrid Material
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pozo Morales, A.R. Materiales Compuestos de Fibras Naturales. Doctoral Dissertation, Universidad Politécnica de Madrid, Madrid, Spain, 2019. [Google Scholar] [CrossRef]
- Luna, P.; Lizarazo-Marriaga, J.M. Natural fibers as reinforcement in polymer matrix composite materials. Momento 2022, 2022, 65–79. [Google Scholar] [CrossRef]
- Mora, W.; Ramon, B.; Moreno, G. Natural fibers as alternative reinforcement in composite materials. A review. Bistua J. Fac. Basic Sci. 2019, 17, 60–72. [Google Scholar]
- Guerrero, V.H.; Pontón, P.; Tamayo, A.; Villacís, H.; Delgado, F.; Galeas, S. Polyester matrix composites reinforced with natural and synthetic fibers. ESPE 2013, 8, 1. [Google Scholar]
- AL-Oqla, F.M.; Salit, M.S. Material selection of natural fiber composites using other methods. In Materials Selection for Natural Fiber Composites; Elsevier: Amsterdam, The Netherlands, 2017; pp. 235–272. [Google Scholar] [CrossRef]
- Miravete, A.; Cuartero, J. Materiales Compuestos 03, AEMAC., Reverté S.A, España, 2003. Volume 1. Available online: https://www.aemac.org/wp/wp-content/uploads/2015/05/MATCOMP03.pdf (accessed on 7 April 2024).
- Vedernikov, A.; Safonov, A.; Tucci, F.; Carlone, P.; Akhatov, I. Analysis of spring-in deformation in L-shaped profiles pultruded at different pulling speeds: Mathematical simulation and experimental results. In Proceedings of the ESAFORM 2021—24th International Conference on Material Forming, Liege, Belgium, 14–16 April 2021. [Google Scholar] [CrossRef]
- Kabir, S.; Shahed, C.A.; Ador, M.S.H.; Choudhury, I.A.; Ahmad, F. Review of the developments in composite materials over the last 15 years. Compr. Mater. Process. 2023, 12, 335–349. [Google Scholar] [CrossRef]
- Waghmare, S.; Shelare, S.; Aglawe, K.; Khope, P. A mini review on fibre reinforced polymer composites. Mater. Today Proc. 2021, 54, 682–689. [Google Scholar] [CrossRef]
- Palanisamy, S.; Vijayananth, K.; Murugesan, T.M.; Palaniappan, M.; Santulli, C. The Prospects of Natural Fiber Composites: A Brief Review. Int. J. Light. Mater. Manuf. 2024, 7, 496–506. [Google Scholar] [CrossRef]
- Batra, N.; Dikshit, I. Evaluation of mechanical properties of polytherimide reinforced carbon/glass/aramid hybrid composites. Mater. Today Proc. 2020, 33, 1472–1476. [Google Scholar] [CrossRef]
- Zuccarello, B.; Zingales, M. Toward high performance renewable agave reinforced biocomposites: Optimization of fiber performance and fiber-matrix adhesion analysis. Compos. Part B Eng. 2017, 122, 109–120. [Google Scholar] [CrossRef]
- Khalid, M.Y.; Imran, R.; Arif, Z.U.; Akram, N.; Arshad, H.; Al Rashid, A.; Márquez, F.P.G. Developments in Chemical Treatments, Manufacturing Techniques and Potential Applications of Natural-Fibers-Based Biodegradable Composites. Coatings 2021, 11, 293. [Google Scholar] [CrossRef]
- Ramesh, M.; Palanikumar, K.; Reddy, K.H. Plant fibre-based bio-composites: Sustainable and renewable green materials. Renew. Sustain. Energy Rev. 2017, 79, 558–584. [Google Scholar] [CrossRef]
- Begum, K.; Islam, M. Natural fiber as a substitute to synthetic fiber in polymer composites: A review. Res. J. Eng. Sci. 2013, 2278, 9472. [Google Scholar]
- Dicker, M.P.; Duckworth, P.F.; Baker, A.B.; Francois, G.; Hazzard, M.K.; Weaver, P.M. Green composites: A review of material attributes and complementary applications. Compos. Part A Appl. Sci. Manuf. 2014, 56, 280–289. [Google Scholar] [CrossRef]
- Peças, P.; Carvalho, H.; Salman, H.; Leite, M. Natural fibre composites and their applications: A review. J. Compos. Sci. 2018, 2, 66. [Google Scholar] [CrossRef]
- Chandgude, S.; Salunkhe, S. In state of art: Mechanical behavior of natural fiber-based hybrid polymeric composites for application of automobile components. Polym. Compos. 2021, 42, 2678–2703. [Google Scholar] [CrossRef]
- Schumann, R.A.; Meyer, J.H.; Antwerpen, V.R. Potential of lignocellulosic fiber reinforced polymer composites for automobile parts production: Current knowledge, research needs, and future direction. Heliyon 2024, 10, e24683. [Google Scholar] [CrossRef]
- Li, M.; Pu, Y.; Thomas, V.M.; Yoo, C.G.; Ozcan, S.; Deng, Y.; Nelson, K.; Ragauskas, A.J. Recent advancements of plant-based natural fiber–reinforced composites and their applications. Compos. Part B Eng. 2020, 200, 108254. [Google Scholar] [CrossRef]
- Manimaran, P.; Sanjay, M.R.; Senthamaraikannan, P.; Jawaid, M.; Saravanakumar, S.S.; George, R. Synthesis and characterization of cellulosic fiber from red banana peduncle as reinforcement for potential applications. J. Nat. Fibers 2018, 16, 768–780. [Google Scholar] [CrossRef]
- Mohammed, L.; Ansari, M.N.M.; Pua, G.; Jawaid, M.; Islam, M.S. A Review on Natural Fiber Reinforced Polymer Composite and Its Applications. Int. J. Polym. Sci. 2015, 2015, 243947. [Google Scholar] [CrossRef]
- Pickering, K.L.; Aruan Efendy, M.G.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Compos. Part A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef]
- Feng, Y.; Hao, H.; Lu, H.; Chow, C.L.; Lau, D. Exploring the development and applications of sustainable natural fiber composites: A review from a nanoscale perspective. Compos. Part B Eng. 2024, 276, 111369. [Google Scholar] [CrossRef]
- Rodríguez, A.; Valín, J.; Díaz, D.; Fonseca, V.; Sanabio, L. Development of a sisal fiber composite material using a thermoset matrix. Mech. Eng. 2014, 17. Available online: http://scielo.sld.cu/scielo.php?pid=S1815-59442014000300008&script=sci_arttext (accessed on 29 March 2024).
- Mora, W.; Ramon, B. Cumare palm natural fiber biocomposite (Astrocaryum chambira) and bioepoxy resin, industrial applications. Rev. Mater. Compuestos 2022, 2, 3. [Google Scholar] [CrossRef]
- Velumani, S.; Navaneethakrishnan, P.; Jayabal, S.; Smart, D.S.R. Optimization of mechanical properties of non-woven short sisal fibre-reinforced vinyl ester composite using factorial design and GA method. Bull. Mater. Sci. 2013, 36, 575–583. [Google Scholar] [CrossRef]
- Jankovic, A.; Chaudhary, G.; Goia, F. Designing the design of experiments (DOE)—An investigation on the influence of different factorial designs on the characterization of complex systems. Energy Build. 2021, 250, 111298. [Google Scholar] [CrossRef]
- Chen, W.-H.; Biswas, P.P.; Ubando, A.T.; Park, Y.-K.; Ashokkumar, V.; Chang, J.-S. Design of experiment for hydrogen production from ethanol reforming: A state-of-the-art review. Fuel 2023, 342, 127871. [Google Scholar] [CrossRef]
- de Olveira, L.; dos Santos, J.C.; Panzera, T.H.; Freire, R.T.S.; Vieira, L.M.G.; Rubio, J.C.C. Investigations on short coir fibre–reinforced composites via full factorial design. Polym. Polym. Compos. 2018, 26, 391–399. [Google Scholar] [CrossRef]
- de Castro, B.D.; Fotouhi, M.; Vieira, L.M.G.; de Faria, P.E.; Rubio, J.C.C. Mechanical Behaviour of a Green Composite from Biopolymers Reinforced with Sisal Fibres. J. Polym. Environ. 2021, 29, 429–440. [Google Scholar] [CrossRef]
- Mori, S.; Tenazoa, C.; Candiotti, S.; Flores, E.; Charca, S. Assessment of Ichu Fibers Extraction and Their Use as Reinforcement in Composite Materials. J. Nat. Fibers 2018, 17, 700–715. [Google Scholar] [CrossRef]
- Sailesh, A.; Palanikumar, K.; Arunkumar, R.; Ramu, P.; Briston, A.M.; Chandrakanth, E. Predicting the Best Flexural Strength of Banana-Bamboo-Glass Fiber Reinforced Natural Fiber Composites Using Taguchi Method. Appl. Mech. Mater. 2015, 766–767, 162–166. [Google Scholar] [CrossRef]
- Haniel; Bawono, B.; Anggoro, P. Optimization of Characteristics Polymer Composite Reinforced Kenaf and Jute Fiber Using Taguchi-Response Surface Methodology Approach. J. Nat. Fibers 2023, 20, 2204453. [Google Scholar] [CrossRef]
- Bezazi, A.; Boumediri, H.; del Pino, G.G.; Bezzazi, B.; Scarpa, F.; Reis, P.N.; Dufresne, A. Alkali Treatment Effect on Physicochemical and Tensile Properties of Date Palm Rachis Fibers. J. Nat. Fibers 2020, 19, 3770–3787. [Google Scholar] [CrossRef]
- Kumar, S.; Balachander, S. Studying the effect of reinforcement parameters on the mechanical properties of natural fibre-woven composites by Taguchi method. J. Ind. Text. 2019, 50, 133–148. [Google Scholar] [CrossRef]
- Sinha, A.K.; Bhattacharya, S.; Narang, H.K. Experimental determination and modelling of the mechanical properties of hybrid abaca-reinforced polymer composite using RSM. Polym. Polym. Compos. 2019, 27, 597–608. [Google Scholar] [CrossRef]
- Aly, M.; Hashmi, M.S.J.; Olabi, A.G.; Benyounis, K.Y.; Messeiry, M.; Hussain, A.I.; Abadir, E.F. Optimization of Alkaline Treatment Conditions of Flax Fiber Using Box-Behnken Method. J. Nat. Fibers 2012, 9, 256–276. [Google Scholar] [CrossRef]
- Salih, A.A.; Zulkifli, R.; Azhari, C.H. Tensile Properties of Single Cellulosic Bamboo Fiber (Gigantochloa Scortechinii) Using Response Surface Methodology. J. Nat. Fibers 2022, 19, 359–368. [Google Scholar] [CrossRef]
- Paredes, J. Optimización de Respuestas Múltiples (DOE/MSR) de Propiedades Mecánicas del Material Híbrido de Matriz Epoxi reforzada con Fibras Sintéticas y Natural (Chambira). Ph.D. Thesis, Universidad Nacional de Educación a Distancia, Madrid, Spain, 2023. Available online: https://hdl.handle.net/20.500.14468/17502 (accessed on 12 April 2024).
- Marín, M.; Millán, B.; Kahn, F. Anatomy and physicochemical properties of the chambira fiber. Rev. Peru. Biol. 2012, 19, 003–010. [Google Scholar] [CrossRef]
- Yukhymets, P.; Dmytriienko, R.I.; Ramadan, I.; Bukharov, S.N. Experimental Characterization of Composite Material Properties. In Non-Destructive Testing and Repair of Pipelines; Springer: Cham, Switzerland, 2018; pp. 227–237. [Google Scholar] [CrossRef]
- Setyabudi, S.A.; Choiron, M.A.; Purnowidodo, A. Effect of angle orientation lay-up on uniaxial tensile test specimen of Fiber carbon composite manufactured by using resin transfer moulding with vacuum bagging. IOP Conf. Ser. Mater. Sci. Eng. 2019, 494, 012020. [Google Scholar] [CrossRef]
- Popineau, V.; Célino, A.; Le Gall, M.; Martineau, L.; Baley, C.; Le Duigou, A. Vacuum-Bag-Only (VBO) Molding of Flax Fiber-reinforced Thermoplastic Composites for Naval Shipyards. Appl. Compos. Mater. 2021, 28, 791–808. [Google Scholar] [CrossRef]
- Juan, P.; Vinicio, S.; Henry, V.; Víctor, E.; Cesar, A. Factorial approach for multiple optimization of mechanical properties of alternative composite material for manufacture/repair flight surfaces (WING TIP—FAIRING ASSY)/CIDFAE. Mater. Today Proc. 2021, 44, 4757–4761. [Google Scholar] [CrossRef]
- Alaba, P.A.; Sani, Y.M.; Mohammed, I.Y.; Abakr, Y.A.; Daud, W.M.A.W. Synthesis of hierarchical nanoporous HY zeolites from activated kaolin, a central composite design optimization study. Adv. Powder Technol. 2017, 28, 1399–1410. [Google Scholar] [CrossRef]
- Yaghoobi, H.; Fereidoon, A. Thermal analysis, statistical predicting, and optimization of the flexural properties of natural fiber biocomposites using Box–Behnken experimental design. J. Nat. Fibers 2018, 16, 987–1005. [Google Scholar] [CrossRef]
- Tharazi, I.; Sulong, A.B.; Salleh, F.M.; Abdullah, A.H.; Ismail, N. Application of Response Surface Methodology for Parameters Optimization in Hot Pressing Kenaf Reinforced Biocomposites. J. Mech. Eng. 2020, 17, 131–144. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, X.; Jiang, S.; Ren, Y. Hybrid effects and interactive failure mechanisms of hybrid fiber composites under flexural loading: Carbon/Kevlar, carbon/glass, carbon/glass/Kevlar. Aerosp. Sci. Technol. 2023, 133, 108105. [Google Scholar] [CrossRef]
- Mohit, H.; Rangappa, S.M.; Gapsari, F.; Siengchin, S.; Marwani, H.M.; Khan, A.; Asiri, A.M. Effect of bio-fibers and inorganic fillers reinforcement on mechanical and thermal characteristics on carbon-kevlar-basalt-innegra fiber bio/ synthetic epoxy hybrid composites. J. Mater. Res. Technol. 2023, 23, 5440–5458. [Google Scholar] [CrossRef]
- Rajak, D.K.; Pagar, D.D.; Kumar, R.; Pruncu, C.I. Recent progress of reinforcement materials: A comprehensive overview of composite materials. J. Mater. Res. Technol. 2019, 8, 6354–6374. [Google Scholar] [CrossRef]
- Gajjar, T.; Shah, D.B.; Joshi, S.; Patel, K. Analysis of Process Parameters for Composites Manufacturing using Vacuum Infusion Process. Mater. Today Proc. 2020, 21, 1244–1249. [Google Scholar] [CrossRef]
- Yalcinkaya, M.A.; Guloglu, G.E.; Pishvar, M.; Amirkhosravi, M.; Sozer, E.M.; Altan, M.C. Pressurized Infusion: A New and Improved Liquid Composite Molding Process. J. Manuf. Sci. Eng. 2018, 141, 367164. [Google Scholar] [CrossRef]
- Zaheer, U.; Zulfiqar, U.; Khurram, A.A.; Subhani, T. Improving the performance of conventional glass fiber epoxy matrix composites by incorporating nanodiamonds. Compos. Interfaces 2018, 25, 1005–1018. [Google Scholar] [CrossRef]
- Fahim, I.S.; Elhaggar, S.M.; Elayat, H. Experimental Investigation of Natural Fiber Reinforced Polymers. Mater. Sci. Appl. 2012, 3, 59–66. [Google Scholar] [CrossRef]
- Bounouri, Y.; Berkani, M.; Zamouche, A.; Rycerz, L. Optimization and modeling of synthesis parameters of neodymium (III) bromide by dry method using full factorial design analysis. Arab. J. Chem. 2020, 13, 366–376. [Google Scholar] [CrossRef]
- Taguchi, G.; Phadke, M.S. Quality engineering through design optimization. In Quality Control, Robust Design, and the Taguchi Method; Springer: Boston, MA, USA, 1989; pp. 77–96. [Google Scholar]
- Hiwa, B.; Ahmed, Y.M.; Rostam, S. Evaluation of tensile properties of Meriz fiber reinforced epoxy composites using Taguchi method. Results Eng. 2023, 18, 101037. [Google Scholar] [CrossRef]
- Raissi, S.; Farsani, R. Statistical Process Optimization Through Multi-Response Surface Methodology. Int. J. Math. Comput. Sci. 2009, 3, 3. [Google Scholar]
- Chaudhuri, S.; Chakraborty, R.; Bhattacharya, P. Optimization of biodegradation of natural fiber (Chorchorus capsularis): HDPE composite using response surface methodology. Iran. Polym. J. 2013, 22, 865–875. [Google Scholar] [CrossRef]
- Caridad, C.; Guerra-Bustillo, W.; Alejandro, L. Mathematical-Statistical Modeling in Response Surface Methodology. Agric. Eng. Mag. 2018, 8, 67–73. [Google Scholar] [CrossRef]
- Benkhelladi, A.; Laouici, H.; Bouchoucha, A. Tensile and flexural properties of polymer composites reinforced by flax, jute and sisal fibres. Int. J. Adv. Manuf. Technol. 2020, 108, 895–916. [Google Scholar] [CrossRef]
- Asma, B.; Hamdi, L.; Ali, B.; Youcef, M. Flexural Mechanical Properties of Natural Fibre Reinforced Polymer Composites—A Statistical Investigation. Fibers Polym. 2020, 21, 2321–2337. [Google Scholar] [CrossRef]
- Mohammed, B.S.; Khed, V.C.; Nuruddin, M.F. Rubbercrete mixture optimization using response surface methodology. J. Clean. Prod. 2018, 171, 1605–1621. [Google Scholar] [CrossRef]
- Costa, N.R.; Lourenço, J.; Pereira, Z.L. Desirability function approach: A review and performance evaluation in adverse conditions. Chemom. Intell. Lab. Syst. 2011, 107, 234–244. [Google Scholar] [CrossRef]
- Lee, D.; Jeong, I.; Kim, K. A desirability function method for optimizing mean and variability of multiple responses using a posterior preference articulation approach. Qual. Reliab. Eng. Int. 2018, 34, 360–376. [Google Scholar] [CrossRef]
- Hasan, M.; Rahman, M.; Chen, Y.; Cicek, N. Optimization of Typha Fibre Extraction and Properties for Bio-Composite Applications Using Desirability Function Analysis. Polymers 2022, 14, 1685. [Google Scholar] [CrossRef] [PubMed]
- Huamani-H, A.; Ponce-Ramírez, J.; Málaga-Juárez, J. Optimization of the quinoa cooking process using the 3k design and the desirability function: Degree of gelatinization, water absorption index, solubility index and cotyledon detachment. Sci. Agropecu. 2020, 11, 381–390. [Google Scholar] [CrossRef]

| Fiber | World Production (103 ton) | Application in Building, Construction and Others |
|---|---|---|
| Hemp fiber | 214 | Construction products, textiles, cordage, geotextiles, paper and packaging, furniture, electrical, manufacture bank notes and manufacture of pipes |
| Flax fiber | 830 | Window frame, panels, decking, railing systems, fencing, tennis racket, bicycle frame, fork, seat post, snowboarding and laptop cases |
| Bagasse fiber | 7500 | Window frame, panels, decking, railing systems and fencing |
| Sisal fiber | 375 | In construction industry such as panels, doors, shutting plate and roofing sheets; also, manufacturing of paper and pulp |
| Kenaf fiber | 970 | Packing material, mobile cases, bags, insulations, clothing-grade cloth, soilless potting mixes, animal bedding, and material that absorbs oil and liquids |
| Coir fibers | 100 | Building panels, flush door shutters, roofing sheets, storage tank, packing material, helmets and postboxes, mirror casing, paper weights, projector cover, voltage stabilizer cover, a filling material for the seat upholstery, brushes and brooms, ropes and yarns for nets, bags, and mats, as well as padding for mattresses, seat cushions |
| Ramie fiber | 100 | Use in products as industrial sewing thread, packing materials, fishing nets, and filter cloths. It is also made into fabrics for household furnishings (upholstery, canvas) and clothing, paper manufacture. |
| Jute fiber | 2300 | Building panels, roofing sheets, door frames, door shutters, transport, packaging, geotextiles, and chip boards. |
| Fiber | Density (g/cm3) | Tensile Strength (MPa) | Young’s Modulus (GPa) | Elongation at Break (%) |
|---|---|---|---|---|
| OPEFB | 0.70–1.55 | 248 | 3.2 | 2.5 |
| Linseed | 1.40 | 88–1500 | 60–80 | 1.2–1.6 |
| Hemp | 1.48 | 550–900 | 70 | 1.6 |
| Jute | 1.46 | 400–800 | 10–30 | 1.8 |
| Coconut fiber | 1.25 | 220 | 6 | 15–25 |
| Sisal | 1.33 | 600–700 | 38 | 2–3 |
| Abaca | 1.50 | 980 | — | — |
| Cotton | 1.51 | 400 | 12 | 3–10 |
| Kenaf (bast) | 1.20 | 295 | — | 2.7–6.9 |
| Bagasse | 1.20 | 20–290 | 19.7–27.1 | 1.1 |
| Henequen | 1.40 | 430–580 | — | 3.0–4.7 |
| Pineapple | 1.50 | 170–1672 | 82 | 1–3 |
| Banana | 1.35 | 355 | 33.8 | 53 |
| Cumare or Chambira | 1.20 | 220.5 | 6.4 | 24.4 |
| Property Mechanical | N. Treatment | Orientation Fiber C1 [Degrees] | Orientation Fiber C2 [Degrees] | Temp [°C] | Fiber | Process | Standard Deviation [S] | Coefficient Variation [CV] | |
|---|---|---|---|---|---|---|---|---|---|
| Maximum Tensile Stress [MPa] | 90 | −45, 0, 45 | −45, 0, 45 | 60, 90, 120 | Carbon | Empty | 115.00 | 17.11 | 14.88% |
| Infusion | 103.66 | 16.52 | 15.94% | ||||||
| Glass | Empty | 81.37 | 13.32 | 16.37% | |||||
| Infusion | 79.52 | 11.64 | 14.64% | ||||||
| Kevlar | Empty | 129.33 | 17.73 | 13.71% | |||||
| Infusion | 126.18 | 16.85 | 13.35% | ||||||
| Modulus Elasticity Tensile [MPa] | 90 | −45, 0, 45 | −45, 0, 45 | 60, 90, 120 | Carbon | Empty | 9999.89 | 1580.55 | 15.81% |
| Infusion | 15,952.37 | 1935.92 | 12.14% | ||||||
| Glass | Empty | 5632.29 | 1025.51 | 18.21% | |||||
| Infusion | 5964.37 | 859.13 | 14.40% | ||||||
| Kevlar | Empty | 13,441.81 | 2124.36 | 15.80% | |||||
| Infusion | 7044.92 | 1191.75 | 16.92% | ||||||
| Elongation [%] | 90 | −45, 0, 45 | −45, 0, 45 | 60, 90, 120 | Carbon | Empty | 6.02 | 1.03 | 17.19% |
| Infusion | 3.14 | 0.57 | 18.20% | ||||||
| Glass | Empty | 7.20 | 1.17 | 16.18% | |||||
| Infusion | 8.41 | 1.59 | 18.90% | ||||||
| Kevlar | Empty | 6.77 | 1.13 | 16.70% | |||||
| Infusion | 11.76 | 2.09 | 17.80% | ||||||
| Maximum Flexure Stress [MPa] | 90 | −45, 0, 45 | −45, 0, 45 | 60, 90, 120 | Carbon | Empty | 49.48 | 8.51 | 17.19% |
| Infusion | 67.90 | 13.51 | 19.90% | ||||||
| Glass | Empty | 69.80 | 13.55 | 19.42% | |||||
| Infusion | 76.12 | 14.16 | 18.61% | ||||||
| Kevlar | Empty | 65.06 | 11.37 | 17.48% | |||||
| Infusion | 68.67 | 12.22 | 17.80% | ||||||
| Modulus Elasticity Flexure [MPa] | 90 | −45, 0, 45 | −45, 0, 45 | 60, 90, 120 | Carbon | Empty | 3238.33 | 631.98 | 19.52% |
| Infusion | 7480.91 | 1233.15 | 16.48% | ||||||
| Glass | Empty | 2920.62 | 578.90 | 19.82% | |||||
| Infusion | 5170.04 | 747.67 | 14.46% | ||||||
| Kevlar | Empty | 2683.98 | 428.80 | 15.98% | |||||
| Infusion | 5018.09 | 847.50 | 16.89% | ||||||
| Deflection [mm] | 90 | −45, 0, 45 | −45, 0, 45 | 60, 90, 120 | Carbon | Empty | 7.37 | 1.43 | 19.44% |
| Infusion | 9.30 | 1.71 | 18.42% | ||||||
| Glass | Empty | 7.73 | 1.40 | 18.17% | |||||
| Infusion | 10.39 | 1.94 | 18.67% | ||||||
| Kevlar | Empty | 7.98 | 1.32 | 16.53% | |||||
| Infusion | 10.09 | 1.93 | 19.11% | ||||||
| Energy Failure [J] | 90 | −45, 0, 45 | −45, 0, 45 | 60, 90, 120 | Carbon | Empty | 2.79 | 0.55 | 19.62% |
| Infusion | 4.26 | 0.81 | 18.91% | ||||||
| Glass | Empty | 5.18 | 0.98 | 18.91% | |||||
| Infusion | 5.33 | 0.99 | 18.61% | ||||||
| Kevlar | Empty | 4.38 | 0.81 | 18.46% | |||||
| Infusion | 4.38 | 0.81 | 18.46% |
| DOE Model Source | Hypothesis | Description |
|---|---|---|
| Molding process | H0 | The average mechanical properties with the vacuum casting and infusion process are similar. |
| H1 | The average mechanical properties with the vacuum casting and infusion process are different. | |
| Synthetic fiber type | H0 | All averages of mechanical properties with the synthetic fiber types glass, carbon and Kevlar are similar. |
| H1 | At least one of the pairs of average mechanical properties with the synthetic fiber types glass, carbon and Kevlar is different. | |
| Orientation FCh. C1 * | H0 | All mechanical property averages with the orientations of the first layer of Chambira natural fiber at −45°, 0° and 45° are similar. |
| H1 | At least one of the pairs of average mechanical properties with the orientations of the first layer of Chambira natural fiber at −45°, 0° and 45° is different. | |
| Orientation FCh. C2 * | H0 | All mechanical property averages with the second layer orientations of Chambira natural fiber at −45°, 0° and 45° are similar. |
| H1 | At least one of the pairs of average mechanical properties with the orientations of the second layer of Chambira natural fiber at −45°, 0° and 45° is different. | |
| Temperature | H0 | All mechanical property averages at the drying temperatures of 60 °C, 90 °C and 120 °C are similar. |
| H1 | At least one of the pairs of average mechanical properties at drying temperatures of 60 °C, 90 °C and 120 °C is different. | |
| Linear and quadratic iterations | H0 | All mechanical property means with linear and quadratic iterations of the model sources are similar. |
| H1 | At least one of the pairs in averages of the mechanical properties with linear and quadratic iterations of the model sources is different. |
| ANOVA | p-Value | ||||||
|---|---|---|---|---|---|---|---|
| Full Factor Model Source | Tensile Stress | Modulus Elasticity Tensile | Elongation | Flexure Stress | Modulus Elasticity Flexure | Deflection | Energy Failure |
| Model | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Linear | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Orientation FCh * C1 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.015 | 0.000 |
| Orientation FCh * C2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Temperature | 0.000 | 0.093 | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 |
| Moldeo | 0.000 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Synthetic Fiber | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Two-term interactions | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Orient. FCh * C1_Moldeo | 0.411 | 0.745 | 0.032 | 0.000 | 0.752 | 0.000 | 0.579 |
| Orient. FCh * C1_Synthetic Fiber | 0.000 | 0.025 | 0.000 | 0.002 | 0.012 | 0.000 | 0.000 |
| Orient. FCh * C2_Moldeo | 0.479 | 0.014 | 0.105 | 0.000 | 0.040 | 0.018 | 0.606 |
| Orient. FCh * C2_ Synthetic Fiber | 0.014 | 0.071 | 0.000 | 0.000 | 0.009 | 0.000 | 0.000 |
| Temperature_Moldeo | 0.414 | 0.007 | 0.086 | 0.000 | 0.000 | 0.000 | 0.637 |
| Temperature_Synthetic Fiber | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Moldeo_Synthetic Fiber | 0.044 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 |
| Three-term interactions | 0.002 | 0.007 | 0.000 | 0.000 | 0.000 | 0.000 | 0.966 |
| Orient. C1_Moldeo_Synthetic Fiber | 0.557 | 0.719 | 0.063 | 0.006 | 0.590 | 0.000 | 0.793 |
| Orient. C2_Moldeo_Synthetic Fiber | 0.050 | 0.006 | 0.163 | 0.068 | 0.000 | 0.286 | 0.732 |
| Temp_Moldeo_Synthetic Fiber | 0.001 | 0.023 | 0.000 | 0.000 | 0.000 | 0.000 | 0.808 |
| Normality (Kolmogorov-Smirnov) | 0.060 | 0.150 | 0.150 | 0.074 | 0.128 | 0.080 | 0.005 |
| Full Factor Model Parameters | |||||||
| S (Standard Deviation) | 0.10 | 0.10 | 0.02 | 0.01 | 0.08 | 0.77 | 0.02 |
| R2 (%) | 85.26 | 95.49 | 94.75 | 81.18 | 96.81 | 87.47 | 91.52 |
| R2 Adjusted (%) | 82.60 | 94.68 | 93.81 | 77.79 | 96.24 | 85.22 | 89.99 |
| R2 Prediction (%) | 79.16 | 93.76 | 92.53 | 73.33 | 95.56 | 82.43 | 88.13 |
| ANOVA | p-Value | ||||||
|---|---|---|---|---|---|---|---|
| Modified Factor Model Source | Tensile Stress | Modulus Elasticity Tensile | Elongation | Flexure Stress | Modulus Elasticity Flexure | Deflection | Energy Failure |
| Model | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Linear | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Orientation FCh * C1 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.016 | 0.000 |
| Orientation FCh * C2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Temperature | 0.000 | 0.091 | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 |
| Moldeo | 0.000 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Synthetic Fiber | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Two-term interactions | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Orient. FCh * C1_Moldeo | 0.418 | 0.743 | 0.035 | 0.000 | 0.751 | 0.000 | 0.570 |
| Orient. FCh * C1_Synthetic Fiber | 0.000 | 0.024 | 0.000 | 0.003 | 0.011 | 0.000 | 0.000 |
| Orient. FCh * C2_Moldeo | 0.485 | 0.014 | 0.112 | 0.000 | 0.039 | 0.018 | 0.596 |
| Orient. FCh * C2_ Synthetic Fiber | 0.015 | 0.069 | 0.000 | 0.000 | 0.009 | 0.000 | 0.000 |
| Temperature_Moldeo | 0.420 | 0.006 | 0.092 | 0.000 | 0.000 | 0.000 | 0.628 |
| Temperature_Synthetic Fiber | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Moldeo_Synthetic Fiber | 0.103 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 |
| Three-term interactions | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | - |
| Orient. C1_Moldeo_Synthetic Fiber | - | 0.007 | - | 0.005 | - | 0.000 | - |
| Orient. C2_Moldeo_Synthetic Fiber | - | - | - | - | 0.000 | - | - |
| Temp_Moldeo_Synthetic Fiber | 0.001 | 0.021 | 0.000 | 0.000 | 0.000 | 0.000 | - |
| Normality (Kolmogorov-Smirnov) | 0.078 | 0.150 | 0.071 | 0.074 | 0.128 | 0.150 | 0.05 |
| Modified Factor Model Parameters | |||||||
| S (Standard Deviation) | 0.11 | 0.10 | 0.02 | 0.01 | 0.08 | 0.77 | 0.02 |
| R2 (%) | 84.47 | 95.45 | 94.41 | 80.45 | 96.77 | 87.20 | 91.34 |
| R2 Adjusted (%) | 82.29 | 94.73 | 93.62 | 77.33 | 96.26 | 85.15 | 90.30 |
| R2 Prediction (%) | 79.59 | 93.90 | 92.58 | 73.43 | 95.67 | 82.66 | 89.18 |
| ANOVA | p-Value | ||||||
|---|---|---|---|---|---|---|---|
| Taguchi Model Source without Iterations | Tensile Stress | Modulus Elasticity Tensile | Elongation | Flexure Stress | Modulus Elasticity Flexure | Deflection | Energy Failure |
| Orientation FCh * C1 | 0.001 | 0.267 | 0.748 | 0.330 | 0.789 | 0.548 | 0.058 |
| Orientation FCh * C2 | 0.000 | 0.132 | 0.601 | 0.000 | 0.000 | 0.000 | 0.227 |
| Temperature | 0.084 | 0.878 | 0.731 | 0.032 | 0.947 | 0.011 | 0.007 |
| Moldeo | 0.031 | 0.916 | 0.032 | 0.000 | 0.000 | 0.000 | 0.005 |
| Synthetic Fiber | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.039 | 0.000 |
| Normality (Kolmogorov-Smirnov) | 0.150 | 0.057 | 0.150 | 0.144 | 0.150 | 0.150 | 0.099 |
| Taguchi Model parameters without iterations | |||||||
| S (Standard Deviation) | 11.76 | 2860.81 | 2.18 | 10.41 | 738.02 | 1.10 | 0.84 |
| R2 (%) | 78.54 | 76.10 | 75.49 | 73.18 | 85.40 | 74.53 | 73.27 |
| R2 Adjusted (%) | 75.69 | 70.29 | 71.68 | 71.98 | 83.47 | 71.16 | 71.09 |
| ANOVA | p-Value | ||||||
|---|---|---|---|---|---|---|---|
| Taguchi Model Source with Iterations | Tensile Stress | Modulus Elasticity Tensile | Elongation | Flexure Stress | Modulus Elasticity Flexure | Deflection | Energy Failure |
| Orientation FCh * C1 | 0.002 | 0.000 | 0.386 | 0.305 | 0.602 | 0.457 | 0.001 |
| Orientation FCh * C2 | 0.000 | 0.000 | 0.192 | 0.000 | 0.000 | 0.000 | 0.019 |
| Temperature | 0.096 | 0.268 | 0.357 | 0.027 | 0.889 | 0.004 | 0.000 |
| Moldeo | 0.035 | 0.678 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Synthetic Fiber | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.024 | 0.000 |
| Orient. FCh * C1_Moldeo | 0.916 | 0.901 | 0.639 | 0.147 | 0.819 | 0.338 | 0.954 |
| Orient. FCh * C1_Synthetic Fiber | 0.470 | 0.824 | 0.188 | 0.567 | 0.845 | 0.281 | 0.000 |
| Orient. FCh * C2_Moldeo | 0.807 | 0.176 | 0.844 | 0.200 | 0.158 | 0.550 | 0.922 |
| Orient. FCh * C2_ Synthetic Fiber | 0.870 | 0.707 | 0.203 | 0.550 | 0.315 | 0.530 | 0.001 |
| Temperature_Moldeo | 0.638 | 0.030 | 0.350 | 0.034 | 0.006 | 0.000 | 0.950 |
| Temperature_Synthetic Fiber | 0.193 | 0.005 | 0.021 | 0.563 | 0.058 | 0.130 | 0.000 |
| Moldeo_Synthetic Fiber | 0.411 | 0.000 | 0.000 | 0.095 | 0.000 | 0.311 | 0.000 |
| Normality (Kolmogorov-Smirnov) | 0.150 | 0.150 | 0.061 | 0.150 | 0.150 | 0.150 | 0.050 |
| Taguchi Model Parameters with Iterations | |||||||
| S (Standard Deviation) | 11.99 | 889.30 | 1.19 | 10.01 | 503.37 | 0.959 | 0.50 |
| R2 (%) | 84.24 | 97.01 | 89.10 | 82.42 | 95.20 | 86.32 | 84.34 |
| R2 Adjusted (%) | 77.71 | 95.20 | 85.52 | 80.95 | 92.31 | 78.06 | 81.30 |
| ANOVA | p-Value | ||||||
|---|---|---|---|---|---|---|---|
| Initial RSM Model Source | Tensile Stress | Modulus Elasticity Tensile | Elongation | Flexure Stress | Modulus Elasticity Flexure | Deflection | Energy Failure |
| Model | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Linear | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Orientation FCh * C1 | 0.486 | 0.446 | 0.455 | 0.202 | 0.031 | 0.081 | 0.018 |
| Orientation FCh *C2 | 0.350 | 0.151 | 0.606 | 0.448 | 0.477 | 0.000 | 0.640 |
| Temperature | 0.001 | 0.114 | 0.000 | 0.000 | 0.067 | 0.000 | 0.014 |
| Moldeo | 0.001 | 0.005 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| Synthetic Fiber | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Square | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Orient. FCh * C1_Orient.FCh * C1 | 0.000 | 0.000 | 0.002 | 0.001 | 0.106 | 0.199 | 0.000 |
| Orient. FCh * C2_Orient. FCh * C2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Temperature _Temperature | 0.078 | 0.220 | 0.915 | 0.441 | 0.027 | 0.000 | 0.000 |
| Two-term interactions | 0.155 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Orient. FCh * C1_Orient. FCh * C2 | 0.535 | 0.002 | 0.675 | 0.000 | 0.408 | 0.177 | 0.043 |
| Orient. FCh * C1_Temperature | 0.645 | 0.930 | 0.057 | 0.573 | 0.566 | 0.856 | 0.014 |
| Orient. FCh * C1_Moldeo | 0.310 | 0.995 | 0.052 | 0.095 | 0.808 | 0.790 | 0.976 |
| Orient. FCh * C1_ Synthetic Fiber | 0.801 | 0.563 | 0.667 | 0.136 | 0.471 | 0.320 | 0.003 |
| Orient. FCh * C2_Temperature | 0.637 | 0.119 | 0.001 | 0.177 | 0.461 | 0.584 | 0.157 |
| Orient. FCh * C2_Moldeo | 0.725 | 0.062 | 0.250 | 0.036 | 0.930 | 0.385 | 0.745 |
| Orient. FCh * C2_Synthetic Fiber | 0.127 | 0.482 | 0.771 | 0.003 | 0.543 | 0.379 | 0.000 |
| Temperature_Moldeo | 0.255 | 0.056 | 0.117 | 0.000 | 0.000 | 0.000 | 0.951 |
| Temperature_Synthetic Fiber | 0.116 | 0.029 | 0.000 | 0.044 | 0.000 | 0.000 | 0.000 |
| Moldeo_Synthetic Fiber | 0.027 | 0.000 | 0.000 | 0.000 | 0.000 | 0.049 | 0.000 |
| Normality (Kolmogorov-Smirnov) | 0.056 | 0.150 | 0.150 | 0.150 | 0.069 | 0.053 | 0.005 |
| Full RSM Model Parameters | |||||||
| S (Standard Deviation) | 0.12 | 0.11 | 0.03 | 0.01 | 0.99 | 1.03 | 0.03 |
| R2 (%) | 85.35 | 94.19 | 89.70 | 83.22 | 94.53 | 75.64 | 82.85 |
| R2 Adjusted (%) | 81.33 | 93.65 | 88.73 | 80.22 | 94.02 | 73.36 | 81.24 |
| R2 Prediction (%) | 78.64 | 93.06 | 87.52 | 76.00 | 93.39 | 70.88 | 79.87 |
| ANOVA | p-Value | ||||||
|---|---|---|---|---|---|---|---|
| Modified RSM Model Source | Tensile Stress | Modulus Elasticity Tensile | Elongation | Flexure Stress | Modulus Elasticity Flexure | Deflection | Energy Failure |
| Model | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Linear | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Orientation FCh * C1 | 0.488 | 0.449 | 0.457 | 0.205 | 0.030 | - | 0.017 |
| Orientation FCh * C2 | 0.353 | 0.154 | 0.608 | 0.451 | 0.475 | 0.000 | 0.638 |
| Temperature | 0.001 | 0.117 | 0.000 | 0.000 | 0.065 | 0.000 | 0.013 |
| Moldeo | 0.001 | 0.005 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| Synthetic Fiber | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Square | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Orient. FCh * C1_Orient. FCh * C1 | 0.000 | 0.000 | 0.002 | 0.001 | - | - | 0.000 |
| Orient. FCh * C2_Orient. FCh * C2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Temperature _Temperature | - | - | - | - | 0.018 | 0.000 | 0.000 |
| Two-term interactions | 0.028 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Orient. FCh * C1_Orient. FCh * C2 | - | 0.002 | 0.001 | 0.000 | - | - | 0.042 |
| Orient. FCh * C1_Temperature | - | - | - | - | - | - | 0.014 |
| Orient. FCh * C1_ Synthetic Fiber | - | - | - | - | - | - | 0.003 |
| Orient. FCh * C2_Temperature | - | - | - | - | - | - | 0.000 |
| Orient. FCh * C2_Moldeo | - | - | - | 0.037 | - | - | - |
| Orient. FCh * C2_Synthetic Fiber | - | - | - | 0.004 | - | - | - |
| Temperature_Moldeo | - | - | - | 0.000 | 0.000 | 0.000 | - |
| Temperature_Synthetic Fiber | - | 0.031 | 0.000 | 0.046 | 0.000 | 0.000 | 0.000 |
| Moldeo_Synthetic Fiber | 0.028 | 0.000 | 0.000 | 0.000 | 0.000 | 0.049 | 0.000 |
| Normality (Kolmogorov-Smirnov) | 0.052 | 0.150 | 0.150 | 0.150 | 0.051 | 0.150 | 0.005 |
| Modified MSR Model Parameters | |||||||
| S (Standard Deviation) | 0.12 | 0.11 | 0.03 | 0.01 | 0,10 | 1.04 | 0.03 |
| R2 (%) | 83.00 | 93.87 | 89.16 | 81.90 | 94.38 | 74.45 | 82.70 |
| R2 Adjusted (%) | 81.11 | 93.56 | 88.61 | 79.74 | 94.09 | 73.26 | 81.38 |
| R2 Prediction (%) | 79.96 | 93.20 | 87.86 | 77.17 | 93.77 | 71.81 | 80.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toapanta, O.G.; Paredes, J.; Meneses, M.; Salinas, G. Validation of DOE Factorial/Taguchi/Surface Response Models of Mechanical Properties of Synthetic and Natural Fiber Reinforced Epoxy Matrix Hybrid Material. Polymers 2024, 16, 2051. https://doi.org/10.3390/polym16142051
Toapanta OG, Paredes J, Meneses M, Salinas G. Validation of DOE Factorial/Taguchi/Surface Response Models of Mechanical Properties of Synthetic and Natural Fiber Reinforced Epoxy Matrix Hybrid Material. Polymers. 2024; 16(14):2051. https://doi.org/10.3390/polym16142051
Chicago/Turabian StyleToapanta, Oscar G., Juan Paredes, Manuel Meneses, and Gabriela Salinas. 2024. "Validation of DOE Factorial/Taguchi/Surface Response Models of Mechanical Properties of Synthetic and Natural Fiber Reinforced Epoxy Matrix Hybrid Material" Polymers 16, no. 14: 2051. https://doi.org/10.3390/polym16142051
APA StyleToapanta, O. G., Paredes, J., Meneses, M., & Salinas, G. (2024). Validation of DOE Factorial/Taguchi/Surface Response Models of Mechanical Properties of Synthetic and Natural Fiber Reinforced Epoxy Matrix Hybrid Material. Polymers, 16(14), 2051. https://doi.org/10.3390/polym16142051








