Aramid Honeycomb Cores under Constant Pressure: Unveiling the Out-of-Plane Compression Deformation
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Materials
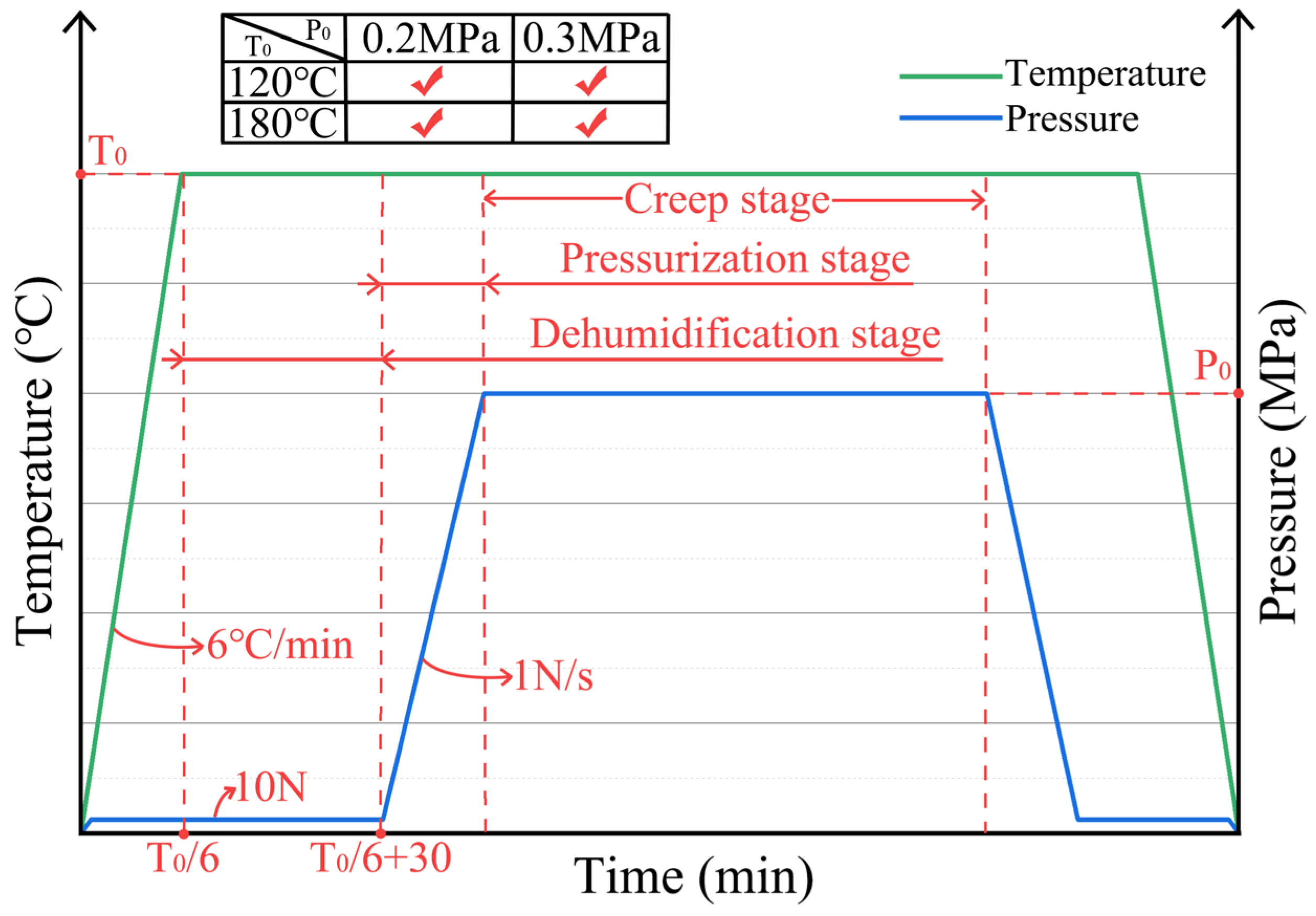
2.2. Experimental Methods
3. Results
3.1. Dehumidification Stage
3.2. Pressurization Stage
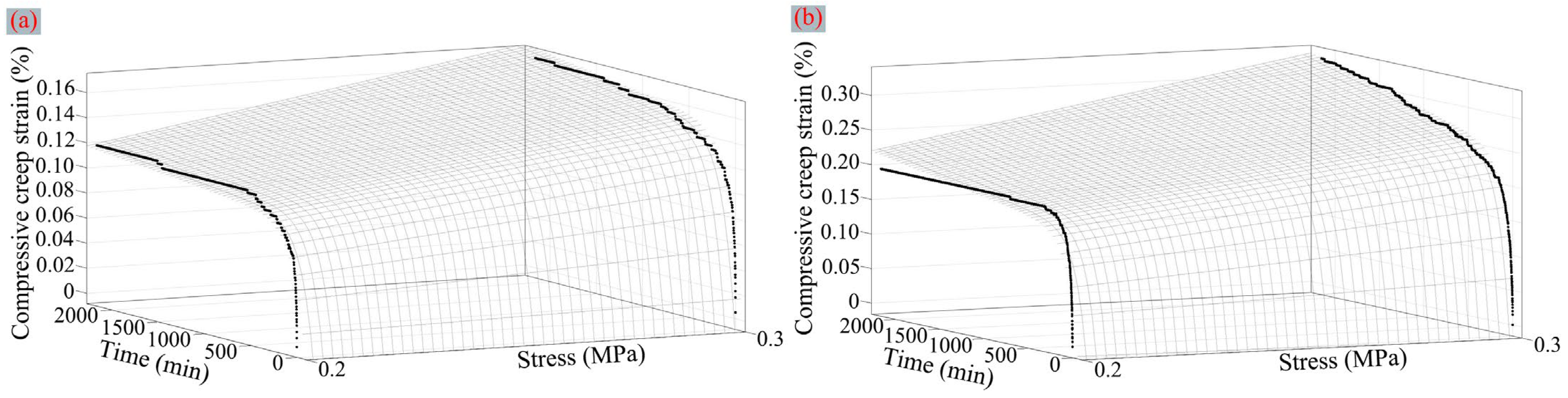
3.3. Creep Stage
3.3.1. Explanation of Creep Stage
3.3.2. Burgers Model Introduction and Fitting Results
4. Conclusions
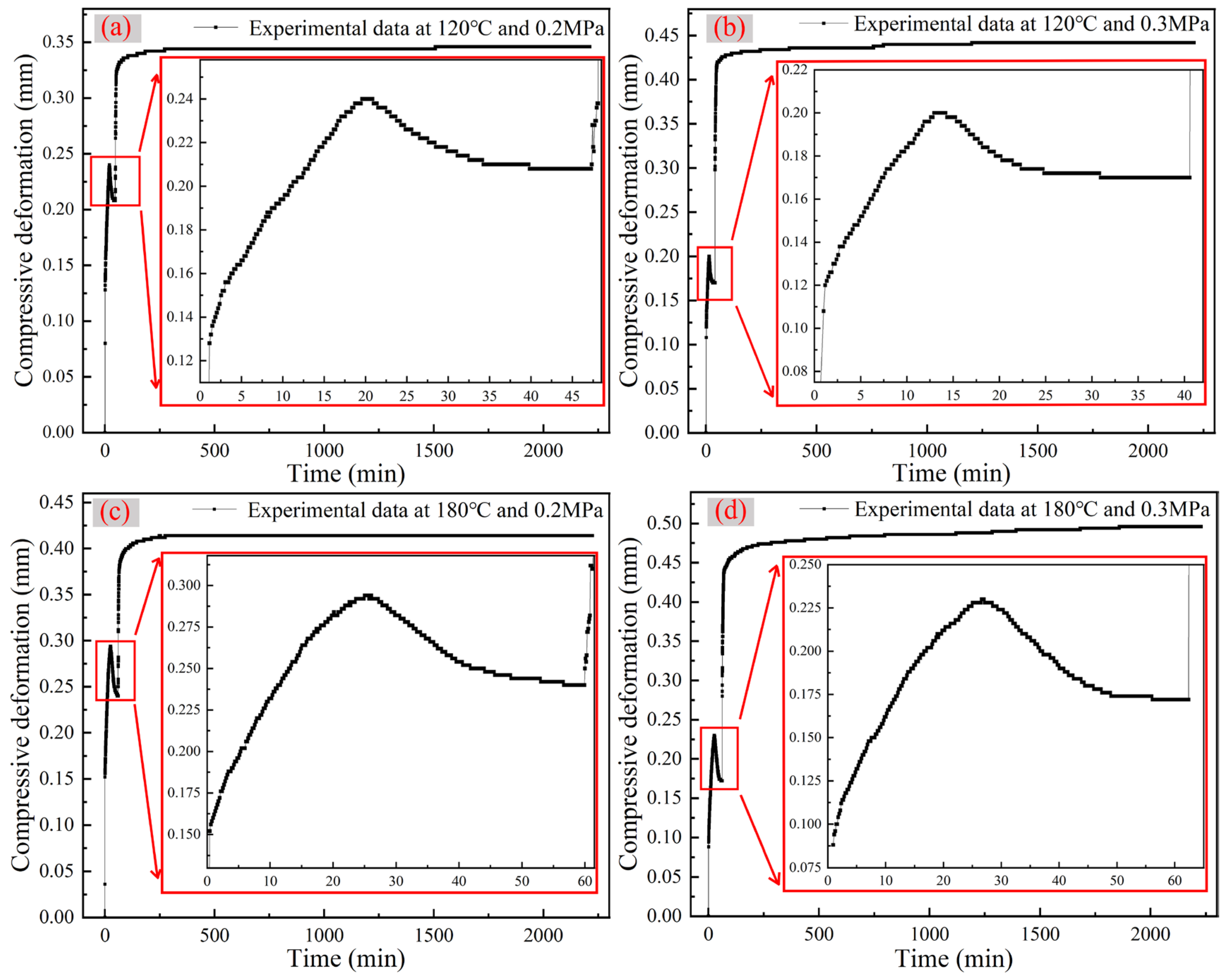
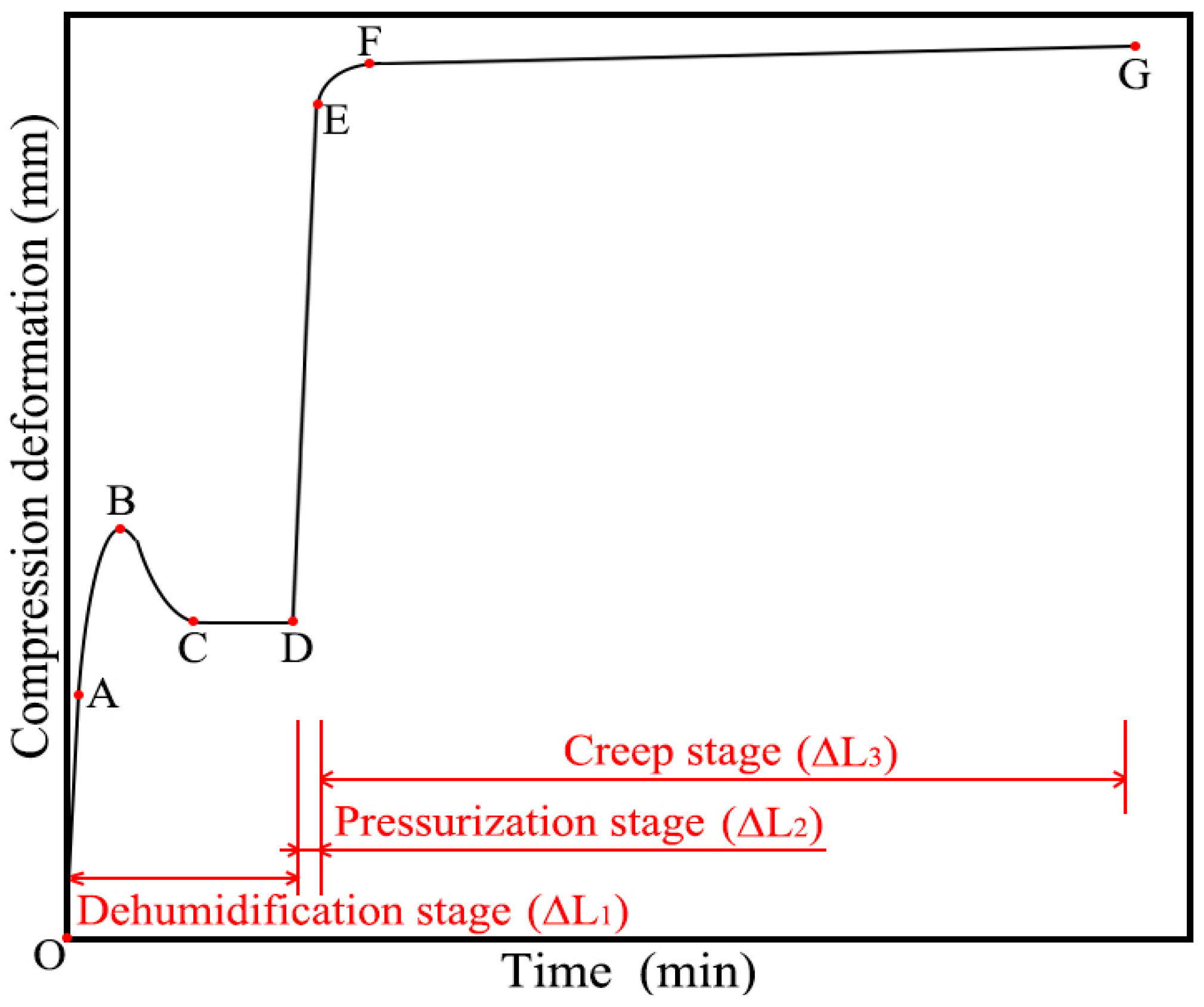
- The out-of-plane compression performance of the aramid honeycomb core was systematically investigated for the first time. Based on the compression deformation curve, the compression behavior can be divided into three stages: the dehumidification stage, the pressurization stage and the creep stage. These stages contribute approximately 35%, 55% and 10%, respectively, to the total deformation.
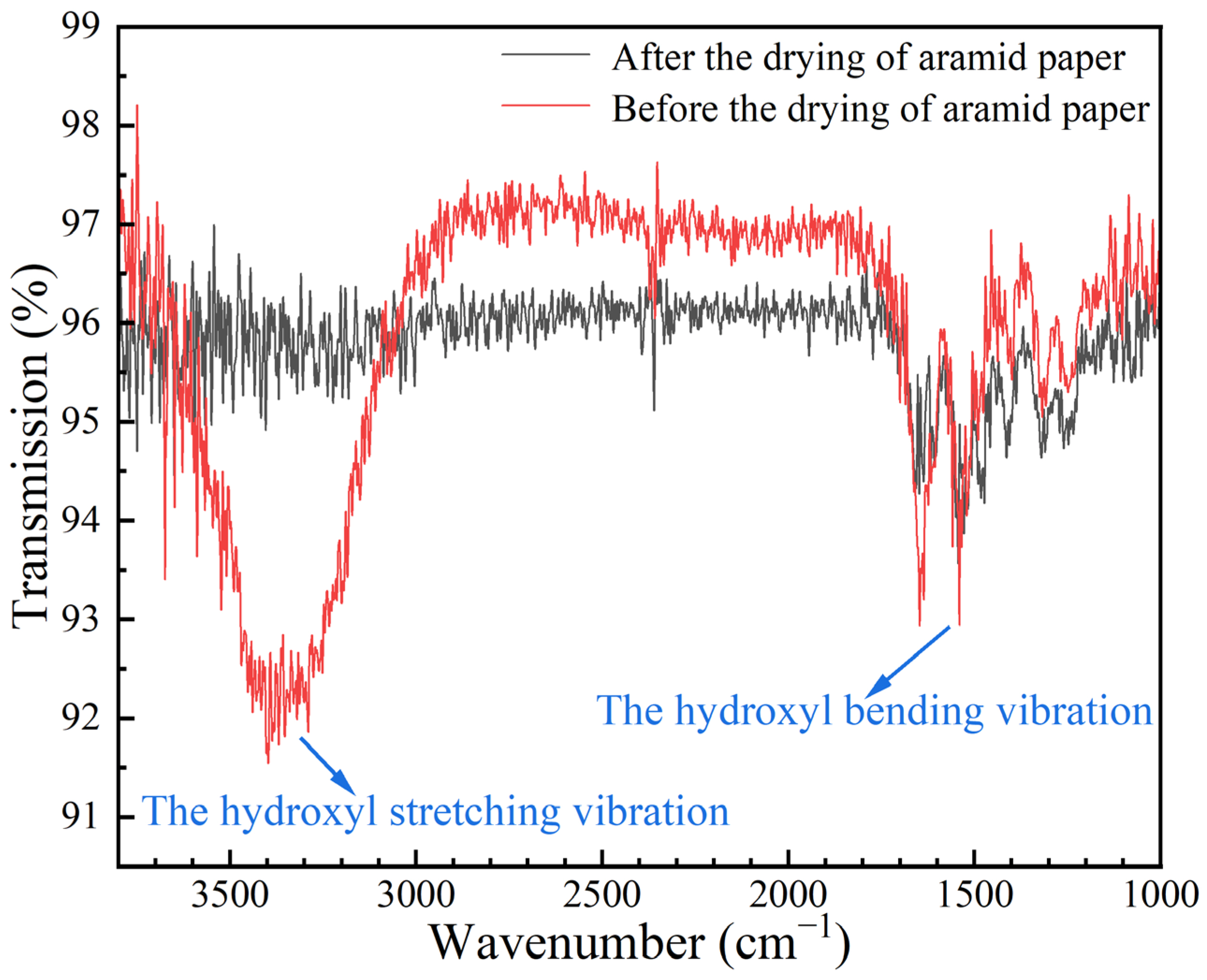
- During the dehumidification stage, the aramid honeycomb core undergoes a process of compression, expansion and plateau. The primary reason for the phenomenon of honeycomb cores is the combined effect of thermal expansion and dehydration shrinkage on aramid honeycomb cores. Prior to the experiment, hydrogen bonds formed between water molecules and the polar groups in the aramid honeycomb core, causing expansion. As the temperature increased, the hydrogen bonds were disrupted, leading to water evaporation and the contraction of the honeycomb core. Further temperature increases weakened intermolecular interactions, increasing the polymer’s free volume and resulting in the overall expansion of the aramid honeycomb core.
- In the pressurization stage, the deformation ΔL2 and pressure exhibit a nonlinear relationship, indicating that the aramid honeycomb core impregnated with phenolic resin is a not purely linear elastomer. Simultaneously, in the creep stage, the aramid honeycomb core exhibits compression creep phenomena related to time, temperature and pressure under high temperature and pressure conditions. Taking into account the aforementioned phenomena, the aramid honeycomb core under high temperature and pressure conditions can be characterized as a viscoelastic material.
- After the out-of-plane compression creep experiment, the nonlinear surface fitting method was employed to fit the creep deformation equations at various stress levels under a constant temperature, resulting in a high degree of fitting accuracy. This method is also capable of predicting the creep deformation behavior under the influence of varying stress levels. Finally, the total height deformation of the aramid honeycomb core under typical manufacturing processes can be obtained by integrating the dehumidification (ΔL1), pressurization (ΔL2) and creep (ΔL3) stages.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, J.P.; Zhan, L.H.; Ma, B.L.; Zhou, H.; Xiong, B.; Guo, J.Z.; Xia, Y.N.; Hui, S.M. Metal-Metal Bonding Process Research Based on Xgboost Machine Learning Algorithm. Polymers 2023, 15, 4085. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zhan, L.H.; Ma, B.L.; Guan, C.L.; Yang, X.B. Simulation and Experimental Study on the Internal Leak Behavior in Carbon Fiber Reinforced Composite Components. Polymers 2023, 15, 2758. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.C.; Zhan, L.H.; Guan, C.L.; Guo, J.Z.; Ma, B.L.; Dai, G.M.; Yao, S.M. Optimization of Vibration Pretreatment Microwave Curing in Composite Laminate Molding Process. Polymers 2023, 15, 296. [Google Scholar] [CrossRef] [PubMed]
- Rathod, S.; Tiwari, G. Structural analysis of cylindrical composite structures for high velocity applications: A parametric optimization study. Thin Walled Struct. 2023, 192, 111178. [Google Scholar] [CrossRef]
- Shan, J.F.; Xu, S.L.; Zhou, L.J.; Wang, D.R.; Liu, Y.G.; Zhang, M.; Wang, P.F. Dynamic fracture of aramid paper honeycomb subjected to impact loading. Compos. Struct. 2019, 223, 110962. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Sun, Y.X.; Li, R.Y.; Sun, Q.R.; Feng, J.T. Response of aramid honeycomb sandwich panels subjected to intense impulse loading by Mylar flyer. Int. J. Impact Eng. 2017, 104, 75–84. [Google Scholar] [CrossRef]
- Kumar, A.; Angra, S.; Chanda, A.K. Fabrication and mechanical characterisation of composite sandwich structure having kevlar honeycomb core. Adv. Mater. Process. Technol. 2023, 1–18. [Google Scholar] [CrossRef]
- Liu, L.Q.; Wang, H.; Guan, Z.W. Experimental and numerical study on the mechanical response Of Nomex honeycomb core under transverse loading. Compos. Struct. 2015, 121, 304–314. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Liu, T.; Tizani, W. Experimental and numerical analysis of dynamic compressive response of Nomex honeycombs. Compos. Part B Eng. 2018, 148, 27–39. [Google Scholar] [CrossRef]
- Liu, L.Q.; Meng, P.; Wang, H.; Guan, Z.W. The flatwise compressive properties of Nomex honeycomb core with debonding imperfections in the double cell wall. Compos. Part B Eng. 2015, 76, 122–132. [Google Scholar] [CrossRef]
- Asprone, D.; Auricchio, F.; Menna, C.; Morganti, S.; Prota, A.; Reali, A. Statistical finite element analysis of the buckling behavior of honeycomb structures. Compos. Struct. 2013, 105, 240–255. [Google Scholar] [CrossRef]
- Yang, W.C.; Zhang, X.F.; Yang, K.J.; Pan, B.; Fei, B.J.; Yi, X.S.; Chen, Y.L. Shear property characterization of aramid paper and its application to the prediction of honeycomb behaviors. Compos. Struct. 2020, 254, 112800. [Google Scholar] [CrossRef]
- Naufal, A.M.; Prabowo, A.R.; Muttaqie, T.; Hidayat, A.; Purwono, J.; Adiputra, R.; Akbar, H.I.; Smaradhana, D.F. Characterization of sandwich materials–Nomex-Aramid carbon fiber performances under mechanical loadings: Nonlinear FE and convergence studies. Rev. Adv. Mater. Sci. 2024, 63, 20230177. [Google Scholar] [CrossRef]
- Kolopp, A.; Rivallant, S.; Bouvet, C. Experimental study of sandwich structures as armour against medium-velocity impacts. Int. J. Impact Eng. 2013, 61, 24–35. [Google Scholar] [CrossRef][Green Version]
- Du, Y.; Yan, N.; Kortschot, M.T. An experimental study of creep behavior of lightweight natural fiber-reinforced polymer composite/honeycomb core sandwich panels. Compos. Struct. 2013, 106, 160–166. [Google Scholar] [CrossRef]
- Ishak, M.R.; Yidris, N.; Zuhri, M.Y.M. Flexural creep response of honeycomb sandwich pultruded GFRP composite cross-arm: Obtaining full-scale viscoelastic moduli and creep coefficients. J. Mater. Res. Technol. 2024, 29, 225–241. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Lin, J.Y.; Huang, J.S. Creep of hexagonal honeycombs with Plateau borders. Compos. Struct. 2005, 67, 477–484. [Google Scholar] [CrossRef]
- Balkan, D.; Mecitoglu, Z. Nonlinear dynamic behavior of viscoelastic sandwich composite plates under non-uniform blast load: Theory and experiment. Int. J. Impact Eng. 2014, 72, 85–104. [Google Scholar] [CrossRef]
- Birman, V.; Kardomateas, G.A. Review of current trends in research and applications of sandwich structures. Compos. Part B Eng. 2018, 142, 221–240. [Google Scholar] [CrossRef]
- Castanie, B.; Bouvet, C.; Ginota, M. Review of composite sandwich structure in aeronautic applications. Compos. Part C Open Access 2020, 1, 100004. [Google Scholar] [CrossRef]
- Sala, G. Composite degradation due to fluid absorption. Compos. Part B Eng. 2000, 31, 357–373. [Google Scholar] [CrossRef]
- Guo, J.Z.; Zhan, L.H.; Ma, B.L.; Zhang, D.C.; Fan, Y.S.; Yao, S.M.; Feng, J.P. A review on failure mechanism and mechanical performance improvement of FRP-metal adhesive joints under different temperature-humidity. Thin Walled Struct. 2023, 188, 110788. [Google Scholar] [CrossRef]
- Viana, G.; Costa, M.; Banea, M.D.; da Silva, L.F.M. A review on the temperature and moisture degradation of adhesive joints. Proc. Inst. Mech. Eng. Part L J. Mater.-Des. Appl. 2017, 231, 488–501. [Google Scholar] [CrossRef]
- Torki, A.M.; Stojanovic, D.B.; Zivkovic, I.D.; Marinkovic, A.; Skapin, S.D.; Uskokovic, P.S.; Aleksic, R.R. The Viscoelastic Properties of Modified Thermoplastic Impregnated Multiaxial Aramid Fabrics. Polym. Compos. 2012, 33, 158–168. [Google Scholar] [CrossRef]
- Obradovic, V.; Simic, D.; Sejkot, P.; Machalicka, K.V.; Vokác, M. Moisture absorption characteristics and effects on mechanical properties of Kolon/epoxy composites. Curr. Appl. Phys. 2021, 26, 16–23. [Google Scholar] [CrossRef]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Northamtonshire, UK, 2003. [Google Scholar]



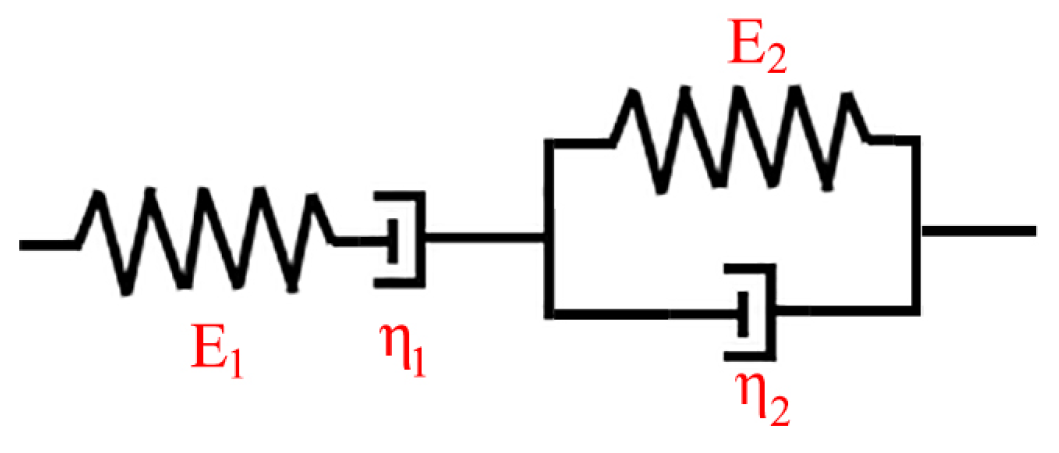
| Experimental Conditions | ΔL11 (mm) | ΔL12 (mm) |
|---|---|---|
| 120 °C, 0.2 MPa | 0.112, 0.118, 0.132 | 0.060, 0.062, 0.066 |
| 120 °C, 0.3 MPa | 0.088, 0.104, 0.110 | 0.046, 0.050, 0.058 |
| 180 °C, 0.2 MPa | 0.100, 0.100, 0.130 | 0.050, 0.058, 0.066 |
| 180 °C, 0.3 MPa | 0.106, 0.106, 0.116 | 0.054, 0.064, 0.064 |
| Overall mean value | 0.110 | 0.058 |
| Sample | Before Drying | After Drying | ||
|---|---|---|---|---|
| Height 1 (mm) | Height 2 (mm) | Height 1 (mm) | Height 2 (mm) | |
| Sample 1 | 19.95 | 19.83 | 19.89 | 19.77 |
| Sample 2 | 20.00 | 20.02 | 19.95 | 19.97 |
| Experimental Conditions | ΔL (mm) | ΔL1 (mm) | ΔL2 (mm) | ΔL3 (mm) | |
|---|---|---|---|---|---|
| ΔL11 (mm) | ΔL12 (mm) | ||||
| 120 °C, 0.2 MPa | 0.392 | 0.110 | 0.058 | 0.198 | 0.026 |
| 120 °C, 0.3 MPa | 0.442 | 0.242 | 0.032 | ||
| 180 °C, 0.2 MPa | 0.430 | 0.224 | 0.038 | ||
| 180 °C, 0.3 MPa | 0.492 | 0.260 | 0.064 | ||
| Parameters | Experimental Conditions | |||
|---|---|---|---|---|
| 120 °C | Error Range | 180 °C | Error Range | |
| 4.616 | (−0.088, +0.087) | 3.481 | (−0.038, +0.039) | |
| 25,580 | (−800, +800) | 8231 | (−59, +58) | |
| 3.571 | (−0.051, +0.051) | 1.862 | (−0.011, +0.01) | |
| 484.1 | (−17.2, +17.2) | 229 | (−3.3, +3.2) | |
| Fitting degrees | 0.9226 | 0.9428 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Hu, X.; Guo, J.; Zhang, D.; Yao, S.; Zhan, L.; Ma, B.; Huang, M.; Zhang, L. Aramid Honeycomb Cores under Constant Pressure: Unveiling the Out-of-Plane Compression Deformation. Polymers 2024, 16, 1974. https://doi.org/10.3390/polym16141974
Huang X, Hu X, Guo J, Zhang D, Yao S, Zhan L, Ma B, Huang M, Zhang L. Aramid Honeycomb Cores under Constant Pressure: Unveiling the Out-of-Plane Compression Deformation. Polymers. 2024; 16(14):1974. https://doi.org/10.3390/polym16141974
Chicago/Turabian StyleHuang, Xinzheng, Xin Hu, Jinzhan Guo, Dechao Zhang, Shunming Yao, Lihua Zhan, Bolin Ma, Minghui Huang, and Lihua Zhang. 2024. "Aramid Honeycomb Cores under Constant Pressure: Unveiling the Out-of-Plane Compression Deformation" Polymers 16, no. 14: 1974. https://doi.org/10.3390/polym16141974
APA StyleHuang, X., Hu, X., Guo, J., Zhang, D., Yao, S., Zhan, L., Ma, B., Huang, M., & Zhang, L. (2024). Aramid Honeycomb Cores under Constant Pressure: Unveiling the Out-of-Plane Compression Deformation. Polymers, 16(14), 1974. https://doi.org/10.3390/polym16141974







