Mixing and Thermal Transport Behavior in a Pin or Non-Pin Extruder Equipped with a Field Synergy Elongation Screw
Abstract
1. Introduction
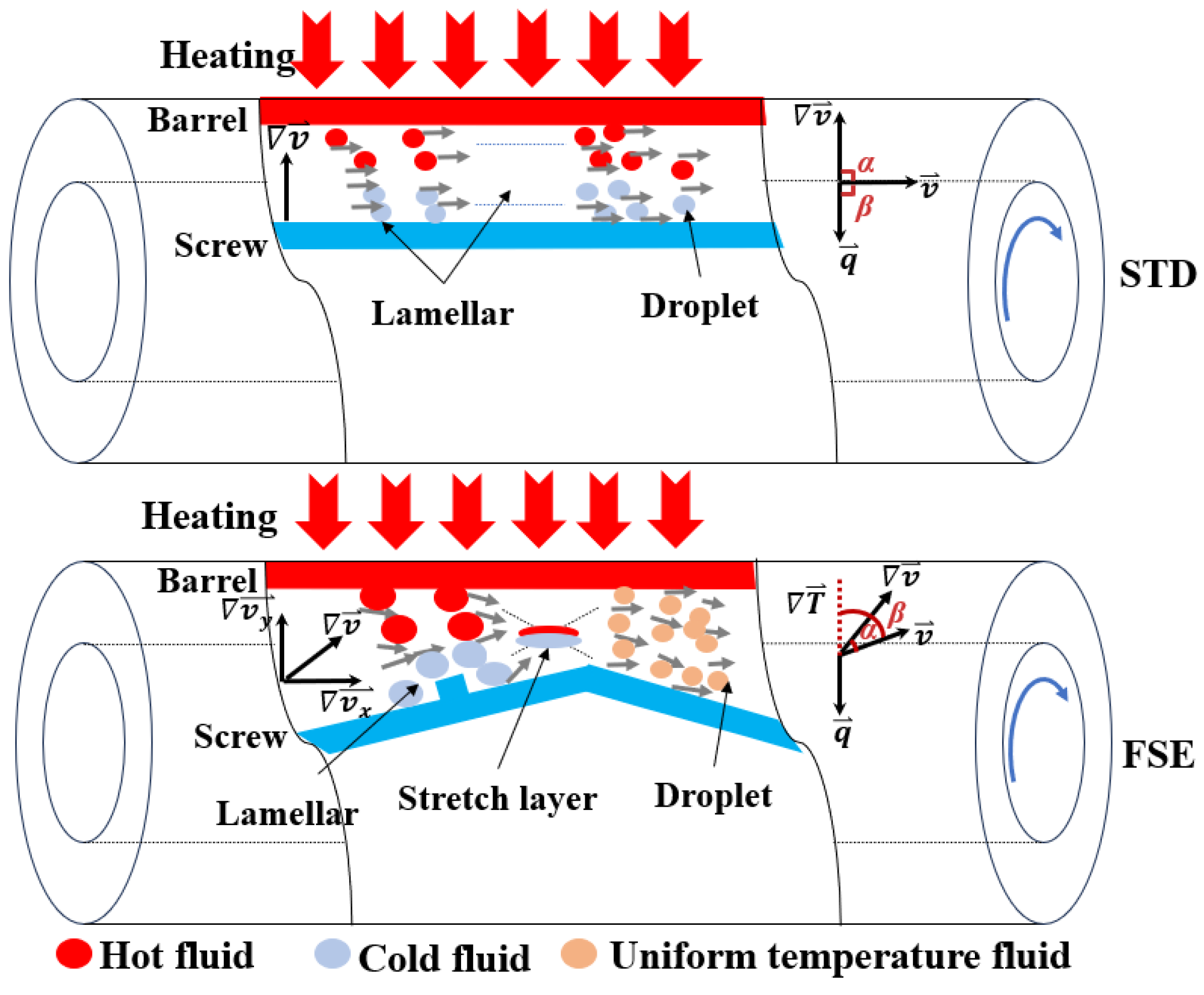
2. Polymeric Field Synergy Principle
3. Mathematical and Physical Models
3.1. Physical Model
3.2. Governing Equations and Boundary Conditions
3.3. Mesh System and Independence Validation
4. Result and Discussion
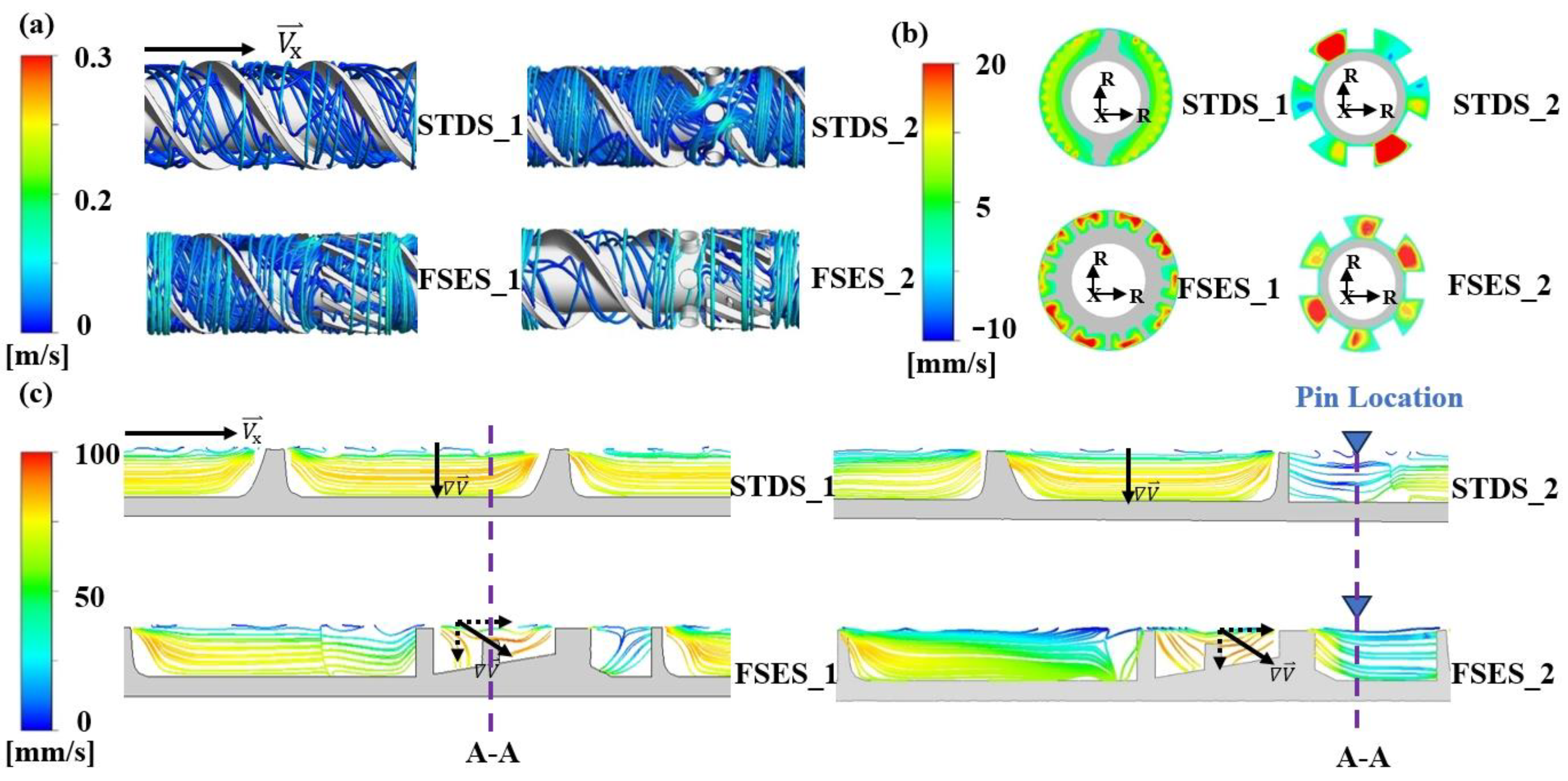
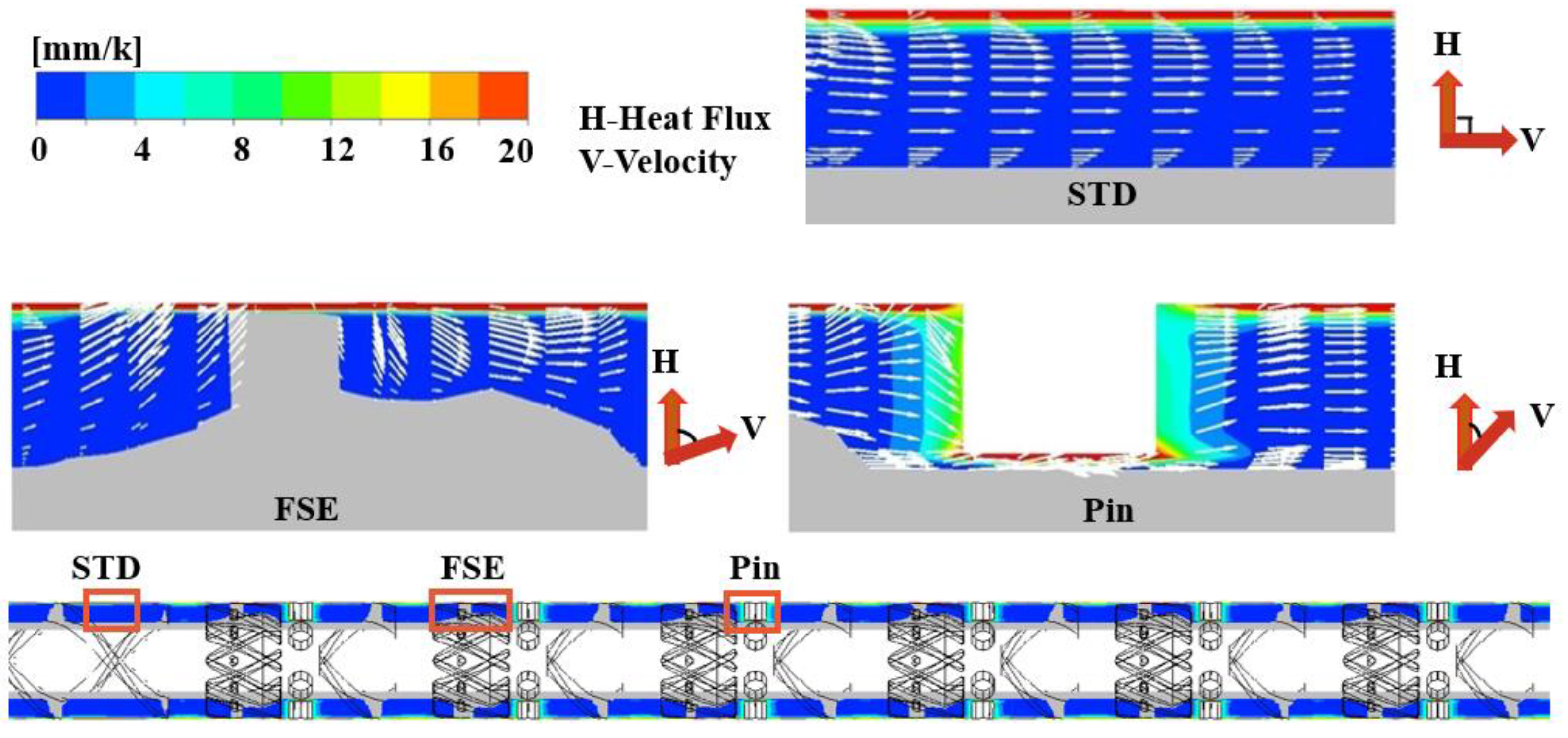
4.1. Flow Filed
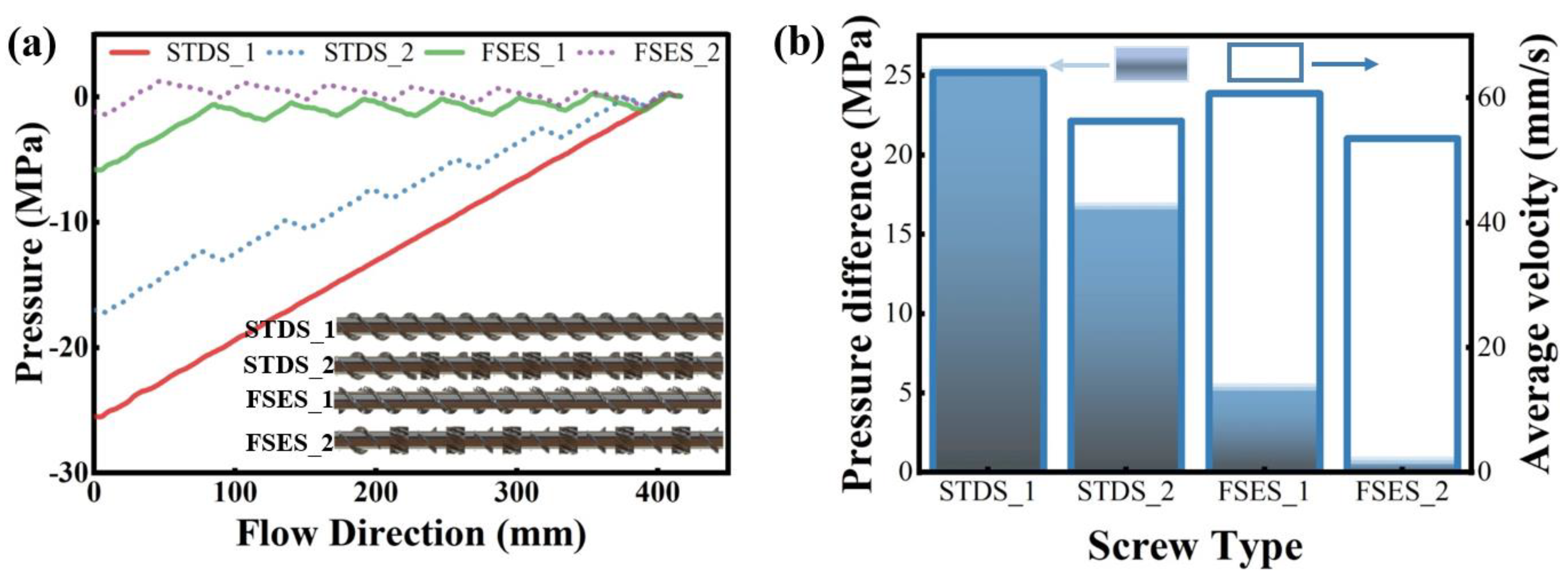
4.2. Pressure Difference and Conveying Capacity
4.3. Particle Trajectories
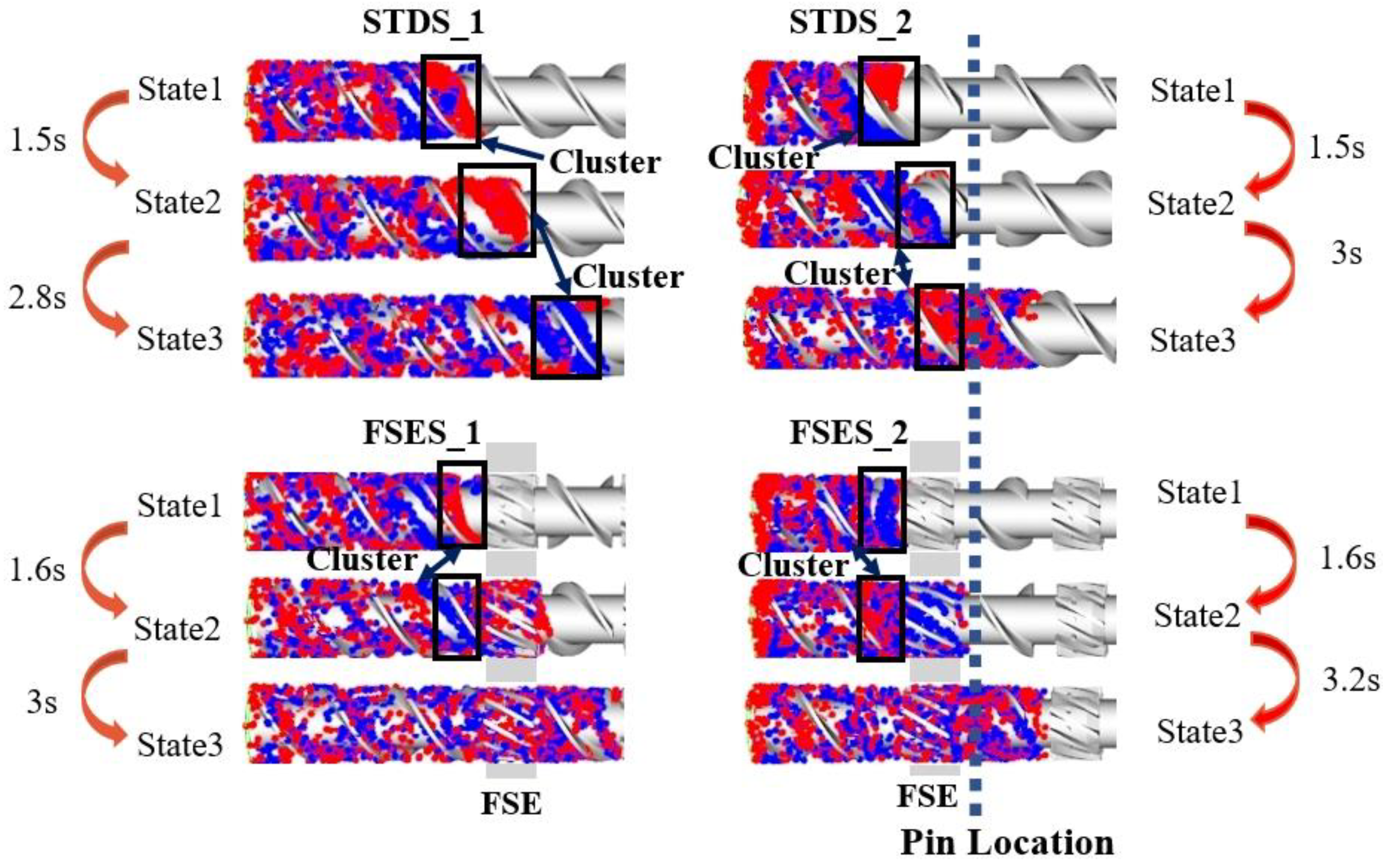
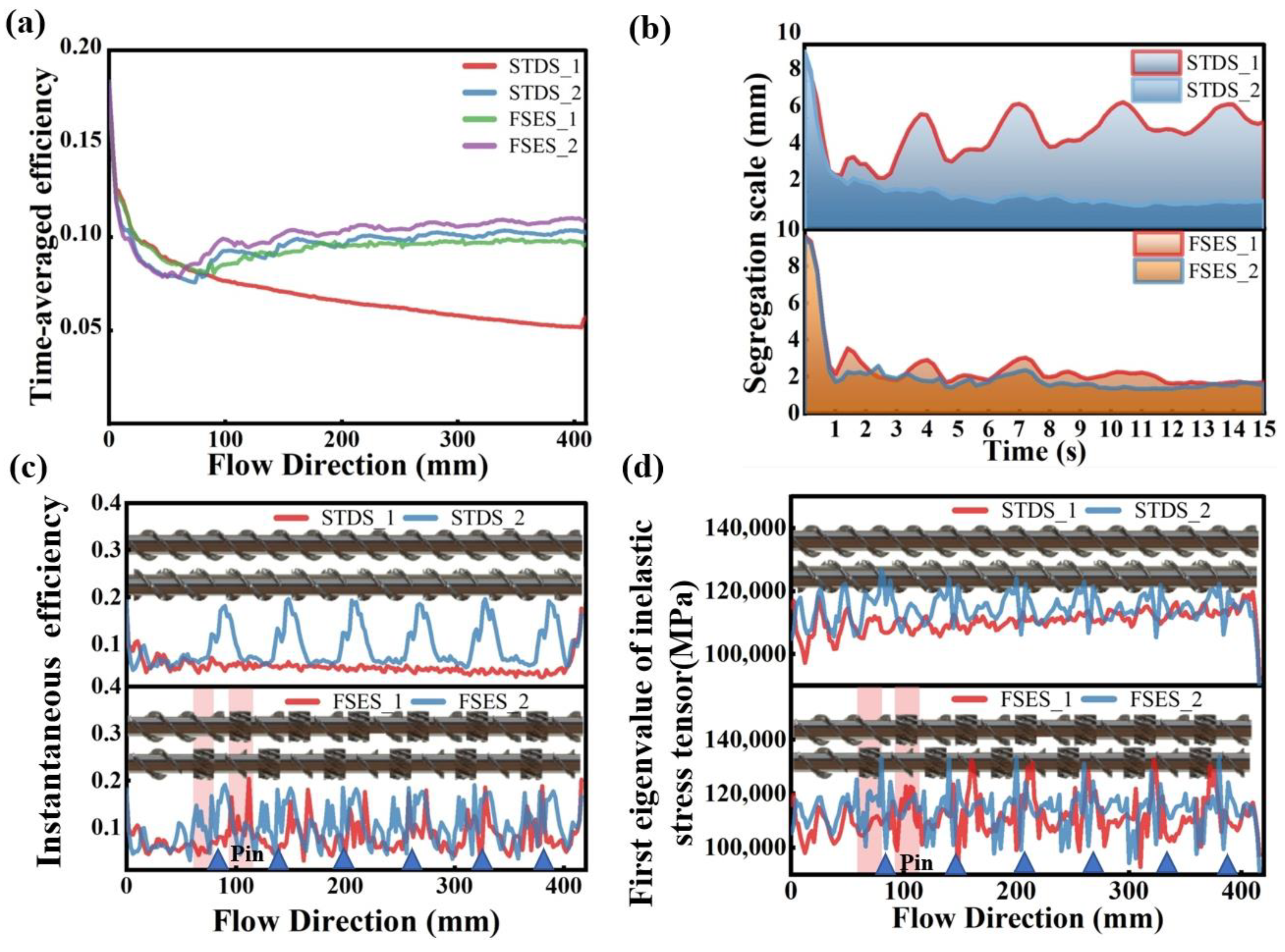
4.4. Mixing Characteristics
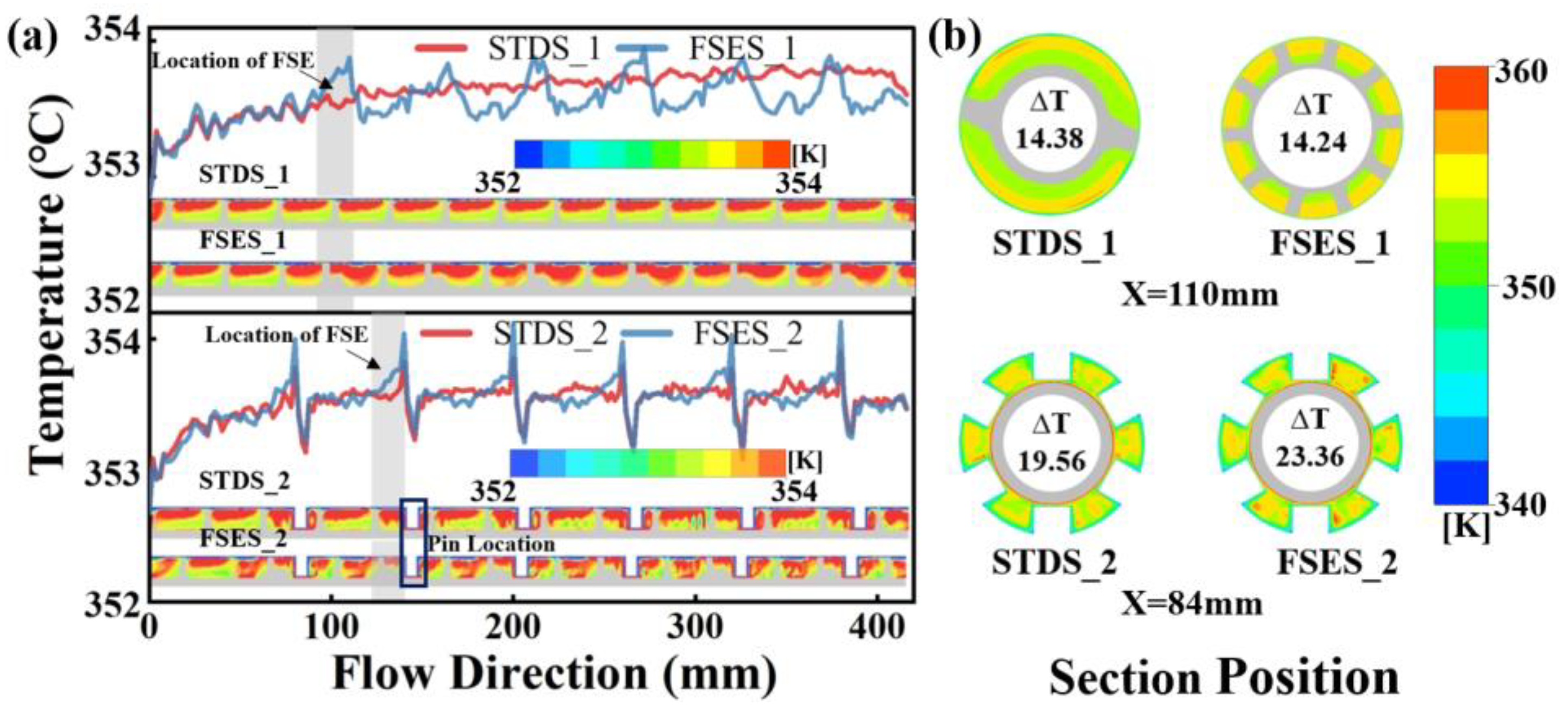
4.5. Temperature Uniformity
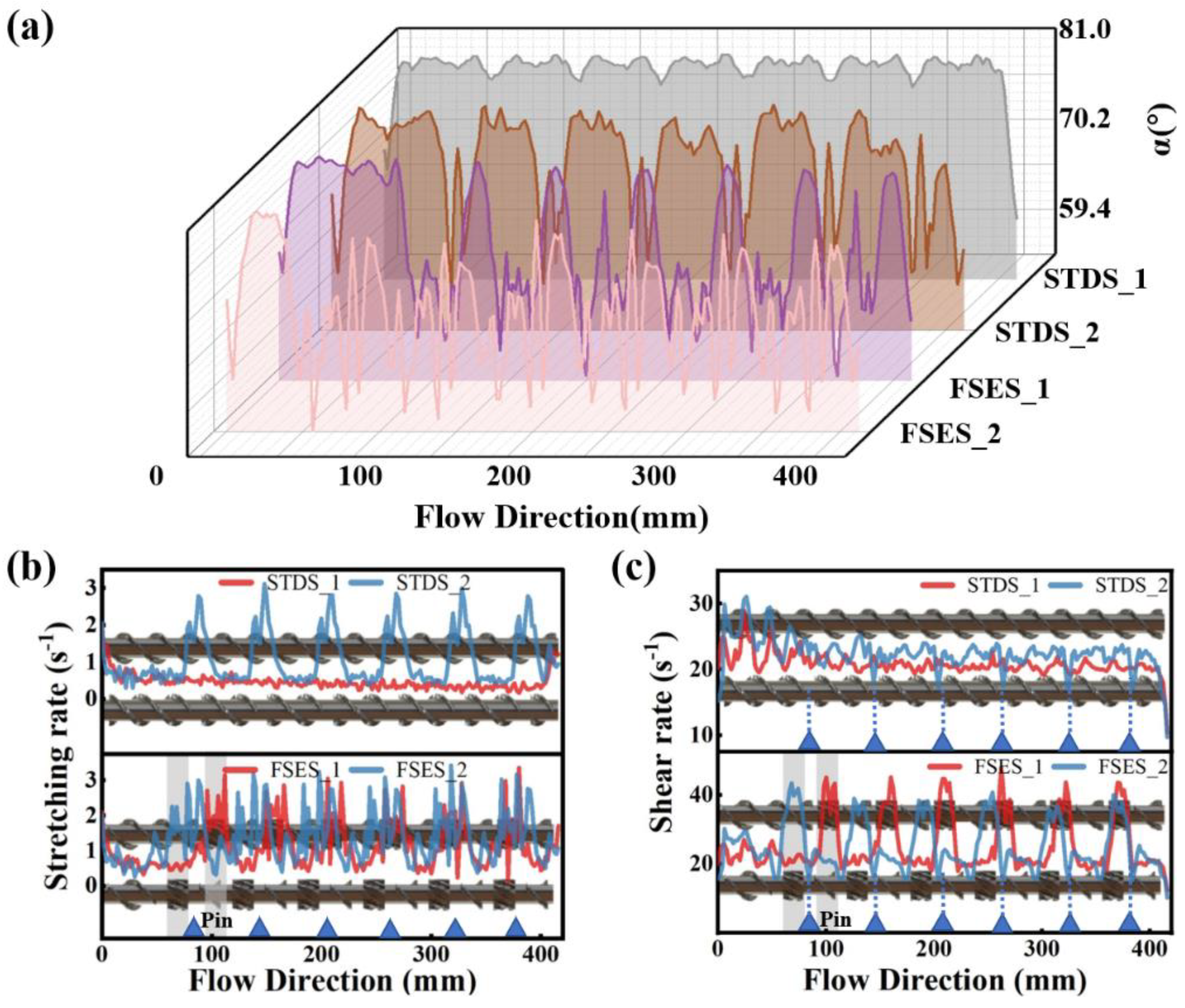
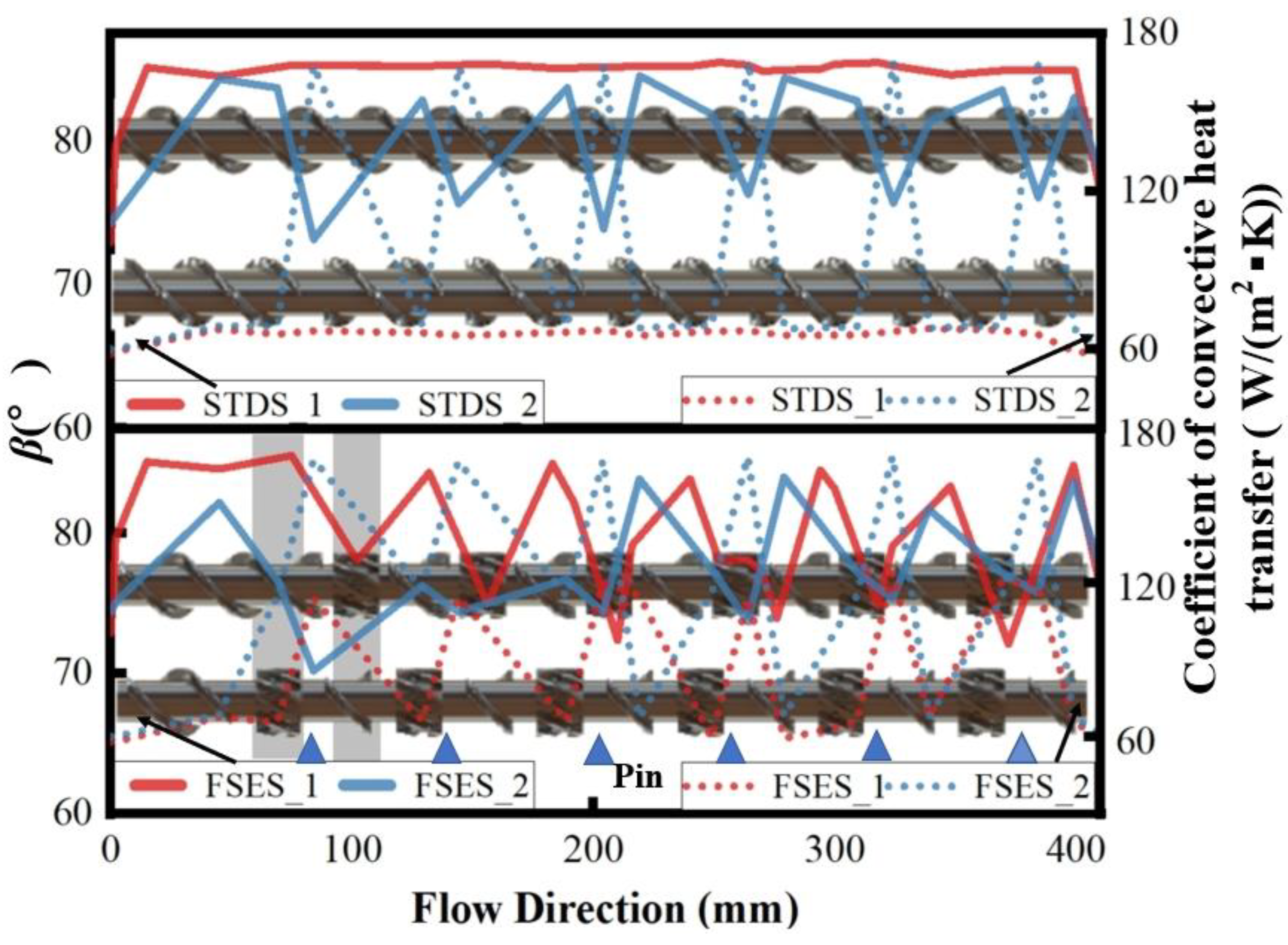
4.6. Field Synergy Analysis
5. Conclusions
- (1)
- Screw structures had a significant influence on the flow pattern and ductile deformation. For the STD configuration, only simple laminar flow was observed. The FSE configuration generated elongational flow in the mixing region, causing the mutual squeezing and thinning of the polymer melt, and facilitated the dispersion and dynamic mixing of aggregates. After being combined with barrel pins, the stretching effect was further improved with a long residence time and large mixing efficiency and thus increased the mixing ability of the entire plasticizing extrusion system.
- (2)
- Due to the unique radial wedge-shaped convergent channel, the heat and mass transport were enhanced in the FSE element, accelerating the heat transfer and mixing. As a result, the temperature uniformity of the polymer melt during extrusion was improved. However, significant temperature fluctuations and viscous heat generation occurred at the pin locations, potentially compromising the overall temperature uniformity of the polymer melt.
- (3)
- The field synergy principle revealed the mechanism of mixing and heat transfer. Compared with the conventional screw, the radial wedge-shaped convergence region of the FSE screw caused a significant radial deviation of the velocity vector in the channel, leading to an improved synergistic effect between the fields of velocity, velocity gradient, and temperature gradient and thus increasing the stretching stress and heat transfer efficiency. Barrel pins further increased the synergistic effect between various physical fields.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Re | Reynolds number |
| velocity vector, m/s | |
| fluid velocity vector, m/s | |
| velocity gradient vector, s−1 | |
| temperature gradient vector, K/m | |
| stress tensor, Pa | |
| viscous dissipation energy | |
| πP | dimensionless pressure gradient |
| stress tensor, Pa | |
| Pr | Prandtl number |
| Nu | Nusselt number |
| ρ | density, kg/m3 |
| vf | fluid average velocity, m/s |
| δ | feature dimension, mm |
| ηf | fluid average viscosity |
| P | pressure, Pa |
| τf | fluid average stress, Pa |
| Cp | constant-pressure specific heat capacity, J/(kg⋅K) |
| λf | fluid average thermal conductivity, W/m·K |
| h | heat convection coefficient, W/(m2·K) |
| α | interaction angle between velocity and velocity gradient, ° |
| β | interaction angle between velocity and temperature gradient, ° |
| L1 | screw length, mm |
| D | screw outer diameter, mm |
| d | screw inner diameter, mm |
| L2 | flow domain length, mm |
| k | thermal conductivity, W/(m·K) |
| η∞ | viscosity at an infinite shear rate, Pa·s |
| η0 | zero shear viscosity, Pa·s |
| λ | natural time, s |
| n | non-Newtonian index |
| f | coefficient of temperature sensibility, K−1 |
| Tα | reference temperature, K |
References
- Rauwendaal, C. Recent advances in barrier screw design. Plast. Addit. Compd. 2005, 7, 36–39. [Google Scholar] [CrossRef]
- Kimura, K.; Nakayama, Y.; Kajiwara, T. Distributive mixing characteristics of a Dulmage-type screw for a single-screw extruder: Experimental and numerical evaluation. Chem. Eng. J. Adv. 2021, 7, 100137. [Google Scholar] [CrossRef]
- Pandey, V.; Maia, J.M. Extension-dominated improved dispersive mixing in single-screw extrusion. Part 1: Computational and experimental validation. J. Appl. Polym. Sci. 2021, 138, 49716. [Google Scholar] [CrossRef]
- Liu, T.-L.; Du, Y.-X.; He, X.-Y. Statistical research on the mixing properties of wave based screws by numerical simulations. Int. Polym. Process. 2023, 38, 200–213. [Google Scholar] [CrossRef]
- He, H.; Li, W.; Huang, Z.; Tian, G.; Zhu, Z. Numerical analysis of a new mound-shaped extensional mixing element designed based on a sine curve in single-screw extrusion. Int. Polym. Process. 2023, 38, 472–482. [Google Scholar] [CrossRef]
- Rauwendaal, C. New screw design for cooling extruders. Plast. Rubber Compos. 2004, 33, 397–399. [Google Scholar] [CrossRef]
- Wang, C.; Bussmann, M.; Park, C. Numerical investigation of the effect of screw geometry on the mixing of a viscous polymer melt. J. Appl. Polym. Sci. 2010, 117, 775–784. [Google Scholar] [CrossRef]
- Chen, J.; Dai, P.; Yao, H.; Chan, T. Numerical analysis of mixing performance of mixing section in pin-barrel single-screw extruder. J. Polym. Eng. 2011, 31, 53–62. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, Y.; Liu, Y.; Huang, J.; Wang, N.; Hu, X. Investigations of the Elongational Deformation Induced by Pins in Pin-Barrel Cold-Feed Extruders. Adv. Polym. Technol. 2022, 2022, 11. [Google Scholar] [CrossRef]
- Bauer, H.; Matić, J.; Evans, R.C.; Gryczke, A.; Ketterhagen, W.; Sinha, K.; Khinast, J. Determining local residence time distributions in twin-screw extruder elements via smoothed particle hydrodynamics. Chem. Eng. Sci. 2022, 247, 117029. [Google Scholar] [CrossRef]
- Connelly, R.K.; Kokini, J.L. Examination of the mixing ability of single and twin screw mixers using 2D finite element method simulation with particle tracking. J. Food Eng. 2007, 79, 956–969. [Google Scholar] [CrossRef]
- Cheng, W.; Xin, S.; Chen, S.; Zhang, X.; Chen, W.; Wang, J.; Feng, L. Hydrodynamics and mixing process in a horizontal self-cleaning opposite-rotating twin-shaft kneader. Chem. Eng. Sci. 2021, 241, 116700. [Google Scholar] [CrossRef]
- Marschik, C.; Osswald, T.A.; Roland, W.; Albrecht, H.; Skrabala, O.; Miethlinger, J. Numerical analysis of mixing in block-head mixing screws. Polym. Eng. Sci. 2019, 59, E88–E104. [Google Scholar] [CrossRef]
- An, Y.; Yang, W.M.; Ding, Y.M. Numerical Investigation of the Effect of Rotors’ Geometric Structure on Mixing Properties of Continuous Mixer. Key Eng. Mater. 2012, 501, 70–75. [Google Scholar] [CrossRef]
- Grosso, G.; Hulsen, M.A.; Overend, A.; Anderson, P.D. Fluid flow and distributive mixing analysis in the cavity transfer mixer. Macromol. Theory Simul. 2018, 27, 1700075. [Google Scholar] [CrossRef]
- Kim, S.J. Dimensionless analysis of three-dimensional residence time distribution in single-screw extrusion processes. Korea-Aust. Rheol. J. 2018, 30, 179–188. [Google Scholar] [CrossRef]
- Yao, W.; Tanifuji, S.; Takahashi, K.; Koyama, K. Mixing efficiency in a pin mixing section for single-screw extruders. Polym. Eng. Sci. 2001, 41, 908–917. [Google Scholar] [CrossRef]
- Xu, B.; Yu, H.; Turng, L.S. Distributive mixing in a corotating twin screw channel using Lagrangian particle calculations. Adv. Polym. Technol. 2018, 37, 2215–2229. [Google Scholar] [CrossRef]
- Lim, K.H.; Hwang, W.R.; Kim, S.J. A finite-element technique for flows in the single screw extruder using a partial periodic unit. Korea-Aust. Rheol. J. 2019, 31, 59–67. [Google Scholar] [CrossRef]
- Jian, R.; Dai, R.; Sain, M.; Yang, W.; He, Y. Ductile behavior and heat transfer efficiency in polymer extrusion by self-controlled “flipping melt-pancakes” with multi-fields synergy. Int. J. Heat Mass Transf. 2022, 186, 122517. [Google Scholar] [CrossRef]

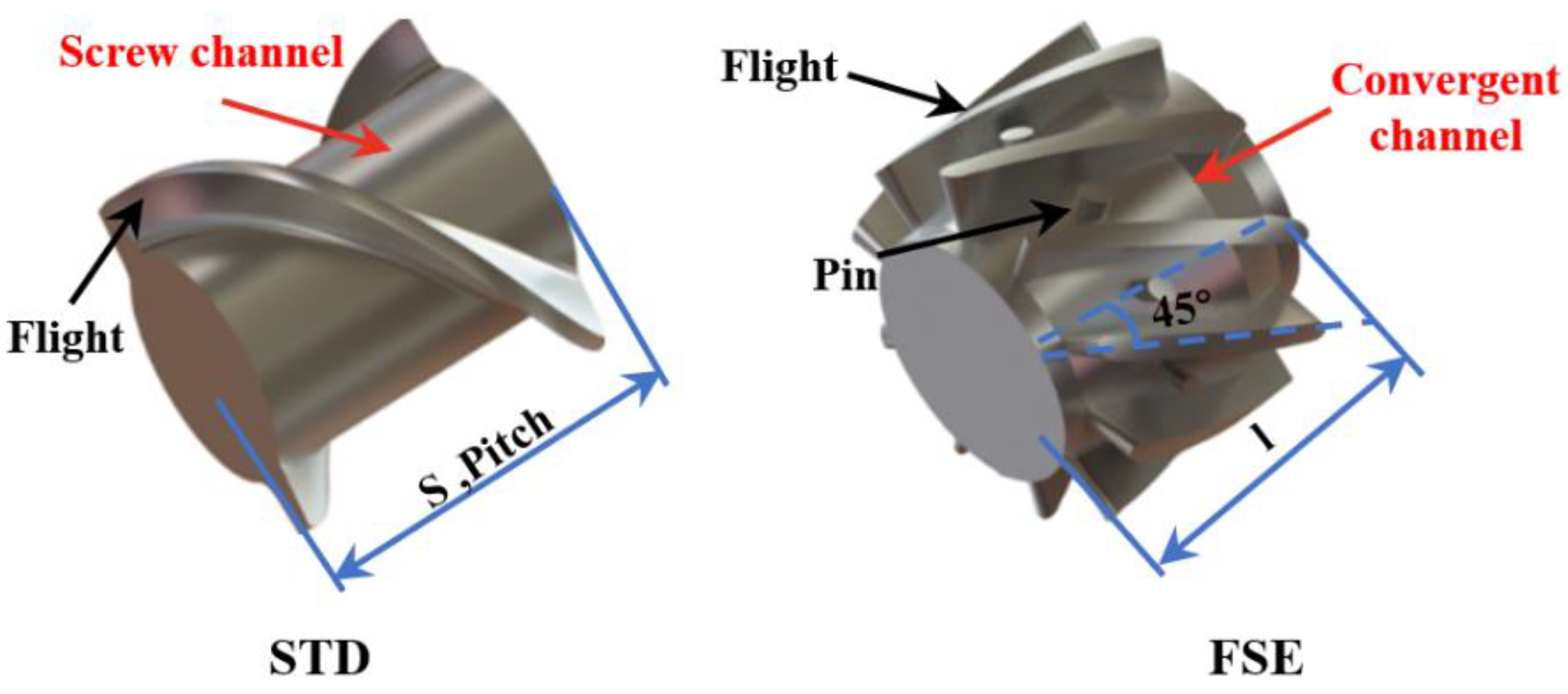
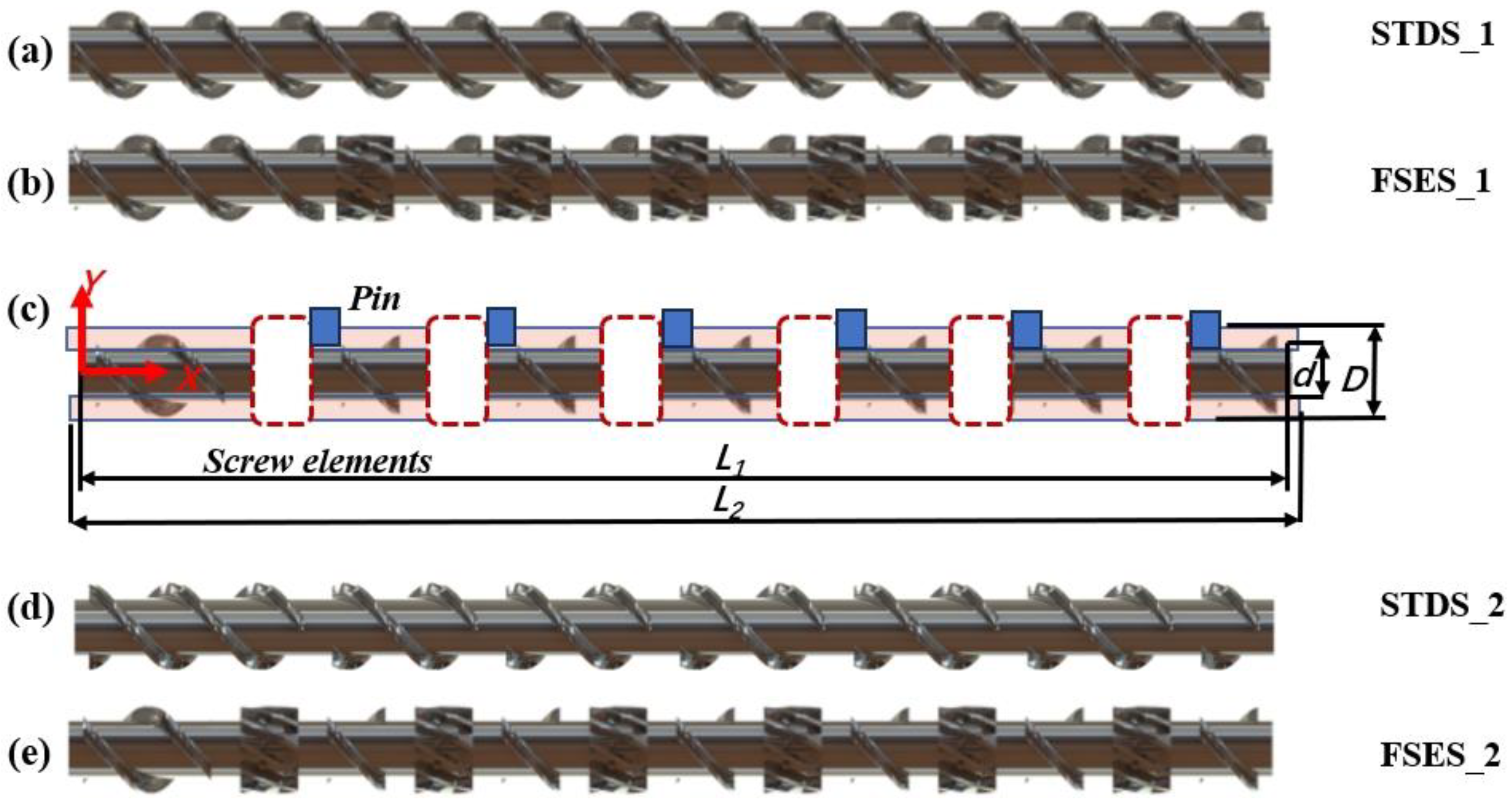

| Parameters | Symbol | Value (mm) |
|---|---|---|
| Screw length | L1 | 414 |
| Screw outer diameter | D | 30 |
| Screw inner diameter | d | 20 |
| Flow domain length | L2 | 418 |
| Parameter | Symbol | Value |
|---|---|---|
| Density | ρ | 1150 Kg/m3 |
| Specific heat capacity | Cp | 1600 J/(Kg·K) |
| Thermal conductivity | k | 0.25 W/(m·K) |
| Viscosity at an infinite shear rate | η∞ | 0 Pa·s |
| Zero shear viscosity | η0 | 175,000 Pa·s |
| Natural time | λ | 14 s |
| Non-Newtonian index | n | 0.408 |
| Coefficient of temperature sensibility | f | 0.0025 K−1 |
| Reference temperature | Tα | 373.15 K |
| Boundary | Flow Conditions | Thermal Conditions |
|---|---|---|
| Inlet | Fully developed, Volumetric flow rate 2.44 × 10−6 m3/s | 353.15 K (80 °C) |
| Outlet | Flow Outflow | Heat outflow |
| Barrel wall | Stationary, No-slip wall | 343.15 K (70 °C) |
| Screw wall | Screw speed 60 r/min | Insulated boundary |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Wang, S.; Huang, S.; Pan, W.; He, Y.; Jian, R. Mixing and Thermal Transport Behavior in a Pin or Non-Pin Extruder Equipped with a Field Synergy Elongation Screw. Polymers 2024, 16, 1793. https://doi.org/10.3390/polym16131793
Sun Y, Wang S, Huang S, Pan W, He Y, Jian R. Mixing and Thermal Transport Behavior in a Pin or Non-Pin Extruder Equipped with a Field Synergy Elongation Screw. Polymers. 2024; 16(13):1793. https://doi.org/10.3390/polym16131793
Chicago/Turabian StyleSun, Yancai, Shilong Wang, Shizheng Huang, Wei Pan, Yan He, and Ranran Jian. 2024. "Mixing and Thermal Transport Behavior in a Pin or Non-Pin Extruder Equipped with a Field Synergy Elongation Screw" Polymers 16, no. 13: 1793. https://doi.org/10.3390/polym16131793
APA StyleSun, Y., Wang, S., Huang, S., Pan, W., He, Y., & Jian, R. (2024). Mixing and Thermal Transport Behavior in a Pin or Non-Pin Extruder Equipped with a Field Synergy Elongation Screw. Polymers, 16(13), 1793. https://doi.org/10.3390/polym16131793







