Optimizing Epoxy Molding Compound Processing: A Multi-Sensor Approach to Enhance Material Characterization and Process Reliability
Abstract
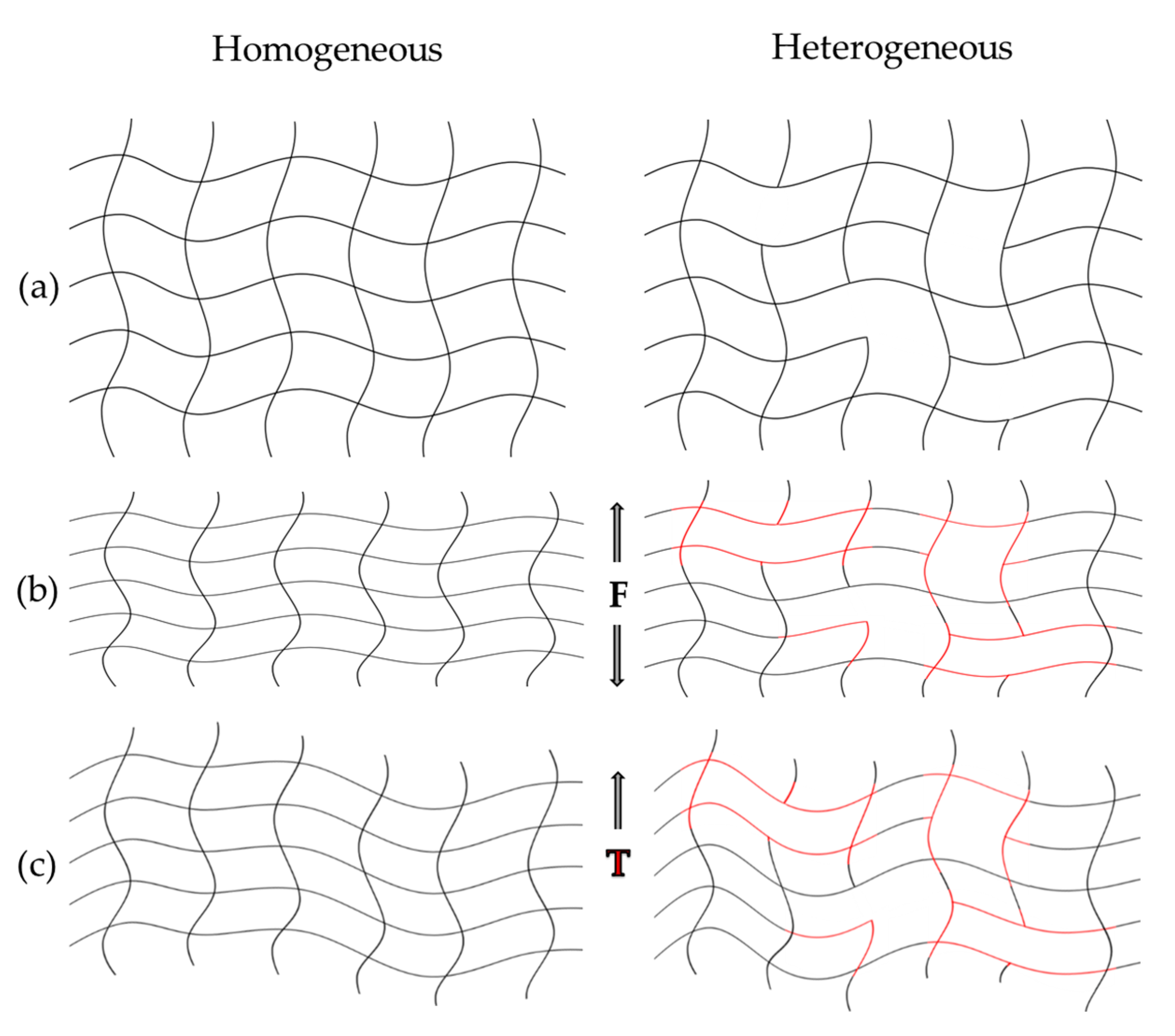
1. Introduction
- ▪
- Reaction mechanisms that favor the formation of regions of higher and lower cross-linking density, e.g., multiple microgels or reaction centers.
- ▪
- Formation of chemical clusters of different natures.
- ▪
- Changes in thermodynamic interactions (number and type of interaction sites).
- ▪
- Increasing molecular weights (before the gel point).
- ▪
- Increasing cross-linking density (after the gel point).
- ▪
- Presence of diluents or additives.
- ▪
2. Materials and Methods
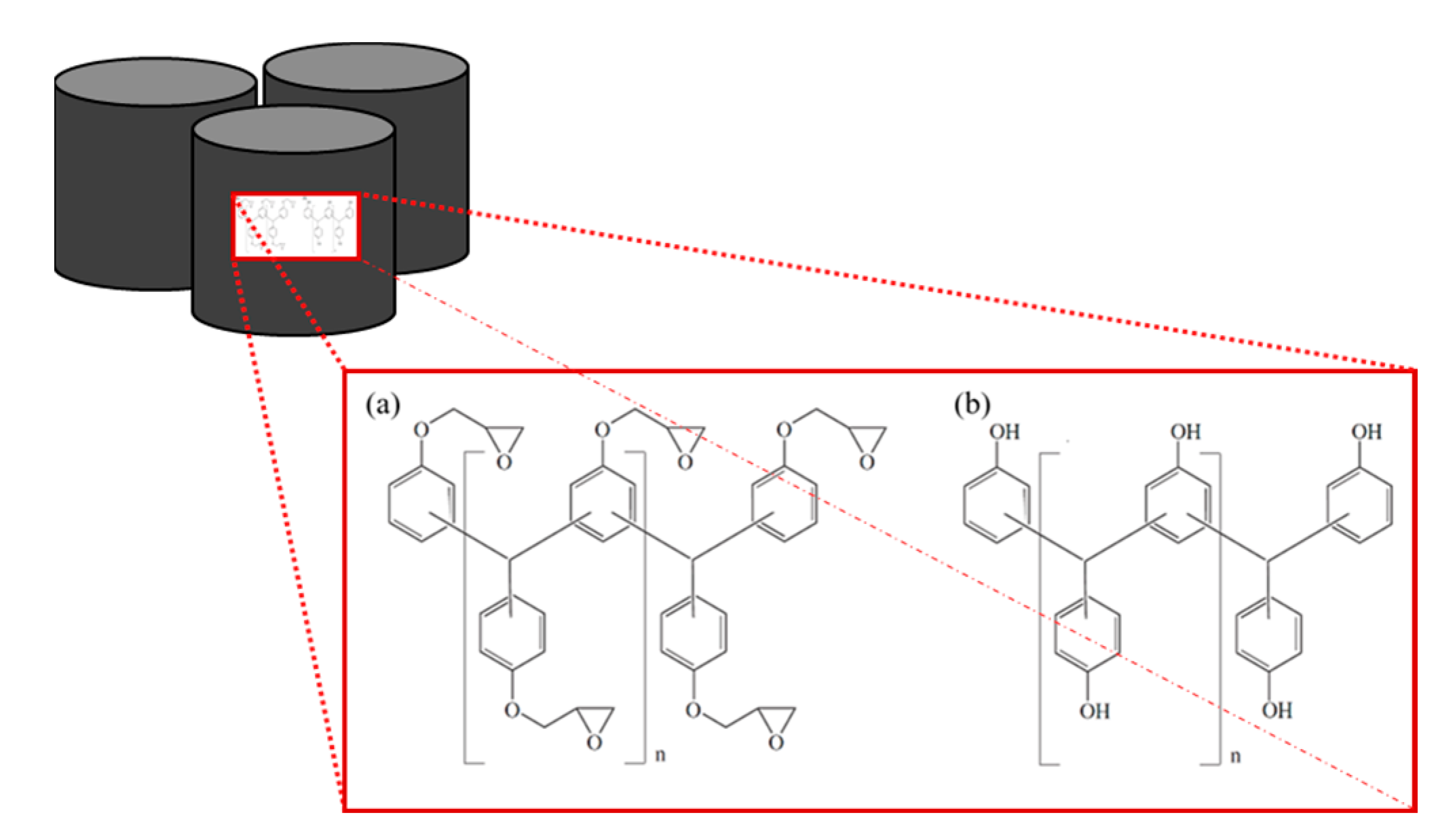
2.1. Materials
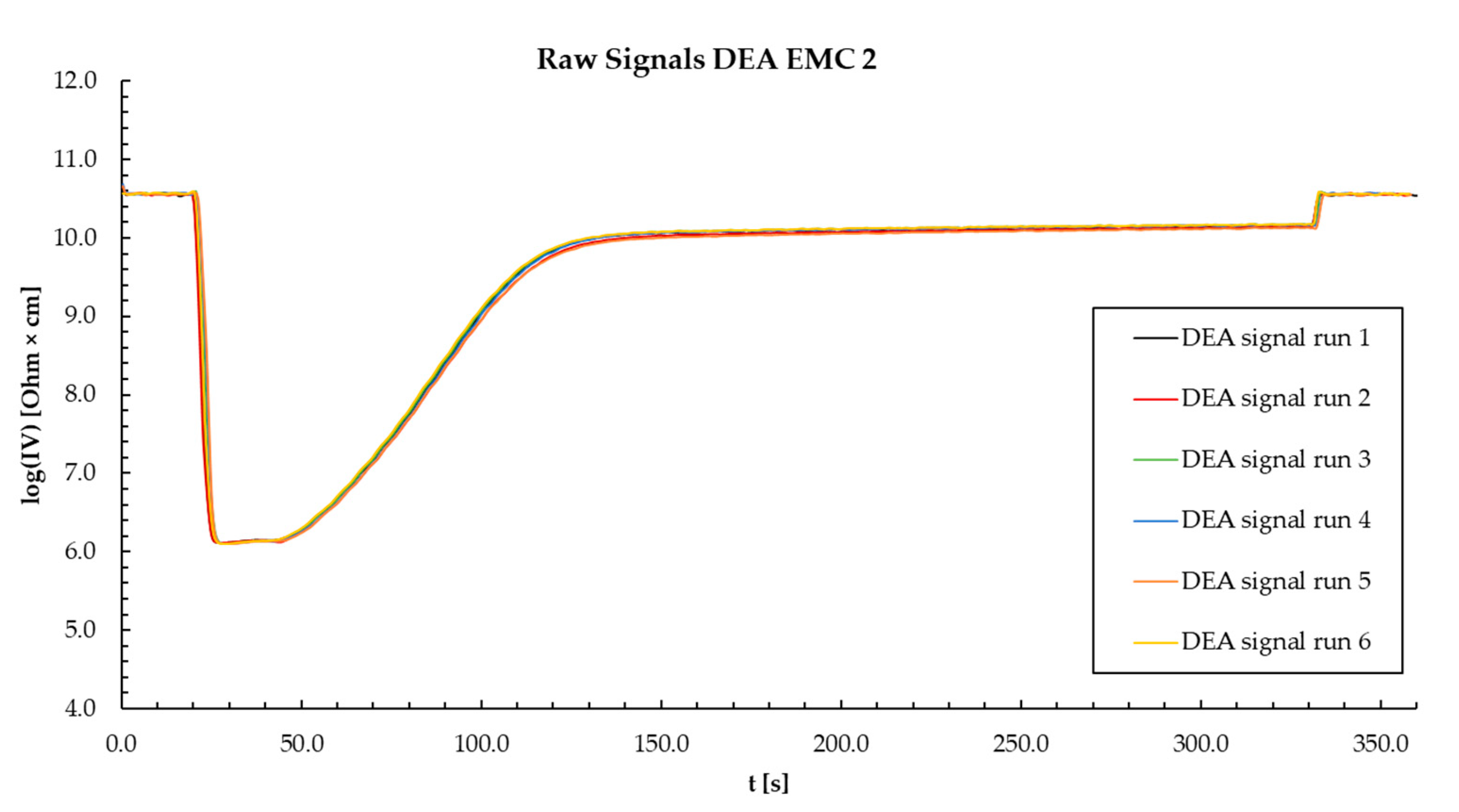
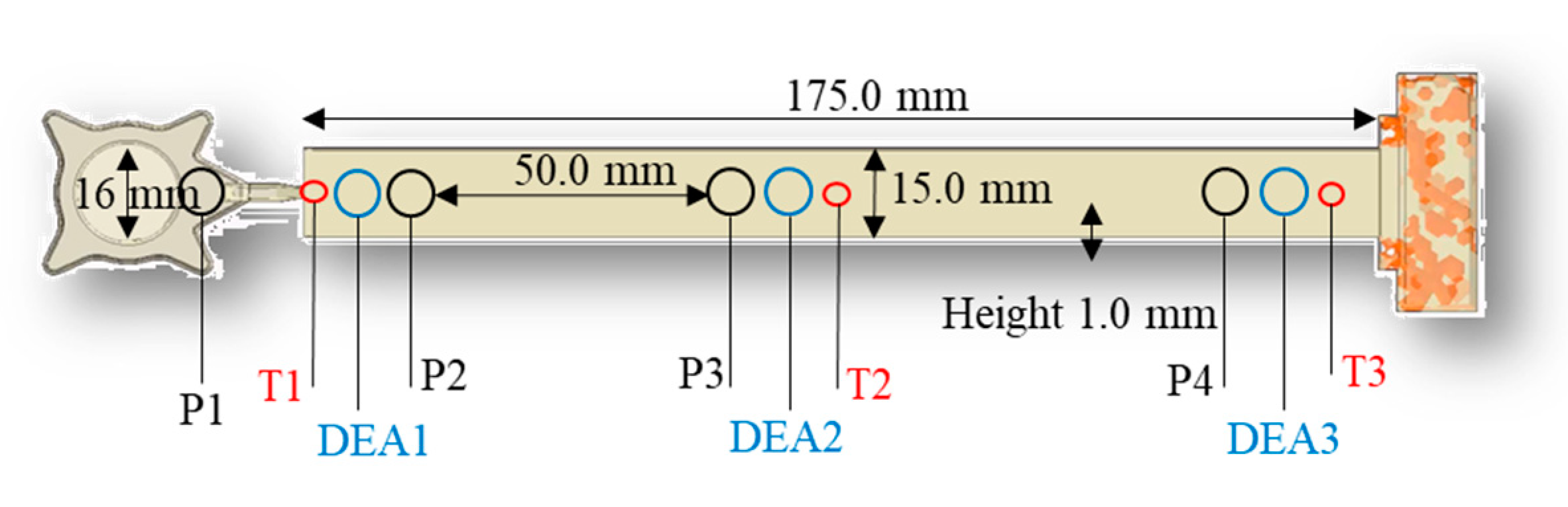
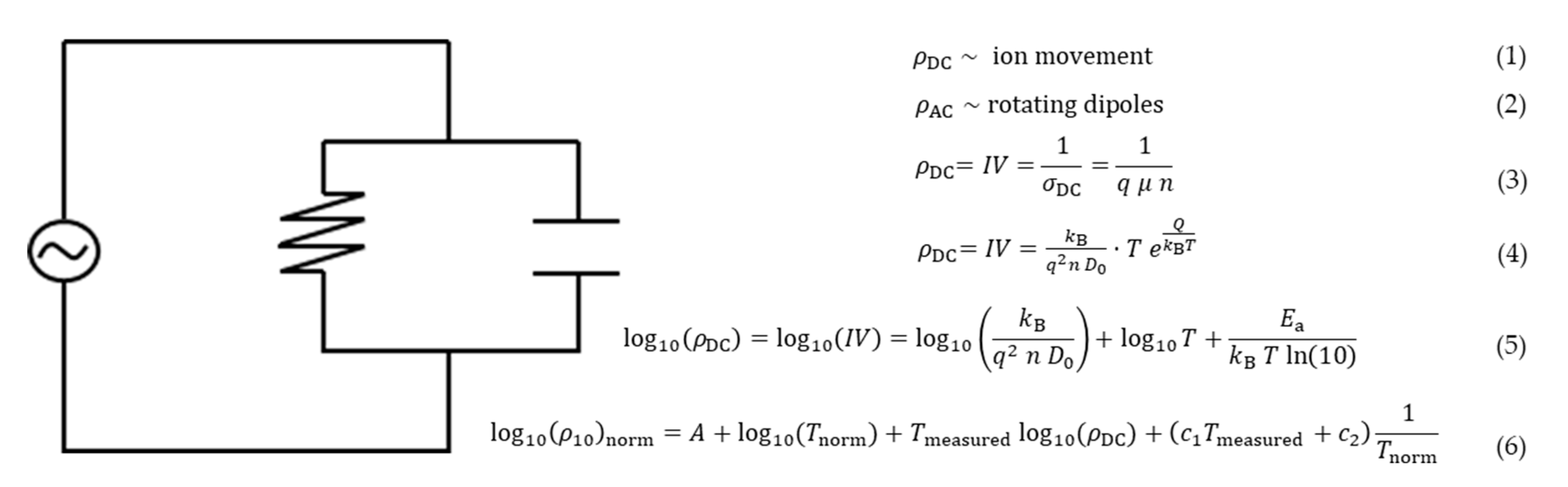
2.2. Dielectric Analysis (DEA) in Transfermold
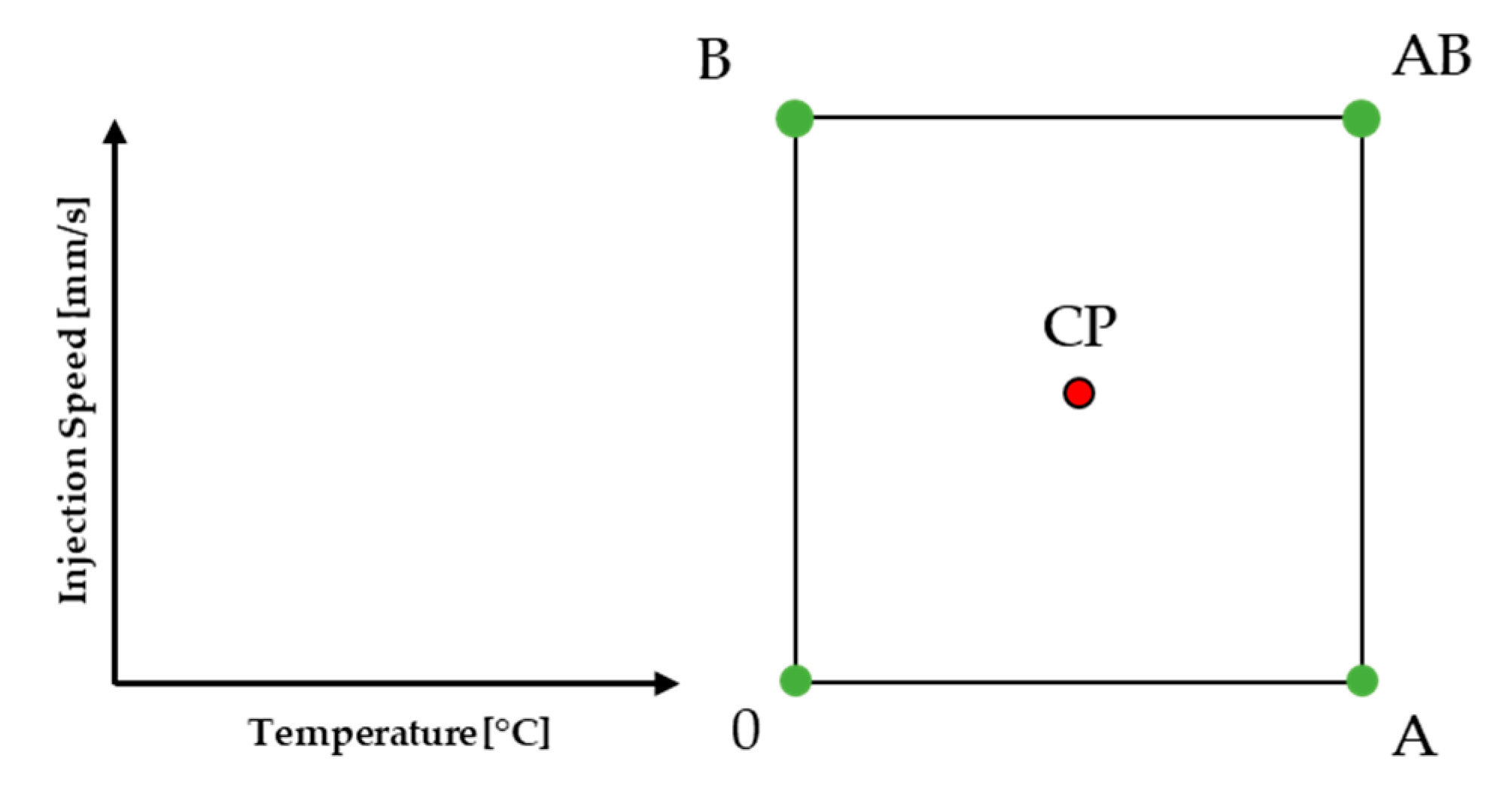
2.3. Design of Experiment (DoE)
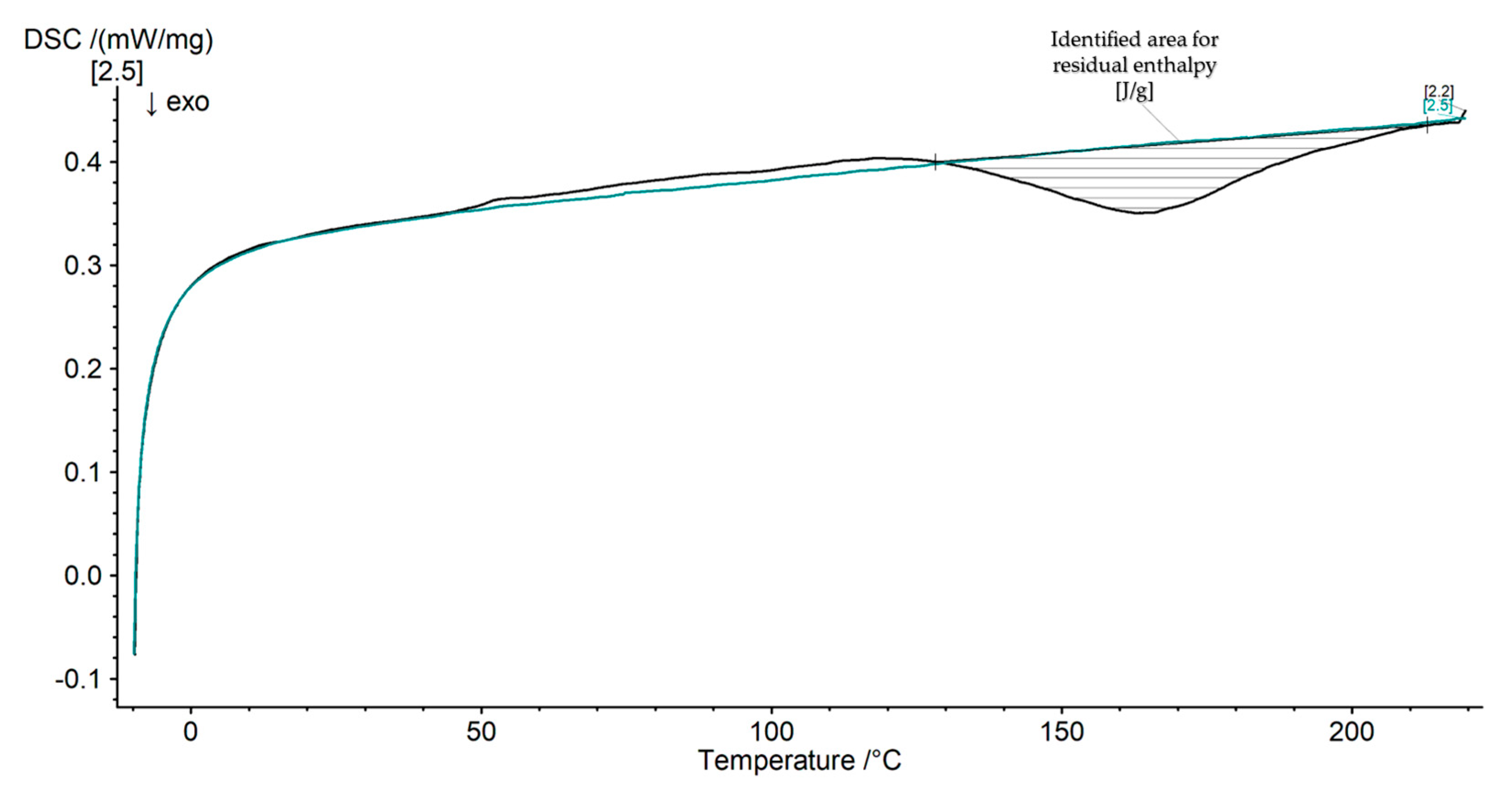
2.4. Residual Enthalpy Measurements via Differential Scanning Calorimetry (DSC)
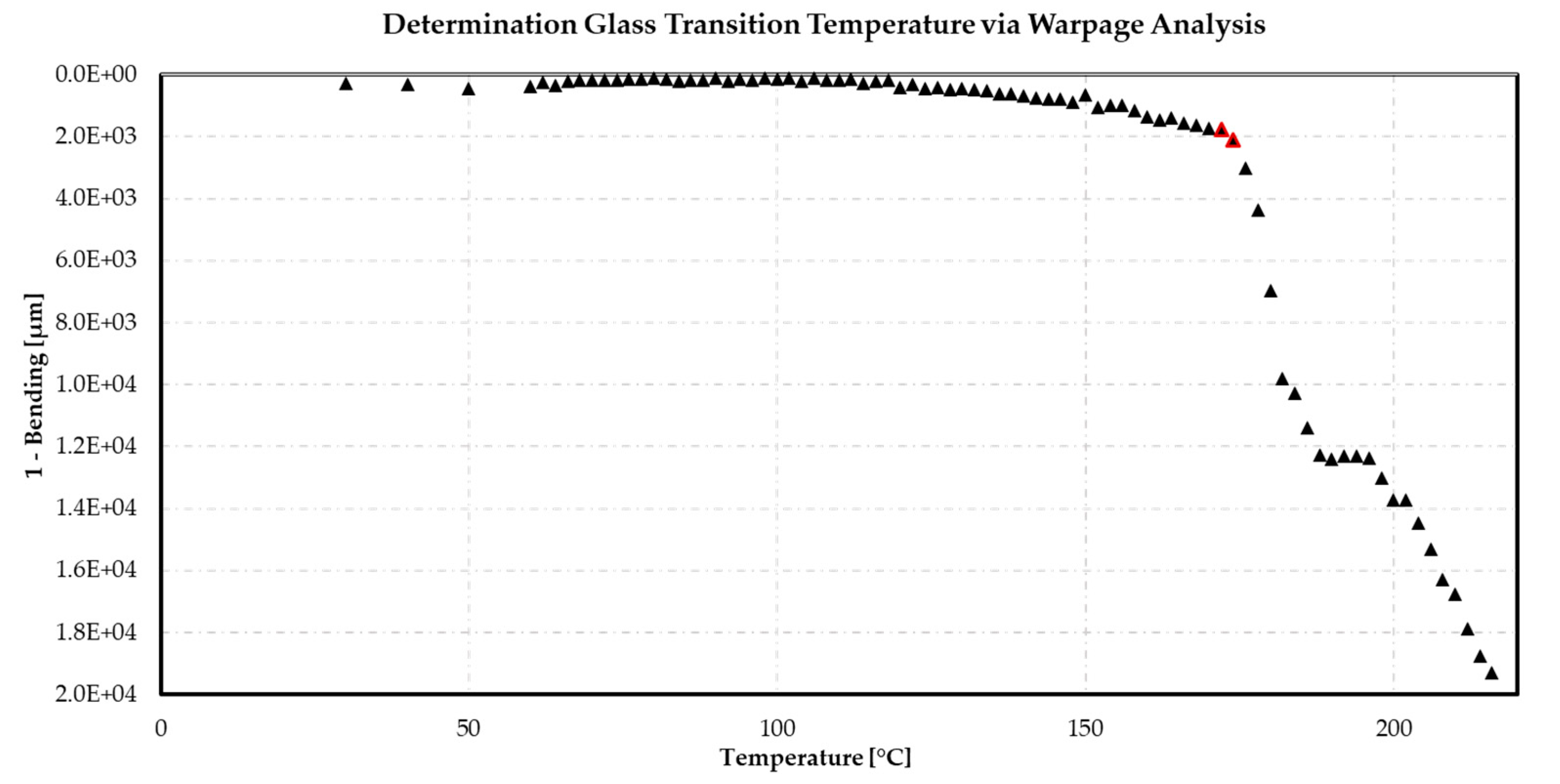
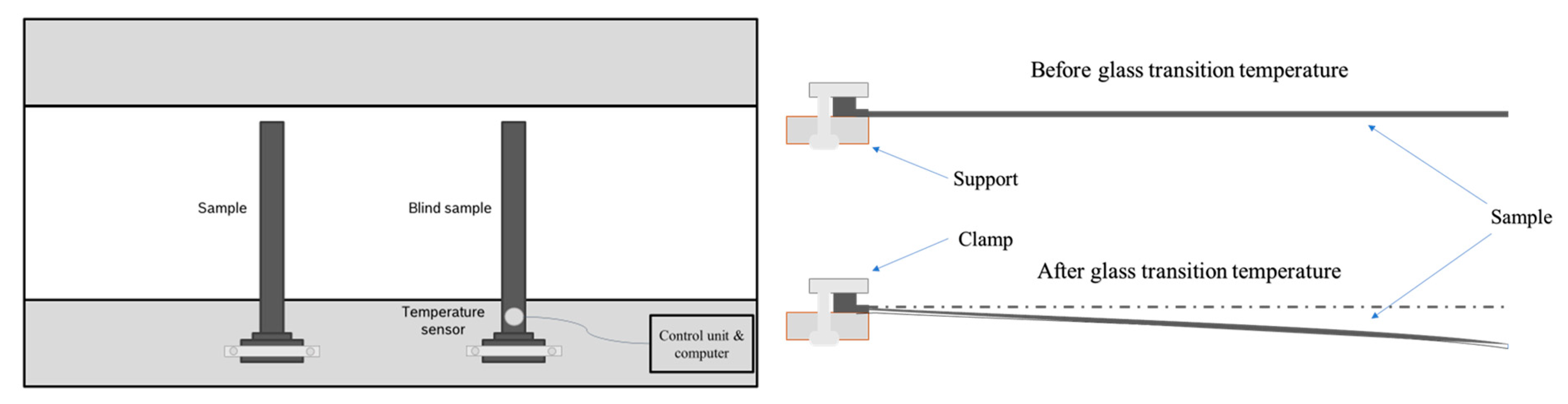
2.5. Determination of the Glass Transition Temperature (Tg) via Warpage Analysis
2.6. Post-Mold-Cure (PMC)
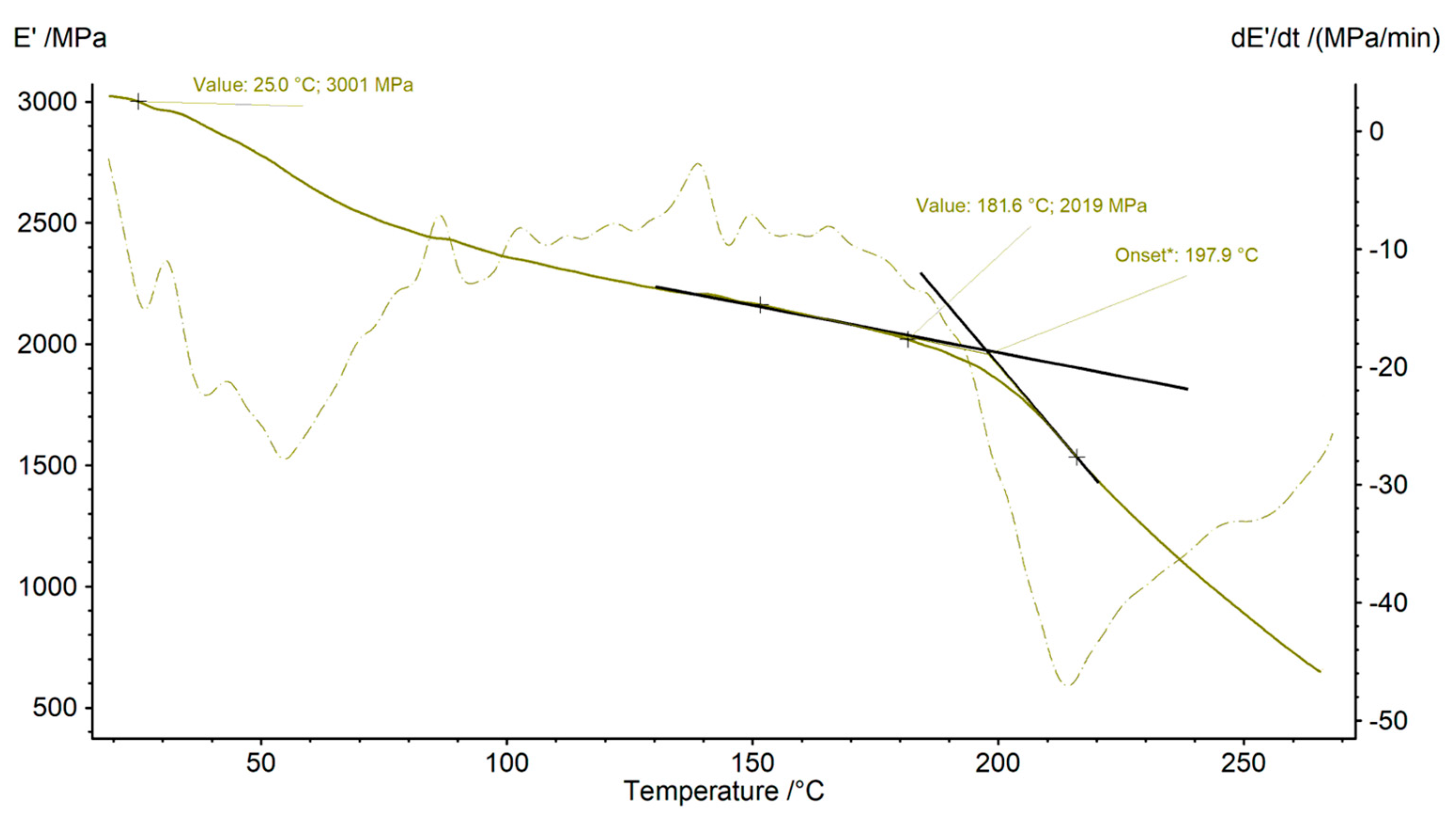
2.7. Dynamic Mechanical Analysis (DMA)
3. Results
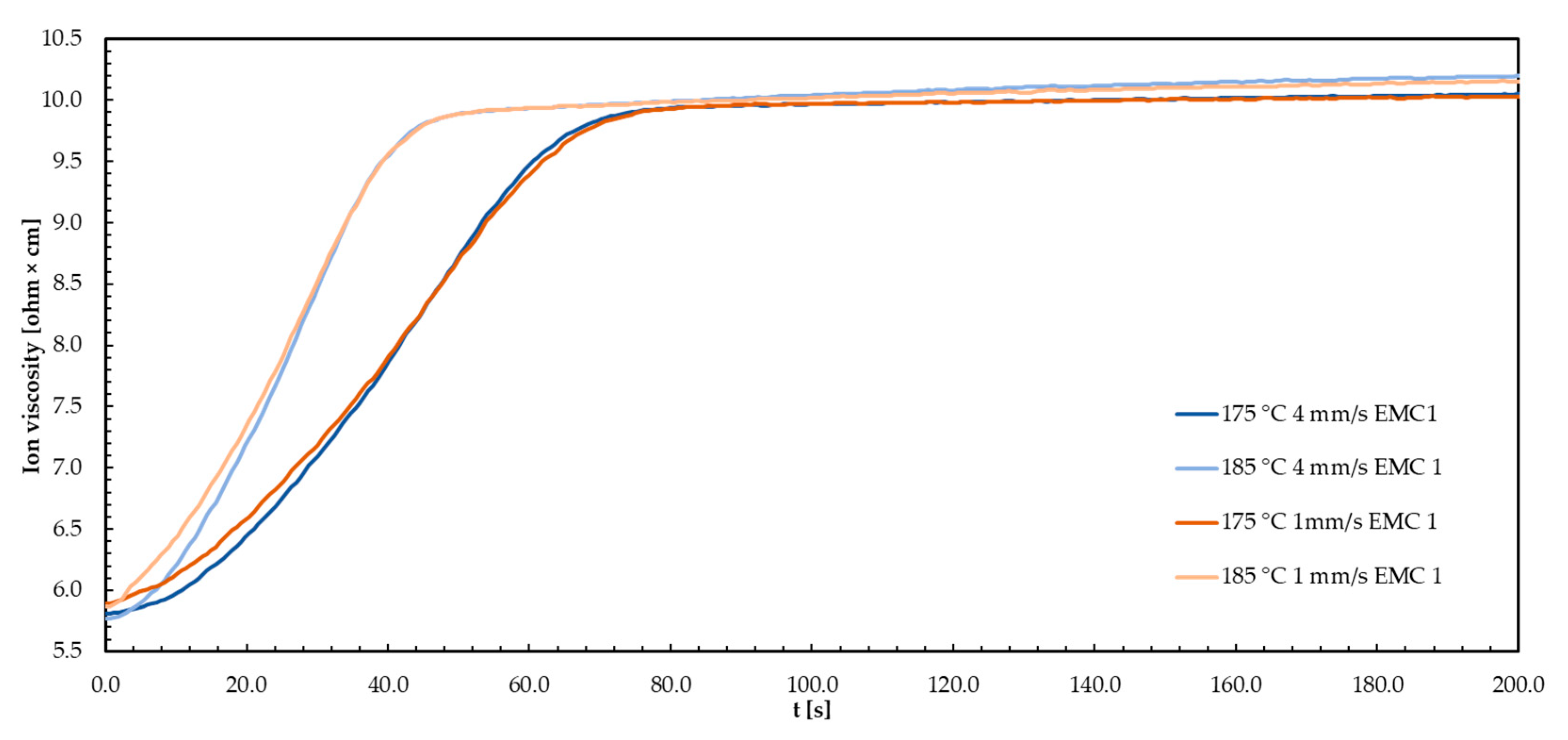
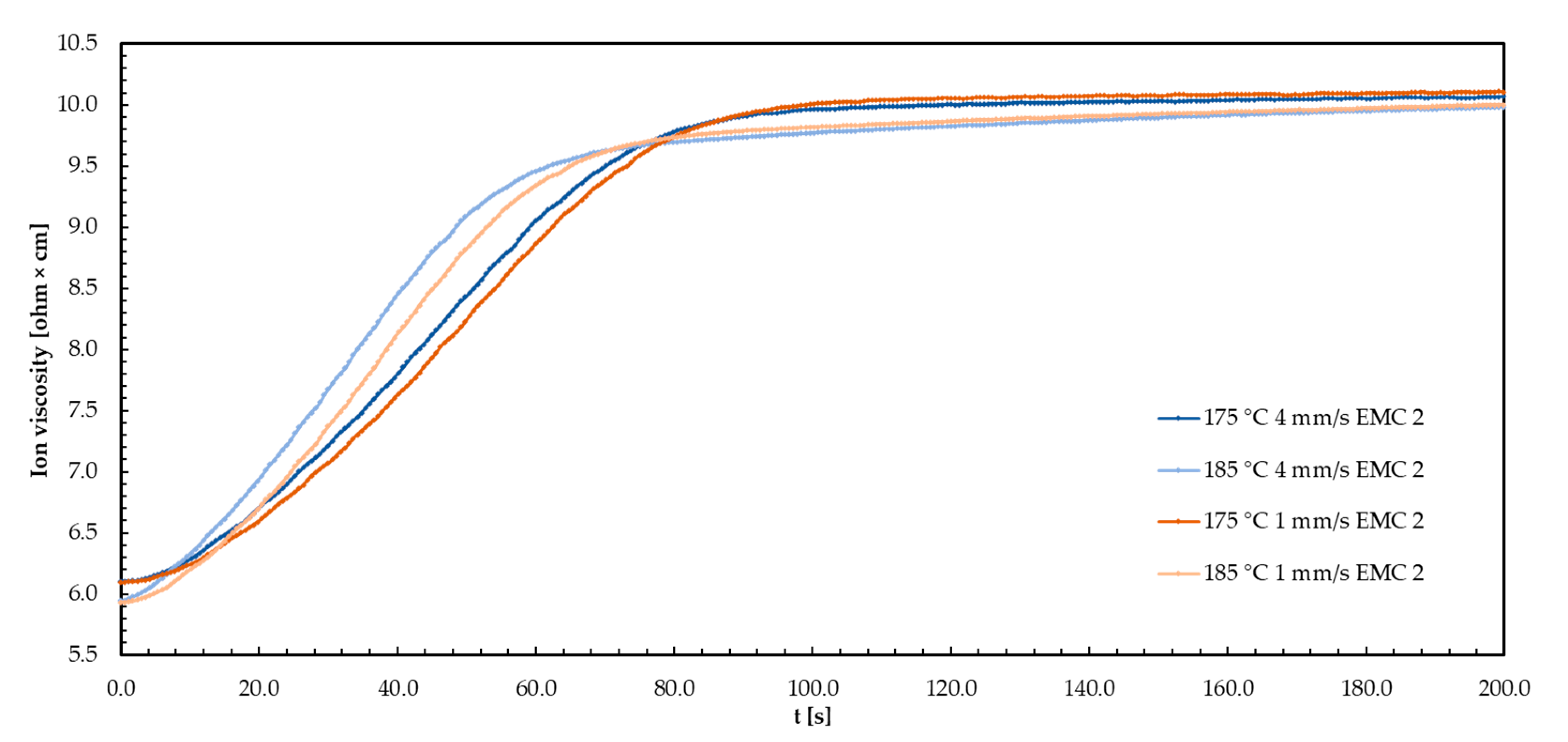
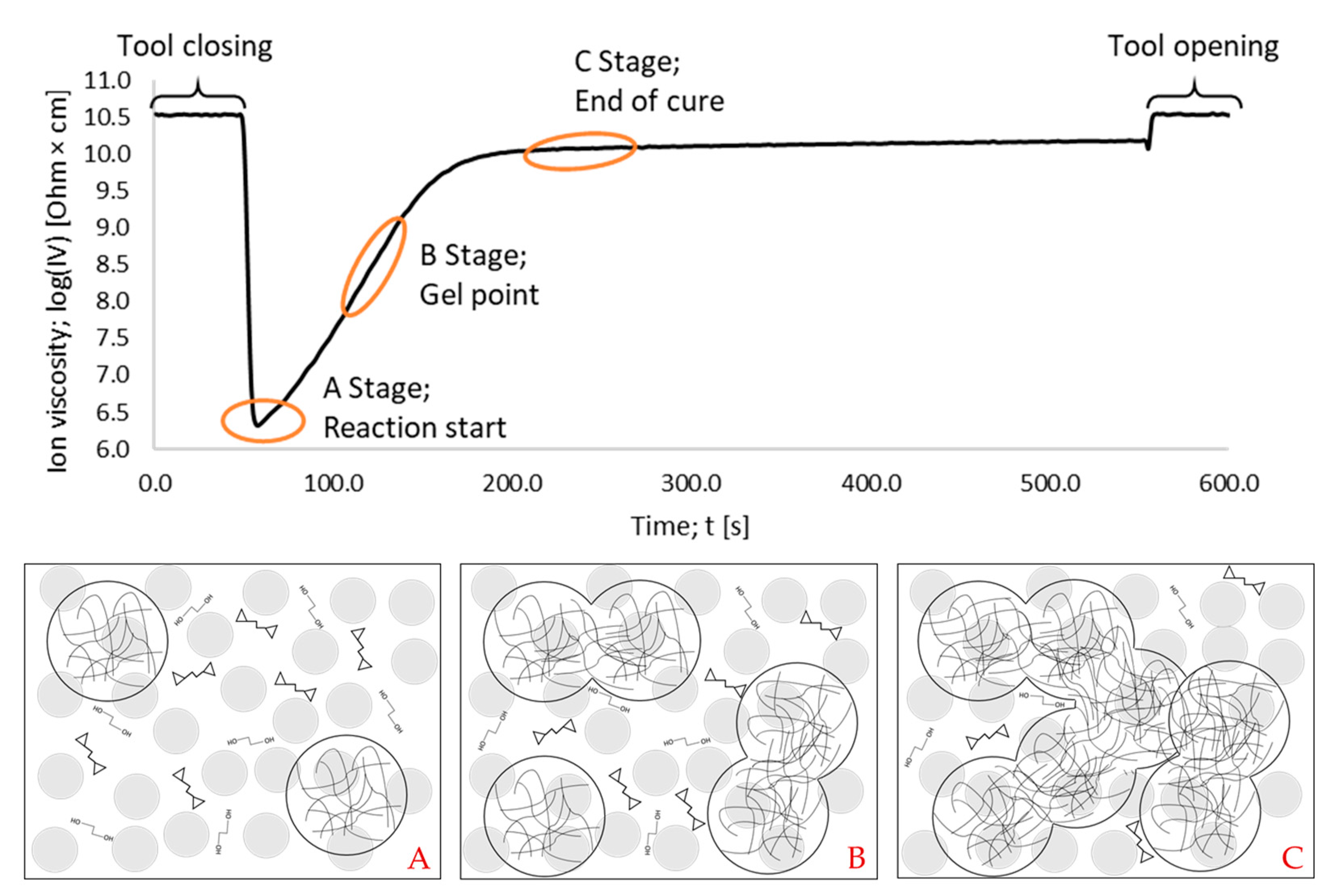
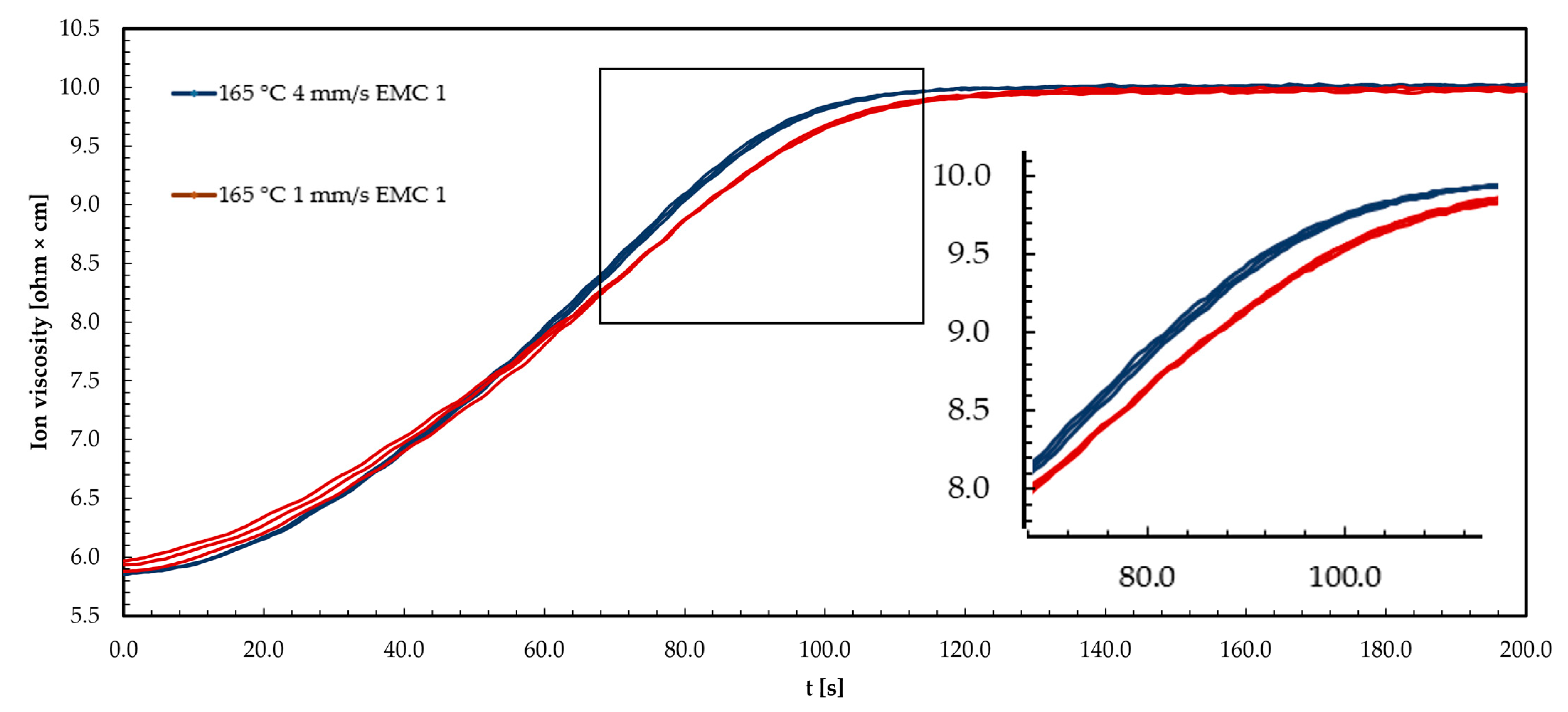
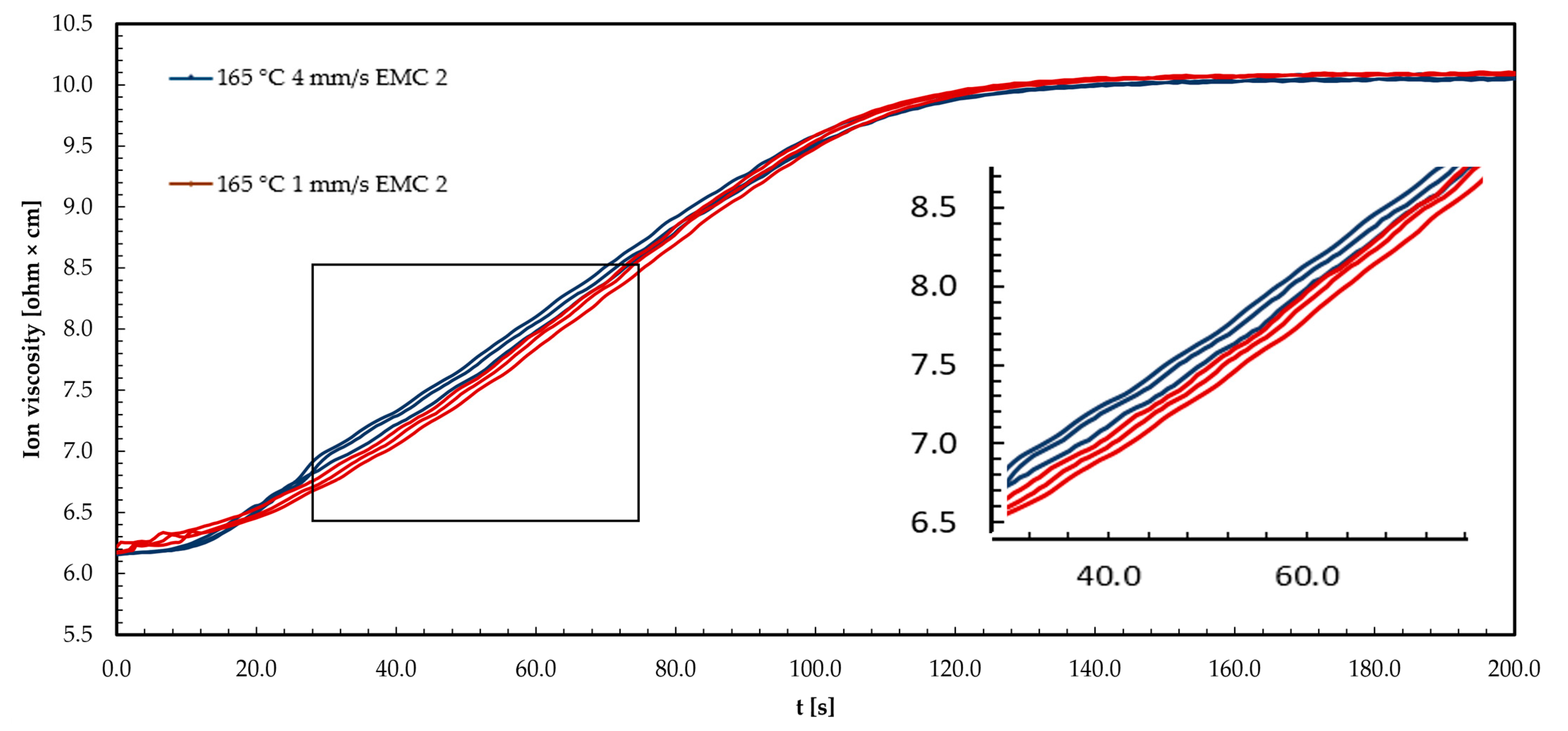
3.1. Effects of Injection Speed on Ion Viscosity (IV) Signal
3.2. Results of the Design of Experiment (DoE)
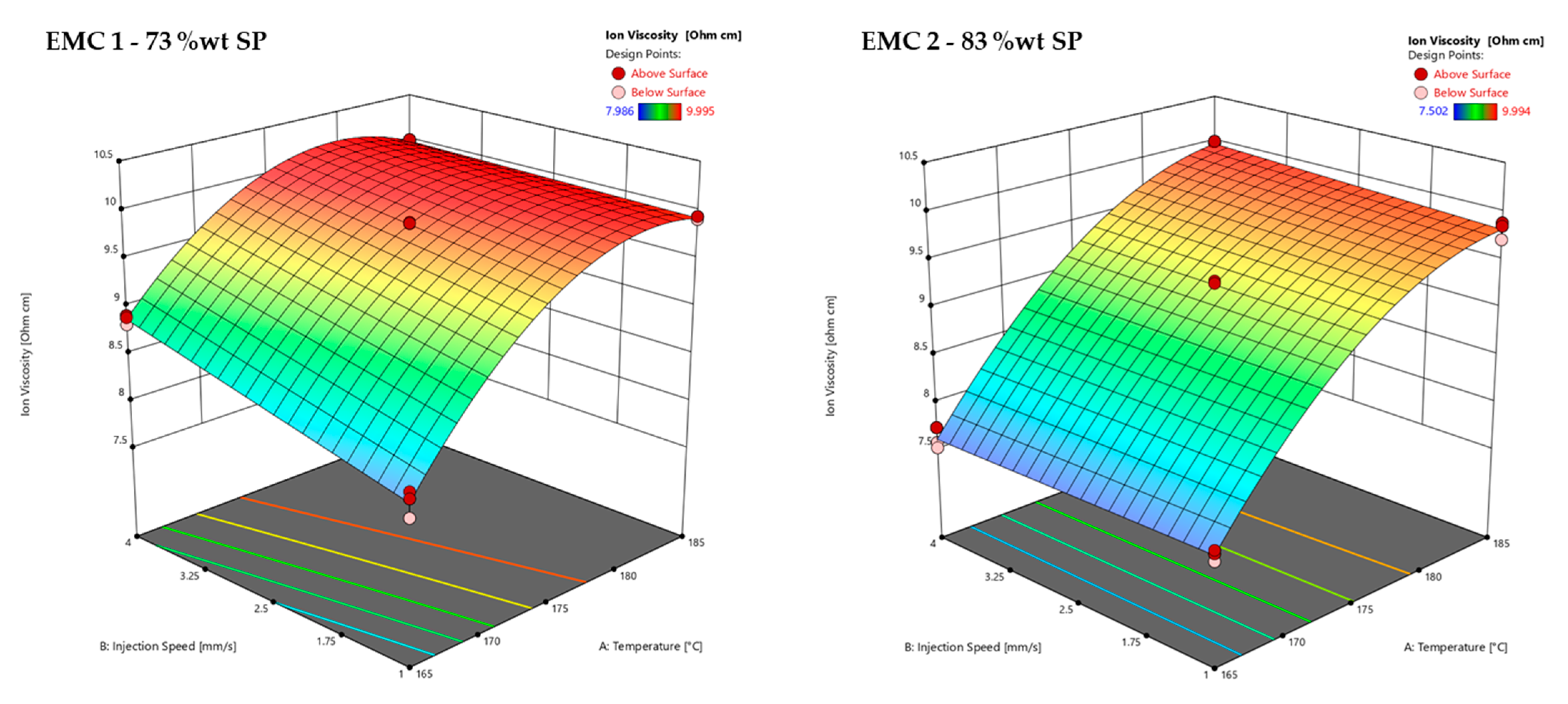
3.2.1. Response Surface of the Ion Viscosity (IV) of EMC 1 and EMC 2
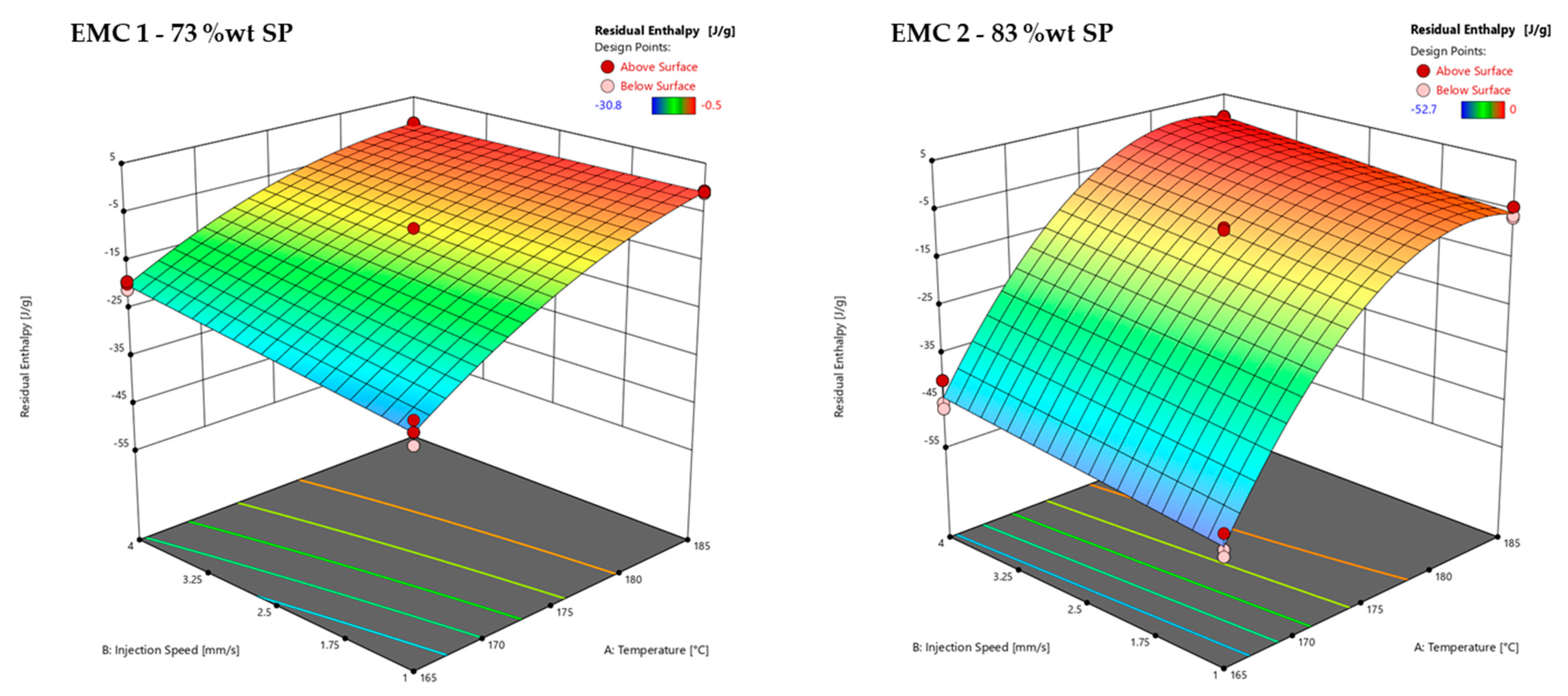
3.2.2. Response Surface of Residual Enthalpy of EMC 1 and EMC 2
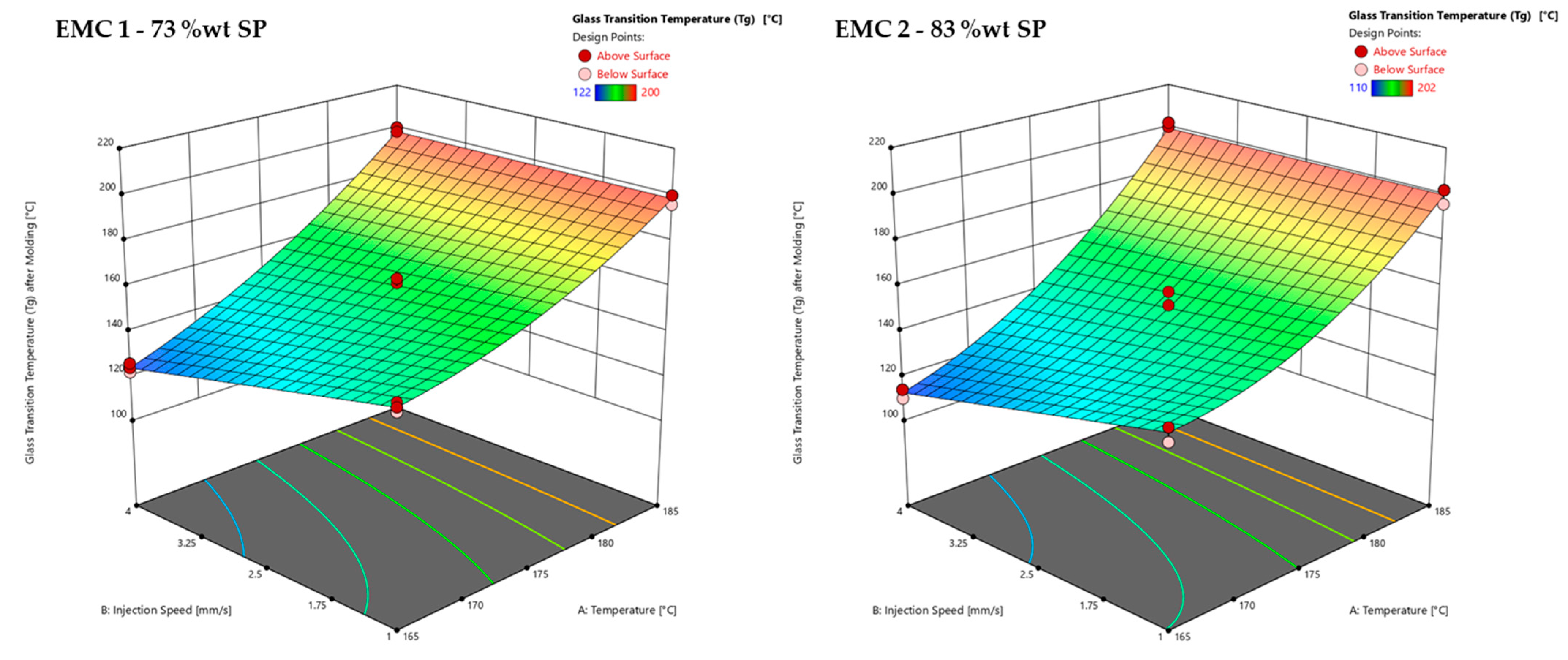
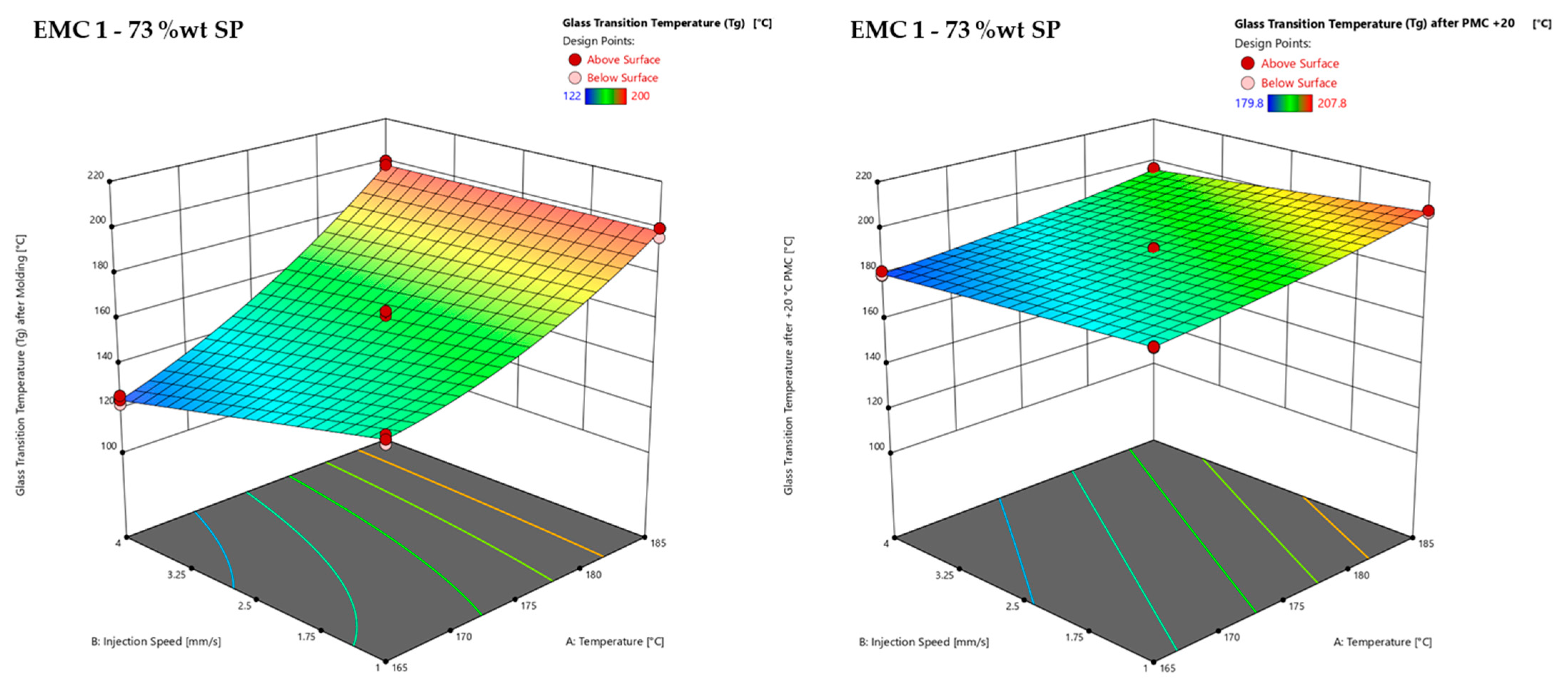
3.2.3. Response Surface of Glass Transition Temperature (Tg) after Molding of EMC 1 and EMC 2
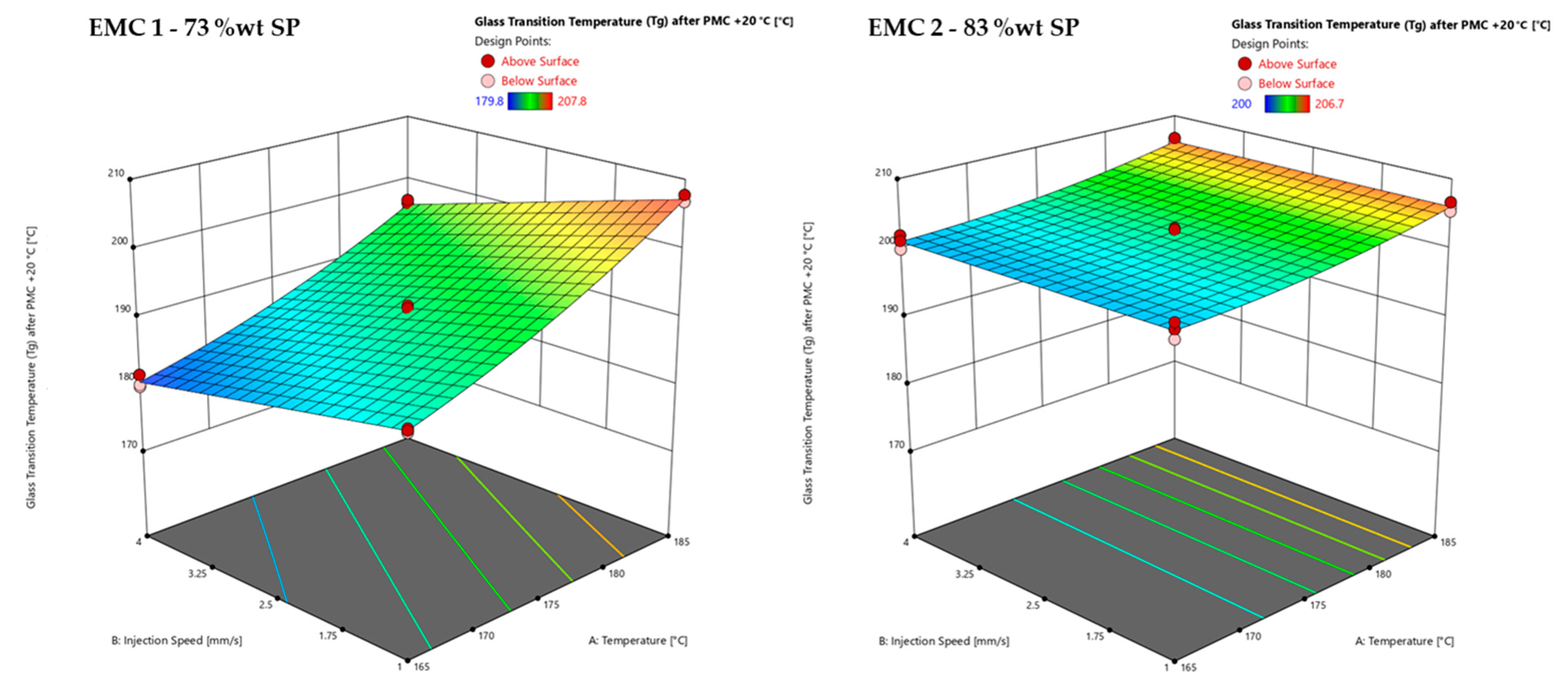
3.2.4. Response Surface of Glass Transition Temperature (Tg) after PMC of EMC 1 and EMC 2
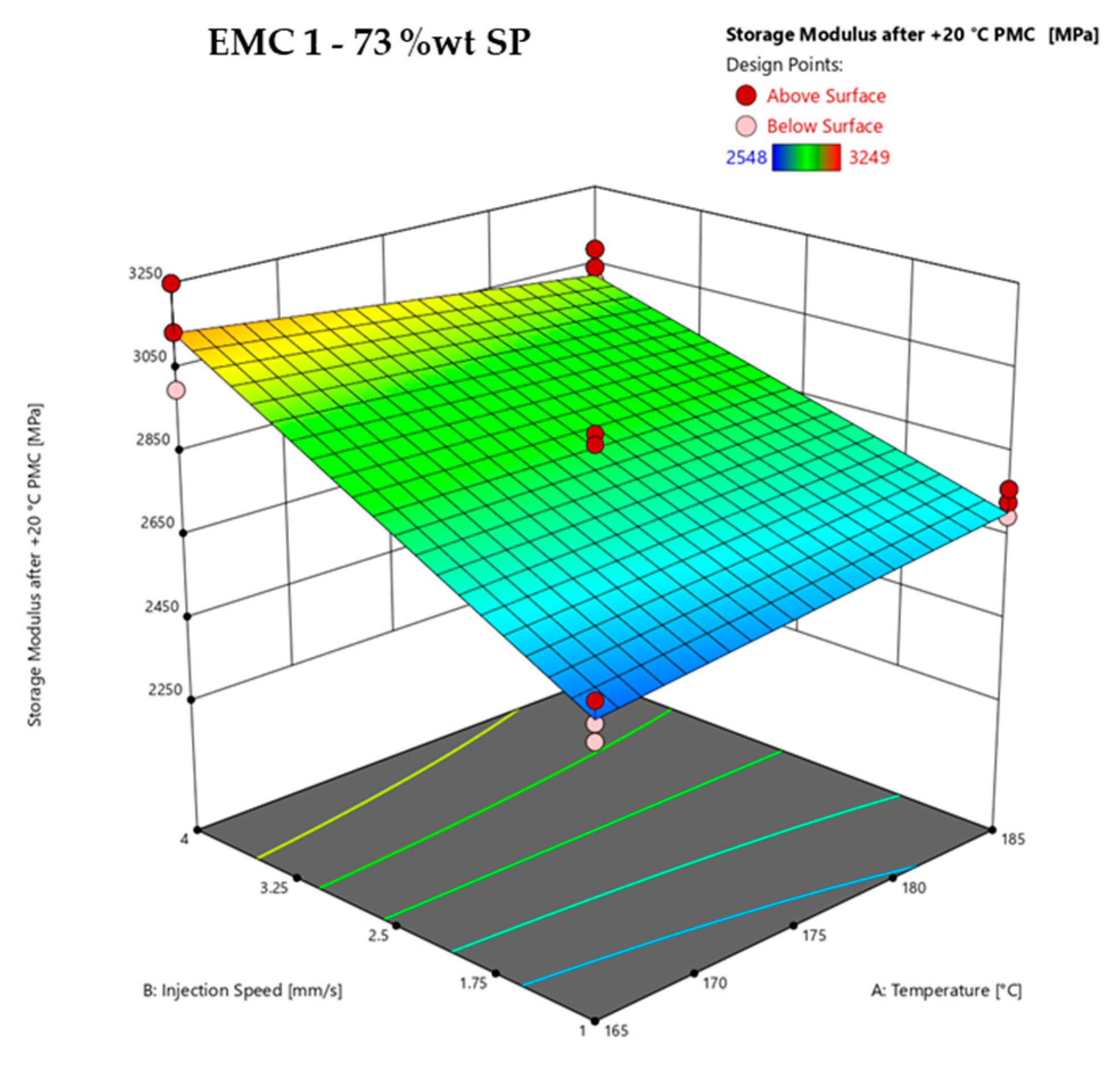
3.2.5. Response Surface of Storage Modulus after PMC of EMC 1 and EMC 2
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Kinjo, N.; Ogata, M.; Nishi, K.; Kaneda, A.; Dušek, K. Epoxy Molding Compounds as Encapsulation Materials for Microelectronic Devices. In Speciality Polymers/Polymer Physics; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–48. [Google Scholar]
- Komori, S.; Sakamoto, Y. Development Trend of Epoxy Molding Compound for Encapsulating Semiconductor Chips. In Materials for Advanced Packaging; Lu, D., Wong, C.P., Eds.; Springer: Boston, MA, USA, 2009; pp. 339–363. [Google Scholar]
- Kamal, M.R.; Isayev, A.I. Injection Molding: Technology and Fundamentals; Carl Hanser Verlag GmbH Co. KG: Munich, Germany, 2012. [Google Scholar]
- Tong, K.W.; Kwong, C.K.; Ip, K.W. Optimization of process conditions for the transfer molding of electronic packages. J. Mater. Process. Technol. 2003, 138, 361–365. [Google Scholar] [CrossRef]
- Zhao, Y.; Drummer, D. Influence of Filler Content and Filler Size on the Curing Kinetics of an Epoxy Resin. Polymers 2019, 11, 1797. [Google Scholar] [CrossRef] [PubMed]
- Dallaev, R.; Pisarenko, T.; Papež, N.; Sadovský, P.; Holcman, V. A Brief Overview on Epoxies in Electronics: Properties, Applications, and Modifications. Polymers 2023, 15, 3964. [Google Scholar] [CrossRef] [PubMed]
- Tarrío-Saavedra, J.; López-Beceiro, J.; Naya, S.; Artiaga, R. Effect of silica content on thermal stability of fumed silica/epoxy composites. Polym. Degrad. Stab. 2008, 93, 2133–2137. [Google Scholar] [CrossRef]
- Linec, M.; Mušič, B. The Effects of Silica-Based Fillers on the Properties of Epoxy Molding Compounds. Materials 2019, 12, 1811. [Google Scholar] [CrossRef] [PubMed]
- Soud, A.A.; Daradkeh, S.I.; Knápek, A.; Holcman, V.; Sobola, D. Electrical characteristics of different concentration of silica nanoparticles embedded in epoxy resin. Phys. Scr. 2023, 98, 125520. [Google Scholar] [CrossRef]
- Altmann, N.; Halley, P.J.; Cooper-White, J.; Lange, J. The effects of silica fillers on the gelation and vitrification of highly filled epoxy-amine thermosets. Macromol. Symp. 2001, 169, 171–177. [Google Scholar] [CrossRef]
- Dutta, A.; Ryan, M.E. Effect of fillers on kinetics of epoxy cure. J. Appl. Polym. Sci. 1979, 24, 635–649. [Google Scholar] [CrossRef]
- Wang, X.; Jin, J.; Song, M.; Lin, Y. Effect of graphene oxide sheet size on the curing kinetics and thermal stability of epoxy resins. Mater. Res. Express 2016, 3, 105303. [Google Scholar] [CrossRef]
- Vogelwaid, J.; Hampel, F.; Bayer, M.; Walz, M.; Kutuzova, L.; Lorenz, G.; Kandelbauer, A.; Jacob, T. In Situ Monitoring of the Curing of Highly Filled Epoxy Molding Compounds: The Influence of Reaction Type and Silica Content on Cure Kinetic Models. Polymers 2024, 16, 1056. [Google Scholar] [CrossRef]
- Nayak, S.K.; Mohanty, S.; Nayak, S.K. Fundamental and innovative approaches for filler design of thermal interface materials based on epoxy resin for high power density electronics application: A retrospective. Multiscale Multidiscip. Model. Exp. Des. 2020, 3, 103–129. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Kamal, M.R.; Sourour, S. Kinetics and thermal characterization of thermoset cure. Polym. Eng. Sci. 1973, 13, 59–64. [Google Scholar] [CrossRef]
- Wuzella, G.; Kandelbauer, A.; Mahendran, A.R.; Teischinger, A. Thermochemical and isoconversional kinetic analysis of a polyester–epoxy hybrid powder coating resin for wood based panel finishing. Prog. Org. Coat. 2011, 70, 186–191. [Google Scholar] [CrossRef]
- Kandelbauer, A.; Wuzella, G.; Mahendran, A.; Taudes, I.; Widsten, P. Using isoconversional kinetic analysis of liquid melamine–formaldehyde resin curing to predict laminate surface properties. J. Appl. Polym. Sci. 2009, 113, 2649–2660. [Google Scholar] [CrossRef]
- Mahendran, A.R.; Wuzella, G.; Kandelbauer, A. Thermal characterization of kraft lignin phenol-formaldehyde resin for paper impregnation. J. Adhes. Sci. Technol. 2010, 24, 1553–1565. [Google Scholar] [CrossRef]
- Alig, I.; Fischer, D.; Lellinger, D.; Steinhoff, B. Combination of NIR, Raman, Ultrasonic and Dielectric Spectroscopy for In-Line Monitoring of the Extrusion Process. Macromol. Symp. 2005, 230, 51–58. [Google Scholar] [CrossRef]
- Hardis, R.; Jessop, J.L.P.; Peters, F.E.; Kessler, M.R. Cure kinetics characterization and monitoring of an epoxy resin using DSC, Raman spectroscopy, and DEA. Compos. Part A Appl. Sci. Manuf. 2013, 49, 100–108. [Google Scholar] [CrossRef]
- Lee, H.L. The Handbook of Dielectric Analysis and Cure Monitoring; Lambient Technology LLC: Boston, MA, USA, 2014; Volume 156. [Google Scholar]
- Kandelbauer, A. Processing and process control. In Handbook of Thermoset Plastics; Elsevier: Amsterdam, The Netherlands, 2022; pp. 1045–1070. [Google Scholar]
- Franieck, E.; Fleischmann, M.; Hölck, O.; Kutuzova, L.; Kandelbauer, A. Cure Kinetics Modeling of a High Glass Transition Temperature Epoxy Molding Compound (EMC) Based on Inline Dielectric Analysis. Polymers 2021, 13, 1734. [Google Scholar] [CrossRef]
- Weiss, S.; Urdl, K.; Mayer, H.A.; Zikulnig-Rusch, E.M.; Kandelbauer, A. IR spectroscopy: Suitable method for determination of curing degree and crosslinking type in melamine–formaldehyde resins. J. Appl. Polym. Sci. 2019, 136, 47691. [Google Scholar] [CrossRef]
- Rosentritt, M.; Behr, M.; Knappe, S.; Handel, G. Dielectric analysis of light-curing dental restorative materials—A pilot study. J. Mater. Sci. 2006, 41, 2805–2810. [Google Scholar] [CrossRef]
- Nasseri, L.; Rosenfeld, C.; Solt-Rindler, P.; Mitter, R.; Moser, J.; Kandelbauer, A.; Konnerth, J.; Van Herwijnen, H.W. Comparison between cure kinetics by means of dynamic rheology and DSC of formaldehyde-based wood adhesives. J. Adhes. 2024, 1–22. [Google Scholar] [CrossRef]
- Nasseri, L.; Rosenfeld, C.; Solt, P.; Mihalic, M.; Kandelbauer, A.; Konnerth, J.; van Herwijnen, H.W. Determination of the Gel Point of Formaldehyde-Based Wood Adhesives by Using a Multiwave Technique. ACS Appl. Polym. Mater. 2023, 5, 6354–6363. [Google Scholar] [CrossRef]
- Franieck, E.; Fleischmann, M.; Hölck, O.; Schneider-Ramelow, M. Inline cure monitoring of epoxy resin by dielectric analysis. In Proceedings of the 2021 23rd European Microelectronics and Packaging Conference & Exhibition (EMPC), Gothenburg, Sweden, 13–16 September 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Vassilikou-Dova, A.; Kalogeras, I.M. Dielectric Analysis (DEA). In Thermal Analysis of Polymers; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2009; pp. 497–613. [Google Scholar]
- Shigue, C.Y.; Santos, R.G.S.D.; De Abreu, M.M.S.P.; Baldan, C.A.; Robin, A.L.M.; Ruppert-Filho, E. Dielectric Thermal Analysis as a Tool for Quantitative Evaluation of the Viscosity and the Kinetics of Epoxy Resin Cure. IEEE Trans. Appl. Supercond. 2006, 16, 1786–1789. [Google Scholar] [CrossRef]
- Bellucci, F.; Valentino, M.; Monetta, T.; Nicodemo, L.; Kenny, J.; Nicolais, L.; Mijovic, J. Impedance spectroscopy of reactive polymers. 1. J. Polym. Sci. Part B Polym. Phys. 1994, 32, 2519–2527. [Google Scholar] [CrossRef]
- Vogelwaid, J.; Bayer, M.; Walz, M.; Kutuzova, L.; Kandelbauer, A.; Jacob, T. Process Optimization of the Morphological Properties of Epoxy Resin Molding Compounds Using Response Surface Design. Polymers 2024, 16, 1102. [Google Scholar] [CrossRef] [PubMed]
- Pascault, J.-P.; Williams, R.J.J. Glass transition temperature versus conversion relationships for thermosetting polymers. J. Polym. Sci. Part B Polym. Phys. 1990, 28, 85–95. [Google Scholar] [CrossRef]
- Vidil, T.; Tournilhac, F.; Musso, S.; Robisson, A.; Leibler, L. Control of reactions and network structures of epoxy thermosets. Prog. Polym. Sci. 2016, 62, 126–179. [Google Scholar] [CrossRef]
- Dušek, K.; Dušková-Smrčková, M. Network structure formation during crosslinking of organic coating systems. Prog. Polym. Sci. 2000, 25, 1215–1260. [Google Scholar] [CrossRef]
- Dušek, K.; Pleštil, J.; Lednický, F.; Luňák, S. Are cured epoxy resins inhomogeneous? Polymer 1978, 19, 393–397. [Google Scholar] [CrossRef]
- Aoki, M.; Shundo, A.; Yamamoto, S.; Tanaka, K. Effect of a heterogeneous network on glass transition dynamics and solvent crack behavior of epoxy resins. Soft Matter 2020, 16, 7470–7478. [Google Scholar] [CrossRef] [PubMed]
- Hoshino, T.; Okamoto, Y.; Yamamoto, A.; Masunaga, H. Heterogeneous dynamics in the curing process of epoxy resins. Sci. Rep. 2021, 11, 9767. [Google Scholar] [CrossRef]
- Shundo, A.; Aoki, M.; Wang, P.; Hoshino, T.; Yamamoto, S.; Yamada, S.; Tanaka, K. Effect of a Heterogeneous Network on the Fracture Behavior of Epoxy Resins. Macromolecules 2023, 56, 3884–3890. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Ediger, M.D. Spatially heterogeneous dynamics in thermoset resins below the glass-transition temperature. J. Polym. Sci. Part B Polym. Phys. 2000, 38, 2232–2239. [Google Scholar] [CrossRef]
- Chevalier, J.; Brassart, L.; Lani, F.; Bailly, C.; Pardoen, T.; Morelle, X.P. Unveiling the nanoscale heterogeneity controlled deformation of thermosets. J. Mech. Phys. Solids 2018, 121, 432–446. [Google Scholar] [CrossRef]
- Kramer, E.J. The stress-strain curve of shear-banding polystyrene. J. Macromol. Sci. Part B 1974, 10, 191–202. [Google Scholar] [CrossRef]
- Eaton, M.D.; Brinson, L.C.; Shull, K.R. Temperature dependent fracture behavior in model epoxy networks with nanoscale heterogeneity. Polymer 2021, 221, 123560. [Google Scholar] [CrossRef]
- Kontou, E.; Spathis, G.; Theocaris, P.S. The heterogeneity of the network structure of epoxy polymers studied by dynamic and DSC tests. J. Polym. Sci. Polym. Chem. Ed. 1985, 23, 1493–1503. [Google Scholar] [CrossRef]
- Morsch, S.; Liu, Y.; Lyon, S.B.; Gibbon, S.R. Insights into Epoxy Network Nanostructural Heterogeneity Using AFM-IR. ACS Appl. Mater. Interfaces 2016, 8, 959–966. [Google Scholar] [CrossRef]
- Nguyen, H.K.; Aoki, M.; Liang, X.; Yamamoto, S.; Tanaka, K.; Nakajima, K. Local Mechanical Properties of Heterogeneous Nanostructures Developed in a Cured Epoxy Network: Implications for Innovative Adhesion Technology. ACS Appl. Nano Mater. 2021, 4, 12188–12196. [Google Scholar] [CrossRef]
- Katahira, C.; Morishita, N.; Ikeda, J.; Lim, P.B.; Inoue, M.; Iwasaki, Y.; Aota, H.; Matsumoto, A. Mechanistic discussion of cationic crosslinking copolymerizations of 1,2-epoxycyclohexane with diepoxide crosslinkers accompanied by intramolecular and intermolecular chain transfer reactions. J. Polym. Sci. Part A Polym. Chem. 2010, 48, 4445–4455. [Google Scholar] [CrossRef]
- Gao, H.; Matyjaszewski, K. Synthesis of functional polymers with controlled architecture by CRP of monomers in the presence of cross-linkers: From stars to gels. Prog. Polym. Sci. 2009, 34, 317–350. [Google Scholar] [CrossRef]
- Jones, B.H.; Alam, T.M.; Lee, S.; Celina, M.C.; Allers, J.P.; Park, S.; Chen, L.; Martinez, E.J.; Unangst, J.L. Curing behavior, chain dynamics, and microstructure of high Tg thiol-acrylate networks with systematically varied network heterogeneity. Polymer 2020, 205, 122783. [Google Scholar] [CrossRef]
- Yamamoto, S.; Ida, R.; Aoki, M.; Kuwahara, R.; Shundo, A.; Tanaka, K. Formation Mechanism of a Heterogeneous Network in Epoxy Resins. Macromolecules 2023, 56, 3913–3921. [Google Scholar] [CrossRef]
- Kim, D.H.; Kim, S.C. Vitrification effect during the reaction injection molding (RIM) process of epoxy resin. Polym. Eng. Sci. 1989, 29, 456–462. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N.; Vyazovkin, S.; Mititelu, A.; Sladic, C.; Vincent, L. A Study of Epoxy-Amine Cure Kinetics by Combining Isoconversional Analysis with Temperature Modulated DSC and Dynamic Rheometry. Macromol. Chem. Phys. 2003, 204, 1815–1821. [Google Scholar] [CrossRef]
- Zheng, X.; Guo, Y.; Douglas, J.F.; Xia, W. Understanding the role of cross-link density in the segmental dynamics and elastic properties of cross-linked thermosets. J. Chem. Phys. 2022, 157, 064901. [Google Scholar] [CrossRef]

| Factor 1 | Factor 2 | Response 1 | Response 2 | Response 3 | Response 4 | Response 5 | |
|---|---|---|---|---|---|---|---|
| Run | A: Temperature [°C] | B: Injection Speed [mm/s] | cm] | Residual Enthalpy [J/g] | Glass Transition Temperature (Tg) after Molding [°C] | Glass Transition Temperature (Tg) after PMC [°C] | Storage Modulus after PMC [MPa] |
| 1 | 165 | 1 | 8.243 | −25.978 | 154 | 188.0 | 2638 |
| 2 | 165 | 1 | 8.174 | −28.252 | 150 | 188.6 | 2548 |
| 3 | 165 | 1 | 7.986 | −30.800 | 152 | 188.3 | 2588 |
| 4 | 185 | 1 | 9.919 | −0.001 | 200 | 207.8 | 2735 |
| 5 | 185 | 1 | 9.939 | −0.001 | 200 | 206.9 | 2767 |
| 6 | 185 | 1 | 9.911 | −0.001 | 196 | 206.8 | 2701 |
| 7 | 165 | 4 | 8.913 | −19.563 | 122 | 181.6 | 3002 |
| 8 | 165 | 4 | 8.891 | −20.796 | 124 | 179.8 | 3136 |
| 9 | 165 | 4 | 8.817 | −19.074 | 126 | 180.1 | 3249 |
| 10 | 185 | 4 | 9.995 | −0.001 | 200 | 195.0 | 3006 |
| 11 | 185 | 4 | 9.973 | −0.001 | 196 | 196.2 | 3089 |
| 12 | 185 | 4 | 9.966 | −0.001 | 198 | 196.7 | 3042 |
| 13 | 175 | 2.5 | 9.882 | −8.100 | 162 | 191.8 | 2899 |
| 14 | 175 | 2.5 | 9.866 | −8.593 | 154 | 191.9 | 2786 |
| 15 | 175 | 2.5 | 9.834 | −8.459 | 164 | 191.5 | 2845 |
| 16 | 175 | 2.5 | 9.871 | −8.448 | 160 | 191.3 | 2807 |
| 17 | 175 | 2.5 | 9.838 | −8.537 | 164 | 191.0 | 2873 |
| Factor 1 | Factor 2 | Response 1 | Response 2 | Response 3 | Response 4 | Response 5 | |
|---|---|---|---|---|---|---|---|
| Run | A: Temperature [°C] | B: Injection Speed [mm/s] | cm] | Residual Enthalpy [J/g] | Glass Transition Temperature (Tg) after Molding [°C] | Glass Transition Temperature (Tg) after PMC [°C] | Storage Modulus after PMC [MPa] |
| 1 | 165 | 1 | 7.647 | −48.118 | 144 | 201.4 | 3015 |
| 2 | 165 | 1 | 7.683 | −51.294 | 138 | 200.1 | 3236 |
| 3 | 165 | 1 | 7.572 | −52.706 | 144 | 202.3 | 2866 |
| 4 | 185 | 1 | 9.716 | −0.004 | 202 | 206.0 | 4545 |
| 5 | 185 | 1 | 9.889 | −6.588 | 202 | 205.4 | 4357 |
| 6 | 185 | 1 | 9.855 | −6.141 | 196 | 206.7 | 4049 |
| 7 | 165 | 4 | 7.560 | −45.371 | 114 | 202.0 | 2537 |
| 8 | 165 | 4 | 7.502 | −46.647 | 114 | 201.2 | 2508 |
| 9 | 165 | 4 | 7.724 | −40.535 | 110 | 200.0 | 2543 |
| 10 | 185 | 4 | 9.969 | 0.000 | 196 | 206.5 | 4002 |
| 11 | 185 | 4 | 9.928 | 0.000 | 200 | 205.5 | 2368 |
| 12 | 185 | 4 | 9.994 | 0.000 | 202 | 205.9 | 3024 |
| 13 | 175 | 2.5 | 9.289 | −9.541 | 150 | 202.9 | 3740 |
| 14 | 175 | 2.5 | 9.265 | −10.647 | 146 | 202.1 | 3686 |
| 15 | 175 | 2.5 | 9.211 | −8.541 | 158 | 203.0 | 2456 |
| 16 | 175 | 2.5 | 9.241 | −9.059 | 148 | 202.8 | 2874 |
| 17 | 175 | 2.5 | 9.234 | −9.488 | 152 | 202.3 | 3452 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 8.5100 | 4 | 2.1300 | 592.08 | <0.0001 |
| A—Temperature | 6.2800 | 1 | 6.2800 | 1747.59 | <0.0001 |
| B—Injection Speed | 0.4732 | 1 | 0.4732 | 131.75 | <0.0001 |
| AB | 0.3512 | 1 | 0.3512 | 97.79 | <0.0001 |
| A2 | 1.4100 | 1 | 1.4100 | 391.18 | <0.0001 |
| Pure Error | 0.0431 | 12 | 0.0036 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 16.4500 | 4 | 4.1100 | 890.03 | <0.0001 |
| A—Temperature | 15.5500 | 1 | 15.5500 | 3365.81 | <0.0001 |
| B—Injection Speed | 0.0082 | 1 | 0.0082 | 1.77 | 0.2078 |
| AB | 0.0250 | 1 | 0.0250 | 5.40 | 0.0385 |
| A2 | 0.8647 | 1 | 0.8647 | 187.12 | <0.0001 |
| Pure Error | 0.0555 | 12 | 0.0046 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 1785.75 | 4 | 446.44 | 396.97 | <0.0001 |
| A—Temperature | 1619.09 | 1 | 1619.09 | 1439.70 | <0.0001 |
| B—Injection Speed | 52.90 | 1 | 52.90 | 47.04 | <0.0001 |
| AB | 56.32 | 1 | 56.32 | 50.08 | <0.0001 |
| A2 | 57.44 | 1 | 57.44 | 51.07 | <0.0001 |
| Pure Error | 13.50 | 12 | 1.12 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 6948.83 | 4 | 1737.21 | 562.64 | <0.0001 |
| A—Temperature | 5966.96 | 1 | 5966.96 | 1932.54 | <0.0001 |
| B—Injection Speed | 111.92 | 1 | 111.92 | 36.25 | <0.0001 |
| A2 | 869.42 | 1 | 869.42 | 281.58 | <0.0001 |
| Pure Error | 37.05 | 12 | 3.09 |
| Source | Sum of Squares | Df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 17,556.93 | 4 | 4389.23 | 324.86 | <0.0001 |
| A—Temperature | 15,696.33 | 1 | 15,696.33 | 1161.74 | <0.0001 |
| B—Injection Speed | 675.00 | 1 | 675.00 | 49.96 | <0.0001 |
| AB | 616.33 | 1 | 616.33 | 45.62 | <0.0001 |
| A2 | 569.26 | 1 | 569.26 | 42.13 | <0.0001 |
| Pure Error | 162.13 | 12 | 13.51 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 16,987.67 | 3 | 5662.56 | 66.17 | <0.0001 |
| A—Temperature | 15,696.33 | 1 | 15,696.33 | 183.41 | <0.0001 |
| B—Injection Speed | 675.00 | 1 | 675.00 | 7.89 | 0.0148 |
| AB | 616.33 | 1 | 616.33 | 7.20 | 0.0188 |
| Pure Error | 954.13 | 12 | 79.51 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 12,288.53 | 4 | 3072.13 | 356.30 | <0.0001 |
| A—Temperature | 10,920.33 | 1 | 10,920.33 | 1266.53 | <0.0001 |
| B—Injection Speed | 616.33 | 1 | 616.33 | 71.48 | <0.0001 |
| AB | 560.33 | 1 | 560.33 | 64.99 | <0.0001 |
| A2 | 191.53 | 1 | 191.53 | 22.21 | 0.0005 |
| Pure Error | 103.47 | 12 | 8.62 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 73.41 | 3 | 24.47 | 49.18 | <0.0001 |
| A—Temperature | 70.08 | 1 | 70.08 | 140.86 | <0.0001 |
| B—Injection Speed | 0.0533 | 1 | 0.0533 | 0.1072 | 0.7486 |
| A2 | 3.28 | 1 | 3.28 | 6.58 | 0.0235 |
| Pure Error | 6.45 | 12 | 0.5379 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 5.817 × 105 | 3 | 1.939 × 105 | 47.80 | <0.0001 |
| A—Temperature | 2670.08 | 1 | 2670.08 | 0.6583 | 0.4318 |
| B—Injection Speed | 5.406 × 105 | 1 | 5.406 × 105 | 133.28 | <0.0001 |
| AB | 38,420.08 | 1 | 38,420.08 | 9.47 | 0.0088 |
| Pure Error | 48,868.00 | 12 | 4072.33 |
| Source | Sum of Squares | Df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 4.806 × 106 | 2 | 2.403 × 106 | 10.74 | 0.0015 |
| A—Temperature | 2.651 × 106 | 1 | 2.651 × 106 | 11.84 | 0.0040 |
| B—Injection Speed | 2.156 × 106 | 1 | 2.156 × 106 | 9.63 | 0.0078 |
| Pure Error | 2.790 × 106 | 12 | 2.325 × 106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vogelwaid, J.; Bayer, M.; Walz, M.; Hampel, F.; Kutuzova, L.; Lorenz, G.; Kandelbauer, A.; Jacob, T. Optimizing Epoxy Molding Compound Processing: A Multi-Sensor Approach to Enhance Material Characterization and Process Reliability. Polymers 2024, 16, 1540. https://doi.org/10.3390/polym16111540
Vogelwaid J, Bayer M, Walz M, Hampel F, Kutuzova L, Lorenz G, Kandelbauer A, Jacob T. Optimizing Epoxy Molding Compound Processing: A Multi-Sensor Approach to Enhance Material Characterization and Process Reliability. Polymers. 2024; 16(11):1540. https://doi.org/10.3390/polym16111540
Chicago/Turabian StyleVogelwaid, Julian, Martin Bayer, Michael Walz, Felix Hampel, Larysa Kutuzova, Günter Lorenz, Andreas Kandelbauer, and Timo Jacob. 2024. "Optimizing Epoxy Molding Compound Processing: A Multi-Sensor Approach to Enhance Material Characterization and Process Reliability" Polymers 16, no. 11: 1540. https://doi.org/10.3390/polym16111540
APA StyleVogelwaid, J., Bayer, M., Walz, M., Hampel, F., Kutuzova, L., Lorenz, G., Kandelbauer, A., & Jacob, T. (2024). Optimizing Epoxy Molding Compound Processing: A Multi-Sensor Approach to Enhance Material Characterization and Process Reliability. Polymers, 16(11), 1540. https://doi.org/10.3390/polym16111540









