Molecular Simulation of Covalent Adaptable Networks and Vitrimers: A Review
Abstract
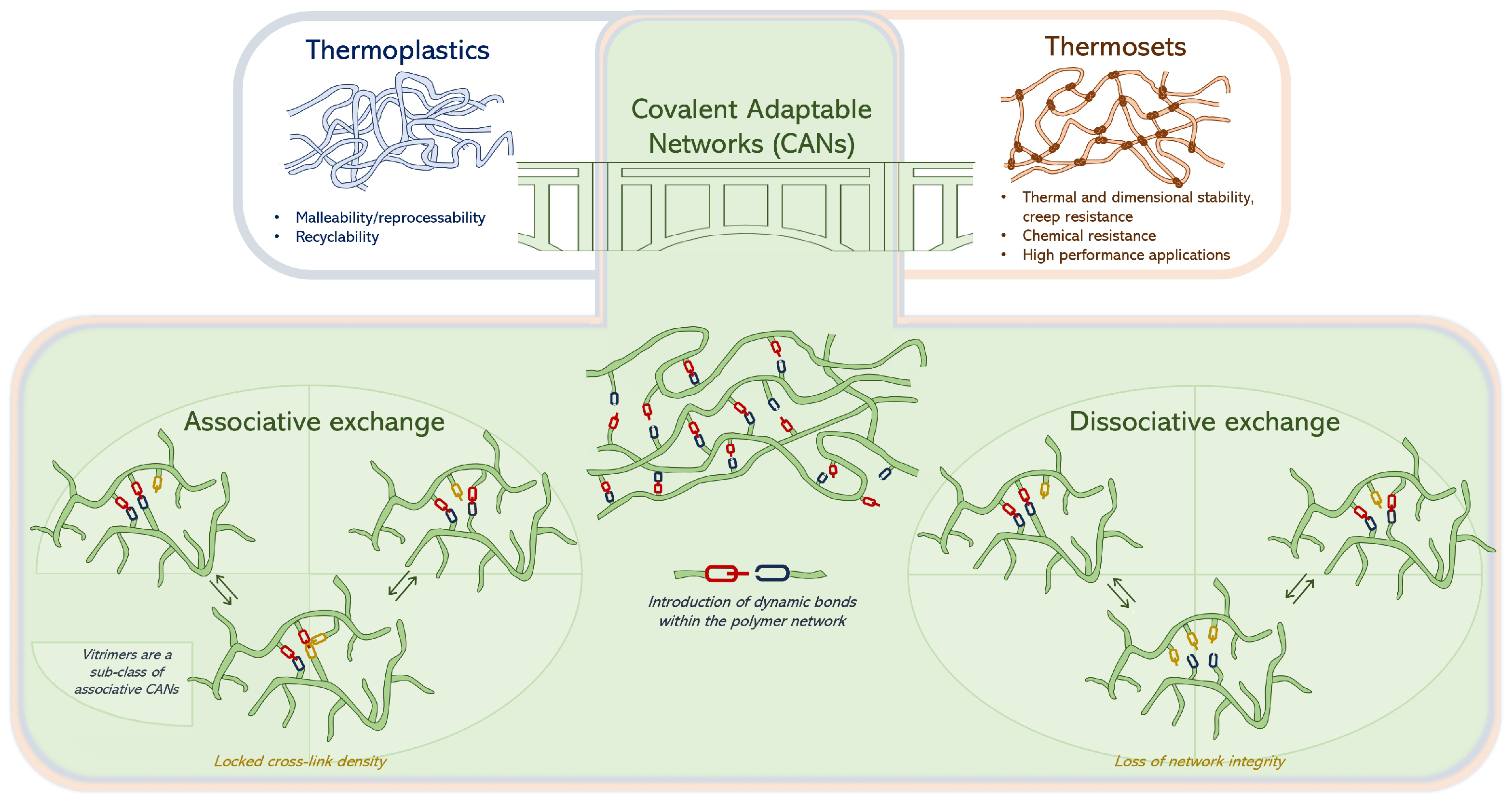
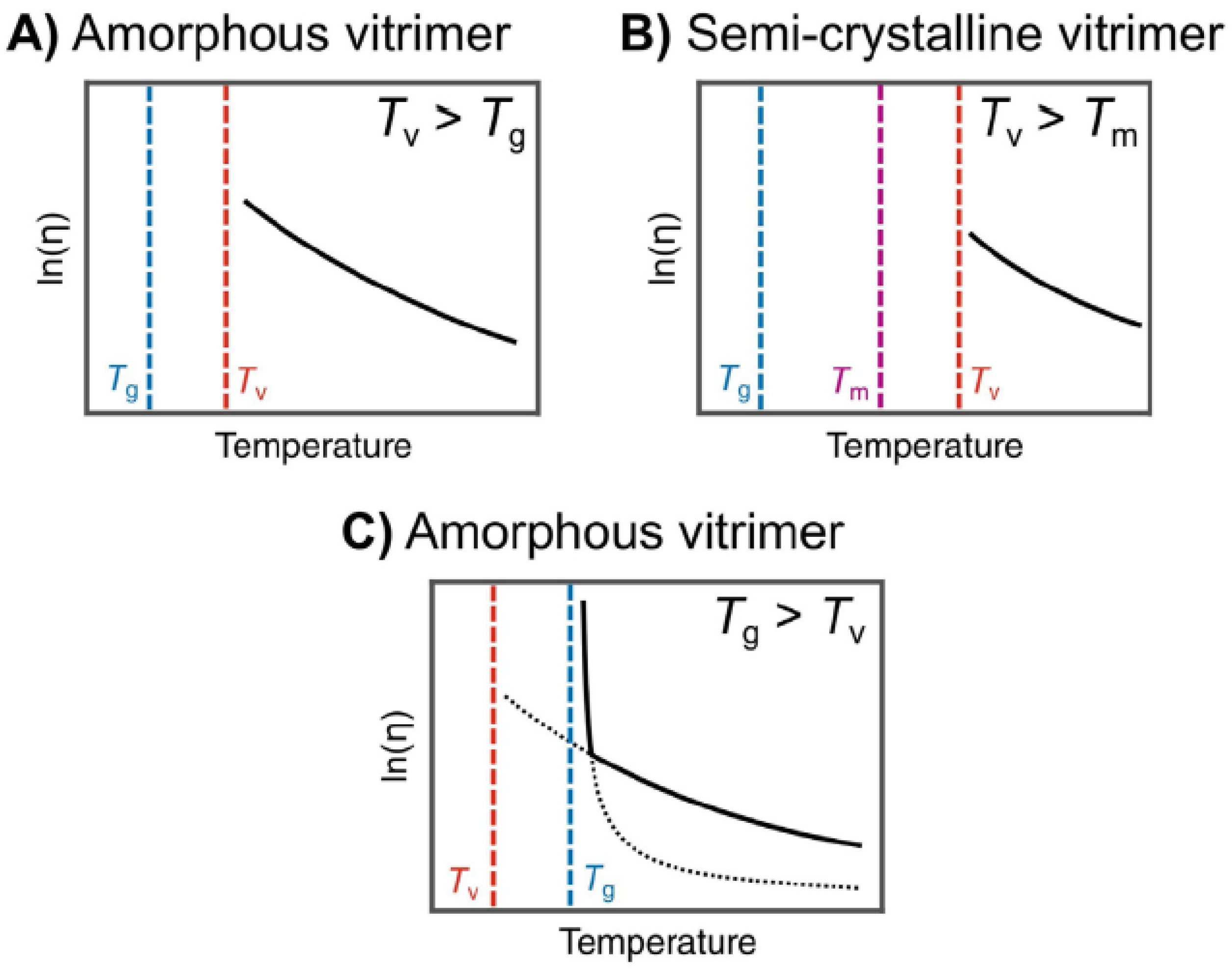
1. Introduction
2. Molecular Dynamics
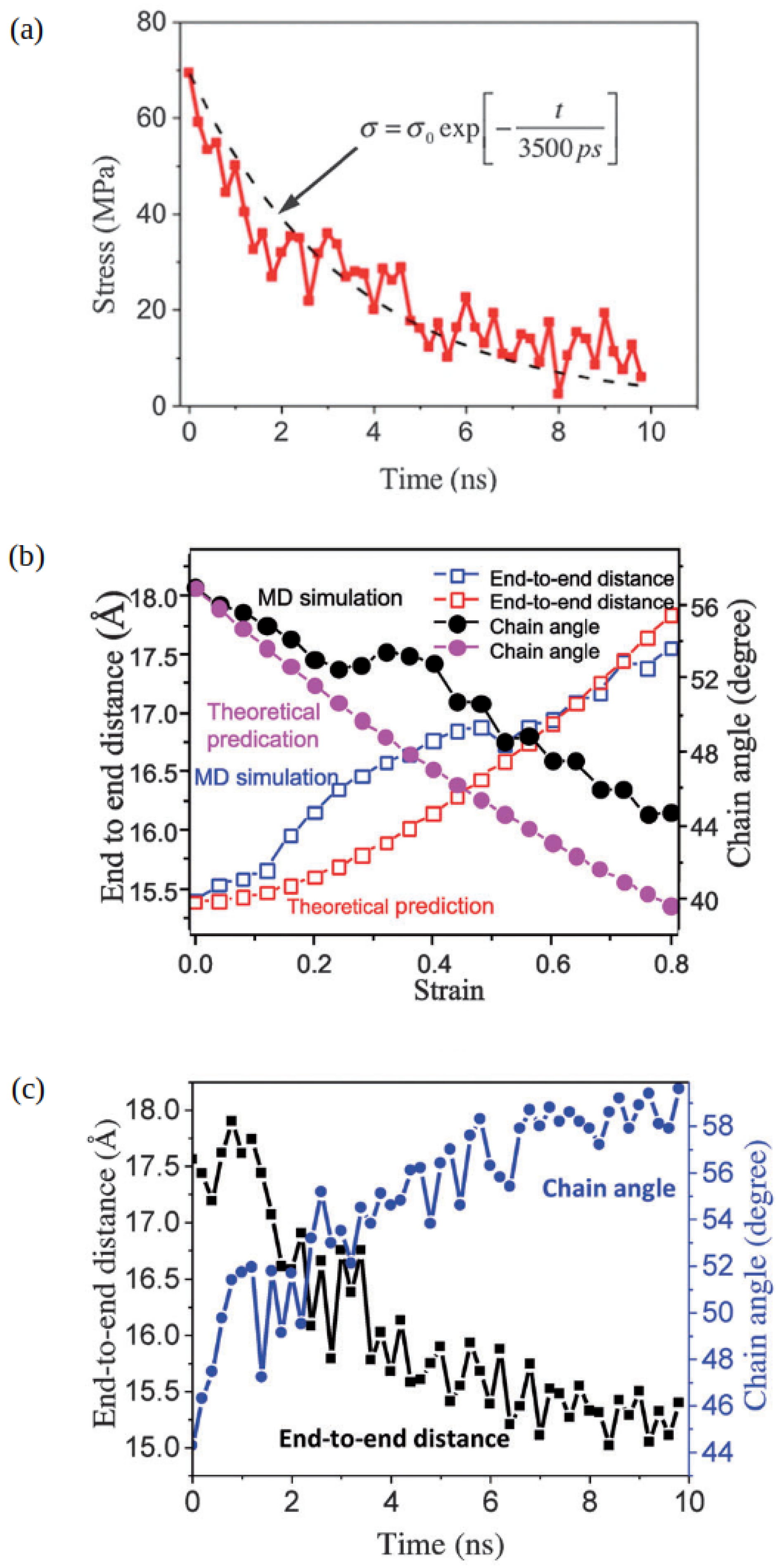
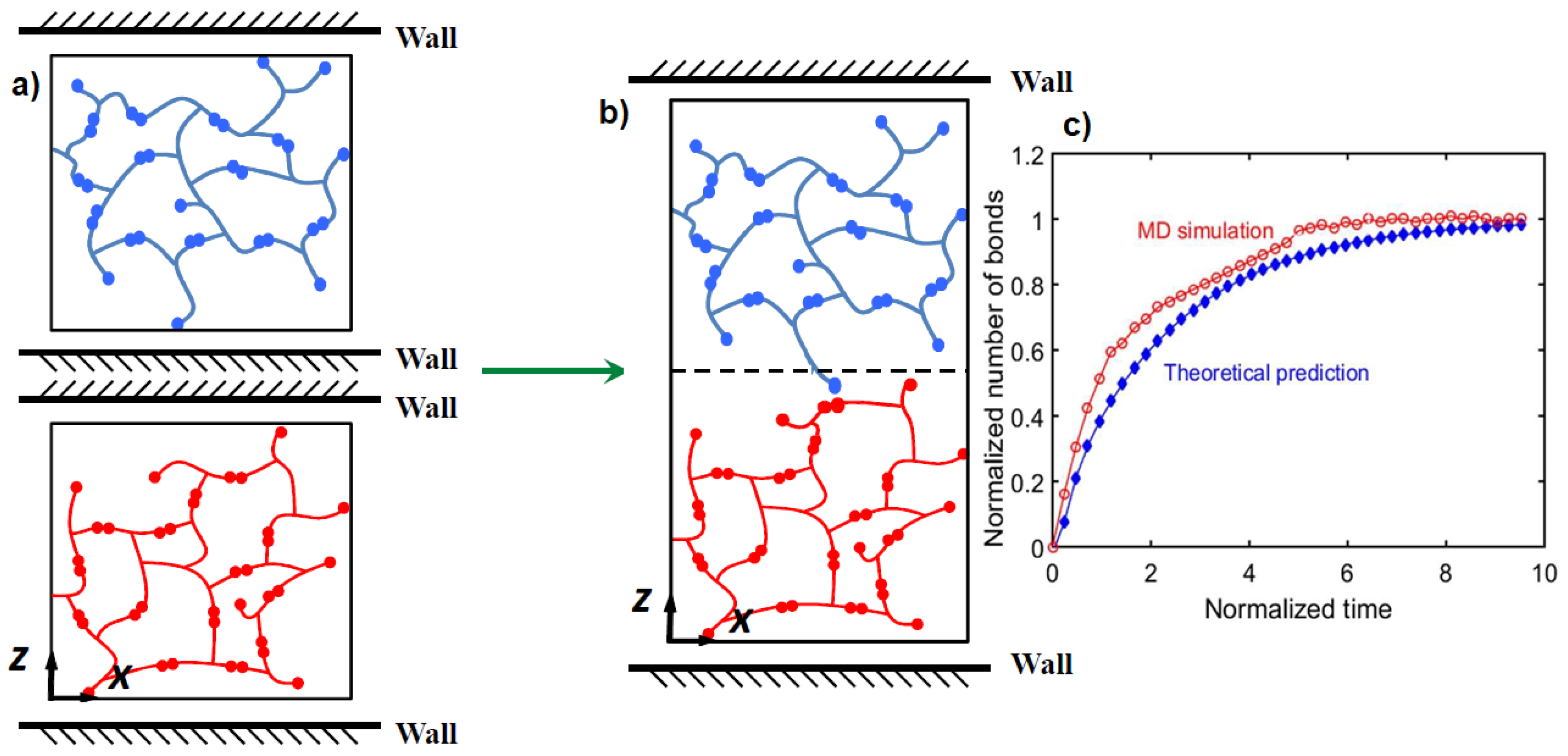
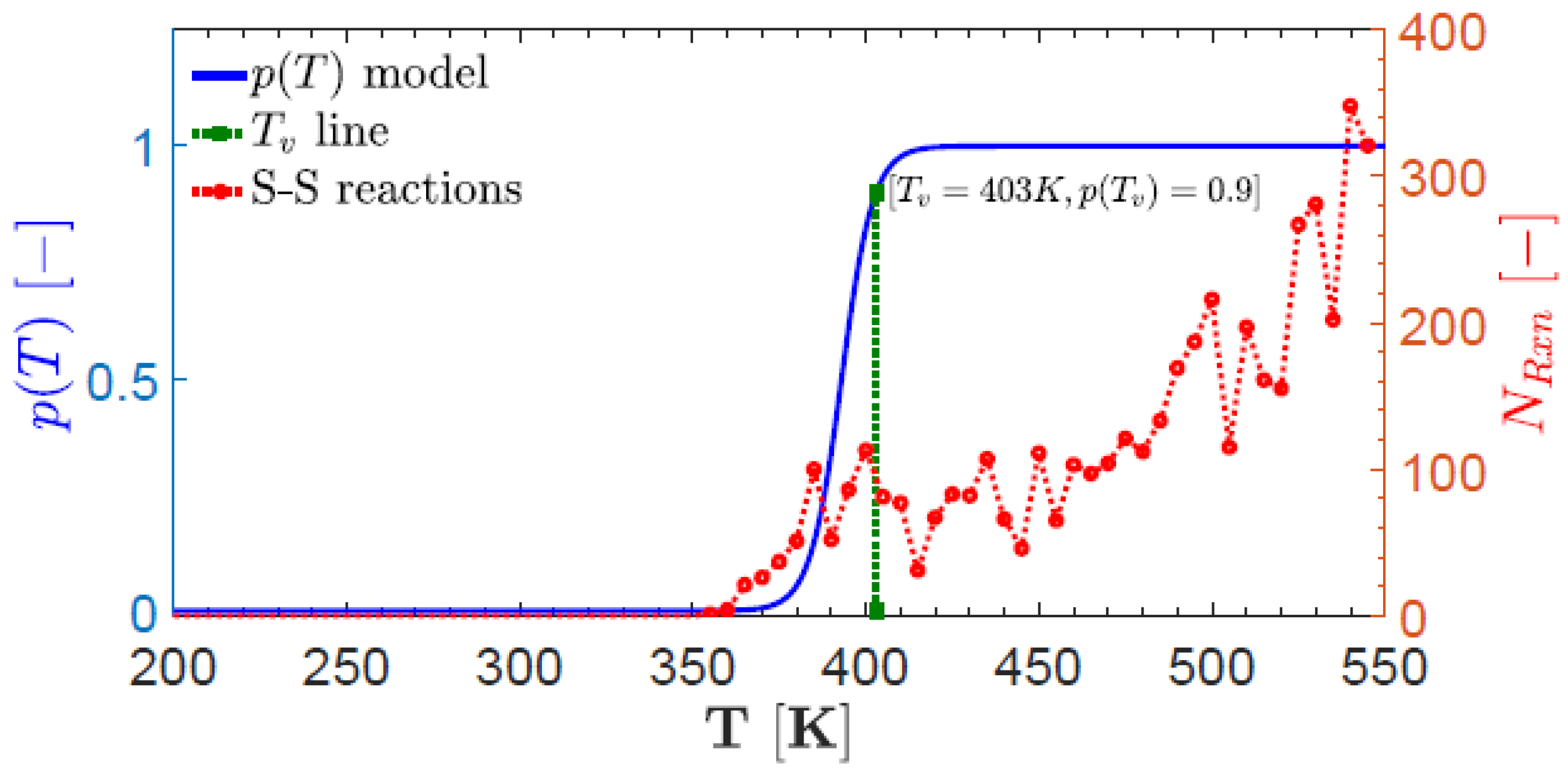
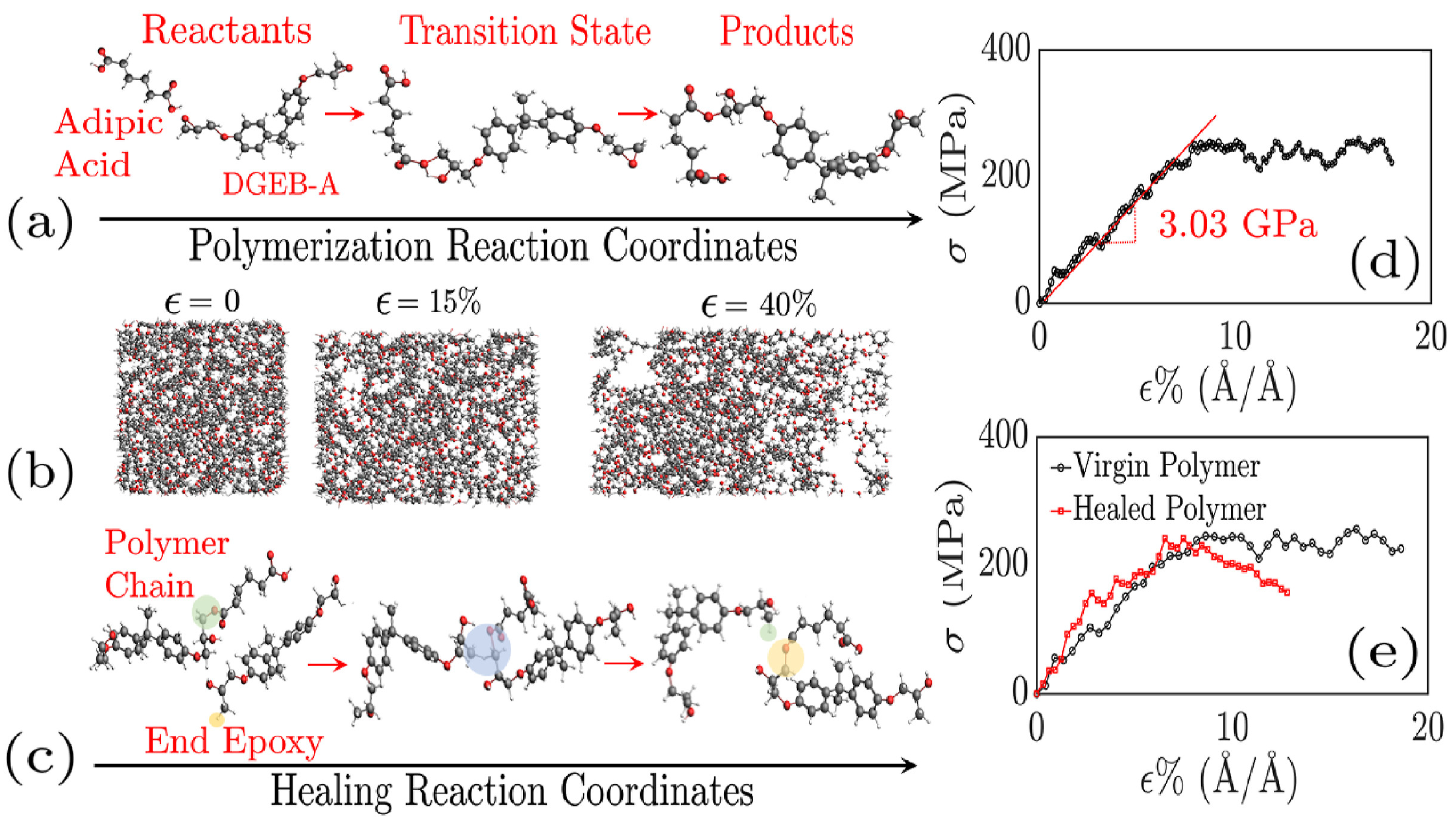
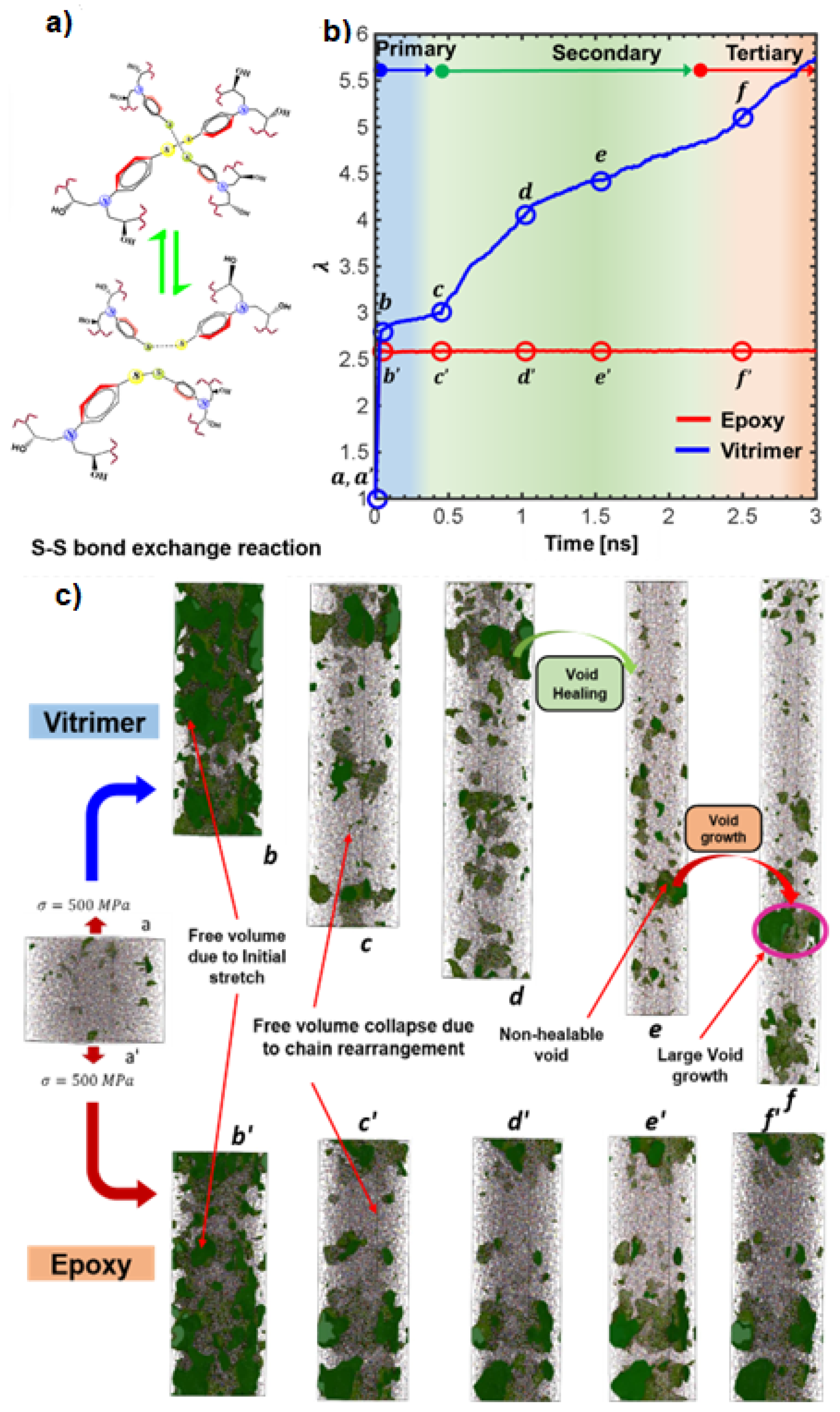
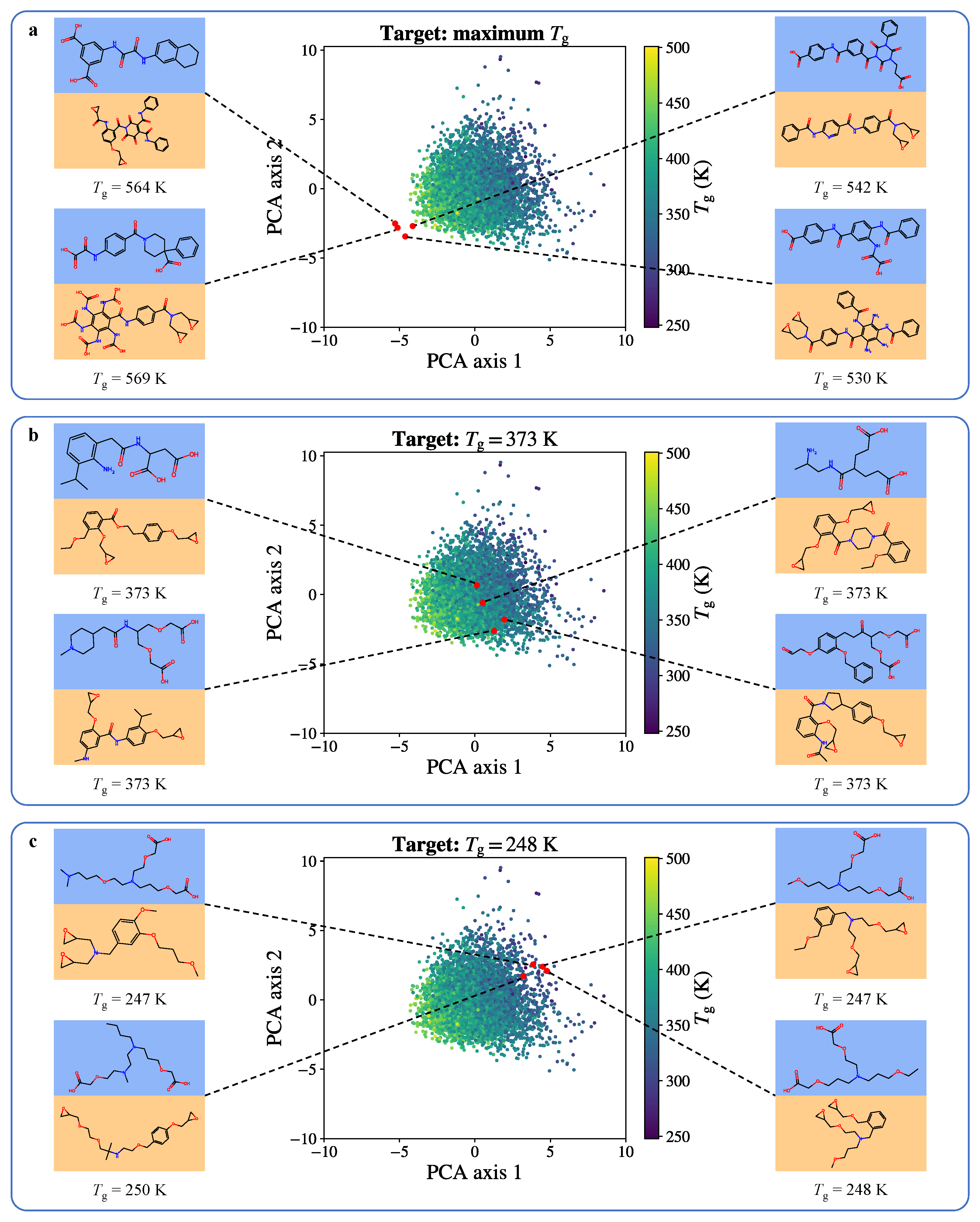
2.1. Atomistic Modeling of CANs and Vitrimers
| Resin | Crosslink Agent | Network | Force Field | Property | Refs. |
|---|---|---|---|---|---|
| DGEBA | tricarballylic acid | aCAN | PCFF | stress/strength | [58,59,60] |
| , welding, creep | |||||
| Tetrafunctional | trifunctional | dCAN | PCFF | welding | [61] |
| furan | maleimide | interfacial strength | |||
| DGEBAEO-2(6) | MPDBMI | dCAN | PCFF | , welding, shape recovery | [62] |
| Polyimine | Bisphenol A | dCAN | PCFF | , stress/strain | [63] |
| welding | |||||
| DGEBA | AFD | vitrimer | CVFF | volume, self-healing | [64] |
| DGEBA | AFD, HT-100 | vitrimer | PCFF | self-healing | [65] |
| DGEBA | adipic acid | vitrimer | ReaxFF | stress, self-healing | [66] |
| DGEBA | AFD | vitrimer | CVFF | volume, creep | [67] |
| DGEBA | fatty acid | aCAN | PCFF | decomposition | [68] |
| Dialdehyde | diamine | aCAN | ML FF | free-energy | [69] |
| Epoxides | carboxylic acid | vitrimer | PCFF | [70] | |
| DGEBA | AFD | vitrimer | PCFF | stress | [71] |
| nanocomposite | self-healing |
2.2. Atomistic Modeling of Vitrimer Nanocomposites
2.3. Coarse-Grained Modeling of CANs and Vitrimers
2.4. Coarse-Grained Modeling on Vitrimer Nanocomposites
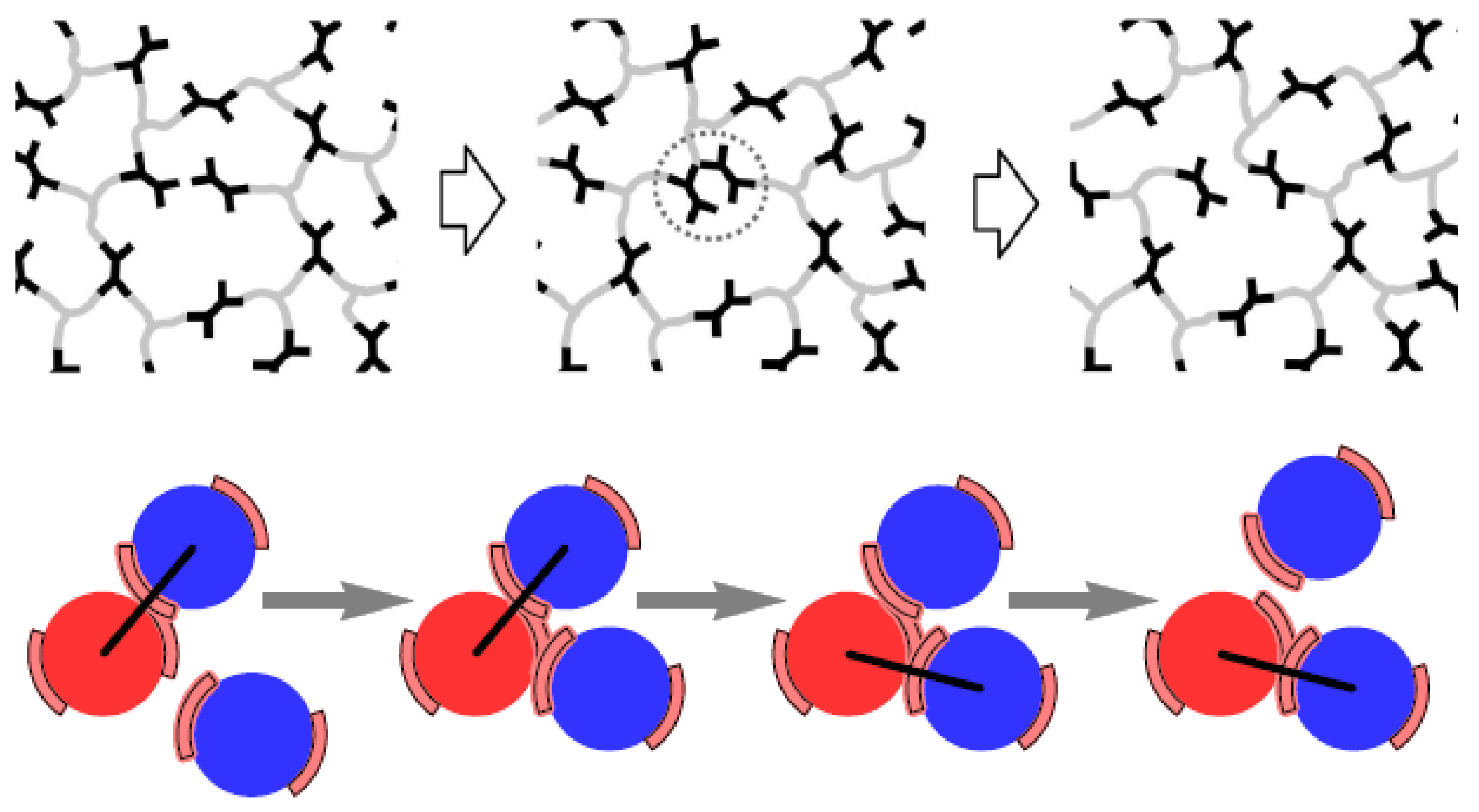
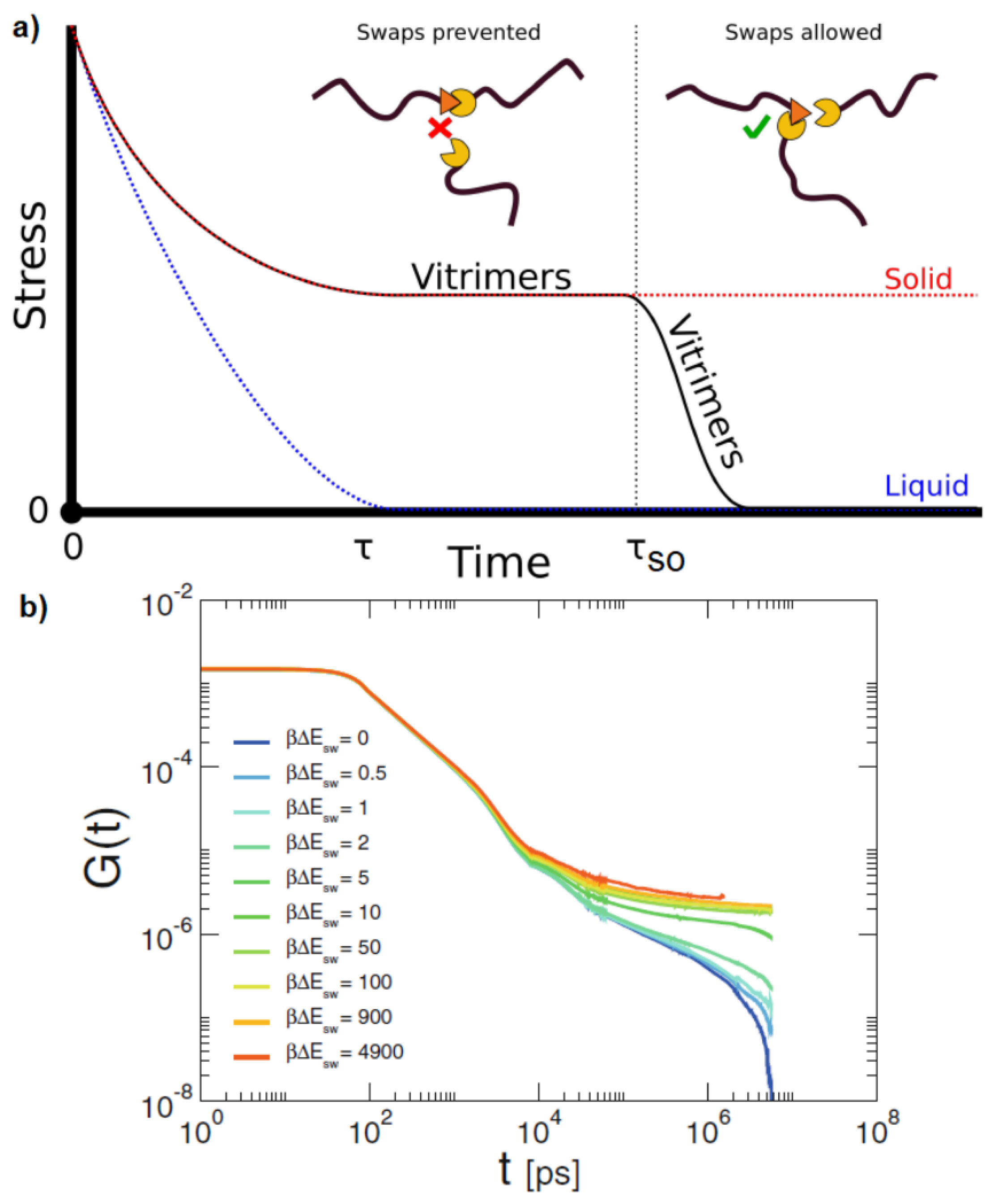
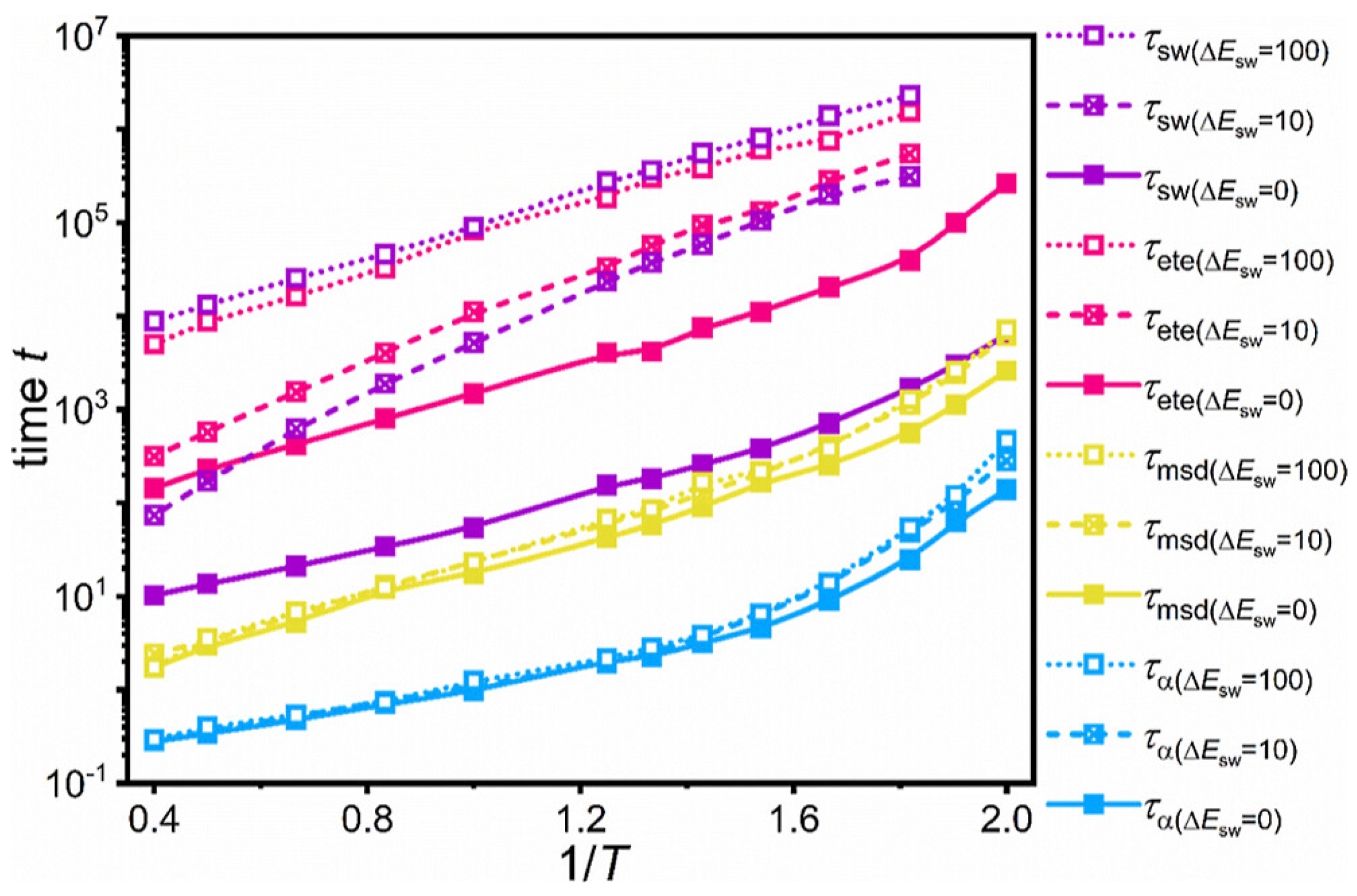
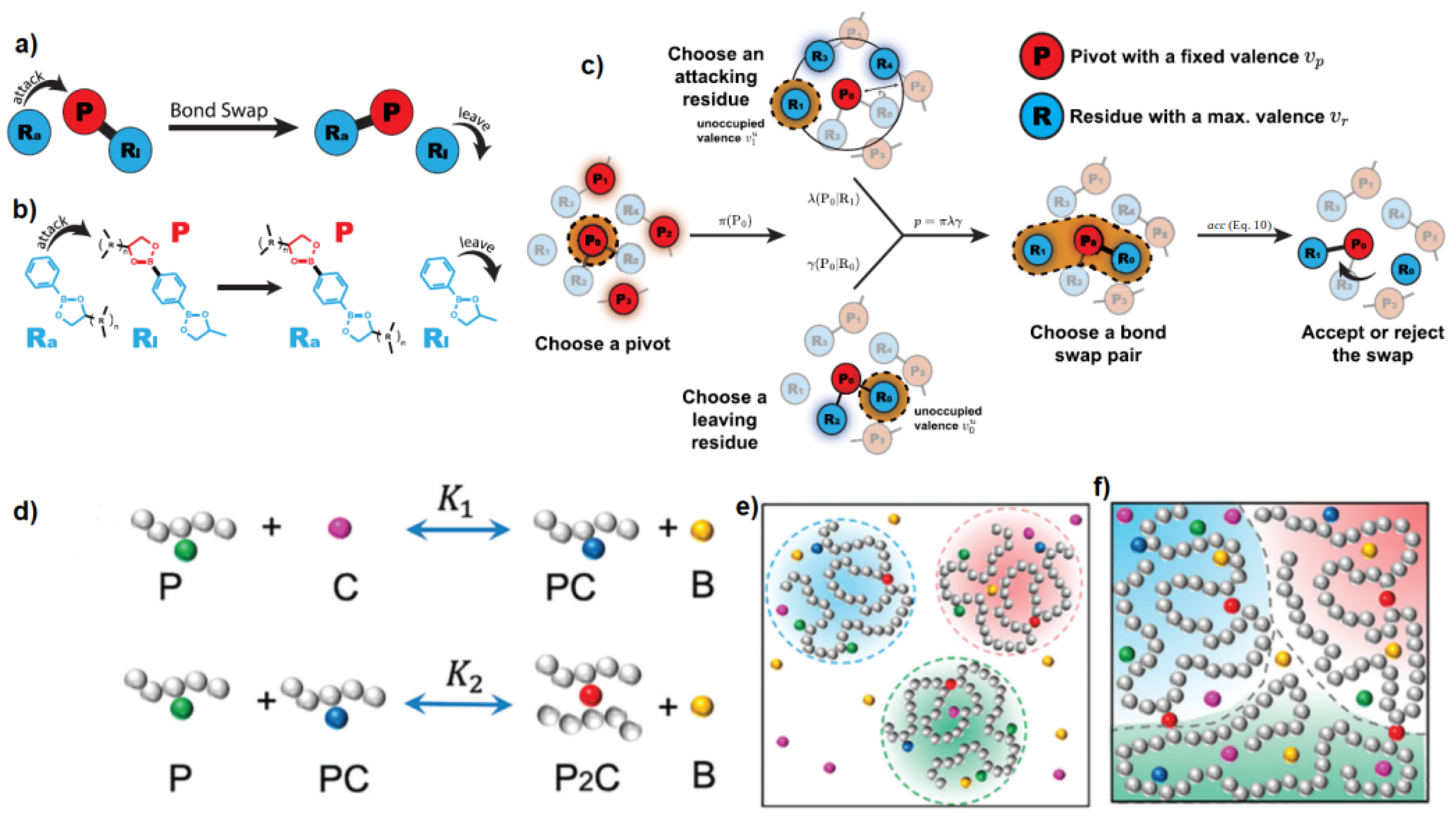
3. Monte Carlo
4. Hybrid Molecular Dynamics/Monte Carlo
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Scheutz, G.M.; Lessard, J.J.; Sims, M.B.; Sumerlin, B.S. Adaptable Crosslinks in Polymeric Materials: Resolving the Intersection of Thermoplastics and Thermosets. J. Am. Chem. Soc. 2019, 141, 16181–16196. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Png, Z.M.; Ng, S.H.; Tham, G.X.; Ye, E.; Goh, S.S.; Loh, X.J.; Li, Z. Vitrimers: Current research trends and their emerging applications. Mater. Today 2021, 51, 586–625. [Google Scholar] [CrossRef]
- Alabiso, W.; Schlögl, S. The Impact of Vitrimers on the Industry of the Future: Chemistry, Properties and Sustainable Forward-Looking Applications. Polymers 2020, 12, 1660. [Google Scholar] [CrossRef] [PubMed]
- Bowman, C.; Du Prez, F.; Kalow, J. Introduction to chemistry for covalent adaptable networks. Polym. Chem. 2020, 11, 5295–5296. [Google Scholar] [CrossRef]
- Zheng, N.; Xu, Y.; Zhao, Q.; Xie, T. Dynamic Covalent Polymer Networks: A Molecular Platform for Designing Functions beyond Chemical Recycling and Self-Healing. Chem. Rev. 2021, 121, 1716–1745. [Google Scholar] [CrossRef]
- Chen, X.; Dam, M.A.; Ono, K.; Mal, A.; Shen, H.; Nutt, S.R.; Sheran, K.; Wudl, F. A Thermally Re-mendable Cross-Linked Polymeric Material. Science 2002, 295, 1698–1702. [Google Scholar] [CrossRef] [PubMed]
- Kloxin, C.J.; Scott, T.F.; Adzima, B.J.; Bowman, C.N. Covalent Adaptable Networks (CANs): A Unique Paradigm in Cross-Linked Polymers. Macromolecules 2010, 43, 2643–2653. [Google Scholar] [CrossRef]
- Kloxin, C.J.; Bowman, C.N. Covalent adaptable networks: Smart, reconfigurable and responsive network systems. Chem. Soc. Rev. 2013, 42, 7161–7173. [Google Scholar] [CrossRef]
- Leibler, L.; Rubinstein, M.; Colby, R.H. Dynamics of reversible networks. Macromolecules 1991, 24, 4701–4707. [Google Scholar] [CrossRef]
- Janssen, L.M. Vitrimers: Combining the best of both polymeric worlds. Europhys. News 2020, 51, 4–5. [Google Scholar]
- Capelot, M.; Montarnal, D.; Tournilhac, F.; Leibler, L. Metal-Catalyzed Transesterification for Healing and Assembling of Thermosets. J. Am. Chem. Soc. 2012, 134, 7664–7667. [Google Scholar] [CrossRef] [PubMed]
- Maurya, M.K.; Singh, M.K. Computational indentation in weakly cross-linked polymer networks. Int. J. Adv. Eng. Sci. Appl. Math. 2023, 15, 196–206. [Google Scholar] [CrossRef]
- Li, L.; Chen, X.; Jin, K.; Torkelson, J.M. Vitrimers Designed Both To Strongly Suppress Creep and To Recover Original Cross-Link Density after Reprocessing: Quantitative Theory and Experiments. Macromolecules 2018, 51, 5537–5546. [Google Scholar] [CrossRef]
- Denissen, W.; Rivero, G.; Nicolaÿ, R.; Leibler, L.; Winne, J.M.; Du Prez, F.E. Vinylogous Urethane Vitrimers. Adv. Funct. Mater. 2015, 25, 2451–2457. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Q.; Wang, T. Dual-Triggered and Thermally Reconfigurable Shape Memory Graphene-Vitrimer Composites. Acs Appl. Mater. Interfaces 2016, 8, 21691–21699. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.X.; Guan, Z. Olefin Metathesis for Effective Polymer Healing via Dynamic Exchange of Strong Carbon–Carbon Double Bonds. J. Am. Chem. Soc. 2012, 134, 14226–14231. [Google Scholar] [CrossRef] [PubMed]
- Denissen, W.; Winne, J.M.; Du Prez, F.E. Vitrimers: Permanent organic networks with glass-like fluidity. Chem. Sci. 2016, 7, 30–38. [Google Scholar] [CrossRef]
- Guerre, M.; Taplan, C.; Winne, J.M.; Du Prez, F.E. Vitrimers: Directing chemical reactivity to control material properties. Chem. Sci. 2020, 11, 4855–4870. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Xu, Y.; Ji, Y.; Wei, Y. Functional epoxy vitrimers and composites. Prog. Mater. Sci. 2021, 120, 100710. [Google Scholar] [CrossRef]
- Dai, C.; Shi, Y.; Li, Z.; Hu, T.; Wang, X.; Ding, Y.; Yan, L.; Liang, Y.; Cao, Y.; Wang, P. The Design, Synthesis, and Characterization of Epoxy Vitrimers with Enhanced Glass Transition Temperatures. Polymers 2023, 15, 4346. [Google Scholar] [CrossRef]
- Tao, Y.; Liang, X.; Zhang, J.; Lei, I.M.; Liu, J. Polyurethane vitrimers: Chemistry, properties and applications. J. Polym. Sci. 2023, 61, 2233–2253. [Google Scholar] [CrossRef]
- Imbernon, L.; Norvez, S. From landfilling to vitrimer chemistry in rubber life cycle. Eur. Polym. J. 2016, 82, 347–376. [Google Scholar] [CrossRef]
- Luo, J.; Demchuk, Z.; Zhao, X.; Saito, T.; Tian, M.; Sokolov, A.P.; Cao, P.F. Elastic vitrimers: Beyond thermoplastic and thermoset elastomers. Matter 2022, 5, 1391–1422. [Google Scholar] [CrossRef]
- Stukenbroeker, T.; Wang, W.; Winne, J.M.; Du Prez, F.E.; Nicolaÿ, R.; Leibler, L. Polydimethylsiloxane quenchable vitrimers. Polym. Chem. 2017, 8, 6590–6593. [Google Scholar] [CrossRef]
- Ahmadi, M.; Hanifpour, A.; Ghiassinejad, S.; van Ruymbeke, E. Polyolefins Vitrimers: Design Principles and Applications. Chem. Mater. 2022, 34, 10249–10271. [Google Scholar] [CrossRef]
- Adjaoud, A.; Puchot, L.; Verge, P. Polybenzoxazine-based covalent adaptable networks: A mini-review. Polymer 2023, 287, 126426. [Google Scholar] [CrossRef]
- Adjaoud, A.; Boina, D.A.; Boulic, V.; Hesse, C.; Jehl, C.; Ziane, C.; Puchot, L.; Shaplov, A.S.; Schmidt, D.F.; Verge, P. Enhancing Sustainable Plastics: Introducing Bio-based Benzoxazines with Dynamic Bonds for Exceptional Performance and Circularity. In ACS Symposium Series; Cheng, H.N., Gross, R.A., Eds.; American Chemical Society: Washington, DC, USA, 2023; Volume 1451, pp. 49–84. [Google Scholar]
- Moghimikheirabadi, A.; Mugemana, C.; Kröger, M.; Karatrantos, A.V. Polymer conformations, entanglements and dynamics in ionic nanocomposites: A molecular dynamics study. Polymers 2020, 12, 2591. [Google Scholar] [CrossRef] [PubMed]
- Mugemana, C.; Moghimikheirabadi, A.; Arl, D.; Addiego, F.; Schmidt, D.F.; Kröger, M.; Karatrantos, A.V. Ionic poly(dimethylsiloxane)-silica nanocomposites: Dispersion and self-healing. MRS Bull. 2022, 47, 1185–1197. [Google Scholar] [CrossRef]
- Nakamura, Y.; Tenjimbayashi, M.; Moriya, A.; Naito, M. Impact of Telechelic Polymer Precursors on the Viscoelastic Properties of Vitrimers. Macromol. Chem. Phys. 2022, 223, 2100433. [Google Scholar] [CrossRef]
- Van Zee, N.J.; Nicolay, R. Vitrimers: Permanently crosslinked polymers with dynamic network topology. Prog. Polym. Sci. 2020, 104, 101233. [Google Scholar] [CrossRef]
- Nishimura, Y.; Chung, J.; Muradyan, H.; Guan, Z. Silyl Ether as a Robust and Thermally Stable Dynamic Covalent Motif for Malleable Polymer Design. J. Am. Chem. Soc. 2017, 139, 14881–14884. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Saed, M.O.; Terentjev, E.M. Rheology of Vitrimers. Nat. Commun. 2022, 13, 5753. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, S.; Novak, P.; Giebler, M.; Gschwandl, M.; Novak, P.; Pilz, G.; Morak, M.; Schlögl, S. The crucial role of external force in the estimation of the topology freezing transition temperature of vitrimers by elongational creep measurements. Polymer 2020, 204, 122804. [Google Scholar] [CrossRef]
- Montarnal, D.; Capelot, M.; Tournilhac, F.; Leibler, L. Silica-Like Malleable Materials from Permanent Organic Networks. Science 2011, 334, 965–968. [Google Scholar] [CrossRef] [PubMed]
- Fang, H.; Ye, W.; Ding, Y.; Winter, H.H. Rheology of the Critical Transition State of an Epoxy Vitrimer. Macromolecules 2020, 53, 4855–4862. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, S.; Zhang, X.; Gao, L.; Wei, Y.; Ji, Y. Detecting topology freezing transition temperature of vitrimers by AIE luminogens. Nat. Commun. 2019, 10, 3165. [Google Scholar] [CrossRef]
- Karimi, M. Diffusion in Polymer Solids and Solutions. In Mass Transfer in Chemical Engineering Processes; Marko, J., Ed.; InTech: Rijeka, Croatia, 2011. [Google Scholar]
- Huang, J.; Sheridan, G.S.; Chen, C.; Ramlawi, N.; Ewoldt, R.H.; Braun, P.V.; Evans, C.M. Reversible Reactions, Mesh Size, and Segmental Dynamics Control Penetrant Diffusion in Ethylene Vitrimers. ACS Macro Lett. 2023, 12, 901–907. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Ramlawi, N.; Sheridan, G.S.; Chen, C.; Ewoldt, R.H.; Braun, P.V.; Evans, C.M. Dynamic Covalent Bond Exchange Enhances Penetrant Diffusion in Dense Vitrimers. Macromolecules 2023, 56, 1253–1262. [Google Scholar] [CrossRef]
- Hubbard, A.M.; Ren, Y.; Picu, C.R.; Sarvestani, A.; Konkolewicz, D.; Roy, A.K.; Varshney, V.; Nepal, D. Creep Mechanics of Epoxy Vitrimer Materials. ACS Appl. Polym. Mater. 2022, 4, 4254–4263. [Google Scholar] [CrossRef]
- Hubbard, A.M.; Ren, Y.; Konkolewicz, D.; Sarvestani, A.; Picu, C.R.; Kedziora, G.S.; Roy, A.; Varshney, V.; Nepal, D. Vitrimer Transition Temperature Identification: Coupling Various Thermomechanical Methodologies. ACS Appl. Polym. Mater. 2021, 3, 1756–1766. [Google Scholar] [CrossRef]
- Sharma, H.; Rana, S.; Singh, P.; Hayashi, M.; Binder, W.H.; Rossegger, E.; Kumar, A.; Schlögl, S. Self-healable fiber-reinforced vitrimer composites: Overview and future prospects. RSC Adv. 2022, 12, 32569–32582. [Google Scholar] [CrossRef] [PubMed]
- Krishnakumar, B.; Prasanna Sanka, R.; Binder, W.H.; Park, C.; Jung, J.; Parthasarthy, V.; Rana, S.; Yun, G.J. Catalyst free self-healable vitrimer/graphene oxide nanocomposites. Compos. Part B Eng. 2020, 184, 107647. [Google Scholar] [CrossRef]
- Hubbard, A.M.; Ren, Y.; Papaioannou, P.; Sarvestani, A.; Picu, C.R.; Konkolewicz, D.; Roy, A.K.; Varshney, V.; Nepal, D. Vitrimer Composites: Understanding the Role of Filler in Vitrimer Applicability. ACS Appl. Polym. Mater. 2022, 4, 6374–6385. [Google Scholar] [CrossRef]
- Legrand, A.; Soulié-Ziakovic, C. Silica–Epoxy Vitrimer Nanocomposites. Macromolecules 2016, 49, 5893–5902. [Google Scholar] [CrossRef]
- Schenk, V.; Labastie, K.; Destarac, M.; Olivier, P.; Guerre, M. Vitrimer composites: Current status and future challenges. Mater. Adv. 2022, 3, 8012–8029. [Google Scholar] [CrossRef]
- Kuncho, C.N.; Liu, W.; Möller, J.; Kammleiter, J.; Stehle, J.; Kokil, A.; Reynaud, E.; Schmidt, D.F. Enhancing the Sustainability of High-Performance Fiber Composites. In Green Polymer Chemistry: New Products, Processes, and Applications; ACS Symposium Series; American Chemical Society: Washington, DC, USA, 2018; pp. 281–295, Chapter 18. [Google Scholar]
- Wagner, R.J.; Hobbs, E.; Vernerey, F.J. A network model of transient polymers: Exploring the micromechanics of nonlinear viscoelasticity. Soft Matter 2021, 17, 8742–8757. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Tran, N.V.; Pan, Y.; Wang, S.; Jin, Z.; Chen, G.; Li, S.; Zheng, J.; Loh, X.J.; Li, Z. Next-Generation Vitrimers Design through Theoretical Understanding and Computational Simulations. Adv. Sci. 2024, 11, 2302816. [Google Scholar] [CrossRef] [PubMed]
- Winne, J.M.; Leibler, L.; Du Prez, F.E. Dynamic covalent chemistry in polymer networks: A mechanistic perspective. Polym. Chem. 2019, 10, 6091–6108. [Google Scholar] [CrossRef]
- Raffaelli, C.; Bose, A.; Vrusch, C.H.M.P.; Ciarella, S.; Davris, T.; Tito, N.B.; Lyulin, A.V.; Ellenbroek, W.G.; Storm, C. Rheology, Rupture, Reinforcement and Reversibility: Computational Approaches for Dynamic Network Materials. In Self-Healing and Self-Recovering Hydrogels; Springer International Publishing: Cham, Switzerland, 2020; Volume 285, pp. 63–126. [Google Scholar]
- Karatrantos, A.; Clarke, N.; Kröger, M. Modeling of polymer structure and conformations in polymer nanocomposites from atomistic to mesoscale: A Review. Polym. Rev. 2016, 56, 385–428. [Google Scholar] [CrossRef]
- Karatrantos, A.; Clarke, N.; Composto, R.J.; Winey, K.I. Polymer conformations in polymer nanocomposites containing spherical nanoparticles. Soft Matter 2015, 11, 382–388. [Google Scholar]
- Ricarte, R.G.; Shanbhag, S. A tutorial review of linear rheology for polymer chemists: Basics and best practices for covalent adaptable networks. Polym. Chem. 2024, 15, 815–846. [Google Scholar] [CrossRef]
- Varshney, V.; Patnaik, S.S.; Roy, A.K.; Farmer, B.L. A Molecular Dynamics Study of Epoxy-Based Networks: Cross-Linking Procedure and Prediction of Molecular and Material Properties. Macromolecules 2008, 41, 6837–6842. [Google Scholar] [CrossRef]
- Lin, P.H.; Khare, R. Molecular Simulation of Cross-Linked Epoxy and Epoxy–POSS Nanocomposite. Macromolecules 2009, 42, 4319–4327. [Google Scholar] [CrossRef]
- Yang, H.; Yu, K.; Mu, X.; Shi, X.; Wei, Y.; Guo, Y.; Qi, H.J. A molecular dynamics study of bond exchange reactions in covalent adaptable networks. Soft Matter 2015, 11, 6305–6317. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Yu, K.; Mu, X.; Wei, Y.; Guo, Y.; Qi, H.J. Molecular dynamics studying on welding behavior in thermosetting polymers due to bond exchange reactions. RSC Adv. 2016, 6, 22476–22487. [Google Scholar] [CrossRef]
- Hanzon, D.W.; He, X.; Yang, H.; Shi, Q.; Yu, K. Creep-induced anisotropy in covalent adaptable network polymers. Soft Matter 2017, 13, 7061–7073. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Yang, H.; Xia, W.; Guo, Y. Molecular dynamics simulations of surface welding in crosslinked networks with thermally reversible linkages. Appl. Surf. Sci. 2020, 527, 146947. [Google Scholar] [CrossRef]
- Yang, H.; Zheng, X.; Sun, Y.; Yu, K.; He, M.; Guo, Y. A molecular dynamics study on the surface welding and shape memory behaviors of Diels-Alder network. Comput. Mater. Sci. 2017, 139, 48–55. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H.; Sun, Y.; Zheng, X.; Guo, Y. A molecular dynamics simulation on tunable and self-healing epoxy-polyimine network based on imine bond exchange reactions. Mol. Simul. 2022, 48, 1605–1615. [Google Scholar] [CrossRef]
- Singh, G.; Sundararaghavan, V. Modeling self-healing behavior of vitrimers using molecular dynamics with dynamic cross-linking capability. Chem. Phys. Lett. 2020, 760, 137966. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, H.; Sun, Y.; Zhang, Y.; Guo, Y. A molecular dynamics simulation on self-healing behavior based on disulfide bond exchange reactions. Polymer 2021, 212, 123111. [Google Scholar] [CrossRef]
- Kamble, M.; Vashisth, A.; Yang, H.; Pranompont, S.; Picu, C.R.; Wang, D.; Koratkar, N. Reversing fatigue in carbon-fiber reinforced vitrimer composites. Carbon 2022, 187, 108–114. [Google Scholar] [CrossRef]
- Singh, G.; Sundararaghavan, V.; Varshney, V. Understanding Creep in Vitrimers: Insights from Molecular Dynamics Simulations. arXiv 2023, arXiv:2304.05518. [Google Scholar]
- Sun, Y.; Yang, H.; Yu, K.; Guo, Y.; Qu, J. A molecular dynamics study of decomposition of covalent adaptable networks in organic solvent. Polymer 2019, 180, 121702. [Google Scholar] [CrossRef]
- Sun, Y.; Wan, K.; Shen, W.; He, J.; Zhou, T.; Wang, H.; Yang, H.; Shi, X. Modeling Exchange Reactions in Covalent Adaptable Networks with Machine Learning Force Fields. Macromolecules 2023, 56, 9003–9013. [Google Scholar] [CrossRef]
- Zheng, Y.; Thakolkaran, P.; Smith, J.A.; Lu, Z.; Zheng, S.; Nguyen, B.H.; Kumar, S.; Vashisth, A. Inverse Design of Vitrimeric Polymers by Molecular Dynamics and Generative Modeling. arXiv 2023, arXiv:2312.03690. [Google Scholar]
- Park, C.; Kim, G.; Jung, J.; Krishnakumar, B.; Rana, S.; Yun, G.J. Enhanced self-healing performance of graphene oxide/vitrimer nanocomposites: A molecular dynamics simulations study. Polymer 2020, 206, 122862. [Google Scholar] [CrossRef]
- Moghimikheirabadi, A.; Karatrantos, A.V.; Kröger, M. Ionic Polymer Nanocomposites Subjected to Uniaxial Extension: A Nonequilibrium Molecular Dynamics Study. Polymers 2021, 13, 4001. [Google Scholar] [CrossRef]
- Wu, P.; Van Der Giessen, E. On improved network models for rubber elasticity and their applications to orientation hardening in glassy polymers. J. Mech. Phys. Solids 1993, 41, 427–456. [Google Scholar] [CrossRef]
- Wu, P.; van der Giessen, E. On improved 3-D non-Gaussian network models for rubber elasticity. Mech. Res. Commun. 1992, 19, 427–433. [Google Scholar] [CrossRef]
- Yu, K.; Taynton, P.; Zhang, W.; Dunn, M.L.; Qi, H.J. Influence of stoichiometry on the glass transition and bond exchange reactions in epoxy thermoset polymers. RSC Adv. 2014, 4, 48682–48690. [Google Scholar] [CrossRef]
- Stukalin, E.B.; Cai, L.H.; Kumar, N.A.; Leibler, L.; Rubinstein, M. Self-Healing of Unentangled Polymer Networks with Reversible Bonds. Macromolecules 2013, 46, 7525–7541. [Google Scholar] [CrossRef]
- Karatrantos, A.; Composto, R.J.; Winey, K.I.; Kröger, M.; Clarke, N. Modeling of Entangled Polymer Diffusion in Melts and Nanocomposites: A Review. Polymers 2019, 11, 876. [Google Scholar] [CrossRef]
- Kito, T.; Hayashi, M. Intrinsic differences of unentangled and highly entangled vitrimer-like materials with bond exchangeable nanodomains. Eur. Polym. J. 2024, 208, 112862. [Google Scholar] [CrossRef]
- Rekondo, A.; Martin, R.; Ruiz de Luzuriaga, A.; Cabanero, G.; Grande, H.J.; Odriozola, I. Catalyst-free room-temperature self-healing elastomers based on aromatic disulfide metathesis. Mater. Horiz. 2014, 1, 237–240. [Google Scholar] [CrossRef]
- Gissinger, J.R.; Jensen, B.D.; Wise, K.E. Modeling chemical reactions in classical molecular dynamics simulations. Polymer 2017, 128, 211–217. [Google Scholar] [CrossRef]
- Chen, M.; Si, H.; Zhang, H.; Zhou, L.; Wu, Y.; Song, L.; Kang, M.; Zhao, X.L. The Crucial Role in Controlling the Dynamic Properties of Polyester-Based Epoxy Vitrimers: The Density of Exchangeable Ester Bonds (υ). Macromolecules 2021, 54, 10110–10117. [Google Scholar] [CrossRef]
- Steudel, R. Properties of Sulfur-Sulfur Bonds. Angew. Chem. Int. Ed. Engl. 1975, 14, 655–664. [Google Scholar] [CrossRef]
- Vashisth, A.; Ashraf, C.; Bakis, C.E.; van Duin, A.C. Effect of chemical structure on thermo-mechanical properties of epoxy polymers: Comparison of accelerated ReaxFF simulations and experiments. Polymer 2018, 158, 354–363. [Google Scholar] [CrossRef]
- Miron, R.A.; Fichthorn, K.A. Accelerated molecular dynamics with the bond-boost method. J. Chem. Phys. 2003, 119, 6210–6216. [Google Scholar] [CrossRef]
- Vashisth, A.; Ashraf, C.; Zhang, W.; Bakis, C.E.; van Duin, A.C.T. Accelerated ReaxFF Simulations for Describing the Reactive Cross-Linking of Polymers. J. Phys. Chem. A 2018, 122, 6633–6642. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Ma, S.; Li, Q.; Xu, X.; Wang, B.; Huang, K.; liu, Y.; Zhu, J. Facile Preparation of Polyimine Vitrimers with Enhanced Creep Resistance and Thermal and Mechanical Properties via Metal Coordination. Macromolecules 2020, 53, 2919–2931. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, H.; Guo, Y. Molecular dynamics simulations of solvent evaporation-induced repolymerization of covalent adaptable networks. Comput. Mater. Sci. 2021, 192, 110412. [Google Scholar] [CrossRef]
- Sterling, T.; Irwin, J.J. ZINC 15 – Ligand Discovery for Everyone. J. Chem. Inf. Model. 2015, 55, 2324–2337. [Google Scholar] [CrossRef] [PubMed]
- Krishnakumar, B.; Singh, M.; Parthasarthy, V.; Park, C.; Sahoo, N.G.; Yun, G.J.; Rana, S. Disulfide exchange assisted self-healing epoxy/PDMS/graphene oxide nanocomposites. Nanoscale Adv. 2020, 2, 2726–2730. [Google Scholar] [CrossRef] [PubMed]
- Smallenburg, F.; Leibler, L.; Sciortino, F. Patchy Particle Model for Vitrimers. Phys. Rev. Lett. 2013, 111, 188002. [Google Scholar] [CrossRef] [PubMed]
- Smallenburg, F.; Sciortino, F. Liquids more stable than crystals in particles with limited valence and flexible bonds. Nat. Phys. 2013, 9, 554–558. [Google Scholar] [CrossRef]
- Wertheim, M.S. Fluids with highly directional attractive forces. I. Statistical thermodynamics. J. Stat. Phys. 1984, 35, 19–34. [Google Scholar] [CrossRef]
- Wertheim, M.S. Fluids with highly directional attractive forces. II. Thermodynamic perturbation theory and integral equations. J. Stat. Phys. 1984, 35, 35–47. [Google Scholar] [CrossRef]
- Ghosh, A.; Schweizer, K.S. Physical Bond Breaking in Associating Copolymer Liquids. ACS Macro Lett. 2021, 10, 122–128. [Google Scholar] [CrossRef]
- Mei, B.; Evans, C.M.; Schweizer, K.S. Self-Consistent Theory for Structural Relaxation, Dynamic Bond Exchange Times, and the Glass Transition in Polymeric Vitrimers. Macromolecules 2024, 57, 3242–3257. [Google Scholar] [CrossRef]
- Ciarella, S.; Sciortino, F.; Ellenbroek, W.G. Dynamics of Vitrimers: Defects as a Highway to Stress Relaxation. Phys. Rev. Lett. 2018, 121, 058003. [Google Scholar] [CrossRef] [PubMed]
- Ciarella, S.; Biezemans, R.A.; Janssen, L.M.C. Understanding, predicting, and tuning the fragility of vitrimeric polymers. Proc. Natl. Acad. Sci. USA 2019, 116, 25013–25022. [Google Scholar] [CrossRef] [PubMed]
- Ciarella, S.; Ellenbroek, W.G. Associative bond swaps in molecular dynamics. SciPost Phys. 2022, 12, 128. [Google Scholar] [CrossRef]
- Sciortino, F. Three-body potential for simulating bond swaps in molecular dynamics. Eur. Phys. J. E 2017, 40, 3. [Google Scholar] [CrossRef] [PubMed]
- Rovigatti, L.; Nava, G.; Bellini, T.; Sciortino, F. Self-Dynamics and Collective Swap-Driven Dynamics in a Particle Model for Vitrimers. Macromolecules 2018, 51, 1232–1241. [Google Scholar] [CrossRef]
- Rao, P.; Xia, X.; Ni, R. A bond swap algorithm for simulating dynamically crosslinked polymers. J. Chem. Phys. 2024, 160, 061102. [Google Scholar] [CrossRef] [PubMed]
- Rouse, P.E., Jr. A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Wittmer, J.P.; Kriuchevskyi, I.; Cavallo, A.; Xu, H.; Baschnagel, J. Shear-stress fluctuations in self-assembled transient elastic networks. Phys. Rev. E 2016, 93, 062611. [Google Scholar] [CrossRef]
- Bomboi, F.; Romano, F.; Fernandez-Castano, J.; Cerbino, R.; Tommaso, B.; Bordi, F.; Filetici, P.; Sciortino, F. Re-entrant DNA gels. Phys. Rev. Lett. 2016, 7, 1391. [Google Scholar] [CrossRef]
- Ciarella, S.; Ellenbroek, W.G. Swap-Driven Self-Adhesion and Healing of Vitrimers. Coatings 2019, 9, 114. [Google Scholar] [CrossRef]
- Ciarella, S. Relaxation Pathways for Soft Materials. Ph.D. Thesis, Technical University of Eindhoven, Eindhoven, UK, 2021. [Google Scholar]
- Tito, N.B.; Creton, C.; Storm, C.; Ellenbroek, W.G. Harnessing entropy to enhance toughness in reversibly crosslinked polymer networks. Soft Matter 2019, 15, 2190–2203. [Google Scholar] [CrossRef] [PubMed]
- Karatrantos, A.V.; Mugemana, C.; Bouhala, L.; Clarke, N.; Kröger, M. From Ionic Nanoparticle Organic Hybrids to Ionic Nanocomposites: Structure, Dynamics, and Properties: A Review. Nanomaterials 2023, 13, 2. [Google Scholar] [CrossRef] [PubMed]
- Kean, Z.S.; Hawk, J.L.; Lin, S.; Zhao, X.; Sijbesma, R.P.; Craig, S.L. Increasing the Maximum Achievable Strain of a Covalent Polymer Gel Through the Addition of Mechanically Invisible Cross-Links. Adv. Mater. 2014, 26, 6013–6018. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Wei, X.; Fang, Y.; Gao, K.; Yue, T.; Zhang, L.; Ganesan, V.; Meng, F.; Liu, J. Molecular Dynamics Simulation of the Structural, Mechanical, and Reprocessing Properties of Vitrimers Based on a Dynamic Covalent Polymer Network. Macromolecules 2022, 55, 1091–1103. [Google Scholar] [CrossRef]
- Wu, J.B.; Li, S.J.; Liu, H.; Qian, H.J.; Lu, Z.Y. Dynamics and reaction kinetics of coarse-grained bulk vitrimers: A molecular dynamics study. Phys. Chem. Chem. Phys. 2019, 21, 13258–13267. [Google Scholar] [CrossRef]
- Zhao, H.; Duan, P.; Li, Z.; Chen, Q.; Yue, T.; Zhang, L.; Ganesan, V.; Liu, J. Unveiling the Multiscale Dynamics of Polymer Vitrimers Via Molecular Dynamics Simulations. Macromolecules 2023, 56, 9336. [Google Scholar] [CrossRef]
- Martins, M.L.; Zhao, X.; Demchuk, Z.; Luo, J.; Carden, G.P.; Toleutay, G.; Sokolov, A.P. Viscoelasticity of Polymers with Dynamic Covalent Bonds: Concepts and Misconceptions. Macromolecules 2023, 56, 8688–8696. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Su, L.; Hu, S.; Xiang, P.; Zhao, X.; Liu, L.; Zhang, L.; Gao, Y. Viscoelasticity and self-healing property of dynamic covalent polymers: A molecular dynamics simulation. Polymer 2024, 295, 126775. [Google Scholar] [CrossRef]
- Karatrantos, A.; Composto, R.J.; Winey, K.I.; Clarke, N. Primitive path network, structure and dynamics of SWCNT/polymer nanocomposites. IOP Conf. Ser. Mat. Sci. Eng. 2012, 40, 012027. [Google Scholar] [CrossRef]
- Duan, P.; Zhao, H.; Chen, Q.; Liu, M.; Wu, X.; Ganesan, V.; Wei, Y.; Liu, J. Insights into Uniaxial Tension and Relaxation of Nanorod-Filled Polymer Vitrimer Nanocomposites: A Molecular Dynamics Simulation. Macromolecules 2023, 56, 4468–4481. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, H.; Duan, P.; Zhang, L.; Liu, J. Manipulating the Properties of Polymer Vitrimer Nanocomposites by Designing Dual Dynamic Covalent Bonds. Langmuir 2024, 40, 7769–7780. [Google Scholar] [CrossRef] [PubMed]
- Oyarzun, B.; Mognetti, B.M. Efficient sampling of reversible cross-linking polymers: Self-assembly of single-chain polymeric nanoparticles. J. Chem. Phys. 2018, 148, 114110. [Google Scholar] [CrossRef] [PubMed]
- Lei, Q.L.; Xia, X.; Yang, J.; Ciamarra, M.P.; Ni, R. Entropy-controlled cross-linking in linker-mediated vitrimers. Proc. Natl. Acad. Sci. USA 2020, 117, 27111–27115. [Google Scholar] [CrossRef] [PubMed]
- Xia, X.; Rao, P.; Yang, J.; Ciamarra, M.P.; Ni, R. Entropy-Driven Thermo-gelling Vitrimer. JACS Au 2022, 2, 2359–2366. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Yang, H.; Huang, S.; Chen, Q. Relationship between Reaction Kinetics and Chain Dynamics of Vitrimers Based on Dioxaborolane Metathesis. Macromolecules 2020, 53, 1180–1190. [Google Scholar] [CrossRef]
- Röttger, M.; Domenech, T.; van der Weegen, R.; Breuillac, A.; Nicolaÿ, R.; Leibler, L. High-performance vitrimers from commodity thermoplastics through dioxaborolane metathesis. Science 2017, 356, 62–65. [Google Scholar] [CrossRef] [PubMed]
- Perego, A.; Khabaz, F. Volumetric and Rheological Properties of Vitrimers: A Hybrid Molecular Dynamics and Monte Carlo Simulation Study. Macromolecules 2020, 53, 8406–8416. [Google Scholar] [CrossRef]
- Perego, A.; Khabaz, F. Effect of bond exchange rate on dynamics and mechanics of vitrimers. J. Polym. Sci. 2021, 59, 2590–2602. [Google Scholar] [CrossRef]
- Perego, A.; Lazarenko, D.; Cloitre, M.; Khabaz, F. Microscopic Dynamics and Viscoelasticity of Vitrimers. Macromolecules 2022, 55, 7605–7613. [Google Scholar] [CrossRef]
- Pandya, H.; Perego, A.; Khabaz, F. Stress-induced dynamics of glassy vitrimers with fast bond exchange rate. J. Appl. Polym. Sci. 2024, 141, e55039. [Google Scholar] [CrossRef]
- Hoy, R.S.; Fredrickson, G.H. Thermoreversible associating polymer networks. I. Interplay of thermodynamics, chemical kinetics, and polymer physics. J. Chem. Phys. 2009, 131, 224902. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Ye, H.; Wang, Q.; Kröger, M.; Li, Y. Sticky Rouse Time Features the Self-Adhesion of Supramolecular Polymer Networks. Macromolecules 2021, 54, 5053–5064. [Google Scholar] [CrossRef]
- Xia, J.; Kalow, J.A.; Olvera de la Cruz, M. Structure, Dynamics, and Rheology of Vitrimers. Macromolecules 2023, 56, 8080–8093. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar] [CrossRef]
- Pant, P.V.K.; Theodorou, D.N. Variable Connectivity Method for the Atomistic Monte Carlo Simulation of Polydisperse Polymer Melts. Macromolecules 1995, 28, 7224–7234. [Google Scholar] [CrossRef]
- Singh, K.; Rabin, Y. Aging of Thermoreversible Gel of Associating Polymers. Macromolecules 2020, 53, 3883–3890. [Google Scholar] [CrossRef]
- Amin, D.; Likhtman, A.E.; Wang, Z. Dynamics in Supramolecular Polymer Networks Formed by Associating Telechelic Chains. Macromolecules 2016, 49, 7510–7524. [Google Scholar] [CrossRef]
- Wilson, M.; Rabinovitch, A.; Baljon, A.R.C. Computational Study of the Structure and Rheological Properties of Self-Associating Polymer Networks. Macromolecules 2015, 48, 6313–6320. [Google Scholar] [CrossRef]
- Wu, S.; Yang, H.; Zhang, Z.; Chen, Q. Elongational Rheology of Entangled Ionomers Based on Poly(hexyl methacrylate). Macromolecules 2023, 56, 9570–9583. [Google Scholar] [CrossRef]
- Karatrantos, A.; Clarke, N. A theoretical model for the prediction of diffusion in polymer/SWCNT nanocomposites. Soft Matter 2011, 7, 7334–7341. [Google Scholar] [CrossRef]
- Karatrantos, A.; Clarke, N.; Composto, R.J.; Winey, K.I. Structure, entanglements and dynamics of polymer nanocomposites containing spherical nanoparticles. IOP Conf. Ser. Mat. Sci. Eng. 2014, 64, 012041. [Google Scholar] [CrossRef]
- Ricarte, R.G.; Tournilhac, F.; Cloître, M.; Leibler, L. Linear Viscoelasticity and Flow of Self-Assembled Vitrimers: The Case of a Polyethylene/Dioxaborolane System. Macromolecules 2020, 53, 1852–1866. [Google Scholar] [CrossRef]
- Jourdain, A.; Asbai, R.; Anaya, O.; Chehimi, M.M.; Drockenmuller, E.; Montarnal, D. Rheological Properties of Covalent Adaptable Networks with 1,2,3-Triazolium Cross-Links: The Missing Link between Vitrimers and Dissociative Networks. Macromolecules 2020, 53, 1884–1900. [Google Scholar] [CrossRef]
- Ricarte, R.G.; Shanbhag, S. Unentangled Vitrimer Melts: Interplay between Chain Relaxation and Cross-link Exchange Controls Linear Rheology. Macromolecules 2021, 54, 3304–3320. [Google Scholar] [CrossRef]
- Karmakar, R.; Himanshu; Sastry, S.; Kumar, S.K.; Patra, T.K. Entropic Cohesion in Vitrimers. arXiv 2024, arXiv:2402.16226. [Google Scholar]
- Clarke, R.W.; Sandmeier, T.; Franklin, K.A.; Reich, D.; Zhang, X.; Vengallur, N.; Patra, T.K.; Tannenbaum, R.J.; Adhikari, S.; Kumar, S.K.; et al. Dynamic crosslinking compatibilizes immiscible mixed plastics. Nature 2023, 616, 731–739. [Google Scholar] [CrossRef] [PubMed]
- Perego, A.; Khabaz, F. Creep and Recovery Behavior of Vitrimers with Fast Bond Exchange Rate. Macromol. Rapid Commun. 2023, 44, 2200313. [Google Scholar] [CrossRef]
- Fricker, H.S. On the Theory of Stress Relaxation by Cross-Link Reorganization. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1973, 335, 289–300. [Google Scholar]
- Robe, D.; Santra, A.; McKinley, G.H.; Prakash, J.R. Evanescent Gels: Competition between Sticker Dynamics and Single-Chain Relaxation. Macromolecules 2024. Ahead of Print. [Google Scholar] [CrossRef]
- Shanbhag, S.; Ricarte, R.G. On the Effective Lifetime of Reversible Bonds in Transient Networks. Macromol. Theory Simul. 2023, 32, 2300002. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, L.; Yang, Y.; Tang, P. Understanding the application of covalent adaptable networks in self-repair materials based on molecular simulation. Soft Matter 2024, 20, 1486–1498. [Google Scholar] [CrossRef]
- Kramers, H. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 1940, 7, 284–304. [Google Scholar] [CrossRef]
- Cordier, P.; Tournilhac, F.; Soulie-Ziakovic, C.; Leibler, L. Self–healing and thermoreversible rubber from supramolecular assembly. Nature 2008, 451, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Ishibashi, J.S.A.; Kalow, J.A. Vitrimeric Silicone Elastomers Enabled by Dynamic Meldrum’s Acid-Derived Cross-Links. ACS Macro Lett. 2018, 7, 482–486. [Google Scholar] [CrossRef]
- Porath, L.E.; Evans, C.M. Importance of Broad Temperature Windows and Multiple Rheological Approaches for Probing Viscoelasticity and Entropic Elasticity in Vitrimers. Macromolecules 2021, 54, 4782–4791. [Google Scholar] [CrossRef]
- Soman, B.; Schweizer, K.S.; Evans, C.M. Fragile Glass Formation and Non-Arrhenius Upturns in Ethylene Vitrimers Revealed by Dielectric Spectroscopy. Macromolecules 2023, 56, 166–176. [Google Scholar] [CrossRef]
- Shao, J.; Jiang, N.; Zhang, H.; Yang, Y.; Tang, P. Sticky Rouse Model and Molecular Dynamics Simulation for Dual Polymer Networks. Macromolecules 2022, 55, 535–549. [Google Scholar] [CrossRef]
- Jiang, N.; Zhang, H.; Yang, Y.; Tang, P. Molecular dynamics simulation of associative polymers: Understanding linear viscoelasticity from the sticky Rouse model. J. Rheol. 2021, 65, 527–547. [Google Scholar] [CrossRef]
- Cui, X.; Jiang, N.; Shao, J.; Zhang, H.; Yang, Y.; Tang, P. Linear and Nonlinear Viscoelasticities of Dissociative and Associative Covalent Adaptable Networks: Discrepancies and Limits. Macromolecules 2023, 56, 772–784. [Google Scholar] [CrossRef]
- Hoy, R.S.; Foteinopoulou, K.; Kröger, M. Topological analysis of polymeric melts: Chain-length effects and fast-converging estimators for entanglement length. Phys. Rev. E 2009, 80, 031803. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karatrantos, A.V.; Couture, O.; Hesse, C.; Schmidt, D.F. Molecular Simulation of Covalent Adaptable Networks and Vitrimers: A Review. Polymers 2024, 16, 1373. https://doi.org/10.3390/polym16101373
Karatrantos AV, Couture O, Hesse C, Schmidt DF. Molecular Simulation of Covalent Adaptable Networks and Vitrimers: A Review. Polymers. 2024; 16(10):1373. https://doi.org/10.3390/polym16101373
Chicago/Turabian StyleKaratrantos, Argyrios V., Olivier Couture, Channya Hesse, and Daniel F. Schmidt. 2024. "Molecular Simulation of Covalent Adaptable Networks and Vitrimers: A Review" Polymers 16, no. 10: 1373. https://doi.org/10.3390/polym16101373
APA StyleKaratrantos, A. V., Couture, O., Hesse, C., & Schmidt, D. F. (2024). Molecular Simulation of Covalent Adaptable Networks and Vitrimers: A Review. Polymers, 16(10), 1373. https://doi.org/10.3390/polym16101373








