Piezoelectric Yield of Single Electrospun Poly(acrylonitrile) Ultrafine Fibers Studied by Piezoresponse Force Microscopy and Numerical Simulations
Abstract
1. Introduction
2. Materials and Methods
2.1. Electrospinning of PAN and PVDF Ultrafine Fibers
2.2. Morphological Characterization
2.3. Infrared Spectroscopy
2.4. Piezoresponse Characterization
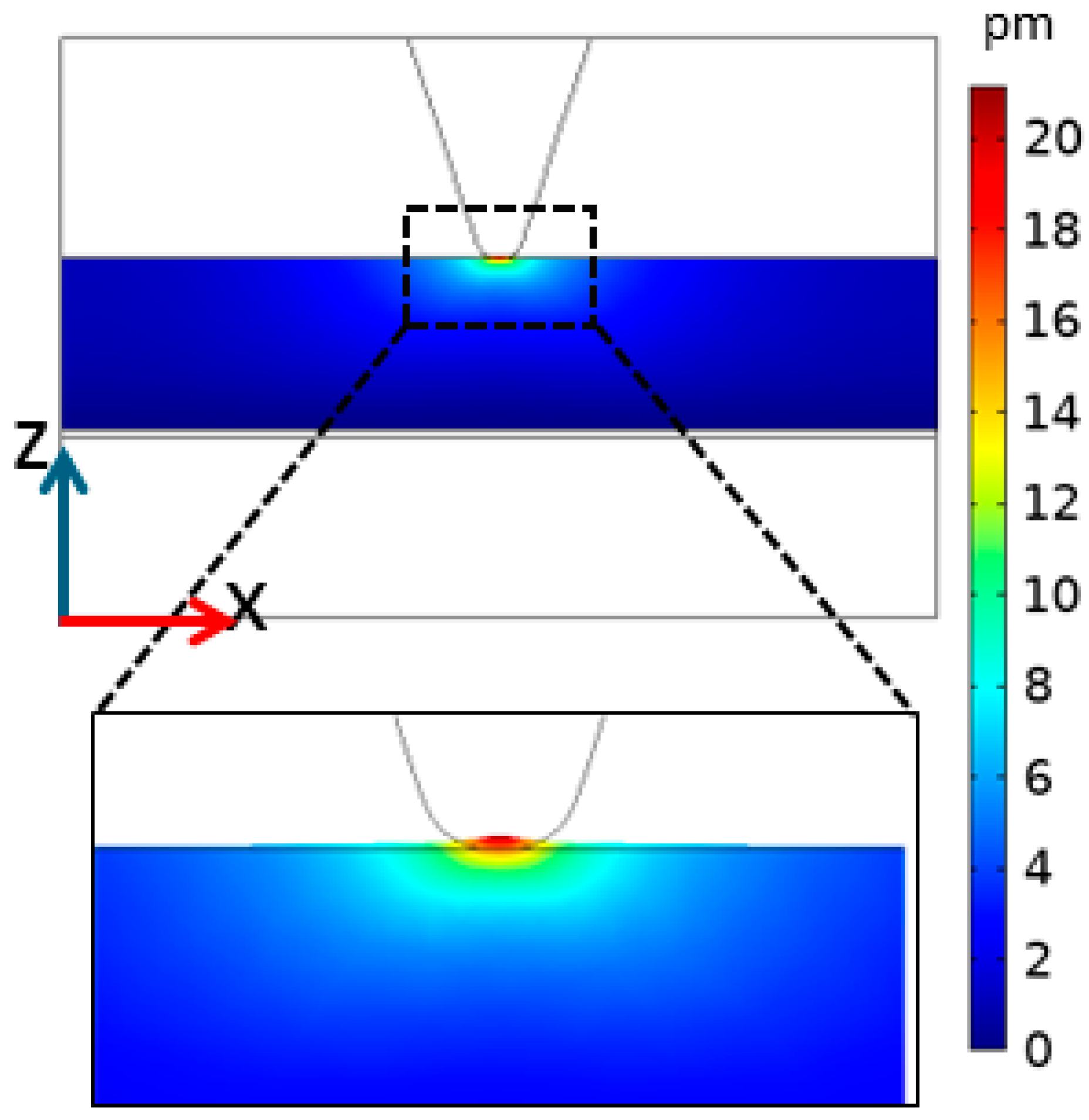
2.5. COMSOL Simulations
3. Results
3.1. Characterization of PAN Fiber Meshes
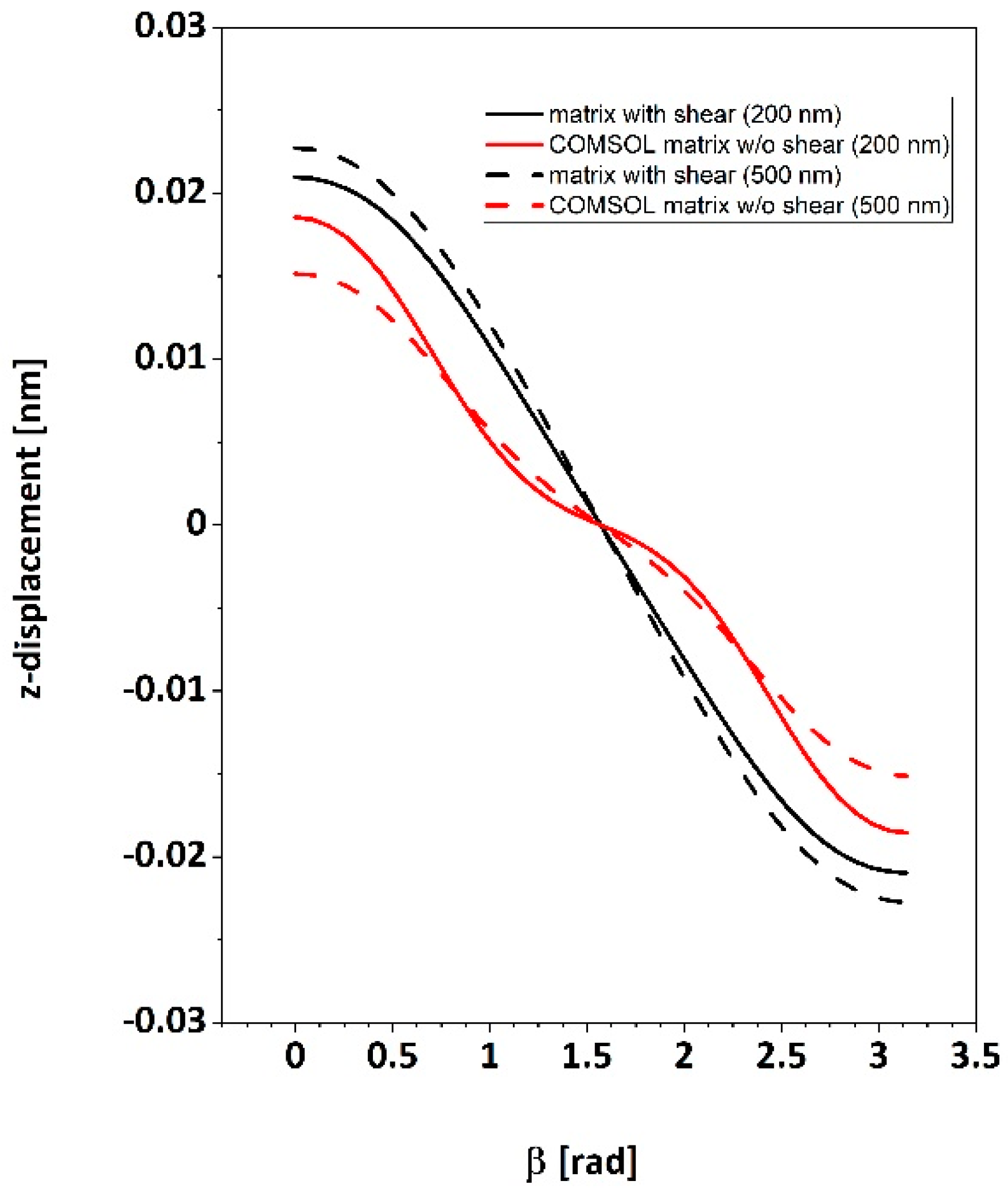
3.2. Results of COMSOL Simulations
4. Discussion
- (i)
- The AC electric field frequency Ω cannot exceed around 100 Hz to allow the correct operation of the AFM frequency-modulation mode [26]; this limits the sampling time (time spent on each measurement pixel of the map) to around 30 ms. A map composed of 256 × 256 pixels takes around one hour to be acquired, as each scan line must be run twice, forward and backward;
- (ii)
- For the correct quantitative operation of the CE-FM mode of PFM, the distance stabilization feedback loop cannot be too fast [26]. Therefore, the scanning speed should be reduced to avoid possible damage or the picking up of organic material by the probe scanning over the fibers. A ruined tip would compromise the quality of the following images, forcing probe replacement to retrieve the proper performance of the microscope. To preserve the probe, we have experienced that the scanning speed should not exceed around 100 nm/s.
- (i)
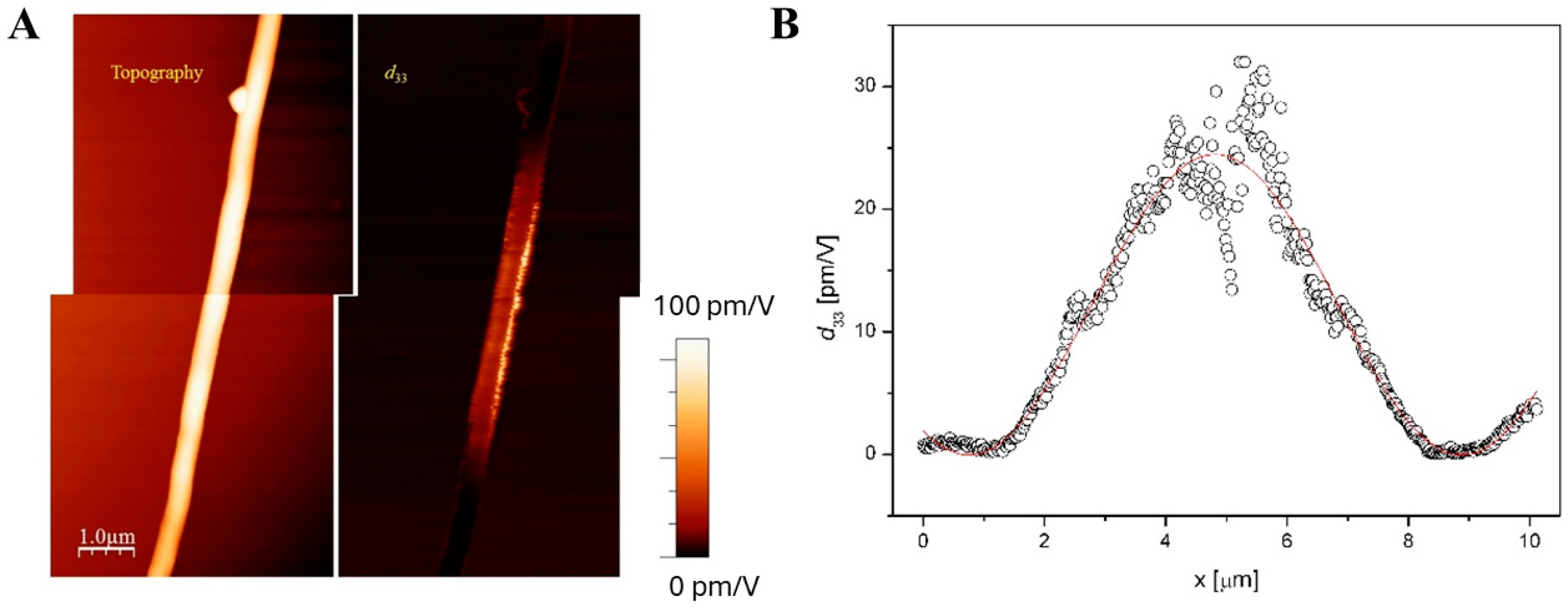
- Uniform piezoresponse is typically detected along the length of single fibers, as in Figure 5. The variability of the reported d33 effective values could be ascribed to the different polar axis directions of fibers lying on the conductive substrate;
- (ii)
- Gradual signal variations at fiber crossing sites are observed. This can be explained by the probe’s greater distance from the substrate and the related decrease in the electric field inside the fibers;
- (iii)
- Occasionally, the piezoresponse of a single fiber may vary even when fully resting on the substrate. This result could be explained by assuming the gradual twisting of the fiber around its longitudinal axis, which may lead to a corresponding rotation of the polar axis of the fiber’s material.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mota, C.; Labardi, M.; Trombi, L.; Astolfi, L.; d’Acunto, M.; Puppi, D.; Gallone, G.; Chiellini, F.; Berrettini, S.; Bruschini, L.; et al. Design, fabrication and characterization of composite piezoelectric ultrafine fibers for cochlear stimulation. Mater. Des. 2017, 122, 206. [Google Scholar] [CrossRef]
- Yu, S.; Milam-Guerrero, J.; Tai, Y.; Yang, S.; Choi, Y.Y.; Nam, J.; Myung, N.V. Maximizing polyacrylonitrile nanofiber piezoelectric properties through the optimization of electrospinning and post-thermal treatment processes. ACS Appl. Polym. Mater. 2022, 4, 635. [Google Scholar] [CrossRef]
- Yu, S.; Tai, Y.; Milam-Guerrero, J.; Nam, J.; Myung, N.V. Electrospun organic piezoelectric nanofibers and their energy and bio applications. Nano Energy 2022, 97, 107174. [Google Scholar] [CrossRef]
- Nishiyama, T.; Sumihara, T.; Sasaki, Y.; Sato, E.; Yamato, M.; Horibe, H. Crystalline structure control of poly(vinylidene fluoride) films with the antisolvent addition method. Polym. J. 2016, 48, 1035. [Google Scholar] [CrossRef]
- Stolze, M.; Sutter, D.H. Molecular g-values, magnetic susceptibility anisotropics, molecular electric quadrupole moments, improved molecular electric dipole moments and 14N-quadrupole coupling constants of acrylonitrile, H2C = CH–CN, and the magnetic susceptibility tensor of the nitrile group. Z. Naturforschung 1985, 40, 998. [Google Scholar]
- Available online: https://pslc.ws/modelhtms/panpdb.htm (accessed on 1 April 2024).
- Henrici-Olivè, G.; Olivè, S. Molecular interactions and macroscopic properties of polyacrylonitrile and model substances. In Chemistry; Springer: Berlin/Heidelberg, Germany, 2005; Volume 32. [Google Scholar] [CrossRef]
- Boyle, A.L. Applications of de novo designed peptides. In Peptide Applications in Biomedicine, Biotechnology and Bioengineering; Elsevier: Amsterdam, The Netherlands, 2018; p. 51. [Google Scholar] [CrossRef]
- Rosenbaum, S. Polyacrylonitrile fiber behavior. I. Mechanisms of tensile response. J. Appl. Polym. Sci. 1965, 9, 2071. [Google Scholar] [CrossRef]
- Hobson, R.J.; Windle, A.H. Crystalline Structure of Atactic Poly (acrylonitrile). Macromolecules 1993, 26, 6903. [Google Scholar] [CrossRef]
- Lindenmeyer, P.H.; Hosemann, R. Application of the theory of paracrystals to the crystal structure analysis of polyacrylonitrile. J. Appl. Phys. 1963, 34, 42. [Google Scholar] [CrossRef]
- Grobelny, J.; Sokbl, M.; Turska, E. A study of conformation, configuration and phase structure of polyacrylonitrile and their mutual dependence by means of WAXS and 1H BL-n.m.r. Polymer 1984, 25, 1415. [Google Scholar] [CrossRef]
- Chorsi, M.T.; Curry, E.J.; Chorsi, H.T.; Das, R.; Baroody, J.; Purohit, P.K.; Ilies, H.; Nguyen, T.D. Piezoelectric biomaterials for sensors and actuators. Adv. Mater. 2019, 31, 1802084. [Google Scholar] [CrossRef]
- Keirouz, A.; Wang, Z.; Reddy, V.S.; Nagy, Z.K.; Vass, P.; Buzgo, M.; Ramakrishna, S.; Radacsi, N. The history of electrospinning: Past, present, and future developments. Adv. Mater. Technol. 2023, 8, 1. [Google Scholar] [CrossRef]
- Taylor, G.I. Electrically driven jets. Proc. R. Soc. Lond. A. Math. Phys. Sci. 1969, 313, 453. [Google Scholar] [CrossRef]
- Bhardwaj, N.; Kundu, S.C. Electrospinning: A fascinating fiber fabrication technique. Biotechnol. Adv. 2010, 28, 325. [Google Scholar] [CrossRef]
- Kawai, H. The piezoelectricity of poly (vinylidene fluoride). Jpn. J. Appl. Phys. 1969, 8, 975. [Google Scholar] [CrossRef]
- Mohammadpourfazeli, S.; Arash, S.; Ansari, A.; Yang, S.; Mallick, K.; Bagherzadeh, R. Future prospects and recent developments of polyvinylidene fluoride (PVDF) piezoelectric polymer; fabrication methods, structure, and electro-mechanical properties. RSC Adv. 2023, 13, 370. [Google Scholar] [CrossRef]
- Lei, T.; Yu, L.; Zheng, G.; Wang, L.; Wu, D.; Sun, D. Electrospinning-induced preferred dipole orientation in PVDF fibers. J. Mater. Sci. 2015, 50, 4342. [Google Scholar] [CrossRef]
- Wang, W.; Zheng, Y.; Jin, X.; Sun, Y.; Lu, B.; Wang, H.; Fang, J.; Shao, H.; Lin, T. Unexpectedly high piezoelectricity of electrospun polyacrylonitrile nanofiber membranes. Nano Energy 2019, 56, 588. [Google Scholar] [CrossRef]
- Yuan, L.; Fan, W.; Yang, X.; Ge, S.; Xia, C.; Foong, S.Y.; Liew, R.K.; Wang, S.; Van Le, Q.; Lam, S.S. Piezoelectric PAN/BaTiO3 nanofiber membranes sensor for structural health monitoring of real-time damage detection in composite. Compos. Commun. 2021, 25, 100680. [Google Scholar] [CrossRef]
- Minagawa, M.; Miyano, K.; Takahashi, M.; Yoshii, F. Infrared characteristic absorption bands of highly isotactic poly (acrylonitrile). Macromolecules 1988, 21, 2387. [Google Scholar] [CrossRef]
- Ueda, H.; Carr, S.H. Piezoelectricity in polyacrylonitrile. Polym. J. 1984, 16, 661. [Google Scholar] [CrossRef]
- Street, R.M.; Minagawa, M.; Vengrenyuk, A.; Schauer, C.L. Piezoelectric electrospun polyacrylonitrile with various tacticities. J. Appl. Polym. Sci. 2019, 136, 2. [Google Scholar] [CrossRef]
- ANSI/IEEE Std 176-1987; IEEE Standard on Piezoelectricity. IEEE: Piscataway, NJ, USA, 1987; p. 10.
- Labardi, M.; Magnani, A.; Capaccioli, S. Piezoelectric displacement mapping of compliant surfaces by constant-excitation frequency-modulation piezoresponse force microscopy. Nanotechnology 2020, 31, 075707. [Google Scholar] [CrossRef] [PubMed]
- Labardi, M. Model of frequency-modulated atomic force microscopy for interpretation of non-contact piezoresponse measurements. Nanotechnology 2020, 31, 245705. [Google Scholar] [CrossRef]
- Protasenko, V.V.; Labardi, M.; Gallagher, A. Conservative and dissipative forces measured by self-oscillator atomic force microscopy at constant-drive amplitude. Phys. Rev. B 2004, 70, 245414. [Google Scholar] [CrossRef]
- Magnani, A.; Capaccioli, S.; Azimi, B.; Danti, S.; Labardi, M. Local piezoelectric response of polymer/ceramic nanocomposite fibers. Polymers 2022, 14, 5379. [Google Scholar] [CrossRef] [PubMed]
- Nix, E.L.; Ward, I.M. The measurement of the shear piezoelectric coefficients of polyvinylidene fluoride. Ferroelectrics 1986, 67, 137. [Google Scholar] [CrossRef]
- Collins, G.; Federici, J.; Imura, Y.; Catalani, L.H. Charge generation, charge transport, and residual charge in the electrospinning of polymers: A review of issues and complications. J. Appl. Phys. 2012, 111, 044701. [Google Scholar] [CrossRef]
- Zavagna, L.; Canelli, E.F.; Azimi, B.; Troisi, F.; Scarpelli, L.; Macchi, T.; Gallone, G.; Labardi, M.; Giovannoni, R.; Milazzo, M.; et al. Electrospun fiber-based tubular structures as 3D scaffolds to generate in vitro models for small intestine. Macromol. Mater. Eng. 2024; submitted. [Google Scholar]
- Montorsi, M.; Pucci, C.; De Pasquale, D.; Marino, A.; Ceccarelli, M.C.; Mazzuferi, M.; Bartolucci, M.; Petretto, A.; Prato, M.; Debellis, D.; et al. Ultrasound-activated piezoelectric nanoparticles trigger microglia activity against glioblastoma cells. Adv. Healthc. Mater. 2024, 230, 4331. [Google Scholar] [CrossRef]
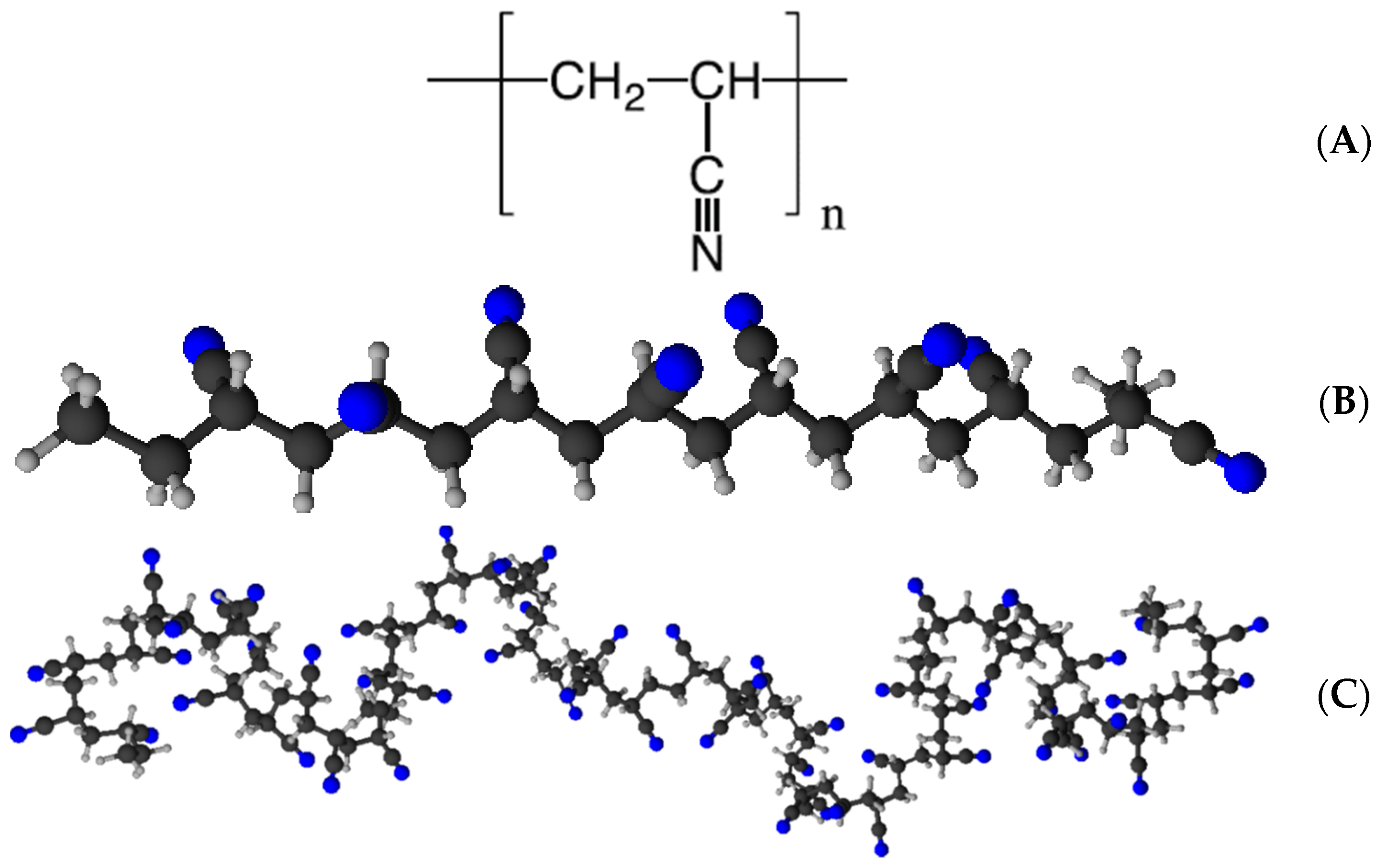






| Material | Sample Type/Treatment | Measuring Method | Piezoelectric Constant/ Voltage Output | Zigzag Content [%] | Reference |
|---|---|---|---|---|---|
| Solvent cast films, poled and stretched. PAN Mw = 35 kDa. Solvent: DMF. | Poled (5 × 104 V/cm) Unstretched | Dynamic stress and piezoelectric polarization (strain of 1.5 × 10−3, oscillating frequency of 11 Hz) used to obtain absolute values of d31. | d31 = 0.32 × 10−8 cgs esu | Not reported | [23] |
| Poled (5 × 104 V/cm) Stretched | d31 = 1.7 × 10−8 cgs esu | ||||
| Poled (10 × 104 V/cm) Stretched | d31 = 3 × 10−8 cgs esu | ||||
| Electrospun fiber meshes with different degrees of alignment. PAN Mw = 90 kDa. Solvent: DMF. | With/without charge removal | Periodic pressure applied. Voltage/current output of the mesh reported. | Voltage outputs of 0.2–1.2 V/cm2 upon compression | 80–86% | [20] |
| Electrospun fiber meshes with different diameter distributions. PAN Mw = 150 kDa. Solvent: DMF. | No annealing | Piezoresponse force microscopy (PFM). d33 of the fibers reported. | d33 = 2–14 pm/V | 55–75% | [2] |
| 60 °C annealing | d33 = 1–16 pm/V | 45–80% | |||
| 95 °C annealing | d33 = 8–40 pm/V | 70–90% | |||
| Electrospun fiber meshes, PAN with various tacticites. Solvent: DMSO. | Commercial (Mw = 300 kDa) | Periodic semi-static normal load method. Effective d33 of the mesh reported. | d33,eff = 0–0.2 pC/N | Not reported | [24] |
| 25% Isotactic (Mw = 857 kDa) | d33,eff = 1.5–2.0 pC/N | ||||
| 52% Isotactic (Mw = 517 kDa) | d33,eff = 0.4–0.6 pC/N | ||||
| Electrospun fiber composite meshes of PAN/BaTiO3. | 0% w BaTiO3 | Periodic pressure applied. Voltage/current output of the mesh reported. | 0.64 V/cm2 | 45% | [21] |
| 5% w BaTiO3 | 0.94 V/cm2 | 50% | |||
| 10% w BaTiO3 | 1.36 V/cm2 | 52% | |||
| 15% w BaTiO3 | 1.86 V/cm2 | 56% | |||
| 20% w BaTiO3 | 1.56 V/cm2 | 53% | |||
| 25% w BaTiO3 | 1.26 V/cm2 | 51% | |||
| Electrospun fiber meshes collected at different rotation speeds. PAN Mw = 150 kDa. Solvent: DMF. | 5 rpm (random) | Piezoresponse force microscopy (PFM). d33 of the fibers reported. | d33 = 88 ± 44 pm/V | 24% | This work |
| 1500 rpm | d33 = 88 ± 58 pm/V | 46% | |||
| 3000 rpm (aligned) | d33 = 17 ± 11 pm/V | 33% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montorsi, M.; Zavagna, L.; Scarpelli, L.; Azimi, B.; Capaccioli, S.; Danti, S.; Labardi, M. Piezoelectric Yield of Single Electrospun Poly(acrylonitrile) Ultrafine Fibers Studied by Piezoresponse Force Microscopy and Numerical Simulations. Polymers 2024, 16, 1305. https://doi.org/10.3390/polym16101305
Montorsi M, Zavagna L, Scarpelli L, Azimi B, Capaccioli S, Danti S, Labardi M. Piezoelectric Yield of Single Electrospun Poly(acrylonitrile) Ultrafine Fibers Studied by Piezoresponse Force Microscopy and Numerical Simulations. Polymers. 2024; 16(10):1305. https://doi.org/10.3390/polym16101305
Chicago/Turabian StyleMontorsi, Margherita, Lorenzo Zavagna, Lorenzo Scarpelli, Bahareh Azimi, Simone Capaccioli, Serena Danti, and Massimiliano Labardi. 2024. "Piezoelectric Yield of Single Electrospun Poly(acrylonitrile) Ultrafine Fibers Studied by Piezoresponse Force Microscopy and Numerical Simulations" Polymers 16, no. 10: 1305. https://doi.org/10.3390/polym16101305
APA StyleMontorsi, M., Zavagna, L., Scarpelli, L., Azimi, B., Capaccioli, S., Danti, S., & Labardi, M. (2024). Piezoelectric Yield of Single Electrospun Poly(acrylonitrile) Ultrafine Fibers Studied by Piezoresponse Force Microscopy and Numerical Simulations. Polymers, 16(10), 1305. https://doi.org/10.3390/polym16101305








