Abstract
The relationships between gas permeability and free volume fraction, intersegmental distance, and glass transition temperature, are investigated. They are analyzed for He, CO2, O2, CH4, and N2 gases and for five similar polyimides with a wide range of permeabilities, from very low to extremely high ones. It has been established here that there is an exponential relationship between permeability and the free volume fraction, and between permeability and the most probable intersegmental distance as measured by WAXS; in both cases, with an exponential coefficient that depends on the kinetic gas diameter as a quadratic polynomial and with a preexponential positive constant. Moreover, it has been proven that the intersegmental distance increases linearly with the free volume fraction. Finally, it has been established that the free volume fraction increases with the glass transition temperature for the polymers tested, and that they depend on each other in an approximate linear way.
1. Introduction
Polyimides play a crucial role in the realm of gas separation membranes, underlining their paramount importance in various industrial applications. Gas separation membranes are essential in processes such as gas purification, carbon capture, and the production of high-purity gases. Polyimides, owing to their unique combination of mechanical strength, thermal stability, and excellent gas permeability, stand out as a preferred material for crafting these membranes. The inherent versatility of polyimides allows for the design and fabrication of membranes with tailored properties, enabling selective gas permeation based on size, shape, and chemical affinity. This selectivity is paramount in industries wherein the separation of specific gases from complex mixtures is imperative. Whether it is enhancing the efficiency of natural gas processing or mitigating greenhouse gas emissions through carbon capture technologies, polyimide-based gas separation membranes contribute significantly to the advancement of environmentally friendly and economically viable processes. The continual research and development in this field underscore the ongoing efforts to optimize polyimide materials for enhanced gas separation performance, further solidifying their indispensable role in shaping the future of sustainable industrial practices.
In general, d-spacing, obtained from wide-angle X-ray diffraction, is accepted to represent intersegmental distance between polymer chains. Long-chain polymers are presumed to have a higher d-spacing value because it seems clear that longer chains induce lower crystallinity leading, for long enough d-spacings, to the transformation from a glassy to a rubbery structure [1]. Moreover, Stadler et al. showed that d-spacing increases with the molecular weight of the polymers [2]. It has also been noted that there is an improvement in gas permeability for longer chain polymers [3]. Therefore, it should be expected that permeability should increase for longer intersegmental distances between polymer chains.
A similar general increase in permeability for increasing free volume fractions seems to be reasonable. Sandhya et al. confirm that, when the gases diffuse through polymeric membranes with low free volume fractions, they cannot penetrate efficiently into the system, thereby decreasing the permeability of the gas [4].
Nevertheless, Bas et al. did not find any clear correlation between neither d-spacing nor free volume with permeability [5]. Park and Paul [6] performed measurements on an extensive collection of rather heterogeneous polyimides and did not find any concluding quantitative dependence of permeability on free volume, perhaps because they used polyimides with similar permeabilities.
We have recently proposed and tested a quantitative correlation of free volume fraction with permeability [7,8,9,10] that we want to verify here for a homologous series of rather similar polyimides with a wide range of permeabilities. We will test as well whether that quantitative correlation can be applied to d-spacing too.
Referring to the dependence of free volume fraction on the glass transition temperature, Tg, Van Krevelen and Nijenhuis [11] reported an increase in free volume with increasing Tg for an extensive assortment of polymers with a positive correlation, although with a considerable scattering. Hensema et al. recognized [12] that the glass transition temperature may be an appropriate way to estimate free volume, although confirming wide deviations from any monotonous fitting line. More recently, White and Lipson [13] showed, by a thermodynamic detailed analysis and experimental testing, that free volume at glass transition temperature must increase in an approximately linear way with Tg. This would justify that, for temperatures below Tg, the same or a similarly linear behavior would hold. This will be tested here for a homologous set of akin polymers, polyimides specifically, with a wide range of permeabilities.
2. Materials and Methods
A wide set of commercial (P84® and Matrimid®) and other polyimides synthetized by us were used to form films for gas separation. P84® was obtained from HP Polymer GmbH (Lenzing, Austria). Matrimid® was obtained from Huntsman Advanced Materials GmbH (Berkamen, Germany). The synthetized polyimides (Pi-HABAc, Pi-DAM, Pi-DAPOH) were formed by the reaction of 4,4′-(Hexafluoroisopropylidene) diphthalic anhydride, 6FDA, from Fluorochem (Glossop, UK) and 3,3′-Dihydroxybenzidine, HAB, 2,4,6-Trimethyl-1,3-benzenediamine, DAM, both from Apollo Scientific (Manchester, UK) or 2,4-Diaminophenol dihydrochloride, DAP, from Merck-Sigma Aldrich (St. Louis, MO, USA), respectively. Diamines and 6FDA were dried before used. A scheme of the corresponding structures is shown in Figure 1.
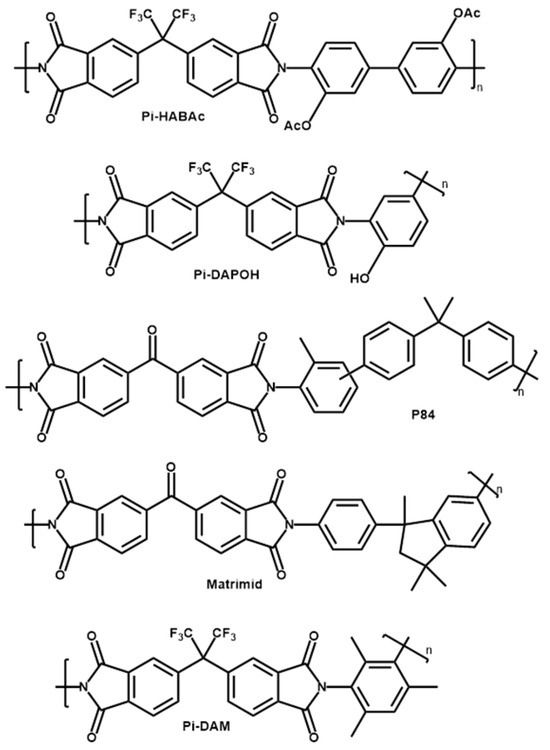
Figure 1.
Scheme of the polyimides tested here.
Anhydrous 1-methyl-2-pyrrolidinone (NMP), anhydrous pyridine (Py), acetic anhydride, and anhydrous chloroform were purchased from Sigma Aldrich, o-xylene was from VWR (Radnor, PA, USA) and ethanol from Quimilid (Laguna de Duero, Valladolid, Spain). All solvents were used as purchased.
2.1. Synthesis of Matrix Polyimides
All the synthetized polyimides were obtained by a two-step polycondensation reaction between 6FDA anhydride and the corresponding diamine reported in previous works [14,15]. A three-necked flask equipped with a mechanical stirrer and gas inlet and outlet was charged with 10 mmol of diamine (HAB, DAM or DAP ·2HCl) and 4 mL of NMP. When using DAP ·2HCl, the salt protection of the amino groups was removed with 100 mmol of pyridine. Then, the mixture was cooled to 0 °C and 10 mmol of 6FDA was added followed by 4 mL of NMP. After stirring for 20 min, the solution was left to warm up to room temperature and left overnight. For HAB and DAM, chemical imidization was carried out by adding 8 mmol of acetic anhydride and 8 mmol of pyridine, left 5 h stirring at room temperature and 1 h at 60 °C to ensure the complete imidization. The resulting polymer was cooled down to room temperature and then precipitated in water, washed firstly with water and afterwards with ethanol and then dried in an oven at 150 °C for 12 h under vacuum. For DAP, an azeotropic imidization was carried out by adding 6 mL of o-xylene to the solution as an azeotropic water remover and it was vigorously stirred and heated for 6 h at 180 °C. During this stage, water was released as a xylene azeotrope. After o-xylene was distilled out from the polymer solution, the solution was cooled down to room temperature and poured on water, washed consecutively with water and ethanol, and then dried at 150 °C for 12 h in a vacuum oven. The synthesized polyimides were designated as Pi-HABAc, Pi-DAM, Pi-DAPOH. The proton NMR spectra were as follows:
Pi-HABAc: 1H NMR (400 MHz, DMSO-d6) δ 8.20 (d, 2H), 7.98 (d, 2H), 7.84 s, 2H), 7.81–7.75 (m, 4H), 7.66 (d, 2H), 2.14 (s, 6H).
Pi-DAM: 1H NMR (400 MHz, DMSO-d6) δ 8.21 (d, 2H), 7.99–7.92 (m, 4H), 7.35 (s, 1H), 2.17 (s, 4H), 1.95 (s, 2H).
Pi-DAPOH: 1H NMR (400 MHz, DMSO-d6) δ 10.33 (s, 1H, OH), 8.20 (dd, 2H), 7.97 (d, 2H), 7.81 (dd, 2H), 7.42 (s, 1H), 7.16 (d, 2H).
The membranes were manufactured by the solution casting method. The solvents used and the drying protocol employed are shown in Table 1. For all the polymers, 10% (w/w) solutions were prepared in the corresponding solvent. Then, the solution was filtered through a 3.1 µm fiberglass filter (Symta, Madrid, Spain), casted onto a glass plate and slowly heated for solvent evaporation under established conditions.

Table 1.
Solvents used during the film formation for the studied polymers.
2.2. Gas Separation Transport Properties
A portion of the uniform membrane was loaded into a 25 mm Millipore high-pressure stainless-steel filter holder (Cat. No. XX4502500) (Millipore Corporation, Burlington, MA, USA) as a permeator cell and left one day in vacuum before the measurement, to remove humidity and adsorbed gases in a handmade constant-volume and variable-pressure permeation system. Single gas permeability coefficients (Pi) of He, N2, O2, CH4 and CO2 were measured at 35 °C and upstream pressure of 3 bar. Helium permeability was measured at three different pressures (1, 2 and 3 bar) as a protocol to determine the absence of pinholes. The permeability coefficient is typically expressed in barrer [1 barrer = 10−10 (cm3 (STP) cm)/(cm2 s cmHg) = 7.5005 × 10−18 m2 s2 Pa−1]. It was obtained with the following equation:
Here, L is the thickness of the membranes, V is the downstream volume, T the temperature, pa the pressure of the feed gas, A the effective area and the slope of downstream versus time. The numeric factors refer to standard pressure and temperature (76 cm Hg y 273.15 K). The thicknesses were measured with a Dualscope MP0R (Fischer Technology, Sindelfingen, Baden Wurtenberg, Germany). The ideal selectivity for a determined gas pair of gases was calculated as the ratio of their single gas permeabilities.
Figure 2 shows the Robeson plot exhibiting selectivity, measured as the ratio of permeabilities of the pair of gases to be separated, versus the permeability of the most permeable gas in a double log plot for the pairs He/CH4 and CO2/CH4. The corresponding upper bound straight, as evaluated by Robeson in 2008 [16], is also shown. These kinds of plots are instrumental in assessing the performance of various membrane materials for gas separation applications. Permeability represents the ease with which a specific gas can pass through a membrane, while selectivity reflects the membrane’s ability to distinguish between different gases. The Robeson plots help to create a visualization of the trade-off between these two properties, providing valuable insights into the membrane’s efficiency and guiding the selection of materials for specific gas separation tasks. By plotting the performance of different membranes on a single graph, researchers can rapidly identify the optimal trade-offs and work toward designing membranes with enhanced gas separation capabilities.
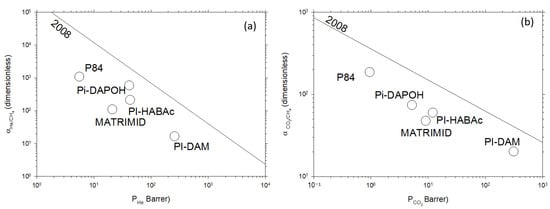
Figure 2.
Robeson’s plots for (a) He/CH4; (b) CO2/CH4 gas pairs for the studied polymers.
The selected membranes, a homologous series of polyimides with rather similar structures, cover a rather wide range of permeability and have selectivities that place their representative points in Robeson’s plots along lines parallel to the successive Robeson limits (selectivities decreasing with permeability increasing), particularly with the 2008 one, as shown in Figure 2.
3. Theory
3.1. Free Volume Fraction
Free volume in a polymer is the portion of the total volume that is not occupied by the polymer chains themselves, allowing for the movement of diffusing molecules. It is typically understood to refer to the spaces or pores between polymer chain segments. The concept is schematically shown in Figure 3. Free volume may depend on the size of the gas molecules permeating the membrane, because free volume should refer to the volume occupiable by the gas molecule to be transported. In our case, all the gases have very similar sizes and all of them should detect similarly small voids opened for transport in such a way that their sizes will not be taken into account to evaluate the free volume.
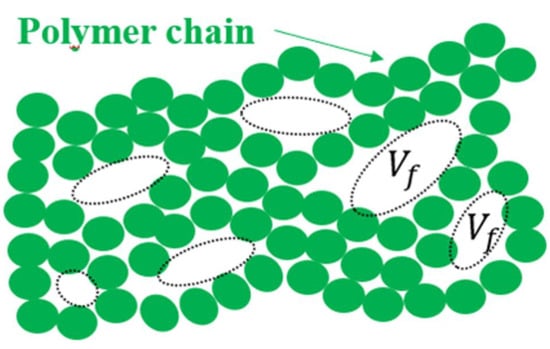
Figure 3.
Scheme of free volume or inter-chain holes contributing to the total free volume.
Densities of the materials can be determined by using a CP225 Analytical Balance from Sartorius (Sartorius, Göttingen, Germany) equipped with a density measurement kit using the Archimedes principle. The Archimedes principle states that a body immersed in a fluid experiments a buoyancy force acting upwards that equals the weight of the fluid displaced by the body. Therefore, the average density can then be obtained as
Here, corresponds to the isooctane’s density, is the sample weight in air and stands for the weight of the sample when submerged in isooctane. This method corresponds to the standard ISO 1183-1/ASTM D792 that requires weighing the samples at room temperature, both in air and convenient liquid. Here, isooctane was chosen as the immersion liquid because it is not absorbed by most polymers, it is not hygroscopic and it does not tend to form bubbles.
The most common method used to evaluate the free volume fraction, FFV, which will be referred to as hereafter for easy notation, can be described as follows:
Here, ( being the density) and is the volume of the chain per unit mass. can be obtained from the van der Waals [11,17,18,19] specific volume, , as
The van der Waals volume can be evaluated by using the Bondi’s group contribution theory [11] or by molecular modeling of the polymer repeating units, with programs like Hyperchem Molecular Modeling (Hypercube, Gainesville, FL, USA) [20,21] or DS BIOVIA Materials Studio software (2023 v23.1.0.3829) (BioVia Dassault Systémes, San Diego, CA, USA) [8,22].
Within the frame of the so-called solution diffusion theory, permeability can be written as (the product of solubility S and diffusivity D). Thornton et al. [23] proposed a dependence of on as given by , Previously, a Doolite type of dependence of D on f (), originally used by Fujita [24] and Lee [25], was accepted. Fractional free volume, f, was moved from the denominator in a Doolittle’s type correlation for the diffusion coefficient to the numerator in the exponent to account for the effect of occupied volume on gas diffusion. Thus, permeability can be written as
Here, we distinguish between the exponential and preexponential factors for diffusivity, and , and those for permeability, and . It can be assumed that Equation (5) holds when the solubility is almost independent of f or depends, like diffusivity, exponentially on f [12]. Several models admit a linear dependence of the exponential constant (α in Equation (5)) on the square of the gas kinetic diameter, dk. These models are based on a reasonable linear dependence of the diffusion activation energy on the transversal area of the penetrant founded, which is reasonable when considering the hard sphere diffusion model wherein diffusion depends on the cross-section area of diffusing molecules [26]. Nevertheless, for the sake of comprehensiveness, a polynomial will be tested here including a linear summand [27]. Thus, using a quadratic polynomial for the constant in the exponent of Equation (5):
The kinetic diameters can be taken from Breck [28], which are widely used. It is true that, as pointed out by Matteucci et al. [29], the value reported as the kinetic diameter by Breck, for example, for CO2, 3.3 Å, is significantly lower than the Lennard–Jones collision diameter (4.05 Å), but Breck himself rationalized this low value on the basis of experimental data of CO2 adsorption on zeolites with known sizes. The shortcomings of Breck’s data have, in fact, led to several alternative proposals of effective molecular sizes leading to different suitable space scales [25,30,31,32]. Nevertheless, here we will use Breck’s kinetic diameters attending to their common usage.
Combining Equations (5) and (6), we obtain
If constants in Equation (6) are assumed as equal for a given ensemble of polymers, the free volume can be referenced to a given polymer by correlating with those of this polymer, and if its free volume fraction is known, we could evaluate all for the polymers in the ensemble [27].
3.2. Glass Transition Temperature
The glass transition temperature, Tg, was determined by using a Differential Scanning Calorimeter DSC 25 from TA Instruments (Waters Co., New Castle, DE, USA). Samples were prepared by encapsulating a single membrane disc using Tzero® Aluminum crucibles from TA Instruments with a nominal mass of 52 mg. Each lid and pan mass were weighted separately with a resolution of ±0.001 mg and were selected to obtain a mass difference between the reference and the empty crucible always lower than ±0.02 mg. Samples, with masses between 0.6 and 2.0 mg, were determined with an error smaller than 0.005 mg. This procedure complies with the instructions of the ISO 11357-2:2020(E) standard. As the glass transition temperatures are high, a preliminary thermal cycle is performed until reaching a temperature high enough to erase the previous thermal history of the material, and afterwards Tg is evaluated in a second heating cycle. The reported Tg are Ti,g (corresponding to the inflection point). All heating and cooling cycles were carried out at a rate of 20 K min−1.
3.3. Intersegmental Distance between Polymer Chains
Wide-angle X-ray scattering (WAXS) was recorded at room temperature by means of a Bruker D8 discover A25 advanced diffractometer equipped with a Goebel mirror with of Cu Kα (λ = 1.542 Å) as the radiation source (Bruker, Billerica, MA, USA). The system worked with a LynxEye detector using a step-scanning mode ranging from 5° to 70° (with time periods of 0.5 s and a 2θ pace of 0.020°). The preferential segmental distance () in the chain-packing of the amorphous polymers was determined using Bragg’s Law according to Equation (8) which refers to Figure 4:
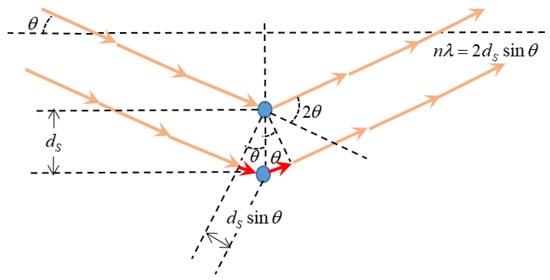
Figure 4.
X-ray diffraction and Bragg’s law.
Here, θ is the scattering angle and, as can be inferred from Figure 4 and Equation (8), smaller angles correspond to longer segmental distances. A plot of the X-ray intensity versus the scattering angle give a certain distribution that, according to Equation (8), for a given wavelength, could be transformed into a distribution. Due to the fact that the polymers tested here are not crystalline, there are wide statistically distributed intersegmental distances showing a most probable that can be taken as representative of the whole distribution of intersegmental distances.
As mentioned, it seems reasonable that an increase in the mean segmental distance would lead to an increase in the gas permeability [33,34]. For example, it is known that the presence of bulky pendant groups in the backbone chain of polymers typically increases with a simultaneous rising of rigidity and permeability [34], although neither the correlation nor any form of analytical correlation has been universally recognized so far. Even some researchers report that does not always correspond to the intermolecular distance governing the diffusivity or permeability of the gas [35].
This work will assume a tentative exponential dependence of permeability on according to
giving a similar dependence to that shown in Equation (5) for on f. Moreover, by analogy with Equation (6), we can assume a quadratic dependence of β on :
Leading to
Analogously to what was deduced from Equation (7), we can see that a plot of permeability as a function of would allow for the evaluation of by assuming now that the parameters in Equation (10) are invariable.
On the other hand,
This relationship states that FFV would be linear with :
Therefore, the free volume fraction should be linear with d-spacing:
With intercept and slope depending on the gas through its kinetic diameter according to Equations (15) and (16), respectively,
Note that the units for the used parameters are
Consequently,
where it is assumed that is the fraction (from 0 to 1) of free volume, and and in Å.
4. Results
4.1. Free Volume
In Figure 5, we show the permeability of CO2, for the membranes that we studied here, as a function of showing the fitted straight line, corresponding to Equation (5). These results for , as obtained by using the Biovia Materials Studio software(DS BIOVIA Materials Studio 2023 v23.1.0.3829), approximately agree with the values collected from the literature when possible [36,37,38]. Molecular dynamics simulations make it possible to estimate FFV by assuming a big enough number of polymer chains that are left to relax inside a box of a given size and using a probe molecule to determine the free volume [39]. This approach allows for accounting for the potential interchain interactions on the packing structure. Additionally, some studies gave comparable values by molecular simulation and via Bondi’s method for free volume fractions [39]. Given that Bondi’s group contributions are not kept truly updated [6,11,40], it seems preferable to use molecular simulations to obtain more accurate estimations of FFV.
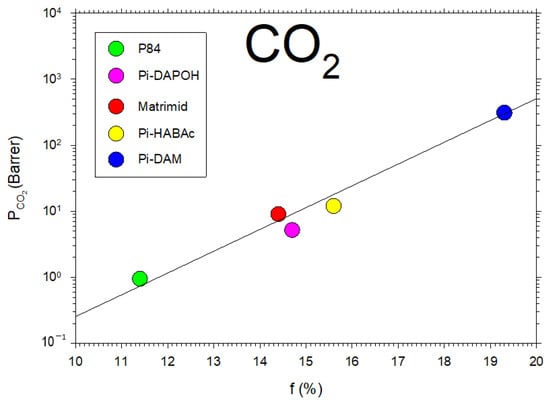
Figure 5.
CO2 permeability versus the free volume for the membranes studied here.
CO2 permeability as a function of the fraction of free volume for several data extracted from the literature [6,41,42,43,44] is shown in Figure 6.
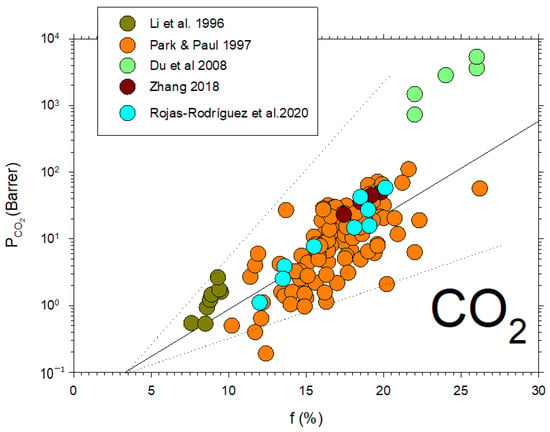
Figure 6.
CO2 permeability versus the free volume fraction from previous literature [6,41,42,43,44].
Figure 7 shows the slope of Figure 5 for CO2 and for the other gases studied here as a function of their kinetic diameter. Note that, in Figure 7, the ordinates correspond to the slope of versus which is proportional to , in accordance with Equations (5) and (7). The constant appears in order to pass from to because and the slope of versus is .
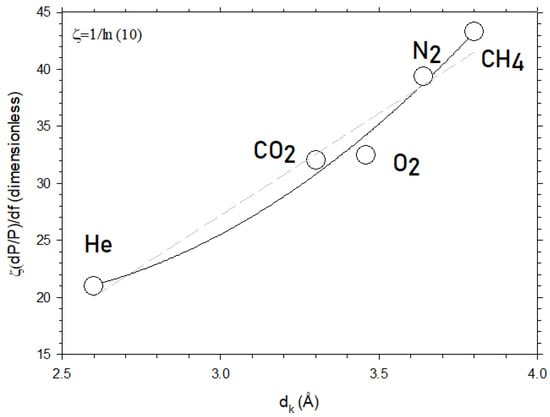
Figure 7.
The slope of ln P for the membranes studied here versus f as a function of dk, i.e., for different kinetic diameters of the permeant. The dashed straight line corresponds to the linear fitting while the continuous line is the best parabolic fitting.
According to Equation (7), this slope should be quadratic with dk, as effectively shown in Figure 7. This confirms that Equation (7) captures the essence of the dependence of permeability on the free volume fraction. Note that the linear dependency could also be possible but with a lower fitting goodness of 0.938 as compared to 0.983 for the quadratic dependence. The values of the parameters of Equation (7) obtained by fitting are shown in Table 2.

Table 2.
Fitted values for the parameters in Equation (7).
4.2. Free Volume Fraction and Glass Transition Temperature
To test the dependence of the glass transition temperature on the fraction of free volume, we plot both of these magnitudes in Figure 8, where it seems clear that they are positively correlated. This dependency is in fact only roughly linear (correlation index < 0.8). This can only be considered as a hint of a tendency of glass transition temperature to increase with free volume or vice versa.
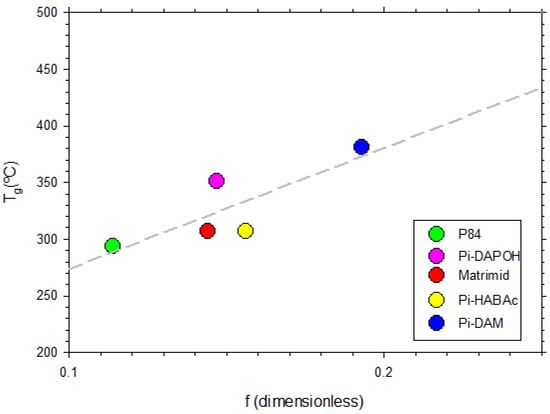
Figure 8.
The glass transition temperature as a function of the free volume fraction. The straight line can only be taken as an eye guide.
It is crucial to keep in mind that we are working with extremely rigid (high Tg) polymers, meaning that chain segments are only given very little mobility. Free volume thus appears as spaces between rigid chains, and more rigid polymers—and occasionally branched ones—are beneficial because they provide larger free volumes and wider pathways for gases to permeate.
4.3. Intersegmental Distance between Polymer Chains
In Figure 9, two examples of d-spacing obtained by WAXS are presented. It is worth noting that they are statistically distributed in accordance with the amorphous nature of polyimides.
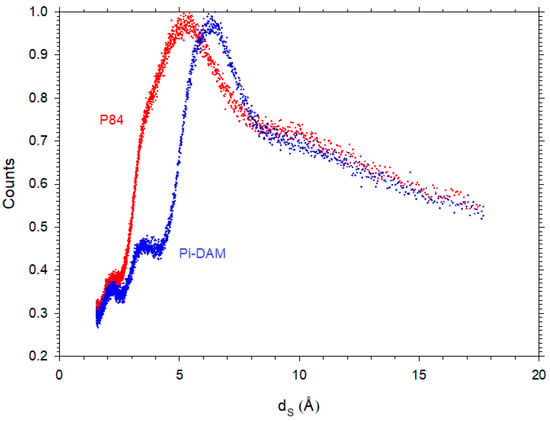
Figure 9.
d-Spacing distribution for P84 and Pi-DAM showing the amorphous nature of our polymers. Note that the counts have been normalized to 1 for the most probable d-spacing.
In Figure 10, the permeability of CO2, for the membranes we studied here, as a function of showing the fitted straight line corresponding to Equation (9), is shown.
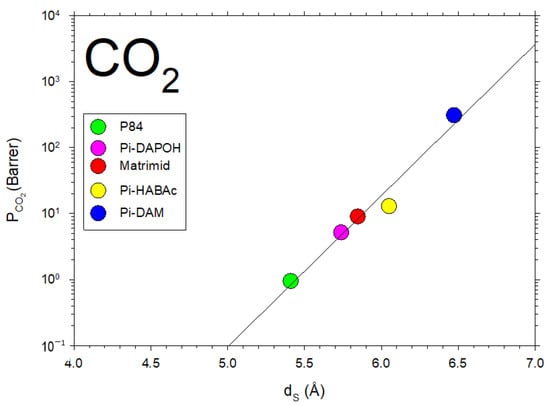
Figure 10.
CO2 permeability as a function of dS for the membranes studied in this article.
Some data from the literature [42,43,44,45,46,47,48,49] on CO2 permeability versus d-spacing are described in Figure 11.
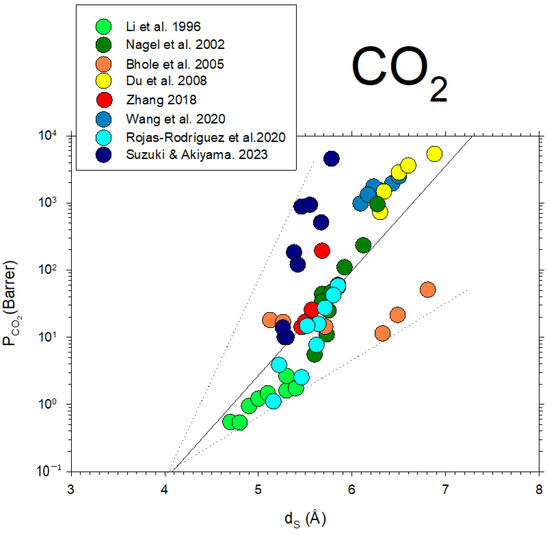
Figure 11.
CO2 permeability as a function of dS from the literature [42,43,44,45,46,47,48,49].
Note that, although in a somehow diffuse way, a certainly linear dependence of on with some divergences could be due to the possible non-homologous series of membranes shown in Figure 11. Better fittings are clearly shown for the membranes studied here, as shown in Figure 10.
In Figure 12, we plot the slope of Figure 10 for CO2 and for the other gases studied here as a function of their kinetic diameter. According to Equation (11), this slope should be quadratic with dk, as effectively shown in Figure 12. Note that the linear dependency could also be possible but with a lower fitting goodness of 0.925, as compared to 0.998 for the quadratic dependence.
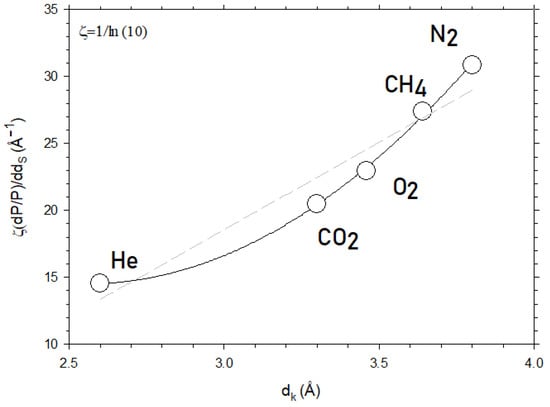
Figure 12.
The slope of ln P versus dS as a function of dk, i.e., for different kinetic diameters of the permeant. The dashed straight line corresponds to the linear fitting while the continuous line is the best parabolic fitting.
In Figure 12, the ordinates correspond to the slope of versus , which is proportional to in accordance with Equations (9) and (11). The constant appears in order to pass from tobecause and the slope of versus is . The values of the parameters of Equation (11) obtained by fitting are shown in Table 3.

Table 3.
Fitted values for the parameters in Equation (11).
4.4. Fractional Free Volume and d-Spacing
Some data from the literature [42,44,45,50,51,52,53] on the free volume fraction versus d-spacing are shown in Figure 13, where it is seen that there is an average linear trend according to Equation (14).
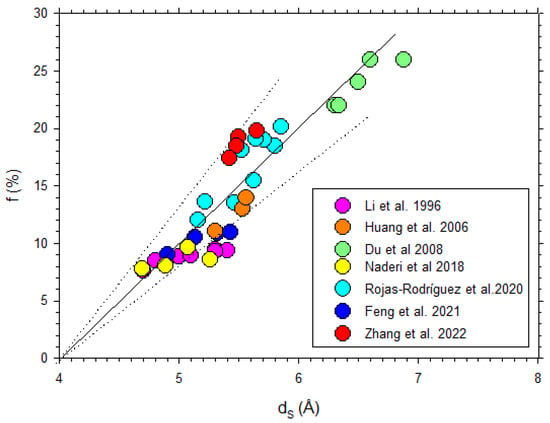
Figure 13.
Fractional free volume as a function of from previous literature [42,44,45,50,51,52,53].
Figure 14 shows versus for our polyimide membranes showing a clear linear dependence.
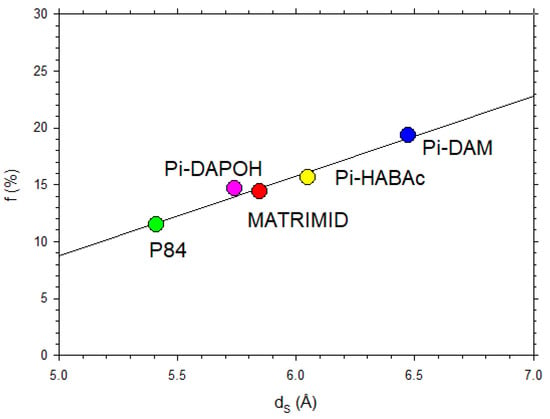
Figure 14.
Fractional free volume as a function of for the membranes studied in this article.
Equations (15) and (16) state that would depend on the permeated gas. In our case, the free volume has been evaluated without taking into account the fraction of void volume effectively accessible to each gas; therefore, the constants and would not depend on . This, attending to Equations (15) and (16), would mean that
In fact, the fitted straight line in Figure 13 corresponds to
While the corresponding ratios of the parameters of Equations (7) and (11) are, according to Table 1 and Table 2,
The accordance means that, in , the slope does not depend on . The ordinate intercept does not depend on either because and depend on , approximately compensating for the dependence of the denominator. In fact, the extreme values of are −0.24 and −0.30, which averaged give −0.27, and this compares nicely to the ordinate intercept in Equation (20).
5. Conclusions
It has been analyzed how free volume fraction, intersegmental distance and glass transition temperature are correlated to each other and with gas permeability for several simple gases including He, CO2, O2, CH4 and N2. This was achieved by using a series of similar polyimides covering a wide range of permeabilities from rather low to very high ones.
In effect, it has been proved that the correlation of permeability with free volume fraction and intersegmental distance are both rather similar exponentials, indicating that permeability increases exponentially with both the free volume fraction and the intersegmental distance. It has also been shown that the pre-multiplicative factors in the exponents depend, in both cases, on the kinetic gas diameter as a quadratic polynomial. Positive preexponential elements are present in both relationships.
It is important to point out that no theoretical background has been proposed for these correlations here. Specifically for the quadratic dependence of on , while no theory had been proposed in the literature for the dependence of permeability on d-spacing. But the correlations tested here have at least a clear phenomenological value. While a convenient justification could be rather interesting, it was not our objective here.
It is worth noting that, because the polymers tested here are amorphous, there are relatively wide statistical distributions for the intersegmental distances that lead to not sharply defined d-spacing values. Moreover, it is also worth considering that free volume is a somehow ambiguous concept that has here been taken as defined by the voids left between the polymer backbones and evaluated by molecular dynamics and density measurements. These factors can explain the difficulties in detecting the dependencies tested here within the literature on the topic. It is also clear that the long-range dependencies can coexist with short-range ones with rather different behaviors, especially when taking into account data from different sources and for rather different polymers.
It has been also confirmed that free volume fraction and intersegmental distance are both linearly positively dependent on each other. This means that there are specific correlations, that have been tested here, between the constants involved in both exponentials.
The existence of monotonous increasing correlations between permeability and free volume fraction and intersegmental distance seems reasonable and has been made plausible in the literature but was never analyzed in depth. The relevance of such correlations is clear when designing polymers for gas separation and should clarify the structure versus function of gas transport through polymeric membranes. With this objective, the correlations shown here should be tested for the specific class of polymers to be used. Of course, some of the details of these relationships should be specific for the polymers studied, but although the details could differ, in our opinion the general trends must be true for any analogous polymeric series, probably excluding polymers with strong affinities for the penetrant.
To conclude, it has been shown that the glass temperature increases with the free volume fraction in our case. Of course, this complies with the largely admitted idea of obtaining higher permeabilities for more rigid glassy polymers. This correlation was never clearly analyzed and could depend on the class of polymers studied.
Author Contributions
Conceptualization and methodology, A.H. and P.P.; software, A.H.; validation, A.T. (Alberto Tena), A.H. and L.P.; investigation, A.T. (Alba Torres), J.C., M.d.l.V. and C.S.; resources, R.M., B.C.-G., M.T.S., I.S. and L.P.; data curation, A.T. (Alba Torres); writing—original draft preparation, A.T. (Alba Torres); writing—review and editing, A.H., P.P. and A.T. (Alba Torres); visualization, A.H. and A.T. (Alba Torres); supervision, A.H.; project administration, A.T. (Alberto Tena); funding acquisition B.C.-G. and R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Project TED2021-131170A-I00 financed by MCIN/AEI /10.13039/501100011033 and by the European Union Next Generation EU/PRTR. We are also grateful to the ECLOSION project MIG-202111071 (Mission 2, Spanish “Plan Estatal I+D+I”), funded by Next Generation EU as well. We are grateful as well to the Regional Government of Castilla y León and the EU-FEDER initiative for their programs CL-EI-2021-07 and UIC082.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
All the relevant data for the research here shown are included within the paper.
Conflicts of Interest
Author María Teresa Simorte and Inmaculada Sanz were employed by the company FCC Medio Ambiente. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Chowdhury, G.; Kruczek, B.; Matsuura, T. Polyphenylene Oxide and Modified Polyphenylene Oxide Membranes. Gas, Vapor and Liquid Separation, 1st ed.; Springer: New York, NY, USA, 2001; ISBN 978-1-4615-1483-1. [Google Scholar]
- Stadler, F.J.; Takahashi, T.; Yonetake, K. Lattice Sizes, Crystallinities, and Spacing between Amorphous Chains—Characterization of Ethene-α-Olefin Copolymers with Various Comonomers and Comonomer Contents Measured by Wide Angle X-ray Scattering. e-Polymers 2009, 9, 1–19. [Google Scholar] [CrossRef]
- Lasseuguette, E.; Malpass-Evans, R.; Carta, M.; McKeown, N.B.; Ferrari, M.-C. Temperature and Pressure Dependence of Gas Permeation in a Microporous Tröger’s Base Polymer. Membranes 2018, 8, 132. [Google Scholar] [CrossRef] [PubMed]
- Sandhya, P.K.; Lakshmipriya, R.; Sreekala, M. Gas Permeability through Thermosets. In Transport Properties of Polymeric Membranes; Thomas, S., Wilson, R., Kumar, A., Goerge, S., Eds.; Elservier: Amsterdam, The Netherlands, 2018; pp. 475–516. ISBN 978-0-12-809884-4. [Google Scholar]
- Bas, C.; Mercier, R.; Dauwe, C.; Albérola, N.D. Microstructural Parameters Controlling Gas Permeability and Permselectivity in Polyimide Membranes. J. Memb. Sci. 2010, 349, 25–34. [Google Scholar] [CrossRef]
- Park, J.Y.; Paul, D.R. Correlation and Prediction of Gas Permeability in Glassy Polymer Membrane Materials via a Modified Free Volume Based Group Contribution Method. J. Memb. Sci. 1997, 125, 23–39. [Google Scholar] [CrossRef]
- Soto, C.; Torres-Cuevas, E.S.; Palacio, L.; Prádanos, P.; Freeman, B.D.; Lozano, Á.E.; Hernández, A.; Comesaña-Gándara, B. Gas Permeability, Fractional Free Volume and Molecular Kinetic Diameters: The Effect of Thermal Rearrangement on Ortho-Hydroxy Polyamide Membranes Loaded with a Porous Polymer Network. Membranes 2022, 12, 200. [Google Scholar] [CrossRef] [PubMed]
- Soto, C.; Carmona, J.; Freeman, B.D.; Palacio, L.; González-Ortega, A.; Prádanos, P.; Lozano, Á.E.; Hernandez, A. Free Volume and Permeability of Mixed Matrix Membranes Made from a Terbutil-M-Terphenyl Polyamide and a Porous Polymer Network. Polymers 2022, 14, 3176. [Google Scholar] [CrossRef]
- Soto, C.; Comesaña-Gandara, B.; Marcos, Á.; Cuadrado, P.; Palacio, L.; Lozano, Á.E.; Álvarez, C.; Prádanos, P.; Hernandez, A. Thermally Rearranged Mixed Matrix Membranes from Copoly(o-Hydroxyamide)s and Copoly(o-Hydroxyamide-Amide)s with a Porous Polymer Network as a Filler—A Comparison of Their Gas Separation Performances. Membranes 2022, 12, 998. [Google Scholar] [CrossRef]
- Soto, C.; Cicuttin, N.; Carmona, F.J.; de la Viuda, M.; Tena, A.; Lozano, E.; Hernández, A.; Palacio, L.; Prádanos, P. Gas Adsorption Isotherm, Pore Size Distribution, and Free Volume Fraction of Polymer-Polymer Mixed Matrix Membranes before and after Thermal Rearrangement. J. Memb. Sci. 2023, 683, 1841. [Google Scholar] [CrossRef]
- Van Krevelen, D.W.; Te Nijenhuis, K. Properties of Polymers. Their Correlation with Chemical Structure. In Their Numerical Estimation and Prediction from Additive Group Contributions, 4th ed.; Elservier: Amsterdam, The Netherlands, 2009; ISBN 978-0-08-054819-7. [Google Scholar]
- Hensema, E.R.; Mulder, M.H.V.; Smolders, C.A. On the Mechanism of Gas Transport in Rigid Polymer Membranes. J. Appl. Polym. Sci. 1993, 49, 2081–2090. [Google Scholar] [CrossRef]
- White, R.P.; Lipson, J.E.G. Polymer Free Volume and Its Connection to the Glass Transition. Macromolecules 2016, 49, 3987–4007. [Google Scholar] [CrossRef]
- Comesaña-Gándara, B.; De La Campa, J.G.; Hernández, A.; Jo, H.J.; Lee, Y.M.; De Abajo, J.; Lozano, A.E. Gas Separation Membranes Made through Thermal Rearrangement of Ortho-Methoxypolyimides. RSC Adv. 2015, 5, 102261–102276. [Google Scholar] [CrossRef]
- Comesaña-Gándara, B.; Hernández, A.; de la Campa, J.G.; de Abajo, J.; Lozano, A.E.; Lee, Y.M. Thermally Rearranged Polybenzoxazoles and Poly(Benzoxazole-Co-Imide)s from Ortho-Hydroxyamine Monomers for High Performance Gas Separation Membranes. J. Memb. Sci. 2015, 493, 329–339. [Google Scholar] [CrossRef]
- Robeson, L.M. The Upper Bound Revisited. J. Memb. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Bondi, A. Van Der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Bondi, A. Physical Properties of Molecular Crystals, Liquids and Glasses; John Wiley & Sons: New York, NY, USA, 1968. [Google Scholar]
- Horn, N.R. A Critical Review of Free Volume and Occupied Volume Calculation Methods. J. Memb. Sci. 2016, 518, 289–294. [Google Scholar] [CrossRef]
- Hypercube Inc. HyperChem Professional. Available online: http://www.hypercubeusa.com/ (accessed on 13 December 2023).
- Díez, B.; Cuadrado, P.; Marcos-Fernández, Á.; de la Campa, J.G.; Tena, A.; Prádanos, P.; Palacio, L.; Lee, Y.M.; Alvarez, C.; Lozano, Á.E.; et al. Thermally Rearranged Polybenzoxazoles Made from Poly(Ortho-Hydroxyamide)s. Characterization and Evaluation as Gas Separation Membranes. React. Funct. Polym. 2018, 127, 38–47. [Google Scholar] [CrossRef]
- Dassault Systèmes BIOVIA Materials Studio. Available online: https://www.3ds.com/es/productos-y-servicios/biovia/ (accessed on 13 December 2023).
- Thornton, A.W.; Nairn, K.M.; Hill, A.J.; Hill, J.M. New Relation between Diffusion and Free Volume: I. Predicting Gas Diffusion. J. Memb. Sci. 2009, 338, 29–37. [Google Scholar] [CrossRef]
- Fujita, H. Diffusion in Polymer-Diluent Systems. In Fortschritte der Hochpolymeren-Forschung; Springer: Berlin/Heidelberg, Germany, 1961; pp. 1–47. [Google Scholar]
- Lee, W.M. Selection of Barrier Materials from Molecular Structure. Polym. Eng. Sci. 1980, 20, 65–69. [Google Scholar] [CrossRef]
- Cohen, M.H.; Turnbull, D. Molecular Transport in Liquids and Glasses. J. Chem. Phys. 1959, 31, 1164–1169. [Google Scholar] [CrossRef]
- Soto, C.; Torres-Cuevas, E.S.; González-Ortega, A.; Palacio, L.; Lozano, Á.E.; Freeman, B.D.; Prádanos, P.; Hernández, A. Gas Separation by Mixed Matrix Membranes with Porous Organic Polymer Inclusions within O-Hydroxypolyamides Containing m-Terphenyl Moieties. Polymers 2021, 13, 931. [Google Scholar] [CrossRef]
- Breck, D.W. Zeolite Molecular Sieves: Structure, Chemistry and Use. Anal. Chim. Acta 1975, 75, 493. [Google Scholar] [CrossRef]
- Matteucci, S.; Yampolskii, Y.; Freeman, B.D.; Pinnau, I. Transport of Gases and Vapors in Glassy and Rubbery Polymers. In Materials Science of Membranes for Gas and Vapor Separation; Yampolskii, Y., Pinnau, I., Freeman, B., Eds.; John Wiley & Sons: Berlin, Germany, 2006; pp. 1–47. [Google Scholar]
- Teplyakov, V.V.; Durgar’yan, S.G. Correlation Analysis of the Gas Permeability Parameters of Polymers. Polym. Sci. USSR 1984, 26, 1498–1505. [Google Scholar] [CrossRef]
- Teplyakov, V.; Meares, P. Correlation Aspects of the Selective Gas Permeabilities of Polymeric Materials and Membranes. Gas Sep. Purif. 1990, 4, 66–74. [Google Scholar] [CrossRef]
- Reynier, A.; Dole, P.; Humbel, S.; Feigenbaum, A. Diffusion Coefficients of Additives in Polymers. I. Correlation with Geometric Parameters. J. Appl. Polym. Sci. 2001, 82, 2422–2433. [Google Scholar] [CrossRef]
- McCormick, H.W.; Brower, F.M.; Kin, L. The Effect of Molecular Weight Distribution on the Physical Properties of Polystyrene. J. Polym. Sci. 1959, 39, 87–100. [Google Scholar] [CrossRef]
- Ismail, A.F.; Khulbe, K.C.; Matsuura, T. Gas Separation Membranes: Polymeric and Inorganic, 1st ed.; Springer Cham: New York, NY, USA, 2015; ISBN 978-3-319-01095-3. [Google Scholar]
- Shimazu, A.; Miyazaki, T.; Ikeda, K. Interpretation of D-Spacing Determined by Wide Angle X-ray Scattering in 6FDA-Based Polyimide by Molecular Modeling. J. Memb. Sci. 2000, 166, 113–118. [Google Scholar] [CrossRef]
- Tin, P.S.; Chung, T.-S.; Liu, Y.; Wang, R. Separation of CO2/CH4 through Carbon Molecular Sieve Membranes Derived from P84 Polyimide. Carbon N. Y. 2004, 42, 3123–3131. [Google Scholar] [CrossRef]
- Xu, S.; Ren, X.; Zhao, N.; Wu, L.; Zhang, Z.; Fan, Y.; Li, N. Self-Crosslinking of Bromomethylated 6FDA-DAM Polyimide for Gas Separations. J. Memb. Sci. 2021, 636, 119534. [Google Scholar] [CrossRef]
- Mazinani, S.; Ramezani, R.; Molelekwa, G.F.; Darvishmanesh, S.; Di Felice, R.; Van der Bruggen, B. Plasticization Suppression and CO2 Separation Enhancement of Matrimid through Homogeneous Blending with a New High Performance Polymer. J. Memb. Sci. 2019, 574, 318–324. [Google Scholar] [CrossRef]
- Abdulhamid, M.A.; Genduso, G.; Wang, Y.; Ma, X.; Pinnau, I. Plasticization-Resistant Carboxyl-Functionalized 6FDA-Polyimide of Intrinsic Microporosity (PIM-PI) for Membrane-Based Gas Separation. Ind. Eng. Chem. Res. 2020, 59, 5247–5256. [Google Scholar] [CrossRef]
- Wu, A.X.; Lin, S.; Rodriguez, K.M.; Benedetti, F.M.; Joo, T.; Grosz, A.F.; Storme, K.R.; Roy, N.; Syar, D.; Smith, Z.P. Revisiting Group Contribution Theory for Estimating Fractional Free Volume of Microporous Polymer Membranes. J. Memb. Sci. 2021, 636, 119526. [Google Scholar] [CrossRef]
- Yampolskii, Y. Polymeric Gas Separation Membranes. Macromolecules 2012, 45, 3298–3311. [Google Scholar] [CrossRef]
- Du, N.; Robertson, G.P.; Song, J.; Pinnau, I.; Thomas-Droz, S.; Guiver, M.D. Polymers of Intrinsic Microporosity Containing Trifluoromethyl and Phenylsulfone Groups as Materials for Membrane Gas Separation. Macromolecules 2008, 41, 9656–9662. [Google Scholar] [CrossRef]
- Zhang, C.; Cao, B.; Li, P. Thermal Oxidative Crosslinking of Phenolphthalein-Based Cardo Polyimides with Enhanced Gas Permeability and Selectivity. J. Memb. Sci. 2018, 546, 90–99. [Google Scholar] [CrossRef]
- Rojas-Rodríguez, M.; Aguilas-Lugo, C.; Lozano, Á.E.; Hernández, A.; Mancilla-Cetina, E.; Alexandrova, L. Synthesis and Properties of Highly Processable Asymmetric Polyimides with Bulky Phenoxy Groups. High Perform. Polym. 2019, 32, 455–468. [Google Scholar] [CrossRef]
- Li, Y.; Ding, M.; Xu, J. Structure/Permeability and Permselectivity Relathionship of Polyetherimides from 1,4-Bis(3,4-Dicarboxyphenoxy)Benzene Dianhydride. Eur. Polym. J. 1996, 32, 1313–1317. [Google Scholar] [CrossRef]
- Nagel, C.; Günther-Schade, K.; Fritsch, D.; Strunskus, T.; Faupel, F. Free Volume and Transport Properties in Highly Selective Polymer Membranes. Macromolecules 2002, 35, 2071–2077. [Google Scholar] [CrossRef]
- Bhole, Y.S.; Kharul, U.K.; Somani, S.P.; Kumbharkar, S.C. Benzoylation of Polyphenylene Oxide: Characterization and Gas Permeability Investigations. Eur. Polym. J. 2005, 41, 2461–2471. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, Q.; Liang, J.; Zhang, Y.; Jin, J. Adamantane-Grafted Polymer of Intrinsic Microporosity with Finely Tuned Interchain Spacing for Improved CO2 Separation Performance. Sep. Purif. Technol. 2020, 233, 116008. [Google Scholar] [CrossRef]
- Suzuki, T.; Akiyama, R. Unexpected Permeability Enhancement of Thermally Rearranged (TR) Copolybenzoxazole Membranes. Mater. Today Commun. 2023, 35, 106120. [Google Scholar] [CrossRef]
- Feng, F.; Liang, C.-Z.; Wu, L.; Weber, M.; Maletzko, C.; Zhang, S.; Chung, T. Polyphenylsulfone (PPSU)-Based Copolymeric Membranes: Effects of Chemical Structure and Content on Gas Permeation and Separation. Polymers 2021, 13, 2745. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.H.; Hu, C.C.; Lee, K.R.; Liaw, D.J.; Lai, J.Y. Gas Separation Properties of Aromatic Poly(Amide-Imide) Membranes. Eur. Polym. J. 2006, 42, 140–148. [Google Scholar] [CrossRef]
- Zhang, B.; Qiao, J.; Wu, D.; He, X.; Liu, J.; Yi, C.; Qi, S. Enhanced Gas Separation by Free Volume Tuning in a Crown Ether-Containing Polyimide Membrane. Sep. Purif. Technol. 2022, 293, 121116. [Google Scholar] [CrossRef]
- Naderi, A.; Yong, W.F.; Xiao, Y.; Chung, T.S.; Weber, M.; Maletzko, C. Effects of Chemical Structure on Gas Transport Properties of Polyethersulfone Polymers. Polymer 2018, 135, 76–84. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).