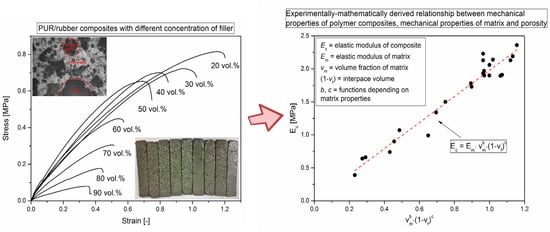
The Influence of Porosity on Mechanical Properties of PUR-Based Composites: Experimentally Derived Mathematical Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
2.3. Characterization Methods
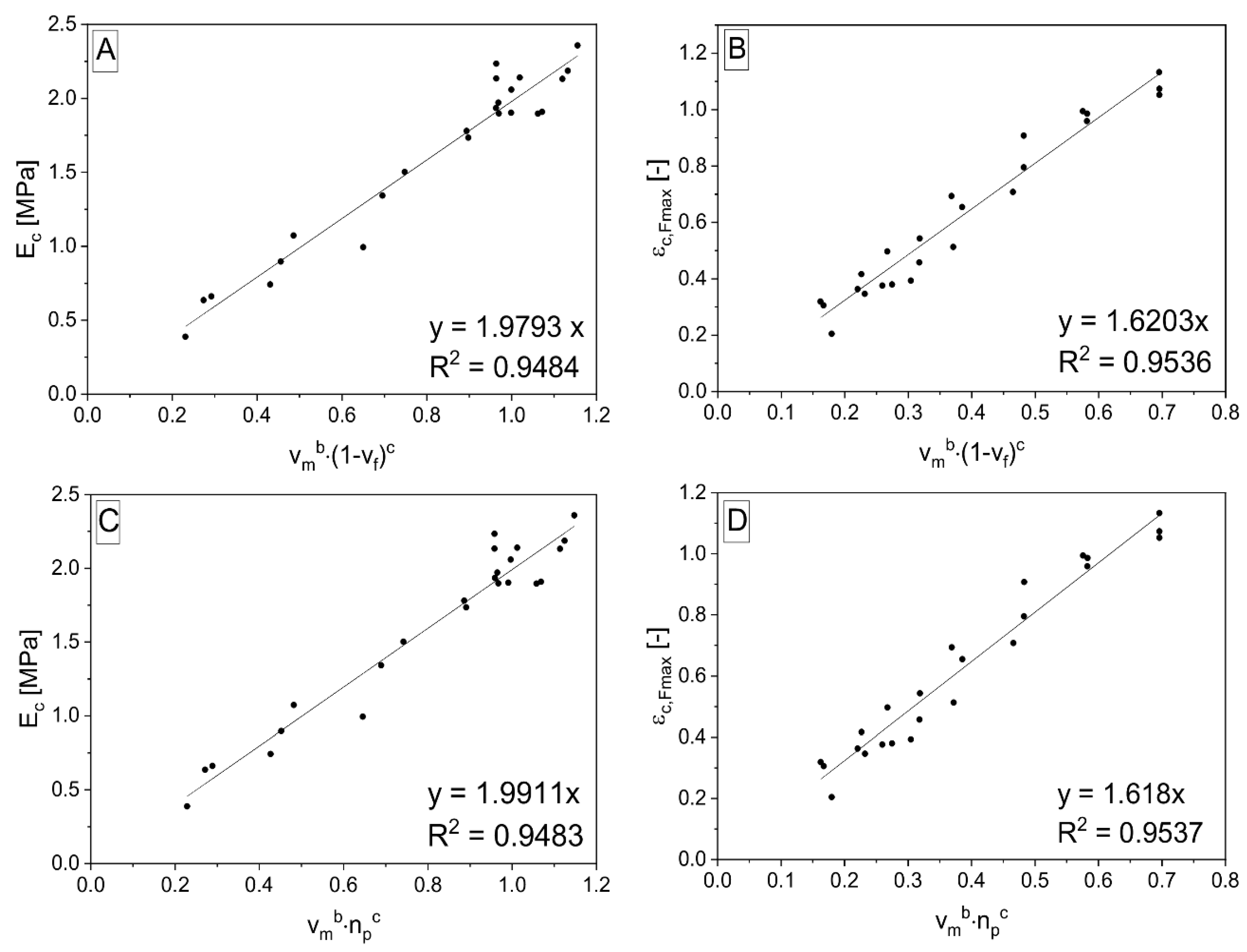
2.4. Basics for Data Processing
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Choren, J.A.; Heinrich, S.M.; Silver-Thorn, M.B. Young’s modulus and volume porosity relationships for additive manufacturing applications. J. Mater. Sci. 2013, 48, 5103–5112. [Google Scholar] [CrossRef]
- Krishna, V.; Bose, S.; Bandyopadhyay, A. Low stiffness porous Ti structures for load-bearing implants. Acta Biomater. 2007, 3, 997–1006. [Google Scholar] [CrossRef] [PubMed]
- Rubshtein, A.P.; Trakhtenberg, I.S.; Makarova, E.B.; Triphonova, E.B.; Bliznets, D.G.; Yakovenkova, L.I.; Vladimirov, A.B. Porous material based on spongy titanium granules: Structure, mechanical properties, and osseointegration. Mat. Sci. Eng. C-Mater. 2014, 35, 363–369. [Google Scholar] [CrossRef] [PubMed]
- Kovacik, J. Correlation between shear modulus and porosity in porous materials. J. Mater. Sci. Lett. 2001, 20, 1953–1955. [Google Scholar] [CrossRef]
- Lian, C.; Zhuge, Y.; Beecham, S. The relationship between porosity and strength for porous concrete. Constr. Build. Mater. 2011, 25, 4294–4298. [Google Scholar] [CrossRef]
- Fan, X.; Case, E.D.; Ren, F.; Shu, Y.; Baumann, M.J. Part II: Fracture strength and elastic modulus as a function of porosity for hydroxyapatite and other brittle materials. J. Mech. Behav. Biomed. 2012, 8, 99–110. [Google Scholar] [CrossRef]
- Karthikeyan, S.; Balasubramanian, V.; Rajendran, R. Developing empirical relationships to estimate porosity and Young’s modulus of plasma sprayed YSZ coatings. Appl. Surf. Sci. 2014, 296, 31–46. [Google Scholar] [CrossRef]
- Kovacik, J. Correlation between Young’s modulus and porosity in porous materials. J. Mater. Sci. Lett. 1999, 18, 1007–1010. [Google Scholar] [CrossRef]
- Kovacik, J. Correlation between elastic modulus, shear modulus, Poisson’s ratio and porosity in porous materials. Adv. Eng. Mater. 2008, 10, 250–252. [Google Scholar] [CrossRef]
- Smolin, L.Y.; Eremin, M.O.; Makarov, M.P.; Evtushenko, E.P.; Kulkov, S.N.; Buyakova, S.P. Brittle Porous Material Mesovolume Structure Models and Simulation of their Mechanical Properties. AIP Conf. Proc. 2014, 1623, 595–598. [Google Scholar] [CrossRef]
- Werner, J.; Aneziris, C.G.; Schaffoner, S. Influence of porosity on Young’s modulus of carbon-bonded alumina from room temperature up to 1450 °C. Ceram. Int. 2014, 40, 14439–14445. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, K.W.; Elias, A.; Dong, Z.G.; Chen, W.X. Porosity dependence of elastic modulus of porous Cr3C2 ceramics. Ceram. Int. 2014, 40, 191–198. [Google Scholar] [CrossRef]
- Sapozhnikov, S.B.; Kudryavtsev, O.A.; Dolganina, N.Y. Experimental and numerical estimation of strength and fragmentation of different porosity alumina ceramics. Mater. Design 2015, 88, 1042–1048. [Google Scholar] [CrossRef]
- Wu, Z.; Sun, L.C.; Wang, J.Y. Synthesis and characterization of porous Y2SiO5 with low linear shrinkage, high porosity and high strength. Ceram. Int. 2016, 42, 14894–14902. [Google Scholar] [CrossRef]
- Sonnenschein, M.F. Porosity-Dependent Young’s Modulus of Membranes from Polyetherether Ketone. J. Polym. Sci. Pol. Phys. 2003, 41, 1168–1174. [Google Scholar] [CrossRef]
- Palchik, V. Influence of porosity and elastic modulus on uniaxial compressive strength in soft brittle porous sandstones. Rock Mech. Rock Eng. 1999, 32, 303–309. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Easterling, K.E. Structure and mechanics of the iris leaf. J. Mater. Sci. 1988, 23, 3041–3048. [Google Scholar] [CrossRef]
- Nielsen, L.F. Elasticity and damping of porous materials and impregnated materials. J. Am. Ceram. Soc. 1984, 67, 93–98. [Google Scholar] [CrossRef]
- Huiru, X.; Quizhen, S. Deformation mechanisms and mechanical properties of porous magnesium/carbon nanofiber composites with different porosities. J. Mater. Sci. 2018, 53, 14375–14385. [Google Scholar] [CrossRef]
- Wagh, A.S.; Poeppel, R.B.; Singh, J.P. Open pore description of mechanical properties of ceramics. J. Mater. Sci. 1991, 26, 3862–3868. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, Y.F. Compressive Strength of Fractal-Textured Foamed Concrete. Fractals 2019, 27, 1940003. [Google Scholar] [CrossRef]
- Bruck, H.A.; Rabin, B.H. Evaluating microstructural and damage effects in rule-of-mixtures predictions of the mechanical properties of Ni-Al2O3 composites. J. Mater. Sci. 1999, 34, 2241–2251. [Google Scholar] [CrossRef]
- Chao, X.J.; Tian, W.L.; Xu, F.; Shou, D.H. A fractal model of effective mechanical properties of porous composites. Compos. Sci. Technol. 2021, 213, 108957. [Google Scholar] [CrossRef]
- Katsube, N.; Wu, Y.N. A constitutive theory for porous composite materials. Int. J. Solids Struct. 1998, 35, 4587–4596. [Google Scholar] [CrossRef]
- Xu, H.; Li, Q. Effect of carbon nanofiber concentration on mechanical properties of porous magnesium composites: Experimental and theoretical analysis. Mater. Sci. Eng. A 2017, 706, 249–255. [Google Scholar] [CrossRef]
- Odhiambo, J.O.; Yoshida, M.; Otsu, A.; Yi, L.-F.; Onda, T.; Chen, Z.-C. Microstructure and tensile properties of in-situ synthesized and hot-extruded aluminum-matrix composites reinforced with hybrid submicron-sized ceramic particles. J. Compos. Mater. 2022, 56, 1987–2001. [Google Scholar] [CrossRef]
- Poh, L.; Della, C.; Ying, S.; Goh, C.; Li, Y. Micromechanics model for predicting effective elastic moduli of porous ceramic matrices with randomly oriented carbon nanotube reinforcements. AIP Adv. 2015, 5, 097153. [Google Scholar] [CrossRef]
- Alam, P. A mixtures model for porous particle-polymer composites. Mech. Res. Commun. 2010, 37, 389–393. [Google Scholar] [CrossRef]
- Choi, H.K.; Son, M.J.; Shin, E.S.; Yu, J. Prediction of thermos-poro-elastic properties of porous composites using an expanded unmixing-mixing model. Compos. Struct. 2018, 188, 387–393. [Google Scholar] [CrossRef]
- Chan, C.; Naguib, H.E. Development and Characterization of Polypyrrole-Polylactide Conductive Open-Porous Composites. J. Appl. Polym. Sci. 2010, 117, 3187–3195. [Google Scholar] [CrossRef]
- Tran, A.T.; Le Quang, H.; He, Q.-C. Computation of the size-dependent elastic moduli of nano-fibrous and nano-porous composites by FFT. Compos. Sci. Technol. 2016, 135, 159–171. [Google Scholar] [CrossRef]
- Khoroshun, L.P.; Shikula, E.N. Nonlinear Straining of Porous Composite Materials. Int. Appl. Mech. 1993, 29, 983–988. [Google Scholar] [CrossRef]
- Cerny, M.; Petrus, J.; Kucera, F.; Pavlinakova, V.; Kupka, V.; Polacek, P.; Chamradova, I. A new approach to the structure-properties relationship evaluation for porous polymer composites. SN Appl. Sci. 2020, 2, 640. [Google Scholar] [CrossRef]
- Keleş, Ö.; Anderson, E.H.; Huynh, J.; Gelb, J.; Freund, J.; Karakoç, A. Stochastic fracture of additively manufactured porous composites. Sci. Rep. 2018, 8, 15437. [Google Scholar] [CrossRef]
- Teng, J.; Yang, B.; Zhang, L.-Q.; Lin, S.-Q.; Xu, L.; Zhong, G.-J.; Tang, J.-H.; Li, Z.-M. Ultra-high mechanical properties of porous composites based on regenerated cellulose and cross-linked poly(ethylene glycole). Carbohydr. Polym. 2018, 179, 244–251. [Google Scholar] [CrossRef]
- Węgrzyk, S.; Herman, D. Strengthening of Al2O3 porous composites with a glass-ceramic binder doped with nanocopper. J. Eur. Ceram. 2021, 41, 5558–5569. [Google Scholar] [CrossRef]
- Olmos, L.; Gonzalés-Pedraza, A.S.; Vergara-Hernández, H.J.; Chávez, J.; Jimenez, O.; Mihalcea, E.; Arteaga, D.; Ruiz-Mondragón, J.J. Ti64/20Ag Porous Composites Fabricated by Powder Metallurgy for Biomedical Applications. Materials 2022, 15, 5956. [Google Scholar] [CrossRef]
- Seuba, J.; Maire, E.; Adrien, J.; Meille, S.; Deville, S. Mechanical properties of unidirectional porous polymer/ceramic composites for biomedical applications. Open Ceram. 2021, 8, 100195. [Google Scholar] [CrossRef]
- Yeboah, A.; Ying, S.; Lu, J.; Xie, Y.; Amoanimaa-Dede, H.; Boateng, K.G.A.; Chen, M.; Yin, X. Castor oil (Ricinus communis): A review on the chemical composition and physicochemical properties. Food. Sci. Technol. 2021, 41, 399–413. [Google Scholar] [CrossRef]
- Vereshchagin, A.G.; Novitskaya, G.V. The triglyceride composition of linseed oil. J. Am. Oil Chem. Soc. 1965, 42, 970–974. [Google Scholar] [CrossRef]

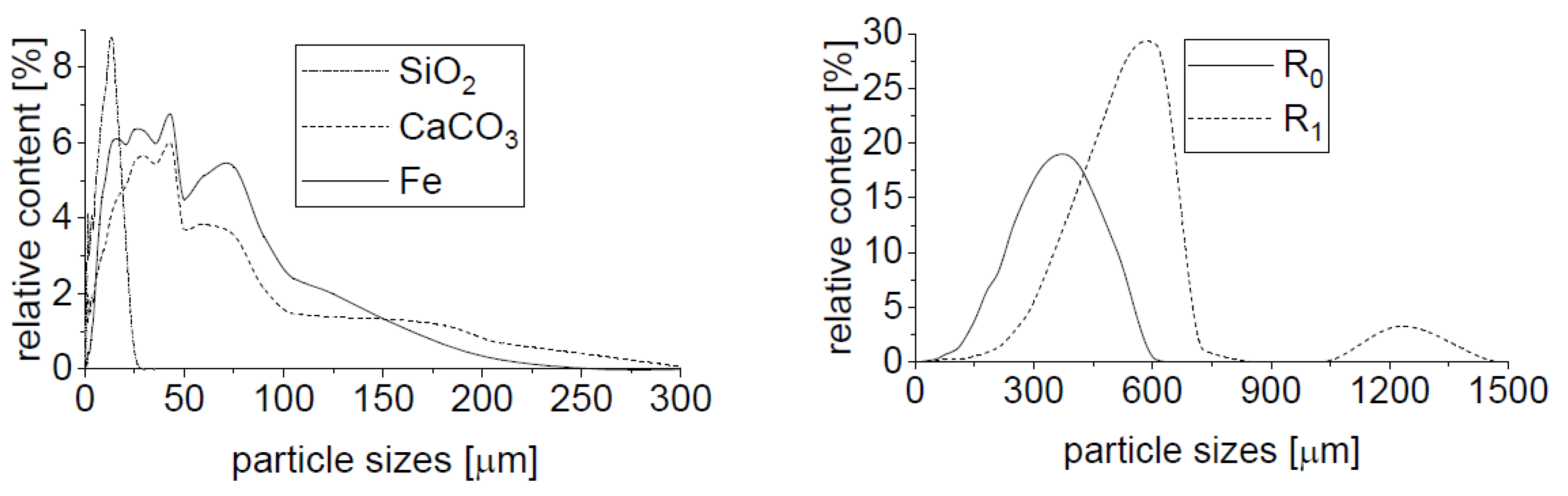



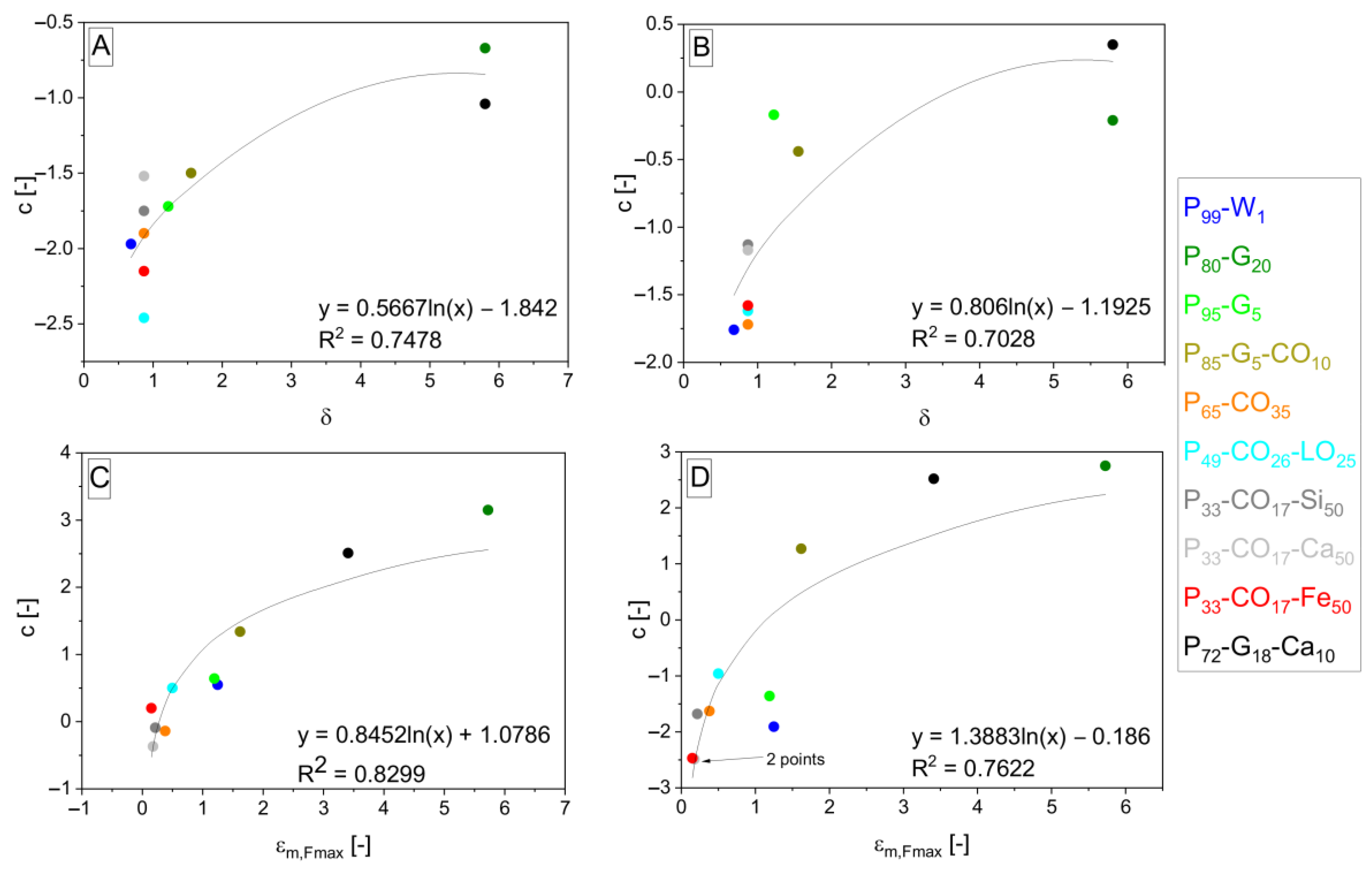
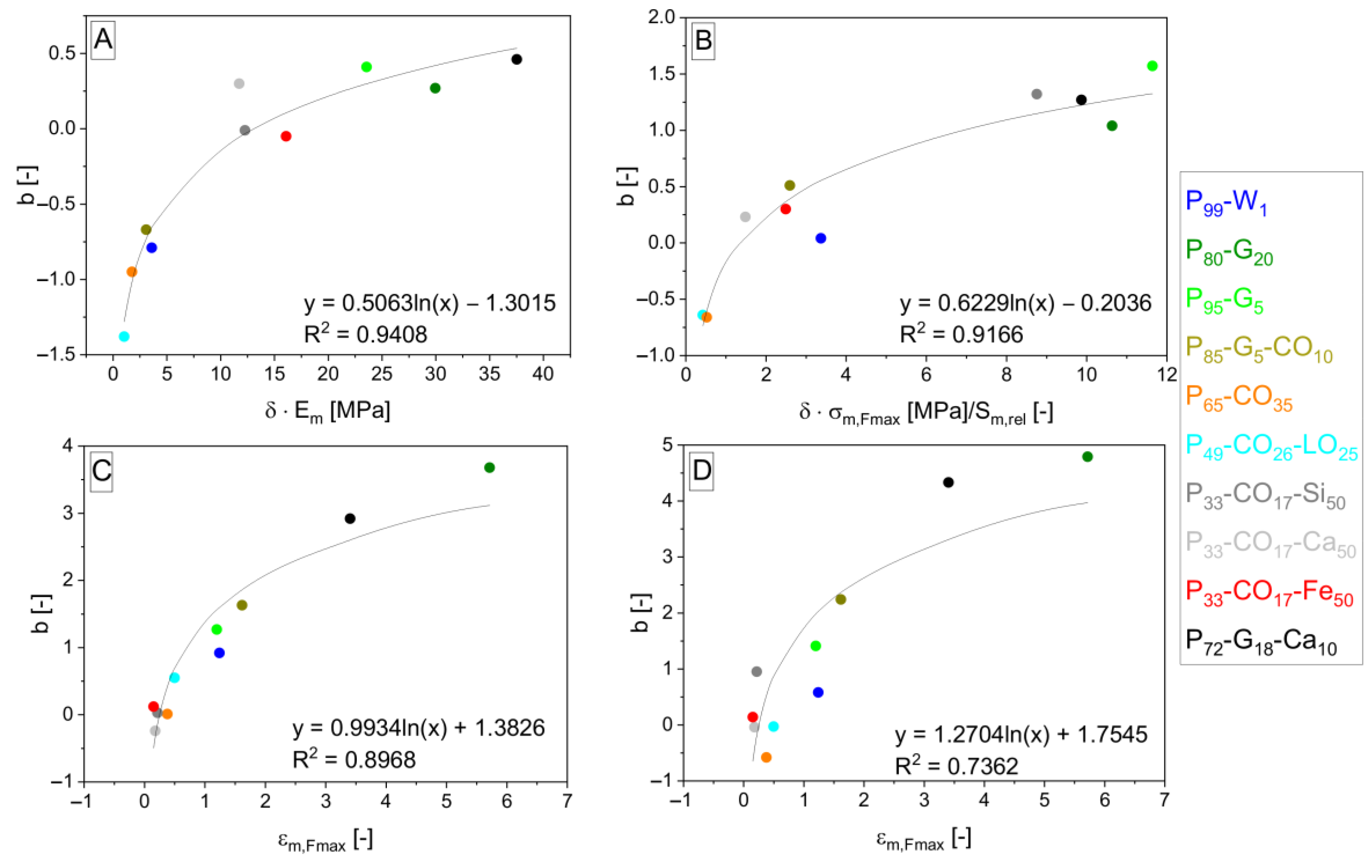
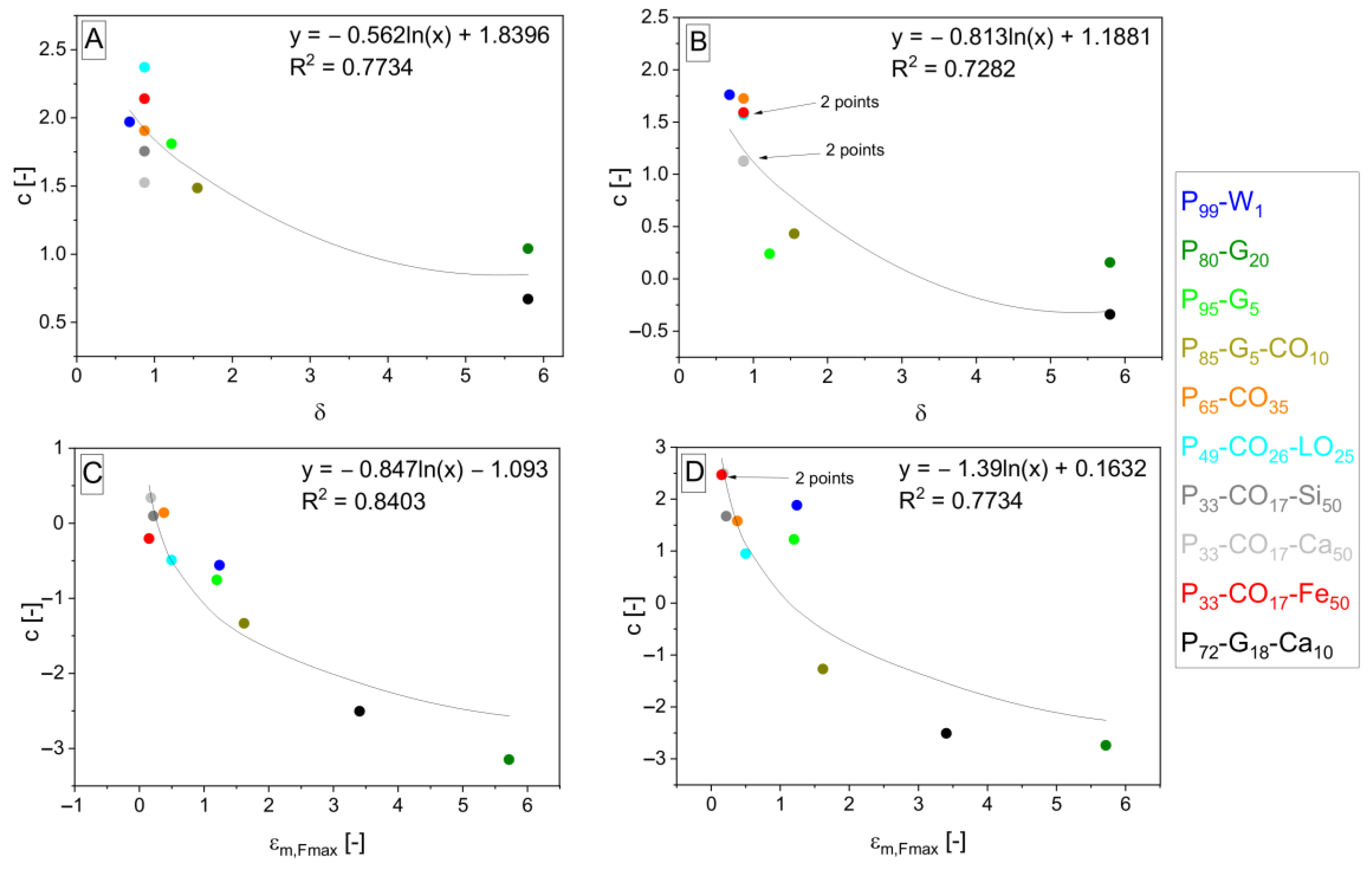
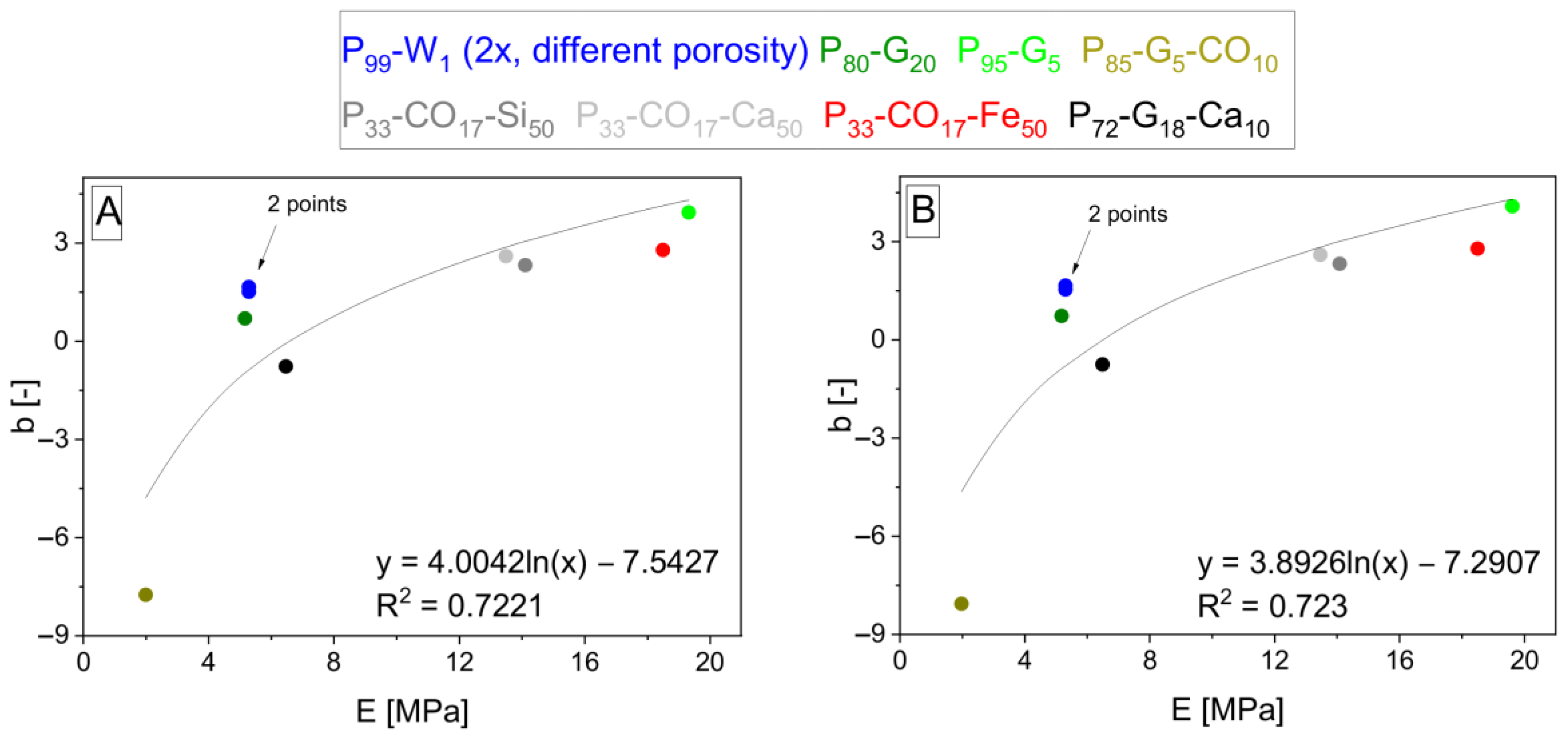
| Designation | PU4223 CS (vol%) | Curing Agent (vol%) | Others (vol%) | δ a (-) | DBTL b (wt%) |
|---|---|---|---|---|---|
| P99-W1 | 99 | 1 (W) | - | 0.68 c | 0.1 |
| P95-G5 | 95 | 5 (G) | - | 1.22 | 0.03 |
| P80-G20 | 80 | 20 (G) | - | 5.79 | 0.03 |
| P85-G5-CO10 | 85 | 5 (G) + 10 (CO) | - | 1.55 | 0.03 |
| P65-CO35 | 65 | 35 (CO) | - | 0.87 | 0.1 |
| P49-CO26-LO25 | 49 | 26 (CO) | 25 (LO) | 0.87 | 0.1 |
| P33-CO17-Si50 | 33 | 17 (CO) | 50 (Si) | 0.87 | 0.1 |
| P33-CO17-Ca50 | 33 | 17 (CO) | 50 (Ca) | 0.87 | 0.1 |
| P33-CO17-Fe50 | 33 | 17 (CO) | 50 (Fe) | 0.87 | 0.1 |
| P72-G18-Ca10 | 72 | 18 (G) | 10 (Ca) | 5.79 | 0.03 |
| Designation | E (MPa) | σFmax (MPa) | εFmax (%) | AFmax (kJ·m−3) | ρt (g·cm−3) | nm (%) |
|---|---|---|---|---|---|---|
| P99-W1 | 1.4 ± 0.3 | 0.56 ± 0.05 | 94 ± 9 | 321 ± 14 | 1.10 a | 57 ± 7 |
| P99-W1 | 4.1 ± 0.1 | 2.7 ± 0.3 | 82 ± 12 | 1400 ± 400 | 1.10 a | 16 ± 2 |
| P95-G5 | 13 ± 2 | 4.7 ± 0.1 | 140 ± 40 | 4100 ± 700 | 1.12 b | 9.5 ± 0.7 |
| P80-G20 | 4.8 ± 0.3 | 1.75 ± 0.08 | 340 ± 20 | 3700 ± 300 | 1.15 b | 10 ± 1 |
| P85-G5-CO10 | 2.3 ± 0.3 | 1.24 ± 0.04 | 100 ± 4 | 700 ± 50 | 1.05 b | 2 ± 2 |
| P65-CO35 | 1.6 ± 0.4 | 0.42 ± 0.03 | 39 ± 4 | 69 ± 6 | 1.04 b | 4 ± 1 |
| P49-CO26-LO25 | 1.1 ± 0.03 | 0.4 ± 0.03 | 68 ± 8 | 90 ± 8 | 1.03 b | 1 ± 2 |
| P33-CO17-Si50 | 9 ± 1 | 2.2 ± 0.3 | 22 ± 1 | 210 ± 40 | 1.85 c | 16 ± 1 |
| P33-CO17-Ca50 | 4.9 ± 0.5 | 0.7 ± 0.04 | 20 ± 1 | 69 ± 9 | 1.86 c | 32 ± 2 |
| P33-CO17-Fe50 | 9.1 ± 0.6 | 1.09 ± 0.09 | 13 ± 1 | 70 ± 10 | 4.04 c | 22.6 ± 0.5 |
| P72-G18-Ca10 | 7.4 ± 0.8 | 1.93 ± 0.06 | 260 ± 30 | 3700 ± 300 | 1.30 c | 16.3 ± 0.6 |
| Parameter | Suitability or Reason for Exclusion |
|---|---|
| 1 − n/np | – nonporous composite: (1 − n) · np = 1 |
| npf/1 − vf | – porous matrix: npf · (1 − vf) = 1 |
| 1 − n/1 − vf; npf/vm; npf/1 − n | – first fitting: Low R2 in comparison with the fitting according to pair np/1 – vf [33] |
| 1 − n/vm; npf/np | – too different slope value in the first fitting in comparison with Table 4 |
| np/1 − vf [33]; vm/1 − vf; vm/np | – suitable for further research |
| Matrix | E (MPa) | σFmax (MPa) | εFmax (-) | AFmax (kJ·m−3) |
|---|---|---|---|---|
| P99-W1 | 5.30/5.31/5.28 | 3.38/3.45/3.39 | 1.25/1.25/1.24 | 2871/2961/2879 |
| P95-G5 | 19.38/19.62/19.32 | 5.17/5.21/5.21 | 1.19/1.19/1.20 | 3377/3448/3416 |
| P80-G20 | 5.17 5.18/5.17 | 1.49/1.49/1.49 | 5.72/5.73/5.72 | 6920/6923/6911 |
| P85-G5-CO10 | 1.98/1.98/1.99 | 1.02/1.02/1.02 | 1.62/1.62/1.62 | 1004/1004/1002 |
| P65-CO35 | 2.02/2.03/2.02 | 0.42/0.42/0.42 | 0.38/0.38/0.38 | 111/111/113 |
| P49-CO26-LO25 | 1.19/1.19/1.20 | 0.29/0.28/0.29 | 0.50/0.50/0.50 | 83/83/83 |
| P33-CO17-Si50 | 14.09/14.09/14.11 | 4.50/4.50/4.49 | 0.22/0.22/0.22 | 435/434/435 |
| P33-CO17-Ca50 | 13.46/13.47/13.48 | 1.28/1.28/1.27 | 0.19/0.19/0.18 | 167/167/168 |
| P33-CO17-Fe50 | 18.53/18.51/18.50 | 1.70/1.70/1.70 | 0.14/0.15/0.15 | 153/152/153 |
| P72-G18-Ca10 | 6.48/6.49/6.47 | 1.62/1.63/1.63 | 3.41/3.41/3.41 | 5320/5309/5299 |
| PUR Matrix | nmax (vf(t))/nmin (vf(t))—(%) (%)/(%) (%), If Filler Is: | ||
|---|---|---|---|
| R2 | R1 | R0 | |
| P99-W1 | 45 (90)/32 (70) | 53 (90)/36 (70) | 54 (90)/28 (50) |
| P95-G5 | 46 (90)/15 (20) | 54 (90)/26 (20) | 45 (90)/24 (20) |
| P80-G20 | 46 (90)/12 (20) | 44 (90)/15 (40) | 46 (80)/14 (30) |
| P85-G5-CO10 | 44 (90)/7 (20) | 42 (90)/12 (20) | 48 (90)/12 (20) |
| P65-CO35 | 46 (90)/10 (30) | 50 (90)/12 (20) | 50 (90)/15 (20) |
| P49-CO26-LO25 | 47 (90)/6 (20) | 49 (90)/4 (20) | 50 (90)/8 (20) |
| P33-CO17-Si50 | 42 (80)/13 (40) | 45 (80)/13 (40) | 43 (70)/12 (30) |
| P33-CO17-Ca50 | 47 (90)/16 (50) | 44 (80)/15 (40) | 47 (80)/18 (30) |
| P33-CO17-Fe50 | 44 (80)/16 (40) | 45 (80)/17 (40) | 47 (80)/15 (30) |
| P72-G18-Ca10 | 44 (90)/13 (50) | 51 (90)/15 (40) | 45 (80)/14 (40) |
| Powered Parameters | Mathematical Treatment | Exponents Behavior (eq.) | Notice |
|---|---|---|---|
| hypothetical nonporous composite | |||
| porous matrix | |||
| porous composite (full equation shape, the example of fitting result) | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Černý, M.; Petruš, J.; Chamradová, I. The Influence of Porosity on Mechanical Properties of PUR-Based Composites: Experimentally Derived Mathematical Approach. Polymers 2023, 15, 1960. https://doi.org/10.3390/polym15081960
Černý M, Petruš J, Chamradová I. The Influence of Porosity on Mechanical Properties of PUR-Based Composites: Experimentally Derived Mathematical Approach. Polymers. 2023; 15(8):1960. https://doi.org/10.3390/polym15081960
Chicago/Turabian StyleČerný, Miroslav, Josef Petruš, and Ivana Chamradová. 2023. "The Influence of Porosity on Mechanical Properties of PUR-Based Composites: Experimentally Derived Mathematical Approach" Polymers 15, no. 8: 1960. https://doi.org/10.3390/polym15081960
APA StyleČerný, M., Petruš, J., & Chamradová, I. (2023). The Influence of Porosity on Mechanical Properties of PUR-Based Composites: Experimentally Derived Mathematical Approach. Polymers, 15(8), 1960. https://doi.org/10.3390/polym15081960