Modelling across Multiple Scales to Design Biopolymer Membranes for Sustainable Gas Separations: 1—Atomistic Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental
Materials
2.2. Gas Solubility and Diffusivity Measurements
2.3. MD Simulations
3. Results and Discussion
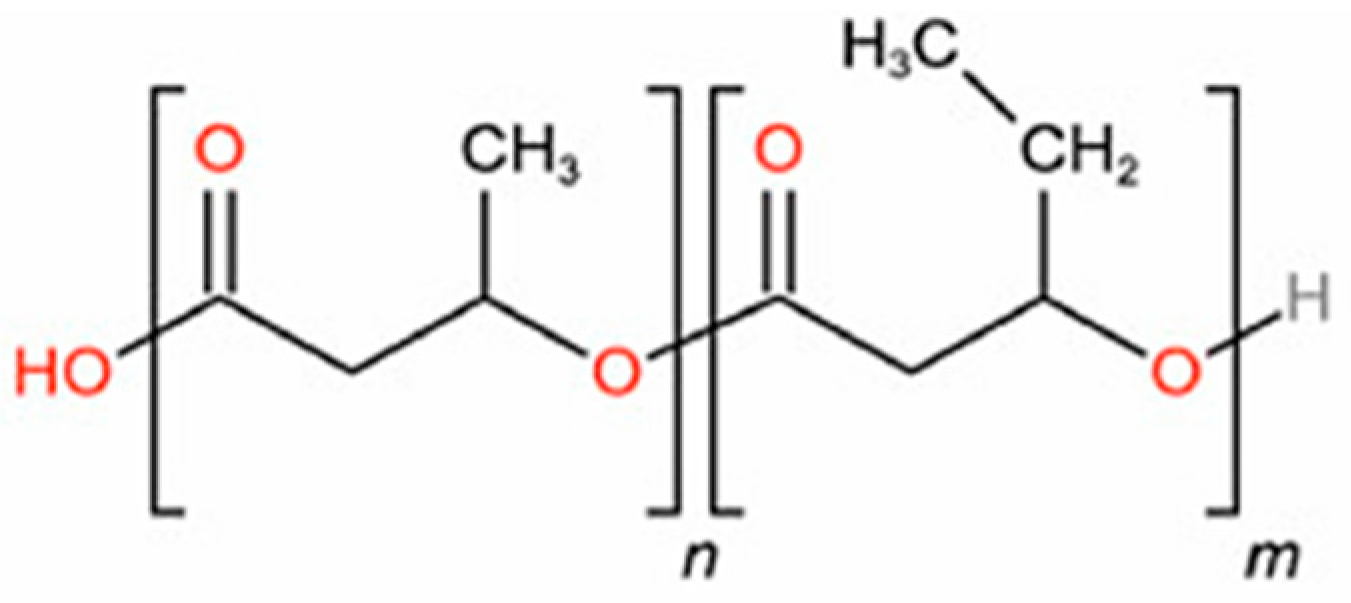
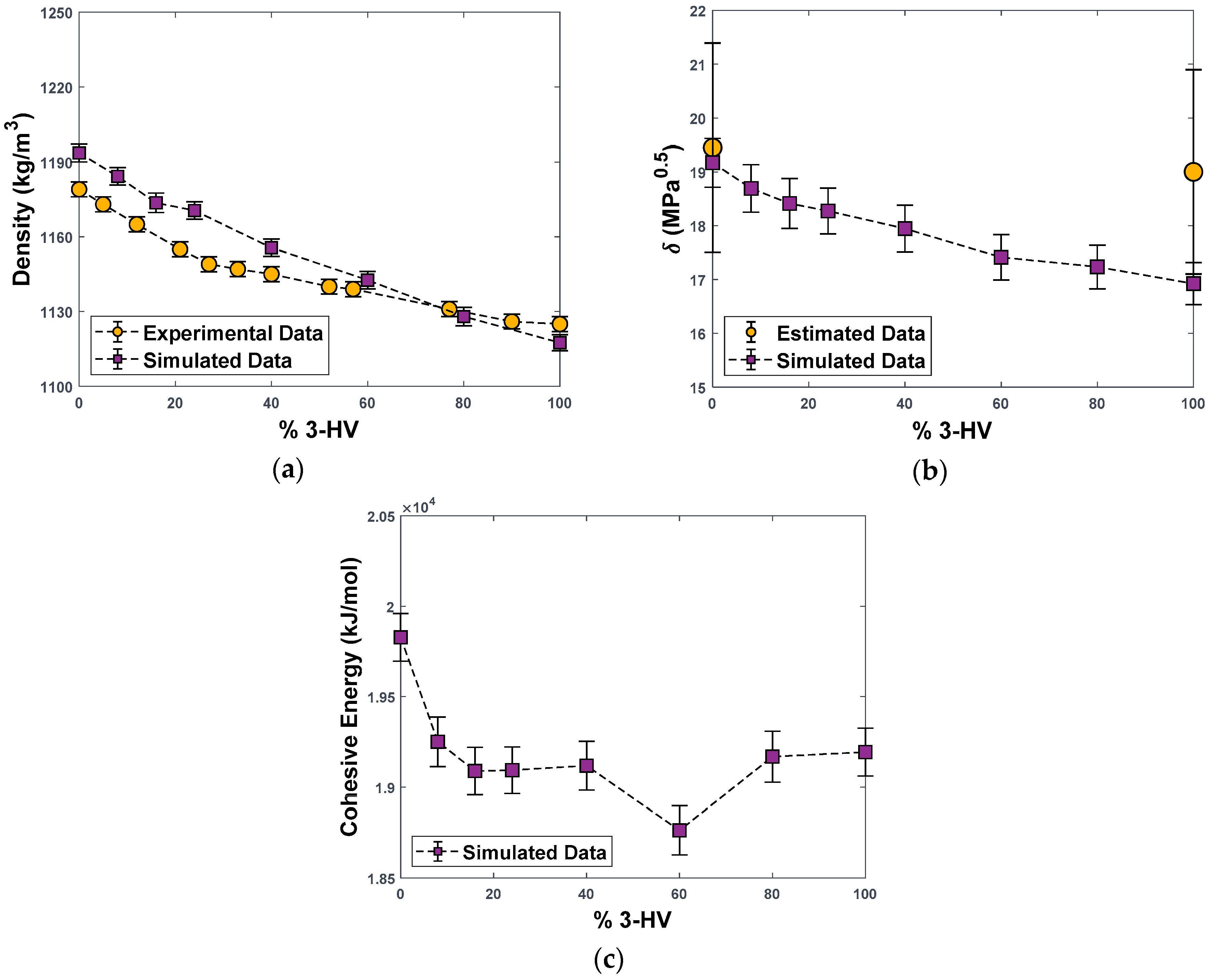
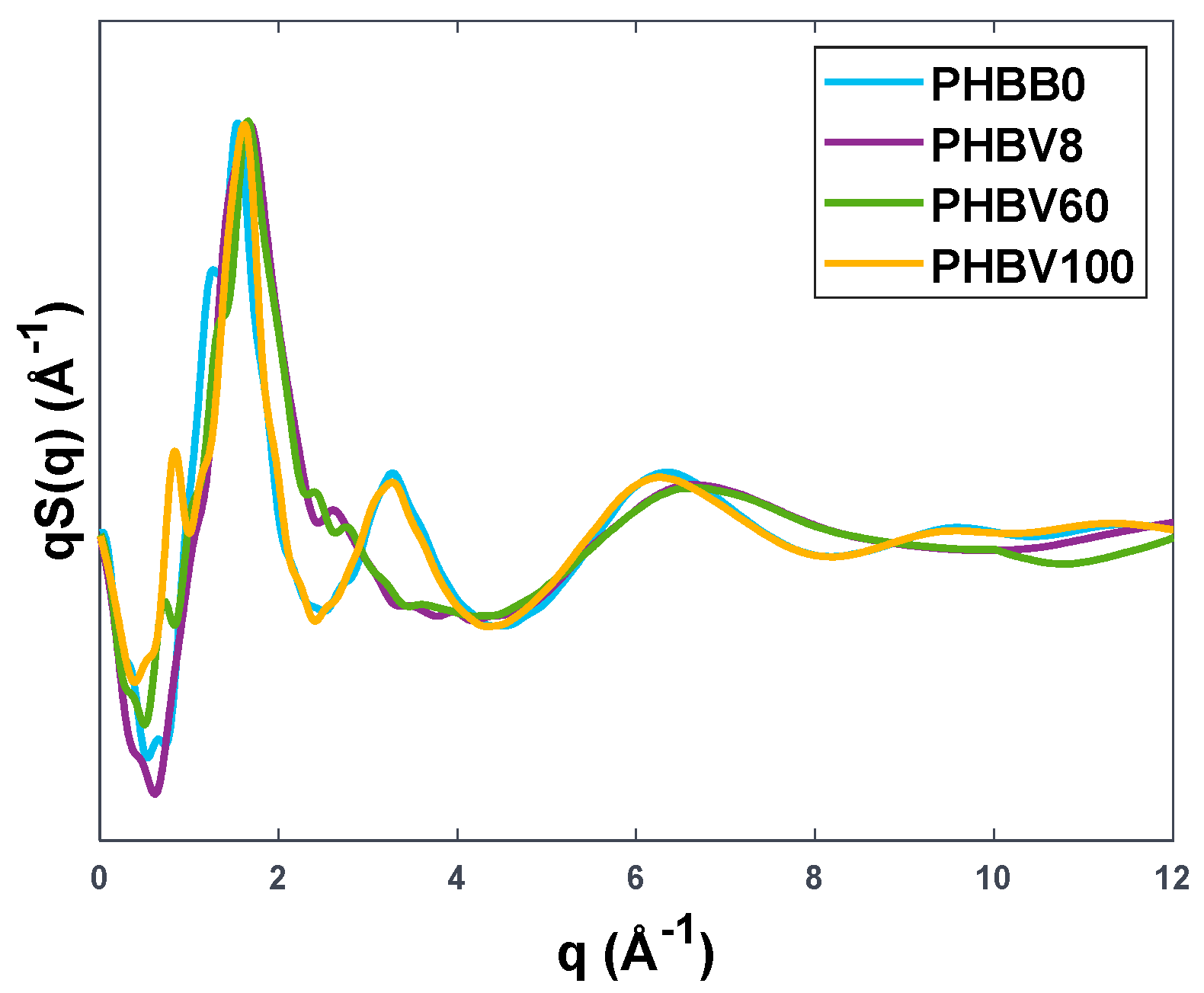
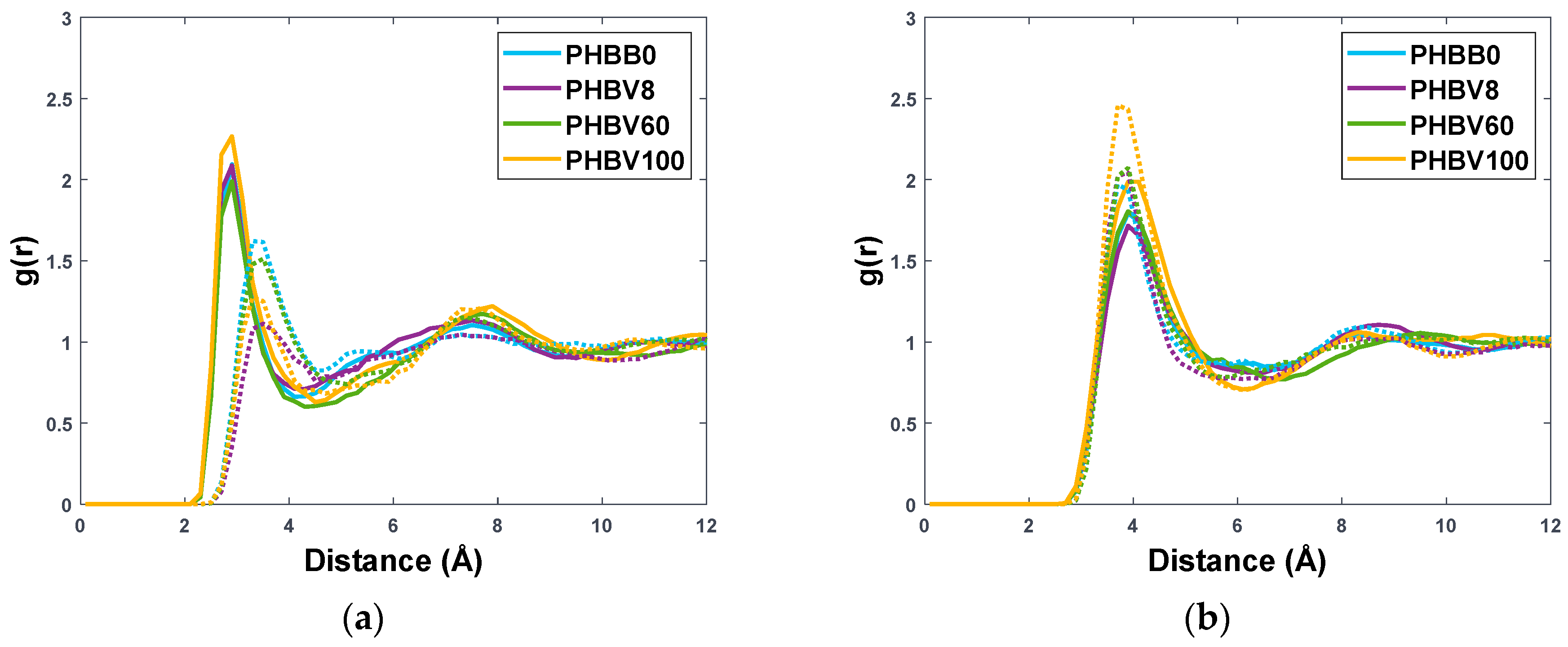
3.1. Validation of the Molecular Polymer Model
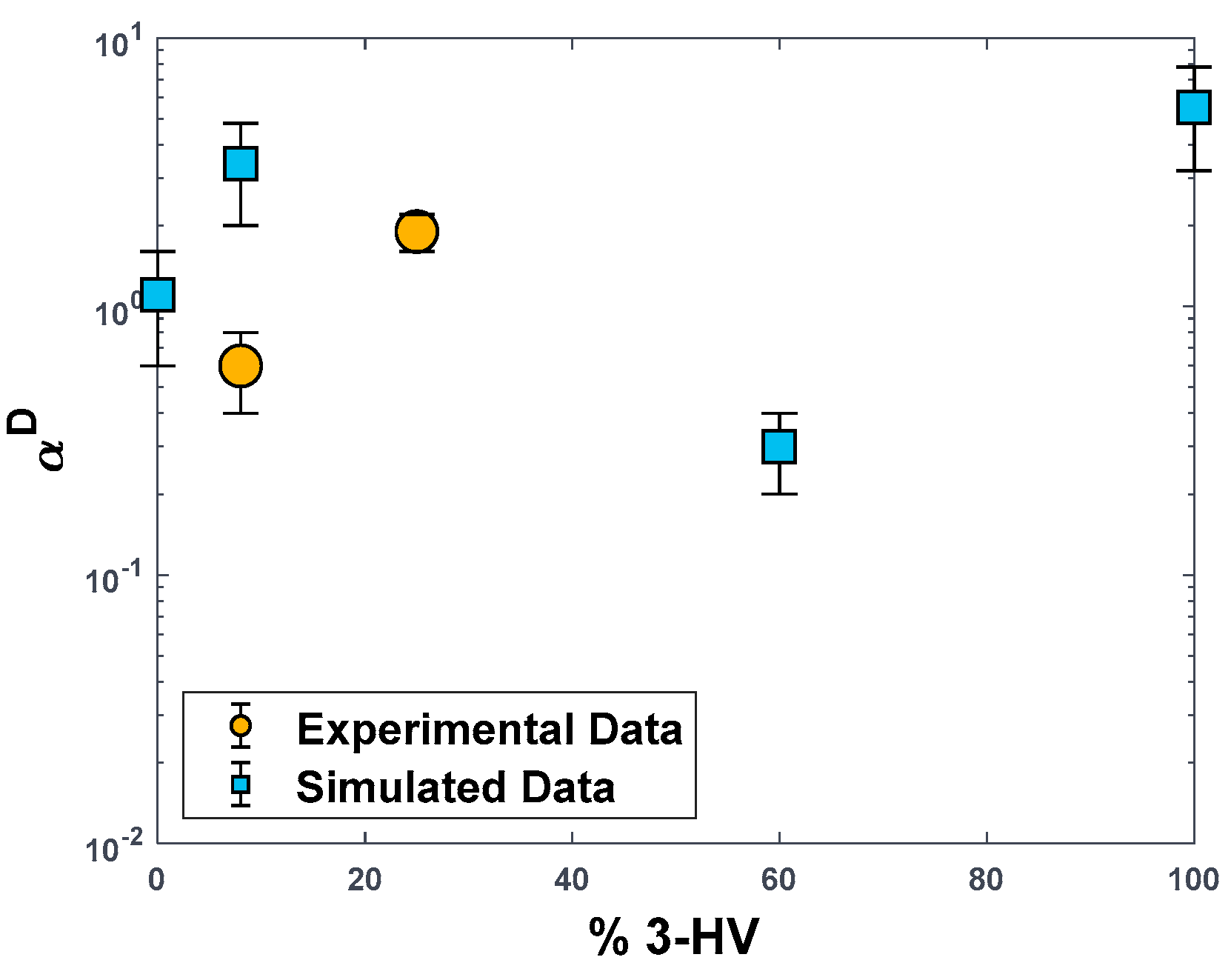
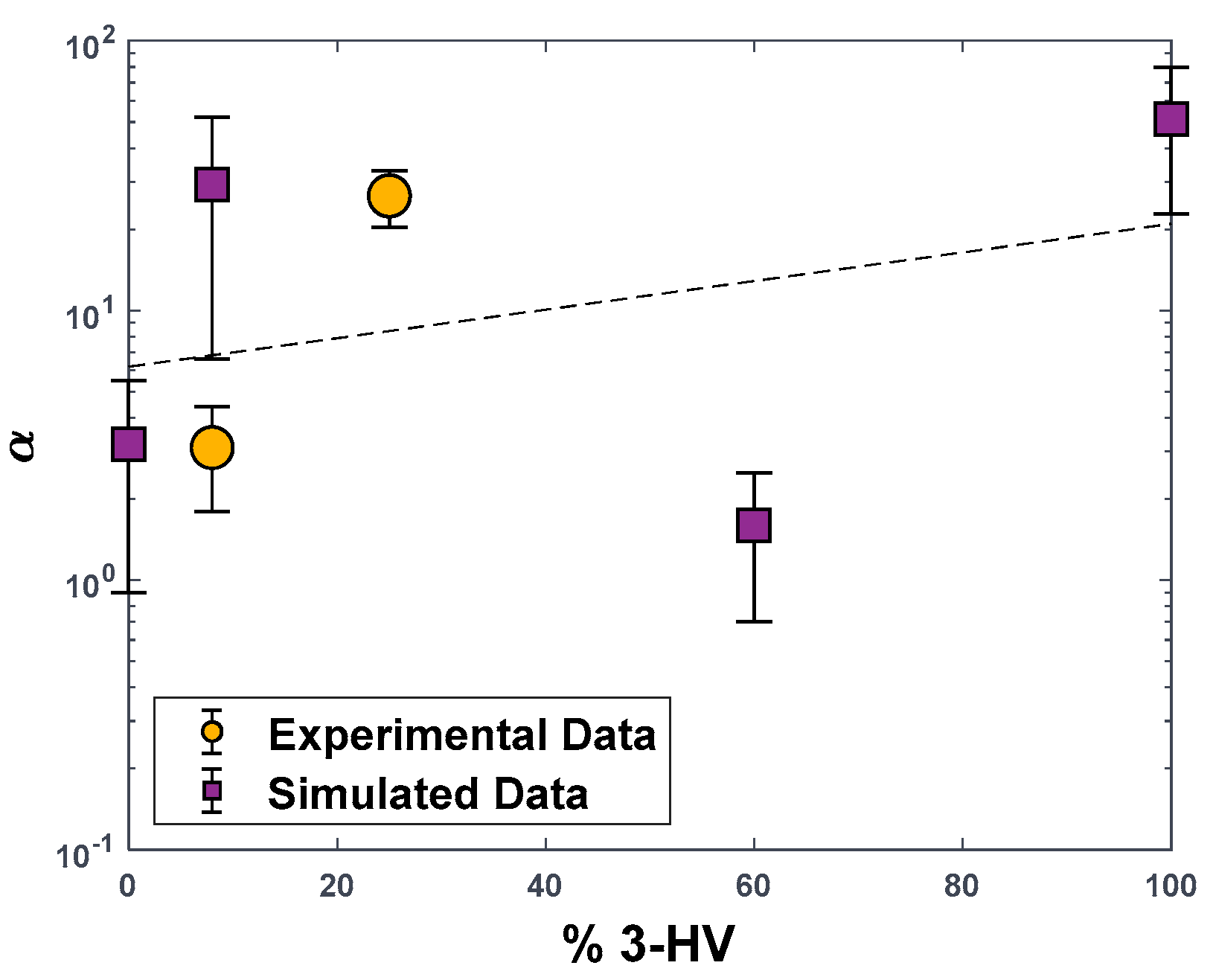
3.2. Gas Separation Performance: Experimental Data and MD Simulations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bernardo, P.; Drioli, E.; Golemme, G. Membrane Gas Separation: A Review/State of the Art. Ind. Eng. Chem. Res. 2009, 48, 4638–4663. [Google Scholar] [CrossRef]
- Russo, F.; Galiano, F.; Iulianelli, A.; Basile, A.; Figoli, A. Biopolymers for Sustainable Membranes in CO2 Separation: A Review. Fuel Process. Technol. 2021, 213, 106643. [Google Scholar] [CrossRef]
- Galizia, M.; Chi, W.S.; Smith, Z.P.; Merkel, T.C.; Baker, R.W.; Freeman, B.D. 50th Anniversary Perspective: Polymers and Mixed Matrix Membranes for Gas and Vapor Separation: A Review and Prospective Opportunities. Macromolecules 2017, 50, 7809–7843. [Google Scholar] [CrossRef]
- Sidhikku Kandath Valappil, R.; Ghasem, N.; Al-Marzouqi, M. Current and Future Trends in Polymer Membrane-Based Gas Separation Technology: A Comprehensive Review. J. Ind. Eng. Chem. 2021, 98, 103–129. [Google Scholar] [CrossRef]
- Baker, R.W.; Low, B.T. Gas Separation Membrane Materials: A Perspective. Macromolecules 2014, 47, 6999–7013. [Google Scholar] [CrossRef]
- Owen, G.; Bandi, M.; Howell, J.A.; Churchouse, S.J. Economic Assessment of Membrane Processes for Water and Waste Water Treatment. J. Membr. Sci. 1995, 102, 77–91. [Google Scholar] [CrossRef]
- Galiano, F.; Briceño, K.; Marino, T.; Molino, A.; Christensen, K.V.; Figoli, A. Advances in Biopolymer-Based Membrane Preparation and Applications. J. Membr. Sci. 2018, 564, 562–586. [Google Scholar] [CrossRef]
- Dong, X.; Lu, D.; Harris, T.A.L.; Escobar, I.C. Polymers and Solvents Used in Membrane Fabrication: A Review Focusing on Sustainable Membrane Development. Membranes 2021, 11, 309. [Google Scholar] [CrossRef]
- Doi, Y.; Kitamura, S.; Abe, H. Microbial Synthesis and Characterization of Poly(3-hydroxybutyrate-co-3-hydroxyhexanoate). Macromolecules 1995, 28, 4822–4828. [Google Scholar] [CrossRef]
- Sudesh, K.; Abe, H.; Doi, Y. Synthesis, Structure and Properties of Polyhydroxyalkanoates: Biological Polyesters. Prog. Polym. Sci. 2000, 25, 1503–1555. [Google Scholar] [CrossRef]
- Winnacker, M. Polyhydroxyalkanoates: Recent Advances in Their Synthesis and Applications. Eur. J. Lipid Sci. Technol. 2019, 121, 1900101. [Google Scholar] [CrossRef]
- Costa, S.S.; Miranda, A.L.; de Morais, M.G.; Costa, J.A.V.; Druzian, J.I. Microalgae as Source of Polyhydroxyalkanoates (PHAs)—A Review. Int. J. Biol. Macromol. 2019, 131, 536–547. [Google Scholar] [CrossRef] [PubMed]
- Hori, Y.; Yamaguchi, A.; Hagiwara, T. Chemical Synthesis of High Molecular Weight Poly(3-hydroxybutyrate-co-4-hydroxybutyrate). Polymer 1995, 36, 4703–4705. [Google Scholar] [CrossRef]
- Boey, J.Y.; Mohamad, L.; Khok, Y.S.; Tay, G.S.; Baidurah, S. A Review of the Applications and Biodegradation of Polyhydroxyalkanoates and Poly(lactic acid) and Its Composites. Polymers 2021, 13, 1544. [Google Scholar] [CrossRef] [PubMed]
- Vert, M. Aliphatic Polyesters: Great Degradable Polymers That Cannot Do Everything. Biomacromolecules 2005, 6, 538–546. [Google Scholar] [CrossRef] [PubMed]
- Degli Esposti, M.; Chiellini, F.; Bondioli, F.; Morselli, D.; Fabbri, P. Highly Porous PHB-Based Bioactive Scaffolds for Bone Tissue Engineering by in Situ Synthesis of Hydroxyapatite. Mater. Sci. Eng. C 2019, 100, 286–296. [Google Scholar] [CrossRef] [PubMed]
- Follain, N.; Chappey, C.; Dargent, E.; Chivrac, F.; Crétois, R.; Marais, S. Structure and Barrier Properties of Biodegradable Polyhydroxyalkanoate Films. J. Phys. Chem. C 2014, 118, 6165–6177. [Google Scholar] [CrossRef]
- Siracusa, V.; Ingrao, C.; Karpova, S.G.; Olkhov, A.A.; Iordanskii, A.L. Gas Transport and Characterization of Poly(3 hydroxybutyrate) Films. Eur. Polym. J. 2017, 91, 149–161. [Google Scholar] [CrossRef]
- Papchenko, K.; Degli Esposti, M.; Minelli, M.; Fabbri, P.; Morselli, D.; De Angelis, M.G. New Sustainable Routes for Gas Separation Membranes: The Properties of Poly(hydroxybutyrate-co-hydroxyvalerate) Cast from Green Solvents. J. Membr. Sci. 2022, 660, 120847. [Google Scholar] [CrossRef]
- Ricci, E.; Minelli, M.; De Angelis, M.G. Modelling Sorption and Transport of Gases in Polymeric Membranes across Different Scales: A Review. Membranes 2022, 12, 857. [Google Scholar] [CrossRef]
- Theodorou, D.N.; Suter, U.W. Detailed Molecular Structure of a Vinyl Polymer Glass. Macromolecules 1985, 18, 1467–1478. [Google Scholar] [CrossRef]
- Antoniadis, S.J.; Samara, C.T.; Theodorou, D.N. Molecular Dynamics of Atactic Polypropylene Melts. Macromolecules 1998, 31, 7944–7952. [Google Scholar] [CrossRef]
- Ricci, E.; Vergadou, N.; Vogiatzis, G.G.; De Angelis, M.G.; Theodorou, D.N. Molecular Simulations and Mechanistic Analysis of the Effect of CO2 Sorption on Thermodynamics, Structure, and Local Dynamics of Molten Atactic Polystyrene. Macromolecules 2020, 53, 3669–3689. [Google Scholar] [CrossRef]
- González Torres, M.; Villarreal-Ramírez, E.; Moyaho-Bernal, M.D.L.A.; Álvarez, M.; González-Valdez, J.; Gutiérrez Uribe, J.A.; Leyva Gómez, G.; Cortez, J.R.C. Insights into the Application of Polyhydroxyalkanoates Derivatives from the Combination of Experimental and Simulation Approaches. J. Mol. Struct. 2019, 1175, 536–541. [Google Scholar] [CrossRef]
- Bejagam, K.K.; Iverson, C.N.; Marrone, B.L.; Pilania, G. Molecular Dynamics Simulations for Glass Transition Temperature Predictions of Polyhydroxyalkanoate Biopolymers. Phys. Chem. Chem. Phys. 2020, 22, 17880–17889. [Google Scholar] [CrossRef] [PubMed]
- Bejagam, K.K.; Iverson, C.N.; Marrone, B.L.; Pilania, G. Composition and Configuration Dependence of Glass-Transition Temperature in Binary Copolymers and Blends of Polyhydroxyalkanoate Biopolymers. Macromolecules 2021, 54, 5618–5628. [Google Scholar] [CrossRef]
- Bejagam, K.K.; Gupta, N.S.; Lee, K.-S.; Iverson, C.N.; Marrone, B.L.; Pilania, G. Predicting the Mechanical Response of Polyhydroxyalkanoate Biopolymers Using Molecular Dynamics Simulations. Polymers 2022, 14, 345. [Google Scholar] [CrossRef]
- Mitomo, H.; Morishita, N. Structural Changes of Poly(3-hydroxybutyrate-co-3-hydroxyvaIerate) Fractionated with Acetone-Water Solution. Polymer 1995, 36, 2573–2578. [Google Scholar] [CrossRef]
- Terada, M.; Marchessault, R.H. Determination of Solubility Parameters for Poly(3-hydroxyalkanoates). Int. J. Biol. Macromol. 1999, 25, 207–215. [Google Scholar] [CrossRef] [PubMed]
- Jacquel, N.; Lo, C.-W.; Wu, H.-S.; Wei, Y.-H.; Wang, S.S. Solubility of Polyhydroxyalkanoates by Experiment and Thermodynamic Correlations. AIChE J. 2007, 53, 2704–2714. [Google Scholar] [CrossRef]
- Capitán, M.J.; Rueda, D.R.; Ezquerra, T.A. Inhibition of the Crystallization in Nanofilms of Poly(3-hydroxybutyrate). Macromolecules 2004, 37, 5653–5659. [Google Scholar] [CrossRef]
- Hurrell, B.L.; Hurrell, B.L. A Wide-Angle X-Ray Scattering Study of the Ageing of Poly(hydroxybutyrate). J. Mater. Sci. 1998, 33, 1709–1713. [Google Scholar] [CrossRef]
- Righetti, M.C.; Aliotta, L.; Mallegni, N.; Gazzano, M.; Passaglia, E.; Cinelli, P.; Lazzeri, A. Constrained Amorphous Interphase and Mechanical Properties of Poly(3-hydroxybutyrate-co-3-hydroxyvalerate). Front. Chem. 2019, 7, 790. [Google Scholar] [CrossRef]
- Minelli, M.; Cocchi, G.; Ansaloni, L.; Baschetti, M.G.; De Angelis, M.G.; Doghieri, F. Vapor and Liquid Sorption in Matrimid Polyimide: Experimental Characterization and Modeling. Ind. Eng. Chem. Res. 2013, 52, 8936–8945. [Google Scholar] [CrossRef]
- Ferrari, M.C.; Galizia, M.; De Angelis, M.G.; Sarti, G.C. Gas and Vapor Transport in Mixed Matrix Membranes Based on Amorphous Teflon AF1600 and AF2400 and Fumed Silica. Ind. Eng. Chem. Res. 2010, 49, 11920–11935. [Google Scholar] [CrossRef]
- Galizia, M.; De Angelis, M.G.; Finkelshtein, E.; Yampolskii, Y.P.; Sarti, G.C. Sorption and Transport of Hydrocarbons and Alcohols in Addition-Type Poly(trimethyl silyl norbornene). I: Experimental Data. J. Membr. Sci. 2011, 385–386, 141–153. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1979; ISBN 978-0-19-853411-2. [Google Scholar]
- Minelli, M.; Baschetti, M.G.; Doghieri, F.; Ankerfors, M.; Lindström, T.; Siró, I.; Plackett, D. Investigation of Mass Transport Properties of Microfibrillated Cellulose (MFC) Films. J. Membr. Sci. 2010, 358, 67–75. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The Solution-Diffusion Model: A Review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- MAPS Platform. Available online: https://www.scienomics.com (accessed on 15 March 2023).
- Ramos, J.; Peristeras, L.D.; Theodorou, D.N. Monte Carlo Simulation of Short Chain Branched Polyolefins in the Molten State. Macromolecules 2007, 40, 9640–9650. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- LAMMPS Molecular Dynamics Simulator. Available online: https://www.lammps.org (accessed on 15 March 2023).
- Sun, H.; Mumby, S.J.; Maple, J.R.; Hagler, A.T. An Ab Initio CFF93 All-Atom Force Field for Polycarbonates. J. Am. Chem. Soc. 1994, 116, 2978–2987. [Google Scholar] [CrossRef]
- Yang, J.; Ren, Y.; Tian, A.; Sun, H. COMPASS Force Field for 14 Inorganic Molecules, He, Ne, Ar, Kr, Xe, H2, O2, N2, NO, CO, CO2, NO2, CS2, and SO2, in Liquid Phases. J. Phys. Chem. B 2000, 104, 4951–4957. [Google Scholar] [CrossRef]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles, 1st ed.; CRC Press: Boca Raton, FL, USA, 1988. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Widom, B. Some Topics in the Theory of Fluids. J. Chem. Phys. 1963, 39, 2808–2812. [Google Scholar] [CrossRef]
- Shing, K.S.; Chung, S.T. Computer Simulation Methods for the Calculation of Solubility in Supercritical Extraction Systems. J. Phys. Chem. 1987, 91, 1674–1681. [Google Scholar] [CrossRef]
- Atiq, O.; Ricci, E.; Baschetti, M.G.; De Angelis, M.G. Modelling Solubility in Semi-Crystalline Polymers: A Critical Comparative Review. Fluid Phase Equilibria 2022, 556, 113412. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J.; Tildesley, D.J. Computer Simulation of Liquids; Oxford Science Publications: Oxford, UK, 1987; Reprinted in Clarendon Press: Oxford, UK, 2017; ISBN 978-0-19-855375-5. [Google Scholar]
- Freeman, B.; Yampolskii, Y.; Pinnau, I.; Yampolskii, Y. Materials Science of Membranes for Gas and Vapor Separation; Yampolskii, Y., Pinnau, I., Freeman, B., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2006; ISBN 978-0-470-02903-9. [Google Scholar]
- Vogiatzis, G.G.; Theodorou, D.N. Local Segmental Dynamics and Stresses in Polystyrene–C60 Mixtures. Macromolecules 2014, 47, 387–404. [Google Scholar] [CrossRef]
- Atomic Form Factors. Available online: http://lampx.tugraz.at/~hadley/ss1/crystaldiffraction/atomicformfactors/formfactors.php (accessed on 15 March 2023).
- Voyiatzis, E.; Stroeks, A. Atomistic Modeling of Hydrogen and Oxygen Solubility in Semicrystalline PA-6 and HDPE Materials. J. Phys. Chem. B 2022, 126, 6102–6111. [Google Scholar] [CrossRef]
- Hofman, D.; Ulbrich, J.; Fritsch, D.; Paul, D. Molecular Modelling Simulation of Gas Transport in Amorphous Polyimide and Poly(amide imide) Membrane Materials. Polymer 1996, 37, 4773–4785. [Google Scholar] [CrossRef]
- Memari, P.; Lachet, V.; Rousseau, B. Molecular Simulations of the Solubility of Gases in Polyethylene below Its Melting Temperature. Polymer 2010, 51, 4978–4984. [Google Scholar] [CrossRef]
- Sun, D.; Zhou, J. Molecular Simulation of Oxygen Sorption and Diffusion in the Poly(lactic acid). Chin. J. Chem. Eng. 2013, 21, 301–309. [Google Scholar] [CrossRef]
- Yang, Y.; Narayanan Nair, A.K.; Sun, S. Sorption and Diffusion of Methane and Carbon Dioxide in Amorphous Poly(alkyl acrylates): A Molecular Simulation Study. J. Phys. Chem. B 2020, 124, 1301–1310. [Google Scholar] [CrossRef] [PubMed]
- Goubko, M.; Miloserdov, O.; Yampolskii, Y.; Alentiev, A.; Ryzhikh, V. A Novel Model to Predict Infinite Dilution Solubility Coefficients in Glassy Polymers. J. Polym. Sci. Part B Polym. Phys. 2017, 55, 228–244. [Google Scholar] [CrossRef]
- Cravo, C.; Duarte, A.R.C.; Duarte, C.M.M. Solubility of Carbon Dioxide in a Natural Biodegradable Polymer: Determination of Diffusion Coefficients. J. Supercrit. Fluids 2007, 40, 194–199. [Google Scholar] [CrossRef]
- Williams, L.L.; Rubin, J.B.; Edwards, H.W. Calculation of Hansen Solubility Parameter Values for a Range of Pressure and Temperature Conditions, Including the Supercritical Fluid Region. Ind. Eng. Chem. Res. 2004, 43, 4967–4972. [Google Scholar] [CrossRef]
- Panayiotou, C.; Hatzimanikatis, V. The Solubility Parameters of Carbon Dioxide and Ionic Liquids: Are They an Enigma? Fluid Phase Equilibria 2021, 527, 112828. [Google Scholar] [CrossRef]
- Tocci, E.; Bellacchio, E.; Russo, N.; Drioli, E. Diffusion of Gases in PEEKs Membranes: Molecular Dynamics Simulations. J. Membr. Sci. 2002, 206, 389–398. [Google Scholar] [CrossRef]
- Barham, P.J.; Keller, A.; Otun, E.L.; Holmes, P.A. Crystallization and morphology of a bacterial thermoplastic: Poly-3-hydroxybutyrate. J. Mater. Sci. 1984, 19, 2781–2794. [Google Scholar] [CrossRef]
- Kamiya, N.; Sakurai, M.; Inoue, Y.; Chujo, R. Isomorphic behavior of random copolymers: Thermodynamic analysis of cocrystallization of poly(3-hydroxybutyrate-co-3-hydroxyvalerate). Macromolecules 1991, 24, 3888–3892. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papchenko, K.; Ricci, E.; De Angelis, M.G. Modelling across Multiple Scales to Design Biopolymer Membranes for Sustainable Gas Separations: 1—Atomistic Approach. Polymers 2023, 15, 1805. https://doi.org/10.3390/polym15071805
Papchenko K, Ricci E, De Angelis MG. Modelling across Multiple Scales to Design Biopolymer Membranes for Sustainable Gas Separations: 1—Atomistic Approach. Polymers. 2023; 15(7):1805. https://doi.org/10.3390/polym15071805
Chicago/Turabian StylePapchenko, Kseniya, Eleonora Ricci, and Maria Grazia De Angelis. 2023. "Modelling across Multiple Scales to Design Biopolymer Membranes for Sustainable Gas Separations: 1—Atomistic Approach" Polymers 15, no. 7: 1805. https://doi.org/10.3390/polym15071805
APA StylePapchenko, K., Ricci, E., & De Angelis, M. G. (2023). Modelling across Multiple Scales to Design Biopolymer Membranes for Sustainable Gas Separations: 1—Atomistic Approach. Polymers, 15(7), 1805. https://doi.org/10.3390/polym15071805








