Optimal Design of Carbon-Based Polymer Nanocomposites Preparation Based on Response Surface Methodology
Abstract
1. Introduction
2. Materials and Methods
2.1. Design of the Central Combination of CNT-GN/RTV Polymer Nanocomposites
2.2. Preparation of Samples
2.3. Sensitivity of CNT-GN/RTV Polymer Nanocomposites
2.4. Compressive Modulus of CNT-GN/RTV Polymer Nanocomposites
3. Results and Discussion
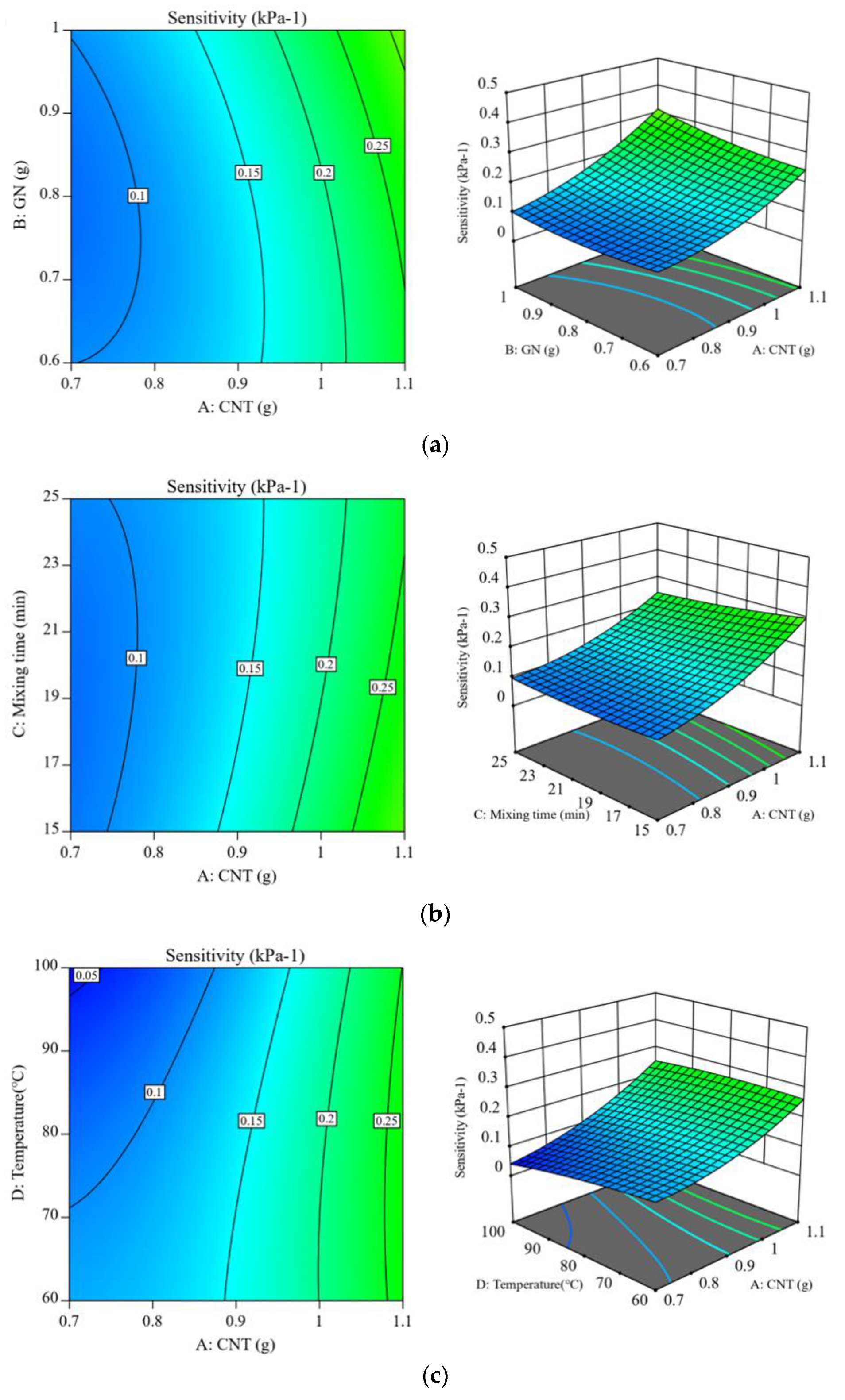
3.1. ANOVA and Model Fitting for CNT/GN-RTV Nanocomposites’ Sensitivity
3.2. ANOVA and Model Fitting for the Compressive Modulus of CNT/GN-RTV Nanocomposites
3.3. Optimal Optimization Range of the CNT/GN-RTV Preparation Process
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Asyraf, M.R.M.; Ishak, M.R.; Syamsir, A.; Nurazzi, N.M.; Sabaruddin, F.A.; Shazleen, S.S.; Norrrahim, M.N.F.; Rafidah, M.; Ilyas, R.A.; Rashid, M.Z.A.; et al. Mechanical Properties of Oil Palm Fibre-Reinforced Polymer Composites: A Review. J. Mater. Res. Technol. 2022, 17, 33–65. [Google Scholar] [CrossRef]
- Du, H.; Fang, C.; Zhang, J.; Xia, X.; Weng, G.J. Segregated Carbon Nanotube Networks in CNT-Polymer Nanocomposites for Higher Electrical Conductivity and Dielectric Permittivity, and Lower Percolation Threshold. Int. J. Eng. Sci. 2022, 173, 103650. [Google Scholar] [CrossRef]
- Jhang, W.-L.; Li, C.-J.; Wang, A.-S.; Liu, C.-W.; Hsu, S.-W. Tunable Optical Property of Plasmonic–Polymer Nanocomposites Composed of Multilayer Nanocrystal Arrays Stacked in a Homogeneous Polymer Matrix. ACS Appl. Mater. Interfaces 2020, 12, 51873–51884. [Google Scholar] [CrossRef] [PubMed]
- Kim, N.K.; Lin, R.; Bhattacharyya, D.; van Loosdrecht, M.C.M.; Lin, Y. Insight on How Biopolymers Recovered from Aerobic Granular Wastewater Sludge Can Reduce the Flammability of Synthetic Polymers. Sci. Total Environ. 2022, 805, 150434. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Feng, Y.; Qin, M.; Gao, L.; Li, Z.; Zhao, F.; Zhang, Z.; Lv, F.; Feng, W. Stress Controllability in Thermal and Electrical Conductivity of 3D Elastic Graphene-Crosslinked Carbon Nanotube Sponge/Polyimide Nanocomposite. Adv. Funct. Mater. 2019, 29, 1901383. [Google Scholar] [CrossRef]
- Gong, S.; Wu, D.; Li, Y.; Jin, M.; Xiao, T.; Wang, Y.; Xiao, Z.; Zhu, Z.; Li, Z. Temperature-Independent Piezoresistive Sensors Based on Carbon Nanotube/Polymer Nanocomposite. Carbon 2018, 137, 188–195. [Google Scholar] [CrossRef]
- Boland, C.S.; Khan, U.; Ryan, G.; Barwich, S.; Charifou, R.; Harvey, A.; Backes, C.; Li, Z.; Ferreira, M.S.; Möbius, M.E.; et al. Sensitive Electromechanical Sensors Using Viscoelastic Graphene-Polymer Nanocomposites. Science 2016, 354, 1257–1260. [Google Scholar] [CrossRef]
- Chen, J.; Zheng, J.; Gao, Q.; Zhang, J.; Zhang, J.; Omisore, O.M.; Wang, L.; Li, H. Polydimethylsiloxane (PDMS)-Based Flexible Resistive Strain Sensors for Wearable Applications. Appl. Sci. 2018, 8, 345. [Google Scholar] [CrossRef]
- Nayak, G.C.; Rajasekar, R.; Das, C.K. Dispersion of SiC Coated MWCNTs in PEI/Silicone Rubber Blend and Its Effect on the Thermal and Mechanical Properties. J. Appl. Polym. Sci. 2011, 119, 3574–3581. [Google Scholar] [CrossRef]
- Jiao, Y.; Young, C.W.; Yang, S.; Oren, S.; Ceylan, H.; Kim, S.; Gopalakrishnan, K.; Taylor, P.C.; Dong, L. Wearable Graphene Sensors with Microfluidic Liquid Metal Wiring for Structural Health Monitoring and Human Body Motion Sensing. IEEE Sens. J. 2016, 16, 7870–7875. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, H.; Yi, K.; Lin, J.; Chen, A.; Chen, L.; Zou, Z.; Liu, M.; Ji, Y.; Dong, L.; et al. Wearable LIG Flexible Stress Sensor Based on Spider Web Bionic Structure. Coatings 2023, 13, 155. [Google Scholar] [CrossRef]
- Tang, D.; Wang, Q.; Wang, Z.; Liu, Q.; Zhang, B.; He, D.; Wu, Z.; Mu, S. Highly Sensitive Wearable Sensor Based on a Flexible Multi-Layer Graphene Film Antenna. Sci. Bull. 2018, 63, 574–579. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Wei, A.; Ma, J.; Shao, L.; Jiang, H.; Dong, D.; Ji, Z.; Wang, Q.; Kang, S. Lightweight, Compressible and Electrically Conductive Polyurethane Sponges Coated with Synergistic Multiwalled Carbon Nanotubes and Graphene for Piezoresistive Sensors. Nanoscale 2018, 10, 7116–7126. [Google Scholar] [CrossRef]
- Gao, H.; Liu, M.; Liu, J.; Dai, H.; Zhou, X.; Liu, X.; Zhuo, Y.; Zhang, W.; Zhang, L. Medium Optimization for the Production of Avermectin B1a by Streptomyces Avermitilis 14-12A Using Response Surface Methodology. Bioresour. Technol. 2009, 100, 4012–4016. [Google Scholar] [CrossRef] [PubMed]
- Flaifel, M.H. An Approach Towards Optimization Appraisal of Thermal Conductivity of Magnetic Thermoplastic Elastomeric Nanocomposites Using Response Surface Methodology. Polymers 2020, 12, 2030. [Google Scholar] [CrossRef]
- Zenoozi, S.; Sadeghi, G.M.M.; Shahrousvand, M.; Rafiee, M. Preparation, and Optimization of Polyurethane/Crosslinked Poly Acrylic Acid Semi-IPNs Containing Multi Wall Carbon Nanotube Applicable for Artificial Tendon. Colloids Surf. A Physicochem. Eng. Asp. 2022, 640, 128415. [Google Scholar] [CrossRef]
- Tanabi, H.; Erdal, M. Effect of CNTs Dispersion on Electrical, Mechanical and Strain Sensing Properties of CNT/Epoxy Nanocomposites. Results Phys. 2019, 12, 486–503. [Google Scholar] [CrossRef]
- Han, H.; Yu, R.; Li, B.; Zhang, Y. Multi-Objective Optimization of Corrugated Tube Inserted with Multi-Channel Twisted Tape Using RSM and NSGA-II. Appl. Therm. Eng. 2019, 159, 113731. [Google Scholar] [CrossRef]
- Bao, L.; Zheng, M.; Zhou, Q.; Gao, P.; Xu, Y.; Jiang, H. Multi-Objective Optimization of Partition Temperature of Steel Sheet by NSGA-II Using Response Surface Methodology. Case Stud. Therm. Eng. 2022, 31, 101818. [Google Scholar] [CrossRef]
- Yanez-Fernandez, A.; Inestrosa-Izurieta, M.J.; Urzua, J.I. Concurrent Magnesium and Boron Extraction from Natural Lithium Brine and Its Optimization by Response Surface Methodology. Desalination 2021, 517, 115269. [Google Scholar] [CrossRef]
- Yan, G.; Han, D.; Li, W.; Qiu, J.; Jiang, C.; Li, L.; Wang, C. Effect of Pyrolysis Carbon Black and Carbon Nanotubes on Properties of Natural Rubber Conductive Composites. J. Appl. Polym. Sci. 2022, 139, 52321. [Google Scholar] [CrossRef]
- Kim, J.Y.; Ji, S.; Jung, S.; Ryu, B.-H.; Kim, H.-S.; Lee, S.S.; Choi, Y.; Jeong, S. 3D Printable Composite Dough for Stretchable, Ultrasensitive and Body-Patchable Strain Sensors. Nanoscale 2017, 9, 11035–11046. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Zheng, L.; Meng, Q.; Tang, R.; Wang, Z.; Dang, B.; Shen, X.; Sun, Q. A Flexible Hydrogel Tactile Sensor with Low Compressive Modulus and Dynamic Piezoresistive Response Regulated by Lignocellulose/Graphene Aerogels. J. Mater. Chem. C 2021, 9, 12895–12903. [Google Scholar] [CrossRef]
- Smith, S.; Chen, X.; Li, Z.; Smith, S.; Chen, M.; Liu, H.; Wu, X. Optimization of Supercritical CO2 Extraction of Moringa Oleifera Seed Oil Using Response Surface Methodological Approach and Its Antioxidant Activity. Curr. Dev. Nutr. 2022, 6, 535. [Google Scholar] [CrossRef]
- Regti, A.; Laamari, M.R.; Stiriba, S.-E.; El Haddad, M. Use of Response Factorial Design for Process Optimization of Basic Dye Adsorption onto Activated Carbon Derived from Persea Species. Microchem. J. 2017, 130, 129–136. [Google Scholar] [CrossRef]
- Ghahramani, P.; Behdinan, K.; Moradi-Dastjerdi, R.; Naguib, H.E. Theoretical and Experimental Investigation of MWCNT Dispersion Effect on the Elastic Modulus of Flexible PDMS/MWCNT Nanocomposites. Nanotechnol. Rev. 2021, 11, 55–64. [Google Scholar] [CrossRef]
- Colonna, S.; Bernal, M.M.; Gavoci, G.; Gomez, J.; Novara, C.; Saracco, G.; Fina, A. Effect of Processing Conditions on the Thermal and Electrical Conductivity of Poly (Butylene Terephthalate) Nanocomposites Prepared via Ring-Opening Polymerization. Mater. Des. 2017, 119, 124–132. [Google Scholar] [CrossRef]
- Wang, Z.; Volinsky, A.A.; Gallant, N.D. Crosslinking Effect on Polydimethylsiloxane Elastic Modulus Measured by Custom-Built Compression Instrument. J. Appl. Polym. Sci. 2014, 131, 41050. [Google Scholar] [CrossRef]
- Han, L.; Xiao, C.; Song, Q.; Yin, X.; Li, W.; Li, K.; Li, Y. Nano-Interface Effect of Graphene on Carbon Nanotube Reinforced Carbon/Carbon Composites. Carbon 2022, 190, 422–429. [Google Scholar] [CrossRef]
- Schneider, F.; Fellner, T.; Wilde, J.; Wallrabe, U. Mechanical Properties of Silicones for MEMS. J. Micromech. Microeng. 2008, 18, 065008. [Google Scholar] [CrossRef]
- Kumar, R. Effects of High Volume Dolomite Sludge on the Properties of Eco-Efficient Lightweight Concrete: Microstructure, Statistical Modeling, Multi-Attribute Optimization through Derringer’s Desirability Function, and Life Cycle Assessment. J. Clean. Prod. 2021, 307, 127107. [Google Scholar] [CrossRef]










| Variable | Symbol | Actual Range | Coded Levels | ||||
|---|---|---|---|---|---|---|---|
| −2 | Low (−1) | Center (0) | High (+1) | +2 | |||
| Amount of CNT (g) | A | 0.8—1.0 | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 |
| Amount of GN (g) | B | 0.7—0.9 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
| Mixing time (min) | C | 15—25 | 10 | 15 | 20 | 25 | 30 |
| Temperature (°C) | D | 60—100 | 40 | 60 | 80 | 100 | 120 |
| Input Variables (Factors) | Responses | |||||
|---|---|---|---|---|---|---|
| Run | A: CNT (g) | B: GN (g) | C: Mixing Time (min) | D: Temperature (°C) | Sensitivity (kPa−1) | Compression Modulus (kPa) |
| 1 | 1 | 1 | −1 | −1 | 0.387 | 559.704 |
| 2 | 0 | 0 | 0 | 0 | 0.129 | 636.943 |
| 3 | 0 | 0 | 0 | 0 | 0.157 | 651.57 |
| 4 | 0 | 0 | −2 | 0 | 0.205 | 602.178 |
| 5 | 0 | −2 | 0 | 0 | 0.197 | 527.573 |
| 6 | −1 | −1 | −1 | 1 | 0.07 | 469.795 |
| 7 | 0 | 0 | 0 | 0 | 0.13 | 622.693 |
| 8 | −2 | 0 | 0 | 0 | 0.062 | 579.748 |
| 9 | 1 | 1 | 1 | 1 | 0.203 | 557.687 |
| 10 | 0 | 0 | 2 | 0 | 0.142 | 687.158 |
| 11 | 1 | −1 | 1 | −1 | 0.192 | 690.491 |
| 12 | 1 | −1 | −1 | 1 | 0.239 | 359.624 |
| 13 | 0 | 0 | 0 | 0 | 0.147 | 484.934 |
| 14 | −1 | −1 | −1 | −1 | 0.09 | 739.168 |
| 15 | −1 | −1 | 1 | 1 | 0.102 | 434.897 |
| 16 | −1 | −1 | 1 | −1 | 0.137 | 702.085 |
| 17 | 0 | 0 | 0 | 0 | 0.124 | 595.274 |
| 18 | −1 | 1 | −1 | 1 | 0.062 | 394.148 |
| 19 | 0 | 2 | 0 | 0 | 0.21 | 580.638 |
| 20 | 0 | 0 | 0 | 2 | 0.085 | 217.341 |
| 21 | −1 | 1 | 1 | 1 | 0.037 | 440.39 |
| 22 | 1 | 1 | 1 | −1 | 0.322 | 681.951 |
| 23 | 2 | 0 | 0 | 0 | 0.49 | 687.609 |
| 24 | 0 | 0 | 0 | 0 | 0.166 | 583.281 |
| 25 | −1 | 1 | 1 | −1 | 0.176 | 557.612 |
| 26 | 1 | 1 | −1 | 1 | 0.338 | 511.452 |
| 27 | −1 | 1 | −1 | −1 | 0.19 | 568.908 |
| 28 | 1 | −1 | −1 | −1 | 0.22 | 490.337 |
| 29 | 0 | 0 | 0 | −2 | 0.136 | 589.762 |
| 30 | 1 | −1 | 1 | 1 | 0.26 | 414.272 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Status |
|---|---|---|---|---|---|---|
| Model | 0.2862 | 14 | 0.0204 | 28.18 | <0.0001 | significant |
| A-CNT | 0.1931 | 1 | 0.1931 | 266.26 | <0.0001 | |
| B-GN | 0.0077 | 1 | 0.0077 | 10.67 | 0.0052 | |
| C-Mixing Time | 0.0036 | 1 | 0.0036 | 4.93 | 0.0422 | |
| D-Temperature | 0.0106 | 1 | 0.0106 | 14.65 | 0.0016 | |
| 0.0047 | 1 | 0.0047 | 6.42 | 0.0229 | ||
| 0.0038 | 1 | 0.0038 | 5.26 | 0.0367 | ||
| 0.0036 | 1 | 0.0036 | 5.00 | 0.0409 | ||
| 0.0060 | 1 | 0.0060 | 8.33 | 0.0113 | ||
| 0.0136 | 1 | 0.0136 | 18.79 | 0.0006 | ||
| 0.0001 | 1 | 0.0001 | 0.1903 | 0.6689 | ||
| 0.0302 | 1 | 0.0302 | 41.57 | <0.0001 | ||
| 0.0062 | 1 | 0.0062 | 8.54 | 0.0105 | ||
| 0.0016 | 1 | 0.0016 | 2.14 | 0.1637 | ||
| 0.0019 | 1 | 0.0019 | 2.55 | 0.1309 | ||
| Residual | 0.0109 | 15 | 0.0007 | |||
| Lack-of-Fit | 0.0094 | 10 | 0.0009 | 3.22 | 0.1045 | not significant |
| Pure Error | 0.0015 | 5 | 0.0003 | |||
| Cor Total | 0.2970 | 29 | ||||
| 0.9634 | ||||||
| 0.9292 | ||||||
| 0.8103 | ||||||
| 14.95 | ||||||
| Model Precision | 22.9879 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Status |
|---|---|---|---|---|---|---|
| Model | 3.623 × | 14 | 25,876.54 | 11.03 | <0.0001 | significant |
| A-CNT | 1264.94 | 1 | 1264.94 | 0.5394 | 0.4740 | |
| B-GN | 249.05 | 1 | 249.05 | 0.1062 | 0.7490 | |
| C-Mixing time | 12,890.35 | 1 | 12,890.35 | 5.50 | 0.0332 | |
| D-Temperature | 1.931 × | 1 | 1.931 × | 82.35 | <0.0001 | |
| 34,313.58 | 1 | 34,313.58 | 14.63 | 0.0017 | ||
| 13,243.35 | 1 | 13,243.35 | 5.65 | 0.0312 | ||
| 3878.02 | 1 | 3878.02 | 1.65 | 0.2179 | ||
| 26.54 | 1 | 26.54 | 0.0113 | 0.9167 | ||
| 14,339.76 | 1 | 14,339.76 | 6.12 | 0.0259 | ||
| 1636.10 | 1 | 1636.10 | 0.6977 | 0.4167 | ||
| 861.48 | 1 | 861.48 | 0.3674 | 0.5535 | ||
| 5600.22 | 1 | 5600.22 | 2.39 | 0.1431 | ||
| 1913.15 | 1 | 1913.15 | 0.8159 | 0.3807 | ||
| 73,960.10 | 1 | 73,960.10 | 31.54 | <0.0001 | ||
| Residual | 35,174.54 | 15 | 2344.97 | |||
| Lack of Fit | 17,200.00 | 10 | 1720.00 | 0.4785 | 0.8497 | not significant |
| Pure Error | 17,974.54 | 5 | 3594.91 | |||
| Cor Total | 3.974 × | 29 | ||||
| 0.9115 | ||||||
| 0.8289 | ||||||
| 0.6856 | ||||||
| CV% | 8.74 | |||||
| Model Precision | 14.8684 |
| Name | Goal | Lower Limit | Upper Limit | Lower Weight | Upper Weight | Importance | Desirability |
|---|---|---|---|---|---|---|---|
| A: CNT | in range | 0.7 | 1.1 | 1 | 1 | 3 | 1 |
| B: GN | in range | 0.6 | 1 | 1 | 1 | 3 | 1 |
| C: Mixing time | in range | 15 | 25 | 1 | 1 | 3 | 1 |
| D: Temperature | in range | 60 | 100 | 1 | 1 | 3 | 1 |
| Sensitivity | maximize | 0.037 | 0.49 | 1 | 1 | 5 | 0.787 |
| Compression modulus | maximize | 217.341 | 739.168 | 1 | 1 | 5 | 0.963 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, S.; Tang, Y.; Bi, G.; Xiao, B.; He, G.; Lin, Y. Optimal Design of Carbon-Based Polymer Nanocomposites Preparation Based on Response Surface Methodology. Polymers 2023, 15, 1494. https://doi.org/10.3390/polym15061494
Yan S, Tang Y, Bi G, Xiao B, He G, Lin Y. Optimal Design of Carbon-Based Polymer Nanocomposites Preparation Based on Response Surface Methodology. Polymers. 2023; 15(6):1494. https://doi.org/10.3390/polym15061494
Chicago/Turabian StyleYan, Shaoqiu, Ying Tang, Gangping Bi, Bowen Xiao, Guotian He, and Yuanchang Lin. 2023. "Optimal Design of Carbon-Based Polymer Nanocomposites Preparation Based on Response Surface Methodology" Polymers 15, no. 6: 1494. https://doi.org/10.3390/polym15061494
APA StyleYan, S., Tang, Y., Bi, G., Xiao, B., He, G., & Lin, Y. (2023). Optimal Design of Carbon-Based Polymer Nanocomposites Preparation Based on Response Surface Methodology. Polymers, 15(6), 1494. https://doi.org/10.3390/polym15061494





