Numerical Simulation of the Pouring Process in Deep-Water Flexible Pipe End Fittings
Abstract
:1. Introduction
2. Methods
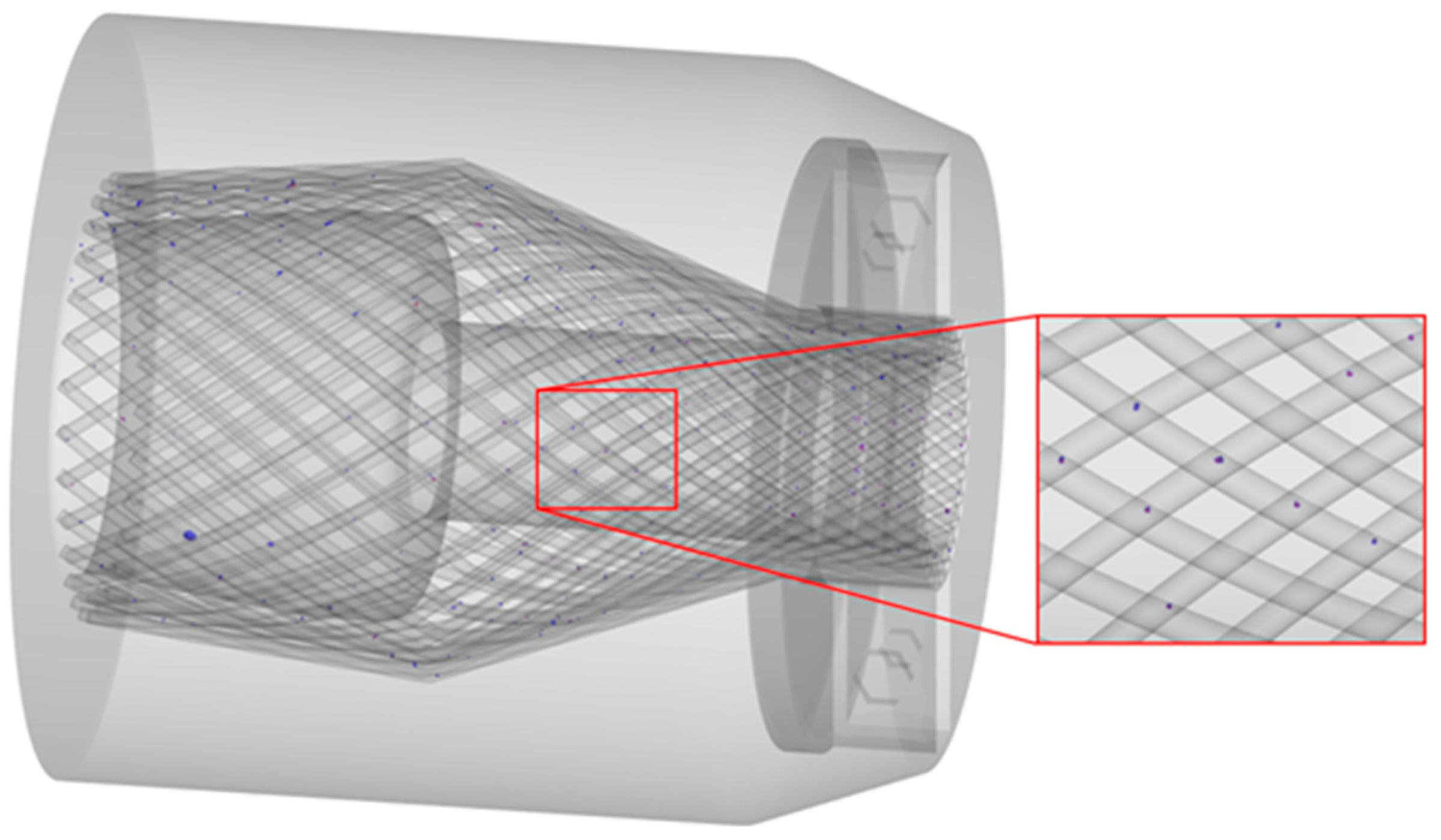
2.1. Geometry and Finite Element Models
2.2. Boundary Conditions
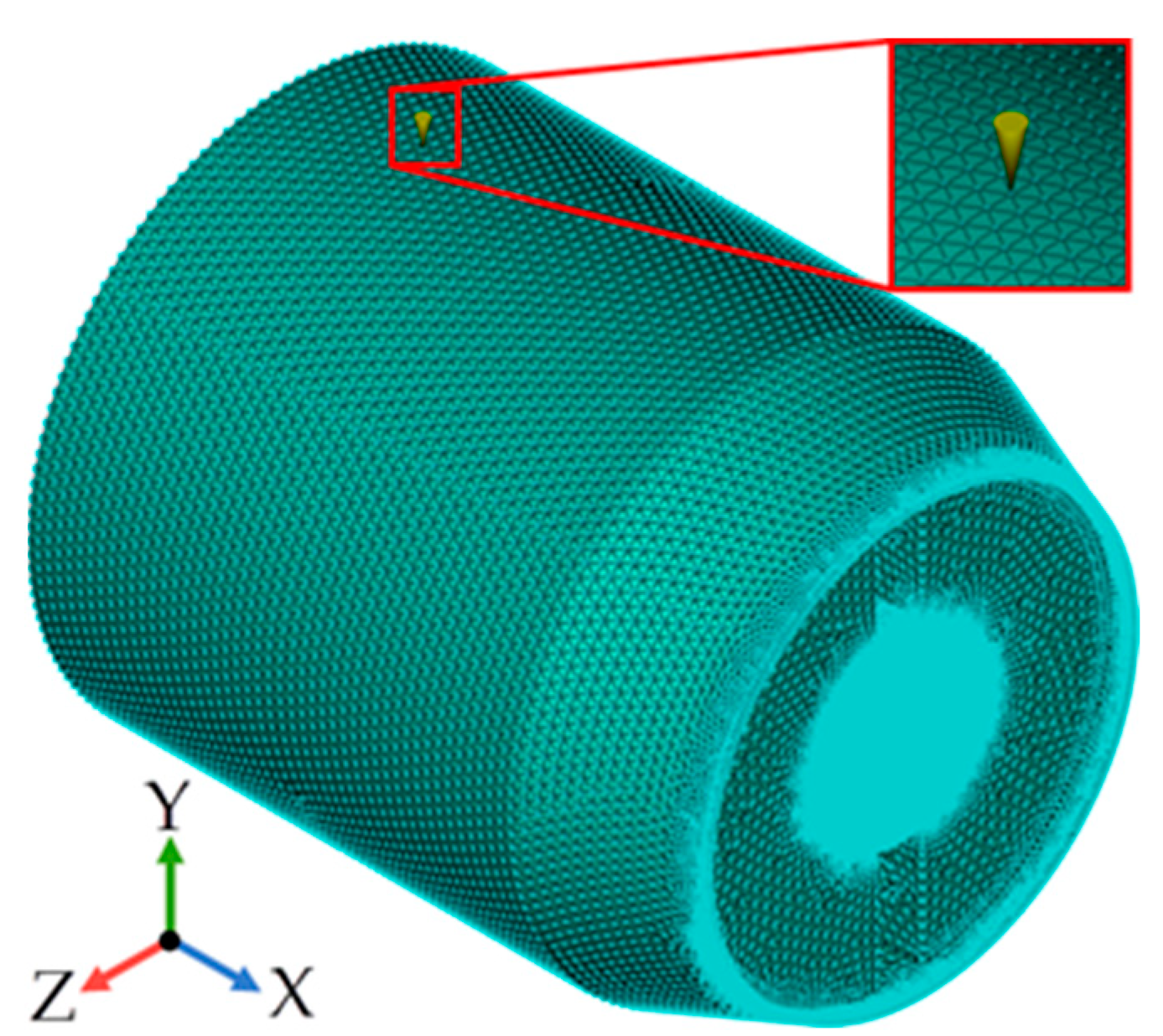
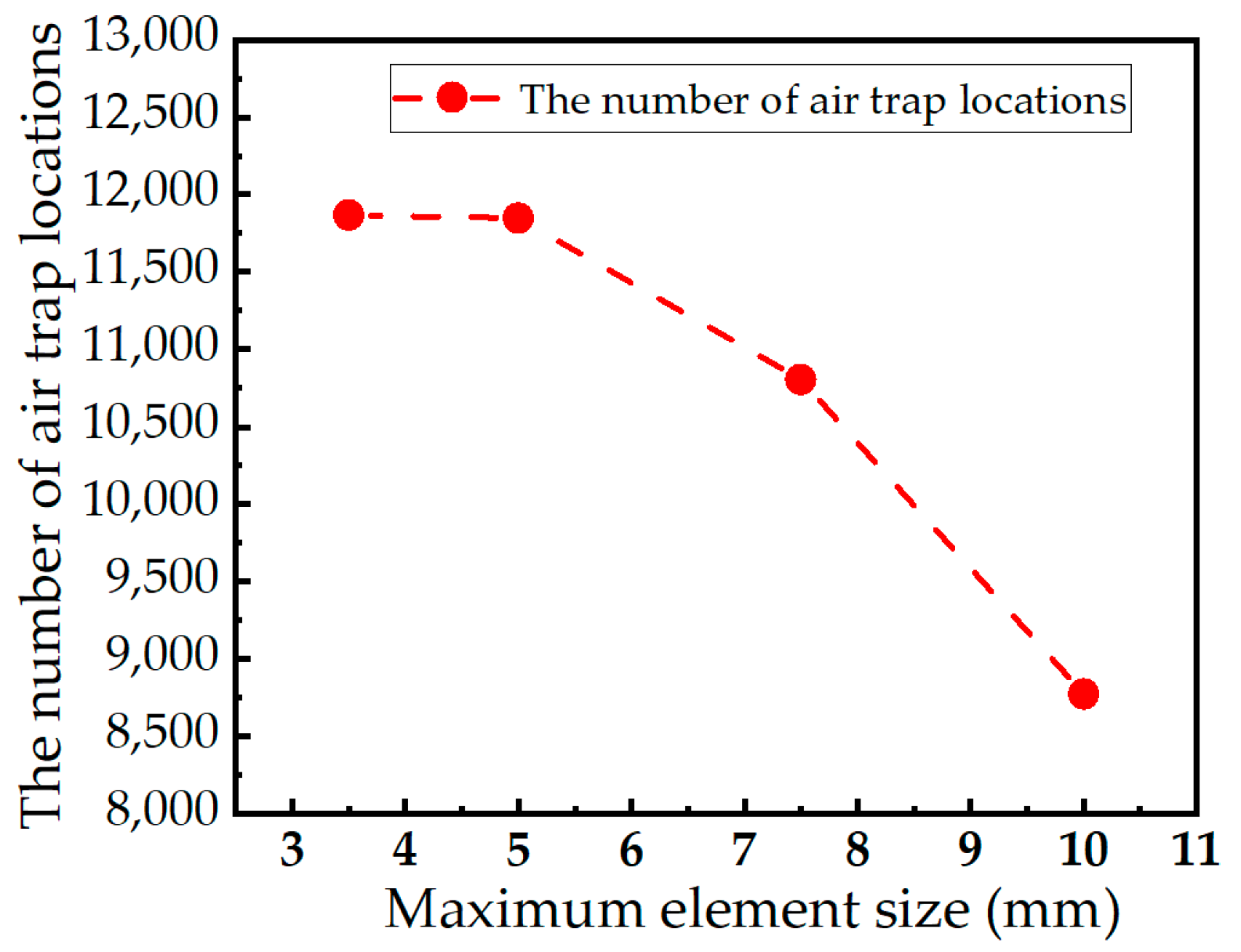
2.3. Mesh Independency
3. Results and Discussion
3.1. Simulation Result and Analysis
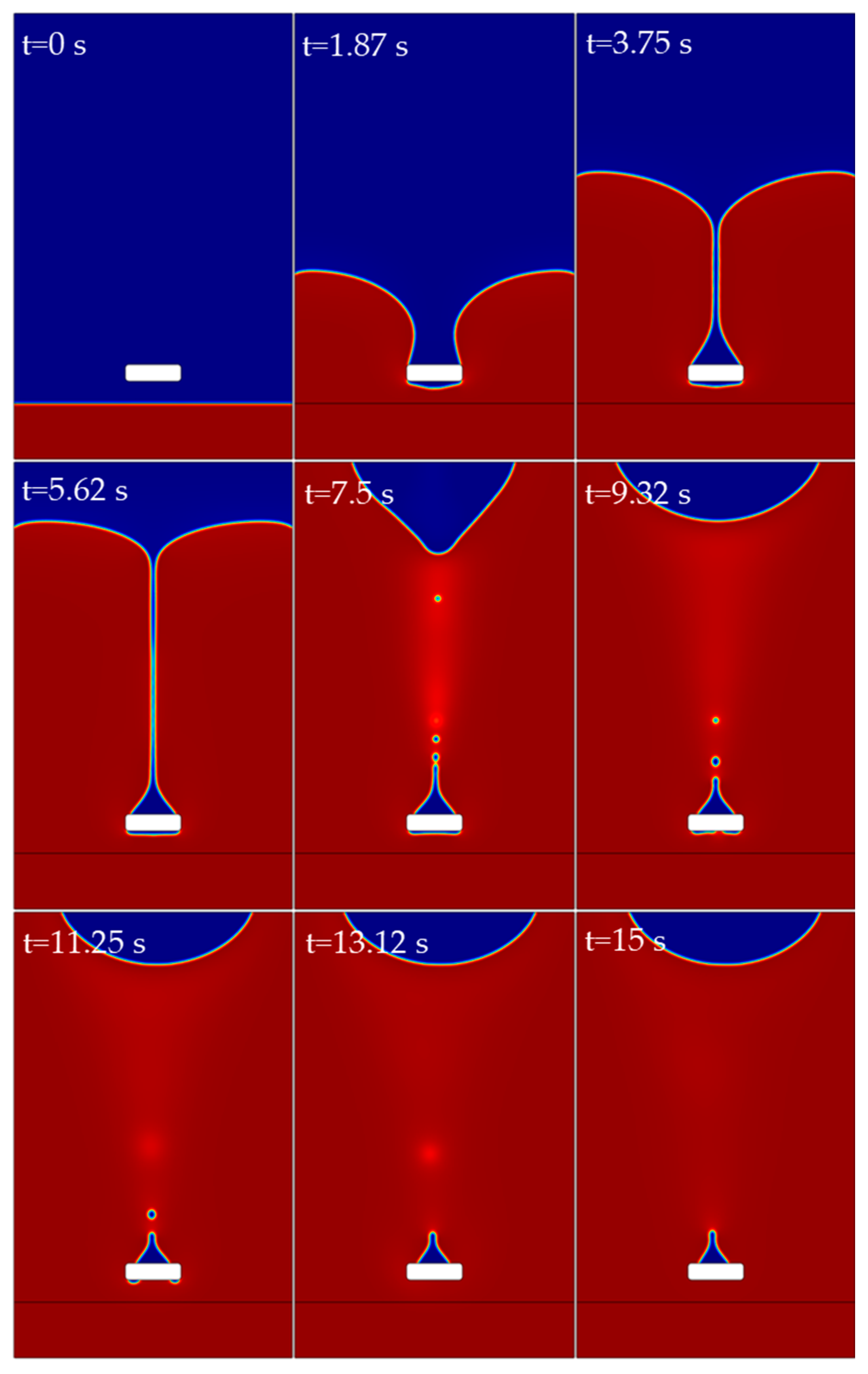
3.1.1. Distribution of Air Traps
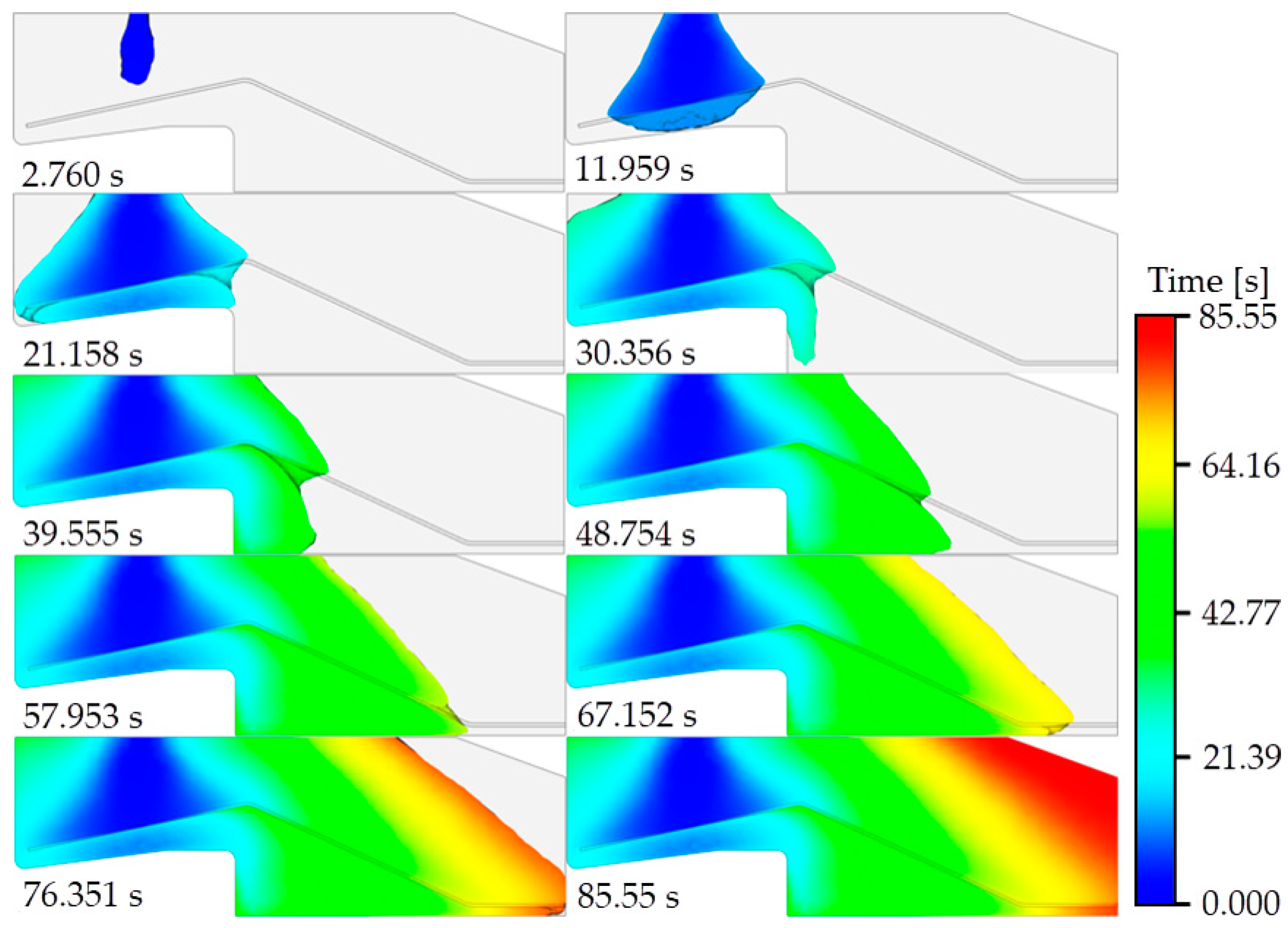
3.1.2. Resin Flow Condition
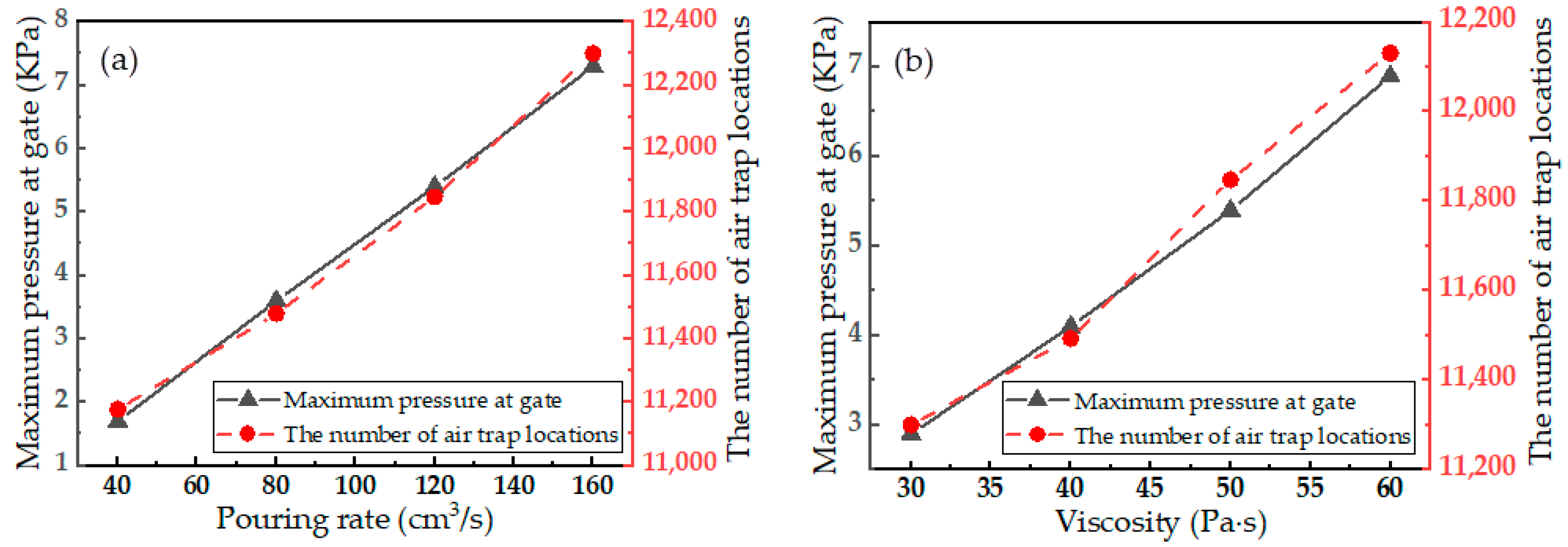
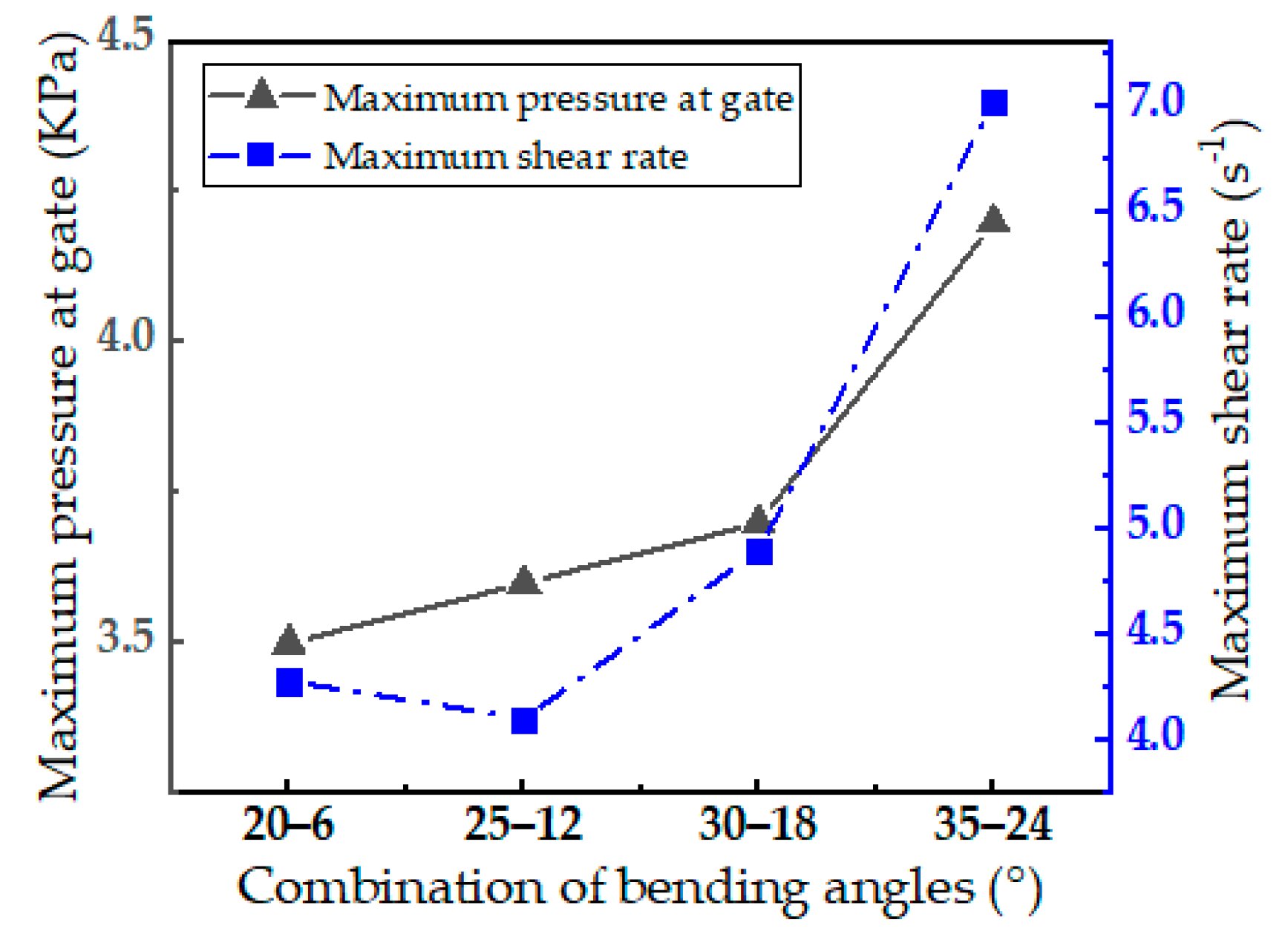
3.1.3. Effect of Process Conditions
3.2. Effect of Tensile Armor Steel Wire on Pouring Quality
3.2.1. Bending Pattern of Steel Wires
3.2.2. Steel Wire Section Shape
3.3. Validation of Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Yang, L. The Strategic Selection for the Exploitation and Utilization of Oil and Gas Resources under the Background of “Double Carbon” Goal and Energy Security in China. Urban Environ. Stud. 2022, 14, 56–69. [Google Scholar]
- Tang, M.; Zhang, Z.; Wu, B.; Chen, C.; Gu, X. Application and Technical Challenge of Flexible Pipe in Deep-sea Mining. Ocean. Eng. Equip. Technol. 2019, 6, 765–770. [Google Scholar]
- Gao, B.; Yang, Z.; Wu, S.; Lu, Q.; Han, H.; Yan, J.; Yue, Q. Study on Prediction Methods of Burst Failure for Marine Unbounded Flexible Pipes Considering Clearance between Pressure Armors. Shipbuild. China 2018, 59, 60–71. [Google Scholar]
- Mao, Q. Key Design Issues of Offshore Flexible Pipe End Fitting. Master’s Thesis, Dalian University of Technology, Dalian, China, 2013. [Google Scholar]
- Tian, K. Digital Design and Manufacturing Technology of Offshore Flexible Pipe End Fitting. Master’s Thesis, Dalian University of Technology, Dalian, China, 2014. [Google Scholar]
- Zhang, L. Analysis and Design of the Sealing System in Unbonded Flexible Pipe End Fitting. Master’s Thesis, Dalian University of Technology, Dalian, China, 2016. [Google Scholar]
- Torres, R.N.; Tanaka, R.L.; Morini, R.G.; Otte Filho, O.O.; Vilela, T. Flexible Pipe Anchoring System: Resin Ratio Effects on Mechanical Properties. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar]
- Xavier, F.G. Avaliação da Vida em Fadiga de um Novo Modelo de Terminal Conector Para Dutos Flexíveis. Ph.D. Thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, 2009. [Google Scholar]
- Bueno, A.F.B. Avaliação das Armaduras de Tração de Riser Flexível Durante Ensaios Axiais de Tração e Fadiga. Ph.D. Thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, 2010. [Google Scholar]
- Otte Filho, O.O.; Tanaka, R.L.; Morini, R.G.; Torres, R.N.; Vilela, T.S.V. Thermal effects on the anchoring of flexible pipe tensile armors. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar]
- Campello, G.; Bertoni, F.; de Sousa, J.R.M.; Carpigiani, M.; Vardaro, E.; Mudry, G. A Novel Concept of Flexible Pipe End Fitting: Tensile Armor Foldless Assembly. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012. [Google Scholar]
- Anastasiadis, P.S.; Theotokoglou, E.E.; Michailides, C. Numerical analysis of stress concentration factors on tensile armour wires inside the end-fitting of an axially tensed unbonded flexible pipe. J. Struct. Integr. Maint. 2020, 5, 72–86. [Google Scholar] [CrossRef]
- Shen, Y.; Ma, F.; Tan, Z.; Sheldrake, T.H. Development of the End Fitting Tensile Wires Fatigue Analysis Model: Sample Tests and Validation in an Unbonded Flexible Pipe. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2008. [Google Scholar]
- Connaire, A.; Smyth, J.; Nestor, R.; Tanaka, R.; Albuquerque, E. Validation of Solid Modeling and Analysis Techniques for Response Prediction of Deepwater Flexible Pipe. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar]
- Zhang, Z.Y.; Zhang, H.G.; Liu, Y.Y.; Hu, Q.X. The Research on Two-Component Materials Mixed Method for Vacuum Casting. Adv. Mater. Res. 2013, 712–715, 729–734. [Google Scholar] [CrossRef]
- Bin Ahmad, M.N.; Maidin, N.A.B.; Rahman, M.H.B.; Bin Osman, M.H.; Bin Wahid, M.K.; Basir, M.F.B. Shrinkage Effect of Vacuum Casting Process Parameters using Taguchi Method. Int. J. Integr. Eng. 2019, 11, 248–254. [Google Scholar]
- Jin, T.; Liu, Y.; Liu, S. Numerical Simulation of Temperature Field in Curing Process for Epoxy Resin Dry-type Transformer Winding. High Volt. Appar. 2008, 44, 385–388. [Google Scholar]
- Fan, X.; Du, C.; Mou, M. Appearance Quality Analysis of Epoxy Resin Vacuum Casting Product. Insul. Mater. 2014, 47, 106–109. [Google Scholar]
- Wu, H. Resin Vacuum Cast Process and Its Points for Attention. Transformer 2000, 37, 33–36. [Google Scholar]
- Li, X. Investigation of Design and Analysis for Unbonded Flexible Pipe end fitting Structural. Master’s Thesis, Dalian University of Technology, Dalian, China, 2014. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; He, C.; Zhang, T.; Lu, Q.; Yan, J. Numerical Simulation of the Pouring Process in Deep-Water Flexible Pipe End Fittings. Polymers 2023, 15, 1397. https://doi.org/10.3390/polym15061397
Li H, He C, Zhang T, Lu Q, Yan J. Numerical Simulation of the Pouring Process in Deep-Water Flexible Pipe End Fittings. Polymers. 2023; 15(6):1397. https://doi.org/10.3390/polym15061397
Chicago/Turabian StyleLi, Hongxia, Chenwei He, Tao Zhang, Qingzhen Lu, and Jun Yan. 2023. "Numerical Simulation of the Pouring Process in Deep-Water Flexible Pipe End Fittings" Polymers 15, no. 6: 1397. https://doi.org/10.3390/polym15061397
APA StyleLi, H., He, C., Zhang, T., Lu, Q., & Yan, J. (2023). Numerical Simulation of the Pouring Process in Deep-Water Flexible Pipe End Fittings. Polymers, 15(6), 1397. https://doi.org/10.3390/polym15061397





