A Class of Algorithms for Recovery of Continuous Relaxation Spectrum from Stress Relaxation Test Data Using Orthonormal Functions
Abstract
1. Introduction
2. Materials and Methods
2.1. Relaxation Spectrum
2.2. Models
2.3. Identification Problem
2.4. Regularization
2.5. Algebraic Background
3. Results and Discussion
3.1. Identification Algorithm
- Choose the time-scaling factor and the number of model components comparing, for different values of , a few first functions from the sequence with the experiment results .
- Compute the matrix (11) and next determine SVD (18).
- Determine GCV function (21), and next compute the optimal regularization parameter minimizing , i.e., solving the optimization task (17).
- Compute the regularized solution according to (19) for .
- For , using computed above, determine the modified spectrum of relaxation frequencies according to:
- Determine the spectrum of relaxation frequencies according to
Two Remarks
- Only the SVD of the matrix, , of computational complexity [45] is a space- and time-consuming task of the scheme. However, the SVD must be computed only once and is accessible in the form of optimized numerical procedures in most commonly used computational packets.
- The matrix depends on the choice of the basis functions as well as the measurement points ; however, it does not depend on the relaxation modulus measurements . Thus, when the identification scheme is applied for successive samples of the same material, step 3 should not be repeated while the same time instants are kept and the same model parameters and are selected in step 2.
3.2. Analysis
- (a)
- The model of the relaxation spectrum that we would obtain on the basis of ideal (undisturbed) measurements of the relaxation modulus:
- (b)
- The model of the relaxation spectrum that we obtain on the basis of the normal solution of the linear-quadratic problem (13) for noise measurements of the relaxation modulus:
- (c)
- The model of the relaxation spectrum that we would obtain on the basis of the normal solution of the linear-quadratic problem (13) for noise-free measurements of the relaxation modulus:
3.2.1. Smoothness
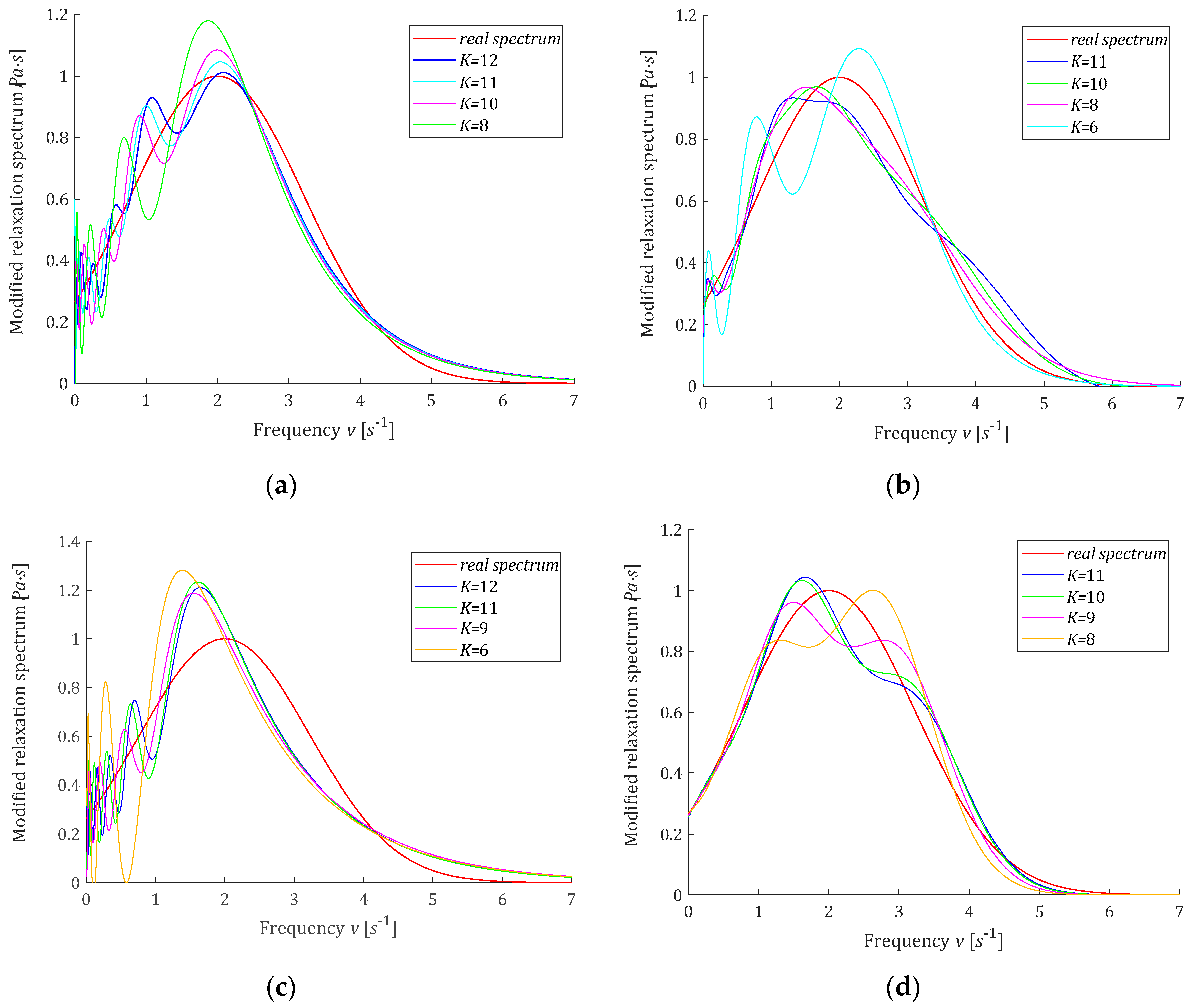
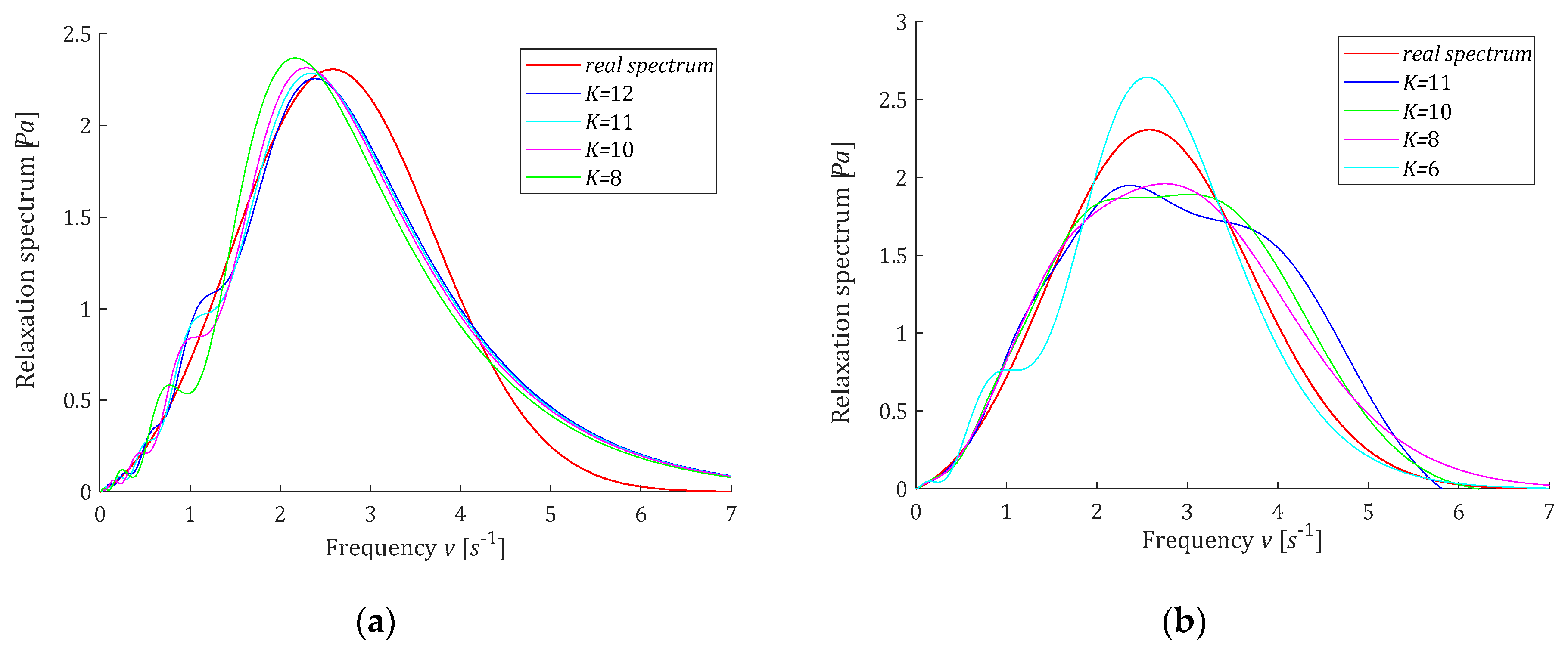
3.2.2. Convergence
3.2.3. Noise Robustness
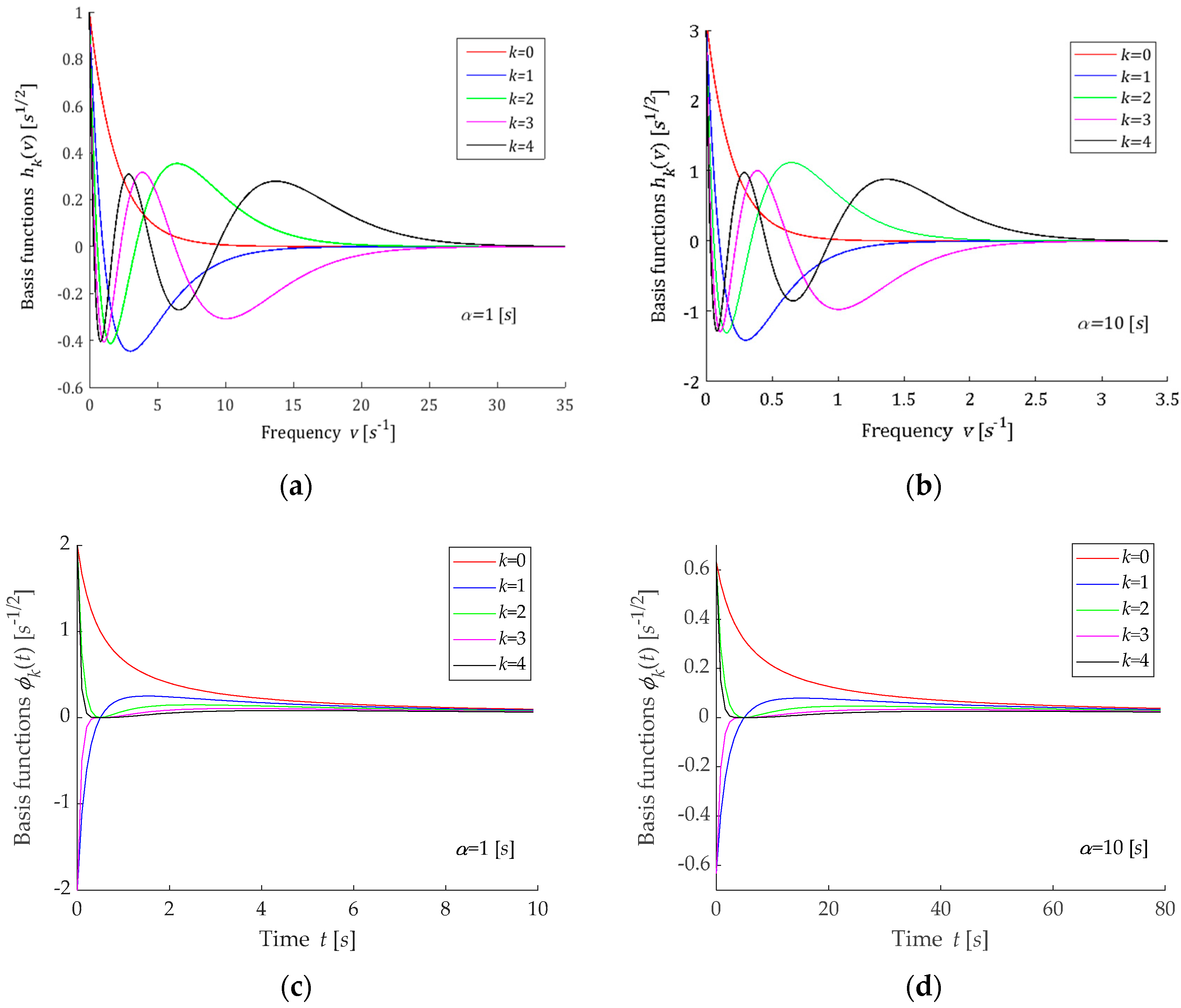
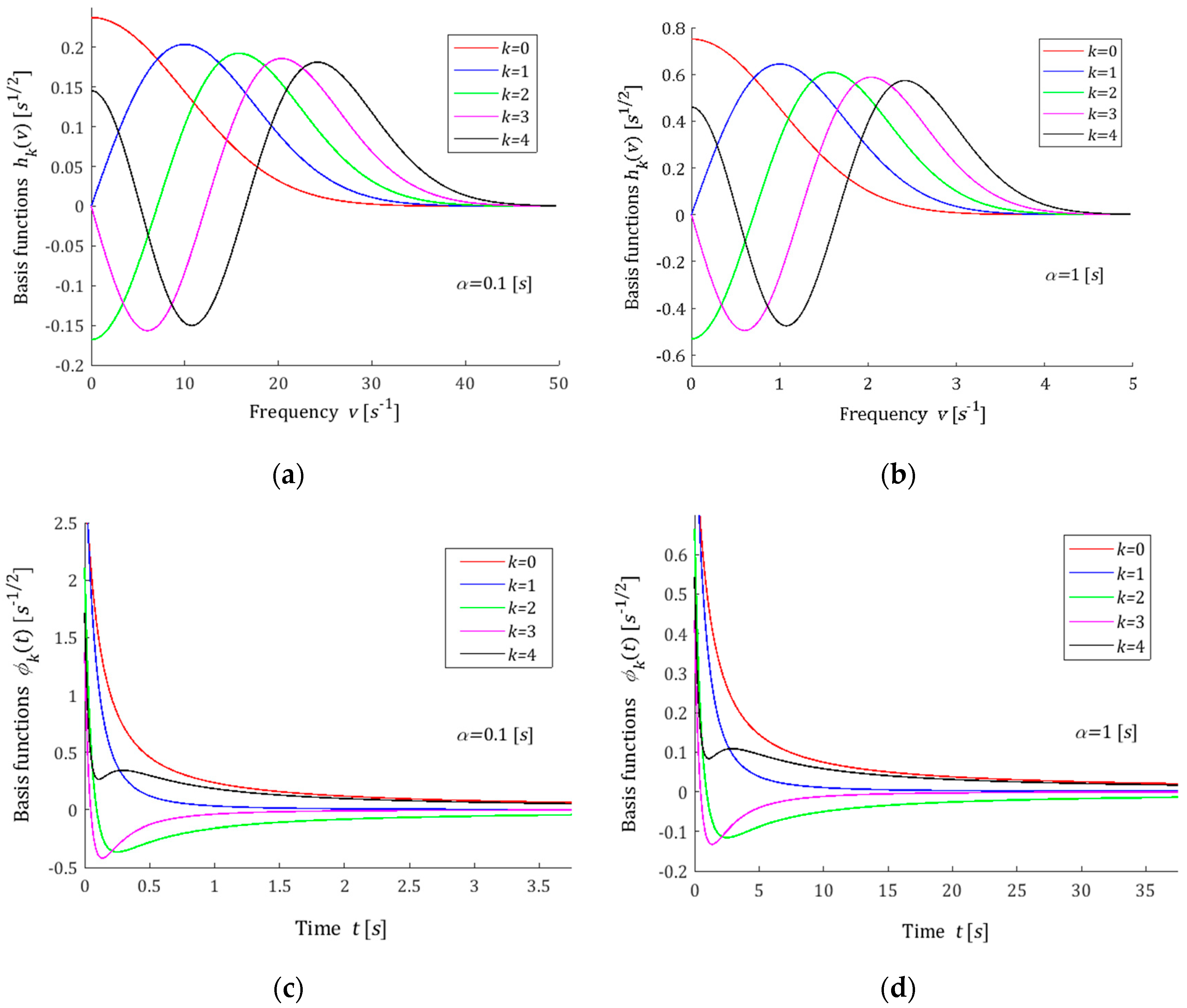
3.3. Legendre Model
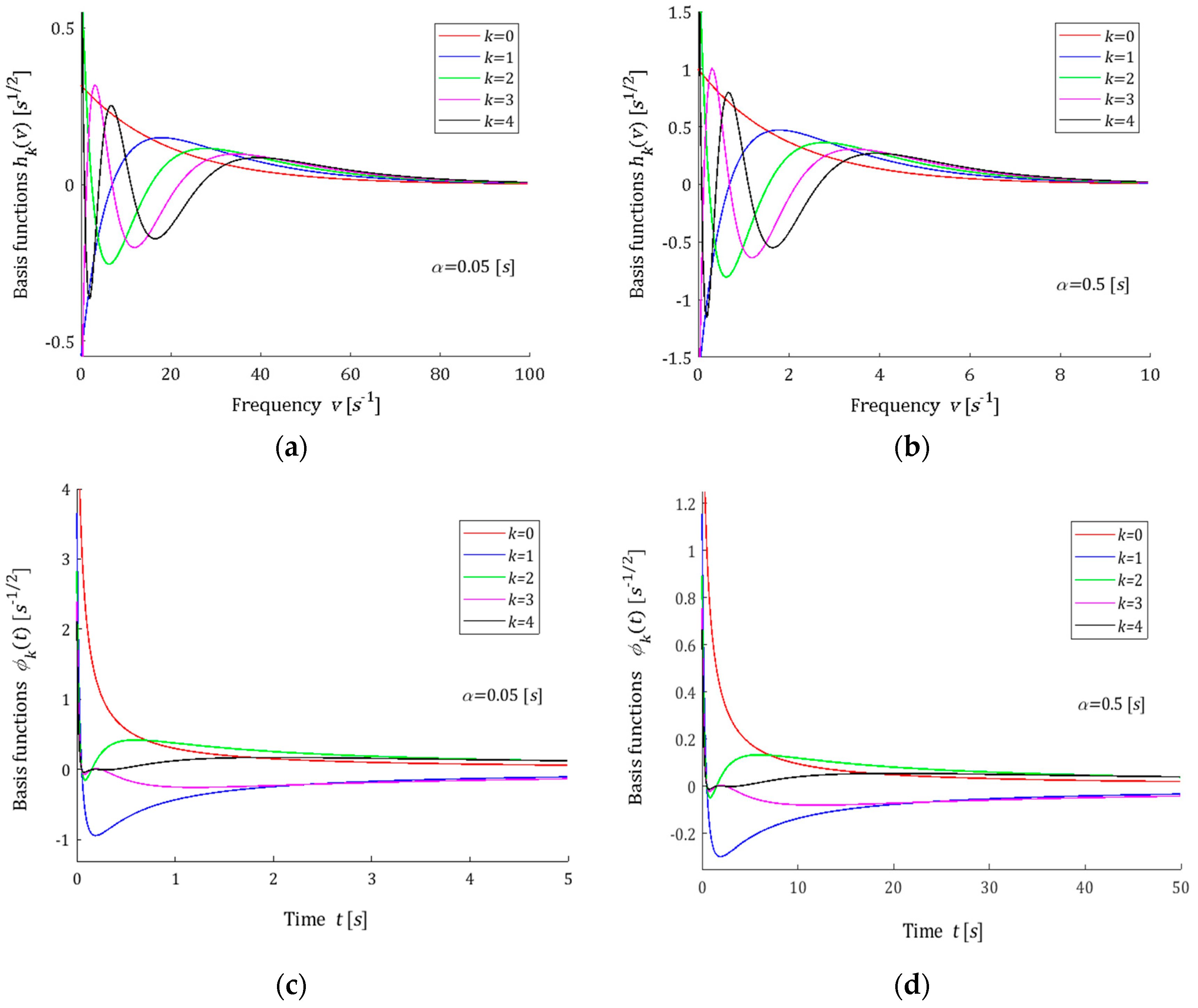
3.4. Laguerre Model
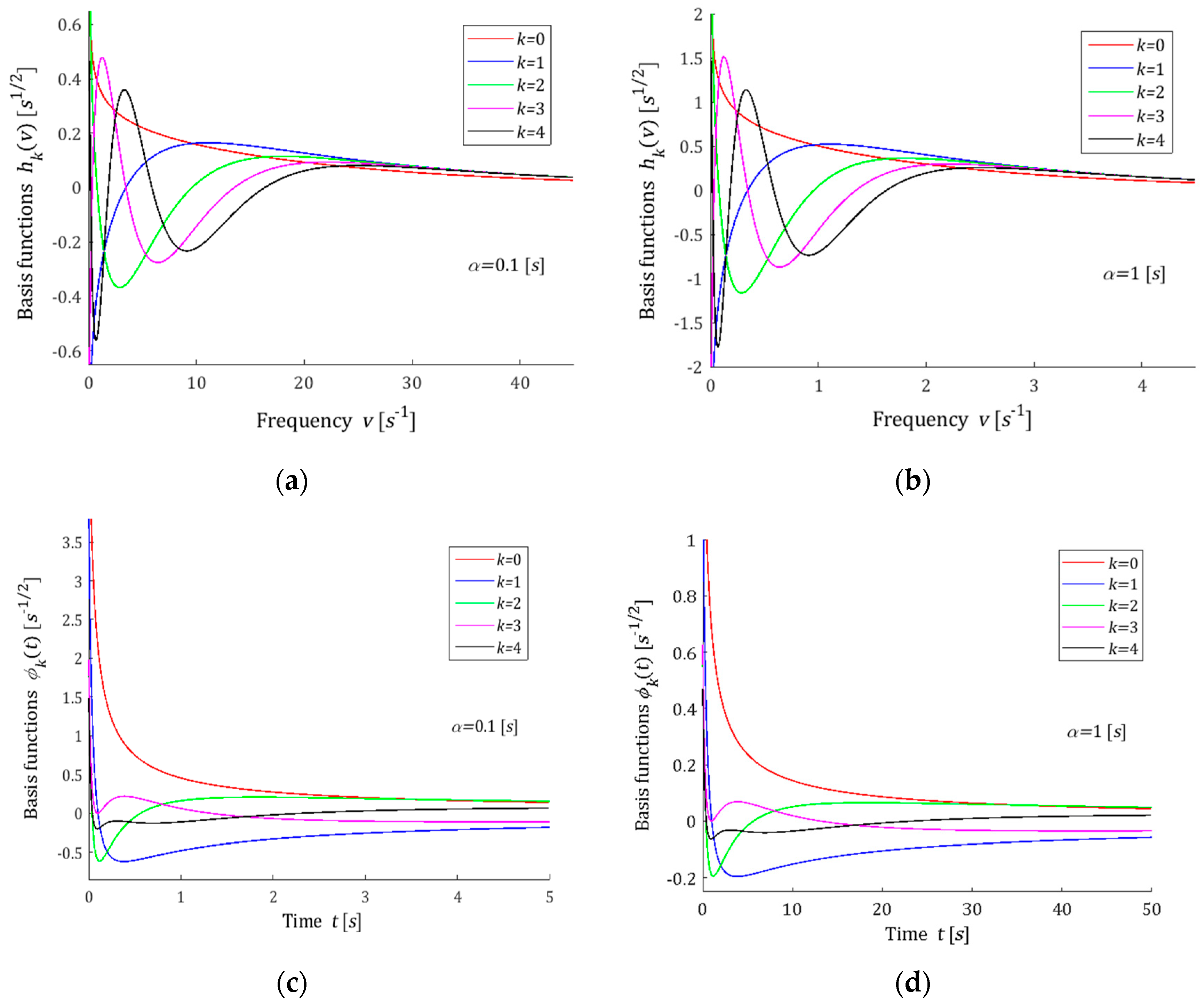
3.5. Chebyshev Model
3.6. Hermite Model
Smoothness
3.7. Choice of the Basis Functions
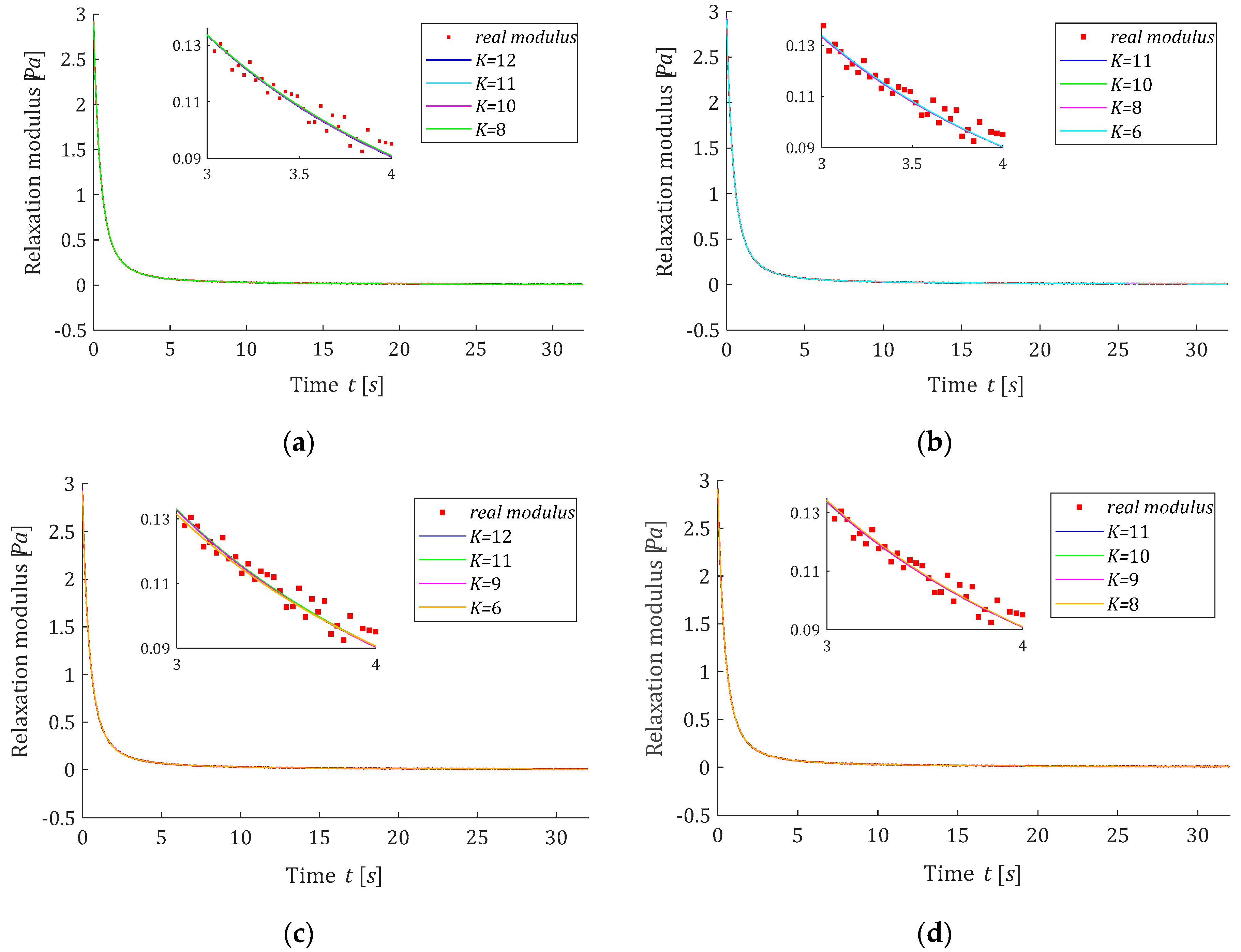
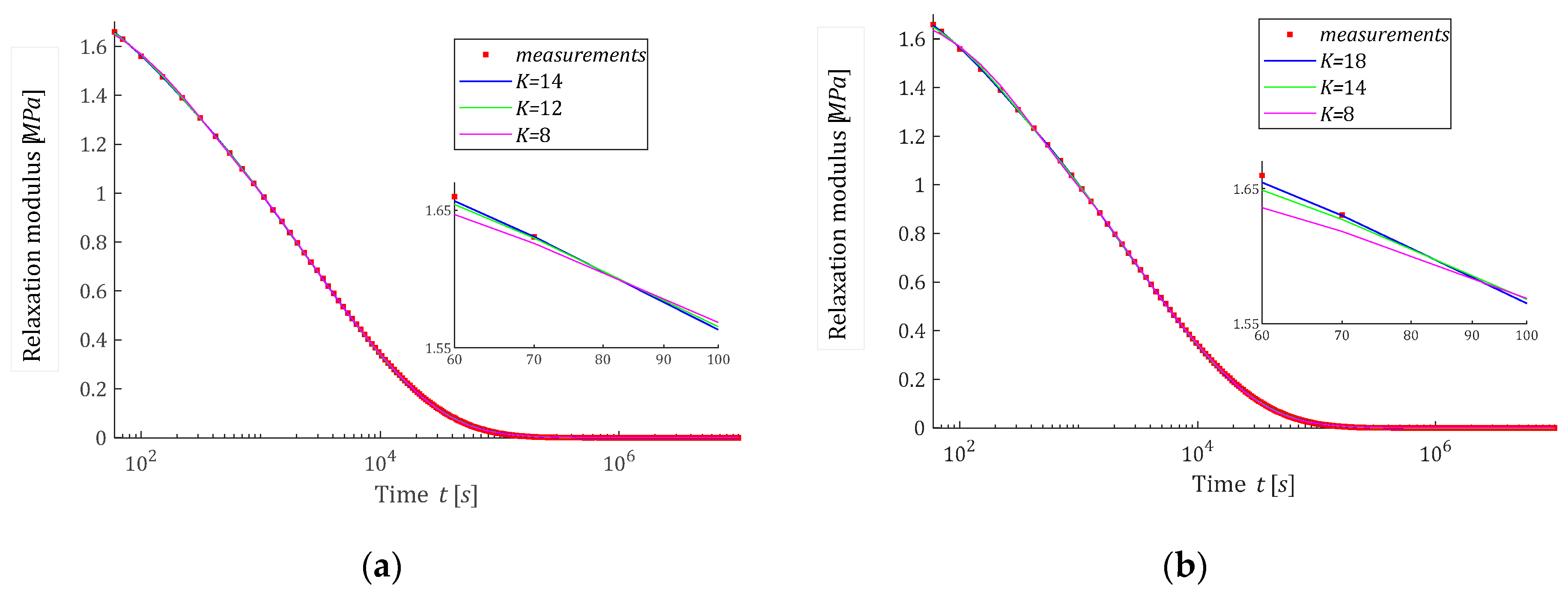
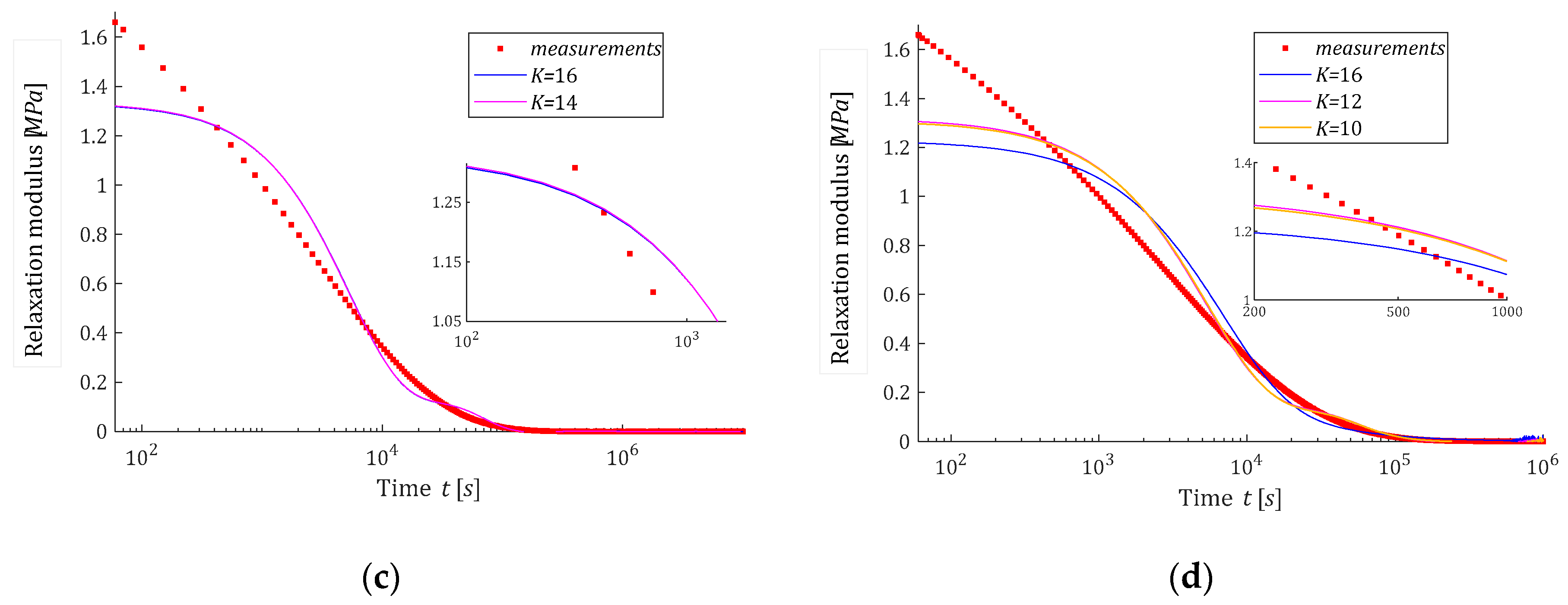
3.8. Example 1
3.9. Example 2
3.10. Remarks
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| noise corrupted | |
| relaxation modulus model corresponding to | |
| dimensional vector of the measurements , Equation (11) | |
| dimensional vector of noise-free measurements | |
| parameters of the , | |
| (8) | |
| solution of regularized task (14) given for regularization parameter by (15) or (19) | |
| solution of regularized task (14) for ideal measurements, Equation (25) | |
| vector of optimal model parameters determined by GCV method | |
| normal solutions of least-squares problem (13) for noise and noise-free measurements of the relaxation modulus | |
| continuous spectrum of relaxation frequencies | |
| model of | |
| model of | |
| model of obtained for ideal measurements, | |
| models of obtained for the normal solutions | |
| basis functions of the , | |
| dimensional identity matrix | |
| number of summands, Equation (7), – | |
| number of measurements in the stress relaxation test, – | |
| square identification index defined by (10), | |
| number of non-zero singular values of , – | |
| time interval from which the sampling instants were generated | |
| orthogonal matrices of singular value decomposition of , Equation (18) | |
| the GCV functional defined by (16) and expressed by (21) | |
| dimensional vector | |
| dimensional vector , | |
| time-scaling factor of the basis functions | |
| regularization parameter introduced in the optimization task (14), – | |
| optimal regularization parameter determined by GCV method, Equation (17) | |
| diagonal matrix defined by (20) | |
| the non-zero singular values of , Equation (18) | |
| diagonal matrix of singular values of , Equation (18) | |
| matrix defined by (11) basis for least-squares task (13) | |
| integral square error of approximation, Equation (60), |
Appendix A
Appendix A.1. Derivation of the Formula (32)
Appendix A.2. Derivation of Formula (35)
Appendix A.3. Derivation of Formulas (40)–(43)
Appendix A.4. Derivation of Formulas (47)–(49)
Appendix A.5. Proof of Formulas (52) and (53)
Appendix A.6. Applicability of the Models for Various Time-Scale Parameters
| Model | Time-Scale Factor | Range 1 of Relaxation Frequency | Range 1 of Time |
|---|---|---|---|
| Legendre model | 0.001 | 5301 | 3.615 |
| 0.01 | 530 | 36.15 | |
| 0.1 | 53 | 361.5 | |
| 1 | 5.3 | 3614.6 | |
| 10 | 0.53 | 36,144.5 | |
| 100 | 0.05301 | 361,445 | |
| 1000 | 0.005301 | 3,614,450 | |
| 10,000 | 0.0005301 | 36,144,500 | |
| Laguerre model | 0.01 | 5256 | 0.995 |
| 0.1 | 525.36 | 9.95 | |
| 1 | 52.5359 | 99.5 | |
| 10 | 5.2536 | 995 | |
| 100 | 0.528 | 9950 | |
| 1000 | 0.0526 | 99,500 | |
| 10,000 | 0.00526 | 995,000 | |
| 100,000 | 0.000526 | 9,950,000 | |
| Chebyshev model | 0.001 | 10,020 | 0.34125 |
| 0.01 | 1002 | 3.4125 | |
| 0.1 | 100.2 | 34.125 | |
| 1 | 10.02 | 341.25 | |
| 10 | 1.002 | 3412.5 | |
| 100 | 0.1002 | 34,125 | |
| 1000 | 0.01002 | 341,250 | |
| 10,000 | 0.001002 | 3,412,500 | |
| 100,000 | 0.0001002 | 34,125,000 | |
| Hermite model | 0.001 | 4797.5 | 0.037639 |
| 0.01 | 479.75 | 0.376394 | |
| 0.1 | 47.975 | 3.7639 | |
| 1 | 4.7975 | 37.63944 | |
| 10 | 0.47975 | 376.3944 | |
| 100 | 0.047975 | 3763.944 | |
| 1000 | 0.0047975 | 37,639.443 | |
| 10,000 | 0.00047975 | 376,394.436 | |
| 100,000 | 0.000047975 | 3,763,944.359 |
Appendix B
| Model | ||||||
|---|---|---|---|---|---|---|
| Legendre model | 0.8222 | 0.8225 | 0.8229 | 0.8232 | 0.8235 | 0.8238 |
| 0.7699 | 0.7695 | 0.7705 | 0.7714 | 0.7723 | 0.7731 | |
| 0.6138 | 0.5979 | 0.5963 | 0.5959 | 0.5963 | 0.5970 | |
| 0.5299 | 0.4503 | 0.4347 | 0.4263 | 0.4215 | 0.4188 | |
| 0.5448 | 0.3564 | 0.3215 | 0.3021 | 0.2889 | 0.2801 | |
| 0.4300 | 0.3190 | 0.2887 | 0.2647 | 0.2490 | 0.2378 | |
| 0.2807 | 0.2442 | 0.2227 | 0.2074 | 0.1966 | ||
| 0.2520 | 0.2185 | 0.1945 | 0.1781 | 0.1663 | ||
| 0.1973 | 0.1742 | 0.1578 | 0.1462 | |||
| 0.1562 | 0.1398 | 0.1280 | ||||
| 0.1264 | 0.1146 | |||||
| 0.1030 | ||||||
| Laguerre model | 0.3277 | 0.3265 | 0.3265 | 0.3266 | 0.3267 | |
| −0.5817 | −0.5814 | −0.5804 | −0.5795 | −0.5805 | ||
| 0.7416 | 0.7908 | 0.7897 | 0.7891 | 0.7856 | ||
| −0.6558 | −0.7164 | −0.7193 | −0.7163 | −0.7109 | ||
| 0.7138 | 0.5043 | 0.5076 | 0.5013 | 0.5015 | ||
| −0.5418 | −0.36570 | −0.3658 | −0.3777 | −0.3717 | ||
| 0.2063 | 0.2083 | 0.2121 | 0.2282 | |||
| −0.0935 | −0.0918 | −0.1178 | −0.1254 | |||
| −0.0054 | 0.0122 | 0.0446 | ||||
| 0.0517 | 0.0269 | |||||
| −0.0712 | ||||||
| Chebyshev model | 0.8227 | 0.8265 | 0.8316 | 0.7988 | 0.8023 | 0.7991 |
| 0.8350 | 0.8226 | 0.8139 | 0.7962 | 0.7905 | 0.7944 | |
| 0.5313 | 0.5312 | 0.5382 | 0.5234 | 0.5287 | 0.5248 | |
| 0.5168 | 0.4545 | 0.4362 | 0.4502 | 0.4397 | 0.4416 | |
| 0.4625 | 0.3392 | 0.3233 | 0.3549 | 0.3426 | 0.3294 | |
| 0.4209 | 0.2912 | 0.2623 | 0.3195 | 0.2992 | 0.2828 | |
| 0.2444 | 0.2138 | 0.2768 | 0.2542 | 0.2403 | ||
| 0.2148 | 0.1899 | 0.2509 | 0.2317 | 0.2146 | ||
| 0.1603 | 0.2270 | 0.2047 | 0.1899 | |||
| 0.2112 | 0.1917 | 0.1752 | ||||
| 0.1734 | 0.1585 | |||||
| 0.1487 | ||||||
| Hermite model | 0.5504 | 0.6391 | 0.5909 | 0.6044 | 0.6051 | |
| 0.7337 | 0.7670 | 0.8046 | 0.8004 | 0.8009 | ||
| 0.7965 | 0.6140 | 0.6703 | 0.6826 | 0.6853 | ||
| 0.6881 | 0.5241 | 0.4749 | 0.5005 | 0.5075 | ||
| 0.4916 | 0.5137 | 0.4089 | 0.3846 | 0.3885 | ||
| 0.7075 | 0.4046 | 0.3715 | 0.2971 | 0.2875 | ||
| 0.2833 | 0.2769 | 0.2366 | 0.2181 | |||
| 0.3419 | 0.2239 | 0.2318 | 0.2207 | |||
| 0.2576 | 0.2218 | 0.2178 | ||||
| 0.1315 | 0.1381 | |||||
| 0.0236 | ||||||
| Model | ||||||
|---|---|---|---|---|---|---|
| Legendre model | 43.80739 | 39.6666 | 37.4618 | 35.1566 | 32.2127 | |
| −29.51378 | −31.6618 | −32.1025 | −32.1325 | −31.6435 | ||
| 8.10418 | 15.9237 | 19.1145 | 21.6308 | 23.8515 | ||
| −2.20279 | −6.1369 | −8.1839 | −10.9840 | −14.3753 | ||
| −3.819709 | 0.0198 | 1.5667 | 3.9792 | 7.5618 | ||
| 32.529089 | 10.4212 | 5.8515 | 2.9019 | −0.9375 | ||
| −10.2725 | −5.9794 | −4.2456 | −1.7853 | |||
| 19.8011 | 11.2957 | 8.1554 | 5.3793 | |||
| −8.6168 | −6.9530 | −5.7798 | ||||
| 12.6105 | 9.3899 | 7.7029 | ||||
| −7.0433 | −6.9429 | |||||
| 8.7841 | 7.9943 | |||||
| −6.6946 | ||||||
| 7.3213 | ||||||
| Laguerre model | 53.0965 | 53.0609 | 53.0093 | 53.0664 | 52.5153 | 52.7585 |
| −1.4762 | 0.2502 | 1.8283 | 0.4988 | 6.3911 | 4.8727 | |
| 6.9102 | 6.5809 | 6.4712 | 5.2459 | 8.0061 | 6.8685 | |
| −0.2900 | −3.7059 | −4.5349 | −6.4194 | −2.4884 | −4.0192 | |
| −10.8544 | −6.2248 | −3.8522 | −3.7269 | −0.8334 | −1.5307 | |
| −10.7846 | −6.6303 | −6.0659 | −6.4034 | −4.9840 | −5.6574 | |
| −8.9629 | −8.7827 | −7.0219 | −6.1421 | −4.2199 | −4.2360 | |
| −28.0790 | −12.2858 | −8.2334 | −6.5918 | −6.1999 | −6.0076 | |
| −6.1049 | −6.7165 | −5.7225 | −5.4599 | −4.9298 | ||
| −18.5624 | −10.7187 | −7.3355 | −6.9589 | −6.0759 | ||
| −4.8687 | −4.0801 | −5.6896 | −4.7692 | |||
| −13.0786 | −8.3498 | −7.4589 | −6.0712 | |||
| −2.0153 | −5.4359 | −4.2447 | ||||
| −9.4015 | −7.7715 | −6.0352 | ||||
| −4.9662 | −3.5890 | |||||
| −7.9368 | −5.9731 | |||||
| −2.9159 | ||||||
| −5.8840 | ||||||
Appendix C
Mathematical Terminology and Special Functions
| complementary error function, Equation (50) | |
| Hermite polynomials, , Equations (45) and (46) | |
| Laguerre polynomials, , Equation (33) | |
| Legendre polynomials, , Equations (A1)–(A3) | |
| Chebyshev polynomials of the first kind, , Equations (36) and (37) | |
| space of real-valued square-integrable functions on the interval | |
| Laplace transform of the function | |
| Euler’s gamma function | |
| square norm in the real Euclidean space and in | |
| find the value of , which minimizes the function |
References
- Anderssen, R.S.; Davies, A.R.; de Hoog, F.R.; Loy, R.J. Derivative based algorithms for continuous relaxation spectrum recovery. J. Non-Newton. Fluid Mech. 2015, 222, 132–140. [Google Scholar] [CrossRef]
- Chang, F.-L.; Bin, H.; Huang, W.-T.; Chen, L.; Yin, X.-C.; Cao, X.-W.; He, G.-J. Improvement of rheology and mechanical properties of PLA/PBS blends by in-situ UV-induced reactive extrusion. Polymer 2022, 259, 125336. [Google Scholar] [CrossRef]
- Ankiewicz, S.; Orbey, N.; Watanabe, H.; Lentzakis, H.; Dealy, J. On the use of continuous relaxation spectra to characterize model polymers. J. Rheol. 2016, 60, 1115–1120. [Google Scholar] [CrossRef]
- Dealy, J.M.; Read, D.J.; Larson, R.G. Structure and Rheology of Molten Polymers, 2nd ed.; Carl Hanser Verlag GmbH & Co. KG: Munich, Germany, 2018; pp. 105–145. [Google Scholar] [CrossRef]
- Pogreb, R.; Loew, R.; Bormashenko, E.; Whyman, G.; Multanen, V.; Shulzinger, E.; Abramovich, A.; Rozban, A.; Shulzinger, A.; Zussman, E.; et al. Relaxation spectra of polymers and phenomena of electrical and hydrophobic recovery: Interplay between bulk and surface properties of polymers. J. Polym. Sci. Part B: Polym. Phys. 2017, 55, 198–205. [Google Scholar] [CrossRef]
- Owens, R.G.; Phillips, T.N. Computational Rheology; World Scientific: London, UK, 2002. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Mead, D.W. Numerical interconversion of linear viscoelastic material functions. J. Rheol. 1994, 38, 1769–1795. [Google Scholar] [CrossRef]
- Hajikarimi, P.; Moghadas Nejad, F. Chapter 6-Interconversion of constitutive viscoelastic functions. In Applications of Viscoelasticity; Hajikarimi, P., Moghadas Nejad, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 107–139. [Google Scholar] [CrossRef]
- Baumgaertel, M.; Winter, H.H. Determination of discrete relaxation and retardation time spectra from dynamic mechanical data. Rheol. Acta 1989, 28, 511–519. [Google Scholar] [CrossRef]
- Honerkamp, J.; Weese, J. Determination of the relaxation spectrum by a regularization method. Macromolecules 1989, 22, 4372–4377. [Google Scholar] [CrossRef]
- Honerkamp, J.; Weese, J. A nonlinear regularization method for the calculation of relaxation spectra. Rheol. Acta 1993, 32, 65–73. [Google Scholar] [CrossRef]
- Malkin, A.Y. The use of a continuous relaxation spectrum for describing the viscoelastic properties of polymers. Polym. Sci. Ser. A 2006, 48, 39–45. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Vasilyev, G.B.; Andrianov, A.V. On continuous relaxation spectrum. Method of calculation. Polym. Sci. Ser. A 2010, 52, 1137–1141. [Google Scholar] [CrossRef]
- Stadler, F.J.; Bailly, C. A new method for the calculation of continuous relaxation spectra from dynamic-mechanical data. Rheol. Acta 2009, 48, 33–49. [Google Scholar] [CrossRef]
- Davies, A.R.; Goulding, N.J. Wavelet regularization and the continuous relaxation spectrum. J. Non-Newton. Fluid Mech. 2012, 189–190, 19–30. [Google Scholar] [CrossRef]
- Cho, K.S. Power series approximations of dynamic moduli and relaxation spectrum. J. Rheol. 2013, 57, 679–697. [Google Scholar] [CrossRef]
- Takeh, A.; Shanbhag, S. A Computer Program to Extract the Continuous and Discrete Relaxation Spectra from Dynamic Viscoelastic Measurements. Appl. Rheol. 2013, 23, 24628. [Google Scholar] [CrossRef]
- Liu, H.; Luo, R.; Lv, H. Establishing continuous relaxation spectrum based on complex modulus tests to construct relaxation modulus master curves in compliance with linear viscoelastic theory. Constr. Build. Mater. 2018, 165, 372–384. [Google Scholar] [CrossRef]
- Luo, L.; Xi, R.; Ma, Q.; Tu, C.; Ibrahim Shah, Y. An improved method to establish continuous relaxation spectrum of asphalt materials. Constr. Build. Mater. 2022, 354, 129182. [Google Scholar] [CrossRef]
- Poudel, S.; Shanbhag, S. Efficient test to evaluate the consistency of elastic and viscous moduli with Kramers–Kronig relations. Korea-Aust. Rheol. J. 2022, 10, 2202. [Google Scholar] [CrossRef]
- Alfrey, T.; Doty, P. The Methods of Specifying the Properties of Viscoelastic Materials. J. Appl. Phys. 1945, 16, 700–713. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Yunping, X. Continuous Retardation Spectrum for Solidification Theory of Concrete Creep. J. Eng. Mech. 1995, 121, 281–288. [Google Scholar] [CrossRef]
- ter Haar, D. An easy approximate method of determining the relaxation spectrum of a viscoelastic materials. J. Polym. Sci. 1951, 6, 247–250. [Google Scholar] [CrossRef]
- Goangseup, Z.; Bažant, Z.P. Continuous Relaxation Spectrum for Concrete Creep and its Incorporation into Microplane Model M4. J. Eng. Mech. 2002, 128, 1331–1336. [Google Scholar] [CrossRef]
- Kurenuma, Y.; Nakano, T. Analysis of stress relaxation on the basis of isolated relaxation spectrum for wet wood. J. Mater. Sci. 2012, 47, 4673–4679. [Google Scholar] [CrossRef]
- Stankiewicz, A. Identification of the relaxation spectrum of viscoelastic materials under strong noise measurement data. Part I. Problem and example. MOTROL. Comm. Mot. Energetics Agric. 2013, 15, 119–126. [Google Scholar]
- Stankiewicz, A. Identification of the relaxation and retardation spectra of plant viscoelastic materials using Chebyshev functions. Part II. Analysis. Teka Comm. Mot. Energetics Agric. 2010, 10, 372–378. [Google Scholar]
- Pillonetto, G.; Chen, T.; Chiuso, A.; De Nicolao, G.; Ljung, L. Regularized System Identification: Learning Dynamic Models from Data, 1st ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Aleksandrov, A.; Lekova, S.; Milenova, M. Generalized model of viscoelastic deformation. Int. J. Pure Appl. Math. 2022, 81, 635–646. Available online: https://ijpam.eu/contents/2012-81-4/11/index.html (accessed on 17 December 2022).
- Cao, J.; Chen, Y.; Wang, Y.; Cheng, G.; Barrière, T. Shifted Legendre polynomials algorithm used for the dynamic analysis of PMMA viscoelastic beam with an improved fractional model. Chaos Solitons Fractals 2020, 141, 110342. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M. The proper orthogonal decomposition modal spectral element method for two-dimensional viscoelastic equation. Thin-Walled Struct. 2021, 161, 107429. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Cho, K.S. Direct conversion of creep data to dynamic moduli using point-wise method. Korea-Aust. Rheol. J. 2021, 33, 105–112. [Google Scholar] [CrossRef]
- Lee, S.H.; Bae, J.-E.; Cho, K.S. Determination of continuous relaxation spectrum based on the Fuoss-Kirkwood relation and logarithmic orthogonal power-series approximation. Korea-Aust. Rheol. J. 2017, 29, 115–127. [Google Scholar] [CrossRef]
- Stankiewicz, A. On determination of the relaxation spectrum of viscoelastic materials from discrete-time stress relaxation data. Teka Comm. Mot. Energetics Agric. 2012, 12, 217–222. [Google Scholar]
- Baumgaertel, M.; Schausberger, A.; Winter, H.H. The relaxation of polymers with linear flexible chains of uniform length. Rheol. Acta 1990, 29, 400–408. [Google Scholar] [CrossRef]
- Baumgaertel, M.; Winter, H.H. Interrelation between continuous and discrete relaxation time spectra. J. Non-Newton. Fluid Mech. 1992, 44, 15–36. [Google Scholar] [CrossRef]
- Povolo, F.; Hermida, É.B. Influence of Intensity of Relaxation on Interconversion between Normalized Distribution Functions. Polym. J. 1992, 24, 1–13. [Google Scholar] [CrossRef]
- Hansen, P.C. Rank-Deficient and Discrete Ill-Posed Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1998. [Google Scholar] [CrossRef]
- Friedrich, C.; Honerkamp, J.; Weese, J. New ill-posed problems in rheology. Rheol. Acta 1996, 35, 186–193. [Google Scholar] [CrossRef]
- Stankiewicz, A. On the existence and uniqueness of the relaxation spectrum of viscoelastic materials. Part II: Other existence conditions. Teka Comm. Mot. Energetics Agric. 2010, 10, 388–395. [Google Scholar]
- Datta, K.B.; Mohan, B.M. Orthogonal Functions in Systems and Control; World Scientific: Singapore, 1995. [Google Scholar]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill-Posed Problems; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Wahba, G. Practical Approximate Solutions to Linear Operator Equations When the Data are Noisy. SIAM J. Numer. Anal. 1977, 14, 651–667. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Pérez-Calixto, D.; Amat-Shapiro, S.; Zamarrón-Hernández, D.; Vázquez-Victorio, G.; Puech, P.-H.; Hautefeuille, M. Determination by Relaxation Tests of the Mechanical Properties of Soft Polyacrylamide Gels Made for Mechanobiology Studies. Polymers 2021, 13, 629. [Google Scholar] [CrossRef]
- Malkin, A.I.A.; Malkin, A.Y.; Isayev, A.I. Rheology: Concepts, Methods and Applications; ChemTec: Deerfield Beach, FL, USA, 2006; Available online: https://books.google.pl/books?id=8rGafjhgz-UC (accessed on 17 December 2022).
- Barata, J.C.A.; Hussein, M.S. The Moore–Penrose Pseudoinverse: A Tutorial Review of the Theory. Braz. J. Phys. 2012, 42, 146–165. [Google Scholar] [CrossRef]
- Szabatin, J. Podstawy Teorii Sygnałów; Wydawnictwa Komunikacji i Łączności: Warszawa, Poland, 1982. (In Polish) [Google Scholar]
- Stankiewicz, A. Identification of the relaxation spectrum of viscoelastic materials under strong noise measurement data. Part II. Identification algorithm as FIR filter. MOTROL. Comm. Mot. Energetics Agric. 2013, 15, 127–134. [Google Scholar]
- Szego, G. Orthogonal Polynomials; American Mathematical Society: Providence, RI, USA, 1975; Available online: https://books.google.nl/books?id=ZOhmnsXlcY0C (accessed on 17 December 2022).
- Lebedev, N.N. Special Functions & Their Applications; Dover Publications: New York, NY, USA, 2012. [Google Scholar]
- Tikhonov, A.N.; Samarskii, A.A. Equations of Mathematical Physics; Dover Publications: New York, NY, USA, 2013. [Google Scholar]
- Boumenir, A. Inverse Spectral Problem for the Laguerre Differential Operator. J. Math. Anal. Appl. 1998, 224, 218–240. [Google Scholar] [CrossRef]
- Wang, L.; Cluett, W.R. Optimal choice of time-scaling factor for linear system approximations using Laguerre models. IEEE Trans. Autom. Control. 1994, 39, 1463–1467. [Google Scholar] [CrossRef]
- Prokhorov, S.A.; Kulikovskikh, I.M. Unique condition for generalized Laguerre functions to solve pole position problem. Signal Process. 2015, 108, 25–29. [Google Scholar] [CrossRef]
- Malti, R.; Maquin, D.; Ragot, J. Some results on the convergence of transfer function expansion on Laguerre series. In Proceedings of the 1999 European Control Conference (ECC), Karlsruhe, Germany, 31 August–3 September 1999; pp. 4649–4655. [Google Scholar] [CrossRef]
- Farikhin; Mohd, I. Orthogonal Functions Based on Chebyshev Polynomials. MATEMATIKA: Malays. J. Ind. Appl. Math. 2011, 27, 97–107. [Google Scholar] [CrossRef]
- Rawitscher, G.; dos Santos Filho, V.; Peixoto, T.C. Chebyshev Polynomials as Basis Functions. In An Introductory Guide to Computational Methods for the Solution of Physics Problems: With Emphasis on Spectral Methods; Springer International Publishing: Cham, Germany, 2018; pp. 43–62. [Google Scholar] [CrossRef]
- Van Assche, W. Ordinary Special Functions. In Encyclopedia of Mathematical Physics; Françoise, J.-P., Naber, G.L., Tsun, T.S., Eds.; Academic Press: Oxford, MI, USA, 2006; pp. 637–645. [Google Scholar] [CrossRef]
- Stankiewicz, A. Identification of the relaxation and retardation spectra of plant viscoelastic materials using Chebyshev functions. Part I. Identification algorithm. Teka Comm. Mot. Energetics Agric. 2010, 10, 363–371. [Google Scholar]
- Celeghini, E.; Gadella, M.; del Olmo, M.A. Hermite Functions and Fourier Series. Symmetry 2021, 13, 853. [Google Scholar] [CrossRef]
- Wayne, C.E.; Zharnitsky, V. Exponential bound of the integral of Hermite functions product with Gaussian weight. J. Math. Anal. Appl. 2023, 517, 126544. [Google Scholar] [CrossRef]
- Deaño, A.; Temme, N.M. Analytical and numerical aspects of a generalization of the complementary error function. Appl. Math. Comput. 2010, 216, 3680–3693. [Google Scholar] [CrossRef]
- Dong, S.-H. Factorization Method in Quantum Mechanics, 1st ed.; Springer Science & Business Media: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Wagner, K.W. Operatorenrechnung Nebst Anwendungen in Physik und Technik, 3rd ed.; J.A. Barth: Leipzig, Germany, 1962. [Google Scholar]


| Model | |||||||
|---|---|---|---|---|---|---|---|
| Legendre model | 6 | 1 | 0.03378 | 0.0088 | 1.5518 | 1.5518 | 2.0782 |
| 8 | 1 | 0.03239 | 0.0083 | 1.4833 | 1.4833 | 2.0643 | |
| 9 | 1 | 0.03186 | 0.0084 | 1.4657 | 1.4657 | 2.0597 | |
| 10 | 1 | 0.03139 | 0.0087 | 1.4537 | 1.4537 | 2.0559 | |
| 11 | 1 | 0.03098 | 0.0089 | 1.4452 | 1.4452 | 2.0529 | |
| 12 | 1 | 0.03062 | 0.0091 | 1.4391 | 1.4391 | 2.0505 | |
| Laguerre model | 6 | 6 | 0.03259 | 0.0084 | 1.4929 | 1.4929 | 1.9914 |
| 8 | 6 | 0.02744 | 0.0093 | 1.4222 | 1.4222 | 2.0414 | |
| 9 | 6 | 0.02560 | 0.0092 | 1.4240 | 1.4240 | 2.0435 | |
| 10 | 6 | 0.0239 | 0.0089 | 1.4262 | 1.4262 | 2.0448 | |
| 11 | 6 | 0.02256 | 0.0088 | 1.4253 | 1.4253 | 2.0444 | |
| Chebyshev model | 6 | 1.5 | 0.03103 | 0.00992 | 1.5215 | 1.5215 | 2.1119 |
| 8 | 1.5 | 0.03077 | 0.00981 | 1.4677 | 1.4677 | 2.0811 | |
| 9 | 1.5 | 0.03062 | 0.0101 | 1.4543 | 1.4543 | 2.0668 | |
| 10 | 1.6 | 0.03165 | 0.0089 | 1.4875 | 1.4875 | 2.0864 | |
| 11 | 1.6 | 0.03148 | 0.0091 | 1.47492 | 1.4749 | 2.0775 | |
| 12 | 1.6 | 0.03126 | 0.009246 | 1.4651 | 1.4651 | 2.0713 | |
| Hermite model | 6 | 1 | 0.00625 | 0.0117 | 1.6405 | 1.6029 | 2.0529 |
| 8 | 1 | 0.00588 | 0.0081 | 1.5077 | 1.4891 | 2.0674 | |
| 9 | 1 | 0.00599 | 0.0080 | 1.4731 | 1.4639 | 2.0592 | |
| 10 | 1 | 0.00599 | 0.0080 | 1.4611 | 1.4569 | 2.0607 | |
| 11 | 1 | 0.00566 | 0.0080 | 1.4600 | 1.4561 | 2.0654 |
| Model | |||||||
|---|---|---|---|---|---|---|---|
| Legendre model | 6 | 950 | 2.72 × 10−6 | 0.003261 | 62.717 | 62.717 | 80.604 |
| 8 | 620 | 4.968 × 10−6 | 0.00135 | 58.9351 | 58.9351 | 79.7444 | |
| 10 | 500 | 6.372 × 10−6 | 0.0007138 | 57.4422 | 57.4422 | 79.7170 | |
| 12 | 400 | 7.754 × 10−6 | 0.000557 | 56.8251 | 56.8251 | 79.7917 | |
| 14 | 300 | 9.226 × 10−6 | 0.000575 | 56.6390 | 56.6390 | 79.8353 | |
| Laguerre model | 8 | 8500 | 2.524 × 10−6 | 0.002722 | 63.0250 | 63.0250 | 82.4674 |
| 10 | 8000 | 3.668 × 10−6 | 0.001494 | 59.7092 | 59.7092 | 81.0828 | |
| 12 | 7500 | 4.840 × 10−6 | 0.0009379 | 58.3032 | 58.3032 | 80.6344 | |
| 14 | 8000 | 5.294 × 10−6 | 0.000711 | 57.3277 | 57.3277 | 80.3069 | |
| 16 | 6000 | 7.498 × 10−6 | 0.000699 | 57.39886 | 57.39886 | 80.4441 | |
| 18 | 6500 | 7.686 × 10−6 | 0.000527 | 56.7967 | 56.7967 | 80.1877 | |
| Chebyshev model | 6 | 31,000 | 6.0 × 10−7 | 0.8259 | 289.32 | 289.32 | |
| 8 | 31,500 | 6.0 × 10−7 | 0.7115 | 346.30 | 346.30 | ||
| 10 | 32,000 | 5.0 × 10−7 | 0.6504 | 376.6564 | 376.66 | ||
| 12 | 33,000 | 5.0 × 10−7 | 0.6344 | 379.0402 | 379.04 | ||
| 14 | 33,000 | 5.0 × 10−7 | 0.6029 | 375.3072 | 375.31 | ||
| 16 | 34,500 | 5.0 × 10−7 | 0.6136 | 382.0129 | 382.01 | ||
| Hermite model | 6 | 27,000 | 1.8 × 10−6 | 3.0971 | 390.24 | 387.13 | |
| 8 | 26,800 | 1.6 × 10−6 | 2.1911 | 452.31 | 445.67 | ||
| 10 | 26,750 | 1.6 × 10−6 | 1.9010 | 440.42 | 436.32 | ||
| 12 | 26,700 | 1.8 × 10−6 | 1.8148 | 389.93 | 378.76 | ||
| 14 | 26,600 | 0.999 × 10−6 | 2.9235 | 472.33 | 467.32 | ||
| 16 | 26,600 | 0.994 × 10−6 | 2.7767 | 467.45 | 461.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stankiewicz, A. A Class of Algorithms for Recovery of Continuous Relaxation Spectrum from Stress Relaxation Test Data Using Orthonormal Functions. Polymers 2023, 15, 958. https://doi.org/10.3390/polym15040958
Stankiewicz A. A Class of Algorithms for Recovery of Continuous Relaxation Spectrum from Stress Relaxation Test Data Using Orthonormal Functions. Polymers. 2023; 15(4):958. https://doi.org/10.3390/polym15040958
Chicago/Turabian StyleStankiewicz, Anna. 2023. "A Class of Algorithms for Recovery of Continuous Relaxation Spectrum from Stress Relaxation Test Data Using Orthonormal Functions" Polymers 15, no. 4: 958. https://doi.org/10.3390/polym15040958
APA StyleStankiewicz, A. (2023). A Class of Algorithms for Recovery of Continuous Relaxation Spectrum from Stress Relaxation Test Data Using Orthonormal Functions. Polymers, 15(4), 958. https://doi.org/10.3390/polym15040958






