Lifetime Predictions for High-Density Polyethylene under Creep: Experiments and Modeling
Abstract
1. Introduction
- To develop a simple model for the viscoelastoplastic response of semicrystalline polymers that involves only seven material parameters. Four of them characterize the viscoelastic behavior, and the remaining three reflect the viscoplastic response.
- To perform short-term tests on HDPE samples at room temperature (uniaxial tension up to breakage of samples with various strain rates, tensile relaxation tests at various strains, and tensile creep tests with various stresses) and to find material parameters by matching the experimental data.
- To validate the model by comparing its predictions with observations on HDPE in independent short- and medium-term (up to several days) creep tests.
- To predict the lifetime of HDPE in long-term creep tests numerically, and to compare these predictions with conventional stress-time-to-failure diagrams.
2. Materials and Methods
2.1. Tensile Tests
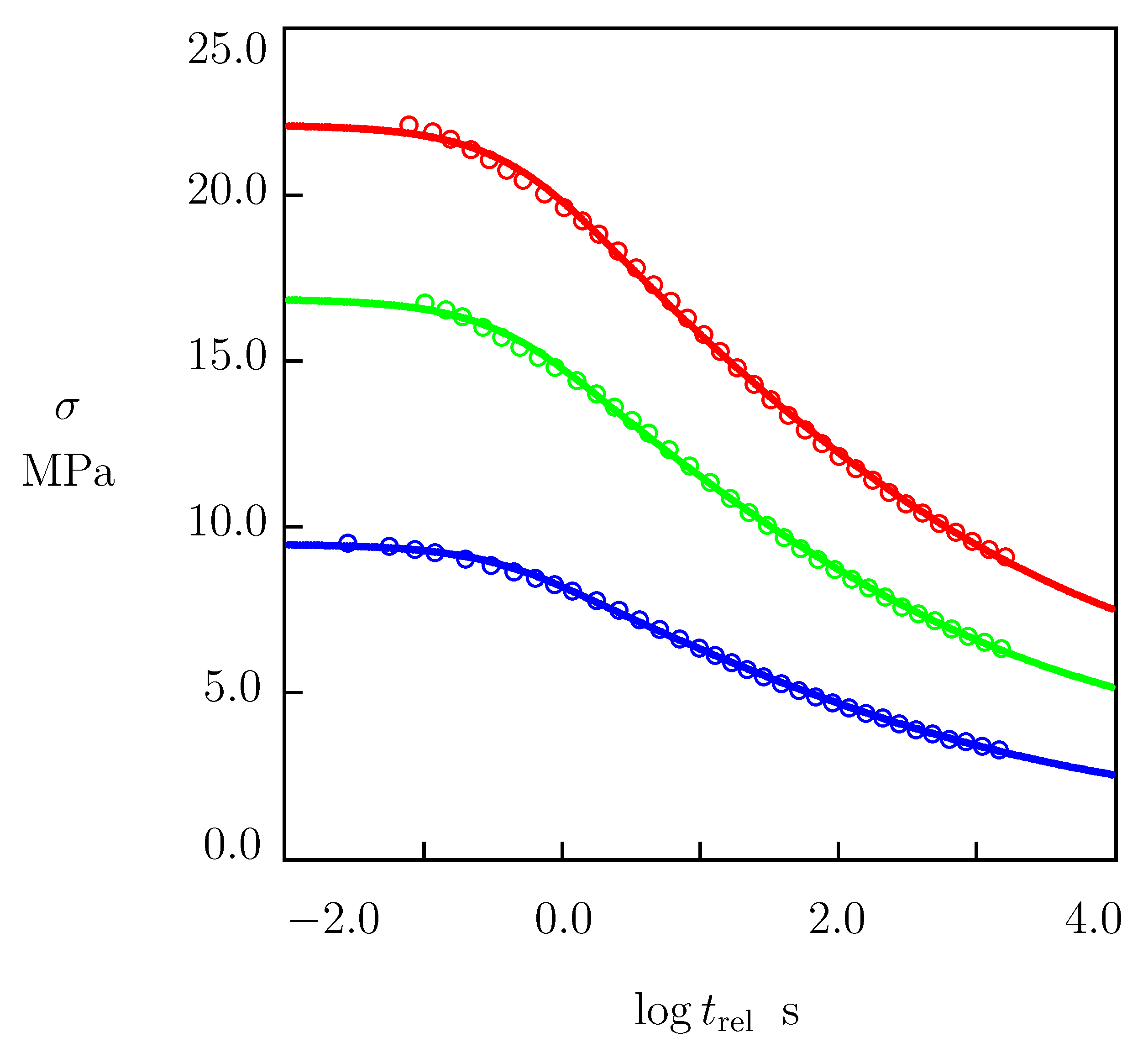
2.2. Relaxation Tests
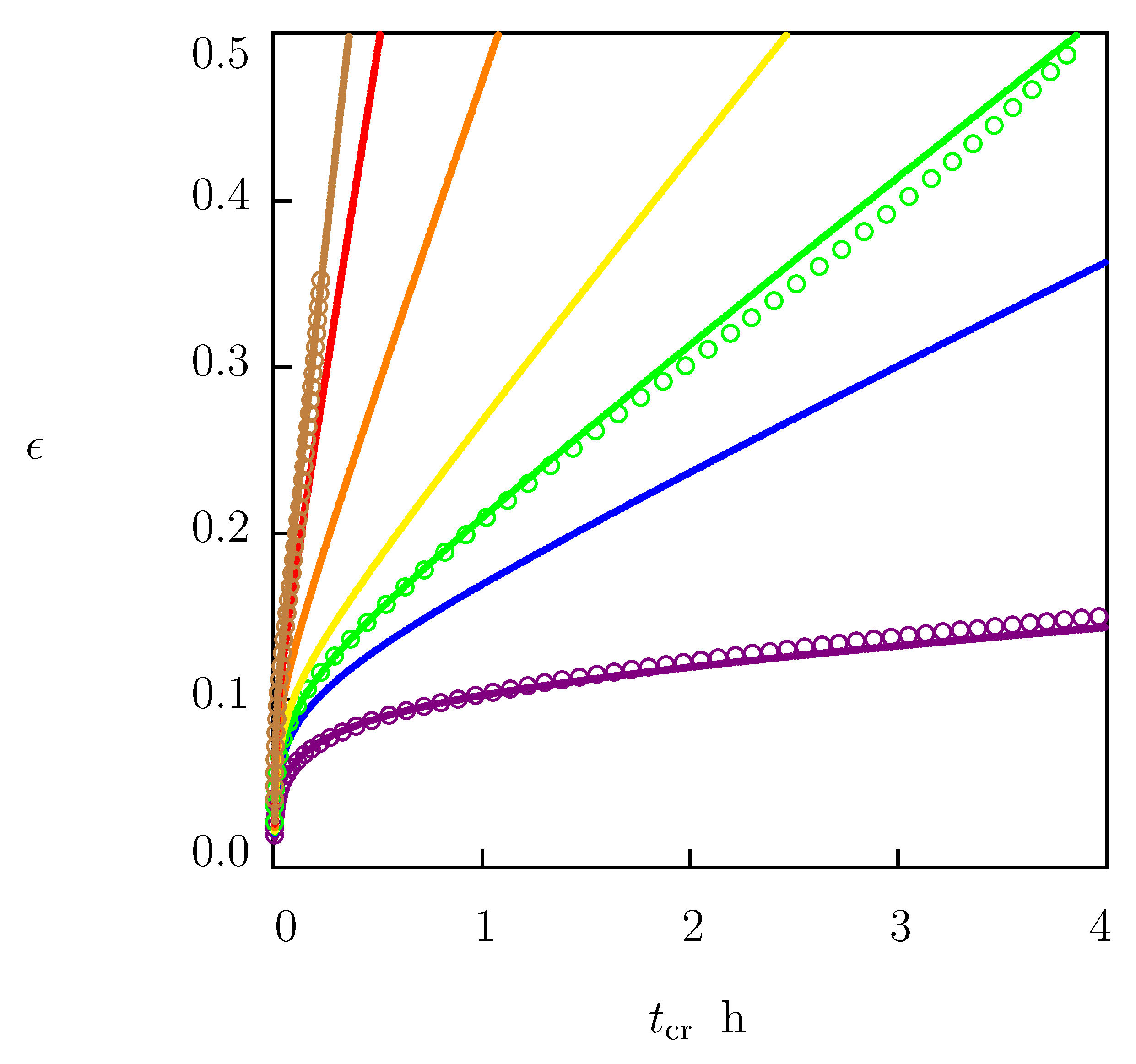
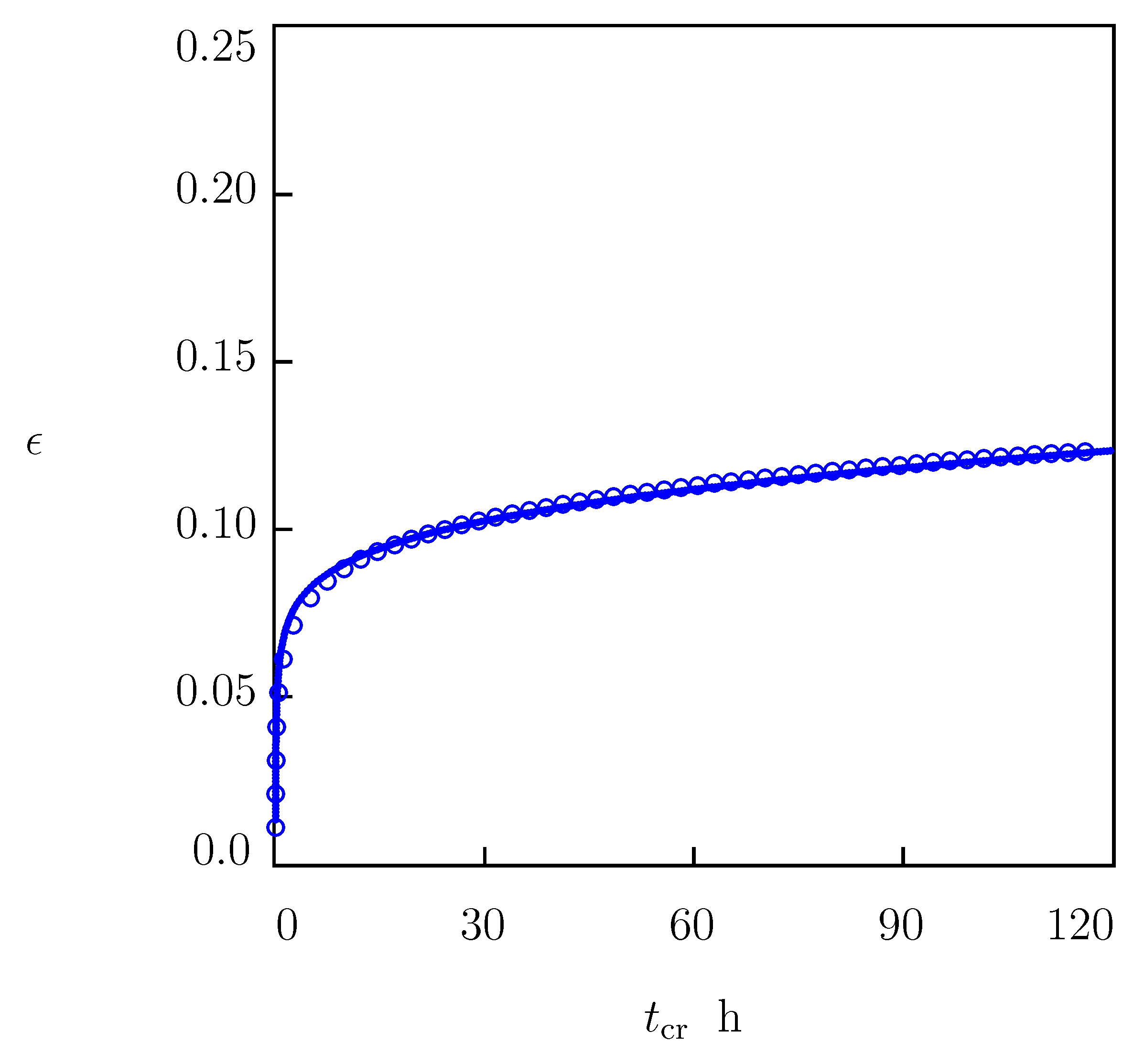
2.3. Creep Tests
3. Constitutive Model
4. Results and Discussion
4.1. Fitting of Experimental Data
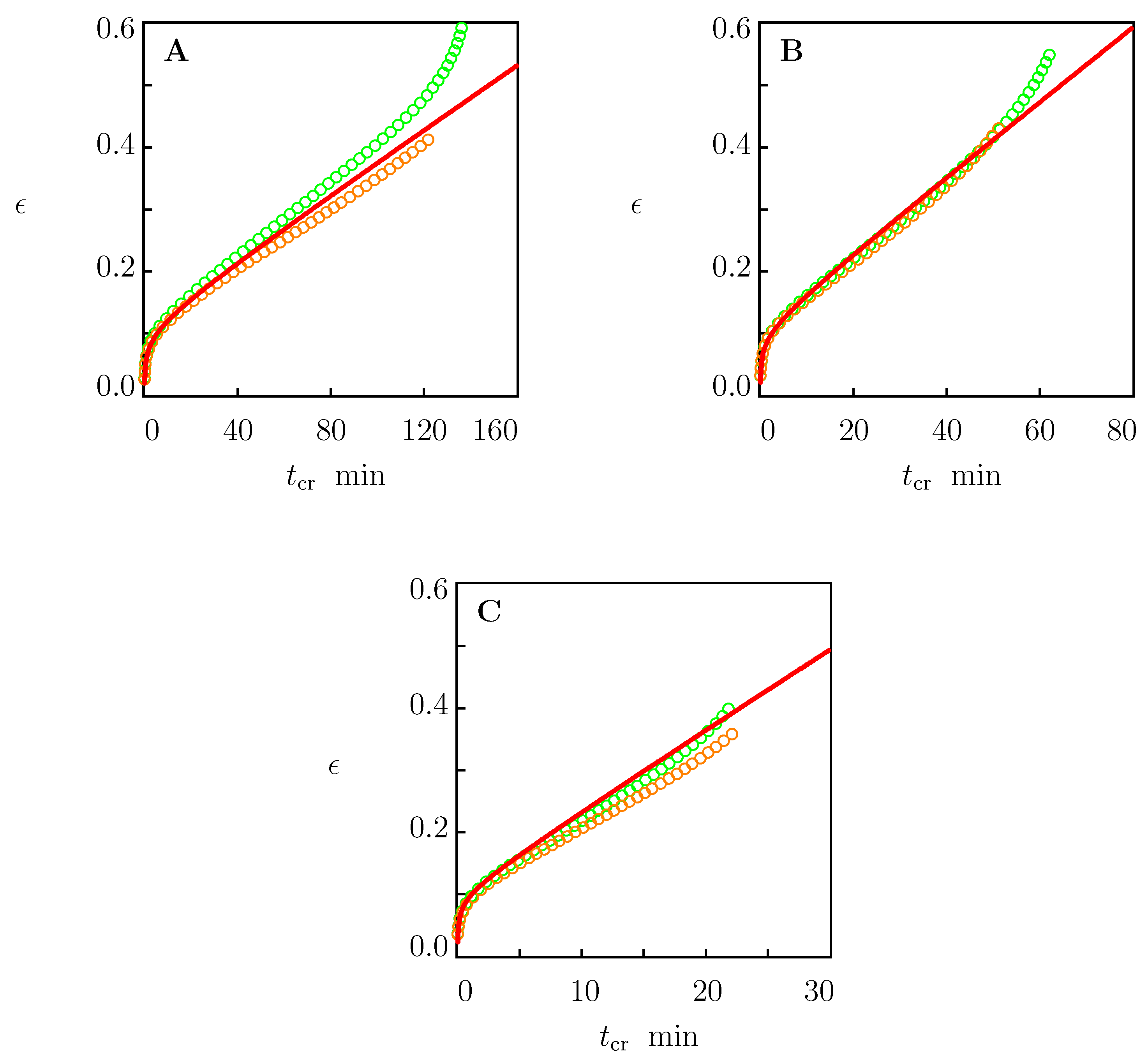
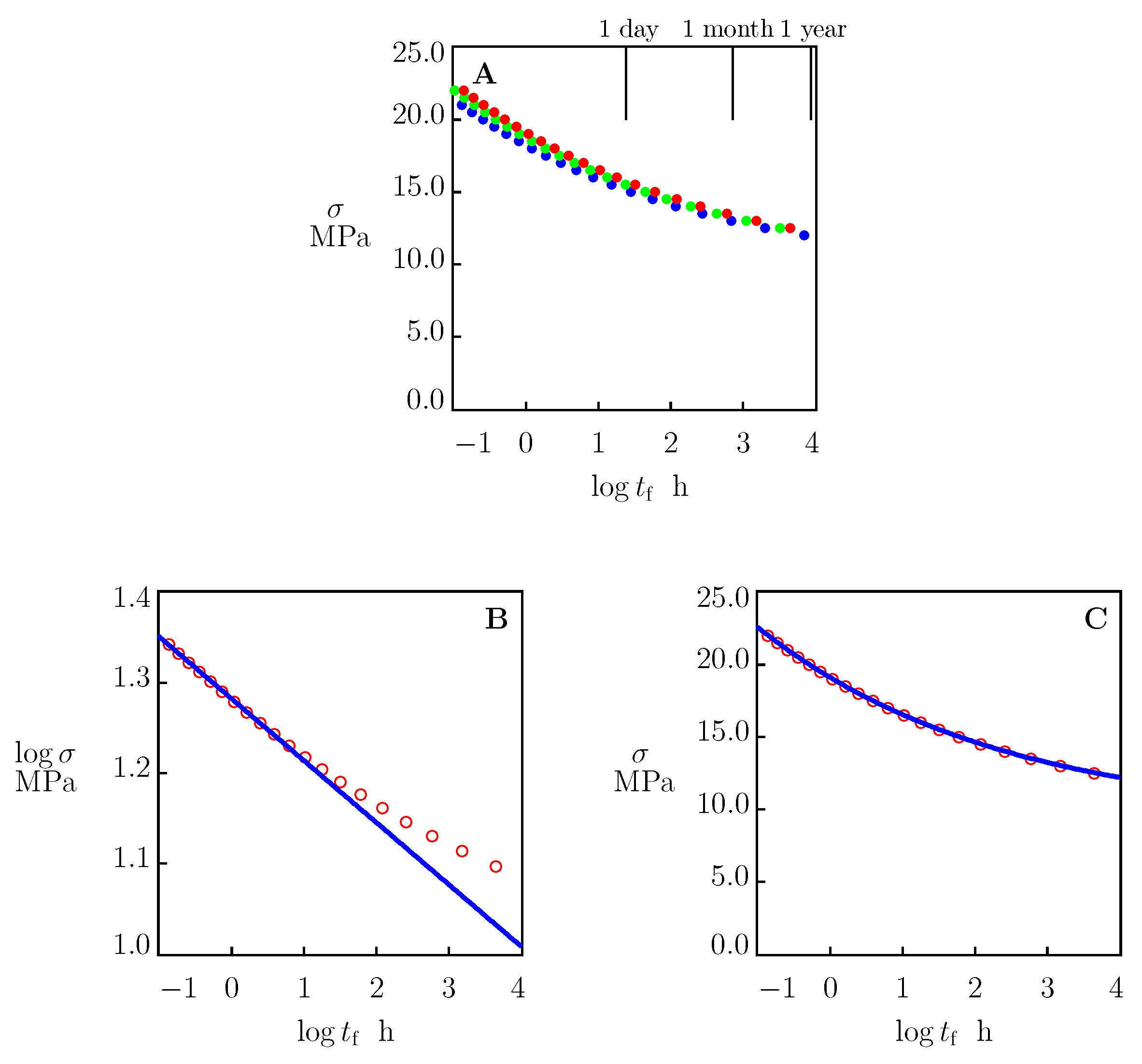
4.2. Validation of the Model
4.3. Stress-Time-to-Failure Diagrams
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guedes, R.M. Lifetime predictions of polymer matrix composites under constant or monotonic load. Compos. A 2006, 37, 703–715. [Google Scholar] [CrossRef]
- Chudnovsky, A.; Zhou, Z.; Zhang, H.; Sehanobish, K. Lifetime assessment of engineering thermoplastics. Int. J. Eng. Sci. 2012, 59, 108–139. [Google Scholar] [CrossRef]
- Laine, E.; Bouvy, C.; Grandidier, J.-C.; Vaes, G. Methodology of accelerated characterization for long-term creep prediction of polymer structures to ensure their service life. Polym. Test. 2019, 79, 106050. [Google Scholar] [CrossRef]
- Sattar, M.; Othman, A.R.; Kamaruddin, S.; Akhtar, M.; Khan, R. Limitations on the computational analysis of creep failure models: A review. Eng. Fail. Anal. 2022, 134, 105968. [Google Scholar] [CrossRef]
- Hutar, P.; Sevcik, M.; Nahlik, L.; Pinter, G.; Frank, A.; Mitev, I. A numerical methodology for lifetime estimation of HDPE pressure pipes. Eng. Fract. Mech. 2011, 78, 3049–3058. [Google Scholar] [CrossRef]
- Majid, F.; Elghorba, M. HDPE pipes failure analysis and damage modeling. Eng. Fail. Anal. 2017, 71, 157–165. [Google Scholar] [CrossRef]
- Zha, S.; Lan, H.-q.; Huang, H. Review on lifetime predictions of polyethylene pipes: Limitations and trends. Int. J. Press. Vessel Pip. 2022, 198, 104663. [Google Scholar] [CrossRef]
- Nikolov, S.; Doghri, I. A micro/macro-constitutive model for the small deformation behavior of polyethylene. Polymer 2000, 41, 1883–1891. [Google Scholar] [CrossRef]
- Drozdov, A.D.; Yuan, Q. The viscoelastic and viscoplastic behavior of low-density polyethylene. Int. J. Solids Struct. 2003, 40, 2321–2342. [Google Scholar] [CrossRef]
- Drozdov, A.D.; Gupta, R.K. Constitutive equations in finite viscoelasticity of semicrystalline polymers. Int. J. Solids Struct. 2003, 40, 6217–6243. [Google Scholar] [CrossRef]
- Dusunceli, N.; Colak, O.U. High density polyethylene (HDPE): Experiments and modeling. Mech. Time-Depend. Mater. 2006, 10, 331–345. [Google Scholar] [CrossRef]
- Drozdov, A.D.; de Christiansen, J.C. Cyclic viscoplasticity of high-density polyethylene: Experiments and modeling. Comput. Mater. Sci. 2007, 39, 465–480. [Google Scholar] [CrossRef]
- Drozdov, A.D.; de Christiansen, J.C. Viscoelasticity and viscoplasticity of semicrystalline polymers: Structure–property relations for high-density polyethylene. Comput. Mater. Sci. 2007, 39, 729–751. [Google Scholar] [CrossRef]
- Brusselle-Dupend, N.; Cangemi, L. A two-phase model for the mechanical behaviour of semicrystalline polymers. Part I: Large strains multiaxial validation on HDPE. Mech. Mater. 2008, 40, 743–760. [Google Scholar] [CrossRef]
- Drozdov, A.D.; de Christiansen, J.C. Thermo-viscoelastic and viscoplastic behavior of high-density polyethylene. Int. J. Solids Struct. 2008, 45, 4274–4288. [Google Scholar] [CrossRef]
- Ayoub, G.; Zairi, F.; Nait-Abdelaziz, M.; Gloaguen, J.M. Modelling large deformation behaviour under loading-unloading of semicrystalline polymers: Application to a high density polyethylene. Int. J. Plast. 2010, 26, 329–347. [Google Scholar] [CrossRef]
- Drozdov, A.D. Cyclic thermo-viscoplasticity of high density polyethylene. Int. J. Solids Struct. 2010, 47, 1592–1602. [Google Scholar] [CrossRef]
- Ayoub, G.; Zairi, F.; Frederix, C.; Gloaguen, J.M.; Nait-Abdelaziz, M.; Seguela, R.; Lefebvre, J.M. Effects of crystal content on the mechanical behaviour of polyethylene under finite strains: Experiments and constitutive modelling. Int. J. Plast. 2011, 27, 492–511. [Google Scholar] [CrossRef]
- Tripathi, A.; Mantell, S.; Le, J.-L. A morphology based constitutive model for high density polyethylene. Mech. Mater. 2019, 137, 103091. [Google Scholar] [CrossRef]
- Amjadi, M.; Fatemi, A. Creep and fatigue behaviors of high-density polyethylene (HDPE): Effects of temperature, mean stress, frequency, and processing technique. Int. J. Fatigue 2020, 141, 105871. [Google Scholar] [CrossRef]
- Ayoub, G.; Rodriguez, A.K.; Mansoor, B.; Colin, X. Modeling the visco-hyperelastic-viscoplastic behavior of photodegraded semi-crystalline low-density polyethylene films. Int. J. Solids Struct. 2020, 204–205, 187–198. [Google Scholar] [CrossRef]
- Yan, Z.; Guo, Q.; Zairi, F.; Zaoui, A.; Jiang, Q.; Liu, X. Continuum-based modeling large-strain plastic deformation of semi-crystalline polyethylene systems: Implication of texturing and amorphicity. Mech. Mater. 2021, 162, 104060. [Google Scholar] [CrossRef]
- Zhang, Y.; Ben Jar, P.-Y.; Xue, S.; Li, L. Quantification of strain-induced damage in semi-crystalline polymers: A review. J. Mater. Sci. 2019, 54, 62–82. [Google Scholar] [CrossRef]
- Hsueh, H.-C.; Kim, J.H.; Orski, S.; Fairbrother, A.; Jacobs, D.; Perry, L.; Hunston, D.; White, C.; Sung, L. Micro and macroscopic mechanical behaviors of high-density polyethylene under UV irradiation and temperature. Polym. Degrad. Stab. 2020, 174, 109098. [Google Scholar] [CrossRef]
- Van Erp, T.B.; Reynolds, C.T.; Peijs, T.; Van Dommelen, J.A.W.; Govaert, L.E. Prediction of yield and long-term failure of oriented polypropylene: Kinetics and anisotropy. J. Polym. Sci. Part B Polym. Phys. 2009, 47, 2026–2035. [Google Scholar] [CrossRef]
- Carneiro Neto, R.M.; Akhavan-Safar, A.; Sampaio, E.M.; Assis, J.T.; da Silva, L.F.M. Assessment of the creep life of adhesively bonded joints using the end notched flexure samples. Eng. Fail. Anal. 2022, 133, 105969. [Google Scholar] [CrossRef]
- Crissman, J.M. On the long time creep and lifetime behavior in uniaxial extension of a linear low density polyethylene. Polym. Eng. Sci. 1991, 31, 541–547. [Google Scholar] [CrossRef]
- Sedighiamiri, A.; Govaert, L.E.; Kanters, M.J.W.; van Dommelen, J.A.W. Micromechanics of semicrystalline polymers: Yield kinetics and long-term failure. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 1664–1679. [Google Scholar] [CrossRef]
- Jar, P.-Y.B. Revisiting creep test on polyethylene pipe—Data analysis and deformation mechanisms. Polym. Eng. Sci. 2021, 61, 586–599. [Google Scholar] [CrossRef]
- Amjadi, M.; Fatemi, A. Tensile behavior of high-density polyethylene including the effects of processing technique, thickness, temperature, and strain rate. Polymers 2020, 12, 1857. [Google Scholar] [CrossRef]
- Zhu, T.; Li, X.; Zhao, X.; Zhang, X.; Lu, Y.; Zhang, L. Stress-strain behavior and corresponding crystalline structures of four types of polyethylene under a wide range of strain rates. Polym. Test. 2022, 106, 107460. [Google Scholar] [CrossRef]
- Drozdov, A.D.; de Christiansen, J.C.; Klitkou, R.; Potarniche, C.G. Viscoelasticity and viscoplasticity of polypropylene/polyethylene blends. Int. J. Solids Struct. 2010, 47, 2498–2507. [Google Scholar] [CrossRef]
- Hiss, R.; Hobeika, S.; Lynn, C.; Strobl, G. Network stretching, slip processes, and fragmentation of crystallites during uniaxial drawing of polyethylene and related copolymers. A comparative study. Macromolecules 1999, 32, 4390–4403. [Google Scholar] [CrossRef]
- Galeski, A.; Bartczak, Z.; Argon, A.S.; Cohen, R.E. Morphological alterations during texture-producing plastic plane strain compression of high-density polyethylene. Macromolecules 1992, 25, 5705–5718. [Google Scholar] [CrossRef]
- Hong, K.; Rastogi, A.; Strobl, G. A model treating tensile deformation of semicrystalline polymers: Quasi-static stress-strain relationship and viscous stress determined for a sample of polyethylene. Macromolecules 2004, 37, 10165–10173. [Google Scholar] [CrossRef]
- Drozdov, A.D.; Gupta, R.K. Nonlinear viscoelasticity and viscoplasticity of isotactic polypropylene. Int. J. Eng. Sci. 2003, 41, 2335–2361. [Google Scholar] [CrossRef]
- Okereke, M.I.; Akpoyomare, A.I. Two-process constitutive model for semicrystalline polymers across a wide range of strain rates. Polymer 2019, 183, 121818. [Google Scholar] [CrossRef]
- Tanaka, F.; Edwards, S.F. Viscoelastic properties of physically cross-linked networks. Transient network theory. Macromolecules 1992, 1992 25, 1516–1523. [Google Scholar] [CrossRef]
- Drozdov, A.D.; Klitkou, R.; de Christiansen, J.C. Cyclic viscoplasticity of semicrystalline polymers with finite deformations. Mech. Mater. 2013, 56, 53–64. [Google Scholar] [CrossRef]
- Naumenko, K.; Altenbach, H.; Gorash, Y. Creep analysis with a stress range dependent constitutive model. Arch. Appl. Mech. 2009, 79, 619–630. [Google Scholar] [CrossRef]
- Derrida, B. Random-energy model: Limit of a family of disordered models. Phys. Rev. Lett. 1980, 45, 79–92. [Google Scholar] [CrossRef]
- Yao, H.-T.; Xuan, F.-Z.; Wang, Z.; Tu, S.-T. A review of creep analysis and design under multi-axial stress states. Nucl. Eng. Des. 2007, 237, 1969–1986. [Google Scholar] [CrossRef]
- Williams, S.J.; Bache, M.R.; Wilshire, B. Recent developments in analysis of high temperature creep and creep fracture behaviour. Mater. Sci. Technol. 2010, 26, 1332–1337. [Google Scholar] [CrossRef]
- Wen, J.-F.; Tu, S.-T.; Xuan, F.-Z.; Zhang, X.-W.; Gao, X.-L. Effects of stress level and stress state on creep ductility: Evaluation of different models. J. Mater. Sci. Technol. 2016, 32, 695–704. [Google Scholar] [CrossRef]
- Khalil, R.; Horani, M.A.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Drozdov, A.D. Fractional differential models in finite viscoelasticity. Acta Mech. 1997, 124, 155–180. [Google Scholar] [CrossRef]
- Sumelka, W. Fractional viscoplasticity. Mech. Res. Comm. 2014, 56, 31–36. [Google Scholar] [CrossRef]
- Schapery, R.A. Theory of crack initiation and growth in viscoelastic media. 3. Analysis of continuous growth. Int. J. Fract. 1975, 11, 549–562. [Google Scholar] [CrossRef]
- Bi, G.; Li, Z.; Wang, Q.; Jiang, D. An examination of creep failure criterion based on a strain threshold identified with a power law model. Mech. Time-Depend. Mater. 2022, 26, 195–209. [Google Scholar] [CrossRef]
- Frank, A.; Arbeiter, F.J.; Berger, I.J.; Hutar, P.; Nahlik, L.; Pinter, G. Fracture mechanics lifetime prediction of polyethylene pipes. J. Pipeline Syst. Eng. Pract. 2019, 10, 04018030. [Google Scholar] [CrossRef]
- Wee, J.-W.; Park, S.-Y.; Choi, B.-H. Modeling and application of discontinuous slow crack growth behaviors of high-density polyethylene pipe with various geometries and loading conditions. Eng. Fract. Mech. 2020, 236, 107205. [Google Scholar] [CrossRef]
- Wee, J.-W.; Chudnovsky, A.; Choi, B.-H. Modeling of multiple crack initiation in polymer pipes under oxidative environment. Int. J. Eng. Sci. 2022, 176, 103686. [Google Scholar] [CrossRef]
- Ojeda, T.; Freitas, A.; Birck, K.; Dalmolin, E.; Jacques, R.; Bento, F.; Camargo, F. Degradability of linear polyolefins under natural weathering. Polym. Degrad. Stabil. 2011, 96, 703–707. [Google Scholar] [CrossRef]
- Grause, G.; Chien, M.-F.; Inoue, C. Changes during the weathering of polyolefins. Polym. Degrad. Stabil. 2020, 181, 109364. [Google Scholar] [CrossRef]


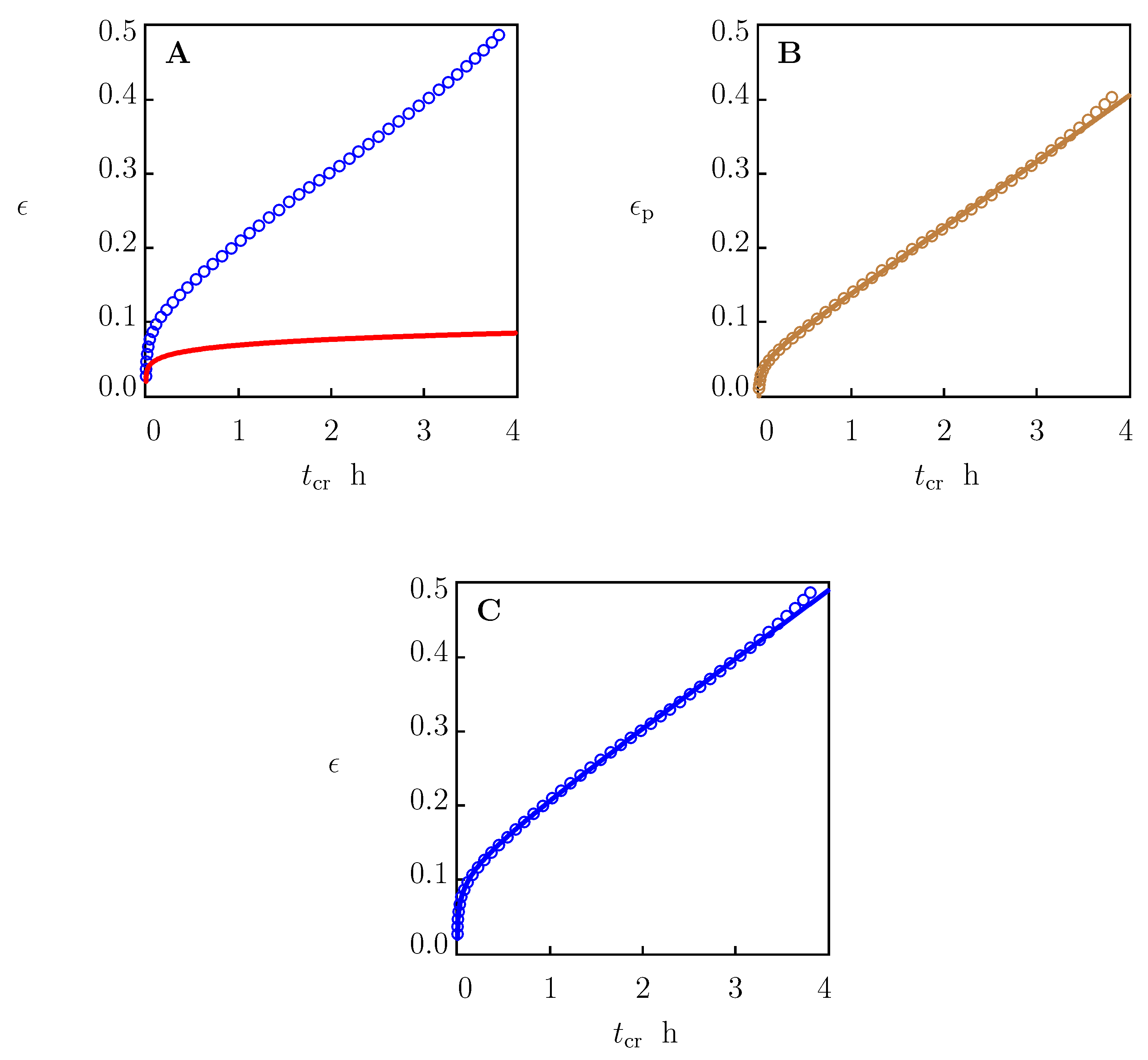

| MPa | s | |||
|---|---|---|---|---|
| 0.01 | 9.52 | 2.1 | 7.2 | 0.862 |
| 0.02 | 16.87 | 1.9 | 6.8 | 0.799 |
| 0.05 | 22.12 | 1.6 | 7.1 | 0.780 |
| Coefficient | |||
|---|---|---|---|
| m | |||
| 1.98 | 7.0 | ||
| A | a | ||
| 0.047 | |||
| B | n | ||
| 8.0 |
| MPa | MPa | |
|---|---|---|
| 9.21 | 9.88 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drozdov, A.D.; Høj Jermiin, R.; de Claville Christiansen, J. Lifetime Predictions for High-Density Polyethylene under Creep: Experiments and Modeling. Polymers 2023, 15, 334. https://doi.org/10.3390/polym15020334
Drozdov AD, Høj Jermiin R, de Claville Christiansen J. Lifetime Predictions for High-Density Polyethylene under Creep: Experiments and Modeling. Polymers. 2023; 15(2):334. https://doi.org/10.3390/polym15020334
Chicago/Turabian StyleDrozdov, A. D., R. Høj Jermiin, and J. de Claville Christiansen. 2023. "Lifetime Predictions for High-Density Polyethylene under Creep: Experiments and Modeling" Polymers 15, no. 2: 334. https://doi.org/10.3390/polym15020334
APA StyleDrozdov, A. D., Høj Jermiin, R., & de Claville Christiansen, J. (2023). Lifetime Predictions for High-Density Polyethylene under Creep: Experiments and Modeling. Polymers, 15(2), 334. https://doi.org/10.3390/polym15020334







