A New Uniaxial Tensile Model for Foam Metal/Epoxy Interpenetrated Phase Composites
Abstract
:1. Introduction
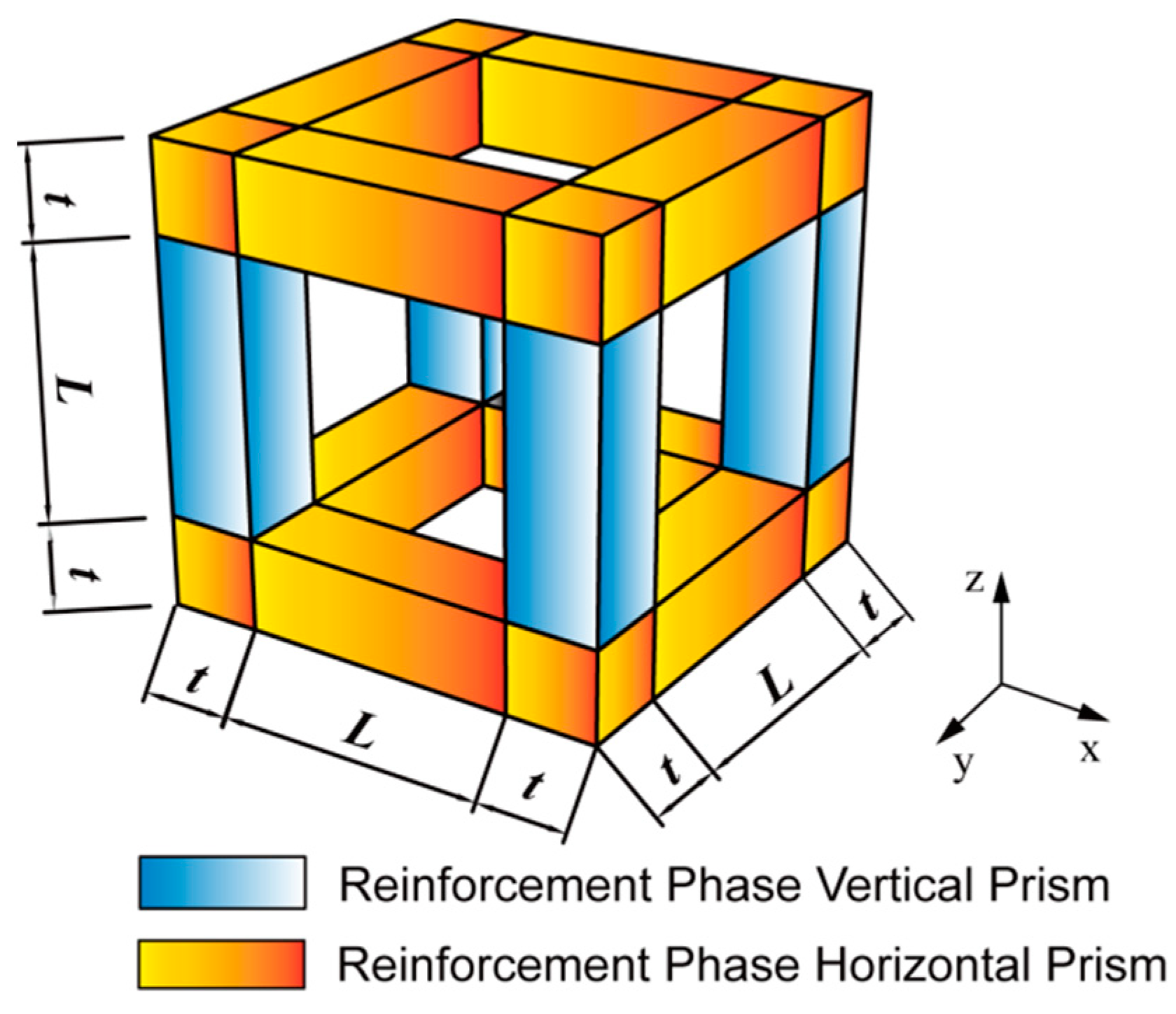
2. Tensile Mesoscopic Model
2.1. Subsection
- The representative volume element is isotropic in mechanical properties; the matrix phase damage is isotropic.
- As the load is in the far-field z-direction, the direction is parallel to the direction normal to the upper surface of the representative volume element.
- Neither the matrix phase nor the reinforced phase undergoes volume change, and Poisson’s ratio is 0.5 in the plastic deformation stage, so the plastic spherical strain is zero in the calculation. The plastic deformation follows the conditions of total strain theory, and the loading mode is simple loading with small deformation.
- Both the reinforcement phases and matrix phases follow the von Mises yielding criterion.
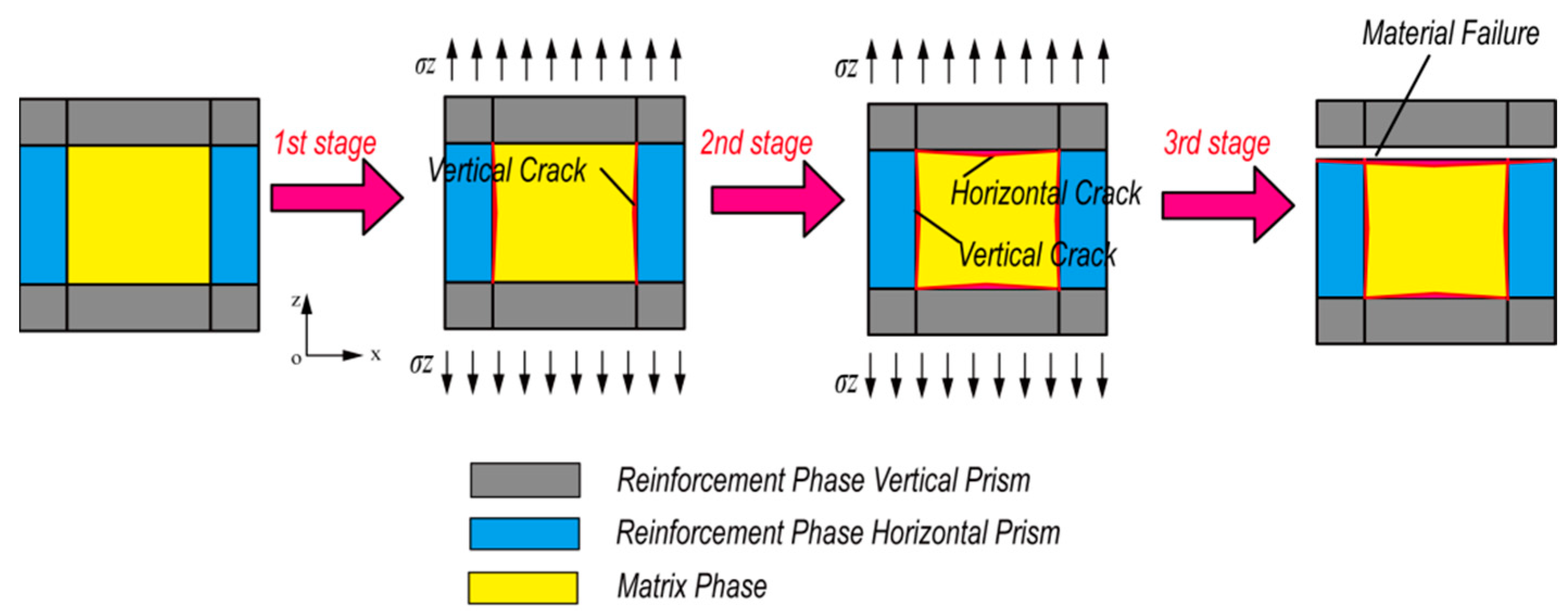
2.2. Deterioration Process Analysis of Mechanical Properties under Tensile Loading
2.3. Damage Variables
3. Tensile Intrinsic Characterization
3.1. Intrinsic Equation of the Representative Volume Element
3.2. Damage Evolution Equation
4. Tensile Test
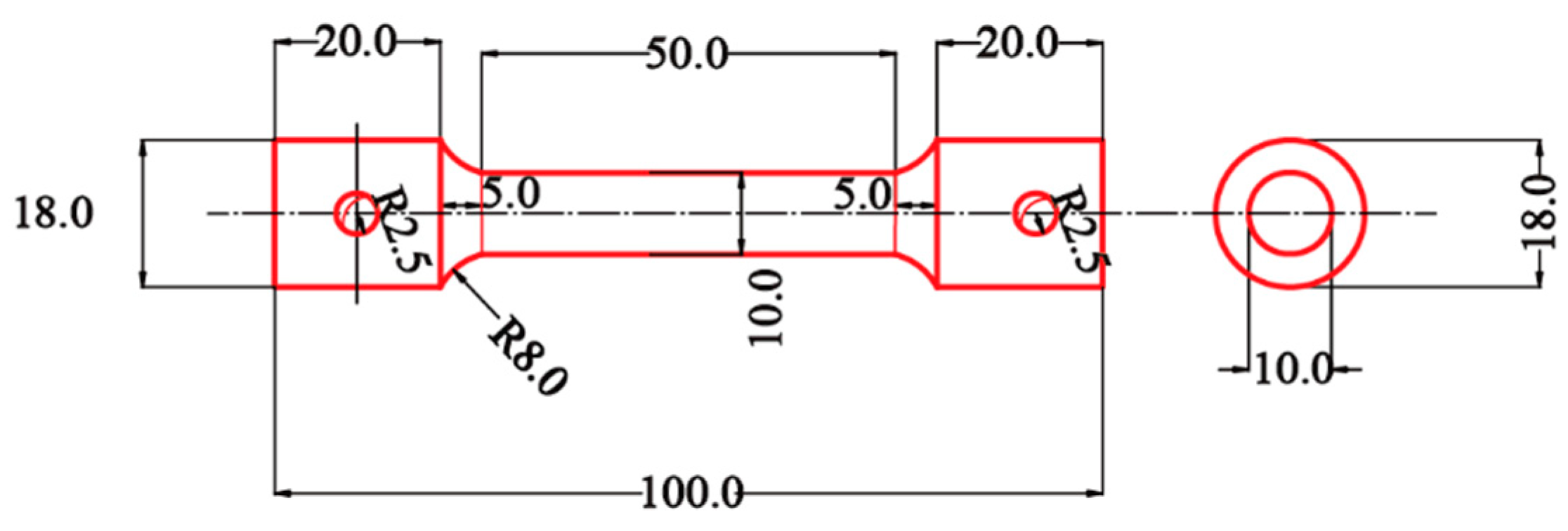
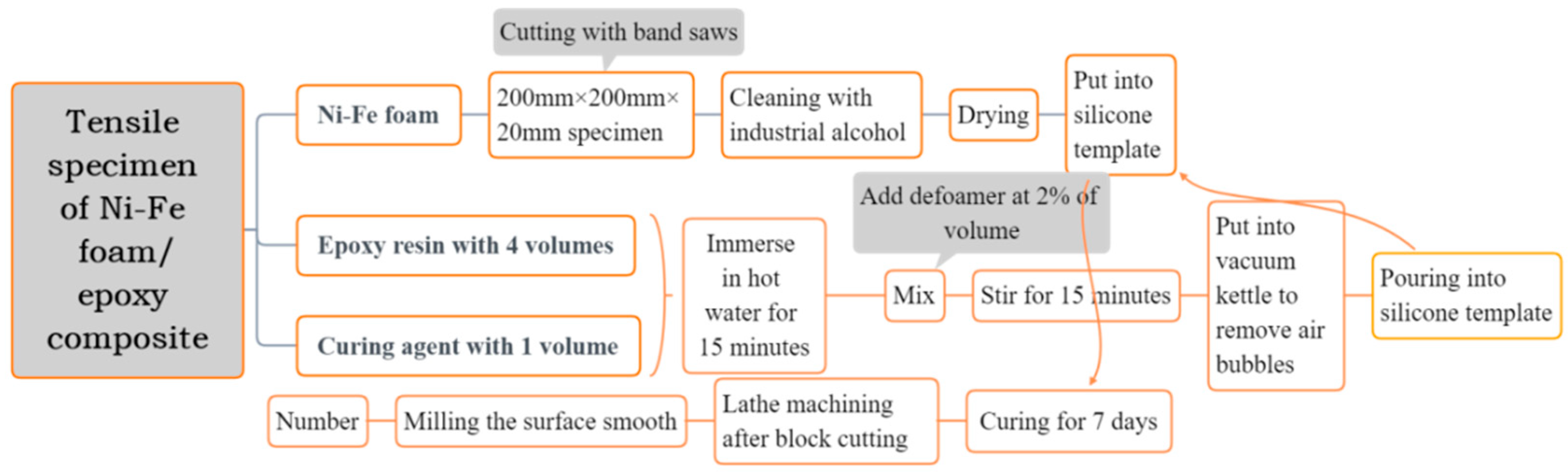
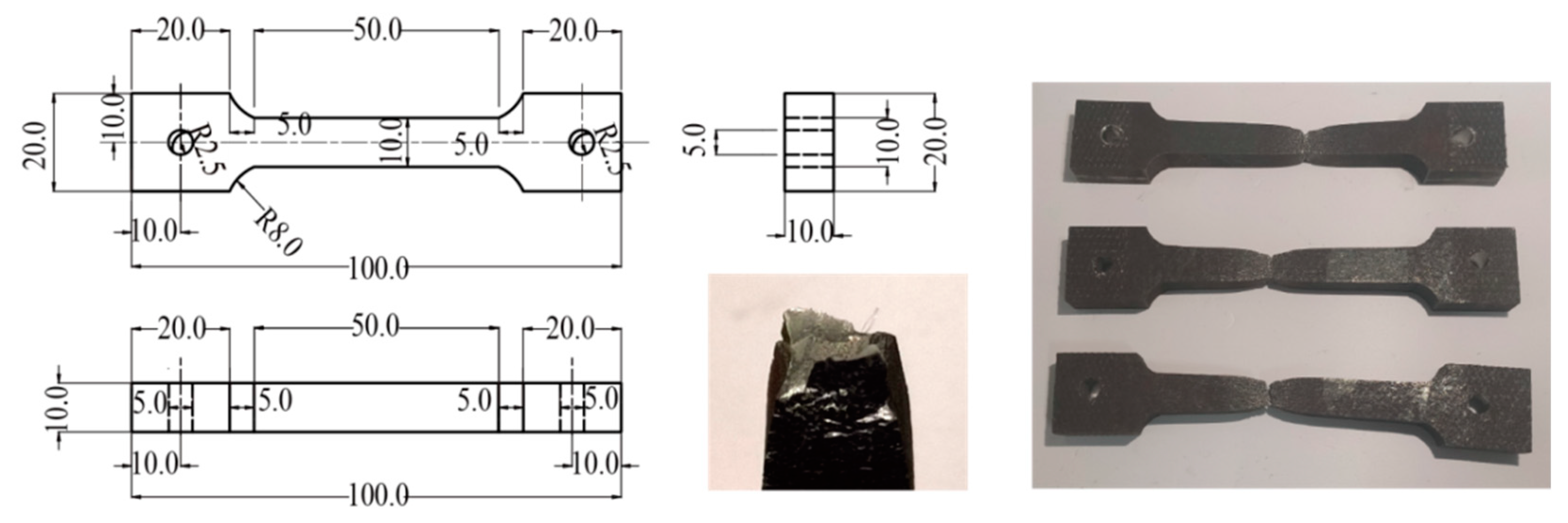
4.1. Specimens of Epoxy Resins and IPC
4.2. Test Instruments and Methods
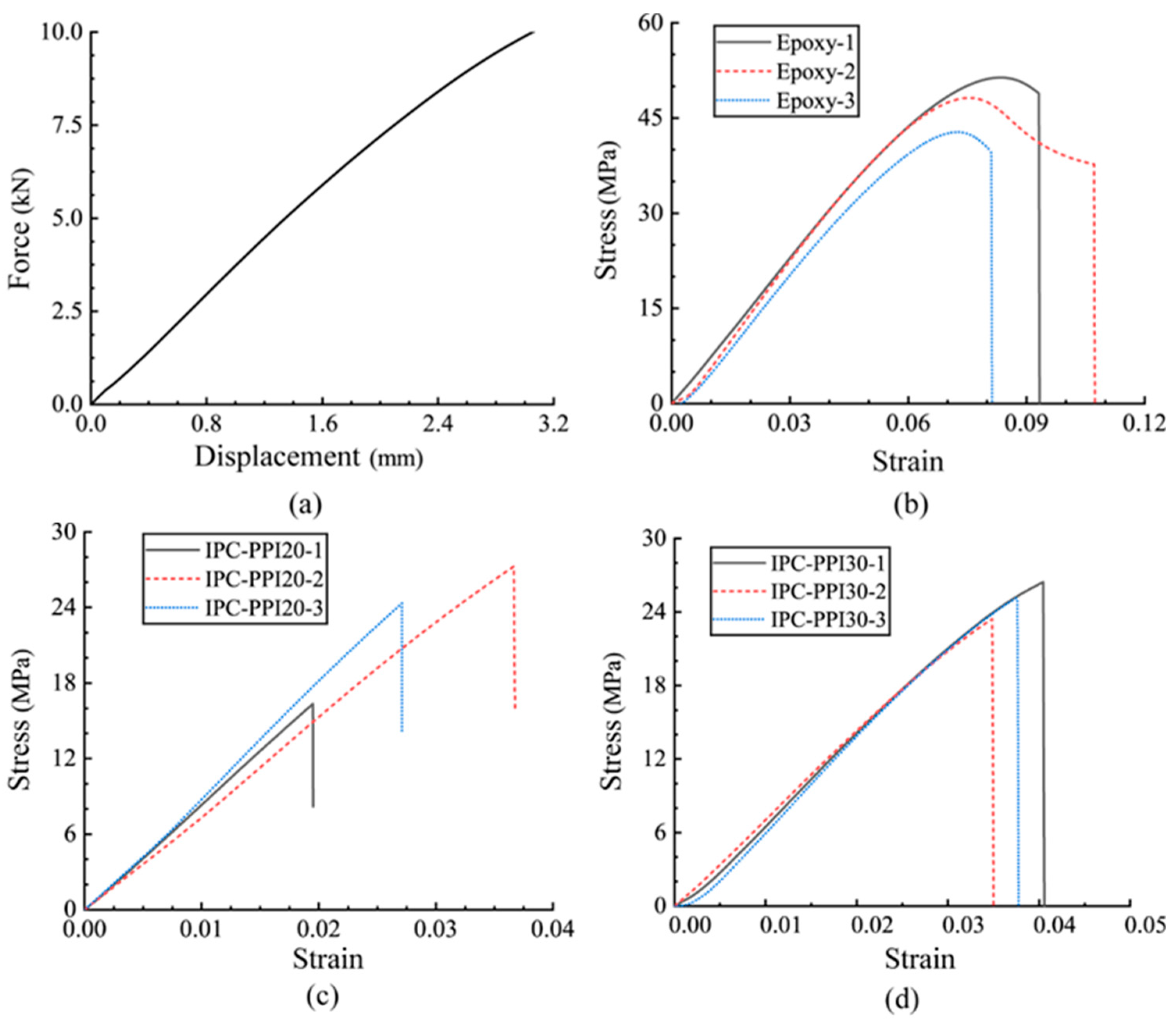
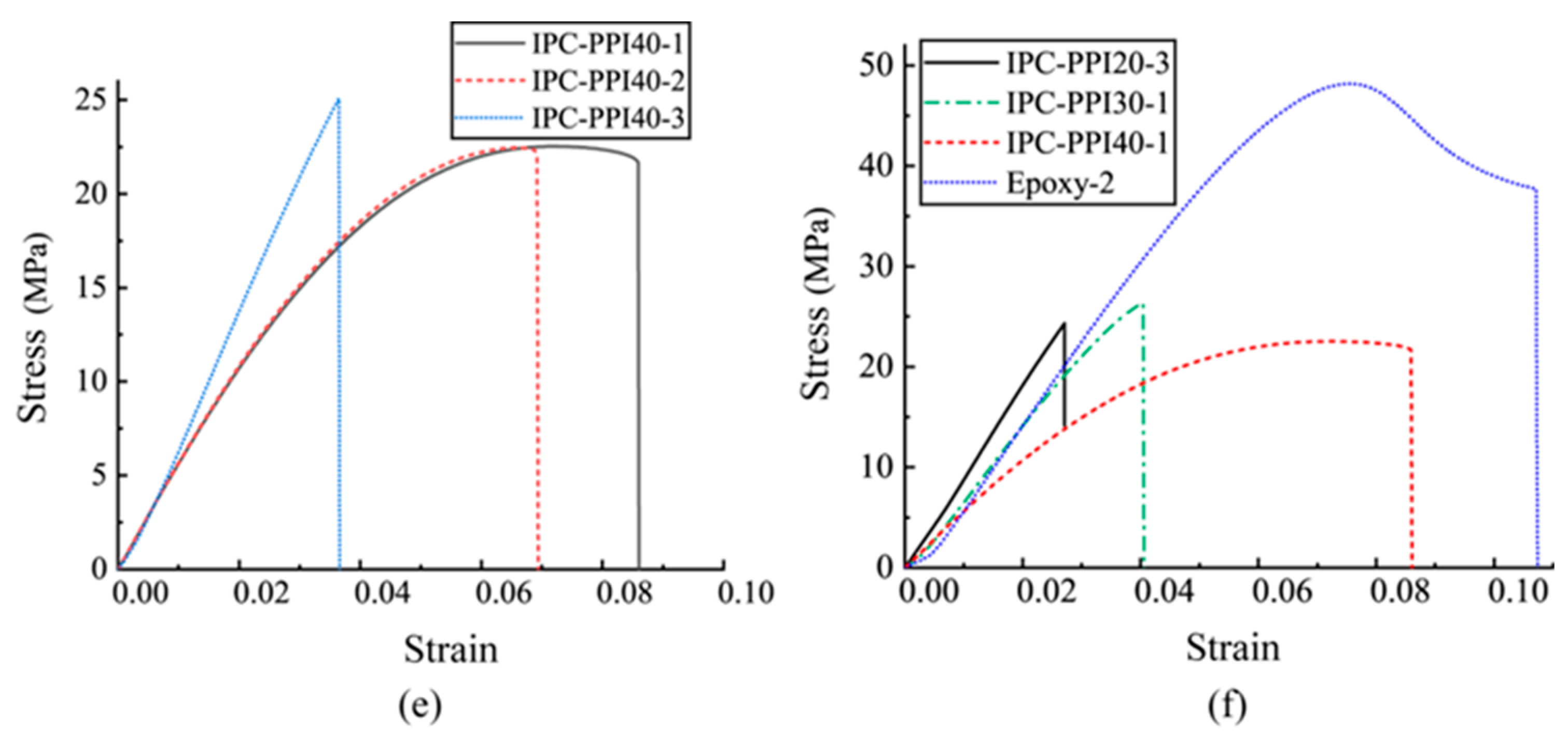
4.3. Test Results and Analysis
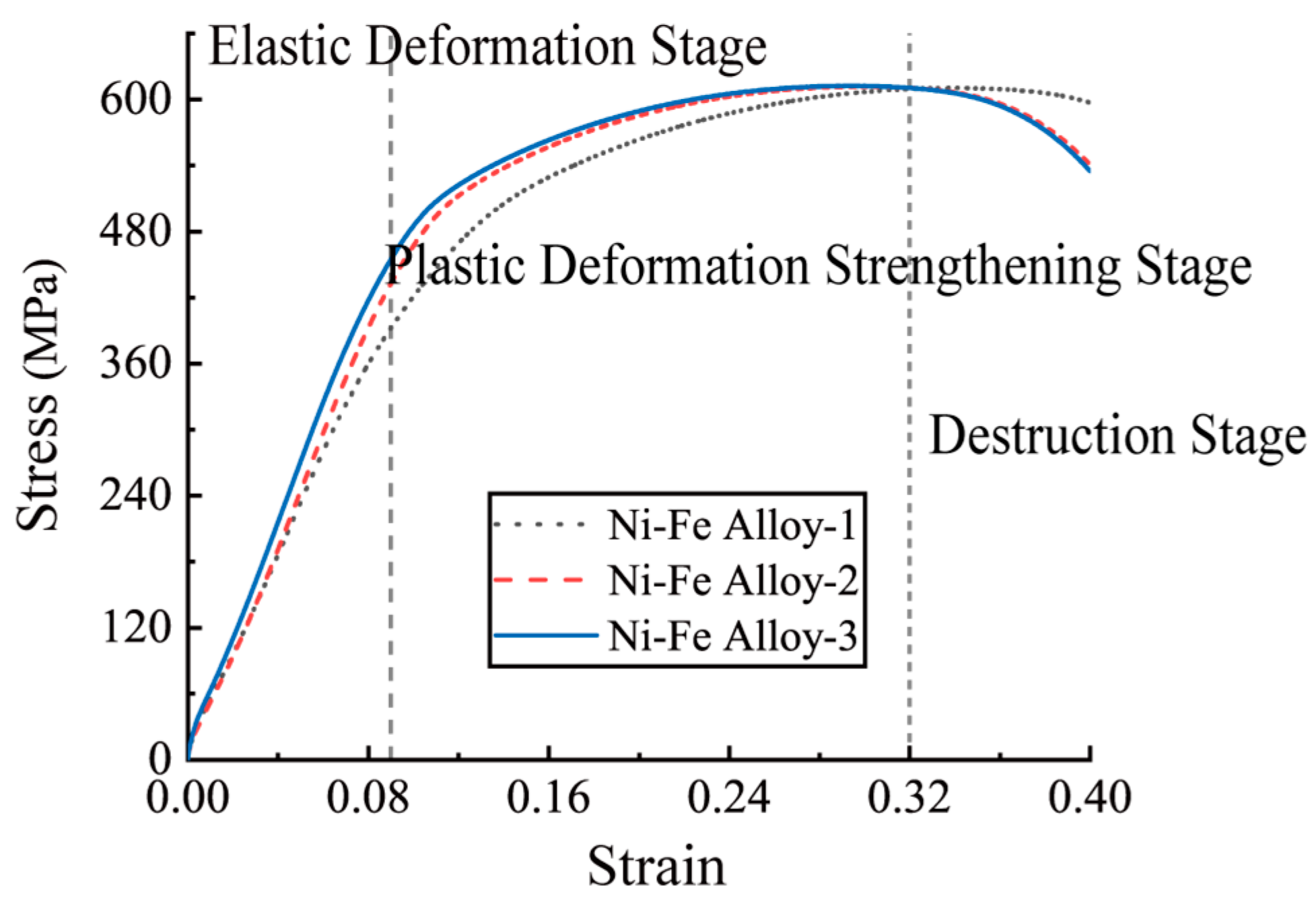
4.4. Tensile Testing of Ni-Fe Alloys
5. Verification
6. Conclusions
- The force characteristics of the foam metal/epoxy IPC are analyzed under uniaxial tensile loading, and a microscopic mechanical model of the tensile representative volume element for the foam metal/epoxy IPC is established. The stress–strain relationships of representative volume elements are derived for foam metal/epoxy IPC in elastic and plastic deformation phases based on the assumptions of equal stress and equal strain; the damage evolution equations of IPC are determined with the effective area of the matrix phase as the damage parameter.
- The uniaxial tensile strengths of PPI20, PPI30, and PPI40 Ni-Fe/epoxy interpenetrated phase composites and their constituent phases (epoxy and Ni-Fe alloy) were tested in three groups each. The results show that the combination of three-dimensional networks interpenetrating does not significantly improve the tensile strength of the composites since the presence of weak interfaces.
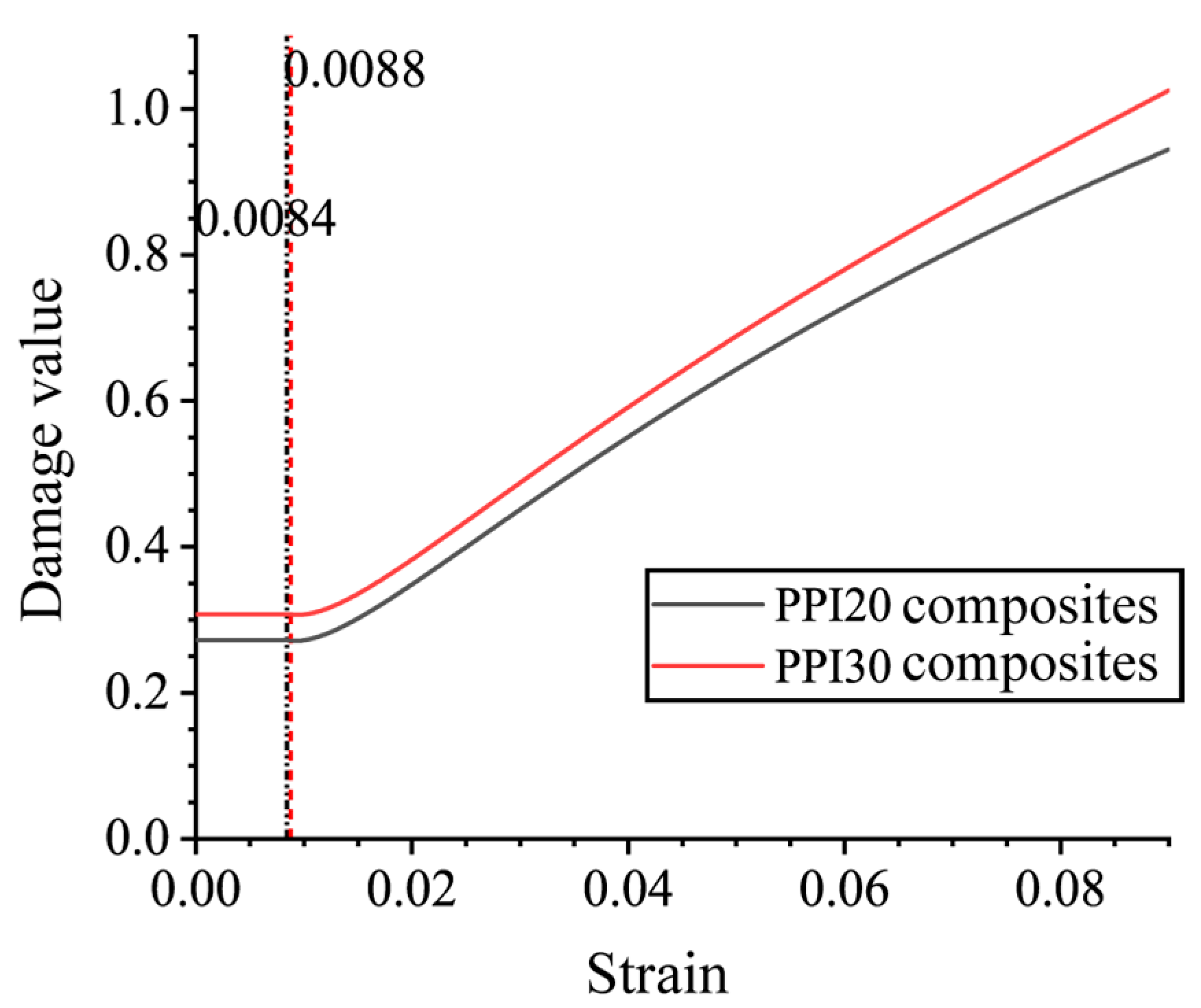
- The damage evolution equations of PPI20 and PPI30 IPC are determined from the measured data of PPI40 Ni-Fe/epoxy composites, geometric data, and the constitutive phase Ni-Fe and epoxy intrinsic relationships, and then the intrinsic equations of PPI20 and PPI30 Ni-Fe/epoxy IPC are predicted. Satisfactory results are obtained in comparison with experimental data, thus verifying the accuracy and applicability of the representative volume element tensile model.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Yang, L.; Deli, D.; Junxiang, W.; Sihan, H.; Shu, L. Tensile Properties of Co-continuous Composites of Nickel Foam/Epoxy Resin/Silicon Carbide. Chin. J. Mater. Res. 2016, 30, 5. [Google Scholar] [CrossRef]
- Kota, N.; Jana, P.; Sahasrabudhe, S.; Roy, S. Processing and characterization of Al-Si alloy/SiC foam interpenetrating phase composite. Mater. Today Proc. 2021, 44, 2930–2933. [Google Scholar] [CrossRef]
- Yu, Y.H. Study on Mechanical Behavior and Application of Aluminum Foam/Epoxy Resin Composites. Ph.D. Thesis, Liaoning University of Engineering and Technology, Fuxin, China, 2007. [Google Scholar]
- Li, H.; Liu, Z.; Yu, W.; Liang, X. Experimental electromagnetic shielding and mechanical properties of aluminum foam/epoxy composites. Mater. Guide 2015, 29, 150–154. [Google Scholar]
- Chen, W.; Guan, C.; Liang, Z.; Yin, H. Current status of application of aluminum foam matrix composites. Therm. Process. Technol. 2019, 48, 22–24. [Google Scholar]
- Liu, S. Experimental Study on Mechanical Properties and Vibration Damping Applications of Aluminum Foam Composites. Ph.D. Thesis, Southeast University, Nanjing, China, 2018. [Google Scholar]
- Xu, X.; Wang, L.; Wang, J.; Wang, Y.; Huang, Q.; Huang, Y. Simulation of heat transfer and thermal storage processes in foam-metal composite PCM microstructures. J. Chem. Eng. 2021, 72, 956–964. [Google Scholar]
- Wang, Z.; Zhang, Z.; Jia, L.; Yang, L. Paraffin and paraffin/aluminum foam composite phase change material heat storage experimental study based on thermal management of Li-ion battery. Appl. Therm. Eng. 2015, 78, 428–436. [Google Scholar] [CrossRef]
- Tuchinskii, L.I. Elastic constants of pseudoalloys with a skeletal structure. Sov. Powder Metall. Met. Ceram. 1983, 22, 588–595. [Google Scholar] [CrossRef]
- Ravichandran, K.S. Deformation behavior of interpenetrating-phase composites. Compos. Sci. Technol. 1994, 52, 541–549. [Google Scholar] [CrossRef]
- Feng, X.Q. Effective Elastic and Plastic Properties of Interpenetrating Multiphase Composites. Appl. Compos. Mater. 2004, 11, 33–55. [Google Scholar] [CrossRef]
- Yu, Y.H.; Liang, B. Prediction of effective elastic modulus of aluminum foam/epoxy composites based on network interwoven composites. Mech. Eng. Mater. 2008, 11, 90–92. [Google Scholar]
- Wegner, L.D.; Gibson, L.J. The mechanical behaviour of interpenetrating phase composites—I: Modelling. Int. J. Mech. Sci. 2000, 42, 925–942. [Google Scholar] [CrossRef]
- Wegner, L.D.; Gibson, L.J. The mechanical behaviour of interpenetrating phase composites—II: A case study of a three-dimensionally printed material. Int. J. Mech. Sci. 2000, 42, 943–964. [Google Scholar] [CrossRef]
- Seetoh, I.; Markandan, K.; Lai, C.Q. Effect of reinforcement bending on the elastic properties of interpenetrating phase composites. Mech. Mater. 2019, 136, 103071. [Google Scholar] [CrossRef]
- Yuan, Z.Y.; Rayess, N.; Dukhan, N. Modeling of the mechanical properties of a polymer-metal foam hybrid. In Proceedings of the 8th International Conference on Porous Metals and Metallic Foams, Raleigh, NC, USA, 23–26 June 2013; pp. 215–219. [Google Scholar]
- Chaturvedi, A.; Gupta, M.K.; Chaturvedi, S. Open-Cell Nickel Alloy Foam–Natural Rubber Hybrid: Compression Energy Absorption Behavior Analysis and Experiment. J. Mater. Eng. Perform. 2021, 30, 885–893. [Google Scholar] [CrossRef]
- Poniznik, Z.; Salit, V.; Basista, M.; Gross, D. Effective elastic properties of interpenetrating phase composites. Comput. Mater. Sci. 2008, 44, 813–820. [Google Scholar] [CrossRef]
- Xie, F.; Lu, Z.; Yuan, Z. Numerical analysis of elastic and elastoplastic behavior of interpenetrating phase composites. Comput. Mater. Sci. 2015, 97, 94–101. [Google Scholar] [CrossRef]
- Agarwal, A.; Singh, I.V.; Mishra, B.K. Numerical prediction of elasto-plastic behaviour of interpenetrating phase composites by EFGM. Compos. Part B Eng. 2013, 51, 327–336. [Google Scholar] [CrossRef]
- Torquato, S. Modeling of physical properties of composite materials. Int. J. Solids Struct. 2000, 37, 411–422. [Google Scholar] [CrossRef]
- Basirat, M.; Shrestha, T.; Potirniche, G.P.; Charit, I.; Rink, K. A study of the creep behavior of modified 9Cr–1Mo steel using continuum-damage modeling. Int. J. Plast. 2012, 37, 95–107. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. ZAMM J. Appl. Math. Mech./Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Wegner, L.D.; Gibson, L.J. The mechanical behaviour of interpenetrating phase composites—III: Resin-impregnated porous stainless steel. Int. J. Mech. Sci. 2001, 43, 1061–1072. [Google Scholar] [CrossRef]
- Liu, Y.; Duan, D.L.; Jiang, S.L.; Li, S. Preparation and its cavitation performance of nickel foam/epoxy/SiC co-continuous composites. Wear 2015, 332–333, 979–987. [Google Scholar] [CrossRef]
- Ying, L.; Xulin, Y.; Wei, F.; Kui, L.; Pan, W.; Zuowan, Z. Preparation Methods of Network Interpenetrating Meta/Polymer Composites and Property Research Progress. J. Chengdu Univ. (Nat. Sci. Ed.) 2021, 40, 89–96. [Google Scholar]
- Wang, X.X.; Zhou, Y.; Li, J.L.; Li, H.J.; Liang, X. Discussion of a new mechanical model for interpenetrating phase composites under compression considering constituent phase interactions. Aip Adv. 2022, 12, 035051. [Google Scholar] [CrossRef]
- Xie, B. Damping and Mechanical Properties of Carbon Nanotube-Modified Nickel Foam/Epoxy Composites. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, 2017. [Google Scholar]
- Broberg, H. Creep Damage and Rupture; Chalmers University of Technology: Gothenberg, Sweden, 1975. [Google Scholar]
- Shen, H. Nonlinear intrinsic equations and dehumidification damage models for highly filled polymer damaged viscoelastic media. J. Solid Mech. 1987, 1, 41–47. [Google Scholar]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990; pp. 121–135. [Google Scholar]






| Material Type | Apparent Density (g·cm−3) | Ni-Fe Alloy Density (g·cm−3) | Young’s Modulus of Ni-Fe Alloy (MPa) |
|---|---|---|---|
| Ni-Fe foam(PPI20) | 0.18 | 8.23 | 22,847 |
| Ni-Fe foam(PPI30) | 0.21 | 8.23 | 22,847 |
| Ni-Fe foam(PPI40) | 0.26 | 8.23 | 22,847 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhang, L.; Zhao, Y.; Li, H. A New Uniaxial Tensile Model for Foam Metal/Epoxy Interpenetrated Phase Composites. Polymers 2023, 15, 812. https://doi.org/10.3390/polym15040812
Wang X, Zhang L, Zhao Y, Li H. A New Uniaxial Tensile Model for Foam Metal/Epoxy Interpenetrated Phase Composites. Polymers. 2023; 15(4):812. https://doi.org/10.3390/polym15040812
Chicago/Turabian StyleWang, Xiaoxing, Lixin Zhang, Yu Zhao, and Huijian Li. 2023. "A New Uniaxial Tensile Model for Foam Metal/Epoxy Interpenetrated Phase Composites" Polymers 15, no. 4: 812. https://doi.org/10.3390/polym15040812
APA StyleWang, X., Zhang, L., Zhao, Y., & Li, H. (2023). A New Uniaxial Tensile Model for Foam Metal/Epoxy Interpenetrated Phase Composites. Polymers, 15(4), 812. https://doi.org/10.3390/polym15040812






