Conformational Parameters and Hydrodynamic Behavior of Poly(2-Methyl-2-Oxazoline) in a Broad Molar Mass Range
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
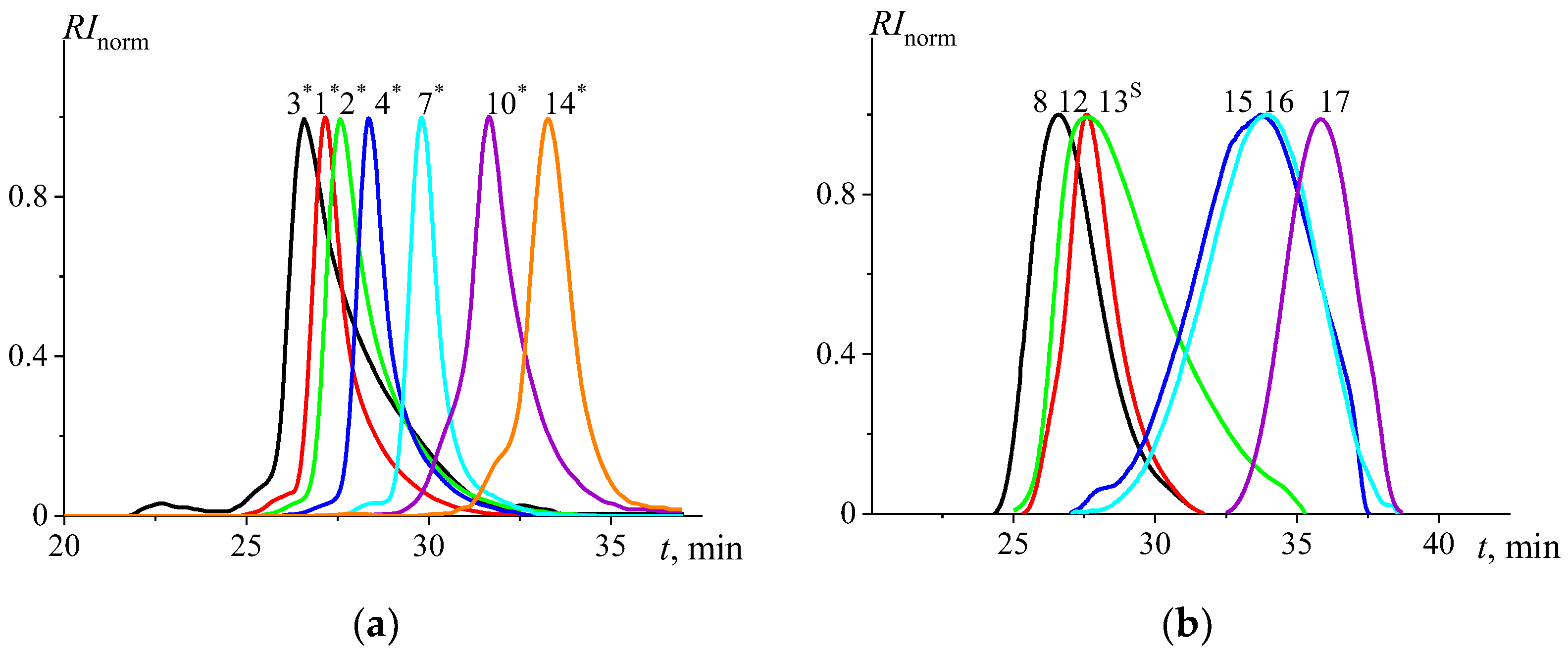
3. Results
4. Discussion
4.1. Kuhn–Mark–Houwink–Sakurada Equations
4.2. Conformation Analysis
4.3. The Specific Hydrodynamic Volume of Relevant Water Soluble Polymers
5. Conclusions
6. Patents
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, L.; Wang, Z.; Wei, X.; Shi, J.; Li, C. Antibodies against polyethylene glycol in human blood: A literature review. J. Pharmacol. Toxicol. Methods 2020, 102, 106678. [Google Scholar] [CrossRef] [PubMed]
- Hoang Thi, T.T.; Pilkington, E.H.; Nguyen, D.H.; Lee, J.S.; Park, K.D.; Truong, N.P. The Importance of Poly(ethylene glycol) Alternatives for Overcoming PEG Immunogenicity in Drug Delivery and Bioconjugation. Polymers 2020, 12, 298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knop, K.; Hoogenboom, R.; Fischer, D.; Schubert, U.S. Poly(ethylene glycol) in Drug Delivery: Pros and Cons as Well as Potential Alternatives. Angew. Chem. Int. Ed. 2010, 49, 6288–6308. [Google Scholar] [CrossRef] [PubMed]
- Garay, R.P.; El-Gewely, R.; Armstrong, J.K.; Garratty, G.; Richette, P. Antibodies against polyethylene glycol in healthy subjects and in patients treated with PEG-conjugated agents. Expert Opin. Drug Deliv. 2012, 9, 1319–1323. [Google Scholar] [CrossRef]
- Braatz, D.; Cherri, M.; Tully, M.; Dimde, M.; Ma, G.; Mohammadifar, E.; Reisbeck, F.; Ahmadi, V.; Schirner, M.; Haag, R. Chemical Approaches to Synthetic Drug Delivery Systems for Systemic Applications. Angew. Chem. Int. Ed. 2022, 61, e202203942. [Google Scholar] [CrossRef]
- Adams, N.; Schubert, U.S. Poly(2-oxazolines) in biological and biomedical application contexts. Adv. Drug Deliv. Rev. 2007, 59, 1504–1520. [Google Scholar] [CrossRef]
- Mero, A.; Pasut, G.; Via, L.D.; Fijten, M.W.M.; Schubert, U.S.; Hoogenboom, R.; Veronese, F.M. Synthesis and characterization of poly(2-ethyl 2-oxazoline)-conjugates with proteins and drugs: Suitable alternatives to PEG-conjugates? J. Control. Release 2008, 125, 87–95. [Google Scholar] [CrossRef]
- Bludau, H.; Czapar, A.E.; Pitek, A.S.; Shukla, S.; Jordan, R.; Steinmetz, N.F. POxylation as an alternative stealth coating for biomedical applications. Eur. Polym. J. 2017, 88, 679–688. [Google Scholar] [CrossRef] [Green Version]
- Sedlacek, O.; de la Rosa, V.R.; Hoogenboom, R. Poly(2-oxazoline)-protein conjugates. Eur. Polym. J. 2019, 120, 109246. [Google Scholar] [CrossRef] [Green Version]
- Sedlacek, O.; Monnery, B.D.; Mattova, J.; Kucka, J.; Panek, J.; Janouskova, O.; Hocherl, A.; Verbraeken, B.; Vergaelen, M.; Zadinova, M.; et al. Poly(2-ethyl-2-oxazoline) conjugates with doxorubicin for cancer therapy: In vitro and in vivo evaluation and direct comparison to poly[N-(2-hydroxypropyl)methacrylamide] analogues. Biomaterials 2017, 146, 1–12. [Google Scholar] [CrossRef]
- Qi, Y.; Chilkoti, A. Protein–polymer conjugation—Moving beyond PEGylation. Curr. Opin. Chem. Biol. 2015, 28, 181–193. [Google Scholar] [CrossRef] [Green Version]
- Hoogenboom, R. Poly(2-oxazoline)s: A Polymer Class with Numerous Potential Applications. Angew. Chem. Int. Ed. 2009, 48, 7978–7994. [Google Scholar] [CrossRef]
- Bouten, P.J.M.; Lava, K.; Van Hest, J.C.M.; Hoogenboom, R. Thermal Properties of Methyl Ester-Containing Poly(2-oxazoline)s. Polymers 2015, 7, 1998–2008. [Google Scholar] [CrossRef] [Green Version]
- Chapman, R.; Bouten, P.J.M.; Hoogenboom, R.; Jolliffe, K.A.; Perrier, S. Thermoresponsive cyclic peptide—poly(2-ethyl-2-oxazoline) conjugate nanotubes. Chem. Commun. 2013, 49, 6522–6524. [Google Scholar] [CrossRef]
- Christova, D.; Velichkova, R.; Loos, W.; Goethals, E.J.; Du Prez, F. New thermo-responsive polymer materials based on poly(2-ethyl-2-oxazoline) segments. Polymer 2003, 44, 2255–2261. [Google Scholar] [CrossRef]
- Lorson, T.; Lübtow, M.M.; Wegener, E.; Haider, M.S.; Borova, S.; Nahm, D.; Jordan, R.; Sokolski-Papkov, M.; Kabanov, A.V.; Luxenhofer, R. Poly(2-oxazoline)s based biomaterials: A comprehensive and critical update. Biomaterials 2018, 178, 204–280. [Google Scholar] [CrossRef]
- Zahoranová, A.; Luxenhofer, R. Poly(2-oxazoline)- and Poly(2-oxazine)-Based Self-Assemblies, Polyplexes, and Drug Nanoformulations—An Update. Adv. Healthc. Mater. 2021, 10, 2001382. [Google Scholar] [CrossRef]
- Nemati Mahand, S.; Aliakbarzadeh, S.; Moghaddam, A.; Salehi Moghaddam, A.; Kruppke, B.; Nasrollahzadeh, M.; Khonakdar, H.A. Polyoxazoline: A review article from polymerization to smart behaviors and biomedical applications. Eur. Polym. J. 2022, 178, 111484. [Google Scholar] [CrossRef]
- Novy, Z.; Lobaz, V.; Vlk, M.; Kozempel, J.; Stepanek, P.; Popper, M.; Vrbkova, J.; Hajduch, M.; Hruby, M.; Petrik, M. Head-To-Head Comparison of Biological Behavior of Biocompatible Polymers Poly(Ethylene Oxide), Poly(2-Ethyl-2-Oxazoline) and Poly[N-(2-Hydroxypropyl)Methacrylamide] as Coating Materials for Hydroxyapatite Nanoparticles in Animal Solid Tumor Model. Nanomaterials 2020, 10, 1690. [Google Scholar] [CrossRef]
- Le, D.; Wagner, F.; Takamiya, M.; Hsiao, I.L.; Gil Alvaradejo, G.; Strähle, U.; Weiss, C.; Delaittre, G. Straightforward access to biocompatible poly(2-oxazoline)-coated nanomaterials by polymerization-induced self-assembly. Chem. Commun. 2019, 55, 3741–3744. [Google Scholar] [CrossRef]
- Moreadith, R.W.; Viegas, T.X.; Bentley, M.D.; Harris, J.M.; Fang, Z.; Yoon, K.; Dizman, B.; Weimer, R.; Rae, B.P.; Li, X.; et al. Clinical development of a poly(2-oxazoline) (POZ) polymer therapeutic for the treatment of Parkinson’s disease—Proof of concept of POZ as a versatile polymer platform for drug development in multiple therapeutic indications. Eur. Polym. J. 2017, 88, 524–552. [Google Scholar] [CrossRef]
- Wyffels, L.; Verbrugghen, T.; Monnery, B.D.; Glassner, M.; Stroobants, S.; Hoogenboom, R.; Staelens, S. μPET imaging of the pharmacokinetic behavior of medium and high molar mass (89)Zr-labeled poly(2-ethyl-2-oxazoline) in comparison to poly(ethylene glycol). J Control. Release 2016, 235, 63–71. [Google Scholar] [CrossRef] [PubMed]
- de la Rosa, V.R.; Bulcke, A.V.D.; Hoogenboom, R. Poly(2-Oxazoline)s: The Versatile Polymer Platform for Biomedicine. Material Matters 2016, 11, 75–79. [Google Scholar]
- Lava, K.; Verbraeken, B.; Hoogenboom, R. Poly(2-oxazoline)s and click chemistry: A versatile toolbox toward multi-functional polymers. Eur. Polym. J. 2015, 65, 98–111. [Google Scholar] [CrossRef] [Green Version]
- Pereira, G.; Huin, C.; Morariu, S.; Bennevault-Celton, V.; Guégan, P. Synthesis of Poly(2-methyl-2-oxazoline) Star Polymers with a β-Cyclodextrin Core. Aust. J. Chem. 2012, 65, 1145–1155. [Google Scholar] [CrossRef]
- Lezov, A.; Gubarev, A.; Mikhailova, M.; Lezova, A.; Mikusheva, N.; Kalganov, V.; Dudkina, M.; Ten’kovtsev, A.; Nekrasova, T.; Andreeva, L.; et al. Star-Shaped poly(2-ethyl-2-oxazoline) and poly(2-isopropyl-2-oxazoline) with central thiacalix [4]Arene fragments: Reduction and stabilization of silver nanoparticles. Polymers 2019, 11, 2006. [Google Scholar] [CrossRef] [Green Version]
- Bauer, M.; Lautenschlaeger, C.; Kempe, K.; Tauhardt, L.; Schubert, U.S.; Fischer, D. Poly(2-ethyl-2-oxazoline) as Alternative for the Stealth Polymer Poly(ethylene glycol): Comparison of in vitro Cytotoxicity and Hemocompatibility. Macromol. Biosci. 2012, 12, 986–998. [Google Scholar] [CrossRef]
- Hoogenboom, R. The future of poly(2-oxazoline)s. Eur. Polym. J. 2022, 179, 111521. [Google Scholar] [CrossRef]
- Olanow, C.W.; Standaert, D.G.; Kieburtz, K.; Viegas, T.X.; Moreadith, R. Once-Weekly Subcutaneous Delivery of Polymer-Linked Rotigotine (SER-214) Provides Continuous Plasma Levels in Parkinson’s Disease Patients. Mov. Disord. 2020, 35, 1055–1061. [Google Scholar] [CrossRef]
- Boerman, M.A.; Roozen, E.; Sánchez-Fernández, M.J.; Keereweer, A.R.; Félix Lanao, R.P.; Bender, J.C.M.E.; Hoogenboom, R.; Leeuwenburgh, S.C.; Jansen, J.A.; Van Goor, H.; et al. Next Generation Hemostatic Materials Based on NHS-Ester Functionalized Poly(2-oxazoline)s. Biomacromolecules 2017, 18, 2529–2538. [Google Scholar] [CrossRef] [Green Version]
- Clinical Safety and Performance of GATT-Patch in Open Liver Surgery. Available online: https://www.clinicaltrials.gov/ct2/show/NCT04819945 (accessed on 3 December 2022).
- Sedlacek, O.; Van Driessche, A.; Uvyn, A.; De Geest, B.G.; Hoogenboom, R. Poly(2-methyl-2-oxazoline) conjugates with doxorubicin: From synthesis of high drug loading water-soluble constructs to in vitro anti-cancer properties. J. Control. Release 2020, 326, 53–62. [Google Scholar] [CrossRef]
- Svoboda, J.; Sedláček, O.; Riedel, T.; Hrubý, M.; Pop-Georgievski, O. Poly(2-oxazoline)s One-Pot Polymerization and Surface Coating: From Synthesis to Antifouling Properties Out-Performing Poly(ethylene oxide). Biomacromolecules 2019, 20, 3453–3463. [Google Scholar] [CrossRef]
- Pidhatika, B.; Rodenstein, M.; Chen, Y.; Rakhmatullina, E.; Mühlebach, A.; Acikgöz, C.; Textor, M.; Konradi, R. Comparative stability studies of poly(2-methyl-2-oxazoline) and poly(ethylene glycol) brush coatings. Biointerphases 2012, 7, 1. [Google Scholar] [CrossRef] [Green Version]
- Konradi, R.; Acikgoz, C.; Textor, M. Polyoxazolines for nonfouling surface coatings—A direct comparison to the gold standard PEG. Macromol. Rapid Commun. 2012, 33, 1663–1676. [Google Scholar] [CrossRef]
- Morgese, G.; Verbraeken, B.; Ramakrishna, S.N.; Gombert, Y.; Cavalli, E.; Rosenboom, J.-G.; Zenobi-Wong, M.; Spencer, N.D.; Hoogenboom, R.; Benetti, E.M. Chemical Design of Non-Ionic Polymer Brushes as Biointerfaces: Poly(2-oxazine)s Outperform Both Poly(2-oxazoline)s and PEG. Angew. Chem. Int. Ed. 2018, 57, 11667–11672. [Google Scholar] [CrossRef] [Green Version]
- Morgese, G.; Benetti, E.M. Polyoxazoline biointerfaces by surface grafting. Eur. Polym. J. 2017, 88, 470–485. [Google Scholar] [CrossRef]
- Yan, Y.H.; Atif, M.; Liu, R.Y.; Zhu, H.K.; Chen, L.J. Design of comb-like poly(2-methyl-2-oxazoline) and its rapid co-deposition with dopamine for the study of antifouling properties. J. Biomater. Sci. Polym. Ed. 2020, 31, 423–438. [Google Scholar] [CrossRef]
- Mansfield, E.D.H.; de la Rosa, V.R.; Kowalczyk, R.M.; Grillo, I.; Hoogenboom, R.; Sillence, K.; Hole, P.; Williams, A.C.; Khutoryanskiy, V.V. Side chain variations radically alter the diffusion of poly(2-alkyl-2-oxazoline) functionalised nanoparticles through a mucosal barrier. Biomater. Sci. 2016, 4, 1318–1327. [Google Scholar] [CrossRef] [Green Version]
- Zakharchenko, A.; Xue, Y.; Keeney, S.; Rock, C.A.; Alferiev, I.S.; Stachelek, S.J.; Takano, H.; Thomas, T.; Nagaswami, C.; Krieger, A.M.; et al. Poly-2-methyl-2-oxazoline–modified bioprosthetic heart valve leaflets have enhanced biocompatibility and resist structural degeneration. Proc. Natl. Acad. Sci. USA 2022, 119, 4119. [Google Scholar] [CrossRef]
- Grube, M.; Leiske, M.N.; Schubert, U.S.; Nischang, I. POx as an alternative to PEG? A hydrodynamic and light scattering study. Macromolecules 2018, 51, 1905–1916. [Google Scholar] [CrossRef]
- He, Z.; Wan, X.; Schulz, A.; Bludau, H.; Dobrovolskaia, M.A.; Stern, S.T.; Montgomery, S.A.; Yuan, H.; Li, Z.; Alakhova, D.; et al. A high capacity polymeric micelle of paclitaxel: Implication of high dose drug therapy to safety and in vivo anti-cancer activity. Biomaterials 2016, 101, 296–309. [Google Scholar] [CrossRef]
- Hwang, D.; Vinod, N.; Skoczen, S.L.; Ramsey, J.D.; Snapp, K.S.; Montgomery, S.A.; Wang, M.; Lim, C.; Frank, J.E.; Sokolsky-Papkov, M.; et al. Bioequivalence assessment of high-capacity polymeric micelle nanoformulation of paclitaxel and Abraxane® in rodent and non-human primate models using a stable isotope tracer assay. Biomaterials 2021, 278, 121140. [Google Scholar] [CrossRef] [PubMed]
- Haider, M.S.; Lübtow, M.M.; Endres, S.; Forster, S.; Flegler, V.J.; Böttcher, B.; Aseyev, V.; Pöppler, A.-C.; Luxenhofer, R. Think Beyond the Core: Impact of the Hydrophilic Corona on Drug Solubilization Using Polymer Micelles. ACS Appl. Mater. Interfaces 2020, 12, 24531–24543. [Google Scholar] [CrossRef] [PubMed]
- Gubarev, A.S.; Monnery, B.D.; Lezov, A.A.; Sedlacek, O.; Tsvetkov, N.V.; Hoogenboom, R.; Filippov, S.K. Conformational properties of biocompatible poly(2-ethyl-2-oxazoline)s in phosphate buffered saline. Polym. Chem. 2018, 9, 2232–2237. [Google Scholar] [CrossRef] [Green Version]
- Monnery, B.D.; Hoogenboom, R. Method for the Preparation of Uniform High Molar Mass Cyclic Imino Ether Polymers. PCT/EP2015/065829, 10 July 2015. [Google Scholar]
- Sedlacek, O.; Monnery, B.D.; Hoogenboom, R. Synthesis of defined high molar mass poly(2-methyl-2-oxazoline). Polym. Chem. 2019, 10, 1286–1290. [Google Scholar] [CrossRef]
- Monnery, B.D.; Jerca, V.V.; Sedlacek, O.; Verbraeken, B.; Cavill, R.; Hoogenboom, R. Defined High Molar Mass Poly(2-Oxazoline)s. Angew. Chem. Int. Ed. 2018, 57, 15400–15404. [Google Scholar] [CrossRef]
- Kratky, O.; Leopold, H.; Stabinger, H. The determination of the partial specific volume of proteins by the mechanical oscillator technique. Methods Enzymol. 1973, 27, 98–110. [Google Scholar] [CrossRef]
- Schuck, P. Size-distribution analysis of macromolecules by sedimentation velocity ultracentrifugation and Lamm equation modeling. Biophys. J. 2000, 78, 1606–1619. [Google Scholar] [CrossRef] [Green Version]
- Lamm, O. Die differentialgleichung der ultrazentrifugierung. Ark. Mat. Astr. Fys. 1929, 21B, 1–4. [Google Scholar]
- Pike, E.R. Photon Correlation and Light Beating Spectroscopy, 1st ed.Springer: New York, NY, USA, 1974; p. 504. [Google Scholar]
- Schärtl, W. Light Scattering from Polymer Solutions and Nanoparticle Dispersions, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2007; p. 191. [Google Scholar]
- Berne, B.J.; Pecora, R. Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics; John Wiley: Hoboken, NJ, USA, 1976; p. 376. [Google Scholar]
- Tsvetkov, V.N. Rigid-Chain Polymers; Consultation Bureau Plenum: London, UK, 1989; p. 490. [Google Scholar]
- Perevyazko, I.; Gubarev, A.S.; Tauhardt, L.; Dobrodumov, A.; Pavlov, G.M.; Schubert, U.S. Linear poly(ethylene imine)s: True molar masses, solution properties and conformation. Polym. Chem. 2017, 8, 7169–7179. [Google Scholar] [CrossRef]
- Huggins, M.L. The Viscosity of Dilute Solutions of Long-Chain Molecules. IV. Dependence on Concentration. J. Am. Chem. Soc. 1942, 64, 2716–2718. [Google Scholar] [CrossRef]
- Kraemer, E.O. Molecular Weights of Celluloses and Cellulose Derivates. Ind. Eng. Chem. 1938, 30, 1200–1203. [Google Scholar] [CrossRef]
- Pamies, R.; Hernandez Cifre, J.G.; Lopez Martinez, M.d.C.; Garcia de la Torre, J. Determination of intrinsic viscosities of macromolecules and nanoparticles. Comparison of single-point and dilution procedures. Colloid. Polym. Sci. 2008, 286, 1223–1231. [Google Scholar] [CrossRef]
- Solomon, O.F.; Ciutǎ, I.Z. Détermination de la viscosité intrinsèque de solutions de polymères par une simple détermination de la viscosité. J. Appl. Polym. Sci. 1962, 6, 683–686. [Google Scholar] [CrossRef]
- Hoogenboom, R.; Thijs, H.M.L.; Jochems, M.J.H.C.; Van Lankvelt, B.M.; Fijten, M.W.M.; Schubert, U.S. Tuning the LCST of poly(2-oxazoline)s by varying composition and molecular weight: Alternatives to poly(N-isopropylacrylamide)? Chem. Commun. 2008, 44, 5758–5760. [Google Scholar] [CrossRef]
- Bloksma, M.M.; Bakker, D.J.; Weber, C.; Hoogenboom, R.; Schubert, U.S. The effect of hofmeister salts on the LCST transition of poly(2-oxazoline)s with varying hydrophilicity. Macromol. Rapid Commun. 2010, 31, 724–728. [Google Scholar] [CrossRef]
- Pavlov, G.M. Different Levels of Self-Sufficiency of the Velocity Sedimentation Method in the Study of Linear Macromolecules. In Analytical Ultracentrifugation: Instrumentation, Software, and Applications; Uchiyama, S., Arisaka, F., Stafford, W., Laue, T., Eds.; Springer: Tokyo, Japan, 2016; pp. 269–307. [Google Scholar]
- Perevyazko, I.Y.; Gubarev, A.S.; Pavlov, G.M. Analytical ultracentrifugation and combined molecular hydrodynamic approaches for polymer characterization. In Molecular Characterization of Polymers: A Fundamental Guide; Malik, M.I., Mays, J., Shah, M.R., Eds.; Elsevier Science: Amsterdam, The Netherlands, 2021; pp. 223–257. [Google Scholar]
- Tsvetkov, V.N.; Lavrenko, P.N.; Bushin, S.V. Hydrodynamic invariant of polymer molecules. J. Polym. Sci., Part A: Polym. Chem. 1984, 22, 3447–3486. [Google Scholar] [CrossRef]
- Pavlov, G.M.; Panarin, E.F.; Korneeva, E.V.; Kurochkin, C.V.; Baikov, V.E.; Ushakova, V.N. Hydrodynamic properties of poly(1-vinyl-2-pyrrolidone) molecules in dilute solution. Makromolek. Chemie 1990, 191, 2889–2899. [Google Scholar] [CrossRef]
- Nischang, I.; Perevyazko, I.; Majdanski, T.; Vitz, J.; Festag, G.; Schubert, U.S. Hydrodynamic Analysis Resolves the Pharmaceutically-Relevant Absolute Molar Mass and Solution Properties of Synthetic Poly(ethylene glycol)s Created by Varying Initiation Sites. Anal. Chem. 2017, 89, 1185–1193. [Google Scholar] [CrossRef]
- Kawaguchi, S.; Imai, G.; Suzuki, J.; Miyahara, A.; Kitano, T.; Ito, K. Aqueous solution properties of oligo- and poly(ethylene oxide) by static light scattering and intrinsic viscosity. Polymer 1997, 38, 2885–2891. [Google Scholar] [CrossRef]
- Dobrun, L.A.; Kuzyakina, E.L.; Rakitina, O.V.; Sergeeva, O.Y.; Mikhailova, M.E.; Domnina, N.S.; Lezov, A.V. Molecular characteristics and antioxidant activity of polyethylene glycols modified by sterically hindered phenols. J. Struct. Chem. 2011, 52, 1161–1166. [Google Scholar] [CrossRef]
- Yamakawa, H.; Fujii, M. Translational Friction Coefficient of Wormlike Chains. Macromolecules 1973, 6, 407–415. [Google Scholar] [CrossRef]
- Stockmayer, W.H.; Fixman, M. On the estimation of unperturbed dimensions from intrinsic viscosities. J. Polym. Sci. Part C Polym. Symp. 1963, 1, 137–141. [Google Scholar] [CrossRef]
- Cowie, J.M.G.; Bywater, S. The use of frictional coefficients to evaluate unperturbed dimensions in dilute polymer solutions. Polymer 1965, 6, 197–204. [Google Scholar] [CrossRef]
- Gray, H.B.; Bloomfield, V.A.; Hearst, J.E. Sedimentation Coefficients of Linear and Cyclic Wormlike Coils with Excluded-Volume Effects. J. Chem. Phys. 1967, 46, 1493–1498. [Google Scholar] [CrossRef]
- Tsuji, T.; Norisuye, T.; Fujita, H. Dilute Solution of Bisphenol A Polycarbonate. Polym. J. 1975, 7, 558. [Google Scholar] [CrossRef] [Green Version]
- Pavlov, G.M.; Harding, S.E.; Rowe, A.J. Normalized scaling relations as a natural classification of linear macromolecules according to size. In Analytical Ultracentrifugation V; Cölfen, H., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 113, pp. 76–80. [Google Scholar]
- Pavlov, G.M. Size and average density spectra of macromolecules obtained from hydrodynamic data. Eur. Phys. J. E 2007, 22, 171–180. [Google Scholar] [CrossRef]



| PMeOx Sample | Đ | |||
|---|---|---|---|---|
| 1 * | 58 | 54 | 1.07 | 43 |
| 2 * | 43 | 39 | 1.10 | 35 |
| 3 * | 73 | 65 | 1.12 | 32 |
| 4 * | 33 | 32 | 1.03 | 25 |
| 5 | 50 | 38 | 1.32 | 20 |
| 6 | 20 | 16 | 1.25 | 17 |
| 7 * | 19 | 18 | 1.06 | 16 |
| 8 | 20 | 16 | 1.25 | 10 |
| 9 | 9.9 | 7.1 | 1.39 | 10 |
| 10 * | 9.5 | 8.7 | 1.09 | 9.5 |
| 11 U | 8.5 | 7.7 | 1.10 | 7.5 |
| 12 | 13 | 12 | 1.08 | 6.8 |
| 13 S | 11 | 8.1 | 1.36 | 5.4 |
| 14 * | 5.1 | 4.8 | 1.06 | 4.2 |
| 15 | 3.6 | 2.8 | 1.29 | 2.3 |
| 16 | 3.3 | 2.6 | 1.27 | 1.6 |
| 17 | 1.8 | 1.5 | 1.20 | 1.2 |
| PMeOx Sample | |||||
|---|---|---|---|---|---|
| 1 * | 60.7 ± 0.3 | 0.36 | 60.4 ± 0.1 | 0.14 | 60.5 |
| 2 * | 55 ± 2 | 0.38 | 55.5 ± 0.9 | 0.14 | 55 |
| 3 * | 52.4 ± 0.9 | 0.49 | 53.4 ± 0.4 | 0.10 | 52.9 |
| 4 * | 41.1 ± 1.3 | 0.38 | 41.1 ± 0.7 | 0.14 | 41.1 |
| 5 | 27.3 ± 0.6 | 0.51 | 27.9 ± 0.1 | 0.10 | 27.6 |
| 6 | 23.5 ± 0.1 | 0.47 | 23.8 ± 0.1 | 0.11 | 23.7 |
| 7 * | 30.1 ± 0.2 | 0.42 | 30.3 ± 0.1 | 0.12 | 30.2 |
| 8 | 19.1 ± 0.1 | 0.53 | 19.5 ± 0.1 | 0.09 | 19.3 |
| 9 | 16.6 ± 0.6 | 0.34 | 16.4 ± 0.4 | 0.15 | 16.5 |
| 10 * | 18.7 ± 0.1 | 0.44 | 18.8 ± 0.1 | 0.10 | 18.8 |
| 11 U | 17.1 ± 0.1 | 0.56 | 17.4 ± 0.1 | 0.07 | 17.2 |
| 12 | 14.5 ± 0.1 | 0.58 | 14.7 ± 0.1 | 0.05 | 14.6 |
| 13 S | 11.5 ± 0.1 | 0.53 | 11.6 ± 0.1 | 0.07 | 11.6 |
| 14 * | - | - | - | - | 11.9 2 |
| 15 | 5.6 ± 0.1 | 0.62 1 | 5.6 ± 0.1 | 0.03 1 | 5.6 |
| 16 | 5.1 ± 0.1 | 0.69 1 | 5.2 ± 0.1 | 0 1 | 5.2 |
| 17 | 3.3 ± 0.1 | 1.3 1 | 3.4 ± 0.1 | -0.4 1 | 3.4 |
| PMeOx Sample | [η] [cm3/g] | <D0>107 [cm2/s] 1 | Rh [nm] | s01013 [s] | MsD10−3 [g/mol] | A01010 | L/A |
|---|---|---|---|---|---|---|---|
| 1 * | 60.5 | 5.5 | 5.8 | 1.81 | 43 | 3.7 | 110 |
| 2 * | 55 | 6 | 5.3 | 1.61 | 35 | 3.7 | 90 |
| 3 * | 52.9 | 6.8 | 4.7 | 1.66 | 32 | 4.0 | 80 |
| 4 * | 41.1 | 7.2 | 4.5 | 1.39 | 25 | 3.6 | 65 |
| 5 | 27.6 | 7.7 | 4.2 | 1.19 | 20 | 3.1 | 50 |
| 6 | 23.7 | 8.9 | 3.6 | 1.16 | 17 | 3.2 | 40 |
| 7 * | 30.2 | 9.3 | 3.4 | 1.1 | 16 | 3.6 | 42 |
| 8 | 19.3 | 10.8 | 3.0 | 0.85 | 10 | 3.1 | 30 |
| 9 | 16.5 | 11.5 | 2.8 | 0.87 | 10 | 3.1 | 30 |
| 10 * | 18.8 | 12.4 | 2.6 | 0.89 | 9.5 | 3.4 | 23 |
| 11 U | 17.2 | 14.1 | 2.3 | 0.8 | 7.5 | 3.5 | 20 |
| 12 | 14.6 | 14.4 | 2.2 | 0.74 | 6.8 | 3.3 | 18 |
| 13 S | 11.6 | 18.4 | 1.7 | 0.75 | 5.4 | 3.6 | 14 |
| 14 * | 11.9 | 18.5 | 1.7 | 0.59 | 4.2 | 3.4 | 11 |
| 15 | 5.6 | 31 | 1.0 | 0.53 | 2.3 | 3.6 | 6 |
| 16 | 5.2 | 39 | 0.8 | 0.48 | 1.6 | 3.9 | 4 |
| 17 | 3.4 | 41 | 0.8 | 0.37 | 1.2 | 3.2 | 3 |
| 0.77 ± 0.04 | 0.015 ± 0.004 | 0.9908 | |
| 0.42 ± 0.02 | 0.019 ± 0.003 | 0.9911 | |
| −0.58 ± 0.02 | 2600 ± 400 | −0.9949 | |
| 0.77 ± 0.03 | 0.017 ± 0.005 | 0.9882 | |
| Theory by | ||||
|---|---|---|---|---|
| Yamakawa–Fujii | 2.7 | 2.7 | 0.3 | 0.4 |
| Fixman–Stockmayer | 1.0 ± 0.1 | |||
| Cowie–Bywater | 1.6 ± 0.1 | |||
| Gray–Bloomfield–Hearst | 1.7 ± 0.1 | 1.7 ± 0.2 | 0.2 ± 0.1 | 0.4 ± 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gubarev, A.S.; Lezov, A.A.; Podsevalnikova, A.N.; Mikusheva, N.G.; Fetin, P.A.; Zorin, I.M.; Aseyev, V.O.; Sedlacek, O.; Hoogenboom, R.; Tsvetkov, N.V. Conformational Parameters and Hydrodynamic Behavior of Poly(2-Methyl-2-Oxazoline) in a Broad Molar Mass Range. Polymers 2023, 15, 623. https://doi.org/10.3390/polym15030623
Gubarev AS, Lezov AA, Podsevalnikova AN, Mikusheva NG, Fetin PA, Zorin IM, Aseyev VO, Sedlacek O, Hoogenboom R, Tsvetkov NV. Conformational Parameters and Hydrodynamic Behavior of Poly(2-Methyl-2-Oxazoline) in a Broad Molar Mass Range. Polymers. 2023; 15(3):623. https://doi.org/10.3390/polym15030623
Chicago/Turabian StyleGubarev, Alexander S., Alexey A. Lezov, Anna N. Podsevalnikova, Nina G. Mikusheva, Petr A. Fetin, Ivan M. Zorin, Vladimir O. Aseyev, Ondrej Sedlacek, Richard Hoogenboom, and Nikolai V. Tsvetkov. 2023. "Conformational Parameters and Hydrodynamic Behavior of Poly(2-Methyl-2-Oxazoline) in a Broad Molar Mass Range" Polymers 15, no. 3: 623. https://doi.org/10.3390/polym15030623
APA StyleGubarev, A. S., Lezov, A. A., Podsevalnikova, A. N., Mikusheva, N. G., Fetin, P. A., Zorin, I. M., Aseyev, V. O., Sedlacek, O., Hoogenboom, R., & Tsvetkov, N. V. (2023). Conformational Parameters and Hydrodynamic Behavior of Poly(2-Methyl-2-Oxazoline) in a Broad Molar Mass Range. Polymers, 15(3), 623. https://doi.org/10.3390/polym15030623









