Impact Response of Monolithic and Laminated Polycarbonate Panels: An Experimental and Numerical Investigation
Abstract
:1. Introduction
2. Experimental Tests
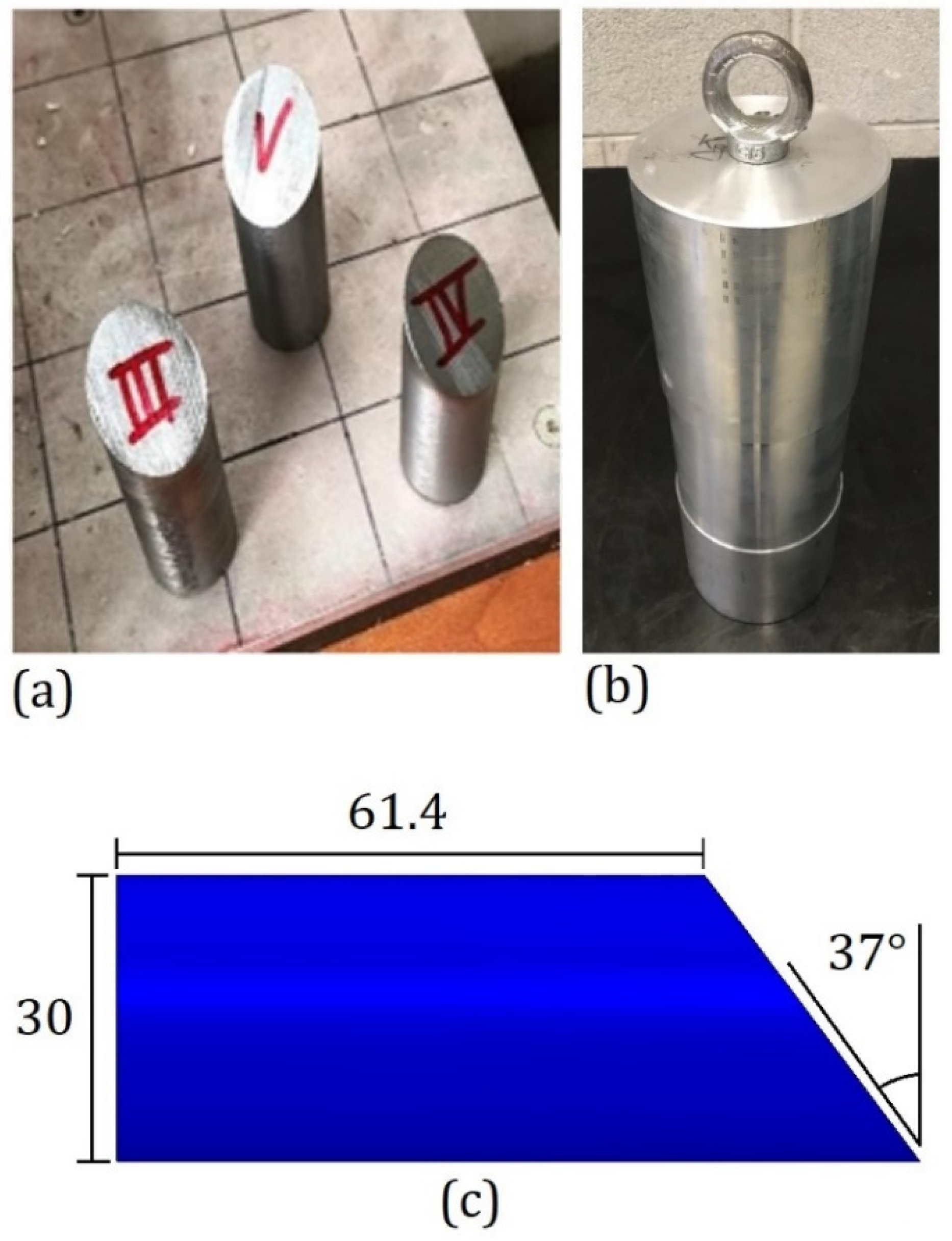
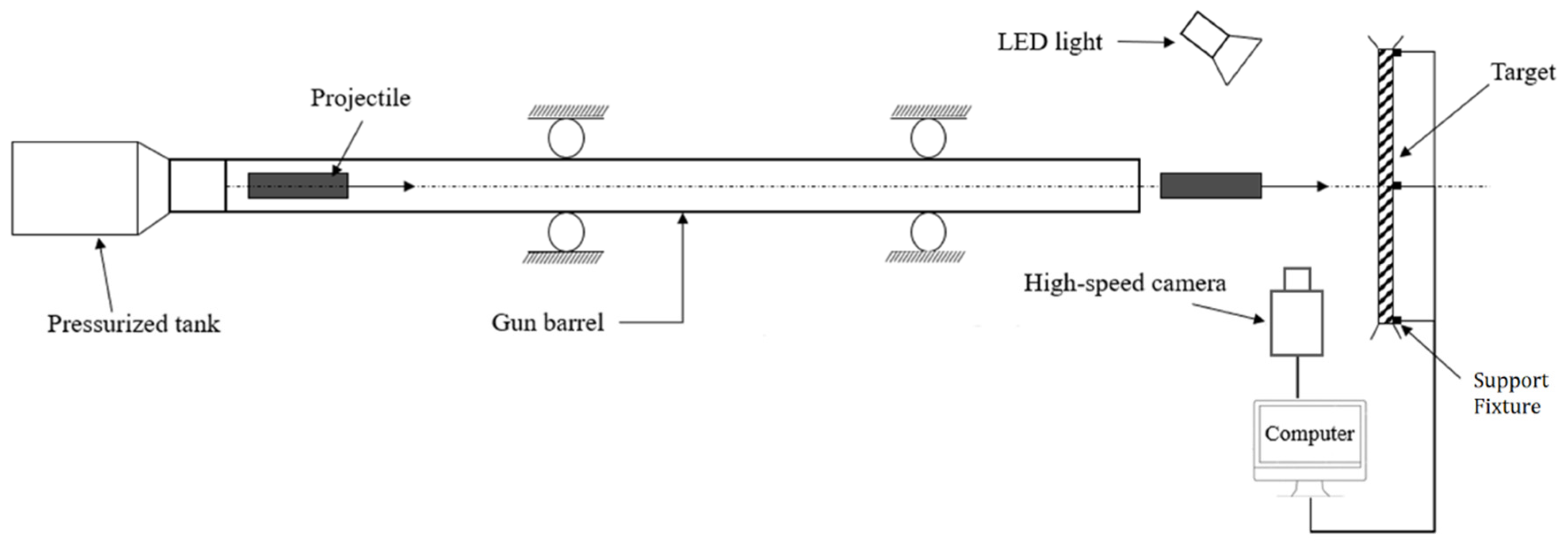
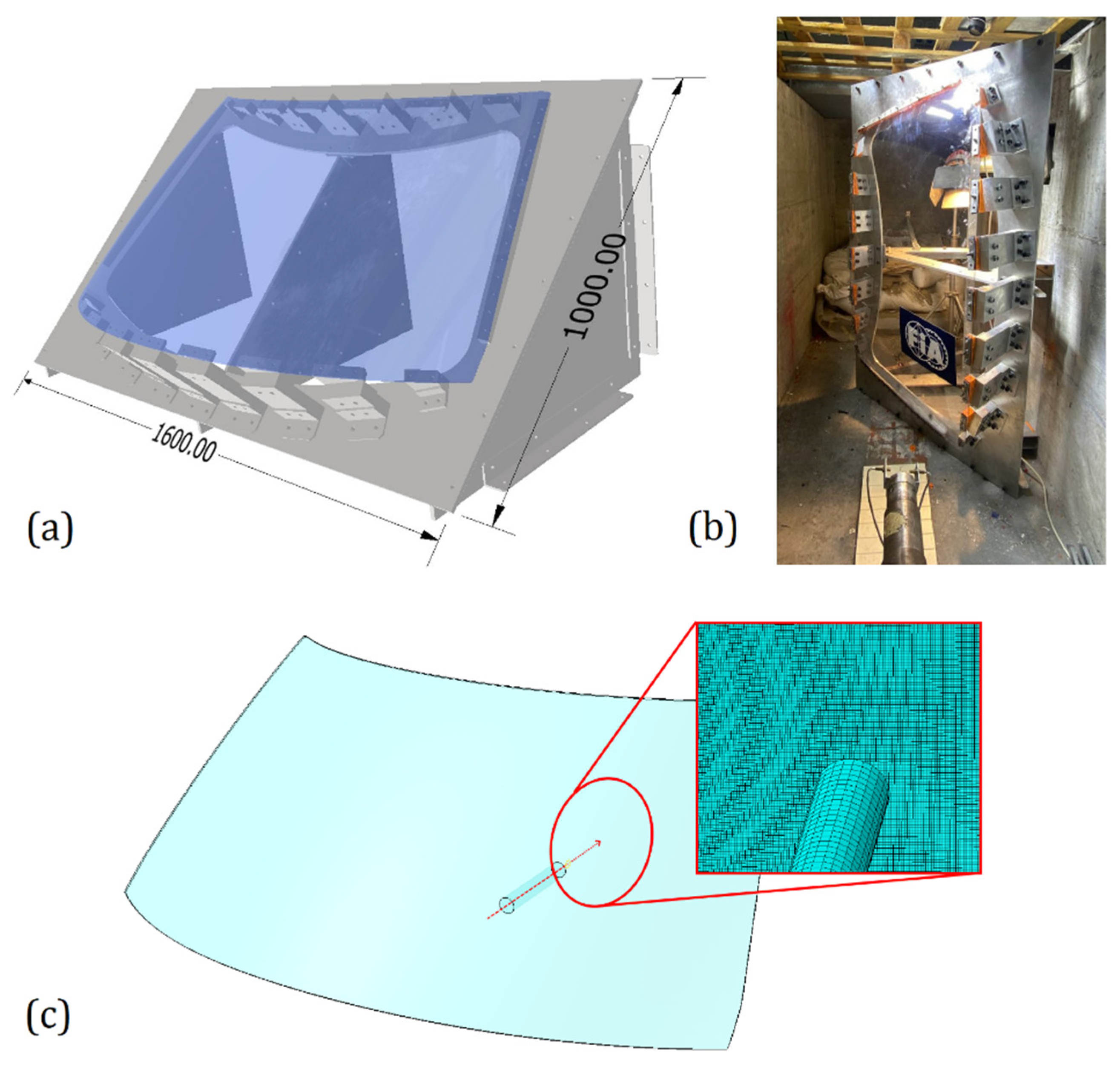
2.1. Drop Weight and Gas Gun Impact Tests Layout
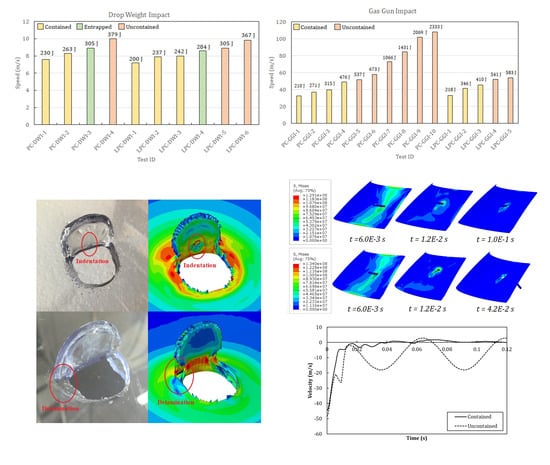
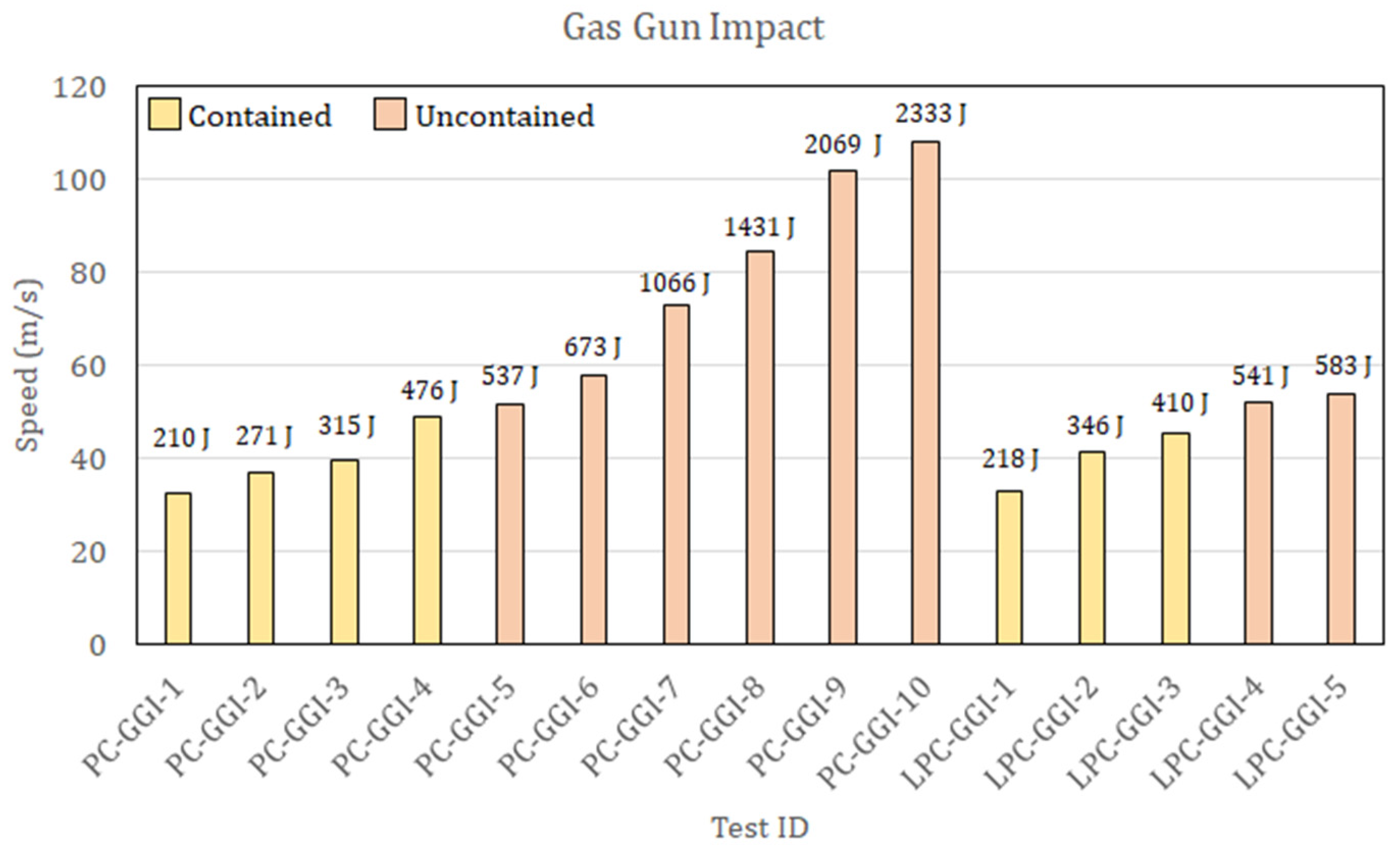
2.2. Drop Weight and Gas Gun Impact Tests Results
3. Numerical Model
3.1. Geometries, Meshes, and Boundary Conditions
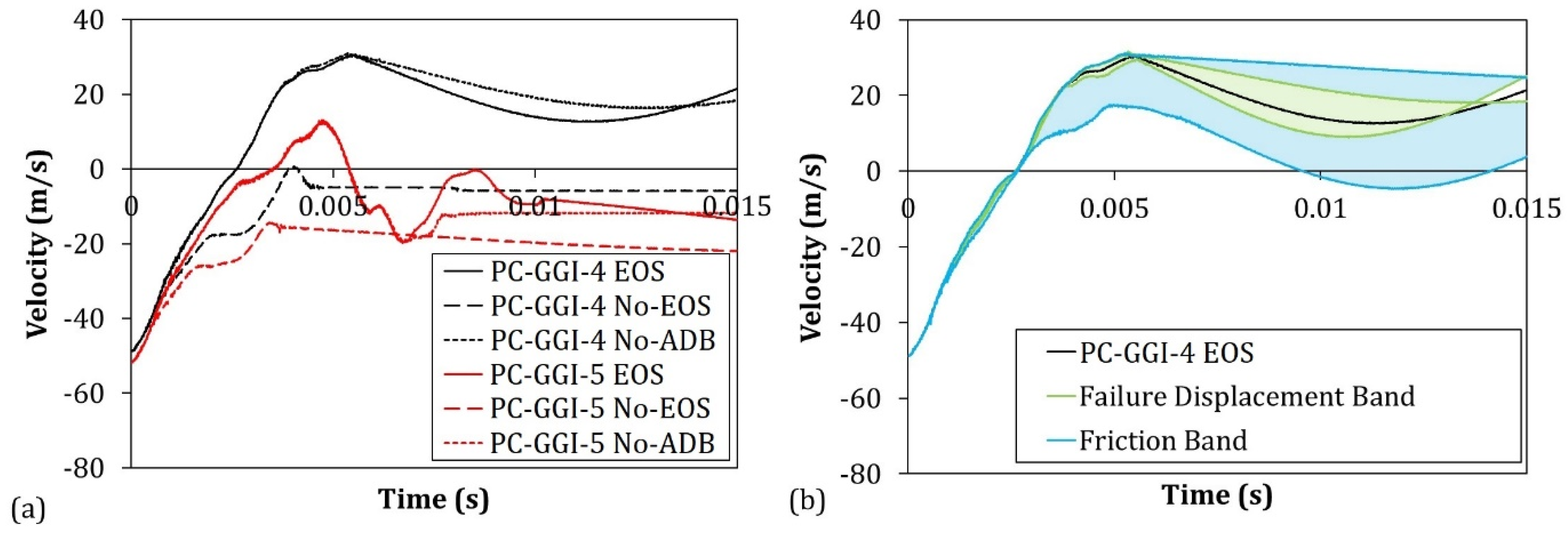
3.2. Adiabatic Condition
3.3. PC Constitutive Laws
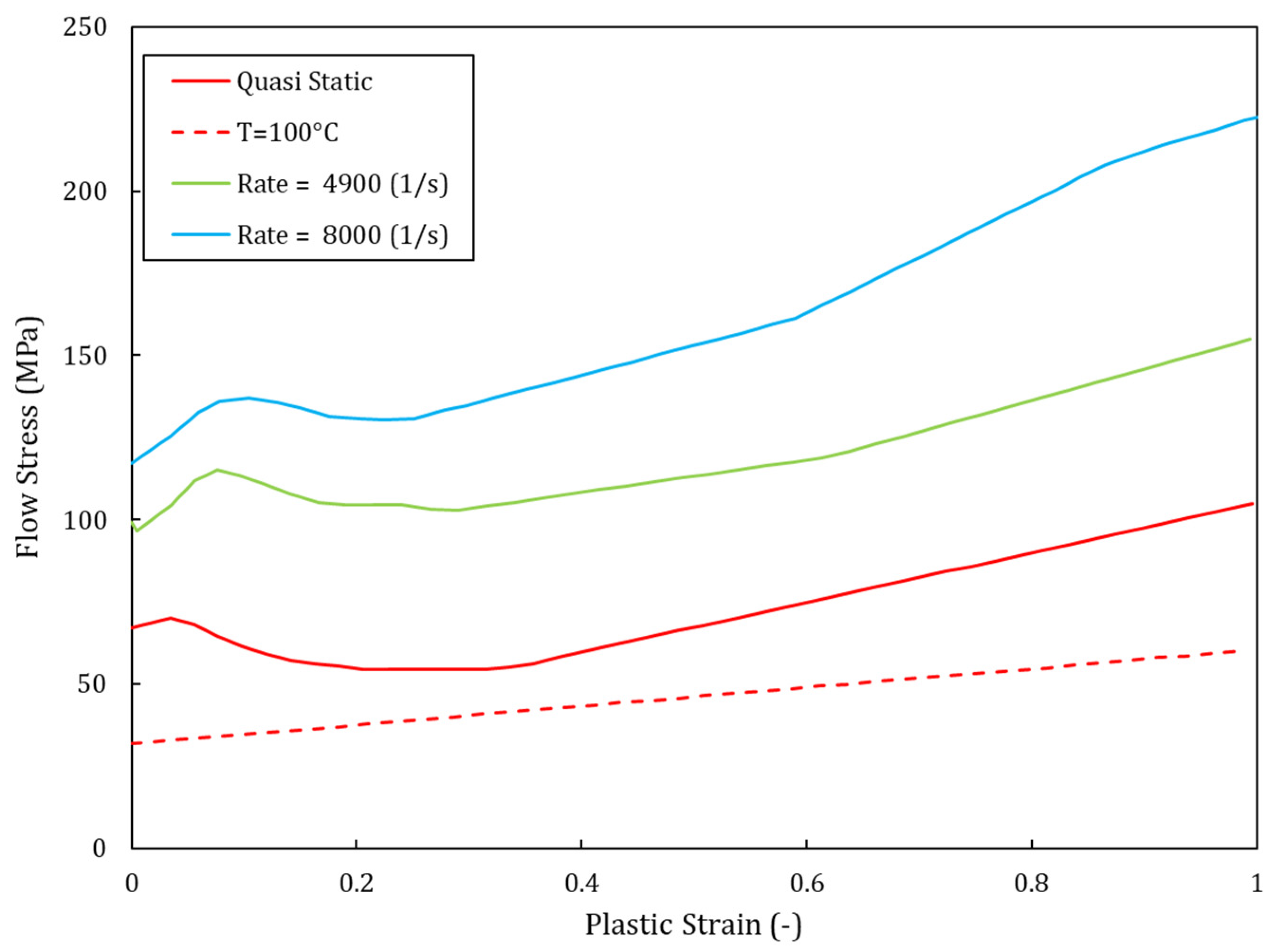
3.3.1. Non-Linear Behavior
3.3.2. Damage Models
3.3.3. Model Parameters and Calibration
| Material | ρ [kg/m3] | G [MPa] | Cp [J/kg·K°] | Inelastic Heat Friction φ | |
|---|---|---|---|---|---|
| PC | 1200 | 0.3 | 803 at T = 0° 80.3 at T = 200° | 1300 | 0.9 |
| Steel | 7800 | 0.37 | 76,600 | 420 | 1.0 |
| Yielding Stress | Ductile Failure | Tensile Failure | ||||
|---|---|---|---|---|---|---|
| Strain Rate | T | Damage Initiation | Damage Evolution | Hydrostatic Cutoff Stress | ||
| Strain Rate | Fracture Strain | Failure Displacement | ||||
| 1/s | °C | MPa | 1/s | - | MPa | |
| 0.001 | 25 | 67.3 | 0.001 | 1 | 80 | 150 |
| 4900 | 25 | 99.3 | 4900 | 0.85 | ||
| 8000 | 25 | 117.2 | 8000 | 0.85 | ||
| 0.001 | 125 | 32.4 | 80,000 | 0.6 | ||
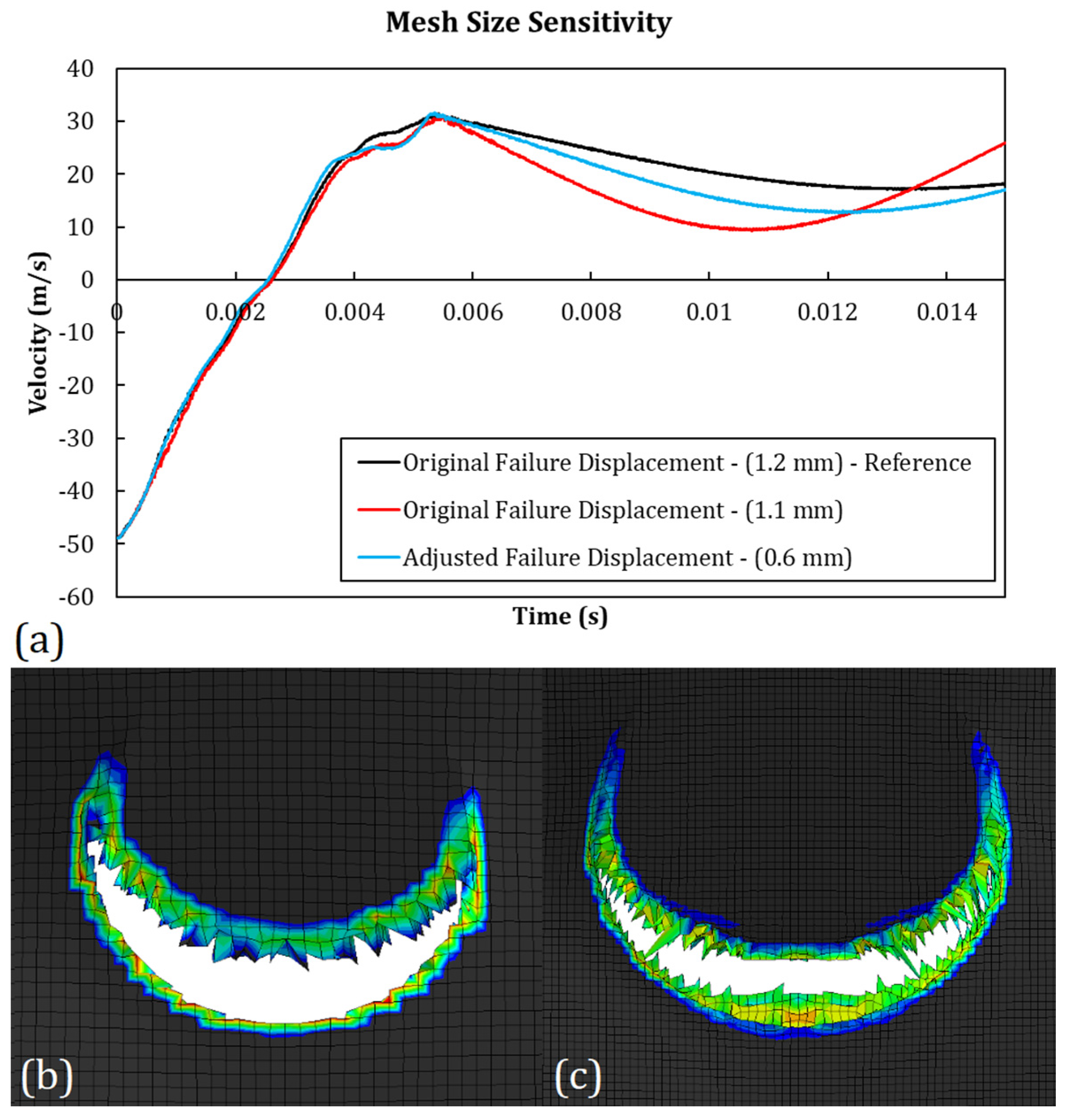
3.3.4. Mesh Size Dependence
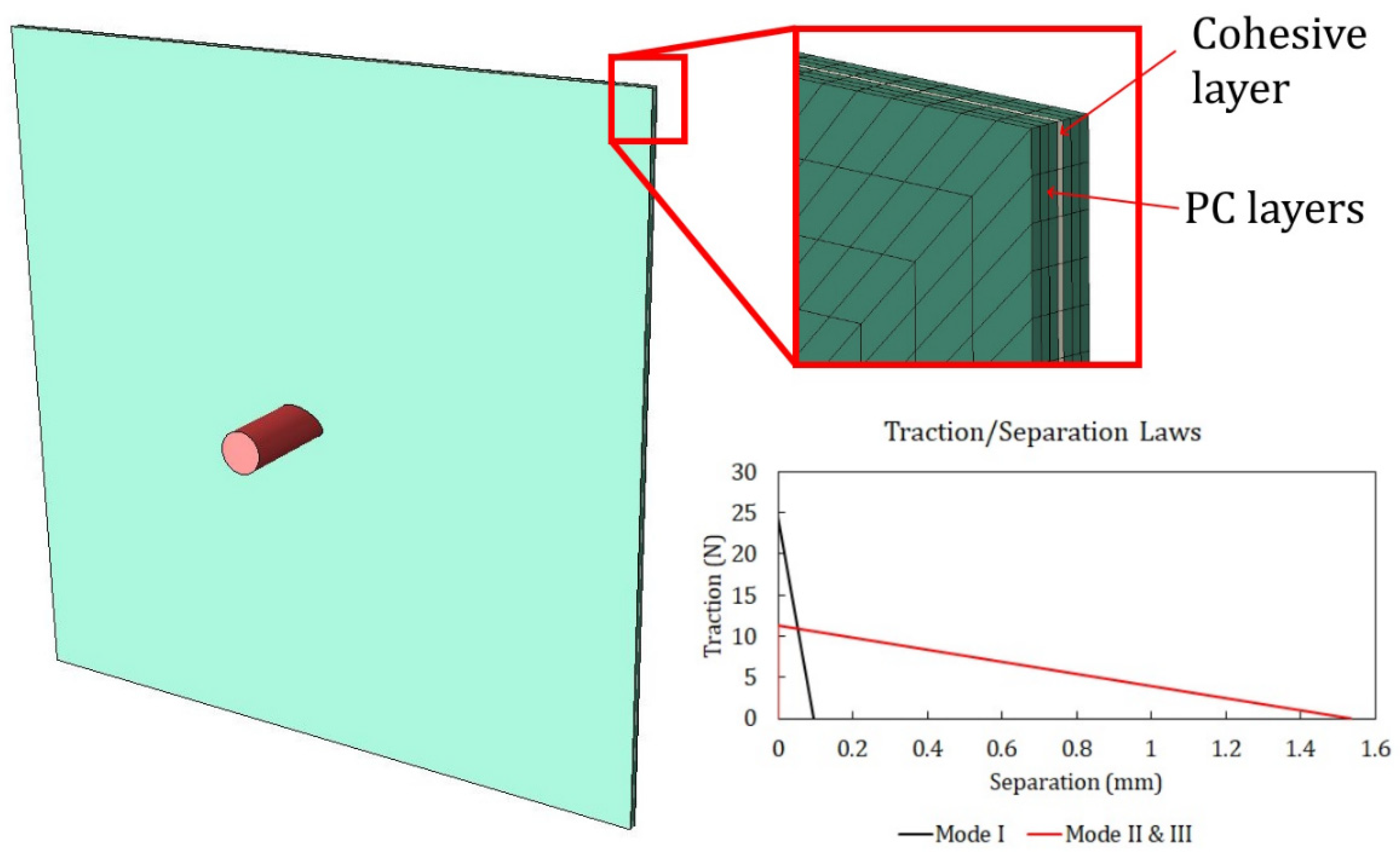
3.4. Polyurethane Adhesive Constitutive Law
4. Numerical Results and Discussion
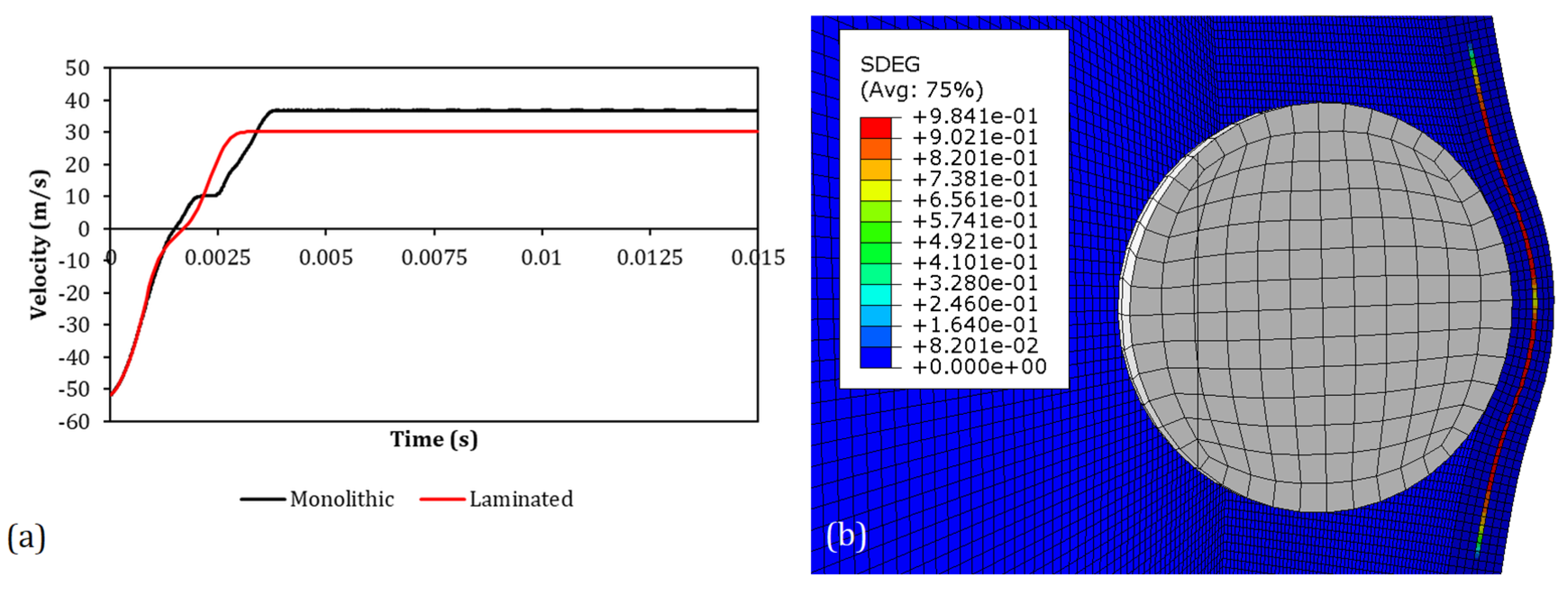
4.1. Threshold Velocities Correlation
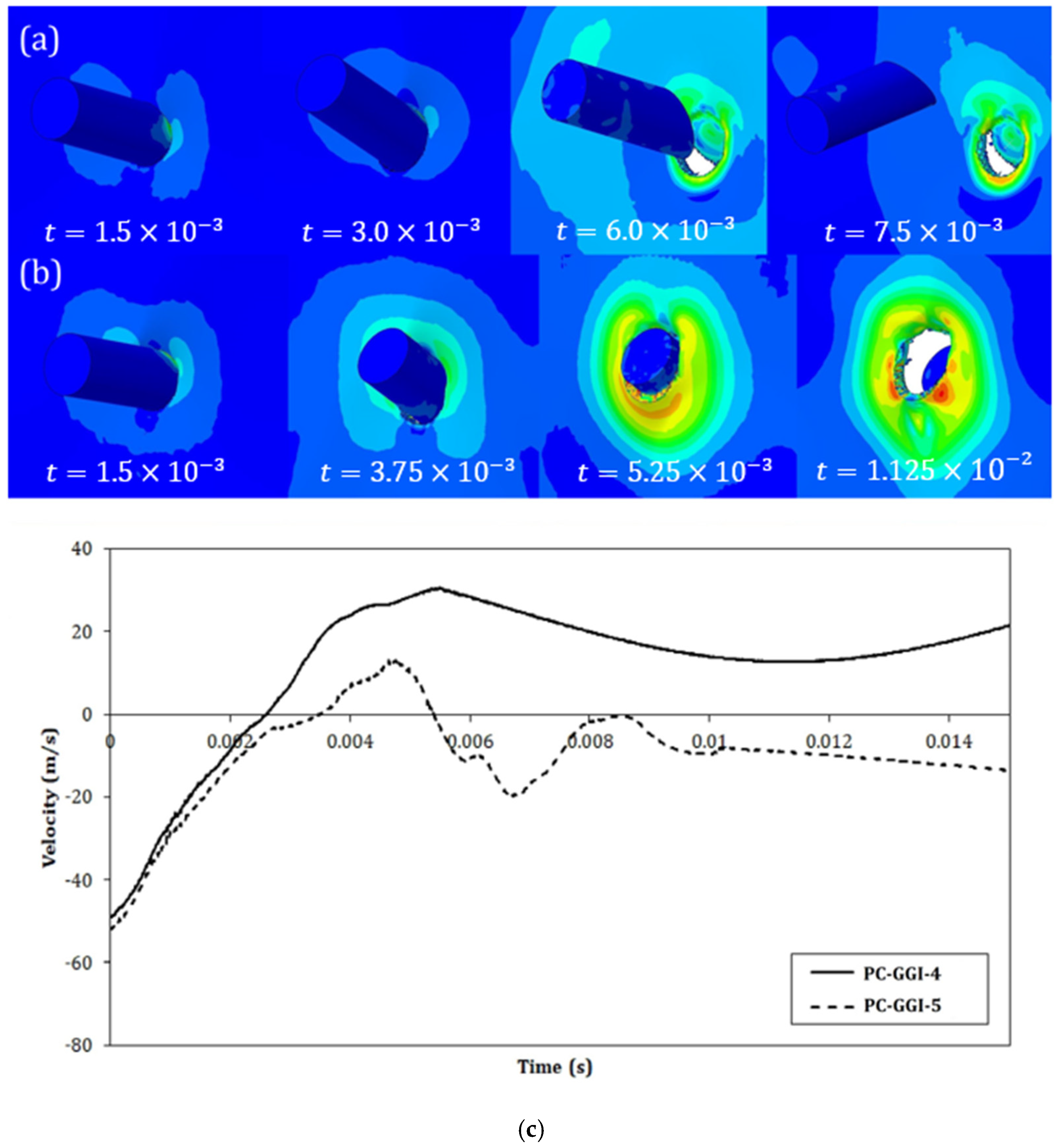
4.2. Numerical Perforation Morphologies Observation
4.3. Numerical Investigation on the Difference between PC and LPC Responses
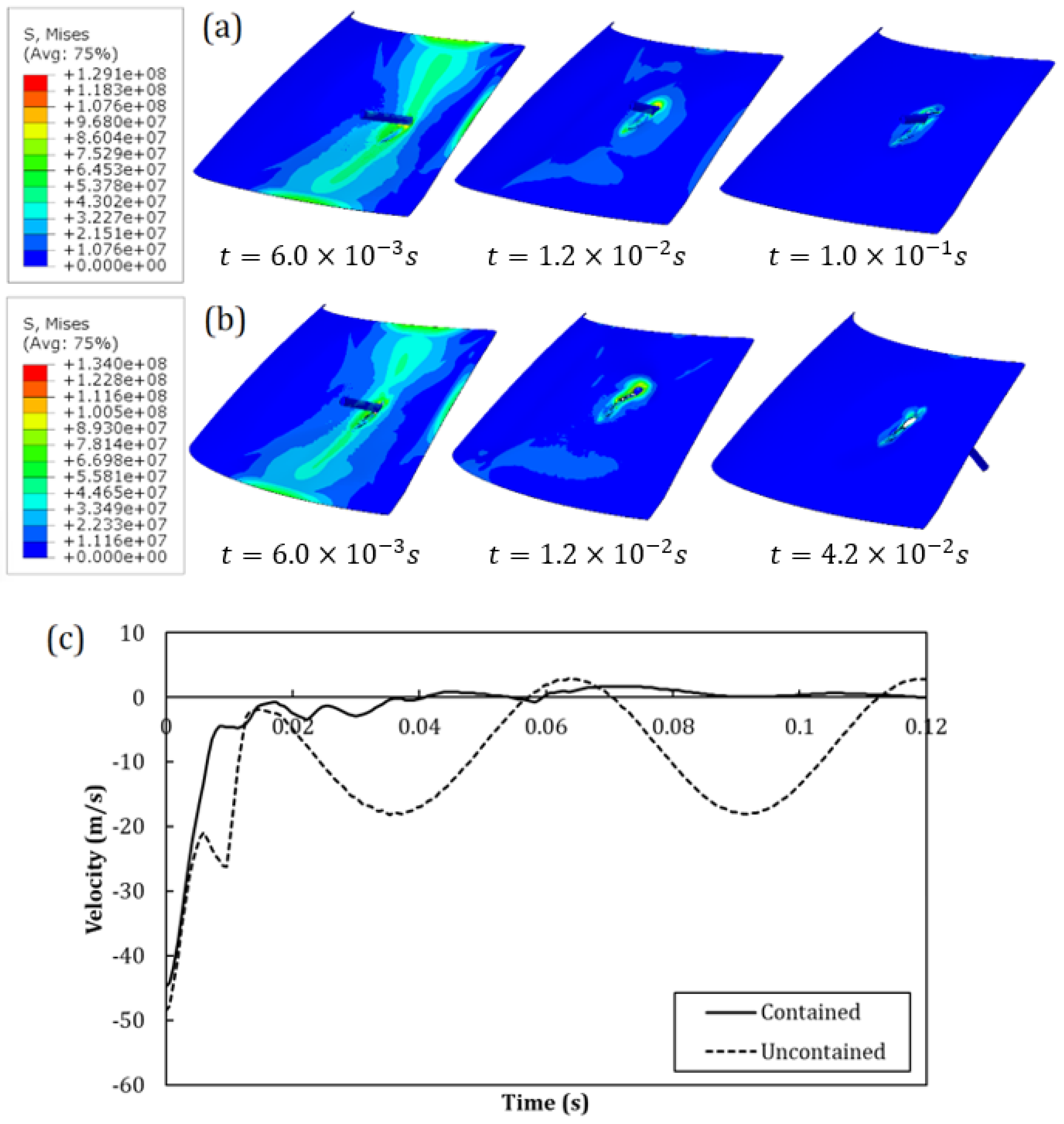
5. Assessment of the Model with a Windshield Test
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sarva, S.; Mulliken, A.D.; Boyce, M.C.; Hsieh, A.J. Mechanics of transparent polymeric material assemblies under projectile impact: Simulation and experiments. In Transformational Science and Technology for the Current and Future Force; World Scientific: Singapore, 2006; pp. 227–234. [Google Scholar] [CrossRef]
- Bardia, P.; Narasimhan, R. Characterization of pressure-sensitive yielding in polymers. Strain 2006, 42, 187–196. [Google Scholar] [CrossRef]
- Rosenberg, Z.; Surujon, Z.; Yeshurun, Y.; Ashuach, Y.; Dekel, E. Ricochet of 0.3″ AP projectile from inclined polymeric plates. Int. J. Impact Eng. 2005, 31, 221–233. [Google Scholar] [CrossRef]
- Mulliken, A.D.; Boyce, M.C. Mechanics of the rate-dependent elastic-plastic deformation of glassy polymers from low to high strain rates. Int. J. Solids Struct. 2006, 43, 1331–1356. [Google Scholar] [CrossRef]
- Bauwens-Crowet, C.; Bauwens, J.-C.; Homès, G. The temperature dependence of yield of PC in uniaxial compression and tensile tests. J. Mater. Sci. 1972, 7, 176–183. [Google Scholar] [CrossRef]
- Hasan, O.A.; Boyce, M.C. A constitutive model for the nonlinear viscoelastic viscoplastic behavior of glassy polymers. Polym. Eng. Sci. 1995, 35, 331–344. [Google Scholar] [CrossRef]
- Song, P.; Trivedi, A.; Siviour, C.R. Tensile testing of polymers: Integration of digital image correlation, infrared thermography and finite element modelling. J. Mech. Phys. Solids 2023, 171, 105161. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, M.; Li, D.; Li, Y. Infrared thermographic evaluation of thermal release phenomena in polycarbonate during plastic deformation. Adv. Ind. Eng. Polym. Res. 2023, 6, 39–48. [Google Scholar] [CrossRef]
- Wright, S.C.; Fleck, N.A.; Stronge, W.J. Ballistic impact of PC-An experimental investigation. Int. J. Impact Eng. 1993, 13, 1–20. [Google Scholar] [CrossRef]
- Li, K.; Goldsmith, W. Perforation of steel and PC plates by tumbling projectiles. Int. J. Solids Struct. 1997, 34, 4581–4596. [Google Scholar] [CrossRef]
- Shah, Q.H.; Abakr, Y.A. Effect of distance from the support on the penetration mechanism of clamped circular PC armor plates. Int. J. Impact Eng. 2008, 35, 1244–1250. [Google Scholar] [CrossRef]
- Shah, Q.H. Impact resistance of a rectangular PC armor plate subjected to single and multiple impacts. Int. J. Impact Eng. 2009, 36, 1128–1135. [Google Scholar] [CrossRef]
- Dorogoy, A.; Rittel, D. Effect of confinement of thick polycarbonate plates impacted by long an AP projectiles. Int. J. Impact Eng. 2015, 36, 38–48. [Google Scholar] [CrossRef]
- Xu, Y.; Lu, H.; Gao, T.; Zhang, W. Predicting the low-velocity impact behavior of polycarbonate: Influence of thermal history during injection molding. Int. J. Impact Eng. 2015, 86, 265–273. [Google Scholar] [CrossRef]
- Stecconi, A.; Landi, L. Finite element analysis for impact tests on polycarbonate safety guards: Comparison with experimental data and statistical dispersion of ballistic limit. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2020, 6, 041004. [Google Scholar] [CrossRef]
- Patalak, J.; Gideon, T. Ballistic Testing of Motorsport Windshields. SAE Int. Transp. Saf. 2013, 1, 127–133. [Google Scholar] [CrossRef]
- Dorogoy, A.; Rittel, D.; Brill, A. A study of inclined impact in polymethylmethacrylate plates. Int. J. Impact Eng. 2010, 37, 285–294. [Google Scholar] [CrossRef]
- Anand, L.; Gurtin, M.E. A theory of amorphous solids undergoing large deformations, with application to polymeric glasses. Int. J. Solids Struct. 2003, 40, 1465–1487. [Google Scholar] [CrossRef]
- Boyce, M.C.; Parks, D.M.; Argon, A.S. Large inelastic deformation of glassy polymers. part I: Rate dependent constitutive model. Mech. Mater. 1988, 7, 15–33. [Google Scholar] [CrossRef]
- Du, S.; Mullins, M.; Hamdi, M.; Sue, H.J. Quantitative modeling of scratch behavior of amorphous polymers at elevated temperatures. Polymer 2020, 197, 122504. [Google Scholar] [CrossRef]
- Esfahlani, S.S. Ballistic performance of polycarbonate and polymethylmethacrylate under normal and inclined dynamic impacts. Heliyon 2021, 7, e06856. [Google Scholar] [CrossRef]
- Sarıkaya, M.; Güden, M.; Kambur, Ç.; Özbek, S.Ç.; Taşdemirci, A. Developmente of the Johnson-Cook flow stress and damage parameters for the impact response of polycarbonate: Experimental and numerical approach. Int. J. Impact Eng. 2023, 179, 104674. [Google Scholar] [CrossRef]
- Bergström, J.S.; Bischoff, J.E. An Advanced Thermomechanical Constitutive Model for UHMWPE. Int. J. Struct. Chang. Solids 2010, 2, 31–39. [Google Scholar]
- Ishikawa, M.; Noarisawa, I.; Ogawa, H. Criterion for Craze Nucleation in PC. J. Polym. Sci. Polym. Phys. Ed. 1977, 15, 1791–1804. [Google Scholar] [CrossRef]
- Nimmer, R.P.; Woods, J.T. An investigation of brittle failure in ductile, notch-sensitive thermoplastics. Polym. Eng. Sci. 1992, 32, 1126–1137. [Google Scholar] [CrossRef]
- Fleischhauer, R.; Dal, H.; Kaliske, M.; Schneider, K. A constitutive model for finite deformation of amorphous polymers. Int. J. Mech. Sci. 2012, 65, 48–63. [Google Scholar] [CrossRef]
- Estevez, R.; Tijssens, M.G.A.; van der Giessen, E. Modeling of the competition between shear yielding and crazing in glassy polymers. J. Mech. Phys. Solids 2000, 48, 2585–2617. [Google Scholar] [CrossRef]
- Fraser, R.A.W.; Ward, I.M. The impact fracture behaviour of notched specimens of PC. J. Mater. Sci. 1977, 12, 459–468. [Google Scholar] [CrossRef]
- Newmann, L.V.; Williams, J.G. A comparative study of the tensile and charpy impact tests from a fracture mechanics viewpoint. Polym. Eng. Sci. 1980, 20, 572–578. [Google Scholar] [CrossRef]
- Gearing, B.P. Constitutive Equations and Failure Criteria for Amorphous Polymeric Solids by Submitted to the Department of Mechanical Engineering. 2002. Available online: https://dspace.mit.edu/handle/1721.1/17543 (accessed on 6 December 2023).
- Torres, J.P.; Frontini, P.M. Mechanics of PC in biaxial impact loading. Int. J. Solids Struct. 2016, 85–86, 125–133. [Google Scholar] [CrossRef]
- Gearing, B.P.; Anand, L. Notch-sensitive fracture of PC. Int. J. Solids Struct. 2004, 41, 827–845. [Google Scholar] [CrossRef]
- Gearing, B.P.; Anand, L. On modeling the deformation and fracture response of glassy polymers due to shear-yielding and crazing. Int. J. Solids Struct. 2004, 41, 3125–3150. [Google Scholar] [CrossRef]
- Kattekola, B.; Ranjan, A.; Basu, S. Three dimensional finite element investigations into the effects of thickness and notch radius on the fracture toughness of PC. Int. J. Fract. 2013, 181, 1–12. [Google Scholar] [CrossRef]
- Dorogoy, A.; Rittel, D.; Brill, A. Experimentation and modeling of inclined ballistic impact in thick PC plates. Int. J. Impact Eng. 2011, 38, 804–814. [Google Scholar] [CrossRef]
- Husain, A.; Ansari, R.; Chan, A.H. Experimental and numerical investigation of perforation of thin polycarbonate plate by projectiles of different nose shape. Lat. Am. J. Solids Struct. 2016, 14, 357–372. [Google Scholar] [CrossRef]
- SIMULIA. Abaqus User Manual. Ver 6.9. 2009. Available online: http://130.149.89.49:2080/v6.9ef/books/usi/default.htm (accessed on 6 December 2023).
- Pouzada, A.S.; Ferreira, E.C.; Pontes, A.J. Friction properties of moulding thermoplastics. Polym. Test. 2006, 25, 1017–1023. [Google Scholar] [CrossRef]
- Lee, J.H.; Xu, G.H.; Liang, H. Experimental and numerical analysis of friction and wear behavior of PC. Wear 2001, 251, 1541–1556. [Google Scholar] [CrossRef]
- Richeton, J.; Ahzi, S.; Vecchio, K.S.; Jiang, F.C.; Adharapurapu, R.R. Influence of temperature and strain rate on the mechanical behavior of three amorphous polymers: Characterization and modeling of the compressive yield stress. Int. J. Solids Struct. 2006, 43, 2318–2335. [Google Scholar] [CrossRef]
- Blumenthal, W.R. Influence of Temperature and Strain Rate on the Compressive Behavior of PMMA and PC Polymers. AIP Conf. Proc. 2003, 620, 665–668. [Google Scholar] [CrossRef]
- Sabet, S.A.; Borst, R. Structural softening, mesh dependence, and regularisation in non-associated plastic flow. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 2170–2183. [Google Scholar] [CrossRef]
- Kanani, A.Y.; Liu, Y.; Hughes, D.J.; Ye, J.; Hou, X. Fracture mechanisms of hybrid adhesive bonded joints: Effects of the stiffness of constituents. Int. J. Adhes. Adhes. 2020, 102, 102649. [Google Scholar] [CrossRef]
- Campilho, R.D.S.G.; Fernandes, T.A.B. Comparative evaluation of single-lap joints bonded with different adhesives by cohesive zone modelling. Procedia Eng. 2015, 114, 102–109. [Google Scholar] [CrossRef]

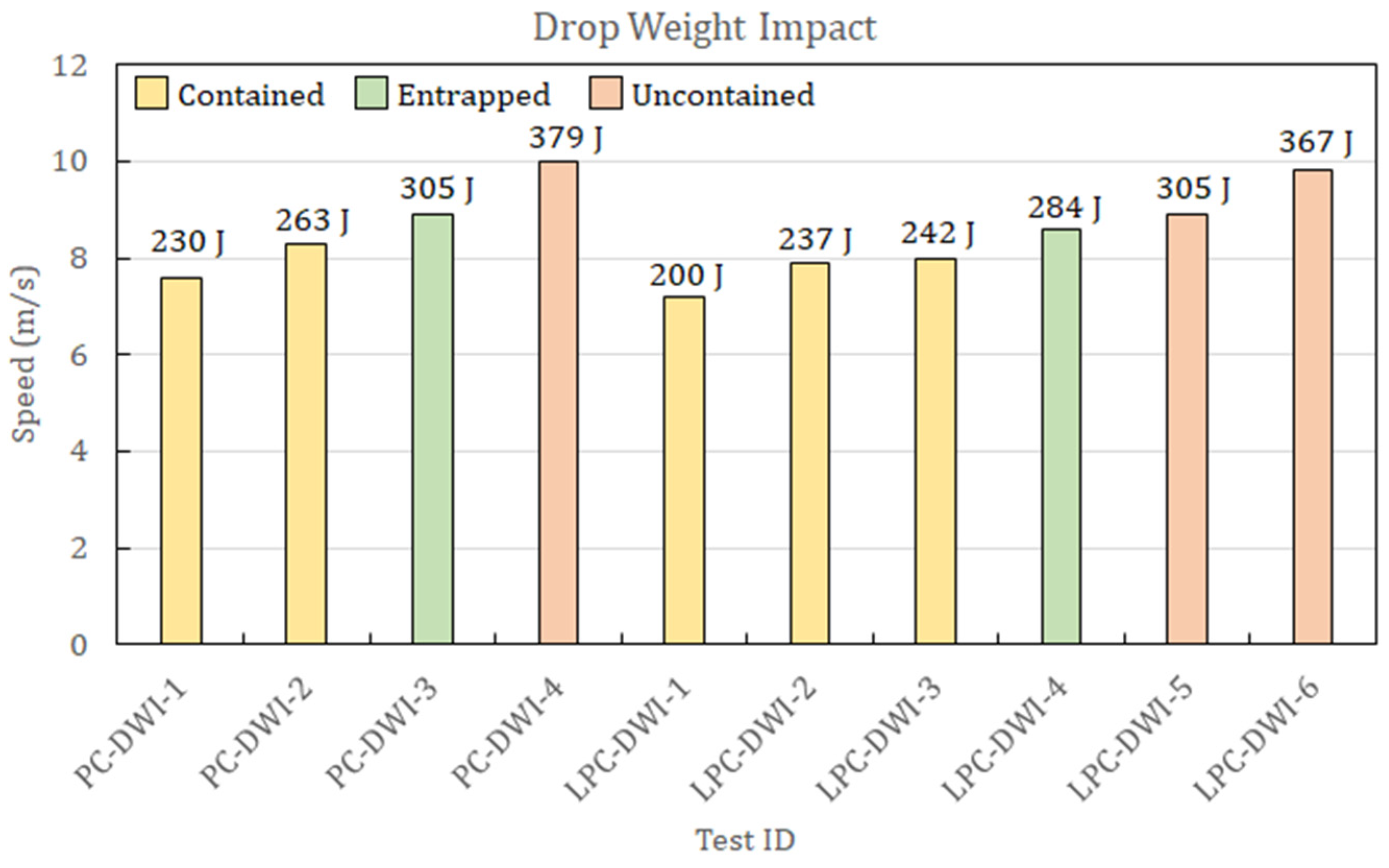






| DWI Threshold | GGI Threshold | |||
|---|---|---|---|---|
| PC | 8.9 m/s | 303 J | 50.8 m/s | 537 J |
| LPC | 8.6 m/s | 283 J | 52.0 m/s | 541 J |
| Non-Linear Behavior | Damage Model | |||
|---|---|---|---|---|
| Law | Data | Law | Data | |
| Deviatoric behavior | Von Mises plasticity | Table 4, Figure 8 | Ductile damage | Table 4 |
| Volumetric behavior | Mie–Grüneisen | Table 5 | Tensile failure | Table 4 |
| c0 (m/s) | s | |
|---|---|---|
| 1933 | 2.65 | 0.61 |
| Property | Value |
|---|---|
| Elastic modulus | 1.79 |
| Shear modulus | 0.25 |
| Normal strength (MPa) | 24.4 |
| Shear strength (MPa) | 11.4 |
| Fracture toughness in tension (N/mm) | 1.18 |
| Fracture toughness in shear (N/mm) | 8.72 |
| Benzeggagh–Kenane power η | 1.8 |
| Test | Panel Type | Threshold Velocity (m/s) | |||
|---|---|---|---|---|---|
| Experimental | Numerical (% Difference) | ||||
| EOS | No-EOS | No-ADB | |||
| DWI | PC | 8.9 | 8.3 (6.7%) | 7.5 (15.7%) | 8.3 (6.7%) |
| LPC | 8.6 | 8.0 (6.9%) | 7.5 (12.8%) | 8.0 (6.9%) | |
| GGI | PC | ||||
| LPC | |||||
| Test | Velocity | Outcome | |
|---|---|---|---|
| Experimental | Numerical | ||
| WS-GGI-1 | 44.8 m/s | Contained | Entrapped |
| WS-GGI-2 | 48.5 m/s | Uncontained | Uncontained |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghavanini, N.; Caporale, A.M.; Astori, P.; Airoldi, A.; Panichelli, P. Impact Response of Monolithic and Laminated Polycarbonate Panels: An Experimental and Numerical Investigation. Polymers 2023, 15, 4677. https://doi.org/10.3390/polym15244677
Ghavanini N, Caporale AM, Astori P, Airoldi A, Panichelli P. Impact Response of Monolithic and Laminated Polycarbonate Panels: An Experimental and Numerical Investigation. Polymers. 2023; 15(24):4677. https://doi.org/10.3390/polym15244677
Chicago/Turabian StyleGhavanini, Navid, Antonio Maria Caporale, Paolo Astori, Alessandro Airoldi, and Paolo Panichelli. 2023. "Impact Response of Monolithic and Laminated Polycarbonate Panels: An Experimental and Numerical Investigation" Polymers 15, no. 24: 4677. https://doi.org/10.3390/polym15244677
APA StyleGhavanini, N., Caporale, A. M., Astori, P., Airoldi, A., & Panichelli, P. (2023). Impact Response of Monolithic and Laminated Polycarbonate Panels: An Experimental and Numerical Investigation. Polymers, 15(24), 4677. https://doi.org/10.3390/polym15244677