Polyelectrolytes: From Seminal Works to the Influence of the Charge Sequence
Abstract
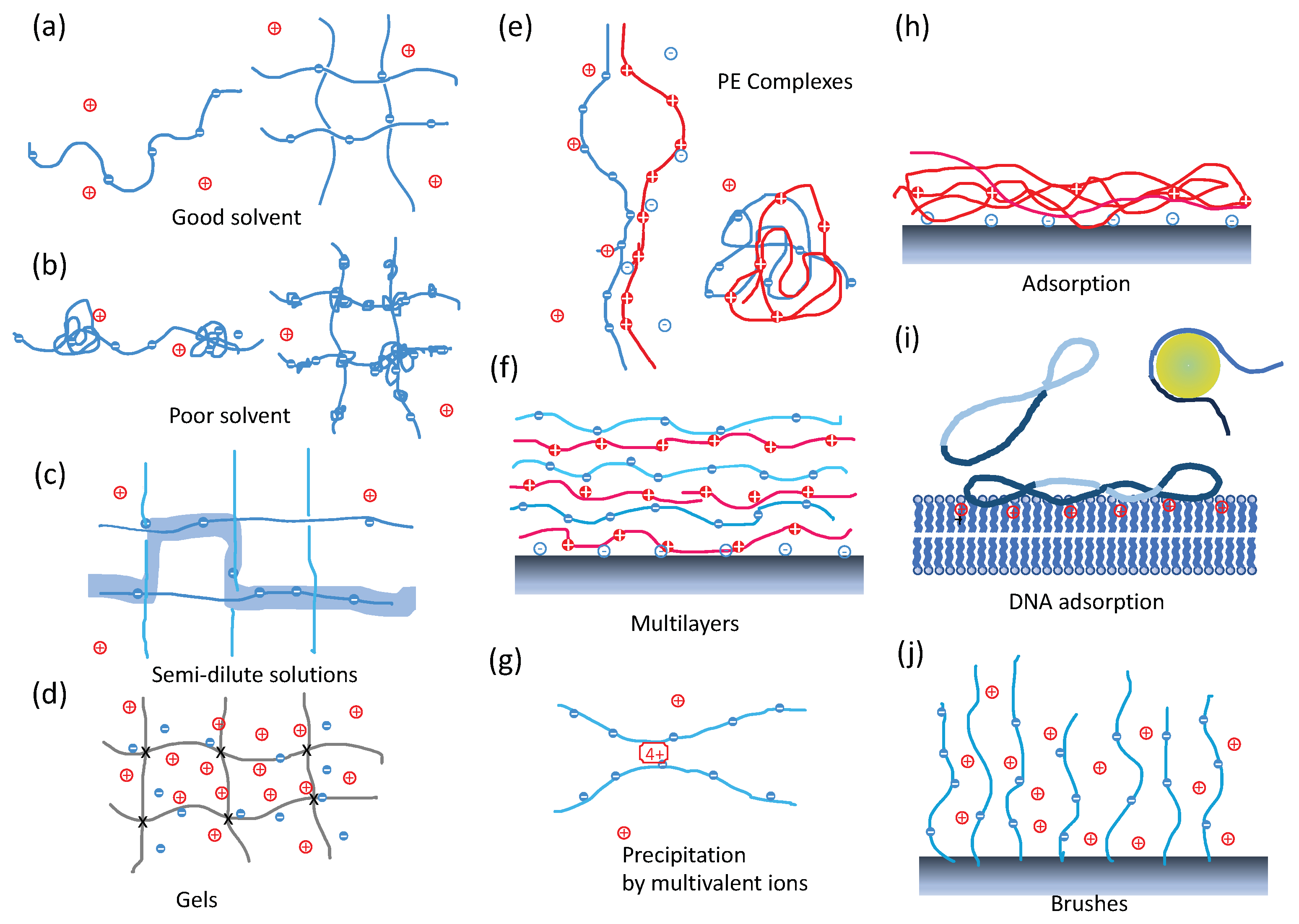
:1. Introduction
2. Generic Descriptions Using Smeared out Charge Distributions
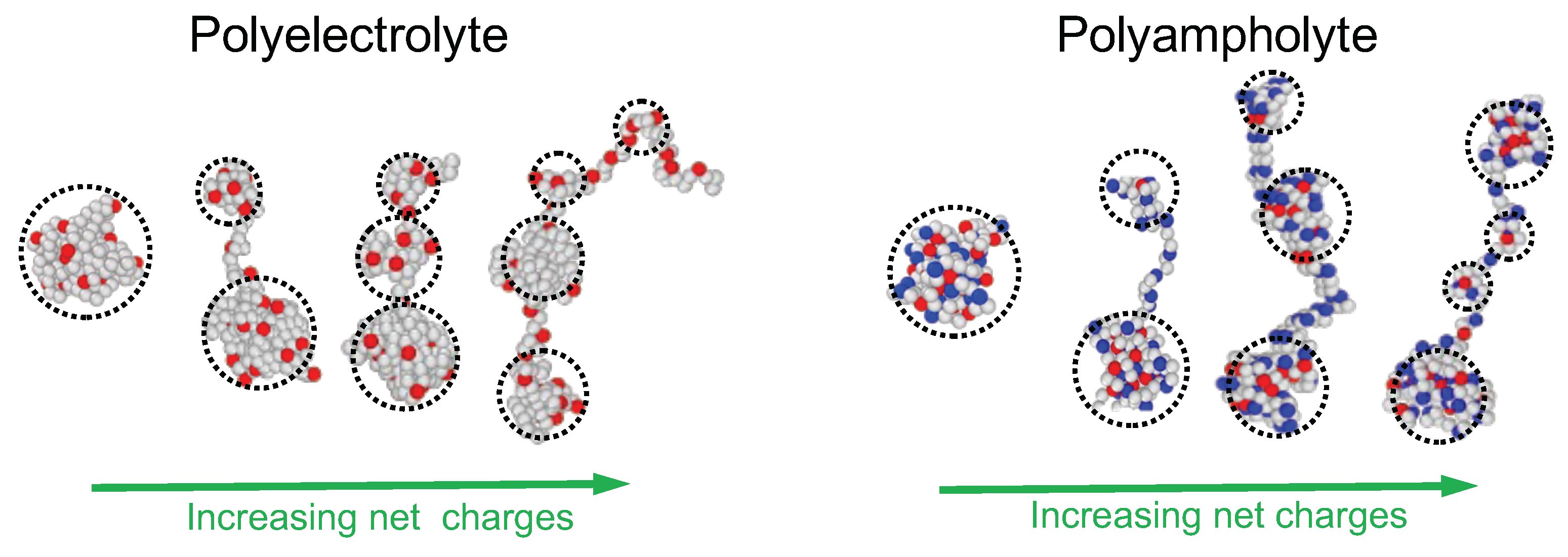
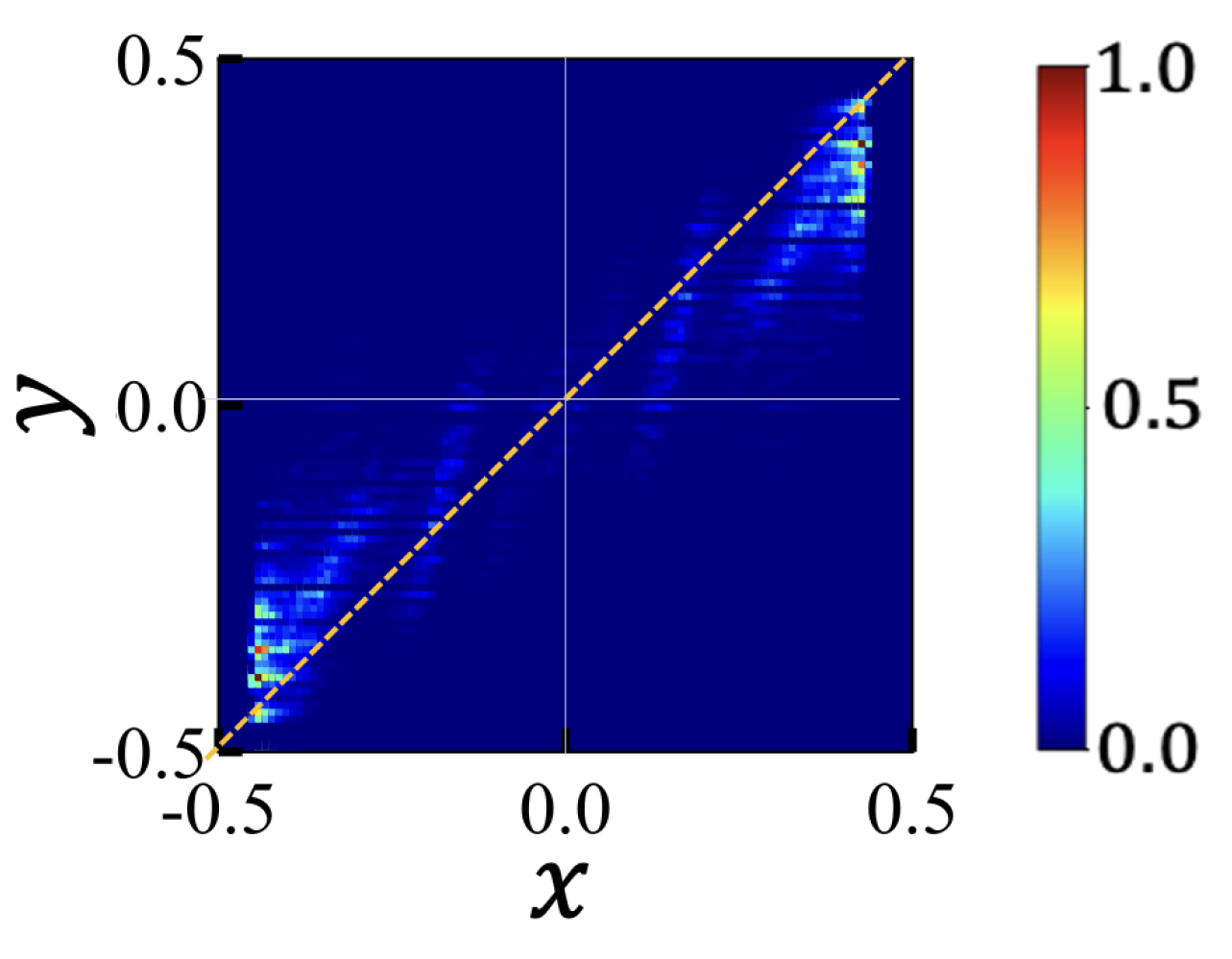
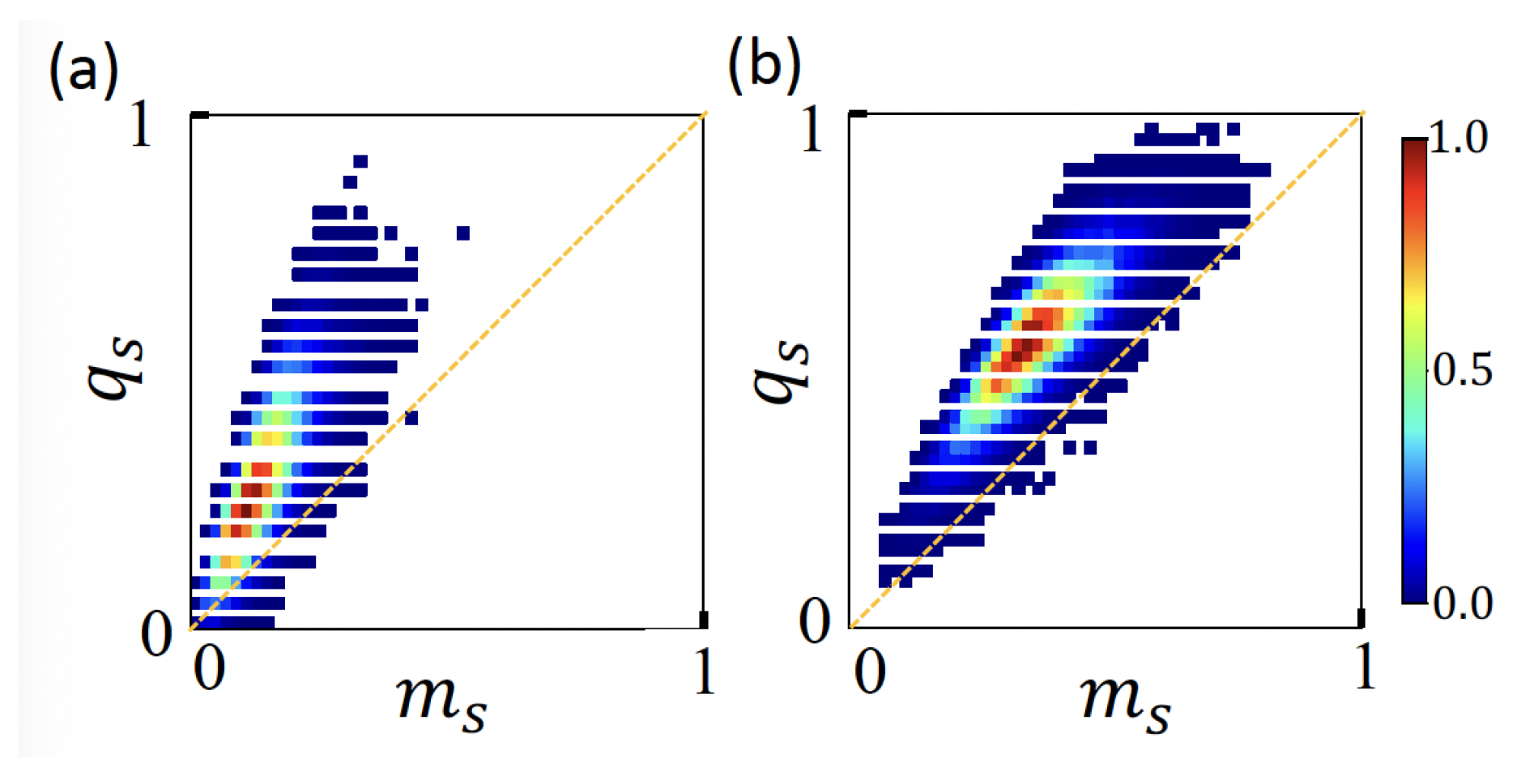
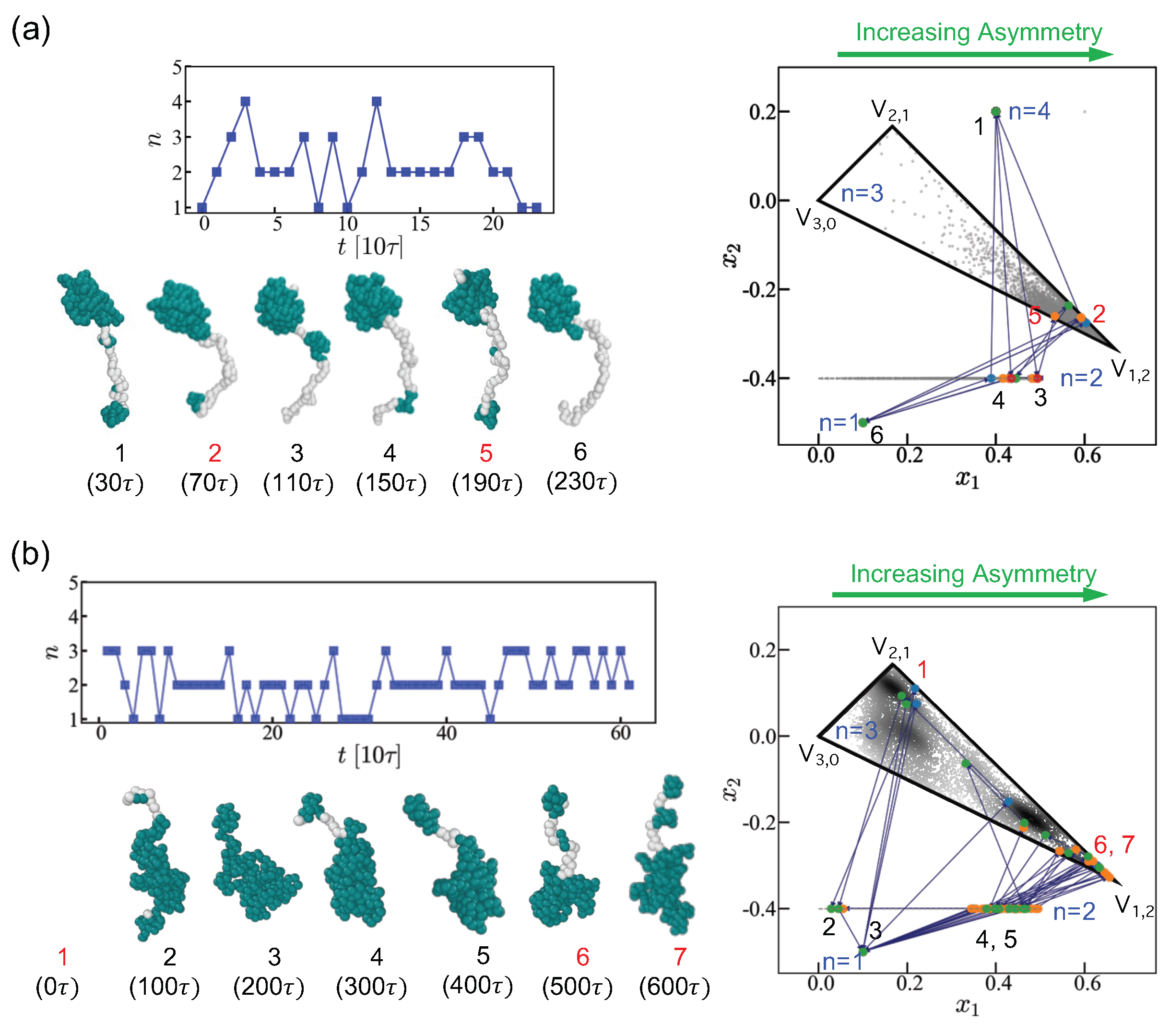
3. Charge Sequence Effects
4. Hydrophobic Polyelectrolytes: Influence of the Charge Sequence
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Staudinger, H. Uber Polymerisation. Ber. Dtsch. Chem. Ges. 1920, 53, 1073–1085. [Google Scholar] [CrossRef]
- Frey, H.; Johann, T. Celebrating 100 years of “polymer science”: Hermann Staudinger’s 1920 manifesto. Polym. Chem. 2020, 11, 8–14. [Google Scholar] [CrossRef]
- Vitz, J.; Majdanski, T.C.; Meier, A.; Lutz, P.J.; Schubert, U.S. Polymerization of ethylene oxide under controlled monomer addition via a mass flow controller for tailor made polyethylene oxides. Polym. Chem. 2016, 7, 4063–4071. [Google Scholar] [CrossRef]
- de Gennes, P.G. A second type of phase separation in polymer solutions. C. R. Acad. Sci. 1991, 313, 1117–1122. [Google Scholar]
- Matsuyama, A.; Tanaka, F. Theory of Solvation-Induced Reentrant Phase Separation in Polymer Solutions. Phys. Rev. Lett. 1990, 65, 341–344. [Google Scholar] [CrossRef] [PubMed]
- Bekiranov, S.; Bruinsma, R.; Pincus, P. Solution behavior of polyethylene oxide in water as a function of temperature and pressure. Phys. Rev. E 1997, 11, 577–585. [Google Scholar] [CrossRef]
- Jarkova, E.; Johner, A.; Maresov, E.A.; Semenov, A.N. Globules of annealed amphiphilic copolymers: Surface structure and interactions. Eur. Phys. J. E 2006, 21, 371–386. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, S. First Observation of the Molten Globule State of a Single Homopolymer Chain. Phys. Rev. Lett. 1996, 77, 3053. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, S. Thermodynamically Stable Globule State of a Single Poly(N-isopropylacrylamide) Chain in Water. Macromolecules 1995, 28, 8388–8390. [Google Scholar] [CrossRef]
- Al Harbi, L. Tuning optical, dielectric, and electrical properties of Polyethylene oxide/Carboxymethyl cellulose doped with mixed metal oxide nanoparticles for flexible electronic devices. J. Mol. Struct. 2023, 1272, 134244. [Google Scholar] [CrossRef]
- Candau, F.; Joanny, J.-F. Polyampholytes; Salamone, J.C., Ed.; CRC Press: Boca Raton, FL, USA, 1996; Volume 7, pp. 5462–5476. [Google Scholar]
- Uversky, V.N. Intrinsically disordered proteins from A to Z. Intl. J. Biochem. Cell Biol. 2011, 43, 1090–1103. [Google Scholar] [CrossRef] [PubMed]
- Müller-Späth, S.; Soranno, A.; Hirschfeld, V.; Hofmann, H.; Rüegger, S.; Reymond, L.; Nettels, D.; Schuler, B. Charge interactions can dominate the dimensions of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA 2010, 107, 14609–14614. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, G.; Longhi, S.; Grandori, R.; Brocca, S. Relevance of Electrostatic Charges in Compactness, Aggregation, and Phase Separation of Intrinsically Disordered Proteins. Int. J. Mol. Sci. 2020, 21, 6208. [Google Scholar] [CrossRef] [PubMed]
- McCarty, J.; Delaney, K.T.; Danielsen, S.P.; Fredrickson, G.H.; Shea, J.-E. Complete phase diagram for liquid–liquid phase separation of intrinsically disordered proteins. J. Phys. Chem. Lett. 2019, 10, 1644–1652. [Google Scholar] [CrossRef] [PubMed]
- Johner, A.; Joanny, J.-F. Translocation of polyampholytes and intrinsically disordered proteins. Eur. Phys. J. E 2018, 41, 78. [Google Scholar] [CrossRef] [PubMed]
- Pappu, R.V.; Cohen, S.R.; Dar, F.; Farag, M.; Kar, M. Phase transitions of associative biomacromolecules. Chem. Rev. 2023, 123, 8945–8987. [Google Scholar] [CrossRef] [PubMed]
- Brangwynne, C.P.; Tompa, P.; Pappu, R.V. Polymer physics of intracellular phase transitions. Nat. Phys. 2015, 11, 899–904. [Google Scholar] [CrossRef]
- Wei, M.T.; Elbaum-Garfinkle, S.; Holehouse, A.S.; Chen, C.C.-H.; Feric, M.; Arnold, C.B.; Priestley, R.D.; Pappu, R.V.; Brangwynne, C.P. Phase behaviour of disordered proteins underlying low density and high permeability of liquid organelles. Nat. Chem. 2017, 9, 1118–1125. [Google Scholar] [CrossRef]
- Nakamura, I.; Wang, Z.G. Effects of dielectric inhomogeneity in polyelectrolyte solutions. Soft Matter 2013, 9, 5686–5690. [Google Scholar] [CrossRef]
- Oosawa, F. Polyelectolytes; Marcel Dekker: New York, NY, USA, 1971. [Google Scholar]
- Mallarino, J.P.; Tellez, G.; Trizac, E. Counterion Density Profile around Charged Cylinders: The Strong-Coupling Needle Limit. J. Phys. Chem. B 2013, 117, 2702–12716. [Google Scholar] [CrossRef]
- Odijk, T. Polyelectrolytes near the rod limit. J. Polym. Sci. 1997, 15, 477–483. [Google Scholar] [CrossRef]
- Barrat, J.L.; Joanny, J.F. Persistence length of polyelectrolyte chains. EPL 1993, 24, 333. [Google Scholar] [CrossRef]
- Ha, B.Y.; Thirumalai, D. Electrostatic persistence length of a polyelectrolyte chain. Macromolecules 1995, 28, 577–581. [Google Scholar] [CrossRef]
- Manghi, M.; Netz, R.R. Variational theory for a single polyelectrolyte chain revisited. EPJE 2004, 14, 67–77. [Google Scholar] [CrossRef] [PubMed]
- Dobrynin, A.M. Electrostatic persistence length of semiflexible and flexible polyelec-trolytes. Macromolecules 2005, 38, 9304–9314. [Google Scholar] [CrossRef]
- Everaers, R.; Milchev, A.; Yamakov, V. The electrostatic persistence length of polymers beyond the OSF limit. Eur. Phys. J. E 2002, 8, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Khokhlov, A.R.; Katchaturian, K.A. On the theory of weakly charged polyelectrolytes. Polymer 1982, 23, 1742–1750. [Google Scholar] [CrossRef]
- Trizac, E.; Shen, T. Bending stiff charged polymers: The electrostatic persistence length. EPL 2016, 116, 18007. [Google Scholar]
- de Gennes, P.G.; Pincus, P.; Velasco, R.M.; Brochard, F. Remarks on Polyelectrolyte Conformation. J. Phys. 1976, 37, 461–1473. [Google Scholar] [CrossRef]
- Doi, M.; Edward, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Essafi, W.; Lafuma, F.; Williams, C.E. Effect of Solvent Quality on the Behaviour of Highly Charged Polyelectrolytes. J. Phys. II 1995, 5, 1269–1275. [Google Scholar] [CrossRef]
- Khokhlov, A. On the collapse of weakly charged polyelectrolytes. J. Phys. A Math. Gen. 1980, 13, 979. [Google Scholar] [CrossRef]
- Borue, V.Y.; Erukhimovich, I.Y. A statistical theory of weakly charged polyelectrolytes: Fluctuations, equation of state and microphase separation. Macromolecules 1988, 21, 3240–3249. [Google Scholar] [CrossRef]
- Leibler, L.; Joanny, J.F. Weakly charged polyelectrolytes in a poor solvent. J. Phys. 1990, 51, 545–557. [Google Scholar]
- Rayleigh, L. On the equilibrium of liquid conducting masses charged with electricity. Lond. Edinburgh Dublin Philos. Mag. J. Sci. 1882, 14, 184–186. [Google Scholar] [CrossRef]
- Dobrynin, A.V.; Rubinstein, M.; Obukhov, S. Cascade of transitions of polyelectrolytes in poor solvents. Macromolecules 1996, 29, 2974–2979. [Google Scholar] [CrossRef]
- Kantor, Y.; Kardar, M. Excess charge in polyampholytes. EPL 1994, 27, 643. [Google Scholar] [CrossRef]
- Barrat, J.L.; Joanny, J.F. Theory of polyelectrolyte solutions. Adv. Chem. Phys. 1996, 94, 1. [Google Scholar]
- Dobrynin, A.; Rubinstein, M. Theory of Polyelectrolyte in Solutions and at Surfaces. Prog. Polym. Sci. 2005, 30, 1049–1118. [Google Scholar] [CrossRef]
- Boroudjerdi, H.; Kim, Y.W.; Naji, A.; Netz, R.; Schlagberger, X.; Serr, A. Statics and Dynamics of Strongly Charged Soft Matter. Phys. Rep.-Rev. Sect. Phys. Lett. 2005, 416, 129–199. [Google Scholar] [CrossRef]
- Kramarenko, E.Y.; Philippova, O.E.; Khokhlov, A.R. Polyelectrolyte networks as highly sensitive polymers. Polym. Sci. Ser. C 2006, 48, 1–20. [Google Scholar] [CrossRef]
- Kabanov, A.V.; Bronich, T.K.; Kabanov, V.A.; Yu, K.; Eisenberg, A. Soluble Stoichiometric Complexes from Poly(N-ethyl-4-vinylpyridinium) Cations and Poly(ethylene oxide)-block-polymethacrylate Anions. Macromolecules 1996, 29, 6797–6802. [Google Scholar] [CrossRef]
- Decher, G. Fuzzy Nanoassemblies: Toward Layered Polymeric Multicomposites. Science 1997, 277, 1232–1237. [Google Scholar] [CrossRef]
- Wittmer, J.P.; Johner, A.J.; Joanny, J.F. Precipitation of polyelectrolytes in the presence of multivalent salts. J. Phys. II Fr. 1995, 5, 635–654. [Google Scholar] [CrossRef]
- Lee, N.; Thirumalai, D. Dynamics of collapse of flexible polyelectrolytes in poor solvents. Macromolecules 2001, 34, 3446–3457. [Google Scholar] [CrossRef]
- Koculi, E.; Lee, N.-K.; Thirumalai, D.; Woodson, S.A. Folding of the Tetrahymena ribozyme by polyamines: Importance of counterion valence and size. J. Mol. Biol. 2004, 341, 27–36. [Google Scholar] [CrossRef] [PubMed]
- Netz, R.R.; Andelman, D. Neutral and charged polymers at interfaces. Phys. Rep.-Rev. Sect. Phys. Lett. 2003, 380, 1–95. [Google Scholar] [CrossRef]
- Pincus, P. Colloid Stabilization with Grafted Polyelectrolytes. Macromolecules 1991, 24, 2912–2919. [Google Scholar] [CrossRef]
- Borisov, O.V.; Zhulina, E.B. Structure of weakly charged polymer brushes: Monomer density profiles. J. Phys. II Fr. 1997, 7, 447–458. [Google Scholar]
- Porcel, C.H.; Schlenoff, J.B. Compact Polyelectrolyte Complexes: Saloplastic Candidates for Biomaterials. Biomacromolecules 2009, 10, 2968–2975. [Google Scholar] [CrossRef]
- Shamoun, R.F.; Reisch, A.; Schlenoff, J.B. Extruded Saloplastic Polyelectrolyte Complexes. Adv. Funct. Mater. 2012, 22, 923–1931. [Google Scholar] [CrossRef]
- Reisch, A.; Roger, E.; Phoeung, T.; Antheaume, C.; Orthlieb, C.; Boulmedais, F.; Lavalle, P.; Schlenoff, J.B.; Frisch, B.; Schaaf, P. On the Benefits of Rubbing Salt in the Cut: Self-Healing of Saloplastic PAA/PAH Compact Polyelectrolyte Complexes. Adv. Mater. 2014, 26, 2547–2551. [Google Scholar] [CrossRef] [PubMed]
- Diddens, D.; Bascnagel, J.; Johner, A. Microscopic Structure of Compacted Polyelectrolyte Complexes: Insights from Molecular Dynamics Simulations. ACS Macro Lett. 2019, 8, 123–127. [Google Scholar] [CrossRef] [PubMed]
- Wittmer, J.; Johner, A.; Joanny, J.F. Random and alternating polyampholytes. EPL 1993, 24, 263. [Google Scholar] [CrossRef]
- Moldakarimov, S.; Johner, A.; Joanny, J.-F. Charge relaxation in polyampholytes of various statistics. Eur. Phys. J. E 2003, 10, 303–318. [Google Scholar] [CrossRef]
- Rumyantsev, A.M.; Jackson, N.E.; Yu, B.; Ting, J.M.; Chen, W.; Tirrell, M.V.; de Pablo, J.J. Controlling Complex Coacervation via Random Polyelectrolyte Sequences. ACS Macro Lett. 2019, 8, 1296–1302. [Google Scholar] [CrossRef]
- Rumyantsev, A.; Jackson, N.E.; de Pablo, J.J. Polyelectrolyte Complex Coacervates: Recent Developments and New Frontiers. Annu. Rev. Condens. Matter Phys. 2021, 12, 155–156. [Google Scholar] [CrossRef]
- Sing, C.E.; Perry, S.L. Recent progress in the science of complex coacervation. Soft Matter 2020, 16, 2885–2914. [Google Scholar] [CrossRef]
- Danielsen, S.P.; McCarty, J.; Shea, J.-E.; Delaney, K.T.; Fredrickson, G.H. Molecular design of self–coacervation phenomena in block polyampholytes. Proc. Natl. Acad. Sci. USA 2019, 116, 8224–8232. [Google Scholar] [CrossRef]
- Rumyantsev, A.M.; Johner, A.; de Pablo, J.J. Sequence blockiness controls the structure of polyampholyte necklaces. ACS Macro Lett. 2021, 10, 1048–1054. [Google Scholar] [CrossRef]
- Lee, N.K.; Jung, Y.; Johner, A.; Joanny, J.F. Globular Polyampholytes: Structure and Translocation. Macromolecules 2021, 54, 2394–2411. [Google Scholar] [CrossRef]
- Chae, M.-K.; Lee, N.-K.; Jung, Y.; Johner, A.; Joanny, J.-F. Partially Globular Conformations from Random Charge Sequences. ACS Macro Lett. 2022, 11, 382–386. [Google Scholar] [CrossRef]
- Chae, M.-K.; Lee, N.-K.; Jung, Y.; Johner, A.; Joanny, J.-F. Structure of a hydrophobic polyelectrolyte chain with a random sequence. Macromolecules 2022, 55, 6275–6285. [Google Scholar] [CrossRef]
- Chae, M.-K.; Lee, N.-K.; Jung, Y.; Johner, A. Shape Fluctuations of Random Polyampholyte and Intrinsically Disordered Protein Sequences. Macromolecules 2023, 56, 785–793. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical Mechanics of Chain Molecules; Oxford University Press: New York, NY, USA, 1988. [Google Scholar]
- Fleer, G.; Stuart, M.C.; Scheutjens, J.; Cosgrove, T.; Vincent, B. Polymers at Interfaces; Springer: London, UK, 1993. [Google Scholar]
- Muthukumar, M. Polymer Translocation; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Muthukumar, M. Physics of Charged Macromolecules; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Lee, N.-K.; Obukhov, S. Collapse dynamics of a polyelectrolyte. EPL 2004, 66, 350. [Google Scholar] [CrossRef]
- Winkler, R. Collapse of polyelectrolyte macromolecules by counterion condensation and ion pair formation: A molecular dynamics simulation stud. Phys. Rev. Lett. 1998, 80, 3731. [Google Scholar] [CrossRef]
- Netz, R.R. Nonequilibrium Unfolding of Polyelectrolyte Condensates in Electric Fields. Phys. Rev. Lett. 2003, 90, 128104. [Google Scholar] [CrossRef]
- Ozmaian, M.; Makarov, D.E. Long–lived metastable knots in polyampholyte chains. PLoS ONE 2023, 18, e0287200. [Google Scholar] [CrossRef]
- Nylander, T.; Samoshina, Y.; Lindman, B. Formation of polyelectrolyte–surfactant complexes on surfaces. Adv. Colloid Interface Sci. 2006, 123–126, 105–123. [Google Scholar] [CrossRef]
- Honig, B.; Nicholls, A. Classical Electrostatics in Biology and Chemistry. Science 1995, 268, 5214. [Google Scholar]
- Hsieh, Y.C.; Delarue, M.; Orland, H.; Koehl, P. Analyzing the Geometry and Dynamics of Viral Structures: A Review of Computational Approaches Based on Alpha Shape Theory, Normal Mode Analysis, and Poisson-Boltzmann Theories. Viruses 2023, 15, 1366. [Google Scholar] [CrossRef] [PubMed]
- Johner, A. Interaction between like-charged surfaces in water: Does mean-field (Poisson Boltzmann) always apply for monovalent counterions? J. Club Condens. Matter Phys. 2020, 35, 551–560. [Google Scholar]
- Zwicker, D.; Decker, M.; Jaensch, S.; Jülicher, F. Centrosomes are autocatalytic droplets of pericentriolar material organized by centrioles. Proc. Natl. Acad. Sci. USA 2014, 111, E2636–E2645. [Google Scholar] [CrossRef]
- Ismail, H.; Liu, X.; Yang, F.; Li, J.; Zahid, A.; Dou, Z.; Liu, X.; Yao, X. Mechanisms and regulation underlying membraneless organelle plasticity control. J. Mol. Cell Biol. 2021, 13, 239–258. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Liao, Q.; Dobrynin, A.V.; Rubinstein, M. Counterion-correlation-induced attraction and necklace formation in polyelectrolyte solutions: Theory and simulations. Macromolecules 2006, 39, 1920–1938. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, N.-K.; Chae, M.-K.; Jung, Y.; Johner, A.; Joanny, J.-F. Polyelectrolytes: From Seminal Works to the Influence of the Charge Sequence. Polymers 2023, 15, 4593. https://doi.org/10.3390/polym15234593
Lee N-K, Chae M-K, Jung Y, Johner A, Joanny J-F. Polyelectrolytes: From Seminal Works to the Influence of the Charge Sequence. Polymers. 2023; 15(23):4593. https://doi.org/10.3390/polym15234593
Chicago/Turabian StyleLee, Nam-Kyung, Min-Kyung Chae, Youngkyun Jung, Albert Johner, and Jean-Francois Joanny. 2023. "Polyelectrolytes: From Seminal Works to the Influence of the Charge Sequence" Polymers 15, no. 23: 4593. https://doi.org/10.3390/polym15234593
APA StyleLee, N.-K., Chae, M.-K., Jung, Y., Johner, A., & Joanny, J.-F. (2023). Polyelectrolytes: From Seminal Works to the Influence of the Charge Sequence. Polymers, 15(23), 4593. https://doi.org/10.3390/polym15234593





