Electrorheological Effect of Suspensions of Polyaniline Nanoparticles with Different Morphologies
Abstract
:1. Introduction
2. Experimental Section
2.1. Materials
2.2. Preparation of PANI Nanoparticles with Different Morphologies
2.3. ER Suspension Preparation
2.4. Characterization and Measurements
3. Simulation Section
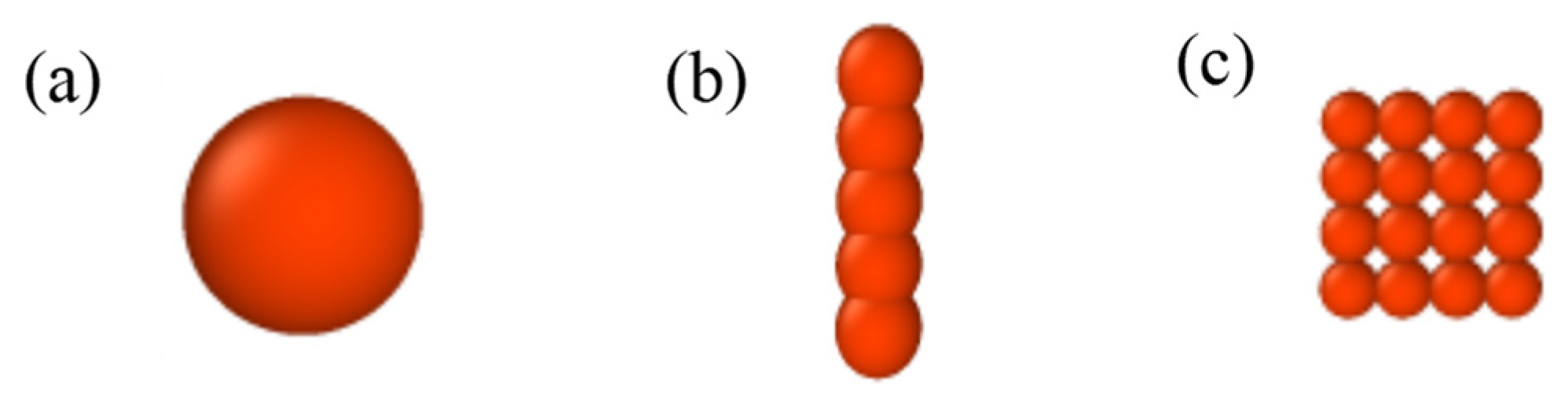
3.1. Models
3.1.1. Electric Dipole Moment of Nanospheres
3.1.2. Electric Dipole Moment of Nanofibers
3.1.3. Electric Dipole Moment of Nanoplates
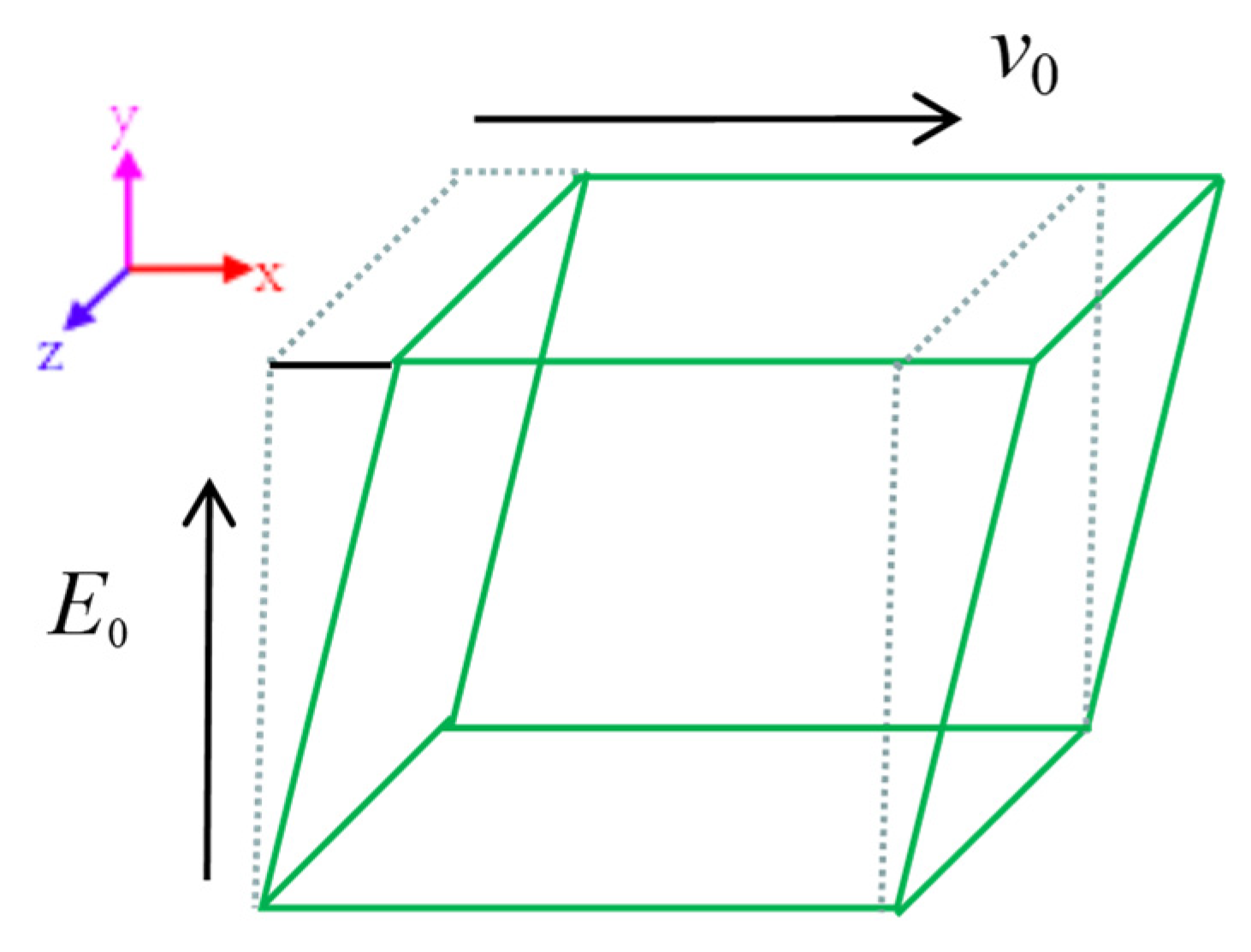
3.2. Definition of Force Field
3.3. Performance Characterization
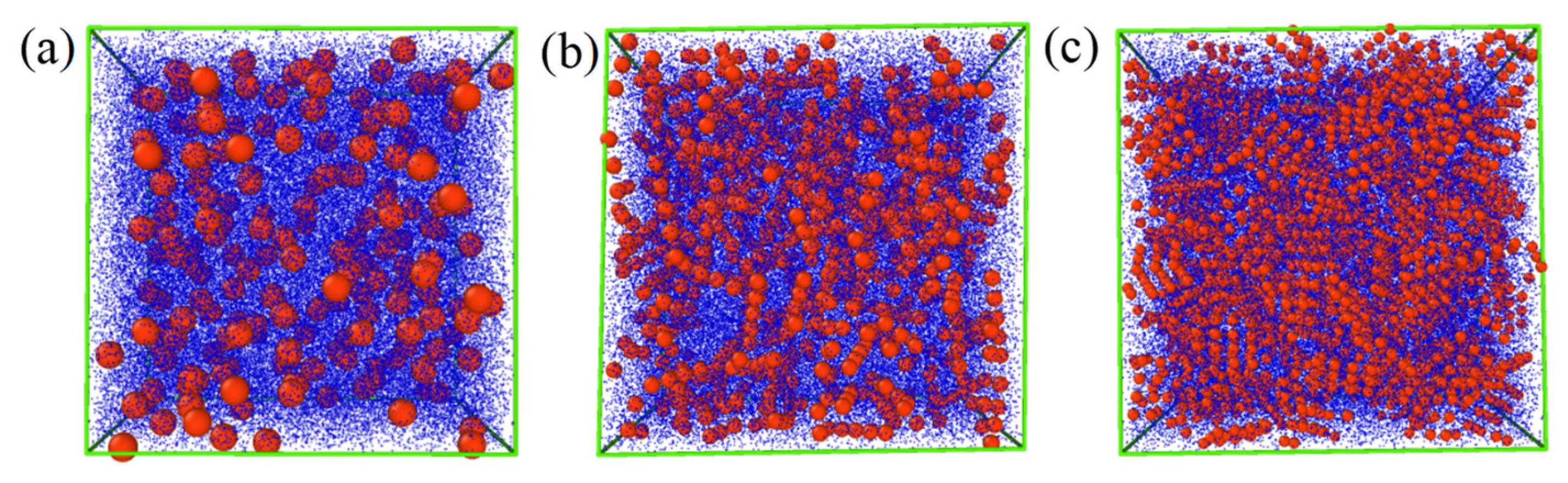
3.4. Simulation Details
4. Results and Discussion
4.1. Particle Structure and Morphology
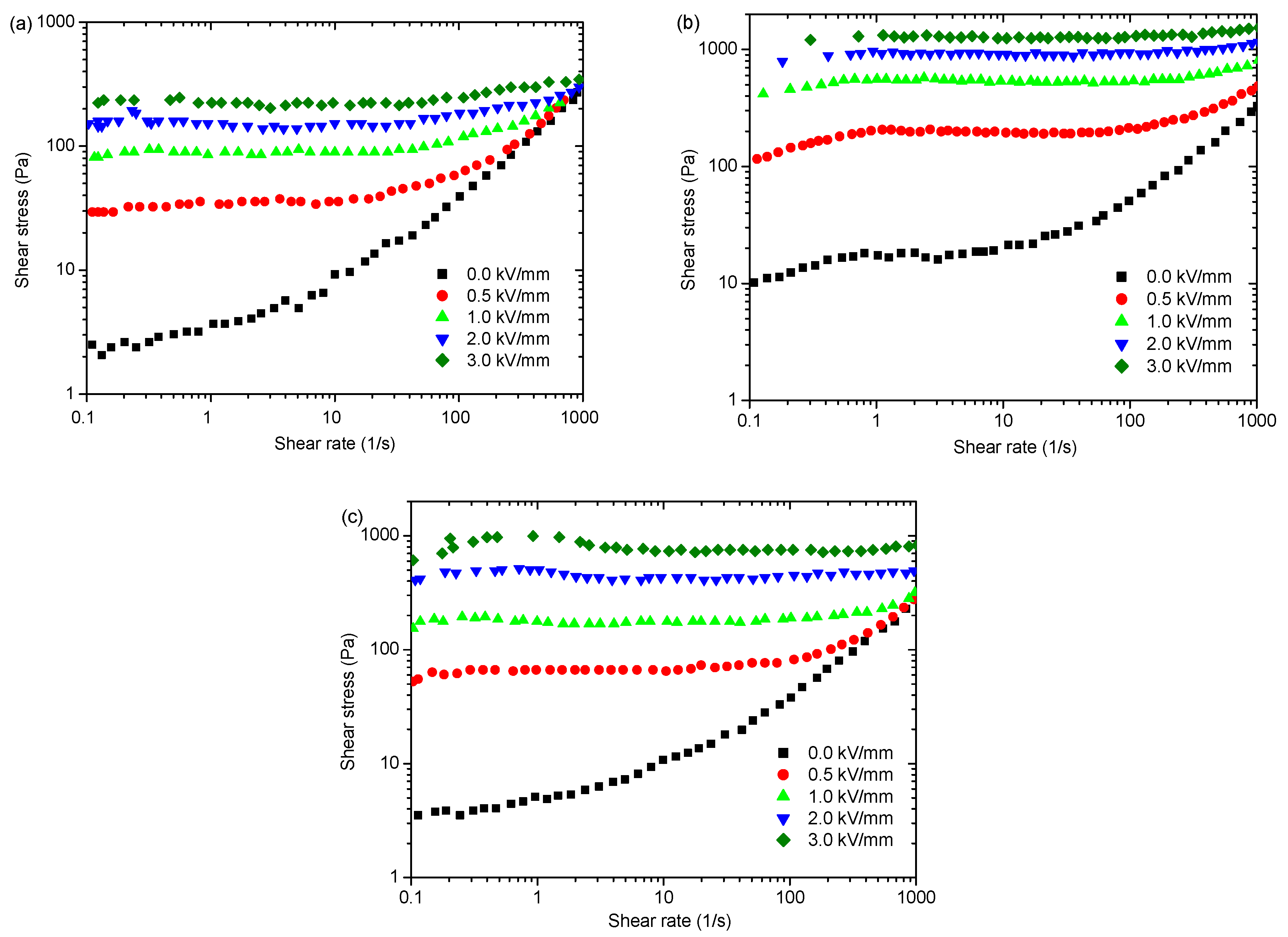
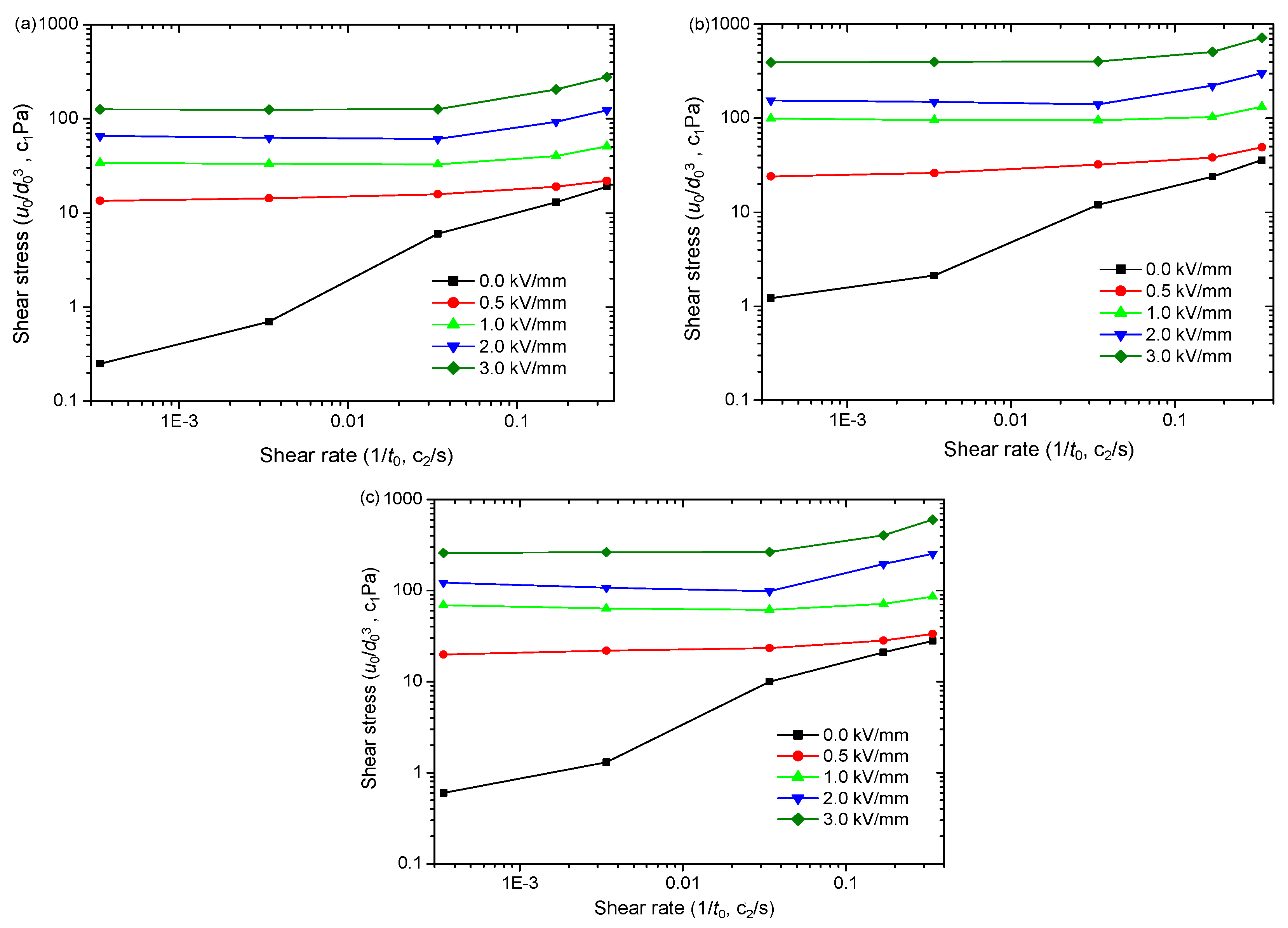
4.2. Impact of Nanoparticle Morphology on ER Effect
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Halsey, T.C. Electrorheological fluids. Science 1992, 258, 761–766. [Google Scholar] [CrossRef] [PubMed]
- Hao, T. Electrorheological fluids. Adv. Mater. 2001, 13, 1847–1857. [Google Scholar] [CrossRef]
- Tao, R.; Tang, H.; Tawhid-Al-Islam, K.; Du, E.; Kim, J. Electrorheology leads to healthier and tastier chocolate. Proc. Nat. Acad. Sci. USA 2016, 113, 7399–7402. [Google Scholar] [CrossRef] [PubMed]
- Wahed, A.K.E.; Stanway, R.; Sproston, J.L. The influence of mechanical input amplitude on the dynamic response of an electrorheological fluid in squeeze flow. J. Vehicle Des. 2003, 33, 153–170. [Google Scholar] [CrossRef]
- Shen, R.; Wang, J.L.; Lu, Y.; Wang, D.; Sun, G.; Cao, Z.X.; Lu, K.Q. Polar-Molecule-Dominated Electrorheological Fluids Featuring High Yield Stresses. Adv. Mater. 2009, 21, 4631–4635. [Google Scholar] [CrossRef]
- Ahn, K.H.; Klingenberg, D.J. Relaxation of polydisperse electrorheological suspensions. J. Rheol. 1994, 38, 713–741. [Google Scholar] [CrossRef]
- Kawai, A.; Uchida, K.; Ikazaki, F. Effects of shape and size of dispersoid on electrorheology. In Proceedings of the 8th International Conference: Electrorheological Fluids and Magnetorheological Suspensions, Nice, France, 9–13 July 2001; Bossis, G., Ed.; World Scientific: Singapore, 2002; pp. 2548–2554. [Google Scholar]
- Allais, C.P.; Foot, P.J.S.; Singer, R.J. Morphology-controlled stabilised polyaniline nanoparticles and their electrorheological properties. Polym. Polym. Compos. 2023, 31, 1–12. [Google Scholar] [CrossRef]
- Kang, S.S.; Choi, H.J. Poly(2,5-dimethoxyaniline) coated polystyrene microspheres and their electrorheological characteristics. Colloids Surf. A 2020, 605, 125375. [Google Scholar]
- Rehman, A.U.; Afzal, A.M.; Iqbal, M.W.; Wabaidur, S.M.; Al-Ammar, E.A.; Mumtaz, S.; Choi, E.H.; Ali, M. Exploring the potential of hydrothermally synthesized AgZnS@Polyaniline composites as electrode material for high-performance supercapattery device. Phys. Scr. 2023, 98, 085009. [Google Scholar] [CrossRef]
- Wang, L.Y.; Li, C.H.; Wang, R.; Lin, Y.S.; Xiong, K.S.; Wang, B.X.; Hao, C.C. The preparation and smart electrorheological behavior of MOF-Ti@PANI core-shell nanoparticles. J. Mol. Liq. 2023, 376, 121373. [Google Scholar] [CrossRef]
- Chen, S.; Cheng, Y.C.; Zhao, Z.H.; Zhang, K.; Hao, T.T.; Sui, Y.; Wang, W.; Zhao, J.P.; Li, Y. Core-shell-structured electrorheological fluid with a polarizabilitytunable nanocarbon shell for enhanced stimuli-responsive activity. ACS Appl. Mater. Interfaces 2023, 15, 35741–35749. [Google Scholar] [CrossRef] [PubMed]
- Ahn, S.Y.; Yu, C.B.; Song, Y.S. Electrorheological behavior of heat-treated sepiolite suspension. Korea-Aust. Rheol. J. 2023, 35, 391–396. [Google Scholar] [CrossRef]
- Chen, P.P.; Cheng, Q.Q.; Wang, L.M.; Liu, Y.D.; Choi, H.J. Fabrication of dual-coated graphene oxide nanosheets by polypyrrole and poly(ionic liquid) and their enhanced electrorheological responses. J. Ind. Eng. Chem. 2019, 69, 106–115. [Google Scholar] [CrossRef]
- He, K.; Wen, Q.K.; Wang, C.W.; Wang, B.X.; Yu, S.S.; Hao, C.C.; Chen, K.Z. The preparation and electrorheological behavior of bowl-like titanium oxide nanoparticles. Soft Matter 2017, 13, 7677–7688. [Google Scholar] [CrossRef] [PubMed]
- Pavlikova, E.; Plachy, T.; Urbanek, M.; Cvek, M. Engineering conductivity and performance in electrorheological fluids using a nanosilica grafting approach. ACS Appl. Nano Mater. 2023, 6, 9768–9776. [Google Scholar] [CrossRef]
- Yatsuzuka, K.; Miura, K.; Kuramoto, N.; Asano, K. Observation of the electrorheological effect of silicone oil/polymer particles suspension. IEEE Trans. Ind. Appl. 1995, 31, 457–463. [Google Scholar] [CrossRef]
- Asano, K.; Suto, H.; Yatsuzuka, K. Influence of the particle configuration on electrorheological effect. J. Electrostat. 1997, 40–41, 573–578. [Google Scholar] [CrossRef]
- Kanu, D.J.; Shaw, M.T. Enhanced electrorheological fluids using anisotropic particles. J. Rheol. 1998, 42, 657–670. [Google Scholar] [CrossRef]
- Otsubo, Y. Electrorheology of whisker suspensions. Colloids Surf. A 1999, 153, 459–466. [Google Scholar] [CrossRef]
- Tsuda, K.; Takeda, Y.; Ogura, H.; Otsubo, Y. Electrorheological behavior of whisker suspensions under oscillatory shear. Colloids Surf. A 2007, 299, 262–267. [Google Scholar] [CrossRef]
- Yin, J.B.; Zhao, X.P. Titanate nano-whisker electrorheological fluid with high suspended stability and ER activity. Nanotechnology 2006, 17, 192–196. [Google Scholar] [CrossRef]
- Lin, C.; Shan, J.B. Electrically tunable viscosity of dilute suspensions of carbon nanotubes. Phys. Fluids 2007, 19, 121702. [Google Scholar] [CrossRef]
- Yin, J.B.; Zhao, X.P.; Xia, X.; Xiang, L.Q.; Qiao, L.Q. Electrorheological fluids based on nano-fibrous polyaniline. Polymer 2008, 49, 4413–4419. [Google Scholar] [CrossRef]
- Yin, J.B.; Xia, X.; Xiang, L.Q.; Qiao, L.Q.; Zhao, X.P. The electrorheological effect of polyaniline nanofiber, nanoparticle and microparticle suspensions. Smart Mater. Struct. 2009, 18, 095007. [Google Scholar] [CrossRef]
- Yin, J.B.; Xia, X.; Xiang, L.Q.; Zhao, X.P. Conductivity and polarization of carbonaceous nanotubes derived from polyaniline nanotubes and their electrorheology when dispersed in silicone oil. Carbon 2010, 248, 2958–2967. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Wu, K.H.; Liu, F.H.; Gu, J.J.; Liu, X.H.; Xu, G.J.; Cui, P. Facile approach to large-scale synthesis of 1D calcium and titanium precipitate (CTP) with high electrorheological activity. ACS Appl. Mater. Interfaces 2010, 2, 621–625. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.D.; Fang, F.F.; Choi, H.J. Silica nanoparticle decorated polyaniline nanofiber and its electrorheological response. Soft Matter 2011, 7, 2782–2789. [Google Scholar] [CrossRef]
- Marins, J.A.; Giulieri, F.; Sorres, B.G.; Bossis, G. Hybrid polyaniline-coated sepiolite nanofiber for ER fluid application. Synth. Met. 2013, 185–186, 9–16. [Google Scholar] [CrossRef]
- Goswami, S.; Brehm, T.; Filonovich, S.; Cidade, M.T. Electrorheological properties of polyaniline-vanadium oxide nanostructures suspended in silicone oil. Smart Mater. Struct. 2014, 23, 105012. [Google Scholar] [CrossRef]
- Wu, J.H.; Jin, T.; Liu, F.H.; Guo, J.J.; Cui, P.; Cheng, Y.C.; Xu, G.J. Preparation of rod-like calcium titanyl oxalate with enhanced electrorheological activity and their morphological effect. J. Mater. Chem. C 2014, 2, 5629–5635. [Google Scholar] [CrossRef]
- Lim, G.H.; Choi, H.J. Fabrication of self-assembled polyaniline tubes and their electrorheological Characteristics. Colloids Surf. A 2017, 530, 227–234. [Google Scholar] [CrossRef]
- Zhang, K.; Gao, C.Y.; Choi, H.J.; Yin, J.B.; Zhao, X.P. Rheological analysis of titanium dioxide nano-whisker based electrorheological fluids. J. Ind. Eng. Chem. 2020, 83, 285–288. [Google Scholar] [CrossRef]
- Tonti, L.; García Daza, F.A.; Patti, A. Kinetics of isotropic to string-like phase switching in electrorheological fluids of nanocubes. J. Chem. Phys. 2022, 157, 224906. [Google Scholar] [CrossRef] [PubMed]
- Hua, H.T.; Wang, X.B.; Wang, J.C. Microwave-assisted covalent modification of graphene nanosheets with chitosan and its electrorheological characteristics. Appl. Surface Sci. 2011, 257, 2637–2642. [Google Scholar] [CrossRef]
- Zhang, W.L.; Liu, Y.D.; Choi, H.J. Fabrication of semiconducting graphene oxide/polyaniline composite particles and their electrorheological response under an applied electric field. Carbon 2012, 50, 290–296. [Google Scholar] [CrossRef]
- Hong, J.; Jang, J. Highly stable, concentrated dispersions of graphene oxide sheets and their electro-responsive characteristics. Soft Matter 2012, 8, 7348–7350. [Google Scholar] [CrossRef]
- Yin, J.B.; Wang, X.X.; Chang, R.T.; Zhao, X.P. Polyaniline decorated graphene sheet suspension with enhanced electrorheology. Soft Matter 2012, 8, 294–297. [Google Scholar] [CrossRef]
- Yin, J.B.; Chang, R.T.; Kai, Y.; Zhao, X.P. Highly stable and AC electric field-activated electrorheological fluid based on mesoporous silica-coated graphene nanosheets. Soft Matter 2013, 9, 3910–3914. [Google Scholar] [CrossRef]
- Li, L.D.; Yin, J.B.; Liu, Y.; Zhao, X.P. Graphene oxide vs. reduced graphene oxide as core substrate for core/shell-structured dielectric nanoplates with different electro-responsive characteristics. J. Mater. Chem. C 2015, 3, 5098–5108. [Google Scholar] [CrossRef]
- Tang, J.; Wen, X.H.; Liu, Z.P.; Wang, J.J.; Zhang, P. Synthesis and electrorheological performances of 2D PANI/TiO2 nanosheets. Colloids Surf. A 2018, 552, 24–31. [Google Scholar] [CrossRef]
- Gao, C.Y.; Kim, M.H.; Jin, H.; Choi, H.J. Synthesis and electrorheological response of graphene oxide/polydiphenylamine microsheet composite particles. Polymers 2020, 12, 1984. [Google Scholar] [CrossRef] [PubMed]
- Davis, L.C. Finite-element analysis of particle-particle forces in electrorheological fluids. Appl. Phys. Lett. 1992, 60, 319–321. [Google Scholar] [CrossRef]
- Sim, H.G.; Ahn, K.H.; Lee, S.J. Three-dimensional dynamics simulation of electrorheological fluids under large amplitude oscillatory shear flow. J. Rheol. 2003, 47, 879–895. [Google Scholar] [CrossRef]
- Blair, M.J.; Patey, G.N. A Monte Carlo study of model electrorheological fluids. J. Chem. Phys. 1999, 111, 3278–3287. [Google Scholar] [CrossRef]
- Kor, Y.K.; See, H. The electrorheological response of elongated particles. Rheol. Acta 2010, 49, 741–756. [Google Scholar] [CrossRef]
- Bonnecaze, R.T.; Brady, J.F. Dynamic simulation of an electrorheological fluid. J. Chem. Phys. 1992, 96, 2183–2202. [Google Scholar] [CrossRef]
- Klingenber, D.J.; Zukoski, C.F.; Hill, J.C. Kinetics of structure formation in electrorheological suspension. J. Appl. Phys. 1993, 73, 4644–4648. [Google Scholar] [CrossRef]
- Lukkarinen, A.; Kaski, K. Computational studies of compressed and sheared electrorheological fluid. J. Phys. D Appl. Phys. 1996, 29, 2729–2732. [Google Scholar] [CrossRef]
- Zhu, S.; Tang, B.; Qu, L.J.; Yuan, W.; Zhang, Q.F. Simulation Studies on Structure-Force Dynamic Coupling of Electrorheological Fluids in a Poiseuille Flow Field. Adv. Mater. Res. 2012, 443–444, 796–801. [Google Scholar] [CrossRef]
- Wan, J.T.K.; Yu, K.W.; Gu, G.Q. Dynamic electrorheological effects and interparticle force between a pair of rotating spheres. Phys. Rev. E 2000, 62, 6846–6850. [Google Scholar] [CrossRef]
- Ihle, T.; Kroll, D.M. Stochastic rotation dynamics. I. Formalism, Galilean invariance, and Green-Kubo relations. Phys. Rev. E 2003, 67, 066705. [Google Scholar] [CrossRef] [PubMed]
- Laganapan, A.M.K.; Videcoq, A.; Bienia, M.; Ala-Nissila, T.; Bochicchio, D.; Ferrando, R. Computation of shear viscosity of colloidal suspensions by SRD-MD. J. Chem. Phys. 2015, 142, 144101. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.H.; Wang, Y.; Xuan, S.H.; Gong, X.L. A hybrid molecular dynamics study on the non-Newtonian rheological behaviors of shear thickening fluid. J. Colloid Interface Sci. 2017, 497, 378–384. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Petersen, M.K.; Lechman, J.B.; Plimpton, S.J.; Grest, G.S.; in’t Veld, P.J.; Schunk, P.R. Mesoscale hydrodynamics via stochastic rotation dynamics: Comparison with Lennard-Jones fluid. J. Chem. Phys. 2010, 132, 174106. [Google Scholar] [CrossRef]
- The Lammps Home Page. Available online: https://www.lammps.org/ (accessed on 8 November 2017).
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ‘t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Long, Y.; Chen, Z.; Wang, N.; Ma, Y.; Zhang, Z.; Zhang, L.; Wan, M. Electrical conductivity of a single conductingpolyaniline nanotube. Appl. Phys. Lett. 2003, 83, 1863–1865. [Google Scholar] [CrossRef]
- Zhang, L.; Wan, M. Self-assembly of polyaniline2 from nanotubes to hollowmicrospheres. Adv. Funct. Mater. 2003, 13, 815–820. [Google Scholar] [CrossRef]
- Seddique, M.A. Preparation and degradation of highly conducting polyanilinedoped with picricacid. Eur. Polym. J. 2002, 38, 1151–1158. [Google Scholar]
- Bell, R.C.; Karli, J.O.; Vavreck, A.N.; Zimmerman, D.T.; Ngatu, G.T.; Wereley, N.M. Magnetorheology of submicron diameter iron microwires dispersed in silicone oil. Smart Mater. Struct. 2008, 17, 015028. [Google Scholar] [CrossRef]
- López-López, M.T.; Kuzhir, P.; Bossis, G. Magnetorheology of fiber. I. Experimental. J. Rheol. 2009, 53, 115–126. [Google Scholar] [CrossRef]
- Gómez-Ramírez, A.; López-López, M.T.; Durán, J.D.G.; González-Caballero, F. Influence of particle shape on the magnetic and magnetorheological properties of nanoparticle suspensions. Soft Matter 2009, 5, 3888–3895. [Google Scholar] [CrossRef]
- Gómez-Ramírez, A.; Kuzhir, P.; López-López, M.T.; Bossis, G.; Meunier, A.; Durán, J.D.G. Steady shear flow of magnetic fiber suspensions: Theory and comparison with experiments. J. Rheol. 2011, 55, 43–67. [Google Scholar] [CrossRef]
- Kuzhir, P.; López-López, M.T.; Bossis, G. Magnetorheology of fiber suspensions. II. Theory. J. Rheol. 2009, 53, 127–151. [Google Scholar] [CrossRef]
- de Vicente, J.; Vereda, F.; Segovia-Gutiérrez, J.P.; Morales, M.P.; Hidalgo-Álvarez, R. Effect of particle shape in magnetorheology. J. Rheol. 2010, 54, 1337–1362. [Google Scholar] [CrossRef]





| Sample | ε′∞ | Δε′ | λ (s) | σ (S/cm) |
|---|---|---|---|---|
| nanosphere | 3.05 | 2.20 | 1.7 × 10−3 | 5.6 × 10−10 |
| nanofiber | 3.02 | 2.21 | 1.3 × 10−3 | 6.2 × 10−10 |
| nanoplate | 3.07 | 2.06 | 1.3 × 10−3 | 6.5 × 10−10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Hu, X.; Zhao, X.; Yin, J. Electrorheological Effect of Suspensions of Polyaniline Nanoparticles with Different Morphologies. Polymers 2023, 15, 4568. https://doi.org/10.3390/polym15234568
Yuan J, Hu X, Zhao X, Yin J. Electrorheological Effect of Suspensions of Polyaniline Nanoparticles with Different Morphologies. Polymers. 2023; 15(23):4568. https://doi.org/10.3390/polym15234568
Chicago/Turabian StyleYuan, Jinhua, Xufeng Hu, Xiaopeng Zhao, and Jianbo Yin. 2023. "Electrorheological Effect of Suspensions of Polyaniline Nanoparticles with Different Morphologies" Polymers 15, no. 23: 4568. https://doi.org/10.3390/polym15234568
APA StyleYuan, J., Hu, X., Zhao, X., & Yin, J. (2023). Electrorheological Effect of Suspensions of Polyaniline Nanoparticles with Different Morphologies. Polymers, 15(23), 4568. https://doi.org/10.3390/polym15234568









