A Light-Powered Liquid Crystal Elastomer Roller
Abstract
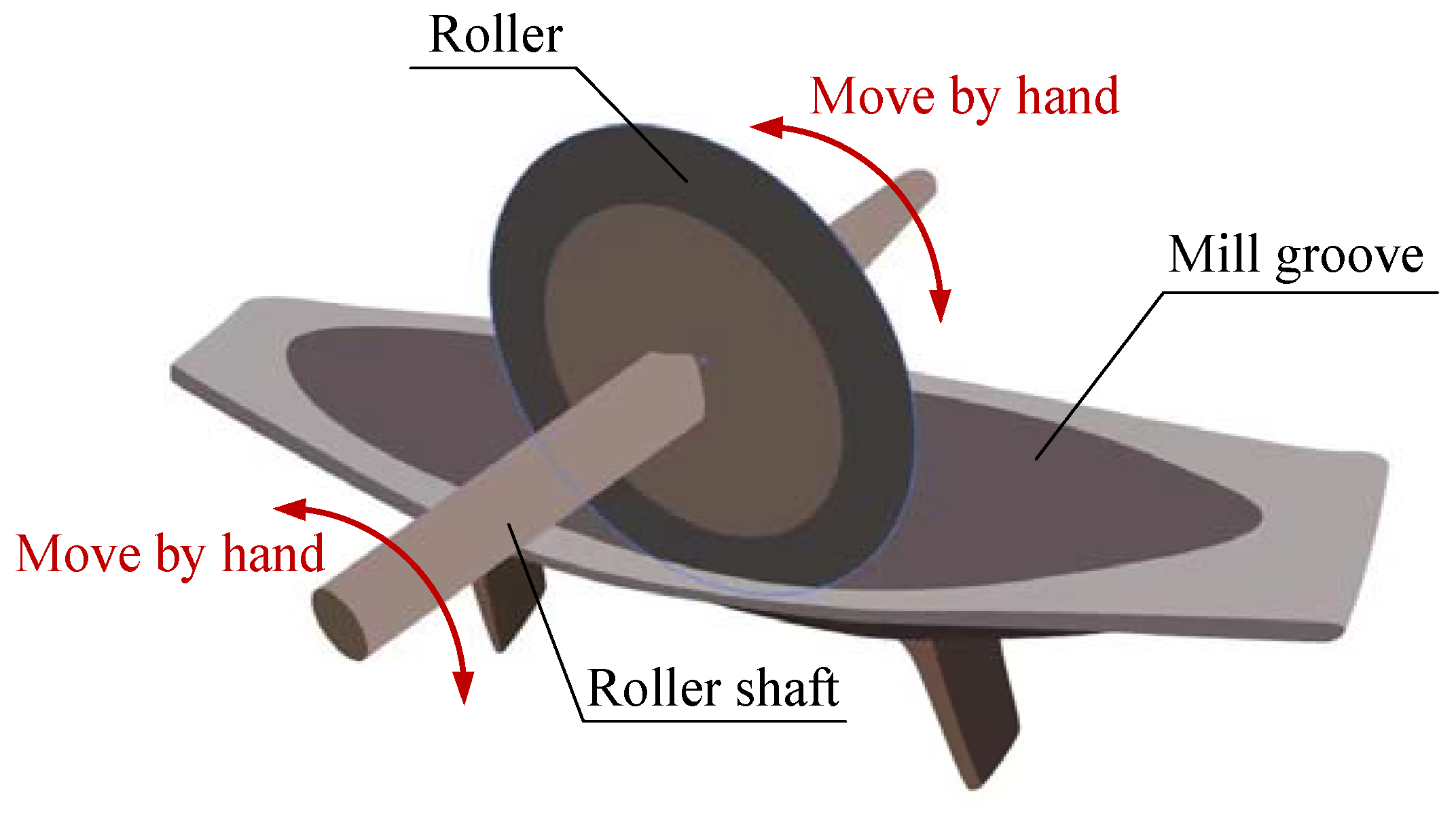
:1. Introduction
2. Model and Formulation
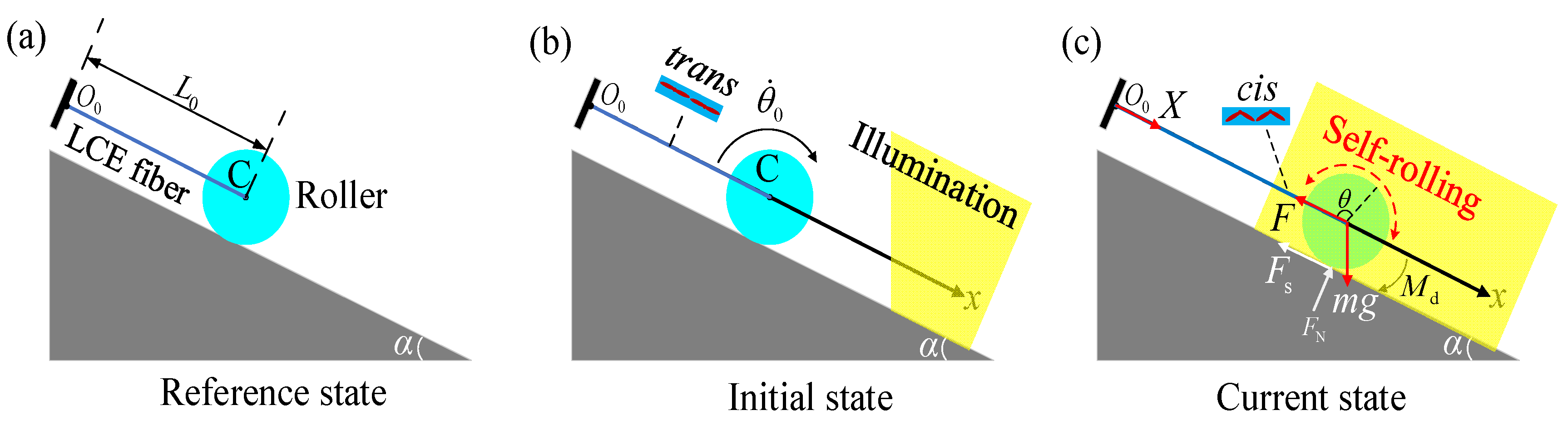
2.1. Dynamics of an LCE Roller
2.2. Tension of LCE Fibers
2.3. Dynamic LCE Model
2.4. Nondimensionalization
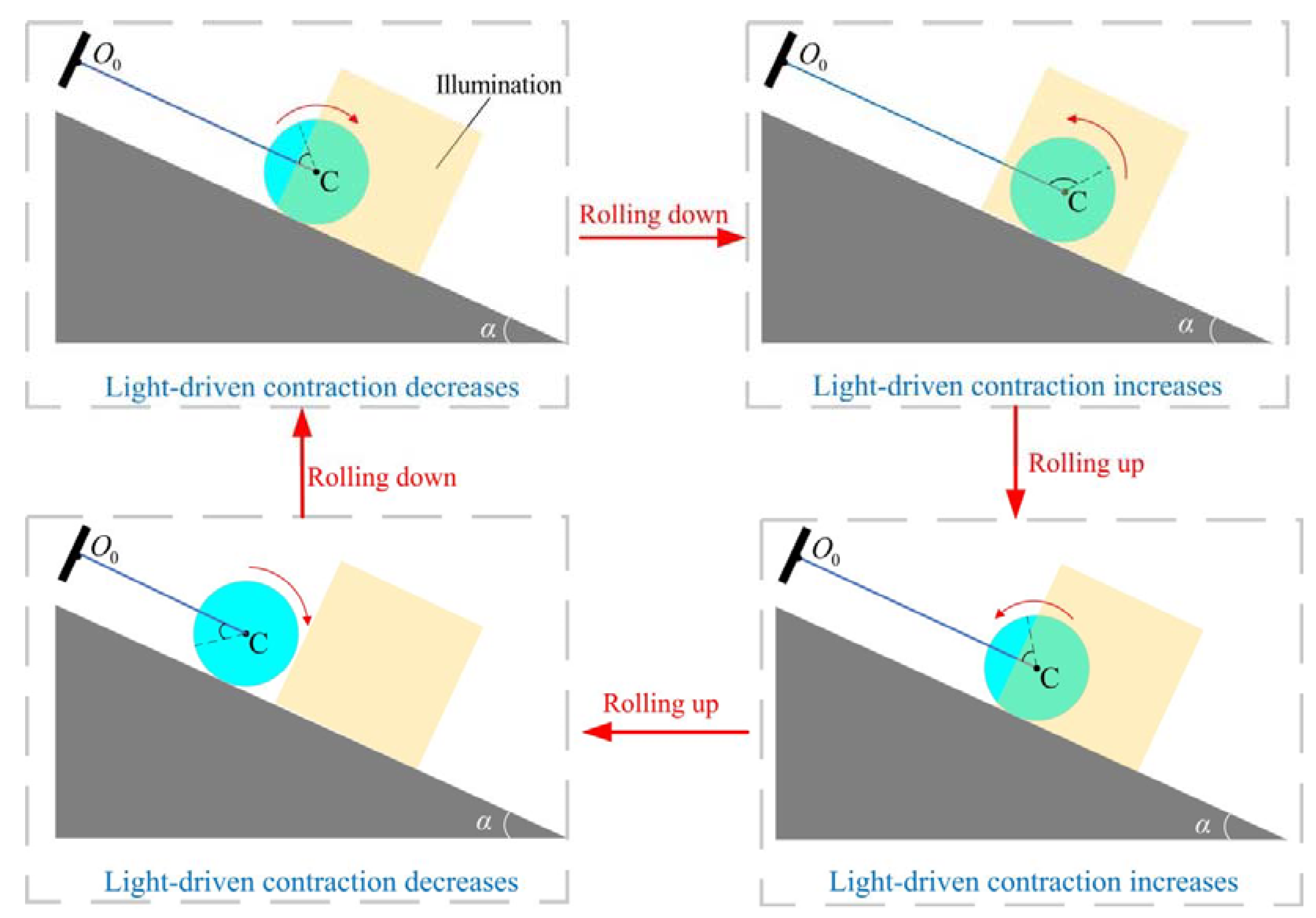
3. Two Motion Regimes and Mechanism of Self-Rolling
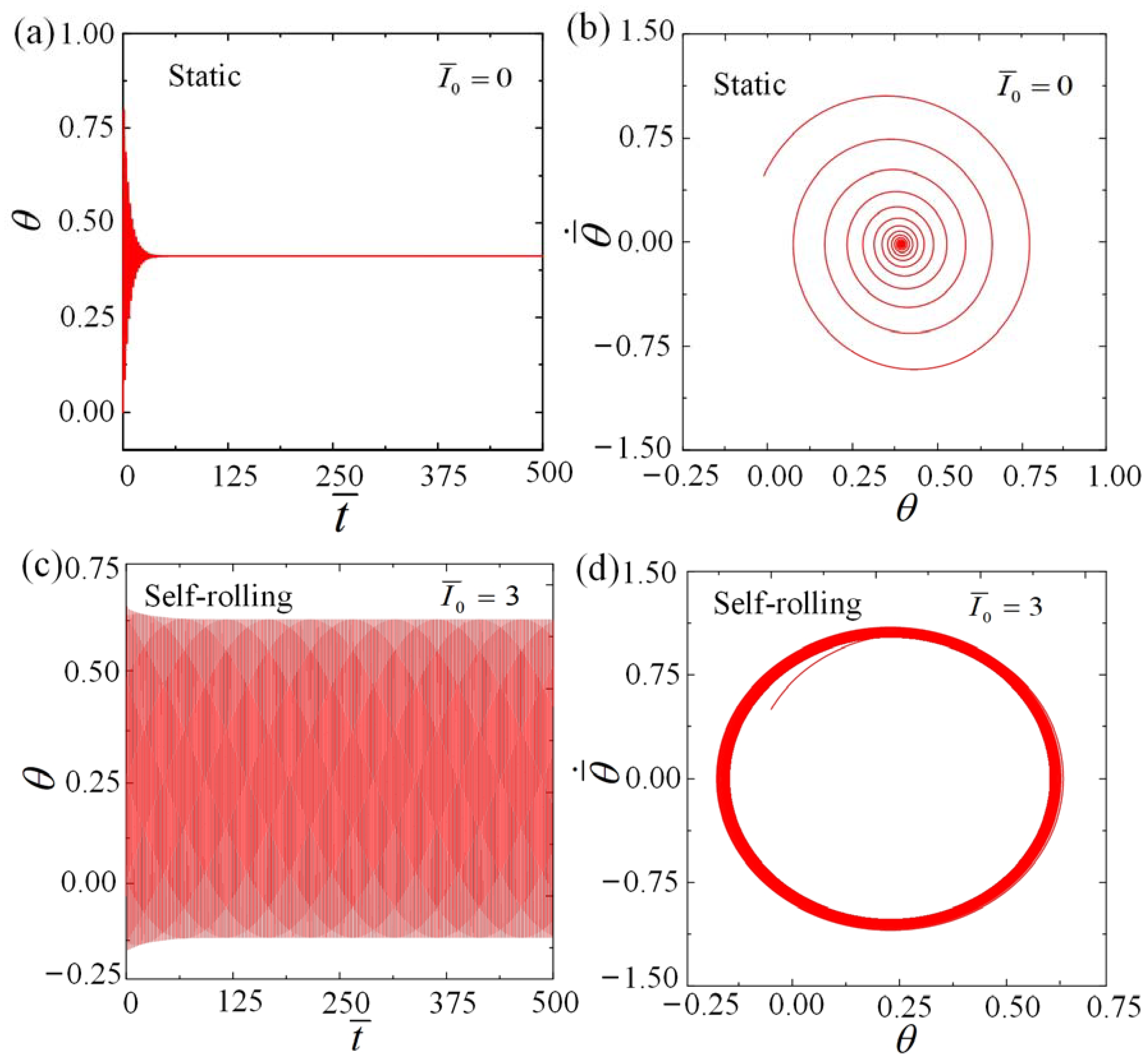
3.1. Two Motion Regimes
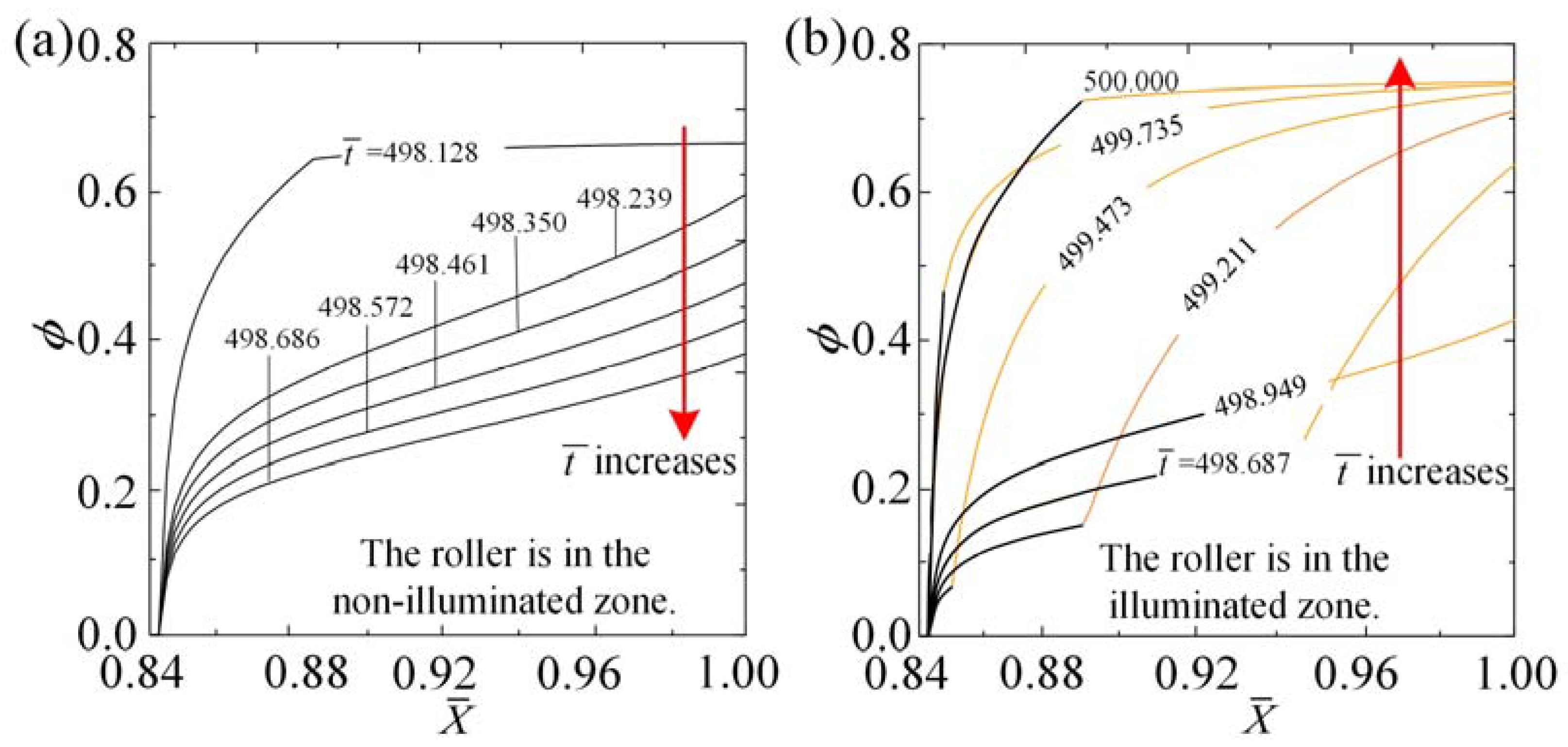
3.2. Mechanism of Self-Rolling
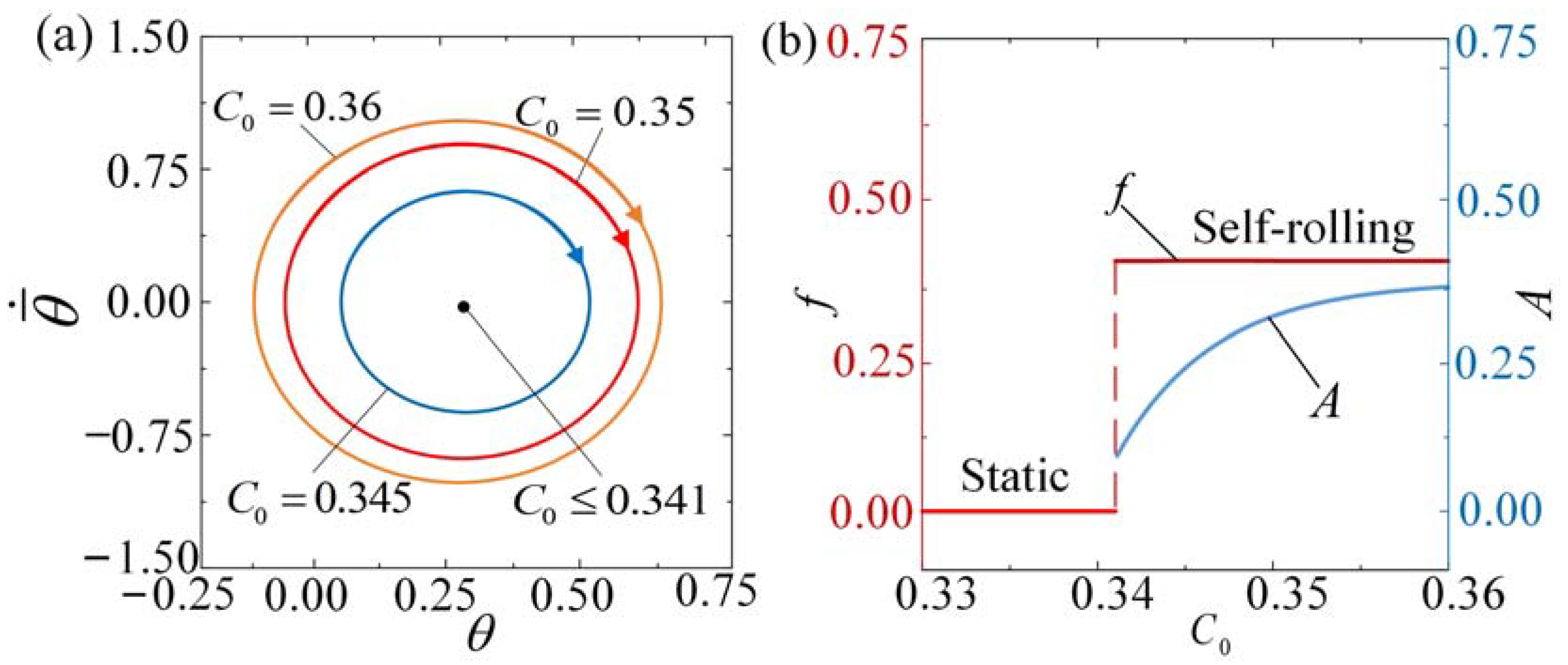
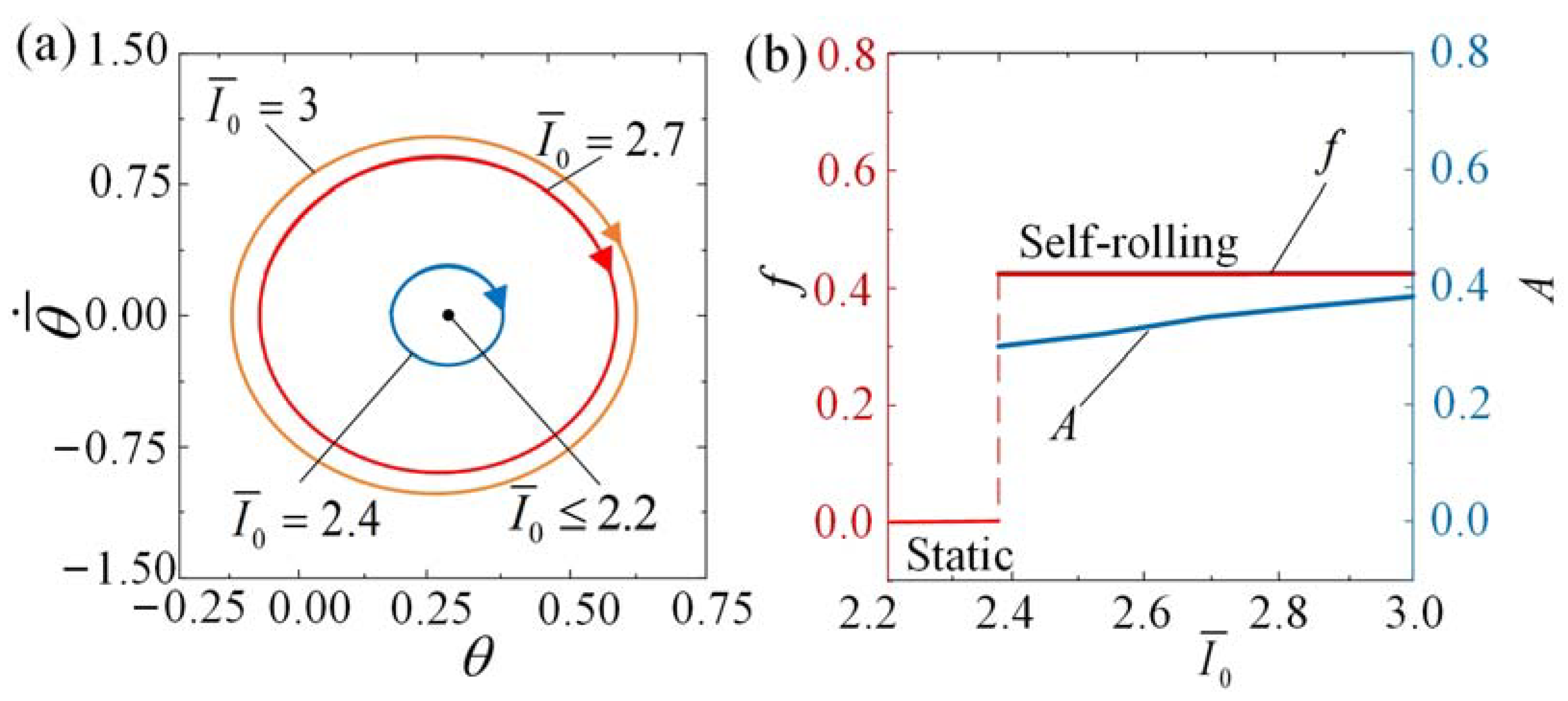
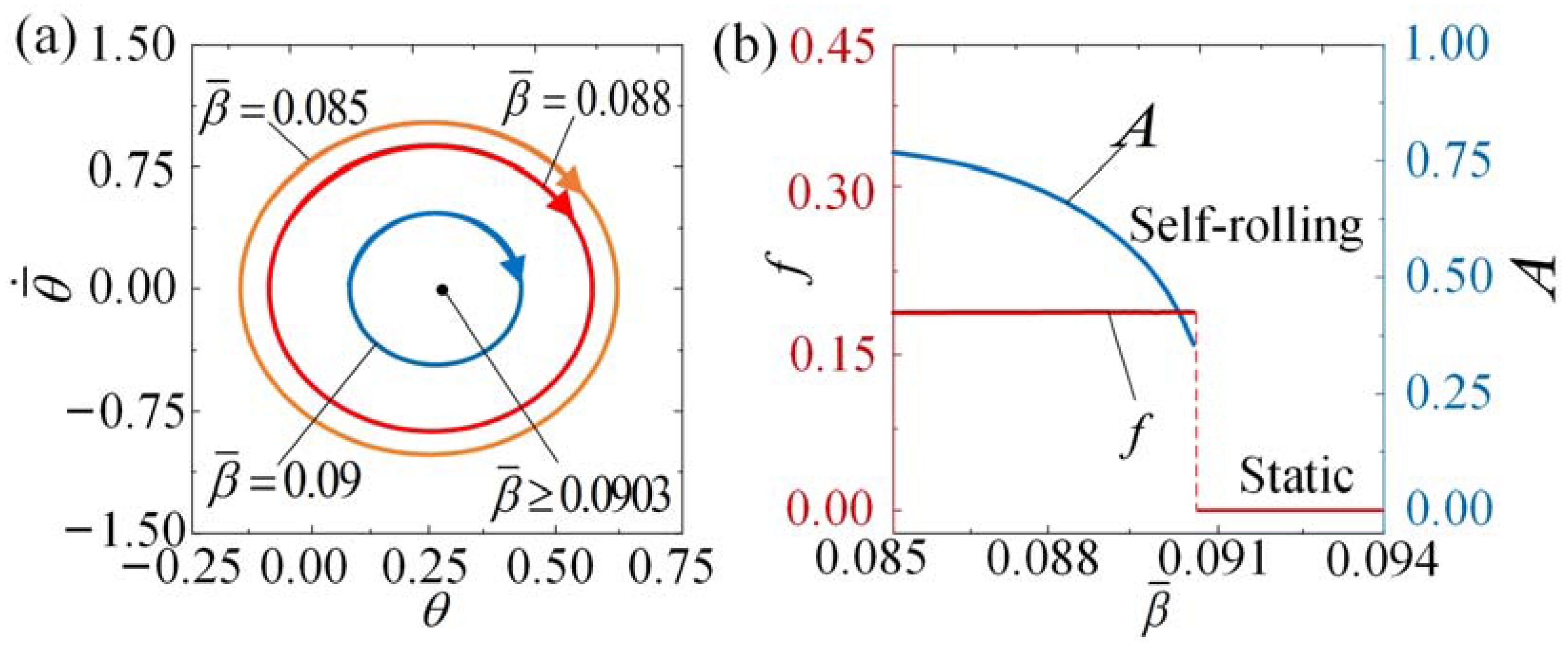
4. Influence of System Parameters on the Self-Rolling
4.1. Effect of the Contraction Coefficient
4.2. Effect of the Light Intensity
4.3. Effect of the Damping Coefficient
4.4. Effect of the Spring Constant
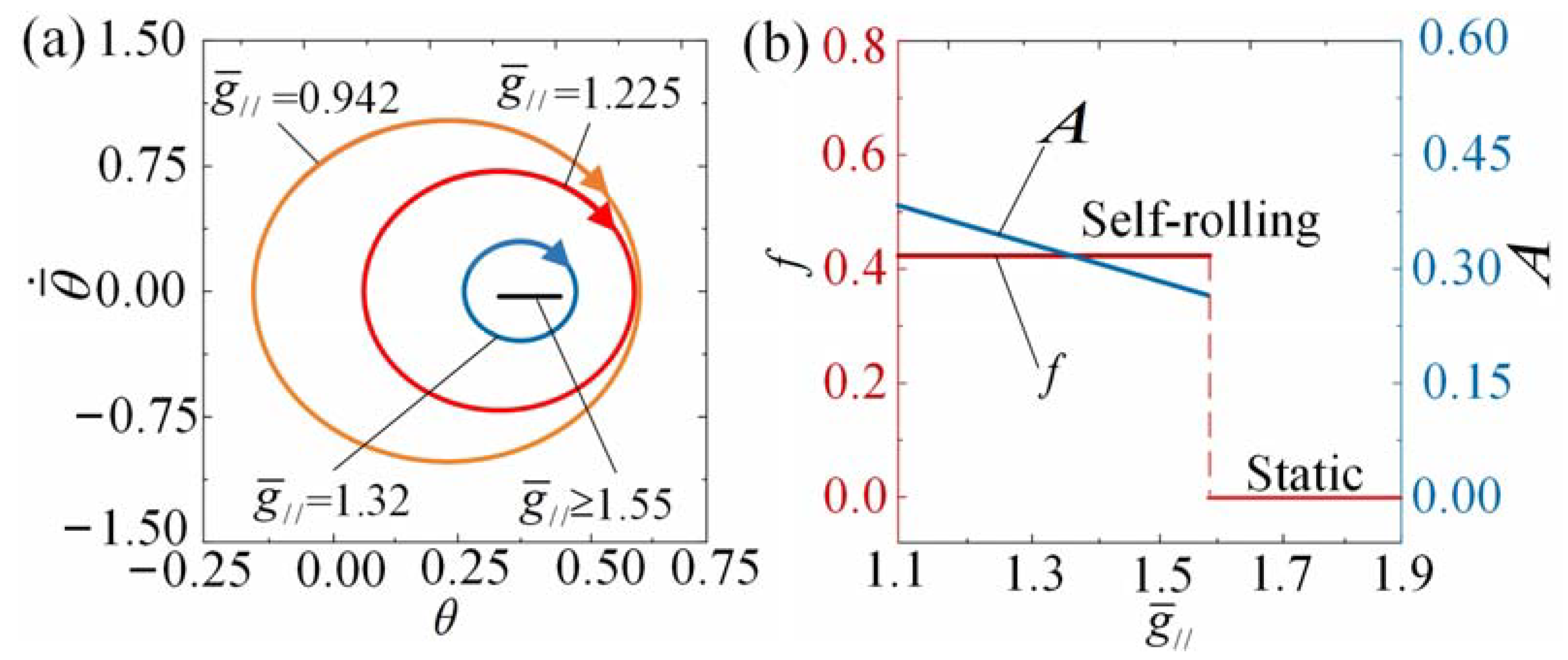
4.5. Effect of the Gravitational Acceleration
4.6. Effect of the Radius of the Roller
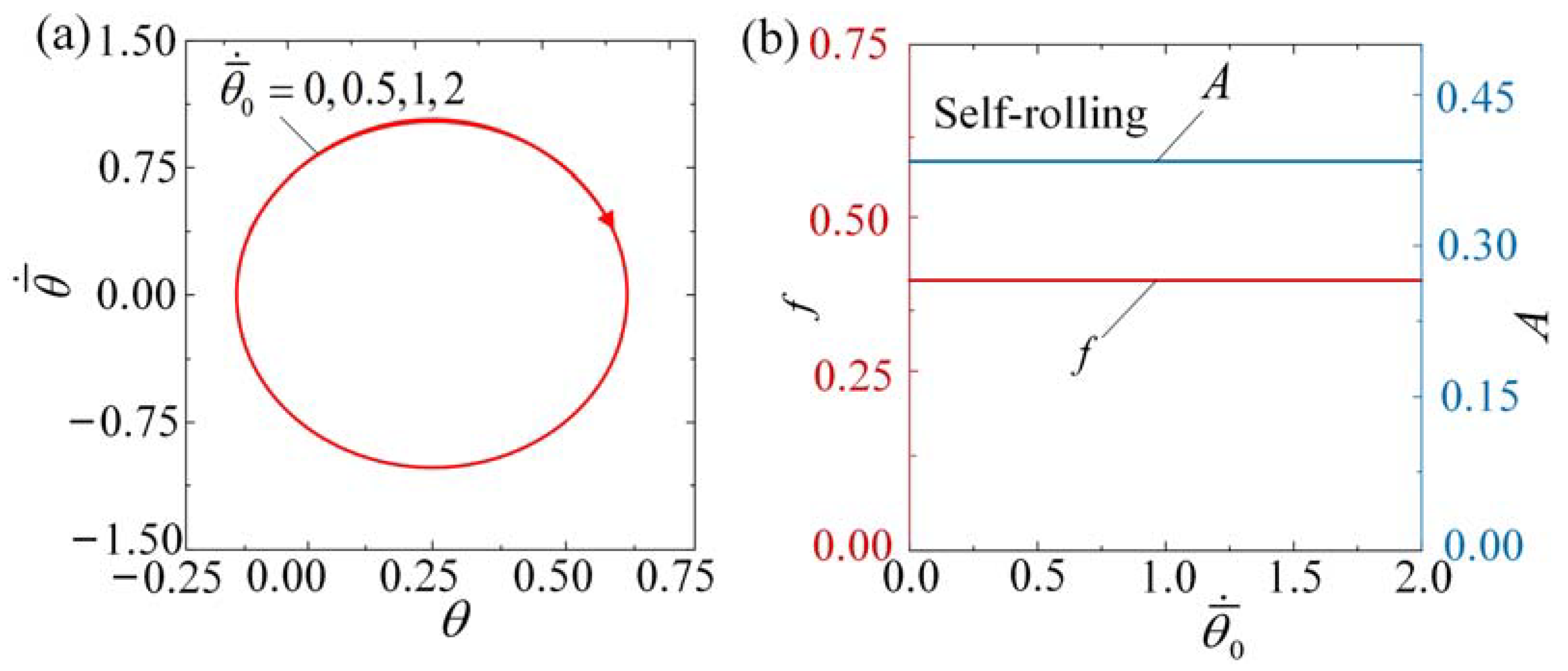
4.7. Effect of the Initial Velocity
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Brighenti, R.; Artoni, F.; Cosma, M.P. Mechanics of materials with embedded unstable molecules. Int. J. Solids. Struct. 2019, 162, 21–35. [Google Scholar] [CrossRef]
- Chen, Y.F.; Zhao, H.C.; Mao, J.; Chirarattananon, P.; Helbling, F.; Hyun, P.N.; Clarke, D.; Wood, R. Controlled flight of a microrobot powered by soft artificial muscles. Nature 2019, 575, 324–329. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, N.W.; Tolley, M.T.; Overvelde, J.T.B.; Weaver, J.C.; Mosadegh, B.; Bertoldi, K.; Whitesides, G.M.; Wood, R.J. A 3D-printed, functionally graded soft robot powered by combustion. Science 2015, 349, 161–165. [Google Scholar] [CrossRef] [PubMed]
- Wehner, M.; Truby, R.L.; Fitzgerald, D.J.; Mosadegh, B.; Whitesides, G.M.; Lewis, J.A.; Wood, R.J. An integrated design and fabrication strategy for entirely soft, autonomous robots. Nature 2016, 536, 451–455. [Google Scholar] [CrossRef] [PubMed]
- Liao, B.; Zang, H.B.; Chen, M.Y.; Wang, Y.J.; Lang, X.; Zhu, N.N.; Yang, Z.; Yi, Y. Soft rod-climbing robot inspired by winding locomotion of snake. Soft Robot 2020, 7, 500–511. [Google Scholar] [CrossRef]
- Hu, W.Q.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Kriegman, S.; Blackiston, D.; Levin, M.; Bongard, J. A scalable pipeline for designing reconfigurable organisms. Proc. Natl. Acad. Sci. USA 2020, 117, 1853–1859. [Google Scholar] [CrossRef]
- Huang, H.B.; Aida, T. Towards molecular motors in unison. Nat. Nanotechnol. 2019, 14, 407. [Google Scholar] [CrossRef]
- Nelson, B.J.; Kaliakatsos, I.K.; Abbott, J.J. Microrobots for minimally invasive medicine. Annu. Rev. Biomed. Eng. 2010, 12, 55–85. [Google Scholar] [CrossRef]
- Sitti, M.; Ceylan, H.; Hu, W.Q.; Giltinan, J.; Turan, M.; Yim, S.; Diller, E. Biomedical applications of untethered mobile milli microrobots. Proc. IEEE 2015, 103, 205–224. [Google Scholar] [CrossRef]
- Sitti, M. Miniature devices: Voyage of the microrobots. Nature 2009, 458, 1121–1122. [Google Scholar] [CrossRef] [PubMed]
- Martella, D.; Nocentini, S.; Parmeggiani, C.; Wiersma, D. Self-regulating capabilities in photonic robotics. Adv. Mater. Technol. 2019, 4, 1800571. [Google Scholar] [CrossRef]
- Karsten, K.; Frank, J. Oscillations in cell biology. Curr. Opin. Cell. Biol. 2015, 17, 20–26. [Google Scholar]
- Yoshida, R. Evolution of self-oscillating polymer gels as autonomous soft actuators. In Soft Actuators: Materials, Modeling, Applications, and Future Perspectives; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Wang, X.Q.; Tan, F.C.; Chan, H.K.; Lu, X.; Zhu, L.L.; Kim, S.W.; Ho, W.G. In-built thermo-mechanical cooperative feedback mechanism for self-propelled multimodal locomotion and electricity generation. Nat. Commun. 2018, 9, 3438. [Google Scholar] [CrossRef]
- Kamlesh, K.; Christopher, K.; David, B.; Mark, A.P.; Heiner, F.; Stefan, H.; Dirk, J.B.; Michael, G.D.; Albertus, P.H.J.S. A chaotic self-oscillating sunlight-driven polymer actuator. Nat. Commun. 2016, 7, 11975. [Google Scholar]
- Rothemund, P.; Ainla, A.; Belding, L.; Preston, D.; Kurihara, S.; Suo, Z.G.; Whitesides, G. A soft, bistable valve for autonomous control of soft actuators. Sci. Robot. 2018, 3, eaar7986. [Google Scholar] [CrossRef] [PubMed]
- Preston, D.; Jiang, H.H.; Joy, S.V.; Rothemund, P.; Rawson, J.; Nemitz, M.; Lee, W.K.; Suo, Z.G.; Walsh, C.; Whitesides, G. A soft ring oscillator. Sci. Robot. 2019, 4, eaaw5496. [Google Scholar] [CrossRef] [PubMed]
- Ding, W.J. Self-Excited Vibration; Tsing-Hua University Press: Beijing, China, 2011. [Google Scholar]
- Sangwan, V.; Taneja, A.; Mukherjee, S. Design of a robust self-excited biped walking mechanism. Mech. Mach. Theory 2004, 39, 1385–1397. [Google Scholar] [CrossRef]
- Chatterjee, S. Self-excited oscillation under nonlinear feedback with time-delay. J. Sound. Vib. 2011, 330, 1860–1876. [Google Scholar] [CrossRef]
- Serak, S.; Tabiryan, N.V.; Vergara, R.; White, T.J.; Vaia, R.A.; Bunning, T.J. Liquid crystalline polymer cantilever oscillators fueled by light. Soft. Matter. 2010, 6, 779–783. [Google Scholar] [CrossRef]
- Zeng, H.; Lahikainen, M.; Liu, L.; Ahmed, Z.; Wani, O.M.; Wang, M.; Priimagi, A. Light-fuelled freestyle self-oscillators. Nat. Commun. 2010, 10, 5057. [Google Scholar]
- White, T.J.; Tabiryan, N.V.; Serak, S.V.; Hrozhyk, U.A.; Tondiglia, V.P.; Koerner, H.; Vaia, R.A.; Bunning, T.J. A high frequency photodriven polymer oscillator. Soft. Matter. 2008, 4, 1796–1798. [Google Scholar]
- Yusuke, H. Function and autonomous behavior of self-oscillating polymer systems. Polymers. 2014, 6, 1958–1971. [Google Scholar]
- Lu, X.; Zhang, H.; Fei, G.; Yu, B.; Tong, X.; Xia, H.; Zhao, Y. Liquid-crystalline dynamic networks doped with gold nanorods showing enhanced photocontrol of actuation. Adv. Mater. 2018, 30, 1706597. [Google Scholar]
- Cheng, Y.; Lu, H.; Lee, X.; Zeng, H. Kirigami-Based Light-Induced Shape-Morphing and Locomotion. Adv. Mater. 2019, 32, 1906233. [Google Scholar]
- Kageyama, Y.; Ikegami, T.; Satonaga, S.; Obara, K.; Sato, H.; Takeda, S. Light-driven flipping of azobenzene assemblies-sparse crystal structures and responsive behavior to polarized light. Chem. Eur. J. 2020, 26, 10759–10768. [Google Scholar]
- Chun, S.; Pang, C.; Cho, S.B. A micropillar-assisted versatile strategy for highly sensitive and efficient triboelectric energy generation under in-plane stimuli. Adv. Mater. 2020, 32, 1905539. [Google Scholar]
- Tang, R.; Liu, Z.; Xu, D.; Liu, J.; Yu, L.; Yu, H. Optical pendulum generator based on photomechanical liquid-crystalline actuators. ACS. Appl. Mater. Interfaces 2015, 7, 8393–8397. [Google Scholar]
- Zhao, D.; Liu, Y. A prototype for light-electric harvester based on light sensitive liquid crystal elastomer cantilever. Energy 2020, 198, 117351. [Google Scholar]
- Yamada, M.; Kondo, M.; Mamiya, J.; Yu, Y.; Kinoshita, M.; Barrett, C.J.; Ikeda, T. Photomobile polymer materials: Towards light-driven plastic motors. Angew. Chem. Int. Edit. 2008, 120, 5064–5066. [Google Scholar]
- Lahikainen, M.; Zeng, H.; Priimagi, A. Reconfigurable photoactuator through synergistic use of photochemical and photothermal effects. Nat. Commun. 2018, 9, 4148. [Google Scholar] [PubMed]
- Boissonade, J.; Kepper, P.D. Multiple types of spatio-temporal oscillations induced by differential diffusion in the Landolt reaction. Phys. Chem. Chem. Phys. 2011, 13, 4132. [Google Scholar]
- Jin, B.; Liu, J.; Shi, Y.; Chen, G.; Zhao, Q.; Yang, S. Solvent-assisted 4D programming and reprogramming of liquid crystalline organogels. Adv. Mater. 2021, 34, 2107855. [Google Scholar]
- Yashin, V.V.; Balazs, A.C. Pattern formation and shape changes in self-oscillating polymer gels. Science 2006, 314, 798–801. [Google Scholar] [PubMed]
- He, X.M.; Aizenberg, M.; Kuksenok, O.; Zarzar, L.D.; Shastri, A.; Balazs, A.C.; Aizenberg, J. Synthetic homeostatic materials with chemo-mechano-chemical selfregulation. Nature 2012, 487, 214–218. [Google Scholar] [PubMed]
- Cunha, M.P.D.; Peeketi, A.R.; Ramgopal, A.; Annabattula, R.K.; Schenning, A.P.H.J. Light-driven continual oscillatory rocking of a polymer film. ChemistryOpen 2020, 9, 1149–1152. [Google Scholar]
- Xu, T.; Pei, D.; Yu, S.; Zhang, X.; Yi, M.; Yi, C. Design of MXene composites with biomimetic rapid and self-oscillating actuation under ambient circumstances. ACS. Appl. Mater. Inter. 2021, 13, 31978–31985. [Google Scholar]
- Cunha, M.; Peeketi, A.R.; Ramgopal, A.; Annabattula, R.K.A. Schenning lightdriven continual oscillatory rocking of a polymer film. ChemistryOpen. 2020, 9, 1149–1152. [Google Scholar]
- Hu, Y.; Ji, Q.X.; Huang, M.J.; Chang, L.F.; Wu, Y.C. Light-driven self-oscillating actuators with pototactic locomotion based on black phosphorus heterostructure. Angew. Chem. Int. Edit. 2021, 60, 20511–20517. [Google Scholar]
- Sun, J.; Hu, W.; Zhang, L.Y.; Lan, R.C.; Yang, H.A.; Yang, D.K. Light-driven self-oscillating behavior of liquid-crystalline networks triggered by dynamic isomerization of molecular motors. Adva. Funct. Mater. 2021, 31, 2103311. [Google Scholar]
- Bazir, A.; Baumann, A.; Ziebert, F.; Kulić, I.M. Dynamics of fiberboids. Soft Matter 2020, 16, 5210–5223. [Google Scholar] [CrossRef] [PubMed]
- Shin, A.; Ha, J.; Lee, M.; Park, K.; Park, G.H.; Choi, T.H.; Cho, K.J.; Kim, H.Y. Hygrobot: A self-locomotive ratcheted actuator powered by environmental humidity. Sci. Robot. 2018, 3, eaar2629. [Google Scholar] [CrossRef] [PubMed]
- Ge, D.L.; Dai, Y.T.; Li, K. Light-powered self-spinning of a button spinner. Int. J. Mech. Sci. 2023, 238, 107824. [Google Scholar] [CrossRef]
- Zhao, Y.; Chi, Y.D.; Hong, Y.Y.; Yin, J. Twisting for soft intelligent autonomous robot in unstructured environments. Proc. Natl. Acad. Sci. USA 2022, 119, e2200265119. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Y.; Lv, J. Phototunable self-oscillating system driven by a self-winding fiber actuator. Nat. Commun. 2021, 12, 3211. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Wang, Z.; Wang, Y.; Wang, Z.; Li, C.; Annapooranan, R.; Zeng, J.; Chen, R.; Cai, S. Electrospun liquid crystal elastomer microfiber actuator. Sci. Robot. 2021, 6, eabi9704. [Google Scholar] [CrossRef]
- Zhou, L.; Dai, Y.T.; Fang, J.G.; Li, K. Light-powered self-oscillation in liquid crystal elastomer auxetic metamaterials with large volume change. Int. J. Mech. Sci. 2023, 254, 108423. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, R.; Jin, L.; Liu, M.; Gao, Y.; Raney, J.; Yang, S. 3D-Printed Photoresponsive Liquid Crystal Elastomer Composites for Free-Form Actuation. Adv. Funct. Mater. 2023, 33, 2210614. [Google Scholar] [CrossRef]
- Cheng, Q.B.; Cheng, W.Y.; Dai, Y.T.; Li, K. Self-oscillating floating of a spherical liquid crystal elastomer balloon under steady illumination. Int. J. Mech. Sci. 2023, 241, 107985. [Google Scholar] [CrossRef]
- Baumann, A.; Sáanchez-Ferrer, A.; Jacomine, L.; Martinoty, P.; Houerou, P.; Ziebert, F.; Kulićc, I. Motorizing fibers with geometric zero-energy modes. Nat. Mater. 2018, 17, 523–527. [Google Scholar] [CrossRef]
- Liu, J.X.; Zhao, J.J.; Wu, H.Y.; Dai, Y.T.; Li, K. Self-Oscillating Curling of a Liquid Crystal Elastomer Beam under Steady Light. Polymers 2023, 15, 344. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Myung, N.V.; Yin, Y. Light-powered soft steam engines for self-adaptive oscillation and biomimetic swimming. Sci. Robot. 2021, 6, eabi4523. [Google Scholar] [CrossRef]
- Shen, B.; Kang, S.H. Designing self-oscillating matter. Matter. 2021, 4, 766–769. [Google Scholar] [CrossRef]
- Kuenstler, A.S.; Chen, Y.; Bui, P.; Kim, H.; DeSimone, A.; Jin, L.; Hayward, R. Blueprinting photothermal shape-morphing of liquid crystal elastomers. Adv. Mater. 2020, 32, 2000609. [Google Scholar] [CrossRef]
- Ge, D.L.; Dai, Y.T.; Li, K. Self-Sustained Euler Buckling of an Optically Responsive Rod with Different Boundary Constraints. Polymers 2023, 15, 316. [Google Scholar] [CrossRef] [PubMed]
- Graeber, G.; Regulagadda, K.; Hodel, P.; Küttel, C.; Landolf, D.; Schutzius, T.; Poulikakos, D. Leidenfrost droplet trampolining. Nat. Commun. 2021, 12, 17–27. [Google Scholar] [CrossRef]
- Kim, Y.; Berg, J.; Crosby, A.J. Autonomous snapping and jumping polymer gels. Nat. Mater. 2021, 20, 1695–1701. [Google Scholar] [CrossRef]
- Lv, X.; Yu, M.; Wang, W.; Yu, H. Photothermal pneumatic wheel with high loadbearing capacity. Compos. Commun. 2021, 24, 100651. [Google Scholar] [CrossRef]
- Xu, P.B.; Wu, H.Y.; Dai, Y.T.; Li, K. Self-sustained chaotic floating of a liquid crystal elastomer balloon under steady illumination. Heliyon 2023, 9, e14447. [Google Scholar] [CrossRef]
- Sepulchre, R.; Paley, D.; Leonard, N. Collective Motion and Oscillator Synchronization; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2004; Volume 309, pp. 466–469. [Google Scholar]
- Vantomme, G.; Elands, L.C.M.; Gelebart, A.H.; Meijer, E.W.; Broer, D.J. Coupled liquid crystalline oscillators in Huygens’ synchrony. Nat. Mater. 2021, 20, 1702–1706. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Zhang, B.; Cheng, Q.B.; Dai, Y.T.; Yu, Y. Light-Fueled Synchronization of Two Coupled Liquid Crystal Elastomer Self-Oscillators. Ploymers 2023, 15, 2886. [Google Scholar] [CrossRef] [PubMed]
- Vantomme, G.; Gelebart, A.H.; Broer, D.J.; Meijer, E.W. A four-blade light-driven plastic mill based on hydrazone liquid-crystal networks. Tetrahedron 2017, 73, 4963–4967. [Google Scholar] [CrossRef]
- Gelebart, A.H.; Mulder, D.J.; Varga, M.; Konya, A.; Vantomme, G.; Meijer, E.W.; Selinger, R.L.B.; Broer, D.J. Making waves in a photoactive polymer film. Nature 2017, 546, 632–636. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Choi, G.P.T.; Mahadevan, L. Self-Excited Motions of Volatile Drops on Swellable Sheets. Phys. Rev. Lett. 2020, 124, 258002. [Google Scholar] [CrossRef] [PubMed]
- Parrany, A.M. Nonlinear light-induced vibration behavior of liquid crystal elastomer beam. Int. J. Mech. Sci. 2018, 136, 179–187. [Google Scholar] [CrossRef]
- Herbert, K.M.; Fowler, H.E.; McCracken, J.M.; Schlafmann, K.R.; Koch, J.A.; White, T.J. Synthesis and alignment of liquid crystalline elastomers. Nat. Rev. Mater. 2021, 7, 23–38. [Google Scholar] [CrossRef]
- Finkelmann, H.; Nishikawa, E.; Pereira, G.G.; Warner, M. A new opto-mechanical effect in solids. Phys. Rev. Lett. 2001, 87, 015501. [Google Scholar] [CrossRef]
- Yu, Y.; Nakano, M.; Ikeda, T. Photomechanics: Directed bending of a polymer film by light-miniaturizing a simple photomechanical system could expand its range of applications. Nature 2003, 425, 145. [Google Scholar] [CrossRef]
- Braun, L.B.; Hessberger, T.; Pütz, E.; Müller, C.; Giesselmann, F.; Serra, C.A.; Zentel, R. Actuating thermo- and photo-responsive tubes from liquid crystalline elastomers. J. Mater. Chem. C 2018, 6, 9093–9101. [Google Scholar] [CrossRef]
- Camacho-Lopez, M.; Finkelmann, H.; Palffy-Muhoray, P.; Shelley, M. Fast liquid-crystal elastomer swims into the dark. Nat. Mater. 2004, 3, 307–310. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Definition | Value | Unit |
|---|---|---|---|
| Damping coefficient | 0~0.001 | mgmm2/s | |
| Contraction coefficient | 0~0.36 | / | |
| Light-absorption constant | 0.0003 | m2/(sW) | |
| Thermal relaxation time from cis-to-trans | 0~100 | ms | |
| Moment of inertia of roller | 0~1 | mgmm2 | |
| Light intensity | 0~100 | kW/m2 | |
| Gravitational acceleration | 0~20 | m/s | |
| Penetration depth | 10−2 | m | |
| Original length of LCE fiber | 0.1 | m | |
| Thickness of LCE fiber | 10−3 | m | |
| Elastic modulus | 5 × 106 | Pa | |
| Spring coefficient | 1~10 | N/m | |
| R | Radius of the roller | 0~0.3 | mm |
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Value | 0~50 | 0~10 | 0~3 | 0~0.1 | 1~10 | 0~2 | 0~0.36 | 0~0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Chen, J.; Hu, H.; Wu, H.; Dai, Y.; Yu, Y. A Light-Powered Liquid Crystal Elastomer Roller. Polymers 2023, 15, 4221. https://doi.org/10.3390/polym15214221
Li K, Chen J, Hu H, Wu H, Dai Y, Yu Y. A Light-Powered Liquid Crystal Elastomer Roller. Polymers. 2023; 15(21):4221. https://doi.org/10.3390/polym15214221
Chicago/Turabian StyleLi, Kai, Jiajing Chen, Haoyu Hu, Haiyang Wu, Yuntong Dai, and Yong Yu. 2023. "A Light-Powered Liquid Crystal Elastomer Roller" Polymers 15, no. 21: 4221. https://doi.org/10.3390/polym15214221
APA StyleLi, K., Chen, J., Hu, H., Wu, H., Dai, Y., & Yu, Y. (2023). A Light-Powered Liquid Crystal Elastomer Roller. Polymers, 15(21), 4221. https://doi.org/10.3390/polym15214221







